Abstract
The mathematical modeling of unsteady flow of micropolar Cu–Al2O3/water nanofluid driven by a deformable sheet in stagnation region with thermal radiation effect has been explored numerically. To achieve the system of nonlinear ordinary differential equations (ODEs), we have employed some appropriate transformations and solved it numerically using MATLAB software (built-in solver called bvp4c). Influences of relevant parameters on fluid flow and heat transfer characteristic are discussed and presented in graphs. The findings expose that double solutions appear in shrinking sheet case in which eventually contributes to the analysis of stability. The stability analysis therefore confirms that merely the first solution is a stable solution. Addition of nanometer-sized particle (Cu) has been found to significantly strengthen the heat transfer rate of micropolar nanofluid. When the copper nanoparticle volume fraction increased from 0 to 0.01 (1%) in micropolar nanofluid, the heat transfer rate increased roughly to an average of 17.725%. The result also revealed that an upsurge in the unsteady and radiation parameters have been noticed to enhance the local Nusselt number of micropolar hybrid nanofluid. Meanwhile, the occurrence of material parameter conclusively decreases it.
1. Introduction
For a number of years, the studies of micropolar fluid flow have captivated the attention of numerous scientists in understanding the fluid behavior especially in the study of rheological complex fluids, as, for example, the colloidal fluids, polymeric suspension, liquid crystals, animal blood, etc. [1]. In sight of these important applications, Eringen [2,3] was the first who originated the microfluid theory in his papers of simple microfluids and theory of micropolar fluids. This kind of fluids demonstrate the micro-rotational effect and micro-rotational inertia. Afterwards, this theory was then extended by Eringen [4] by taking into account the thermal effect and thus established the thermomicropolar fluids theory. Implementing the idea of Eringen, the micropolar fluid flow using a boundary layer approximation has been derived by many researchers in various problems such as in stagnation region [5], semi-infinite plate [6], cylinder [7], and rotating surface [8]. After some years, Nazar et al. [9] initiated the theoretical study of micropolar fluid flow when the sheet is stretch in the stagnation region, and soon after, Ishak et al. [10] and Yacob and Ishak [11] analyzed the same fluid induced by a shrinking sheet and observed the existence of nonunique solutions. Afterwards, Sandeep and Sulochana [12] undertook a numerical research of unsteady magnetohydrodynamic (MHD) micropolar fluid in both permeable shrinking and stretching sheet. The heat transfer characteristic of micropolar fluid flow driven by a shrinking sheet was discussed by Mishra et al. [13]. Soon after, Lund et al. [14] noticed the existence of triple solutions at specific values of suction parameter in micropolar fluid when the sheet is shrunk exponentially and conducted the stability analysis. Further, a number of attempts toward this path have been made in the investigations of [15,16,17].
The inclusion of nanoparticles in a conventional fluid can literally change the flow and heat transfer capabilities, thereby can boost the thermal conductivity of the conventional fluid. It seems that Choi and Eastman [18] was the earlier person who conceived the idea of nanofluid, i.e., nanoparticle suspended in base fluid. Since then, nanofluids have been widely used in industrial cooling application [19], biomedical technology [20], solar thermal application [21], and many more. Numerous researchers, such as Gangadhar et al. [22], Chaudhary and Kanika [23], Naqvi et al. [24] and Anuar et al. [25,26], have scrutinized the concept of nanofluid flow and its heat transfer in their work. However, less studies are observed in micropolar nanofluid. The investigation of micropolar nanofluid driven by a stretching sheet was explored numerically by Hussain et al. [27]. Afterwards, Bourantas and Loukopoulos [28] and Noor et al. [29] scrutinized the micropolar nanofluid flow in an inclined square and vertical plate, respectively. The numerical investigation of micropolar nanofluid driven by a shrinking and stretching sheet have been made by Gangadhar et al. [30] and they pointed out that double solutions exist in certain range of parameters. Meanwhile, Dero et al. [31] point out the existence of triple solutions in their research involving micropolar nanofluid when the sheet is stretch/shrunk exponentially. The studies of micropolar nanofluid in an inclined stretching/shrinking have been scrutinized by Lund et al. [32] with consideration of convective boundary conditions. They also observed the occurrence of nonunique solutions in their work and performed the stability analysis. Recently, Abdal et al. [33], Amjad et al. [34], Rafique et al. [35] and many others have explored the micropolar nanofluid flow problem in different surfaces and aspects.
Nevertheless, a new modern kind of nanofluid which can efficiently improve the heat transfer are later being introduced in the industry are recognized as hybrid nanofluid, i.e., mixture of two types of nanoparticle dispersed into a base fluid. This new kind of fluid, however, shows a great advance in heat conductivity and it proved by the work of Madhesh and Kalaiselvam [36], Tahat and Benim [37], Devi and Devi [38], etc. Following this, mathematical investigation specifically in boundary layer flow in hybrid nanofluid has attracted a few researchers to explore it in various surfaces such as in stretching/shrinking sheet [39], curved surface [40], thin needle [41], Riga plate [42], etc. By opting the novel idea of hybrid nanofluid, Subhani and Nadeem [43] scrutinized the behavior of hybrid nanofluid (Cu-TiO2/water) in micropolar fluid in a porous medium past an exponentially stretching sheet and point out that the heat transfer rate for micropolar hybrid nanofluid is greater than micropolar nanofluid. Afterwards, by taking into attention the simultaneous effects of MHD and slip, Nadeem and Abbas [44] examined the micropolar hybrid nanofluid flow past a circular cylinder. In another study of Abbas et al. [45] and Al-Hanaya [46], a theoretical investigation of micropolar hybrid nanofluid using carbon nanotubes (SWCNT and MWCNT) as a nanoparticle over an exponentially stretching Riga plate and curved stretching sheet have been investigated. Apparently, the research related to micropolar hybrid nanofluids are limited in number. Hence, the principal goal of this investigation is to address the behavior of micropolar hybrid nanofluid in a deformable sheet, i.e., stretching and shrinking. It is important to note that deformable sheet is not a new crucial topic among the researchers in the fluid field since their applications are well recognized in processing industries especially in polymer processing, glass fiber production, cooling, and drying of paper and many others [47].
The impact of thermal radiation is also discussed in this paper, where this effect is crucial in solar power technology, electrical power generation, astrophysical flows, and other industrial fields. In the scenario of high-temperature flow processes, thermal radiation effects are also extremely important [48]. There is a lot of comprehensive literature now available that concerns with the thermal radiation effect on the flow of the boundary layer. For instance, Sajid and Hayat [49] have been analyzing the thermal radiation effect on the viscous flow as the sheet is stretch exponentially and realized that the thermal boundary layer thickness thickens as the radiation parameter increase. Afterwards, Nadeem et al. [50] extend the investigations of [49] by considering it in Jeffrey fluid. The numerical investigation of micropolar nanofluid over the stretching sheet with the effect of thermal radiation, MHD, and heat source/sink have been examined by Pal and Mandal [51]. Again, Gireesha et al. [52] addresses the Jeffrey nanofluids problem driven by a nonlinearly permeable stretching sheet under the effect of radiation and magnetohydrodynamic. In a recent study, Yashkun et al. [53] noticed the occurrence of dual solutions in their work of MHD hybrid nanofluid past a deformable sheet with thermal radiation effect. Hence, motivated by the aforementioned work, our aim here is to scrutinize the influence of thermal radiation towards the heat transfer of micropolar hybrid nanofluid.
In brief, this research paper is an extended work of Nazar et al. [9] to the case of unsteady two-dimensional hybrid nanofluid in shrinking sheet and take into attention the effect of thermal radiation. Given the above-mentioned study, the utilization of hybrid nanofluid (Cu and Al2O3) as the new heat transfer fluid for the micropolar flow problem with the thermal radiation effect, has not been performed up to now. In addition, this analysis also comprises a novel era for scientists to discover the shrinking features of micropolar hybrid nanofluids. Furthermore, the novelty of this study can also be seen in the discovery of non-unique solutions and the execution of stability analysis. To the best of authors’ knowledge, the results of the present work is new and still not considered and published by any researchers. Therefore, current studies are expected to bring good benefits to researchers who are experimentally working on micropolar hybrid nanofluids, and these results are also expected to reduce the cost of experimental work in the future.
2. Mathematical Framework
2.1. Basic Equations
The unsteady two-dimensional flow of micropolar Cu–Al2O3/water nanofluid past a deformable sheet in the stagnation region with the influence of thermal radiation impact are investigated in this work as exemplified in Figure 1. The Cartesian coordinates used are and , given that axis is considered along the sheet while axis normal to it, respectively, the sheet is located in the plane and the fluid fill the half space at . The temperature far from the surface (inviscid flow) and at the surface are represented by and . The sheet is stretch and shrunk along the axis with velocity and the free stream velocity is denoted by .
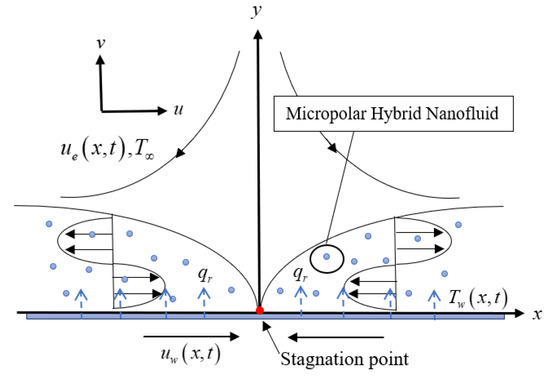
Figure 1.
Schematic model of shrinking sheet.
From all of the above circumstance, the partial differential equations which govern the flow are stated as (see Nazar et al. [9], Bhattacharyya et al. [54], Roy et al. [55]):
Here, the velocity component in the direction is denoted as whereas is the velocity component along axis, t and are time and temperature, refers to the angular velocity (microrotation) in the plane, signifies the radiative heat flux, is the vortex viscosity and is the micro inertial density. In addition, is the spin gradient viscosity given by (Ahmadi [6])
where is specified as the reference length. Further, and are the thermal conductivity, density, dynamic viscosity, and heat capacity of Cu–Al2O3/water.
The accompanying conditions are
where is the constant in the range of . It is worthwhile to note that for which implies that near the wall, exemplifies the microelements near the wall surface are incapable to rotate, i.e., concentrated particle flows (Jena and Mathur [56]) or also denoted as strong concentration of microelements (Guram and Smith [57]). However, for the case which refer to a weak concentration of microelements, the disappearing of anti-symmetric part of the stress tensor is noted (Ahmadi [6]). Further, the case is utilized for the modelling of turbulent boundary layer flows (Peddieson [58]). While the velocity of deformable sheet, free stream and temperature at the surface are referred from the work of Zainal et al. [59] which given as
here, and are constants, measures the unsteadiness of the problem and is the reference temperature.
Using the Rosseland’s approximation (Brewster [60]), the term can be expressed clearly as below
where and signify the constant of Stefan–Boltzmann and mean absorption’s coefficient. Implementing the Taylor series and ignored the higher-order terms, is expanded about hence, we have . Subsequently, Equation (4) become
2.2. Thermophysical Traits of Hybrid Nanofluid
The physical traits of hybrid nanofluids are prescribed in Table 1. In Table 1, the subscript and signify the hybrid nanofluid, nanofluid, fluid and nanoparticle, whereas and symbolize the first nanoparticle and second nanoparticle, respectively. Furthermore, represents the first nanoparticle volume fraction while denotes the second nanoparticle volume fraction. In this investigation, copper (Cu) is picked as the second nanoparticle volume fraction, alumina (Al2O3) is picked as the first nanoparticle volume fraction and water act as a base fluid. Table 2 displays the thermophysical traits of nanoparticles and base fluid. It is important to note that Al2O3 is originally disseminated into the water to achieve the appropriated hybrid nanofluid, i.e., Cu-Al2O3/water, and then Cu is disseminated into the Al2O3/water nanofluid. Additionally, the volume fraction of Al2O3 nanoparticle is set to 1% and Cu is fluctuated from 0 to 2%.

Table 1.
Physical traits of hybrid nanofluids (Devi and Devi [38]).

Table 2.
Thermo physical properties (Oztop and Abu-Nada [61]).
2.3. Similarity Solutions
In this work, the subsequent similarity transformation is introduced (Roy et al. [55])
where and are the fluid kinematic viscosity and similarity variable, while and are the dimensionless function. Further, primes signify the differentiation with respect to , while the stream function is specified as and .
Invoking the similarity variables (10), Equation (1) is identically fulfilled and Equations (2), (3) and (9) are reduced into the following similarity equations
Here, the material parameter, unsteady parameter, Prandtl number and radiation parameter which denoted by and are defined by
The conditions (6) become
where the stretching/shrinking parameter is denoted by with signifies the sheet is stretch, refers to static plate and denotes the sheet is shrunk.
In this investigation, the physical quantities of interest are specified as
here, is the skin friction coefficient and is the Nusselt number. Using variables (10) and (16), the following local skin friction coefficient and local Nusselt number (heat transfer rate) are achieved
where is the local Reynolds number.
3. Stability of the Solutions
Due to the occurrence of non-uniqueness in the present research, the stability analysis is executed by referring to the work of Merkin [62], Weidman et al. [63], and Harris et al. [64]. These analyses have been implemented by other researchers too (see for example the work of [14,15,16,25,26,32,39,59]). Some important steps are implemented to identify the stability of solutions, i.e., (i) introducing a new dimensionless time variables and similarity variables, (ii) implement the linear eigenvalue equations, and (iii) relax the boundary conditions.
3.1. New Similarity Transformation
A new dimensionless time variable need to be introduced as follows (Zainal et al. [59])
while the similarity variables (10) are replaced by
By applying Equations (18) and (19) in Equations (1)–(3) and (9), the new transformed differential equations are attained
and the conditions become
3.2. Introducing Linear Eigenvalue Equations
The stability of the steady flow solutions can be explored by setting , and , where it satisfied the boundary value problems (11)–(13) and (15). Thus, the following equations are introduced (Weidman et al. [63]):
where and their derivatives are small then and . In addition, is the unknown eigenvalue which will be used to specify the stability of the solutions. Substitute Equation (24) into (20)–(22) and let , in which , and , thereby the linearized eigenvalue equations relevant to the problem are
The conditions now take the following form
3.3. Relaxation of Boundary Conditions
To solve the stability model, we need to relax the boundary conditions as proposed by Harris et al. [64]. For that reason, the conditions as can be replaced by new conditions . It must be pointed out that the linearized boundary value problem (25)–(28) together with new conditions will yield the unlimited set of unknown eigenvalues . If the smallest eigenvalues show a positive sign, the solutions observed an initial decay of perturbation and accordingly indicates a stable solution. On the other hand, as the smallest eigenvalues show a negative sign, an early growth of disruption is noticed which consequently signifies unstable solution.
4. Numerical Solutions
To solve the boundary value problems (11)–(13) with boundary conditions given by (15), we have adopted a built-in function called bvp4c from Matlab package. Further, to access the precision of current algorithm, the current results of skin friction coefficient are compared with previously reported solutions of Ishak et al. [10], who used Keller-box method in their work, Mahapatra and Nandy [65], who pursued the shooting method for their computation and Zainal et al. [59] which employed the bvp4c solver. These comparative solutions are revealed in Table 3 for selected values of shrinking parameter . It can be point out from these tables that there is good agreement with these methods (error is relatively small), thereby confirming the consistency of the approach used. Furthermore, this validates the present model and proves the accuracy of the bvp4c solver in solving a boundary layer problem as the present results able to withstand the Keller-box method and shooting method which have been employed by Ishak et al. [10] and Mahapatra and Nandy [65]. In this part, the results of local skin friction , Nusselt number , velocity profile microrotation profile as well as temperature profile are illustrated graphically to explore the influence of some governing parameters such as Cu nanoparticle volume fraction unsteady parameter , material parameter and radiation parameter .

Table 3.
Comparison values of when and for different values.
The effect of Cu nanoparticle volume fraction against stretching or shrinking parameter on the local skin friction and Nusselt number as given in Equation (17) are shown in Figure 2a,b. It is apparent from these figures that for shrinking parameter the occurrence of dual solutions is noted. However, it is remarked that no solution exists when which indicates that the boundary layer is detach from the surface and the principle of boundary layer theory are no longer valid. Moreover, is the critical point that connected the first and second solutions. In addition, a unique solution is noticed when the sheet is stretched . It is clear that for the problem reduces to the micropolar nanofluid. From these figures, it is discovered that upsurge in Cu nanoparticle volume fraction enhances the local skin friction and local Nusselt number for all domains of stretching and shrinking parameter in first solution but a small change is noted for the second solution. This finding proves that the increment of Cu nanoparticle volume fraction can improve the heat transfer efficiency. This also implies that hybrid nanofluid provides a better heat performance than nanofluid. Furthermore, the enhancement of Cu nanoparticle volume fraction on local skin friction and Nusselt number fasten the detachment of boundary layer flow. Figure 3a–c exemplify the impact of Cu nanoparticle volume fraction parameter on the velocity profile , microrotation profile and temperature profile for shrinking sheet . It reveals that augmentation of Cu nanoparticle volume fraction depreciates the momentum and microrotation boundary layer thickness in first and second solutions. Meanwhile, the thermal boundary layer thickness increases as Cu nanoparticle volume fraction increases for the first solution, however a contrary observation is noted for the second solution. Furthermore, one can see that the boundary layer thickness of the first solution was slimmer than second solution. In addition, all the profiles published are asymptotically satisfied the boundary conditions (15) and eventually supported the findings obtained in Figure 2a,b.
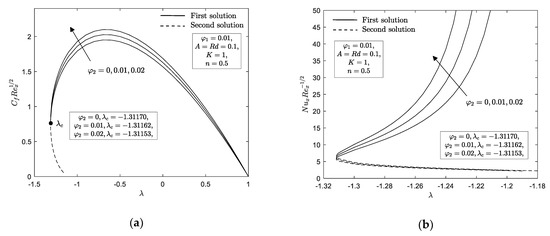
Figure 2.
(a) ; (b) with for various .
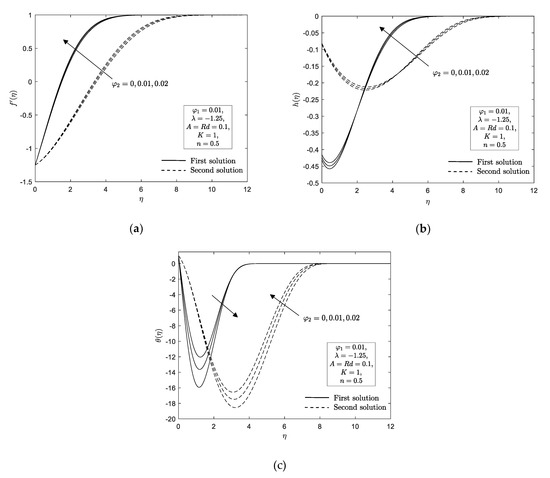
Figure 3.
(a) ; (b) ; (c) for various .
Figure 4a,b show the impact of unsteady parameter on the local skin friction and Nusselt number towards stretching/shrinking parameter . The occurrence of unsteady parameter consequently elevates the local skin friction and Nusselt number . It must be noted that the flow corresponds to the steady micropolar flow when and it is numerically observed that dual solution exists as and a unique solution exists when . However, the physical character of flow changes when the flow becomes unsteady. For instance, as the unsteadiness parameter increase, i.e., and , the range of similarity solutions to exist also increases where dual solutions is observed in the range of and , respectively. The unique solution however only exists as for both case of and concurrently no solution is noticed when . In short, a raise in unsteady parameter act in postponing the boundary layer detachment. On the other side, Figure 5a–c portray the discrepancy of velocity , microrotation and temperature profiles when unsteady parameter fluctuates from 0 to 0.15. For the first solution, the diminished of momentum boundary layer thickness is observed when the unsteady parameter increases as shown in Figure 5a, but a reverse observation is remarked for the second solution. Furthermore, the microrotation boundary layer thickness diminishes with an increment of unsteady parameter values in the first solution except near the sheet, while an opposing trend is remarked for the second solution. It is also interesting to observe from these figures that for both solutions, the thermal boundary layer thickness increase with an upsurge of unsteady parameter
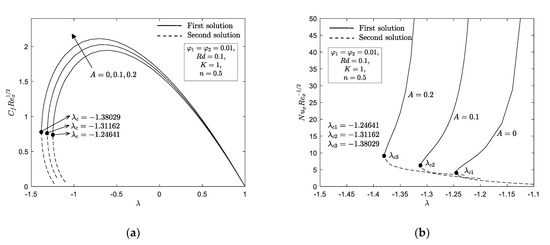
Figure 4.
(a) ; (b) with for various .
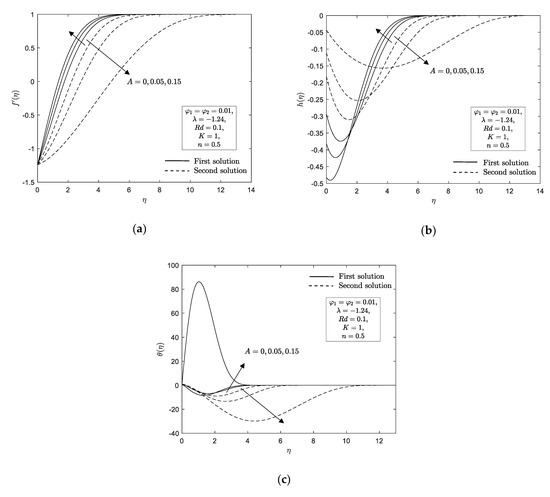
Figure 5.
(a) ; (b) ; (c) for various .
Figure 6a,b and Figure 7a–c are portray to discuss the effect of material parameter on the local skin friction , local Nusselt number , velocity profile , microrotation profile and temperature profile for Cu-Al2O3/water. It is obvious that existence of material parameter give rises to the local skin friction if compared to the absence of material parameter , i.e., no vortex viscosity. However, different results are observed for the local Nusselt number where the nonexistence of micropolar fluid cause an enhancement in comparison with the existence of material parameter . This phenomenon reveals the fact that upsurge value of material parameter gives rise on the vortex viscosity in the fluid flow which consequently enhance the skin friction at the wall and decrease the rate of heat transfer at the wall. Additionally, we observed that an upsurge values of material parameter prompt the domain of similarity solutions to exist become narrow. For instance, the similarity solutions in the nonexistence of material parameter are noted in the range of while in the existence of material parameter , the range of solutions are observed to be and . Furthermore, an upsurge values of material parameter causing the thickness of the momentum and thermal boundary layer to increase in first and second solutions. We can see from Figure 7b that the microrotation boundary layer thickness for first and second solutions near the sheet decreases when this parameter rises while the contrary trend is observed for the large .
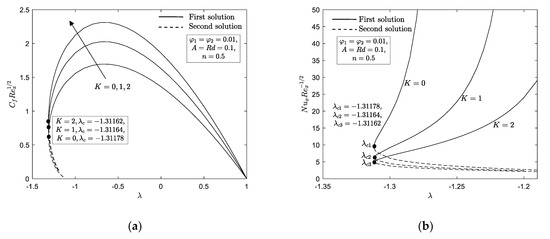
Figure 6.
(a) ; (b) with for various .
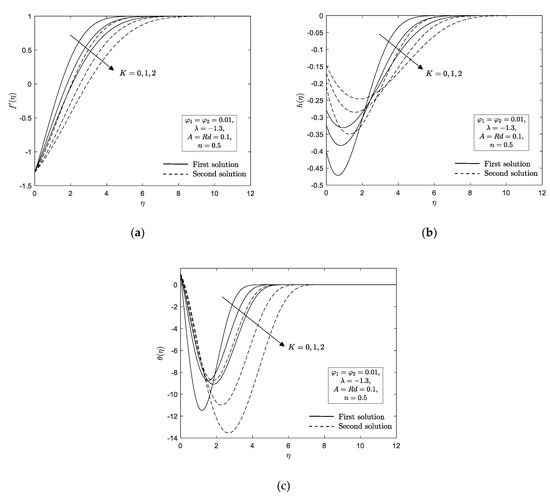
Figure 7.
(a) ; (b) ; (c) for various .
The influence of radiation parameter on the local Nusselt number and temperature profile are portrayed in Figure 8a,b, respectively. We have noticed that the radiation parameter has no control on the flow field, which is evident from Equations (11)–(13). The local Nusselt number is discovered to increase with an upsurge values in radiation parameter . Furthermore, the thermal boundary layer thickness become thicker when this parameter raises in the first solution and it became slimmer in the second solution. As can be seen from Figure 8b, this parameter however does not give effect on the range of similarity solutions to occur, i.e., the critical value for stretching/shrinking parameter is the same for all values of radiation parameter . It is noteworthy that the distribution of temperature in the fluid is significantly affected by the radiation parameter . Physically, this is due to the fact that the heat is produced due to the radiation process and therefore, enhances the fluid temperature.
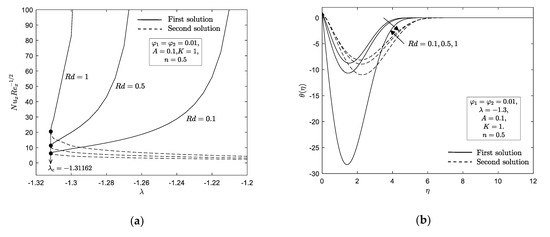
Figure 8.
(a) with ; (b) for various .
The boundary value problems (11)–(13) together with boundary conditions (15) observe the occurrence of non–unique solutions for some governing parameters. The phenomenon of non-unique solutions namely first and second solutions are proved and portrayed as in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. Accordingly, an investigation on the stability analysis has been executed in this present work so that we can identified the most stable solutions. Therefore, the linearized Equations (25)–(27) along with conditions (28) have been solved with the aid of the bvp4 function in MATLAB numerically. The smallest eigenvalues on the selected parameter and from Figure 4a,b are listed in Table 4. This table shown that the second solution displays the negative values of , whereas the first solution demonstrates the positive values of . The smallest eigenvalues against have been plotted in Figure 9. This figure eventually supported the findings obtained from Table 4 except when the values of stretching/shrinking parameter approach its critical value where we observed unstable solutions for both solutions. In reference from the previous literature, we can deduce that the first solution is stable, on the contrary, the second solution is unstable. It worth noting that this analysis is important in identifying the stable solution when there is exist non-unique solutions so that the flow behavior can be predict accurately.

Table 4.
Smallest eigenvalues for selected and when , , and .
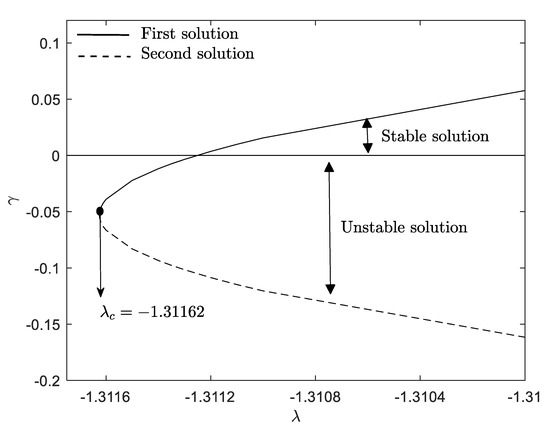
Figure 9.
Smallest eigenvalues against when .
5. Conclusions
Theoretical studies of unsteady micropolar Cu–Al2O3/water flow over a deformable sheet with thermal radiation effect has been examined numerically. The similarity solutions were produced by utilizing the bvp4c function from MATLAB software. The impact of emerging parameters has been examined and illustrated graphically. Thus, the conclusions can be outlined as follows:
- The presence of double solutions is noticeable for shrinking sheet whereas a unique solution is observed for stretching sheet.
- The stability analysis was carried out and the first solution has proven to be a stable solution, whereas the other solution is not a stable solution.
- A raise in Cu nanoparticle volume fraction in micropolar nanofluid has tendency to improve the local Nusselt number and local skin friction for all domain of stretching/shrinking parameter .
- The heat transfer rate increased roughly to an average of 17.725% when the copper nanoparticle volume fraction increased from 0 to 0.01 (1%) in a micropolar nanofluid.
- The rising of unsteady parameter and radiation parameter in micropolar hybrid nanofluid increase the local Nusselt number while the reverse trend is observed with an increase of material parameter .
- The local skin friction enhances as the value of unsteady parameter and material parameter increase.
- The domains of the similarity solutions decrease with a raise in Cu nanoparticle volume fraction and material parameter , therefore fastens the boundary layer separation. However, upsurge value of unsteady parameter delays the boundary layer separation.
Author Contributions
Conceptualization, N.S.A. and N.B.; methodology, formal analysis and validation, N.S.A.; writing—original draft preparation, N.S.A.; writing—review and editing, supervision and funding acquisition N.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Fundamental Research Grant Scheme (FRGS) under Ministry of Education with project number FRGS/1/2018/STG06/UPM/02/4.
Institutional Review Board Statement
Not applicable
Informed Consent Statement
Not applicable
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to its large size.
Acknowledgments
The authors wish to express their sincere thanks to the very competent reviewers for the good comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| positive constants [s−1] | |
| unsteady parameter [-] | |
| skin friction coefficient [-] | |
| specific heat at constant pressure [Jkg−1K−1] | |
| dimensionless stream function [-] | |
| dimensionless angular velocity [-] | |
| microinertia density [m2] | |
| thermal conductivity [Wm−1K−1] | |
| mean absorption coefficient [m−1] | |
| dimensionless material parameter [-] | |
| positive constant [s−1] | |
| angular velocity [ms−1] | |
| local Nusselt number [-] | |
| Prandtl number [-] | |
| radiative heat flux [Wm−2] | |
| radiation parameter [-] | |
| local Reynolds number [-] | |
| time [s] | |
| temperature [K] | |
| velocities component in the and directions, respectively [ms−1] | |
| velocity of inviscid flow [ms−1] | |
| stretching/shrinking velocity [ms−1] | |
| cartesian coordinates along the surface and normal to it, respectively [m] | |
| Greek Symbols | |
| nanoparticle volume fractions for Al2O3 (alumina) [-] | |
| nanoparticle volume fractions for Cu (copper) [-] | |
| dimensionless temperature [-] | |
| unknown eigenvalues [-] | |
| stretching/shrinking parameter [-] | |
| similarity variable [-] | |
| dynamic viscosity [N s m−2] | |
| kinematic viscosity [m2s−1] | |
| density [kgm−3] | |
| dimensionless time variable [-] | |
| Stefan–Boltzmann constant [Wm−2K−4] | |
| stream function [-] | |
| heat capacity [JK−1m−3] | |
| spin gradient viscosity [kg m s−1] | |
| vortex viscosity [kg m−1s−1] | |
| Subscripts | |
| base fluid | |
| hybrid nanofluid | |
| solid component for Al2O3 (alumina) | |
| solid component for Cu (copper) | |
| condition at the surface | |
| ambient condition | |
| Superscript | |
| differentiation with respect to | |
References
- Ariman, T.; Turk, M.A.; Sylvester, N.D. Microcontinuum fluid mechanics—a review. Int. J. Eng. Sci. 1973, 11, 905–930. [Google Scholar] [CrossRef]
- Eringen, A.C. Simple microfluids. Int. J. Eng. Sci. 1964, 2, 205–217. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of micropolar fluids. J. Math. Mech. 1966, 16, 1–18. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of thermomicrofluids. J. Math. Anal. Appl. 1972, 38, 480–496. [Google Scholar] [CrossRef]
- Ebert, F. A similarity solution for the boundary layer flow of a polar fluid. Chem. Eng. J. 1973, 5, 85–92. [Google Scholar] [CrossRef]
- Ahmadi, G. Self-Similar solution of imcompressible micropolar boundary layer flow over a semi-infinite plate. Int. J. Eng. Sci. 1976, 14, 639–646. [Google Scholar] [CrossRef]
- Gorla, R.S.R. Buoyancy effects on the boundary layer flow of a micropolar fluid along a vertical cylinder. Int. J. Eng. Sci. 1988, 26, 883–892. [Google Scholar] [CrossRef]
- Gorla, R.S.R.; Takhar, H.S. Boundary layer flow of micropolar fluid on rotating axisymmetric surfaces with a concentrated heat source. Acta Mech. 1994, 105, 1–10. [Google Scholar] [CrossRef]
- Nazar, R.; Amin, N.; Filip, D.; Pop, I. Stagnation point flow of a micropolar fluid towards a stretching sheet. Int. J. Non Linear Mech. 2004, 39, 1227–1235. [Google Scholar] [CrossRef]
- Ishak, A.; Lok, Y.Y.; Pop, I. Stagnation-Point flow over a shrinking sheet in a micropolar fluid. Chem. Eng. Commun. 2010, 197, 1417–1427. [Google Scholar] [CrossRef]
- Yacob, N.A.; Ishak, A. Micropolar fluid flow over a shrinking sheet. Meccanica 2012, 47, 293–299. [Google Scholar] [CrossRef]
- Sandeep, N.; Sulochana, C. Dual solutions for unsteady mixed convection flow of MHD micropolar fluid over a stretching/shrinking sheet with non-uniform heat source/sink. Eng. Sci. Technol. Int. J. 2015, 18, 738–745. [Google Scholar] [CrossRef]
- Mishra, S.R.; Khan, I.; Al-Mdallal, Q.M.; Asifa, T. Free convective micropolar fluid flow and heat transfer over a shrinking sheet with heat source. Case Stud. Therm. Eng. 2018, 11, 113–119. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Raza, J.; Sherif, E.S.M.; Seikh, A.H. Magnetohydrodynamic (MHD) flow of micropolar fluid with effects of viscous dissipation and joule heating over an exponential shrinking sheet: Triple solutions and stability analysis. Symmetry 2020, 12, 142. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, M.N.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N.; Pop, I. Mixed convective flow and heat transfer of a dual stratified micropolar fluid induced by a permeable stretching/shrinking sheet. Entropy 2019, 21, 1162. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Baleanu, D.; Sooppy Nisar, K. Triple solutions and stability analysis of micropolar fluid flow on an exponentially shrinking surface. Crystals 2020, 10, 283. [Google Scholar] [CrossRef]
- Ahmad, F.; Almatroud, A.O.; Hussain, S.; Farooq, S.E.; Ullah, R. Numerical solution of nonlinear diff. Equations for heat transfer in micropolar fluids over a stretching domain. Mathematics 2020, 8, 854. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J. Enhancing thermal conductivity of fluids with nanoparticles. ASME Publ. Fed. 1995, 231, 99–103. [Google Scholar]
- Rafati, M.; Hamidi, A.A.; Niaser, M.S. Application of nanofluids in computer cooling systems (heat transfer performance of nanofluids). Appl. Therm. Eng. 2012, 45, 9–14. [Google Scholar] [CrossRef]
- Sheikhpour, M.; Arabi, M.; Kasaeian, A.; Rabei, A.R.; Taherian, Z. Role of nanofluids in drug delivery and biomedical technology: Methods and applications. Nanotechnol. Sci. Appl. 2020, 13, 47. [Google Scholar] [CrossRef]
- Nagarajan, P.K.; Subramani, J.; Suyambazhahan, S.; Sathyamurthy, R. Nanofluids for solar collector applications: A review. Energy Procedia 2014, 61, 2416–2434. [Google Scholar] [CrossRef]
- Gangadhar, K.; Kannan, T.; Sakthivel, G.; DasaradhaRamaiah, K. Unsteady free convective boundary layer flow of a nanofluid past a stretching surface using a spectral relaxation method. Int. J. Ambient Energy 2020, 41, 609–616. [Google Scholar] [CrossRef]
- Chaudhary, S.; Kanika, K.M. Viscous dissipation and Joule heating in MHD Marangoni boundary layer flow and radiation heat transfer of Cu–water nanofluid along particle shapes over an exponential temperature. Int. J. Comput. Math. 2020, 97, 943–958. [Google Scholar] [CrossRef]
- Naqvi, S.M.R.S.; Muhammad, T.; Saleem, S.; Kim, H.M. Significance of non-uniform heat generation/absorption in hydromagnetic flow of nanofluid due to stretching/shrinking disk. Phys. Stat. Mech. Appl. 2020, 553, 123970. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Arifin, N.M.; Rosali, H. Role of multiple solutions in flow of nanofluids with carbon nanotubes over a vertical permeable moving plate. Alex. Eng. J. 2020, 59, 763–773. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Arifin, N.M.; Rosali, H. MHD flow past a nonlinear stretching/shrinking sheet in carbon nanotubes: Stability analysis. Chin. J. Phys. 2020, 65, 436–446. [Google Scholar] [CrossRef]
- Hussain, S.T.; Nadeem, S.; Haq, R.U. Model-Based analysis of micropolar nanofluid flow over a stretching surface. Eur. Phys. J. Plus 2014, 129, 161. [Google Scholar] [CrossRef]
- Bourantas, G.C.; Loukopoulos, V.C. MHD natural-convection flow in an inclined square enclosure filled with a micropolar-nanofluid. Int. J. Heat Mass Transf. 2014, 79, 930–944. [Google Scholar] [CrossRef]
- Noor, N.F.M.; Haq, R.U.; Nadeem, S.; Hashim, I. Mixed convection stagnation flow of a micropolar nanofluid along a vertically stretching surface with slip effects. Meccanica 2015, 50, 2007–2022. [Google Scholar] [CrossRef]
- Gangadhar, K.; Kannan, T.; Jayalakshmi, P. Magnetohydrodynamic micropolar nanofluid past a permeable stretching/shrinking sheet with Newtonian heating. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 4379–4391. [Google Scholar] [CrossRef]
- Dero, S.; Rohni, A.M.; Saaban, A. MHD micropolar nanofluid flow over an exponentially stretching/shrinking surface: Triple solutions. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 56, 165–174. [Google Scholar]
- Lund, L.A.; Omar, Z.; Khan, U.; Khan, I.; Baleanu, D.; Nisar, K.S. Stability analysis and dual solutions of micropolar nanofluid over the inclined stretching/shrinking surface with convective boundary condition. Symmetry 2020, 12, 74. [Google Scholar] [CrossRef]
- Abdal, S.; Ali, B.; Younas, S.; Ali, L.; Mariam, A. Thermo-Diffusion and multislip effects on MHD mixed convection unsteady flow of micropolar nanofluid over a shrinking/stretching sheet with radiation in the presence of heat source. Symmetry 2020, 12, 49. [Google Scholar] [CrossRef]
- Amjad, M.; Zehra, I.; Nadeem, S.; Abbas, N. Thermal analysis of Casson micropolar nanofluid flow over a permeable curved stretching surface under the stagnation region. J. Therm. Anal. Calorim. 2020, 1–13. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M.; Khan, I.; Baleanu, D.; Nisar, K.S.; Seikh, A.H. Hydromagnetic flow of micropolar nanofluid. Symmetry 2020, 12, 251. [Google Scholar] [CrossRef]
- Madhesh, D.; Kalaiselvam, S. Experimental analysis of hybrid nanofluid as a coolant. Procedia Eng. 2014, 97, 1667–1675. [Google Scholar] [CrossRef]
- Tahat, M.S.; Benim, A.C. Experimental analysis on thermophysical properties of Al2O3/CuO hybrid nano fluid with its effects on flat plate solar collector. Defect Diffus. Forum 2017, 374, 148–156. [Google Scholar] [CrossRef]
- Devi, S.U.; Devi, S.A. Heat transfer enhancement of Cu-Al2O3/water hybrid nanofluid flow over a stretching sheet. J. Niger. Math. Soc. 2017, 36, 419–433. [Google Scholar]
- Anuar, N.S.; Bachok, N.; Pop, I. Cu-Al2O3/Water hybrid nanofluid stagnation point flow past MHD stretching/shrinking sheet in presence of homogeneous-heterogeneous and convective boundary conditions. Mathematics 2020, 8, 1237. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N.; Malik, M.Y. Inspection of hybrid based nanofluid flow over a curved surface. Comput. Methods Programs Biomed. 2020, 189, 105193. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow past a permeable moving thin needle. Mathematics 2020, 8, 612. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, M.N.; Pop, I. Mixed convective stagnation point flow towards a vertical riga plate in hybrid Cu-Al2O3/Water nanofluid. Mathematics 2020, 8, 912. [Google Scholar] [CrossRef]
- Subhani, M.; Nadeem, S. Numerical analysis of micropolar hybrid nanofluid. Appl. Nanosci. 2019, 9, 447–459. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N. On both MHD and slip effect in micropolar hybrid nanofluid past a circular cylinder under stagnation point region. Can. J. Phys. 2019, 97, 392–399. [Google Scholar] [CrossRef]
- Abbas, N.; Nadeem, S.; Malik, M.Y. Theoretical study of micropolar hybrid nanofluid over Riga channel with slip conditions. Phys. Stat. Mech. Appl. 2020, 124083. [Google Scholar] [CrossRef]
- Al-Hanaya, A.M.; Sajid, F.; Abbas, N.; Nadeem, S. Effect of SWCNT and MWCNT on the flow of micropolar hybrid nanofluid over a curved stretching surface with induced magnetic field. Sci. Rep. 2020, 10, 1–18. [Google Scholar] [CrossRef]
- Bhattacharyya, K. Dual solutions in boundary layer stagnation-point flow and mass transfer with chemical reaction past a stretching/shrinking sheet. Int. Commun. Heat Mass Transf. 2011, 38, 917–922. [Google Scholar] [CrossRef]
- Bestman, A.R.; Adjepong, S.K. Unsteady hydromagnetic free-convection flow with radiative heat transfer in a rotating fluid. Astrophys. Space Sci. 1988, 143, 73–80. [Google Scholar] [CrossRef]
- Sajid, M.; Hayat, T. Influence of thermal radiation on the boundary layer flow due to an exponentially stretching sheet. Int. Commun. Heat Mass Transf. 2008, 35, 347–356. [Google Scholar] [CrossRef]
- Nadeem, S.; Zaheer, S.; Fang, T. Effects of thermal radiation on the boundary layer flow of a Jeffrey fluid over an exponentially stretching surface. Numer. Algorithms 2011, 57, 187–205. [Google Scholar] [CrossRef]
- Pal, D.; Mandal, G. Thermal radiation and MHD effects on boundary layer flow of micropolar nanofluid past a stretching sheet with non-uniform heat source/sink. Int. J. Mech. Sci. 2017, 126, 308–318. [Google Scholar] [CrossRef]
- Gireesha, B.J.; Umeshaiah, M.; Prasannakumara, B.C.; Shashikumar, N.S.; Archana, M. Impact of nonlinear thermal radiation on magnetohydrodynamic three dimensional boundary layer flow of Jeffrey nanofluid over a nonlinearly permeable stretching sheet. Phys. Stat. Mech. Appl. 2020, 124051. [Google Scholar] [CrossRef]
- Yashkun, U.; Zaimi, K.; Bakar, N.A.A.; Ishak, A.; Pop, I. MHD hybrid nanofluid flow over a permeable stretching/shrinking sheet with thermal radiation effect. Int. J. Numer. Methods Heat Fluid Flow 2020. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Mukhopadhyay, S.; Layek, G.C.; Pop, I. Effects of thermal radiation on micropolar fluid flow and heat transfer over a porous shrinking sheet. Int. J. Heat Mass Transf. 2012, 55, 2945–2952. [Google Scholar] [CrossRef]
- Roy, N.C.; Hossain, M.; Pop, I. Analysis of dual solutions of unsteady micropolar hybrid nanofluid flow over a stretching/shrinking sheet. J. Appl. Comput. Mech. 2020. [Google Scholar] [CrossRef]
- Jena, S.K.; Mathur, M.N. Similarity solutions for laminar free convection flow of a thermomicropolar fluid past a non-isothermal vertical flat plate. Int. J. Eng. Sci. 1981, 19, 1431–1439. [Google Scholar] [CrossRef]
- Guram, G.S.; Smith, A.C. Stagnation flows of micropolar fluids with strong and weak interactions. Comput. Math. Appl. 1980, 6, 213–233. [Google Scholar] [CrossRef]
- Peddieson, J., Jr. An application of the micropolar fluid model to the calculation of a turbulent shear flow. Int. J. Eng. Sci. 1972, 10, 23–32. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Unsteady stagnation point flow of hybrid nanofluid past a convectively heated stretching/shrinking sheet with velocity slip. Mathematics 2020, 8, 1649. [Google Scholar] [CrossRef]
- Brewster, M.Q. Thermal Radiative Transfer and Properties; John Wiley & Sons: Hoboken, NJ, USA, 1992. [Google Scholar]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary layer flow near the stagnation point on a vertical surface in porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Nandy, S.K. Slip effects on unsteady stagnation-point flow and heat transfer over a shrinking sheet. Meccanica 2013, 48, 1599–1606. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).