A Lochs-Type Approach via Entropy in Comparing the Efficiency of Different Continued Fraction Algorithms

Abstract

We investigate the efficiency of several types of continued fraction expansions of a number in the unit interval using a generalization of Lochs theorem from 1964. Thus, we aim to compare the efficiency by describing the rate at which the digits of one number-theoretic expansion determine those of another. We study Chan’s continued fractions, $\theta$-expansions, N-continued fractions, and Rényi-type continued fractions. A central role in fulfilling our goal is played by the entropy of the absolutely continuous invariant probability measures of the associated dynamical systems.

1. Introduction

The purpose of this paper is to compare the efficiency of some continued fractions in approximating a real number in the unit interval. For any irrational $x\in (0,1)$, suppose we have two known expansions $x={[a_1,a_2,\dots ]}_1$ and $x={[b_1,b_2,\dots ]}_2$. A natural question is: Which of these continued fraction expansions is more “efficient”? In mathematical terms, “efficiency” means: Which of the two sequences ${[a_1,a_2,\dots ,a_n]}_1$ and ${[b_1,b_2,\dots ,b_n]}_2$ converges more quickly to x as $n\to \infty$? It is therefore relevant to ask how much information (e.g., in terms of the digits in the second expansion) can be determined once we know n digits of the first expansion. Suppose we approximate x by keeping the first n digits of its first expansion. To attain the same degree of accuracy, we need to keep the first $m=m(n,x)$ digits of the second expansion. What can we say about the ratio $m(n,x)/n$ in general? We show that the relative speed of approximation of two different expansions (almost everywhere) is related to the quotient of the entropies of the transformations that generate these expansions. The strategy used in this paper fits for all pairs of number-theoretic fibered maps (NTFMs) for which the generating partition has finite entropy.

1.1. Motivation

The ancient charms of number theory have been replaced by the modern fascination of an algorithmic thinking. When analytic number theory was being formulated in the nineteenth century, probability theory was not yet a reputable branch of mathematics. Nowadays, probabilistic techniques are routinely used in number theory. The field of probabilistic number theory is currently evolving very rapidly and uses more and more refined probabilistic tools and results. It is well-known that continued fractions lie at the heart of a number of classical algorithms such as Euclid’s greatest common divisor or the lattice reduction algorithm of Gauss [1]. Thus, continued fractions arise naturally in the theory of approximation to real numbers by rationals. To this day, the Gauss map, on which metrical theory of regular continued fraction is based, has fascinated researchers from various branches of mathematics and science, with many applications in computer science, cosmology, and chaos theory. Apart from the regular continued fraction expansion, many other continued fraction expansions have been studied. In the last century, mathematicians broke new ground in this area. Since there are several continued fraction algorithms, we ask ourselves which of them provides the best approximation of a real number. The representation of a real number by a continued fraction can be viewed as a source of information about the number. For this purpose, we need the notion of entropy, a rigorous tool at the crossroads of probability, information theory, and dynamical systems [2,3].

1.2. Entropy

As is well known, entropy is an important concept of information in physics, chemistry, and information theory [4]. The connection between entropy and the transmission of information was first studied by Shannon [5]. Thus, entropy can be seen as a measure of randomness of the system or the average information acquired under a single application of the underlying map. Entropy also plays an important role in ergodic theory. Thus, Shannon’s probabilistic notion of entropy was first introduced into the ergodic theory by Kolmogorov [6] via a measure theoretic approach. The contribution of Kolmogorov to modern dynamics was the discovery of the concept of entropy, which was made rigorous by Sinai [7]. This concept provides an important generalization of Shannon entropy. Kolmogorov–Sinai (K-S) entropy measures the maximal loss of information for the iteration of finite partitions in a measure preserving transformation. The concept has shown its strength through the adequate answers to problems in the classification of dynamical systems. Two metrically isomorphic dynamical systems have the same K-S entropy, so this concept is a tool for distinguishing non-isomorphic (non-conjugate) dynamical systems.

We briefly review this very important concept of K-S entropy in Ergodic Theory. Given a measure preserving system $\left(X,\mathcal{X},\mu ,T\right)$, we say $\alpha =\{A_i:i\in I\}$ is a partition of X if $X={\bigcup }_{i\in I}{A}_i$, where $A_i\in \mathcal{X}$ for each $i\in I$ and $A_i\cap A_j=\varnothing$ for $i\ne j$, $i,j\in I$. Here, I is a finite or countable index set. For a partition $\alpha$ of X, we define the entropy of the partition $\alpha$ as

$$H\left(\alpha \right):=-\sum _{A\in \alpha }\mu \left(A\right)log\mu \left(A\right).$$

(1)

In this definition, T does not appear. However, the entropy of the dynamical system is defined by the entropy of the transformation T as follows.

Given a partition $\alpha$, we consider the partition

$${\alpha }_n:=\underset{i=0}{\overset{n-1}{\bigvee }}{T}^{-i}\alpha =\left\{\bigcap _{i=0}^{n-1}{T}^{-i}{A}_i:A_i\in \alpha ,i=0,1,\dots ,n-1\right\}.$$

(2)

Then, the entropy of transformation T with respect to $\alpha$ is given by

$$h(\alpha ,T):=\underset{n\to \infty }{lim}\frac{1}{n}H\left({\alpha }_n\right).$$

(3)

The entropy of T is defined as

$$h\left(T\right):=sup\left\{h(\alpha ,T):\alpha \mathrm{partition} \mathrm{of} X\mathrm{such} \mathrm{that}H\left(\alpha \right)<\infty \right\}.$$

(4)

In general, it does not seem possible to calculate the entropy straight from its definition. First, let us define that a partition $\alpha$ of X is a generator with respect to a non-invertible transformation T if

$$\sigma \left(\underset{i=0}{\overset{\infty }{\bigvee }}{T}^{-i}\alpha \right)=\mathcal{X}\mathrm{up} \mathrm{to} \mathrm{sets} \mathrm{of} \mu \text{-}\mathrm{measure} \mathrm{zero}.$$

(5)

In computation of $h\left(T\right)$, the K-S Theorem is very useful. For completeness, we recall this theorem. Let $\alpha$ be a partition of X such that $H\left(\alpha \right)<\infty$. If $\alpha$ is a generator with respect to T, then $h\left(T\right)=h(\alpha ,T)$.

We also have the following classical Shannon–McMillan–Breiman theorem [8]. Let $\left(X,\mathcal{X},\mu ,T\right)$ be an ergodic measure preserving system and let $\alpha$ be a finite or countable partition of X satisfying $H\left(\alpha \right)<\infty$. The Shannon–McMillan–Breiman theorem says, if $A_n\left(x\right)$ denotes the unique element $A_n\in {\alpha }_n$ such that $x\in A_n$, then for almost every $x\in X$ we have:

$$\underset{n\to \infty }{lim}-\frac{1}{n}log\mu \left(A_n\left(x\right)\right)=h(\alpha ,T).$$

(6)

In 1964, Rohlin [9] showed that, when Rényi’s condition is satisfied, the entropy of a $\mu$-measure preserving operator $T:X\to X$ is given by the formula:

$$h\left(T\right):={\int }_{X}log\left|T^{\prime }\left(x\right)\right|\mathrm{d}\mu \left(x\right).$$

(7)

The Rény’s condition means that there is a constant $C\ge 1$ such that

$$\underset{x,y\in T^n\left({\alpha }_n\right)}{sup}\frac{\left|u_n^{\prime }\left(x\right)\right|}{\left|u_n^{\prime }\left(y\right)\right|}\le C,$$

(8)

where $u_n:={\left({\left.T^n\right|}_{{\alpha }_n}\right)}^{-1}$.

2. Lochs’ Theorem

Expansions that furnish increasingly good approximations to real numbers are usually related to dynamical systems. In 1964, Lochs [10] compared the decimal expansion and the regular continued fraction (RCF) expansion. Although comparing dynamical systems seems difficult, using detailed knowledge of the continued fraction operator, Lochs was able to relate the relative speed of approximation of decimal and regular continued fraction expansions (almost everywhere) to the quotient of the entropies of their dynamical systems. Thus, roughly 97 RCF digits are determined by 100 decimal digits, which indicates that the RCF expansion is slightly more efficient compared to the decimal expansion at representing irrational numbers.

2.1. Decimal Expansions

It is a common known fact that any real number $x\in [0,1)$ can be written as

$$x=\sum _{i=1}^{\infty }\frac{d_i\left(x\right)}{{10}^i},$$

(9)

where $d_i=d_i\left(x\right)\in \{0,1,2,\dots ,9\}$ for $i\in {\mathbb{N}}_{+}:=\{1,2,3,\dots \}$. The representation of x in (9), denoted by $x=0.d_1{d}_2\dots$, is called the decimal expansion of x. We can generate the decimal expansions by iterating the decimal map

$$T_d:[0,1)\to [0,1);T_d\left(x\right)=10x-\lfloor 10x\rfloor ,$$

(10)

where $\lfloor ·\rfloor$ denotes the floor (or entire) function. In other words, $T_d$ is given by

$$T_d\left(x\right)=10x-i\mathrm{if}\frac{1}{10}\le x<\frac{i+1}{10},i=0,1,2,\dots ,9.$$

(11)

Thus, we obtain:

$$x=\frac{d_1}{10}+\frac{d_2}{{10}^2}+\dots +\frac{d_n}{{10}^n}+\frac{T_d^n\left(x\right)}{{10}^n},$$

(12)

where

$$d_1=d_1\left(x\right)=\lfloor 10x\rfloor$$

(13)

and

$$d_n=d_n\left(x\right)=d_1\left(T_d^{n-1}\left(x\right)\right),n\ge 2.$$

(14)

Since $0\le T_d^n\left(x\right)<1$, we obtain

$$\sum _{i=1}^n\frac{d_i}{{10}^i}\to x\mathrm{as}n\to \infty .$$

(15)

2.2. Regular Continued Fraction Expansions

Beside decimal expansions, there are many other possible representations of real numbers in terms of a sequence of integers. We refer to the regular continued fractions as another famous example. Any irrational number $x\in [0,1)$ has a unique regular continued fraction expansion

$${\displaystyle x=\frac{1}{{\displaystyle a_1+\frac{1}{a_2+\ddots }}},}$$

(16)

where $a_n\in {\mathbb{N}}_{+}$ for any $n\ge 1$. This expansion is obtained by applying repeatedly the Gauss map or the regular continued fraction transformation

$$T_G:[0,1)\to [0,1);T_G\left(0\right)=0,T_G\left(x\right)=\frac{1}{x}-⌊\frac{1}{x}⌋.$$

(17)

Therefore, it follows that the digits $a_1,a_2,\dots$ are related by

$$a_n=a_n\left(x\right)=a_1\left(T_G^{n-1}\left(x\right)\right),n\ge 2,$$

(18)

where

$$a_1=a_1\left(x\right)=⌊\frac{1}{x}⌋.$$

(19)

If we denote by ${[a_1,a_2,\dots ]}_G$ the expansion in (16), we have

$${[a_1,a_2,\dots ,a_n]}_G\to x\mathrm{as}n\to \infty .$$

(20)

2.3. Comparing the Efficiency of Decimal Expansion and RCF Expansion

In [10], Lochs answered the question which of these developments is more efficient, namely which of the two sequences in (15) and (20) converges more quickly to x as $n\to \infty$.

Suppose that the irrational number $x\in (0,1)$ has the decimal expansion $x=0.d_1{d}_2\dots$ and the RCF expansion $x={[a_1,a_2,\dots ]}_G$. Let $y=0.d_1{d}_2\dots d_n$ be the rational number determined by the first n decimal digits of x, and let $z=y+{10}^{-n}$. Then, $[y,z]$ is the nth-order decimal cylinder containing x, which we also denote by $C_n\left(x\right)$. Now, let $y={[b_1,\dots ,b_l]}_G$ and $z={[c_1,c_2,\dots ,c_k]}_G$ be the RCF expansions of y and z. Let

$$m(n,x):=max\{i\le max(l,k):\mathrm{for} \mathrm{all}j\le i,b_j=c_j\}.$$

(21)

In other words, $m(n,x)$ is the largest integer such that $C_n\left(x\right)\subset D_{m(n,x)}\left(x\right)$, where $D_j\left(x\right)$ denotes the jth-order RCF cylinder containing x. Lochs [10] proved that, for almost every irrational $x\in (0,1)$, we have

$$\underset{n\to \infty }{lim}\frac{m(n,x)}{n}=\frac{6log2log10}{{\pi }^2}=0.97027014\dots$$

(22)

For example, Lochs [11] computed the first 968 RCF digits of $\pi$ from its first 1000 decimals, and Brent and McMillan [12] computed the first 29,200 RCF digits of Euler–Mascheroni constant from its first 30,100 decimals.

2.4. Extended Lochs’ Theorem

Dajani and Fieldsteel [13] proved a generalization of Lochs’ theorem showing that we can compare any two expansions of numbers which are generated by number-theoretic fibered maps, i.e., surjective interval maps $S:[0,1)\to [0,1)$ that satisfy the following conditions:

(1)

There exists a finite or countable partition of $[0,1)$ into intervals such that S restricted to each interval is strictly monotonic and continuous.

(2)

S is ergodic with respect to Lebesgue measure $\lambda$, and there exists an S invariant probability measure $\mu$ equivalent to $\lambda$ (i.e., $\mu \left(A\right)=0$ if and only if $\lambda \left(A\right)=0$ for all Lebesgue sets A) with bounded density (both ${\displaystyle \frac{\mathrm{d}\mu }{\mathrm{d}\lambda }}$ and ${\displaystyle \frac{\mathrm{d}\lambda }{\mathrm{d}\mu }}$ are bounded).

Consider NTFMs $S_1$ and $S_2$ on $[0,1)$ with invariant measures ${\mu }_1$ and ${\mu }_2$ (equivalent to Lebesgue measure) and with partitions P and Q, respectively. Denote by $P_n\left(x\right)$ the nth-order cylinder that contains $x\in [0,1)$ (a similar definition for $Q_n\left(x\right)$). Let

$$m_{S_1,S_2}(n,x)=sup\{m:P_n\left(x\right)\subset Q_m\left(x\right)\}.$$

(23)

Under the conditions just stated and with the understanding that $m_{S_1,S_2}(n,x)$ is exactly the number of digits in the $S_2$-expansion of x that can be determined from knowing the first n digits in the $S_1$-expansion, we have

$$\underset{n\to \infty }{lim}\frac{m_{S_1,S_2}(n,x)}{n}=\frac{h\left(S_1\right)}{h\left(S_2\right)}\lambda -\mathrm{a}.\mathrm{e}.$$

(24)

where $h\left(S_1\right)$ and $h\left(S_2\right)$ denote the entropy of $S_1$ and $S_2$, respectively, with $h\left(S_1\right)>0$ and $h\left(S_2\right)>0$.

3. Other Continued Fraction Expansions

Apart from the RCF expansions, there is a wide variety of continued fraction expansions. Here, we mention only a few of the expansions studied from the metrical point of view by the authors over time, namely Chan’s continued fractions [14,15], $\theta$-expansions [16,17], N-continued fraction expansions [18,19], and Rényi-type continued fraction expansions [20,21,22].

In this paper, we ask the question which of these expansions is more effective. To apply the result of Dajani and Fieldsteel [13] in Section 2.4, we briefly present these expansions, calculating the entropy of each map that generates these expansions.

3.1. Chan’s Continued Fractions

Fix an integer $\ell \ge 2$. Then, any $x\in \left[0,1\right)$ can be written in the form

$$x=\frac{{\ell }^{-a_1\left(x\right)}}{{\displaystyle 1+\frac{(\ell -1){\ell }^{-a_2\left(x\right)}}{{\displaystyle 1+\frac{(\ell -1){\ell }^{-a_3\left(x\right)}}{{\displaystyle 1+\ddots }}}}}}=:{[a_1\left(x\right),a_2\left(x\right),a_3\left(x\right),\dots ]}_{\ell },$$

(25)

where $a_n\left(x\right)$s are non-negative integers. Define $\frac{p_{\ell ,n}\left(x\right)}{q_{\ell ,n}\left(x\right)}:={[a_1\left(x\right),a_2\left(x\right),\dots ,a_n\left(x\right)]}_{\ell }$ the n-convergent of x by truncating the expansion on the right-hand side of (25), that is,

$${[a_1\left(x\right),a_2\left(x\right),\dots ,a_n\left(x\right)]}_{\ell }\to x(n\to \infty ).$$

(26)

This continued fraction is associated with the following transformation $T_{\ell }$ on $[0,1]$:

$$T_{\ell }\left(x\right):=\left\{\begin{array}{ccc}{\displaystyle \frac{{\ell }^{\frac{log{x}^{-1}}{log\ell }-⌊\frac{log{x}^{-1}}{log\ell }⌋}-1}{\ell -1},}\hfill & \mathrm{if}\hfill & x\ne 0\hfill \\ 0,\hfill & \mathrm{if}\hfill & x=0.\hfill \end{array}\right.$$

(27)

We notice that $T_{\ell }$ maps the set of irrationals in $[0,1]$ into itself. For any $x\in (0,1)$, put

$$a_n=a_n\left(x\right)=a_1\left(T_{\ell }^{n-1}\left(x\right)\right),n\in {\mathbb{N}}_{+},$$

(28)

with $T_{\ell }^0\left(x\right)=x$ and

$$a_1=a_1\left(x\right)=\left\{\begin{array}{ccc}\lfloor log{x}^{-1}/log\ell \rfloor ,\hfill & \mathrm{if}\hfill & x\ne 0\hfill \\ \infty ,\hfill & \mathrm{if}\hfill & x=0.\hfill \end{array}\right.$$

(29)

The transformation $T_{\ell }$ which generates the continued fraction expansion (25) is ergodic with respect to an invariant probability measure, $G_{\ell }$, where

$$G_{\ell }\left(A\right):=k_{\ell }{\int }_A\frac{\mathrm{d}x}{\left(\right(\ell -1)x+1)\left(\right(\ell -1)x+\ell )},A\in {\mathcal{B}}_{[0,1]},$$

(30)

with

$$k_{\ell }:=\frac{{(\ell -1)}^2}{log\left({\ell }^2/(2\ell -1)\right)}$$

(31)

and ${\mathcal{B}}_{[0,1]}$ is the $\sigma$-algebra of Borel subsets of $[0,1]$.

An n-block $(a_1,a_2,\dots ,a_n)$ is said to be admissible for the expansion in (25) if there exists $x\in [0,1)$ such that $a_i\left(x\right)=a_i$ for all $1\le i\le n$. If $(a_1,a_2,\dots ,a_n)$ is an admissible sequence, we call the set

$$I_{\ell }(a_1,a_2,\dots ,a_n)=\{x\in [0,1]:a_1\left(x\right)=a_1,a_2\left(x\right)=a_2,\dots ,a_n\left(x\right)=a_n\},$$

(32)

the nth-order cylinder.

Define ${\left(u_{\ell ,i}\right)}_{i\in \mathbb{N}}$ by

$$u_{\ell ,i}:[0,1]\to [0,1];u_{\ell ,i}\left(x\right):=\frac{{\ell }^{-i}}{1+(\ell -1)x}.$$

(33)

For each $i\in \mathbb{N}$, $u_{\ell ,i}={\left({\left.T_{\ell }\right|}_{I_{\ell }\left(a_1\right)}\right)}^{-1}$. Let

$$u_{\ell ,a_1{a}_2\dots a_n}\left(t\right):=\left(u_{\ell ,a_1}\circ u_{\ell ,a_2}\circ \dots \circ u_{\ell ,a_n}\right)\left(t\right)=\frac{{\ell }^{-a_1\left(x\right)}}{{\displaystyle 1+\frac{(\ell -1){\ell }^{-a_2\left(x\right)}}{{\displaystyle 1+\ddots +\frac{(\ell -1){\ell }^{-a_n}}{1+(\ell -1)t}}}}}.$$

(34)

We observe that $u_{\ell ,a_1{a}_2\dots a_n}={\left({\left.T_{\ell }^n\right|}_{I_{\ell }(a_1,a_2,\dots ,a_n)}\right)}^{-1}$. Therefore,

$$I_{\ell }(a_1,a_2,\dots ,a_n)=\{u_{\ell ,a_1\dots a_n}\left(t\right):t\in [0,1)\}$$

(35)

which is an interval with the endpoints $\frac{p_{\ell ,n}}{q_{\ell ,n}}$ and $\frac{p_{\ell ,n}+(\ell -1){\ell }^{a_n}{p}_{\ell ,n-1}}{q_{\ell ,n}+(\ell -1){\ell }^{a_n}{q}_{\ell ,n-1}}$. Such intervals form a partition of $[0,1]$.

Before applying Rohlin’s formula, we must check Rényi condition (8). We use directly, without mentioning them here, some properties proved in [14]. Thus, we have

$$\frac{\left|u_{\ell ,a_1\dots a_n}^{\prime }\left(t\right)\right|}{\left|u_{\ell ,a_1\dots a_n}^{\prime }\left(r\right)\right|}={\left(\frac{q_{\ell ,n}+r(\ell -1){\ell }^{a_n}{q}_{\ell ,n-1}}{q_{\ell ,n}+t(\ell -1){\ell }^{a_n}{q}_{\ell ,n-1}}\right)}^2\le {\left(\frac{q_{\ell ,n}+(\ell -1){\ell }^{a_n}{q}_{\ell ,n-1}}{q_{\ell ,n}}\right)}^2\le {\ell }^2.$$

(36)

Applying Rohlin’s formula (7), we obtain:

$$\begin{array}{cc}\hfill h\left(T_{\ell }\right)=& {\int }_0^{1}log\left|T_{\ell }^{\prime }\left(x\right)\right|\mathrm{d}{G}_{\ell }={\int }_0^{1}log\left(\frac{{\ell }^{-a_1\left(x\right)}}{(\ell -1)x^2}\right)\mathrm{d}{G}_{\ell }\hfill \\ \hfill =& {\int }_0^1\left(2log(1/x)-a_1\left(x\right)log\ell -log(\ell -1)\right)\mathrm{d}{G}_{\ell }\hfill \\ \hfill =& 2k_{\ell }{\int }_0^1\frac{log(1/x)}{\left(\right(\ell -1)x+1)\left(\right(\ell -1)x+\ell )}\mathrm{d}x\hfill \\ \hfill & -k_{\ell }(log\ell ){\int }_0^1\frac{a_1\left(x\right)}{\left(\right(\ell -1)x+1)\left(\right(\ell -1)x+\ell )}\mathrm{d}x-log(\ell -1).\hfill \end{array}$$

(37)

As examples, we have the values of $h\left(T_{\ell }\right)$ for different values of ℓ and the graph of $h\left(T_{\ell }\right)$ in

Table 1. Entropies $h\left(T_{\ell }\right)$, $h\left(T_{\theta }\right)$, $h\left(T_N\right)$ and $h\left(R_N\right)$ for different values of the parameters involved.

ℓ	$\mathit{h}\left({\mathit{T}}_{\mathit{\ell }}\right)$	s	$\mathit{h}\left({\mathit{T}}_{\mathit{\theta }}\right)$	N	$\mathit{h}\left({\mathit{T}}_{\mathit{N}}\right)$	N	$\mathit{h}\left({\mathit{R}}_{\mathit{N}}\right)$
$\ell =2$	$1.62258$	$s=1$	$2.37314$	$N=1$	$2.37314$	$N=2$	$2.37314$
$\ell =3$	$1.26775$	$s=3$	$3.24705$	$N=3$	$3.24705$	$N=3$	$2.905$
$\ell =5$	$0.996315$	$s=5$	$3.70244$	$N=5$	$3.70244$	$N=5$	$3.50063$
$\ell =10$	$0.765943$	$s=10$	$4.35074$	$N=10$	$4.35074$	$N=10$	$4.25052$
$\ell =50$	$0.476521$	$s=50$	$5.92195$	$N=50$	$5.92195$	$N=50$	$5.90194$
$\ell =100$	$0.406218$	$s=100$	$6.61015$	$N=100$	$6.61015$	$N=100$	$6.60015$
$\ell =200$	$0.350849$	$s=1000$	$8.90825$	$N=1000$	$8.90825$	$N=1000$	$8.90726$

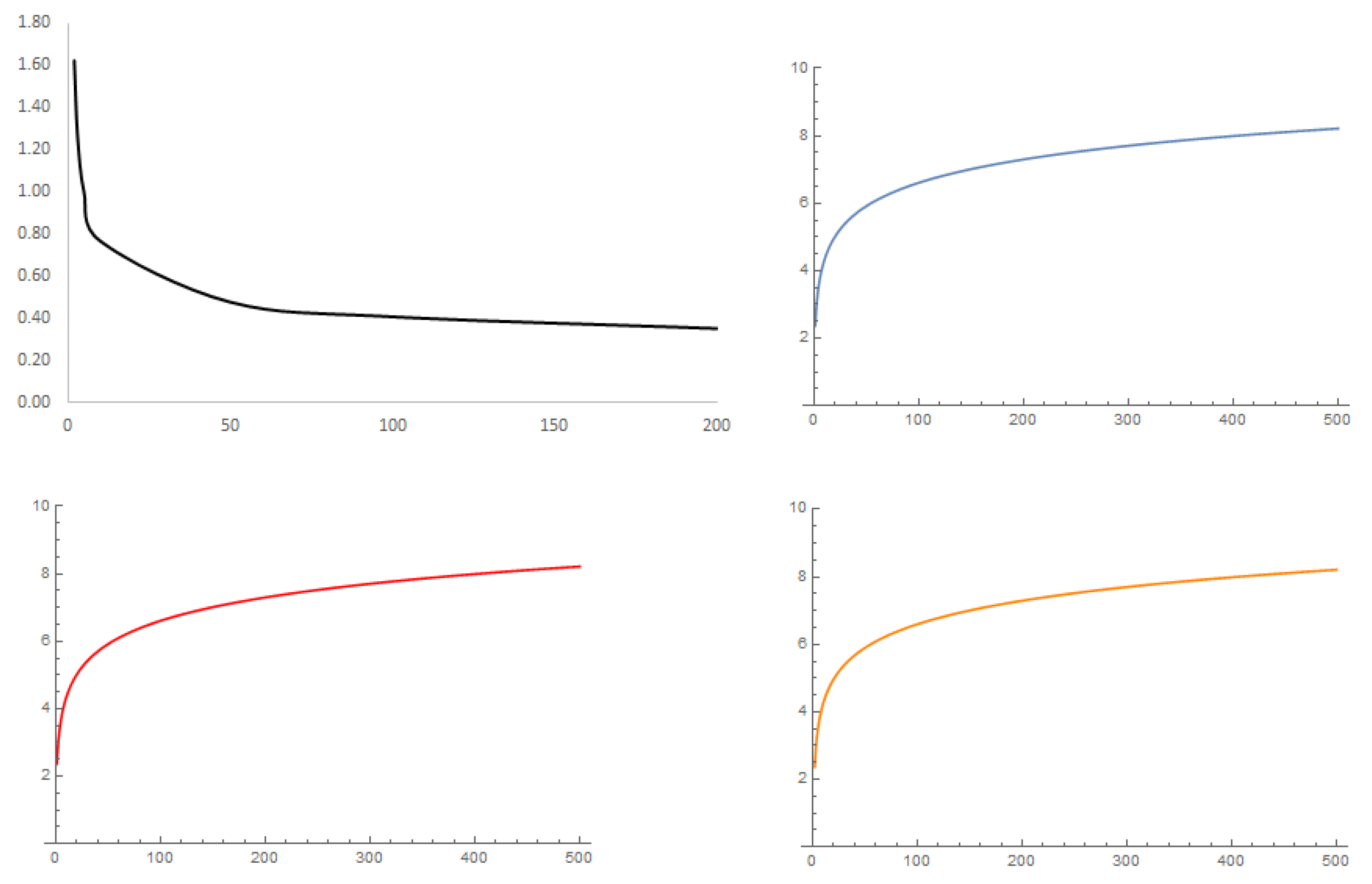
and Figure 1, respectively.

3.2. $\theta$-Expansions

For a fixed irrational $\theta \in (0,1)$, we consider a generalization of the Gauss map, $T_{\theta }:[0,\theta ]\to [0,\theta ]$ defined as

$$T_{\theta }\left(x\right):=\left\{\begin{array}{cc}{\displaystyle \frac{1}{x}-\theta ⌊\frac{1}{x\theta }⌋},\hfill & {\displaystyle \mathrm{if}x\in (0,\theta ],}\hfill \\ 0,\hfill & \mathrm{if}x=0.\hfill \end{array}\right.$$

(38)

The transformation $T_{\theta }$ is connected with the $\theta$-expansion for a number in $(0,\theta )$ as follows. The numbers $\theta ⌊\frac{1}{y\theta }⌋$ obtained by taking y successively equal to x, $T_{\theta }\left(x\right)$, $T_{\theta }^2\left(x\right)$, …, lead to the $\theta$-expansion of x as

$$x=\frac{1}{{\displaystyle {\vartheta }_1\theta +\frac{1}{{\displaystyle {\vartheta }_2\theta +\frac{1}{{\displaystyle {\vartheta }_3\theta +\ddots }}}}}}=:{[{\vartheta }_1,{\vartheta }_2,{\vartheta }_3,\dots ]}_{\theta },$$

(39)

where ${\vartheta }_n\in {\mathbb{N}}_{+}$ for all $n\in {\mathbb{N}}_{+}$. The positive integers ${\vartheta }_n={\vartheta }_n\left(x\right)={\vartheta }_1\left(T_{\theta }^{n-1}\left(x\right)\right)$, $n\in {\mathbb{N}}_{+}$, with $T_{\theta }^0\left(x\right)=x$ and ${\vartheta }_1={\vartheta }_1\left(x\right)=⌊\frac{1}{x\theta }⌋$ are called the digits of x with respect to the $\theta$-expansion in (39), and we have that the finite truncation of (39), $p_{\theta ,n}/q_{\theta ,n}:={[{\vartheta }_1,{\vartheta }_2,\dots ,{\vartheta }_n]}_{\theta }$, tends to x as $n\to \infty$.

If ${\theta }^2=1/s$, $s\in {\mathbb{N}}_{+}$, the digits ${\vartheta }_n$s take values greater or equal to s, and the transformation $T_{\theta }$ is ergodic with respect to an absolutely continuous invariant probability measure

$$G_{\theta }\left(A\right):=\frac{1}{log\left(1+{\theta }^2\right)}{\int }_A\frac{\theta \mathrm{d}x}{1+x\theta },A\in {\mathcal{B}}_{[0,1]}.$$

(40)

An n-block $({\vartheta }_1,{\vartheta }_2,\dots ,{\vartheta }_n)$ is said to be admissible for the expansion in (39) if there exists $x\in [0,\theta )$ such that ${\vartheta }_i\left(x\right)={\vartheta }_i$ for all $1\le i\le n$. If $({\vartheta }_1,{\vartheta }_2,\dots ,{\vartheta }_n)$ is an admissible sequence, we call the set

$$I_{\theta }({\vartheta }_1,{\vartheta }_2,\dots ,{\vartheta }_n)=\{x\in [0,\theta ]:{\vartheta }_1\left(x\right)={\vartheta }_1,{\vartheta }_2\left(x\right)={\vartheta }_2,\dots ,{\vartheta }_n\left(x\right)={\vartheta }_n\},$$

(41)

the nth-order cylinder.

Define ${\left(u_{\theta ,i}\right)}_{i\ge s}$ by

$$u_{\theta ,i}:[0,\theta ]\to [0,\theta ];u_{\theta ,i}\left(x\right):=\frac{1}{i\theta +x}.$$

(42)

For each $i\ge s$, $u_{\theta ,i}={\left({\left.T_{\theta }\right|}_{I_{\theta }\left(a_1\right)}\right)}^{-1}$. Let

$$u_{\theta ,{\vartheta }_1{\vartheta }_2\dots {\vartheta }_n}\left(t\right):=\left(u_{\theta ,{\vartheta }_1}\circ u_{\theta ,{\vartheta }_2}\circ \dots \circ u_{\theta ,{\vartheta }_n}\right)\left(t\right)=\frac{1}{{\displaystyle {\vartheta }_1\theta +\frac{1}{{\displaystyle {\vartheta }_2\theta +\ddots +\frac{1}{{\vartheta }_n\theta +t}}}}}.$$

(43)

We observe that $u_{\theta ,{\vartheta }_1{\vartheta }_2\dots {\vartheta }_n}={\left({\left.T_{\theta }^n\right|}_{I_{\theta }({\vartheta }_1,{\vartheta }_2,\dots ,{\vartheta }_n)}\right)}^{-1}$. Therefore,

$$I_{\theta }({\vartheta }_1,{\vartheta }_2,\dots ,{\vartheta }_n)=\{u_{\theta ,{\vartheta }_1\dots {\vartheta }_n}\left(t\right):t\in [0,\theta )\}$$

(44)

which is an interval with the endpoints $\frac{p_{\theta ,n}}{q_{\theta ,n}}$ and $\frac{p_{\theta ,n}+\theta p_{\theta ,n-1}}{q_{\theta ,n}+\theta q_{\theta ,n-1}}$. Such intervals form a partition of $[0,\theta ]$.

We now check Rényi condition (8). We use directly, without mentioning them here, some properties proved in [16]. Thus, we have

$$\frac{\left|u_{\theta ,{\vartheta }_1\dots {\vartheta }_n}^{\prime }\left(t\right)\right|}{\left|u_{\theta ,{\vartheta }_1\dots {\vartheta }_n}^{\prime }\left(r\right)\right|}={\left(\frac{q_{\theta ,n}+r{q}_{\theta ,n-1}}{q_{\theta ,n}+t{q}_{\theta ,n-1}}\right)}^2\le {\left(\frac{q_{\theta ,n}+\theta q_{\theta ,n-1}}{q_{\theta ,n}}\right)}^2\le {\left(1+{\theta }^2\right)}^2.$$

(45)

We compute the entropy $h\left(T_{\theta }\right)$ by the Rohlin’s formula (7):

$$\begin{array}{ccc}\hfill h\left(T_{\theta }\right)& =& {\int }_0^{\theta }log\left|T_{\theta }^{\prime }\left(x\right)\right|\mathrm{d}{G}_{\theta }\left(x\right)={\int }_0^{\theta }\frac{-log{x}^2}{log(1+{\theta }^2)}\frac{\theta \mathrm{d}x}{1+\theta x}\hfill \\ & =& \frac{-2\theta }{log(1+{\theta }^2)}{\int }_0^{\theta }\frac{logx}{1+\theta x}\mathrm{d}x.\hfill \end{array}$$

(46)

As examples, we have the values of $h\left(T_{\theta }\right)$ for different values of $s=1/{\theta }^2$ and the graph of $h\left(T_{\theta }\right)$ in Table 1 and Figure 1, respectively.

3.3. N-Continued Fraction Expansions

Fix an integer $N\ge 1$. The measure-theoretical dynamical system $([0,1],{\mathcal{B}}_{[0,1]},T_N,G_N)$ is defined as follows:

$$T_N:[0,1]\to [0,1];T_N\left(x\right):=\left\{\begin{array}{cc}{\displaystyle \frac{N}{x}-⌊\frac{N}{x}⌋},\hfill & \mathrm{if}x\in (0,1],\hfill \\ 0,\hfill & \mathrm{if}x=0\hfill \end{array}\right.$$

(47)

and

$$G_N\left(A\right):=\frac{1}{log\frac{N+1}{N}}{\int }_A\frac{\mathrm{d}x}{x+N},A\in {\mathcal{B}}_{[0,1]}.$$

(48)

The probability measure $G_N$ is $T_N$-invariant, and the dynamical system $([0,1],{\mathcal{B}}_{[0,1]},T_N,G_N)$ is ergodic.

For any $0<x<1$, put ${\epsilon }_1\left(x\right)=\lfloor N/x\rfloor$ and ${\epsilon }_n\left(x\right)={\epsilon }_1\left(T_N^{n-1}\left(x\right)\right)$, $n\in {\mathbb{N}}_{+}$, with $T_N^0\left(x\right)=x$. Then, every irrational $0<x<1$ can be written in the form

$${\displaystyle x=\frac{N}{{\displaystyle {\epsilon }_1+\frac{N}{{\displaystyle {\epsilon }_2+\frac{N}{{\epsilon }_3+\ddots }}}}}=:{[{\epsilon }_1,{\epsilon }_2,{\epsilon }_3,\dots ]}_N,}$$

(49)

where ${\epsilon }_n$s are non-negative integers, ${\epsilon }_n\ge N$, $n\in {\mathbb{N}}_{+}$. We call (49) the N-continued fraction expansion of x and $p_{N,n}\left(x\right)/q_{N,n}\left(x\right):={[{\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_n]}_N$ the nth-order convergent of $x\in [0,1]$. Then, $p_{N,n}\left(x\right)/q_{N,n}\left(x\right)\to x$, $n\to \infty$.

An n-block $({\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_n)$ is said to be admissible for the expansion in (49) if there exists $x\in [0,1)$ such that ${\epsilon }_i\left(x\right)={\epsilon }_i$ for all $1\le i\le n$. If $({\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_n)$ is an admissible sequence, we call the set

$$I_N({\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_n)=\{x\in [0,1]:{\epsilon }_1\left(x\right)={\epsilon }_1,{\epsilon }_2\left(x\right)={\epsilon }_2,\dots ,{\epsilon }_n\left(x\right)={\epsilon }_n\},$$

(50)

the nth-order cylinder.

Define ${\left(u_{N,i}\right)}_{i\ge N}$ by

$$u_{N,i}:[0,1]\to [0,1];u_{N,i}\left(x\right):=\frac{N}{i+x}.$$

(51)

For each $i\ge N$, $u_{N,i}={\left({\left.T_N\right|}_{I_N\left({\epsilon }_1\right)}\right)}^{-1}$. Let

$$u_{N,{\epsilon }_1{\epsilon }_2\dots {\epsilon }_n}\left(t\right):=\left(u_{N,{\epsilon }_1}\circ u_{N,{\epsilon }_2}\circ \dots \circ u_{N,{\epsilon }_n}\right)\left(t\right)=\frac{N}{{\displaystyle {\epsilon }_1+\frac{N}{{\displaystyle {\epsilon }_2+\ddots +\frac{N}{{\epsilon }_n+t}}}}}.$$

(52)

We observe that $u_{N,{\epsilon }_1{\epsilon }_2\dots {\epsilon }_n}={\left({\left.T_N^n\right|}_{I_N({\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_n)}\right)}^{-1}$. Therefore,

$$I_N({\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_n)=\{u_{N,{\epsilon }_1\dots {\epsilon }_n}\left(t\right):t\in [0,1]\}$$

(53)

which is an interval with the endpoints $\frac{p_{N,n}}{q_{N,n}}$ and $\frac{p_{N,n}+p_{N,n-1}}{q_{N,n}+q_{N,n-1}}$. Such intervals form a partition of $[0,1]$.

We now check Rényi condition (8). We use directly, without mentioning them here, some properties proved in [19]. Thus, we have

$$\frac{\left|u_{N,{\epsilon }_1\dots {\epsilon }_n}^{\prime }\left(t\right)\right|}{\left|u_{N,{\epsilon }_1\dots {\epsilon }_n}^{\prime }\left(r\right)\right|}={\left(\frac{q_{N,n}+r{q}_{N,n-1}}{q_{N,n}+t{q}_{N,n-1}}\right)}^2\le {\left(\frac{q_{N,n}+q_{N,n-1}}{q_{N,n}}\right)}^2\le {\left(\frac{N+1}{N}\right)}^2.$$

(54)

Using Rohlin’s entropy formula (7), we have:

$$\begin{array}{ccc}\hfill h\left(T_N\right)& =& {\int }_0^{1}log\left|T_N^{\prime }\left(x\right)\right|\mathrm{d}{G}_N\left(x\right)=\frac{1}{log\frac{N+1}{N}}{\int }_0^1\frac{log\left(\frac{N}{x^2}\right)}{x+N}\mathrm{d}x\hfill \\ & =& \frac{\frac{{\pi }^2}{3}+2{\mathrm{Li}}_2(N+1)+log(N+1)logN}{log\frac{N+1}{N}},\hfill \end{array}$$

(55)

where ${\mathrm{Li}}_2$ denotes the dilogarithm function, defined by

$${\mathrm{Li}}_2\left(x\right)={\int }_0^x\frac{lnt}{1-t}\mathrm{d}t\mathrm{or}{\mathrm{Li}}_2\left(x\right)=\sum _{k=1}^{\infty }\frac{x^k}{k^2}.$$

(56)

As examples, we have the values of $h\left(T_N\right)$ for different values of N and the graph of $h\left(T_N\right)$ in Table 1 and Figure 1, respectively.

3.4. Rényi-Type Continued Fraction Expansions

Fix an integer $N\ge 2$. Let the Rényi-type continued fraction transformation$R_N:[0,1]\to [0,1]$ be given by

$$R_N\left(x\right):=\left\{\begin{array}{cc}{\displaystyle \frac{N}{1-x}-⌊\frac{N}{1-x}⌋},\hfill & \mathrm{if}x\in [0,1),\hfill \\ 0,\hfill & \mathrm{if}x=1.\hfill \end{array}\right.$$

(57)

For any irrational $x\in [0,1]$, $R_N$ generates a new continued fraction expansion of x of the form

$${\displaystyle x=1-\frac{N}{{\displaystyle 1+r_1-\frac{N}{{\displaystyle 1+r_2-\frac{N}{1+r_3-\ddots }}}}}=:{[r_1,r_2,r_3,\dots ]}_R.}$$

(58)

Here, $r_n$s are non-negative integers greater than or equal to N defined by

$$r_1:=r_1\left(x\right)=⌊\frac{N}{1-x}⌋,x\ne 1;r_1\left(1\right)=\infty$$

(59)

and

$$r_n:=r_n\left(x\right)=r_1\left(R_N^{n-1}\left(x\right)\right),n\ge 2,$$

(60)

with $R_N^0\left(x\right)=x$. The sequence of rationals $\left\{p_{R,n}/q_{R,n}\right\}:={[r_1,r_2,\dots ,r_n]}_R$, $n\in {\mathbb{N}}_{+}$ are the convergents to x in $[0,1]$.

The dynamical system $\left([0,1],{\mathcal{B}}_{[0,1]},R_N,{\rho }_N\right)$ is measure preserving and ergodic, where the probability measure ${\rho }_N$ is defined by

$${\rho }_N\left(A\right):=\frac{1}{log\left(\frac{N}{N-1}\right)}{\int }_A\frac{\mathrm{d}x}{x+N-1\prime }A\in {\mathcal{B}}_{[0,1]}.$$

(61)

An n-block $(r_1,r_2,\dots ,r_n)$ is said to be admissible for the expansion in (58) if there exists $x\in [0,1)$ such that $r_i\left(x\right)=r_i$ for all $1\le i\le n$. If $(r_1,r_2,\dots ,r_n)$ is an admissible sequence, we call the set

$$I_R(r_1,r_2,\dots ,r_n)=\{x\in [0,1]:r_1\left(x\right)=r_1,r_2\left(x\right)=r_2,\dots ,r_n\left(x\right)=r_n\},$$

(62)

the nth-order cylinder.

Define ${\left(u_{R,i}\right)}_{i\ge N}$ by

$$u_{R,i}:[0,1]\to [0,1];u_{R,i}\left(x\right):=1-\frac{N}{i+x}.$$

(63)

For each $i\ge N$, $u_{R,i}={\left({\left.R_N\right|}_{I_R\left(r_1\right)}\right)}^{-1}$. Let

$$u_{R,r_1{r}_2\dots r_n}\left(t\right):=\left(u_{R,r_1}\circ u_{R,r_2}\circ \dots \circ u_{R,r_n}\right)\left(t\right)=1-\frac{N}{{\displaystyle 1+r_1-\frac{N}{{\displaystyle 1+r_2-\ddots -\frac{N}{r_n+t}}}}}.$$

(64)

We observe that $u_{R,r_1{r}_2\dots r_n}={\left({\left.R_N^n\right|}_{I_R(r_1,r_2,\dots ,r_n)}\right)}^{-1}$. Therefore,

$$I_R(r_1,r_2,\dots ,r_n)=\{u_{R,r_1\dots r_n}\left(t\right):t\in [0,1]\}$$

(65)

which is the interval $\left[\frac{p_{R,n}-p_{R,n-1}}{q_{R,n}-q_{R,n-1}},\frac{p_{R,n}}{q_{R,n}}\right)$. Such intervals form a partition of $[0,1]$.

Before applying Rohlin’s formula, we must check Rényi condition (8). We use directly, without mentioning them here, some properties proved in [20]. Thus, we have

$$\frac{\left|u_{R,r_1\dots r_n}^{\prime }\left(t\right)\right|}{\left|u_{R,r_1\dots r_n}^{\prime }\left(r\right)\right|}={\left(\frac{q_{R,n}+(r-1)q_{R,n-1}}{q_{R,n}+(t-1)q_{R,n-1}}\right)}^2\le {\left(\frac{q_{R,n}}{q_{R,n}-q_{R,n-1}}\right)}^2\le {\left(\frac{N}{N-1}\right)}^2.$$

(66)

The entropy $h\left(R_N\right)$ is given by

$$\begin{array}{ccc}\hfill h\left(R_N\right)& =& {\int }_0^{1}log\left|R_N^{\prime }\left(x\right)\right|\mathrm{d}{\rho }_N\left(x\right)=\frac{1}{log\frac{N}{N-1}}{\int }_0^1\frac{log\frac{N}{{(1-x)}^2}}{x+N-1}\mathrm{d}x\hfill \\ & =& logN+\frac{2{\mathrm{Li}}_2\left(\frac{1}{N}\right)}{log\frac{N}{N-1}},\hfill \end{array}$$

(67)

where ${\mathrm{Li}}_2$ is as in (56). As examples, we have the values of $h\left(R_N\right)$ for different values of N and the graph of $h\left(R_N\right)$ in Table 1 and Figure 1, respectively.

4. Comparing the Efficiency of Some Expansions

In this section, we apply the Extended Lochs’ theorem presented in Section 2.4 and compare two by two the expansions presented in the previous section. First, we observe that, for various values of the parameters involved, the entropies $h\left(T_{\theta }\right)$ and $h\left(T_N\right)$ are equal. Since entropy is an isomorphism invariant, we conjecture the following result.

Conjecture 1.

For an irrational$\theta \in (0,1)$and a non-negative integer$N\ge 2$with$1/{\theta }^2=N$, the transformations$T_{\theta }$in (38) and $T_N$ in (47) are isomorphic.

For this reason, we make only the following pairs: N-continued fractions and Chan’s continued fractions, N-continued fractions and Rényi-type continued fractions, and Rényi-type continued fractions and Chan’s continued fractions.

We observe that the transformations $T_N$, $T_{\ell }$ and $R_N$ satisfy the two conditions from Extended Lochs’ theorem (see Section 2.4).

4.1. N-Continued Fractions and Chan’s Continued Fractions

Let $I_N^x({\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_n)$ denote the nth-order cylinder of the N-continued fraction that contains x and $I_{\ell }^x(a_1,a_2,\dots ,a_m)$ denote the mth-order cylinder of the Chan’s continued fraction that contains x. Then,

$$m_{N\ell }(n,x):=\sup \left\{m:I_N^x({\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_n)\subset I_{\ell }^x(a_1,a_2,\dots ,a_m)\right\}$$

(68)

represents the number of digits in the Chan’s expansion of x in (25) that can be determined from knowing the first n digits in the N-continued fraction in (49). Therefore, applying (24), we have

$$\underset{n\to \infty }{lim}\frac{m_{N\ell }(n,x)}{n}=\frac{h\left(T_N\right)}{h\left(T_{\ell }\right)}$$

(69)

where $h\left(T_N\right)$ and $h\left(T_{\ell }\right)$ are as in (55) and (37), respectively. Given the values in Table 1, we observe that N-continued fraction expansion is more effective than Chan’s continued fraction expansion regardless of the values taken by the parameters N and ℓ, respectively.

As examples, we have,

$$\underset{n\to \infty }{lim}\frac{m_{12}(n,x)}{n}=1.462571953\dots \mathrm{or}\underset{n\to \infty }{lim}\frac{m_{32}(n,x)}{n}=2.001164812\dots$$

(70)

Thus, roughly, if we approximate a number from the unit interval by keeping the first 1000 digits of the N-continued fraction expansion, to retain the same degree of accuracy, we need to keep about 1462 digits in the Chan’s continued fraction expansion.

4.2. N-Continued Fractions and Rényi-Type Continued Fractions

Let $I_N^x({\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_n)$ denote the nth-order cylinder of the N-continued fraction that contains x and $I_R^x(r_1,r_2,\dots ,r_m)$ denote the mth-order cylinder of the Rényi-type continued fraction that contains x. Then,

$$m_{NR}(n,x):=\sup \left\{m:I_N^x({\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_n)\subset I_R^x(r_1,r_2,\dots ,r_m)\right\}$$

(71)

represents the number of digits in the Rényi-type continued fraction of x in (58) that can be determined from knowing the first n digits in the N-continued fraction in (49). Therefore, applying (24), we have

$$\underset{n\to \infty }{lim}\frac{m_{NR}(n,x)}{n}=\frac{h\left(T_N\right)}{h\left(R_N\right)}$$

(72)

where $h\left(T_N\right)$ and $h\left(R_N\right)$ are as in (55) and (67), respectively. Given the values in Table 1, we observe that N-continued fraction expansion is more effective than Rényi-type continued fraction expansion regardless of the values taken by the parameter N.

We notice that $h\left(T_1\right)=h\left(R_2\right)$. We also have

$$\underset{n\to \infty }{lim}\frac{m_{33}(n,x)}{n}=1.117745267\dots \mathrm{or}\underset{n\to \infty }{lim}\frac{m_{55}(n,x)}{n}=1.057649623\dots$$

(73)

As N grows, the entropies are very close, which means that the efficiency of the two continued fraction expansions are about the same.

4.3. Rényi-Type Continued Fractions and Chan’s Continued Fractions

Let $I_R^x(r_1,r_2,\dots ,r_n)$ denote the nth-order cylinder of the Rényi-type continued fraction that contains x and $I_{\ell }^x(a_1,a_2,\dots ,a_m)$ denote the mth-order cylinder of the Chan’s continued fraction that contains x. Then,

$$m_{R\ell }(n,x):=\sup \left\{m:I_R^x(r_1,r_2,\dots ,r_n)\subset I_{\ell }^x(a_1,a_2,\dots ,a_m)\right\}$$

(74)

represents the number of digits in the Chan’s continued fraction of x in (25) that can be determined from knowing the first n digits in the Rényi-type continued fraction in (58). Therefore, applying (24), we have

$$\underset{n\to \infty }{lim}\frac{m_{R\ell }(n,x)}{n}=\frac{h\left(R_N\right)}{h\left(T_{\ell }\right)}$$

(75)

where $h\left(R_N\right)$ and $h\left(T_{\ell }\right)$ are as in (67) and (37), respectively. Given the values in Table 1, we observe that Rényi-type continued fraction expansion is more effective than Chan’s continued fraction expansion regardless of the values taken by the parameters N and ℓ, respectively.

As examples, we have,

$$\underset{n\to \infty }{lim}\frac{m_{22}(n,x)}{n}=1.462571953\dots \mathrm{or}\underset{n\to \infty }{lim}\frac{m_{23}(n,x)}{n}=1.871930586\dots$$

(76)

5. Final Remarks

N-continued fractions are more efficient than Rényi-type continued fractions at representing a number in the unit interval. Since the entropies are $h\left(T_N\right)\ge 2.37314$ for $N\ge 1$, $h\left(R_N\right)\ge 2.37314$ for $N\ge 2$ and $h\left(T_G\right)={\pi }^2/(6log2)=2.37314$, it follows that N-continued fractions and Rényi-type continued fractions are more efficient than regular continued fractions (RCFs). Since the entropy is $h\left(T_{\ell }\right)\le 1.62258$ for $\ell \ge 2$, it follows that RCFs are more efficient than Chan’s continued fractions. Thus, N-continued fractions are the most efficient at representing a number in the unit interval, with a very close efficiency being Rényi-type continued fractions.

Our paper is a systematic presentation of continued fraction expansions that have been investigated by us during the last ten years. Having always in view the classical RCF expansion, we consider some interval maps that generate expansions and that admit an invariant density with suitable ergodic properties. However, these ergodic properties, recently studied, are not enough to yield rates of convergence for mixing properties. For this a Gauss–Kuzmin-type theorem is needed. There are still many open questions closely related to this problem. On the other hand, to extend our references list [14,15,16,17,18,19,20,21,22], we consider the opportunity of starting new investigations such as the efficiency of pairs of maps for which the generating partition has finite entropy. In these circumstances, we review sufficient conditions on the latter to belong to a class of number-theoretic fibered maps for which the generating partition has finite entropy.