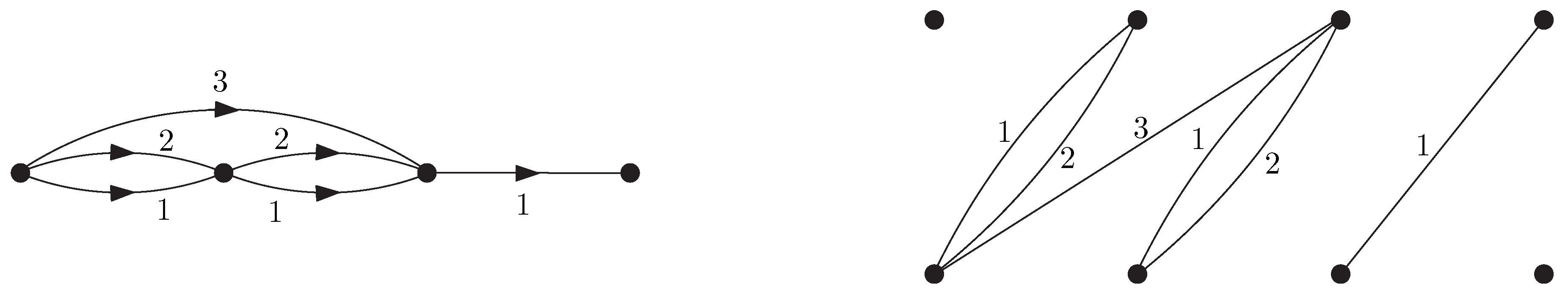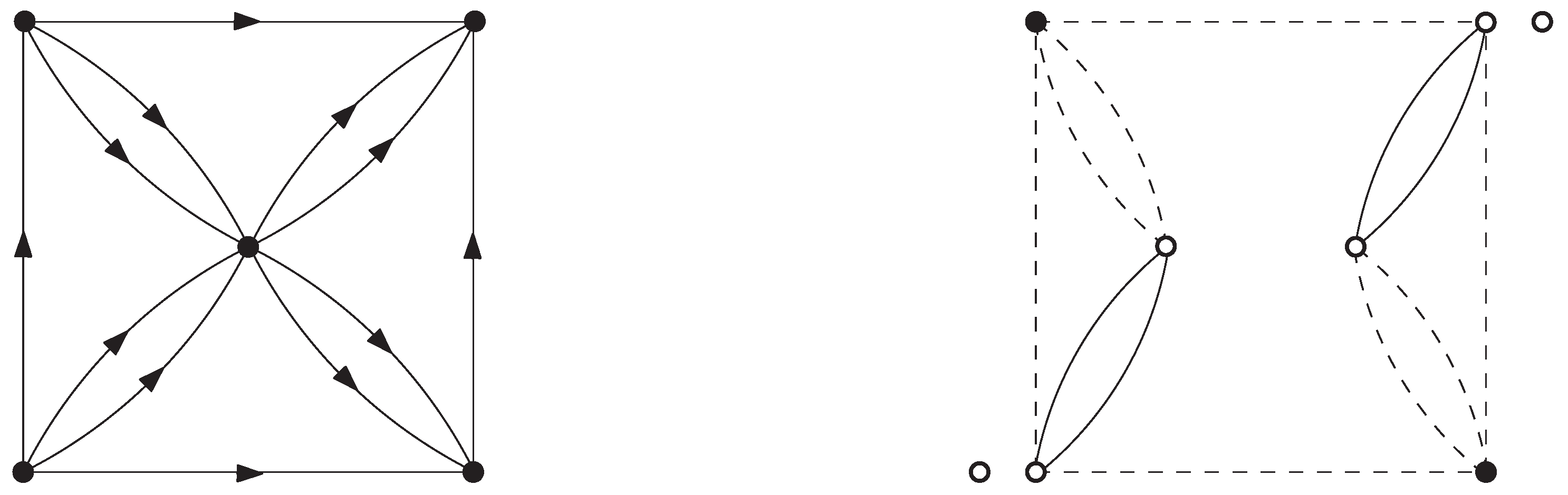Some Remarks on Odd Edge Colorings of Digraphs

Abstract

The principal aim of this article is to initiate a study of the following coloring notion for digraphs. An odd k-edge coloring of a general digraph (directed pseudograph) D is a (not necessarily proper) coloring of its edges with at most k colors such that for every vertex v and color c holds: if c is used on the set ${\partial }_D\left(v\right)$ of edges incident with v, then c appears an odd number of times on each non-empty set from the pair ${\partial }_D^{+}\left(v\right),{\partial }_D^{-}\left(v\right)$ of, respectively, outgoing and incoming edges incident with v. We show that it can be decided in polynomial time whether D admits an odd 2-edge coloring. Throughout the paper, several conjectures, questions and open problems are posed. In particular, we conjecture that for each odd edge-colorable digraph four colors suffice.

1. Introduction

Throughout the article, we follow general terminology and notation from [1]. All considered graphs and digraphs are finite. Loops, parallel edges and parallel arcs are admissible, i.e., strictly speaking, we consider the general setup of pseudographs and directed pseudographs, but to avoid lengthy terminology, we refer to them as ‘graphs’ and ‘digraphs’, respectively.

As introduced in [2], an odd edge coloring of a graph G is a (not necessarily proper) coloring of its edges such that every color class induces a graph in which all vertices are of odd degree. An odd edge coloring of G that uses at most k colors is an odd k-edge coloring. Then, G is said to be odd k-edge-colorable. Recently, Kano, Katona and Varga [3] characterized the family of graphs that are odd 2-edge-colorable, and gave a polynomial time algorithm that finds such a coloring or shows its non-existence. The purpose of this short article is to discuss the analogous coloring notion for digraphs.

General terminology, notation and facts.

If X and Y are (not necessarily disjoint) sets of vertices of a graph G, we denote by $E_G[X,Y]$ the set of edges of G with one end in X and the other end in Y, and by $e_G(X,Y)$ its cardinality. A graph G is connected if for every partition of its vertex set l$V\left(G\right)$ into two non-empty sets X and Y, it holds that $E_G[X,Y]\ne \varnothing$. The maximal connected subgraphs of a graph are called its components. The problem of determining the components is solvable in linear time (see [4]).

Given a graph G and an even-sized subset T of $V\left(G\right)$, a T-join of G is a spanning subgraph H such that $d_H\left(v\right)$, the degree of v in regard to H, is odd for all $v\in T$ and even for all $v\in V\left(G\right)\setminus T$. Observe that for another even-sized subset S of $V\left(G\right)$, the symmetric difference of a T-join and an S-join is clearly a $T\oplus S$-join. From this it readily follows that if G is connected, then it admits a T-join, and a T-join of G can always be found in polynomial time (see [5]). In particular, every even-ordered connected graph G contains an odd factor (i.e., a $V\left(G\right)$-join).

An edge coloring of a graph G (resp. digraph D) with color set S is an assignment $E\left(G\right)\to S$ (resp. $A\left(D\right)\to S$). Every T-join of G can be interpreted as an edge coloring with color set $\{1,2\}$ such that 1 is used an odd number of times at each $v\in T$ and an even number of times (possibly zero) at each $v\in V\left(G\right)\setminus T$; color class 1 forms the edge set of the T-join.

Given a digraph D and a vertex $v\in V\left(D\right)$, the size of the set ${\partial }_D^{-}\left(v\right)$, of ingoing edges at v, (resp. ${\partial }_D^{+}\left(v\right)$, of outgoing edges at v,) is the in-degree $d_D^{-}\left(v\right)$ (resp. out-degree $d_D^{+}\left(v\right)$) of the vertex v; we call each of ${\partial }_D^{-}\left(v\right)$ and ${\partial }_D^{+}\left(v\right)$ (resp. $d_D^{-}\left(v\right)$ and $d_D^{+}\left(v\right)$) a semi-cut (resp. semi-degree) of v. Since loops are allowed, let us clarify that ${\partial }_D^{-}\left(v\right)\cap {\partial }_D^{+}\left(v\right)$ constitutes the set of loops at v; in other words, any loop at vertex v contributes 1 to each semi-degree of v, i.e., strictly speaking $d_D^{-}\left(v\right)$ and $d_D^{+}\left(v\right)$ are the semi-pseudodegrees of v (the in-pseudodegree and out-pseudodegree, respectively). The sum $d_D\left(v\right)=d_D^{-}\left(v\right)+d_D^{+}\left(v\right)$ is the degree of v; a vertex of degree 0 is said to be isolated. Given a non-isolated vertex v, if $d_D^{-}\left(v\right)=0$ (resp. $d_D^{+}\left(v\right)=0$), then v is a source (resp. sink) of D. Any source or sink is a peripheral vertex of D, whereas a non-isolated vertex that is neither a source nor a sink is an internal vertex.

The split (or bipartite representation), $\mathrm{BG}\left(D\right)$, of a digraph D is the bipartite graph G whose partite sets $V^{+}$, $V^{-}$ are copies of $V\left(D\right)$. For each $v\in V\left(D\right)$, there is one vertex $v^{+}\in V^{+}$ and one $v^{-}\in V^{-}$. For each $uv$-arc in D, there is an edge with endpoints $u^{+}$ and $v^{-}$ in G. Hence, the degrees of the vertices $v^{+}$, $v^{-}$ in the split of D are precisely the out-degree and in-degree of v in D, respectively; the pair $(v^{+},v^{-})$ is obtained by splitting v in regard to D. The re-identification of each such pair $(v^{+},v^{-})$ (into v) results in the so-called underlying graph of D. Furthermore, any balanced bipartite graph G is a split of some digraph D, i.e., can be ‘transformed’ into D by reversing the described procedure.

Other way around, any graph G can be regarded as a digraph $D\left(G\right)$, by replacing each of its edges by two oppositely oriented arcs with the same ends (each loop of G gives rise to two directed loops on the same vertex); this digraph is the associated digraph of G. One may also obtain a digraph D from a graph G by replacing each edge by one arc on the same endpoints; such a digraph D is an orientation of G. Conversely, the underlying graph $G\left(D\right)$ of a digraph D is obtained by ‘forgetting orientation’.

2. Basic Definitions and Questions

In the realm of digraphs D, two options come to mind for the definition of the notion ‘odd edge coloring’. Initially, one may be tempted of obtaining a ‘directed version’ of this coloring notion by requiring that for every vertex $v\in V\left(D\right)$ and every color c it holds:

$\left({\mathcal{O}}^{\prime }\right).$On every semi-cut of v that uses c, color c appears an odd number of times.

However, the above ‘definition’ fails to capture the essence of digraphs since it basically ignores the fact that arc sets ${\partial }_D^{-}\left(v\right)$ and ${\partial }_D^{+}\left(v\right)$ are incident with a common vertex (namely v). Actually, a moment’s thought reveals that if we decide to adopt the above ‘definition’, then this coloring notion for digraphs would be merely a ‘disguise’ of odd edge coloring of bipartite graphs with equally sized partite sets. Indeed, it is readily seen that an edge coloring of D satisfies the condition $\left({\mathcal{O}}^{\prime }\right)$ if and only if the associated edge coloring on $\mathrm{BG}\left(D\right)$ is odd.

Before we introduce a (more appropriate) definition of odd edge coloring of digraphs, let us return briefly to graphs to gain further insight. If a graph G admits an odd edge coloring, then the odd chromatic index of G, ${\chi }_o^{\prime }\left(G\right)$, is the minimum integer k for which G is odd k-edge-colorable. Necessary and sufficient for odd edge-colorability of graph G is that there are no vertices incident only to loops. Apart from this, loops have no other influence on the existence or value of ${\chi }_o^{\prime }\left(G\right)$. Along with the introduction of this coloring notion, Pyber [2] studied the odd edge-colorability of simple graphs and proved the following result.

Theorem 1.

(Pyber, 1991) Every simple graph G is odd 4-edge-colorable.

In view of the graph $W_4$, wheel on four spokes, which does not admit an odd 3-edge coloring, the bound ${\chi }_o^{\prime }\left(G\right)\le 4$ is tight for the class of simple graphs G. As further support to this bound, Matrai [6] described a construction of an infinite family of connected simple graphs with odd chromatic index equal to 4.

Moving to the larger class of loopless graphs, the upper bound of 4 (colors) for the odd chromatic index does not hold anymore. Indeed, the second graph in Figure 1 below requires as much as six colors for an odd edge coloring, whereas the first requires five colors. The easiest way to see this is by noting that these two graphs are examples (the smallest ones) of loopless graphs on three pairwise adjacent vertices such that at most one bouquet (the complete set of parallel edges on a pair of vertices) is odd-sized. Every such graph belongs to the family of so-called Shannon triangles; in particular, we speak of a Shannon triangle of type $(2,2,1)$ (resp. $(2,2,2)$) if one (resp. none) of its bouquets is odd-sized.

The main result in [7] states that every connected loopless graph G admits an odd 6-edge coloring; moreover, six colors are necessary if and only if G is a Shannon triangle of type $(2,2,2)$. Recently, the following improvement was given in [8].

Theorem 2.

A connected loopless graph G is odd 4-edge-colorable if and only if it is not a Shannon triangle of type $(2,2,1)$ or $(2,2,2)$.

In view of the existing connection between condition $\left({\mathcal{O}}^{\prime }\right)$ for arbitrary digraph D and the associated edge coloring of its split $\mathrm{BG}\left(D\right)$, the following result is a straightforward consequence of Theorem 2.

Corollary 1.

Every digraph D admits a 4-edge coloring that satisfies condition $\left({\mathcal{O}}^{\prime }\right)$.

A more appropriate definition of the notion ‘odd edge coloring’ for digraphs, the one we shall adopt in this study, is obtained through the following reasoning. Any graph G can be seen as a digraph, namely the associated digraph $D=D\left(G\right)$. In the obvious fashion, every edge coloring $\phi$ of G can be interpreted as an edge coloring ${\phi }_D$ of $D\left(G\right)$. Notice that if $\phi$ is odd then ${\phi }_D$ satisfies a stronger requirement than the one posed with condition $\left({\mathcal{O}}^{\prime }\right)$. Indeed, for every vertex $v\in V\left(D\right)$ and every color c it holds that:

$\left(\mathcal{O}\right).$If the cut ${\partial }_D\left(v\right)$ uses c, then c appears an odd number of times on each non-empty semi-cut of v.

In case v is a sink (resp. source) of a given digraph D, each of the requirements $\left({\mathcal{O}}^{\prime }\right)$ and $\left(\mathcal{O}\right)$ amounts to the appearance of c an odd number of times on the incut ${\partial }_D^{-}\left(v\right)$ (resp. outcut ${\partial }_D^{+}\left(v\right)$). 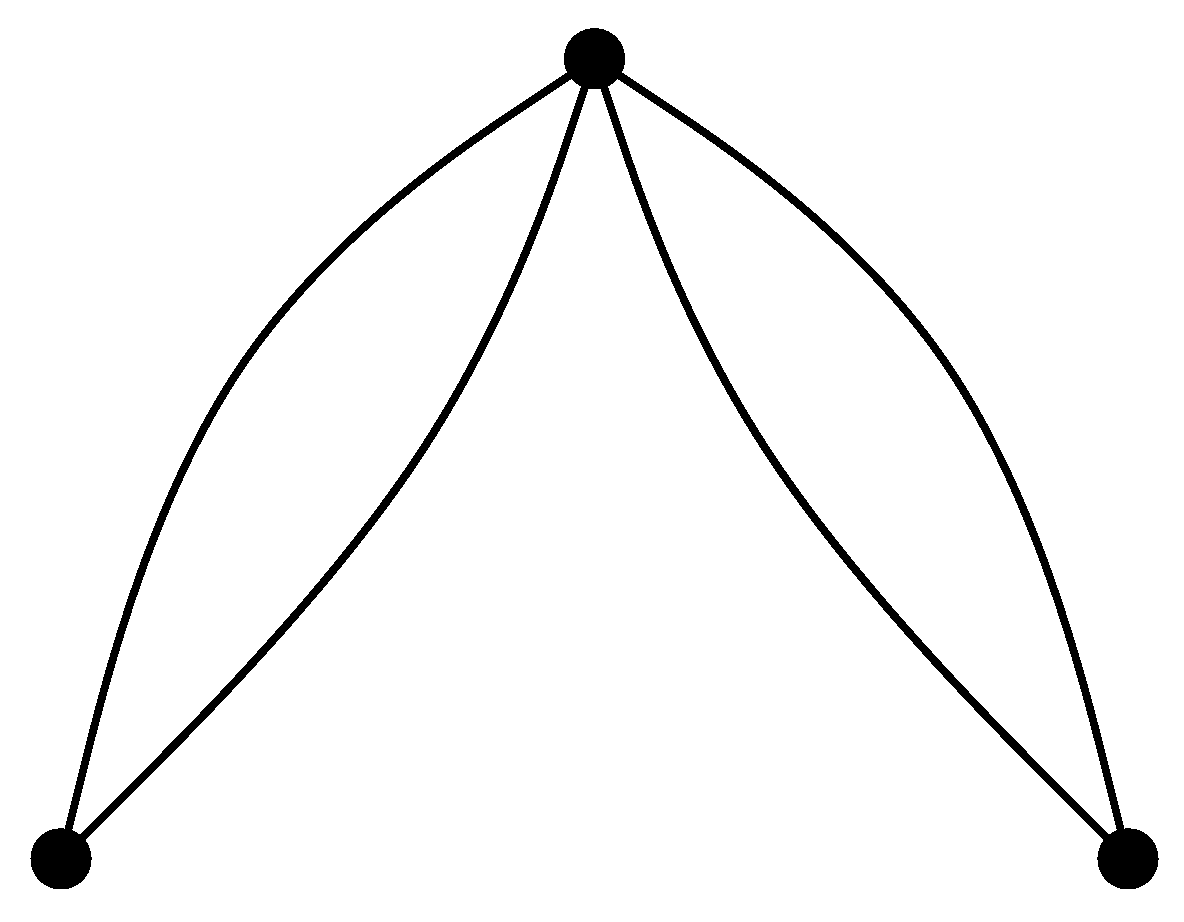The difference between the former and the latter requirement is reflected at the internal vertices of D. For example, the edge coloring of the digraph depicted in Figure 2 meets the former, but fails to meet the later requirement. In fact, this digraph does not admit an edge coloring that fulfills the latter requirement, i.e., presents an example of a digraph which is not odd edge-colorable.

An obvious necessary condition for odd edge-colorability of a digraph D is that for each internal vertex $v\in V\left(D\right)$ the degree $d_D\left(v\right)$ is even; call every such digraph internally even. However, the digraph D from Figure 2, although internally even, fails to be odd edge-colorable. Perhaps the reason for this failure lies in the fact that D contains a vertex v with distinct semi-degrees, i.e., $d_D^{-}\left(v\right)\ne d_D^{+}\left(v\right)$, such that $1\le min\{d_D^{-}\left(v\right),d_D^{+}\left(v\right)\}\le 2$. 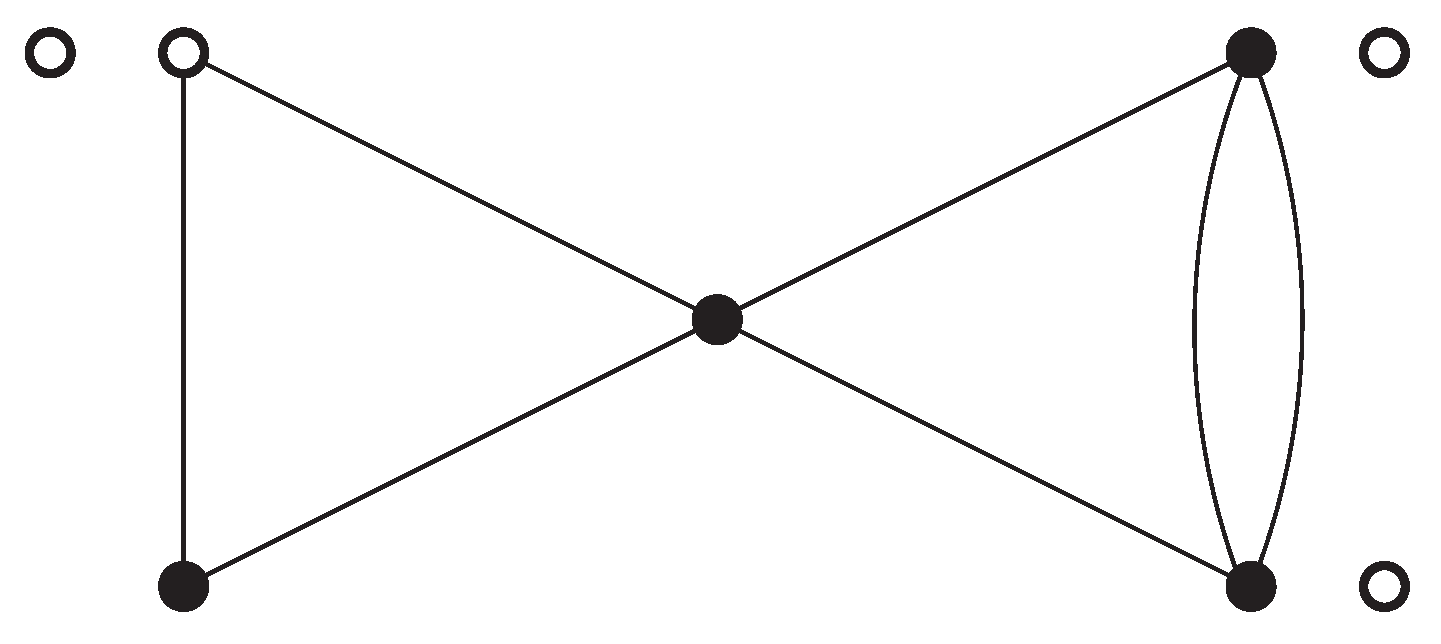Call such (internal) vertices deficient. Another example of an internally even digraph that is not odd edge-colorable (by virtue of containing a deficient vertex) is given on the left in Figure 3.

We are tempted to pose the following.

Conjecture 1.

Every internally even digraph that is free of deficient vertices admits an odd edge coloring.

If a given digraph D is odd edge-colorable, then the minimum number of colors in an odd edge coloring of D is the odd chromatic index, denoted ${\chi }_{\mathrm{o}}^{\prime }\left(D\right)$. An odd edge coloring of D using at most k colors is referred to as an odd k-edge coloring, and any such D is said to be odd k-edge-colorable. Hence, ${\chi }_{\mathrm{o}}^{\prime }\left(D\right)$ is the minimum k for which D is odd k-edge-colorable. Recall that in the realm of graphs the odd chromatic index is bounded (by 6). A natural question that comes to mind is whether this remains true for digraphs. In view of Corollary 1, we believe the following holds.

Conjecture 2.

For every odd edge-colorable digraph D it holds that${\chi }_{\mathrm{o}}^{\prime }\left(D\right)\le 4$.

Notice that if true, the conjectured bound cannot be improved. Indeed, the digraph depicted on the right in Figure 3 has odd chromatic index equal to 4.

We end this section with an easy result about associated digraphs that supports Conjecture 2.

Proposition 1.

Given a connected graph G, it holds that

$${\chi }_{\mathrm{o}}^{\prime }\left(D\left(G\right)\right)\le 4.$$

(1)

Moreover, equality is achieved for every:

$\left(a\right)$

Shannon triangle G of type $(2,2,1)$ that contains a bouquet of size 1;

$\left(b\right)$

bipartite graph G with ${\chi }_{\mathrm{o}}^{\prime }\left(G\right)=4$.

Proof. 

If the order of G is 1, let k be its size. Assuming $k>0$, the arc set of $D\left(G\right)$ consists of $2k$ directed loops. Color $2k-1$ of these loops by 1, and the remaining one by 2. This clearly gives an odd 2-edge coloring of $D\left(G\right)$.

Let the order of G be greater than 1. Observe that every odd k-edge coloring of G readily gives an odd k-edge coloring of $D\left(G\right)$: indeed, if a $vw$-edge of G (vertices v and w being not necessarily distinct) is colored by c, then color the corresponding $vw$-arc and $wv$-arc of $D\left(G\right)$ by c as well. Consequently, ${\chi }_{\mathrm{o}}^{\prime }\left(D\left(G\right)\right)\le {\chi }_{\mathrm{o}}^{\prime }\left(G\right)$. Therefore, as no loop in G influences the value of ${\chi }_o^{\prime }\left(G\right)$, we may use Theorem 2 to conclude that $D\left(G\right)$ is surely odd 4-edge-colorable if G is not a Shannon triangle of type $(2,2,1)$ or $(2,2,2)$. Let us consider now the two ‘excepted’ types of Shannon triangles.

First, assume G is a Shannon triangle of type $(2,2,1)$. We show that ${\chi }_o^{\prime }\left(D\left(G\right)\right)$ equals 4 or 3 depending on whether a bouquet of size 1 exists or not in G. Let $V\left(G\right)=\{u,v,w\}$ so that the bouquet ${\mathcal{B}}_{vw}$ is odd-sized, and consider the split $\mathrm{BG}\left(D\right(G\left)\right)$ (c.f. Figure 4, where each pair of dots depicts an arbitrary even number, including zero, of parallel edges).

• Beginning with the case when $|{\mathcal{B}}_{vw}|=1$, suppose that ${\chi }_{\mathrm{o}}^{\prime }\left(D\left(G\right)\right)\le 3$. Equivalently, our supposition is that $\mathrm{BG}\left(D\right(G\left)\right)$ admits an odd 3-edge coloring such that for each vertex $x\in V\left(G\right)$ the same set of colors is used at $x^{+}$ and $x^{-}$. Then, as the vertices $u^{+},u^{-}$ are of even degree in $\mathrm{BG}\left(D\right(G\left)\right)$, precisely two colors, say 1 and 2, are used at each of them. Upon symmetry, we may assume that each of the colors 1 and 2 appears an odd number of times on the bouquet ${\mathcal{B}}_{u^{-}{w}^{+}}$. Consequently, as ${\mathcal{B}}_{v^{+}{w}^{-}}$ is a 1-bouquet, it must be that ${\mathcal{B}}_{u^{-}{v}^{+}}$ is monochromatic, say colored entirely by 1. Therefore, only color 1 is used at $v^{+}$; thus, only color 1 is used at $v^{-}$ as well. However, then surely the edge $v^{-}{w}^{+}$ is colored by 1, which in turn implies that color 1 appears an even (positive) number of times at $w^{+}$, a contradiction. This yields the inequality ${\chi }_{\mathrm{o}}^{\prime }\left(D\left(G\right)\right)\ge 4$. On the other hand, an odd 4-edge coloring of $D\left(G\right)$ is easily obtained via the following odd 4-edge coloring of $\mathrm{BG}\left(D\right(G\left)\right)$: color ${\mathcal{B}}_{u^{-}{v}^{+}}$ by 1 and 2 such that each of the two colors is used an odd number of times; in the same manner color ${\mathcal{B}}_{u^{-}{w}^{+}}$ by 3 and 4, ${\mathcal{B}}_{u^{+}{w}^{-}}$ by 1 and 4, and ${\mathcal{B}}_{u^{+}{v}^{-}}$ by 2 and 3; finish by coloring $v^{+}{w}^{-}$ with 3 and $v^{-}{w}^{+}$ with 1.
• Let us now consider the case when $|{\mathcal{B}}_{vw}|\ge 3$ (the split of $D\left(G\right)$ is depicted on the right in Figure 4). This time, an odd 3-edge coloring of $D\left(G\right)$ can be easily constructed. Indeed, looking at $\mathrm{BG}\left(D\right(G\left)\right)$ once again, color as follows: for ${\mathcal{B}}_{v^{+}{w}^{-}}$ use each of the colors $1,2,3$ an odd number of times; on ${\mathcal{B}}_{v^{-}{w}^{+}}$ use only color 3; for each of the bouquets ${\mathcal{B}}_{u^{-}{w}^{+}}$ and ${\mathcal{B}}_{u^{+}{v}^{-}}$ use both the colors 1 and 2 an odd number of times; finally, color ${\mathcal{B}}_{u^{-}{v}^{+}}$ and ${\mathcal{B}}_{u^{+}{w}^{-}}$ with 1. Suppose ${\chi }_{\mathrm{o}}^{\prime }\left(D\left(G\right)\right)\le 2$. Then $\mathrm{BG}\left(D\right(G\left)\right)$ would surely admit an odd 2-edge coloring. However, under such a coloring, the edge collection ${\mathcal{B}}_{u^{-}{v}^{+}}\cup {\mathcal{B}}_{v^{+}{w}^{-}}\cup {\mathcal{B}}_{w^{-}{u}^{+}}$ would have to be monochromatic, and the same would have to hold for the edge collection ${\mathcal{B}}_{u^{-}{w}^{+}}\cup {\mathcal{B}}_{w^{+}{v}^{-}}\cup {\mathcal{B}}_{v^{-}{u}^{+}}$. However, this would contradict the coloring being odd (at $u^{+}$ and $u^{-}$).

Next, assume G is a Shannon triangle of type $(2,2,2)$. We show that ${\chi }_o^{\prime }\left(D\left(G\right)\right)$ equals 2. Indeed, as $\mathrm{BG}\left(D\right(G\left)\right)$ is a Euler graph of even order, take an odd factor H of $\mathrm{BG}\left(D\right(G\left)\right)$, color $E\left(H\right)$ by 1 and color the rest of $E\left(\mathrm{BG}\right(D\left(G\right)\left)\right)$ by 2. The corresponding 2-edge coloring of $D\left(G\right)$ is clearly odd. This settles the ‘inequality part’ of the statement of Proposition 1 and confirms the sufficiency of condition $\left(a\right)$ for equality in (1).

In regard to the sufficiency of condition $\left(b\right)$ for equality in (1), taking into account the fact that the inequality ${\chi }_{\mathrm{o}}^{\prime }\left(D\left(G\right)\right)\le {\chi }_{\mathrm{o}}^{\prime }\left(G\right)$ holds in general, it clearly suffices to show that every bipartite graph G satisfies ${\chi }_{\mathrm{o}}^{\prime }\left(D\left(G\right)\right)={\chi }_{\mathrm{o}}^{\prime }\left(G\right)$. We prove the last equality by showing that ${\chi }_{\mathrm{o}}^{\prime }\left(D\left(G\right)\right)\ge {\chi }_{\mathrm{o}}^{\prime }\left(G\right)$. Start by observing that $\mathrm{BG}\left(D\right(G\left)\right)=G⊍G$, i.e., $\mathrm{BG}\left(D\right(G\left)\right)$ consists of two vertex-disjoint copies of G. Indeed, if $G=G[V_1,V_2]$ then by the definition of the notion ‘split of digraph’, we have that $\mathrm{BG}\left(D\left(G\right)\right)=G[V_1^{+},V_2^{-}]⊍G[V_1^{-},V_2^{+}]$. Thus, ${\chi }_o^{\prime }\left(\mathrm{BG}\left(D\left(G\right)\right)\right)={\chi }_o^{\prime }\left(G\right)$. Also note that for any given digraph D, as each odd k-edge coloring of D naturally induces an odd k-edge coloring of $\mathrm{BG}\left(D\right)$, it holds that ${\chi }_o^{\prime }\left(\mathrm{BG}\left(D\right)\right)\le {\chi }_o^{\prime }\left(D\right)$. Consequently, we deduce the desired inequality ${\chi }_o^{\prime }\left(D\left(G\right)\right)\ge {\chi }_o^{\prime }\left(G\right)$. □

In view of Proposition 1, we are tempted to ask whether the given sufficient conditions for equality in (1) might turn out to be necessary as well.

Question 1.

For a connected non-bipartite graph G, does${\chi }_{\mathrm{o}}^{\prime }\left(D\left(G\right)\right)=4$amount to G being a Shannon triangle of type$(2,2,1)$containing a bouquet of size 1?

We end this section by noting that there are plenty of bipartite graphs with odd chromatic index equal to 4.

Proposition 2.

Given an odd integer $n\ge 3$, there exists a connected bipartite graph G of order n such that ${\chi }_{\mathrm{o}}^{\prime }\left(G\right)=4$.

Proof. 

The graph depicted in Figure 5 proves our point if $n=3$.

Assuming there is a bipartite graph G of order n that meets all requirements, apply the following construction: select an edge $e\in E\left(G\right)$, replace it with a path $P_e$ of length 3 and then add an edge parallel to the internal edge of $P_e$. The obtained graph H is clearly connected, bipartite, and of order $n+2$. Moreover, it holds that ${\chi }_o^{\prime }\left(H\right)={\chi }_o^{\prime }\left(G\right)$. Indeed, denote $K=H\left[E\right(H)\setminus E(G\left)\right]$, i.e., $H=(G-e)\cup K$. As ${\chi }_o^{\prime }\left(K\right)=1$, we have ${\chi }_o^{\prime }\left(H\right)\le {\chi }_o^{\prime }\left(G\right)$. In view of Theorem 2, the reversed inequality follows by observing that in any odd 3-edge coloring of K the two pendant edges are colored the same. □

3. Odd 2-Edge-Colorability of Digraphs

In this section, we consider the following decision problem: Given an internally even digraph, find out whether it admits an odd 2-edge coloring. We shall show that this problem is always solvable in polynomial time, and in the affirmative case such a coloring can be efficiently found. Our solution makes use of a graph construction defined as follows.

The partial split, $\mathrm{PS}\left(D\right)$, of given digraph D is a graph obtained by splitting (regarding D) only those vertices $v\in V\left(D\right)$ for which at least one semi-degree is even (including zero), and then forgetting orientation. In other words, $\mathrm{PS}\left(D\right)$ is the graph obtained from $\mathrm{BG}\left(D\right)$ by re-identifying each pair $(u^{+},u^{-})$ for which both $d_D^{+}\left(u\right)$ and $d_D^{-}\left(u\right)$ are odd (c.f. Figure 6). In particular, if no vertex of D has only odd-sized semi-cuts, then $\mathrm{PS}\left(D\right)$ is the same graph as the split $\mathrm{BG}\left(D\right)$; contrarily, if every non-isolated vertex of D has only odd-sized semi-cuts, then $\mathrm{PS}\left(D\right)$ is the same as the underlying graph $G\left(D\right)$. However, in general, these three graphs related to D differ from each other.

We distinguish between two types of vertices in $\mathrm{PS}\left(D\right)$ inducing a 2-partition $\{V^{\prime },V^{″}\}$ of $V\left(\mathrm{PS}\right(D\left)\right)$:

• the first type of vertices, constituting $V^{\prime }$, are the members u of $V\left(D\right)\cap V\left(\mathrm{PS}\right(D\left)\right)$, i.e., the vertices u of D with odd semi-degrees $d_D^{+}\left(u\right),d_D^{-}\left(u\right)$, and the members v of $V\left(\mathrm{PS}\right(D\left)\right)\setminus V\left(D\right)$ that have odd degree $d_{\mathrm{PS}\left(D\right)}\left(v\right)$;
• the second type of vertices, forming $V^{″}$, are the members w of $V\left(\mathrm{PS}\right(D\left)\right)\setminus V\left(D\right)$ that have even degree $d_{\mathrm{PS}\left(D\right)}\left(w\right)$.

Let us use the partial split $\mathrm{PS}\left(D\right)$ from Figure 6 to exemplify the 2-partition $\{V^{\prime },V^{″}\}$ of $V\left(\mathrm{PS}\right(D\left)\right)$: in Figure 7 below the vertices comprising $V^{\prime }$ are depicted as black, whereas those forming $V^{″}$ are white.

Notice that for an internally even digraph D, each vertex $x\in V\left(D\right)\setminus V\left(\mathrm{PS}\right(D\left)\right)$ gives rise to two vertices $x^{+}$ and $x^{-}$ in $\mathrm{PS}\left(D\right)$ such that either both $x^{+},x^{-}\in V^{″}$ or one of them belongs to $V^{\prime }$ and the other one is an isolated vertex belonging to $V^{″}$.

For simplicity of presentation, we shall employ the following ad-hoc notation:

• let $\mathcal{X}$ be the set of components of $\mathrm{PS}\left(D\right)\left[V^{\prime }\right]$, and
• let $\mathcal{Y}$ be the set of components of $\mathrm{PS}\left(D\right)\left[V^{″}\right]$ that are not isolated vertices of $\mathrm{PS}\left(\mathrm{D}\right)$.

For example, the digraph D from Figure 6 clearly has $\left|\mathcal{X}\right|=\left|\mathcal{Y}\right|=1$ (c.f. Figure 7 once again); moreover, for the unique members $X\in \mathcal{X}$ and $Y\in \mathcal{Y}$ it holds that: $e_{\mathrm{PS}\left(D\right)}(V\left(X\right)$, $V\left(Y\right))=2$ and $\left|V\right(Y\left)\right|=1$. Theorem 3 below gives an explanation why this yields the conclusion that D is not odd 2-edge-colorable. (In fact, it is readily checked that the digraph D is another example of an internally even digraph that is not odd edge-colorable at all.) We shall abbreviate $\equiv \left(\mathrm{mod}2\right)$ to ${\equiv }_2$.

Theorem 3.

An internally even digraph D is odd 2-edge-colorable if and only if there exists a subset $\mathcal{S}\subseteq \mathcal{X}$ such that for each $Y\in \mathcal{Y}$ it holds that

$$e_{\mathrm{PS}\left(D\right)}(\bigcup _{X\in \mathcal{S}}V\left(X\right),V\left(Y\right)){\equiv }_2\left|V\left(Y\right)\right|.$$

(2)

Proof. 

Assuming that D is odd 2-edge-colorable, apply one such coloring with color set $\{1,2\}$ to its edges. Consider the accompanying edge coloring of $\mathrm{PS}\left(D\right)$. Observe that for every $X\in \mathcal{X}$ the edge set $E_{\mathrm{PS}\left(D\right)}[V\left(X\right),V\left(\mathrm{PS}\left(D\right)\right)]$ is monochromatic; indeed, for every $x\in V^{\prime }$ it holds that $E_{\mathrm{PS}\left(D\right)}\left(x\right)$ is monochromatic. Define $\mathcal{S}$ to be the collection of those X’s belonging to $\mathcal{X}$ whose incident edges are colored with 1, and denote ${\mathcal{S}}^c=\mathcal{X}\setminus \mathcal{S}$. Thus, for each $Y\in \mathcal{Y}$ all $E_{\mathrm{PS}\left(D\right)}[{\bigcup }_{X\in \mathcal{S}}V\left(X\right),V\left(Y\right)]$ is colored with 1, whereas all $E_{\mathrm{PS}\left(D\right)}[{\bigcup }_{X\in {\mathcal{S}}^c}V\left(X\right),V\left(Y\right)]$ is colored with 2. For each vertex $v\in V\left(\mathrm{PS}\right(D\left)\right)$, let $d_1\left(v\right)$ denote the degree of v in the spanning subgraph of $\mathrm{PS}\left(D\right)$ whose edge set is color class 1. Clearly, if a vertex $y\in V^{″}$ is non-isolated in $\mathrm{PS}\left(D\right)$ then $d_1\left(y\right)$ is odd. Therefore

$$e_{\mathrm{PS}\left(D\right)}(\bigcup _{X\in \mathcal{S}}V\left(X\right),V\left(Y\right)){\equiv }_2\sum _{y\in V\left(Y\right)}{d}_1\left(y\right){\equiv }_2\left|V\left(Y\right)\right|,$$

which gives (2).

Proving the other direction, now let $\mathcal{S}\subseteq \mathcal{X}$ be such that (2) is fulfilled for each $Y\in \mathcal{Y}$, and again let ${\mathcal{S}}^c$ be its set complement with respect to $\mathcal{X}$. Color with 1 all the edges incident to ${\bigcup }_{X\in \mathcal{S}}V\left(X\right)$, and color with 2 all the edges incident to ${\bigcup }_{X\in {\mathcal{S}}^c}V\left(X\right)$. Thus, the remaining uncolored part of $E\left(\mathrm{PS}\right(D\left)\right)$ is the edge set of $\mathrm{PS}\left(D\right)\left[{\bigcup }_{Y\in \mathcal{Y}}V\left(Y\right)\right]$, i.e., ${\bigcup }_{Y\in \mathcal{Y}}E\left(Y\right)$. We extend the coloring to $E\left(Y\right)$ for each $Y\in \mathcal{Y}$ as described below. With the same meaning of $d_1\left(v\right)$, consider the set $T_Y$ defined by

$$T_Y=\{y:y\in V\left(Y\right)\mathrm{and}{d}_1\left(y\right)\mathrm{is}\mathrm{even}\}.$$

Observe that

$$\left|V\left(Y\right)\right|{\equiv }_2\left|T_Y\right|+e_{\mathrm{PS}\left(D\right)}(\bigcup _{X\in \mathcal{S}}V\left(X\right),V\left(Y\right)).$$

(3)

Indeed, the last congruence holds since

$$\begin{array}{ccc}\hfill \left|V\right(Y\left)\right|& =& \left|\right\{y:y\in V\left(Y\right)\mathrm{and}{d}_1\left(y\right)\mathrm{is}\mathrm{even}\left\}\right|\hfill \\ & & +\left|\right\{y:y\in V\left(Y\right)\mathrm{and}{d}_1\left(y\right)\mathrm{is}\mathrm{odd}\left\}\right|\hfill \\ & {\equiv }_2& |\{y:y\in V\left(Y\right)\mathrm{and}{d}_1\left(y\right)\mathrm{is}\mathrm{even}\}|+\sum _{y\in V\left(Y\right)}{d}_1\left(y\right)\hfill \\ & =& |T_Y|+e_{\mathrm{PS}\left(D\right)}(\bigcup _{X\in \mathcal{S}}V\left(X\right),V\left(Y\right)).\hfill \end{array}$$

From (2) and (3) it follows that $T_Y$ is even-sized. Color with 1 the edges of an arbitrary $T_Y$-join of Y, and color with 2 the rest of $E\left(Y\right)$. This completes an edge coloring of $\mathrm{PS}\left(D\right)$ which corresponds to an odd 2-edge coloring of D. Indeed, by the definition of $T_Y$, in the constructed edge coloring of $\mathrm{PS}\left(D\right)$ color 1 (as well as color 2) appears an odd number of times on each non-empty semi-cut of every vertex $v\in V^{″}$. □

As another example, consider the digraph D depicted in Figure 8 below. Here $\left|\mathcal{X}\right|=\left|\mathcal{Y}\right|=2$ ($\mathcal{X}$ constitutes of two copies of $K_2$, and $\mathcal{Y}$ of two copies of $K_1$), but as for each pair of members $X\in \mathcal{X}$ and $Y\in \mathcal{Y}$ it still holds that $e_{\mathrm{PS}\left(D\right)}(V\left(X\right),V\left(Y\right))=2$ and $\left|V\right(Y\left)\right|=1$, once again D is not odd 2-edge-colorable.

However, if we slightly modify the last example by adding a pair of arcs (c.f. Figure 9) we obtain an odd 2-edge-colorable digraph. Indeed, again $\left|\mathcal{X}\right|=\left|\mathcal{Y}\right|=2$ (now $\mathcal{X}$ is comprised of two copies of $K_1$, and $\mathcal{Y}$ of two copies of $C_2$); however, this time for each pair of members $X\in \mathcal{X}$ and $Y\in \mathcal{Y}$ it holds that $e_{\mathrm{PS}\left(D\right)}(V\left(X\right),V\left(Y\right))=3$ and $\left|V\right(Y\left)\right|=2$, which enables $\mathcal{S}=\mathcal{X}$ to meet the requirements of Theorem 3. As the only other solution is $\mathcal{S}=\varnothing$, this digraph is (upon permutation of colors) uniquely odd 2-edge-colorable.

The characterization of odd 2-edge-colorability of digraphs stated in Theorem 3 can also be interpreted as the solvability of a characteristic system $\left(S\right)$ of linear equations over the field $\mathrm{GF}\left(2\right)$.

Theorem 4.

Given an internally even digraph D, let $G[\mathcal{X},\mathcal{Y}]$ be the simple bipartite graph constructed as follows: the partite sets of G are $\mathcal{X}=\{X_1,X_2,\dots ,X_r\}$ and $\mathcal{Y}=\{Y_1,Y_2,\dots ,Y_s\}$, and vertex $X_i$ is joined by an edge with vertex $Y_j$ if and only if $e_G(V\left(X_i\right),V\left(Y_j\right))$ is odd. Relate to each $X_i$ a variable $x_i$ and consider a system $\left(S\right)$ consisting of s linear equations over the field $\mathrm{GF}\left(2\right)$ where the j-th equation $(j=1,2,\dots ,s)$ reads

$$\sum _{X_i\in N_G\left(Y_j\right)}{x}_i{\equiv }_2\left|V\left(Y_j\right)\right|.$$

Then D admits an odd 2-edge coloring if and only if the system $\left(S\right)$ is solvable.

Proof. 

Consider an arbitrary subset $\mathcal{S}\subseteq \mathcal{X}$, and define $x\left(\mathcal{S}\right)={\left(x_i\right)}_{i=1}^r$ as follows: $x_i=1$ if $X_i\in \mathcal{S}$, and $x_i=0$ otherwise. It suffices to observe that for any $Y\in \mathcal{Y}$, the subset $\mathcal{S}$ satisfies (2) if and only if the r-tuple $x\left(\mathcal{S}\right)$ satisfies

$$\sum _{X_i\in N_G\left(Y\right)}{x}_i{\equiv }_2\left|V\left(Y\right)\right|.$$

 □

For example, the characteristic system $\left(S\right)$ accompanying the digraph from Figure 9 consists of two identical equations $x_1+x_2=0$. Its only solutions are $(x_1,x_2)=(0,0)$ and $(x_1,x_2)=(1,1)$. Contrarily, the system corresponding to the digraph from Figure 8 (that is not odd 2-edge-colorable) comprises a pair of identical equations $0=1$, and is clearly unsolvable.

Since row reduction (also known as Gaussian elimination) is an efficient algorithm for solving a system of linear equations over any given field (see e.g., [9]), Theorem 4 and its proof imply the following:

Corollary 2.

The decision problem whether digraph D admits an odd 2-edge coloring is solvable in polynomial time. Moreover, in the affirmative case, such a coloring can be found in polynomial time.

The algebraic interpretation concerning odd 2-edge-colorability of digraphs described in Theorem 4, although basic, is nevertheless interesting in light of the relevance in current literature to find new relations between Graph Theory and Algebra. In this regard, any possible analogue of Theorem 4 concerning odd k-edge-colorability of digraphs, for given $k\ge 3$, would be interesting. Please note that the reasoning applied in the proof of Theorem 3 does not apply straightforwardly when $k\ge 3$ since there are, in general, more than one way of representing an odd natural number as a sum of k odd natural numbers. We are therefore tempted to end this section by asking the following:

Question 2.

Given an integer$k\ge 3$, is the decision problem whether digraph D admits an odd k-edge coloring solvable in polynomial time?

4. Further Work

Every bipartite graph admits an orientation free of internal vertices. Consequently, every bipartite graph admits an odd edge-colorable orientation.

Problem 1.

Characterize graphs that admit an odd edge-colorable orientation.

Given a graph G, a vertex $x\in V\left(G\right)$ is said to be even (resp. odd) if $d_G\left(x\right)$ is even (resp. odd). The set of even (resp. odd) vertices of G is denoted $\mathrm{EvenV}\left(G\right)$ (resp. $\mathrm{OddV}\left(G\right)$). An obvious necessary condition for a graph G to admit an odd edge-colorable orientation is that the induced subgraph $G\left[\mathrm{OddV}\right(G\left)\right]$ is bipartite. One wonders whether this condition is also sufficient for the existence of an odd-edge-colorable orientation. In view of the results of the previous section, we believe that the following related problem is solvable in polynomial time.

Problem 2.

Given a graph G such that $G\left[\mathrm{OddV}\right(G\left)\right]$ is bipartite, characterize the existence of an odd 2-edge-colorable orientation of G.