Efficient or Fractal Market Hypothesis? A Stock Indexes Modelling Using Geometric Brownian Motion and Geometric Fractional Brownian Motion
Abstract
1. Introduction
2. Research Methodology
2.1. Geometric Brownian Motion (GBM)
- 1.
- For any moments of time, the incrementsare independent;
- 2.
- Each increment is a Gaussian random variable of zero mean and variance t − s, so:,
- 3.
- B(0) = 0.
- BM trajectories are continuous and not derivable;
- Stochastic processes, andare martingale, and, reciprocally, ifis a continuous process such thatand (are martingale, thenis a BM;
- Stochastic processis a martingale for anyreal and reciprocally. Ifis a continuous process such thatis a martingale for anyreal, thenis a Brownian motion.
2.2. Geometric Fractional Brownian Motion (GFBM)
- 1.
- is a centered Gaussian process,;
- 2.
- the autocovariance of the increments is given by
- 3.
- .If, FBM is a BM, in which case the increments are independent.The main properties of FBM are [93]:
- stochastic processis an FBM with Hurst parameter (self-similarity property);
- , the increments of the processhave a Gaussian distribution of zero mean and variance(stationarity property of the increments);and,, for each time instant, the incrementsare not independent (the non-independence property of increments); the stochastic processhas continuous trajectories, i.e., there is asuch that:for(property—Hölder continuous sample paths); stochastic processdoes not admit derivative with respect to time (property of no differentiable sample paths); stochastic processis not a semimartingale, except for(no semimartingale property).
- 1.
- if, this situation implies that the FBM increments are negatively correlated, which means that the process is anti-persistent (the process is mean-reverting);
- 2.
- if, this implies that the FBM increments are independent, which means that the process is a BM or Wiener process;
- 3.
- if, this implies that the FBM increments are positively correlated, suggesting that the process is persistent.
2.3. Hurst
2.3.1. Rescaled Range (RS) Computation Methodology
2.3.2. Periodogram Method (PE)
2.4. Mean Absolute Percentage Error (MAPE)
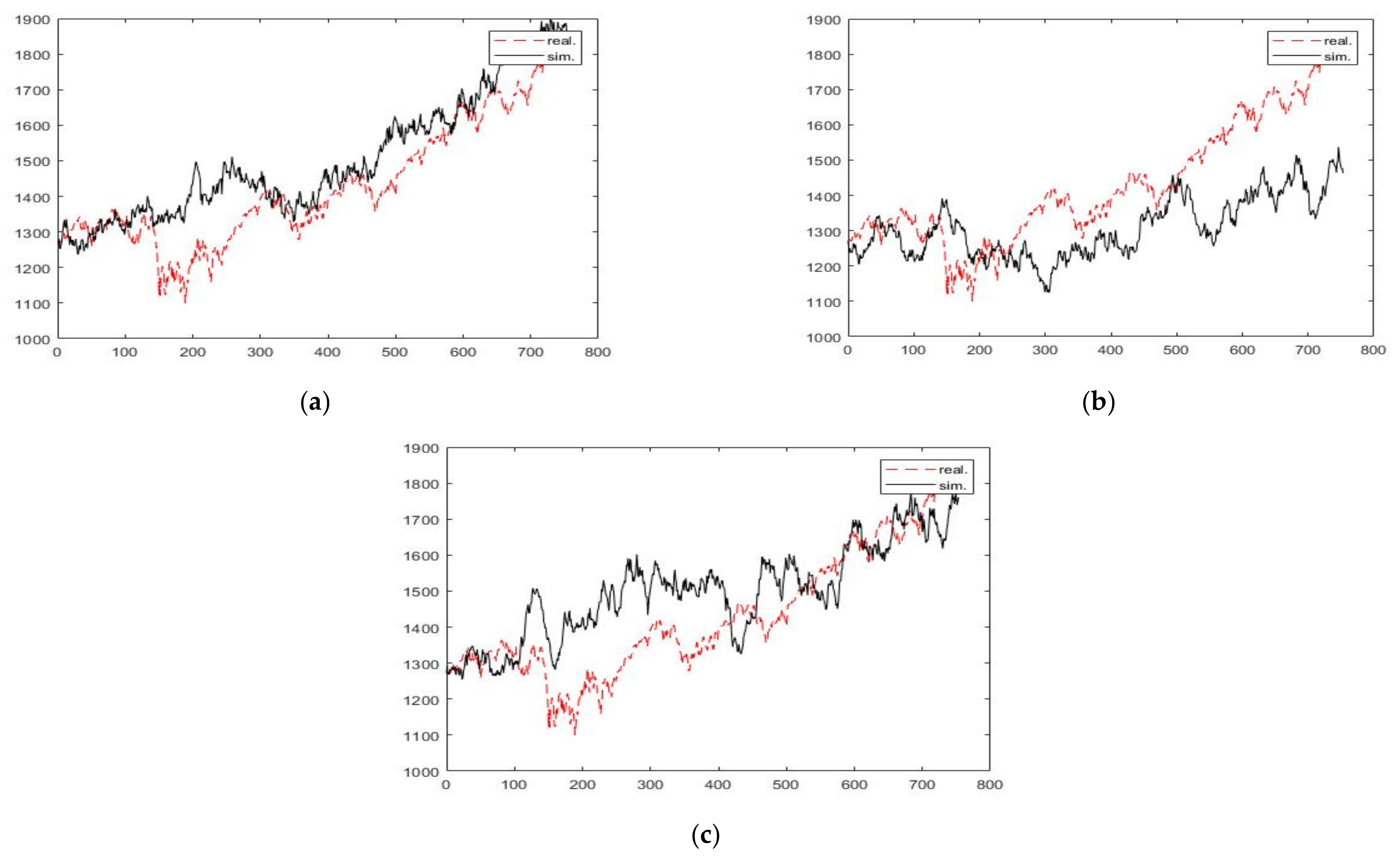
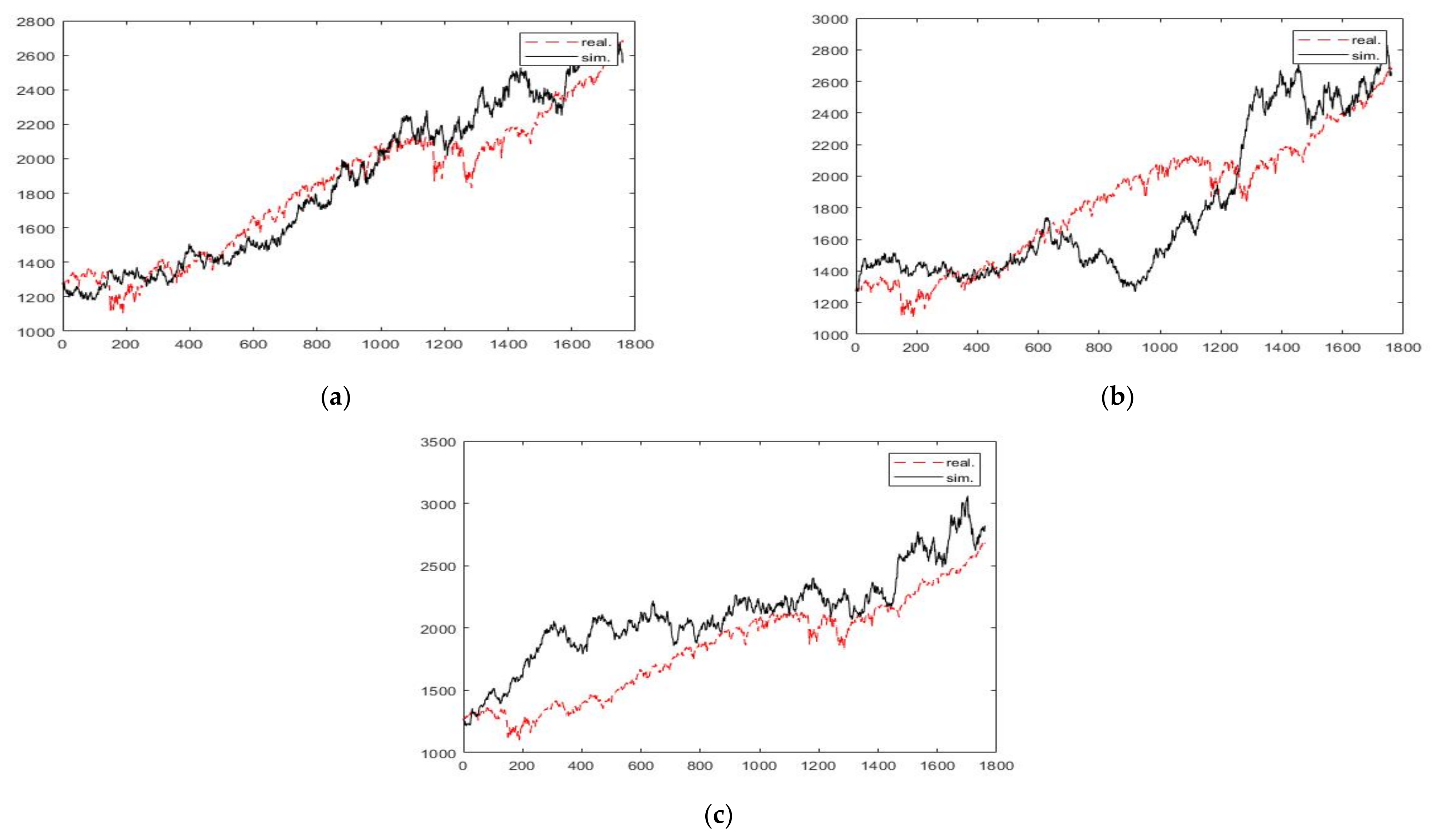
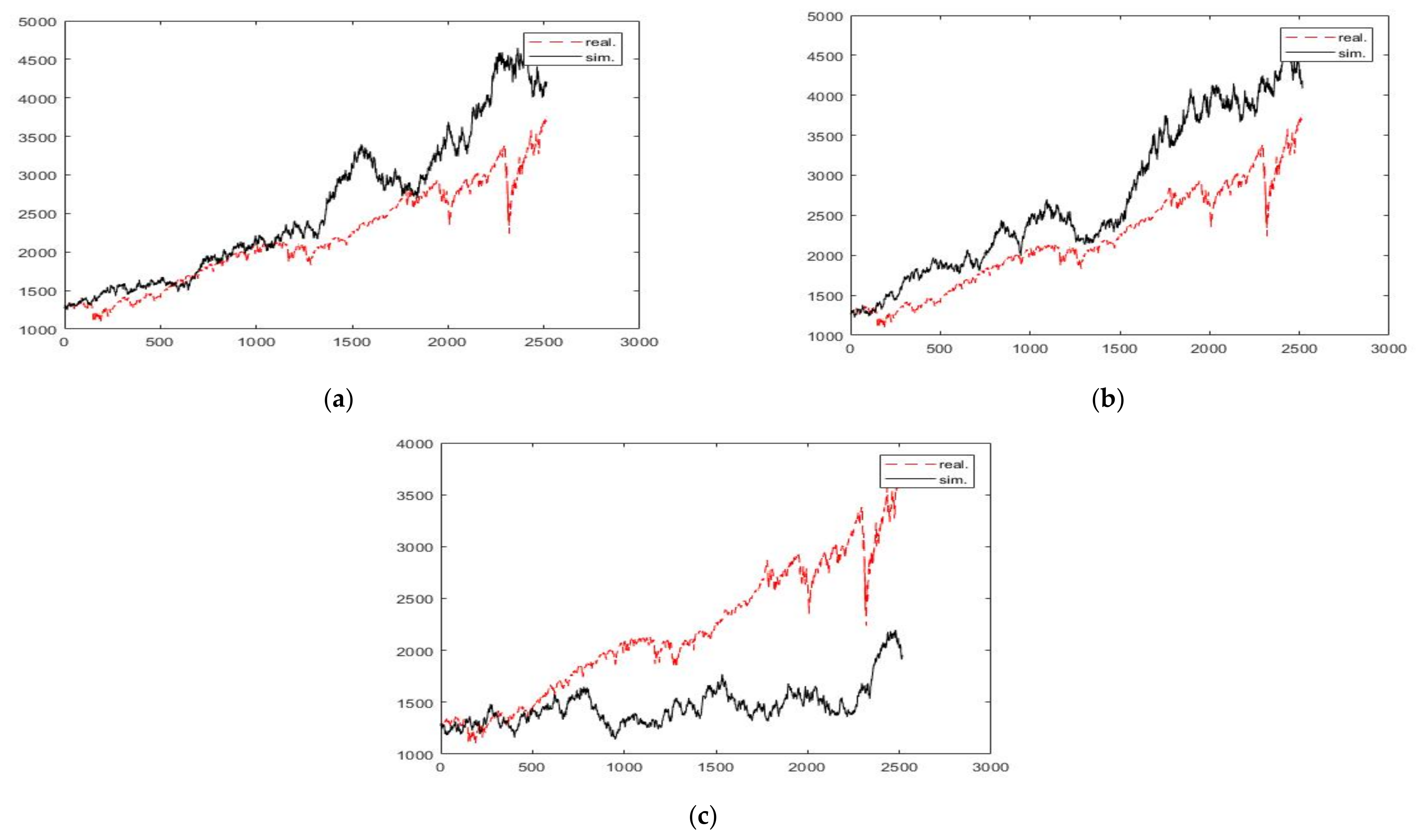
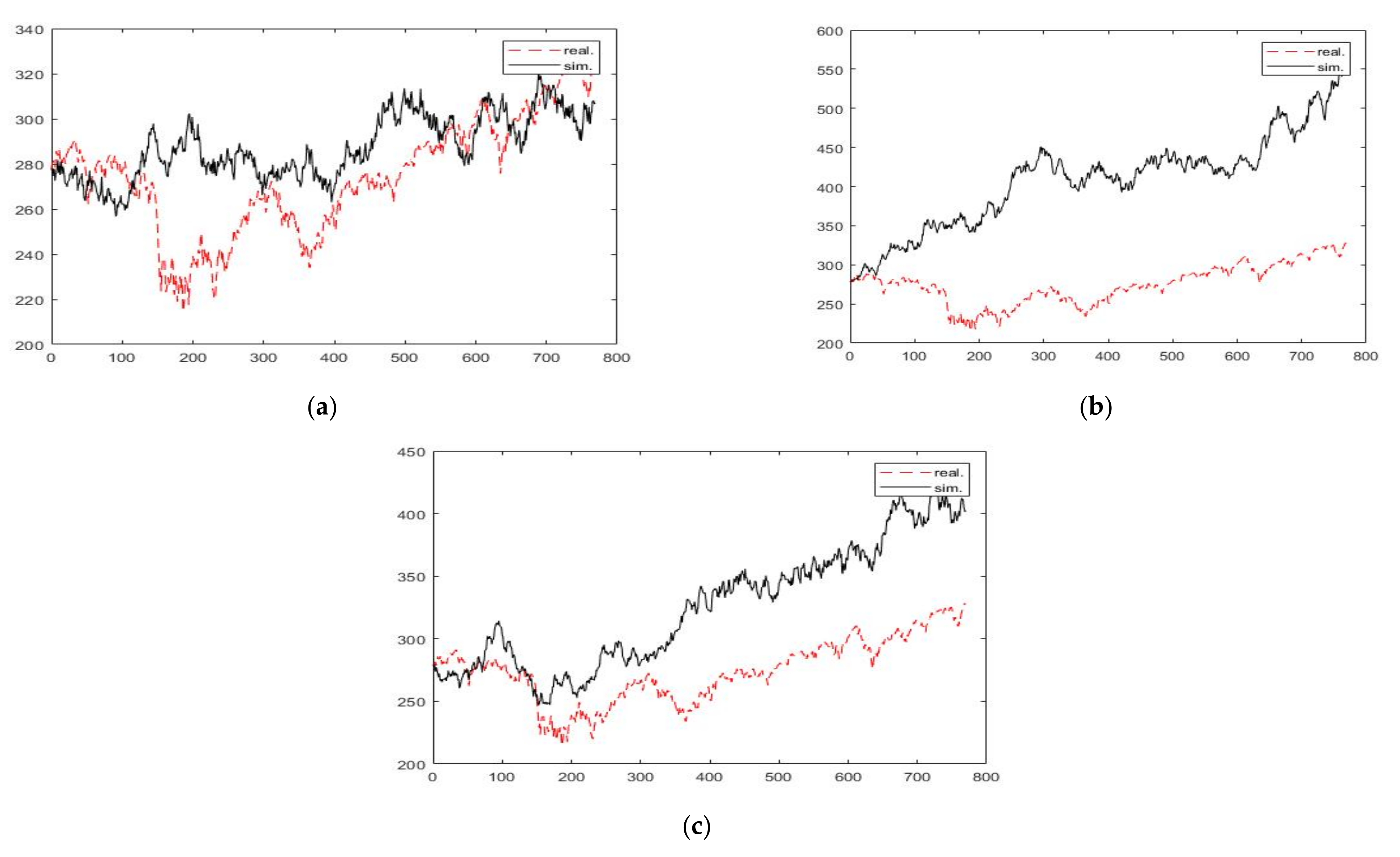
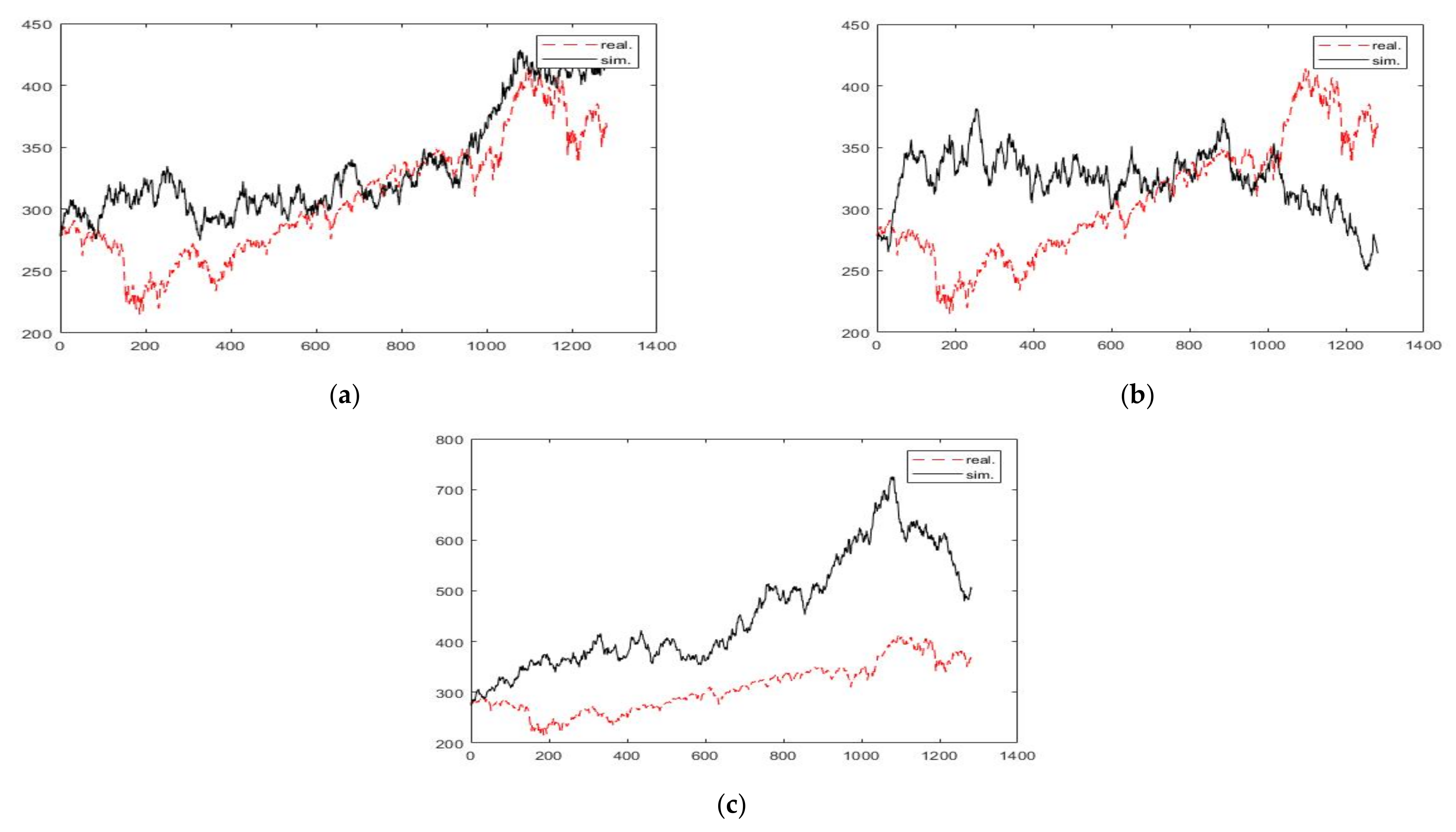
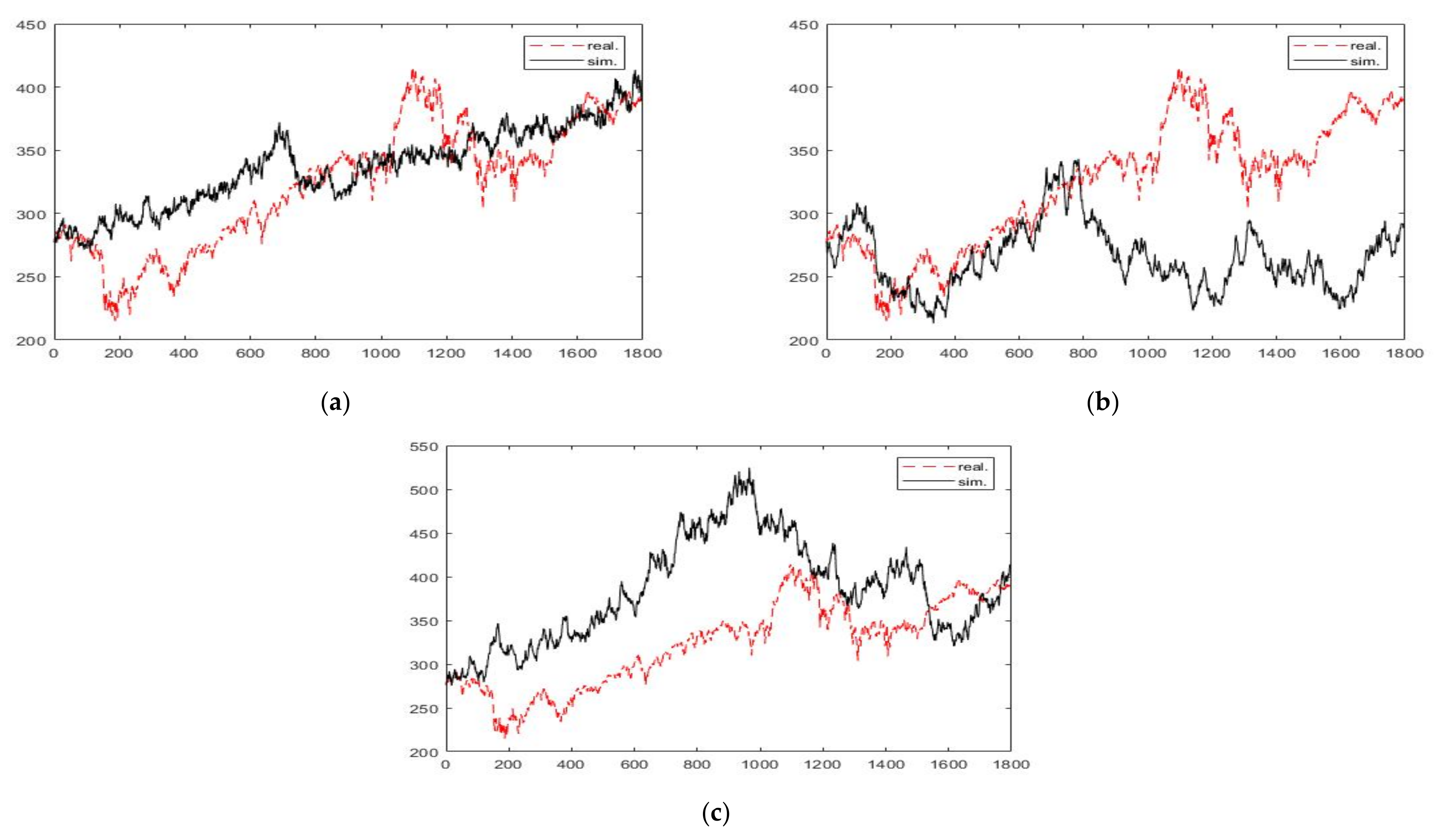
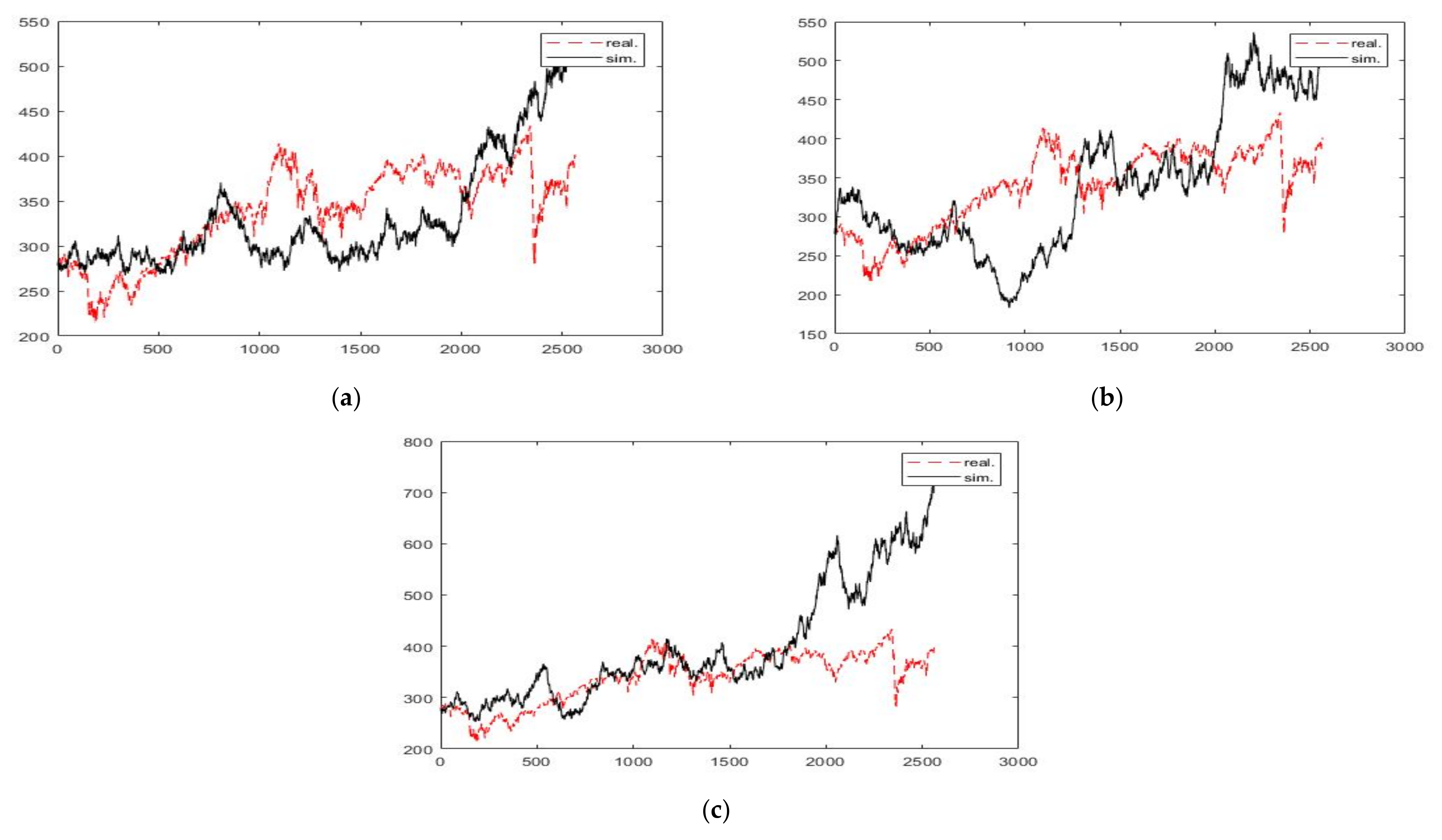
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Cootner, P. The Random Character of Stock Market Prices; MIT Press: Cambridge, MA, USA, 1964. [Google Scholar]
- Samuelson, P.A. Proof that properly anticipated prices fluctuate randomly. Ind. Manag. Rev. 1965, 6, 41–49. [Google Scholar]
- Fama, E. The behavior of stock market prices. J. Bus. 1965, 38, 34–105. [Google Scholar]
- Fama, E. Efficient capital markets: A review of theory and empirical work. J. Financ. 1970, 25, 383–417. [Google Scholar] [CrossRef]
- Persaran, H. Market Efficiency Today, IERP Working Paper, 05.41; Institute of Economic Policy Research, University of Southern California: Los Angeles, CA, USA, 2005; Available online: http://ww.e-m-h.org/Pesaran05.pdf (accessed on 21 June 2021).
- Karp, A.; Van Vuuren, G. Investment Implications of the Fractal Market Hypothesis. Ann. Financ. Econ. 2019, 14, 1950001. [Google Scholar] [CrossRef]
- Wiener, N. Diferențial space. J. Math. Phys. 1923, 2, 131–174. [Google Scholar]
- Greene, M.T.; Fielitz, B.D. Long-term dependence in common stock returns. J. Financ. Econ. 1977, 4, 339–349. [Google Scholar]
- Hampton, J. Rescaled range analysis: Approaches for the financial practitioners, Part 3. Neuro Vest J. 1996, 4, 27–30. [Google Scholar]
- Lillo, F.; Farmer, J.D. The Long Memory of the Efficient Market. Stud. Nonlinear Dyn. E. 2004, 8, 1–19. [Google Scholar]
- Panas, E. Estimating fractal dimension using stable distributions and exploring long memory through ARFIMA models in Athens Stock Exchange. Appl Financ Econ 2001, 11, 395–402. [Google Scholar]
- Peters, E.E. R/S Analysis Using Logarithmic Returns. Financ. Anal J. 1992, 48, 32–37. [Google Scholar]
- Borgesa, M.R. Efficient market hypothesis in European stock markets. Eur. J. Financ. 2010, 16, 711–726. [Google Scholar]
- Chen, F.; Jarrett, J.E. Financial crisis and the market efficiency in the Chinese equity markets. J. Asia Pac. Econ. 2011, 16, 456–463. [Google Scholar] [CrossRef]
- Ito, M.; Noda, A.; Wada, T. The evolution of stock market efficiency in the US: A nonBayesian time-varying model approach. Appl. Econ. 2016, 48, 621–635. [Google Scholar] [CrossRef]
- Urquhart, A. The Euro and European stock market efficiency. Appl. Financ. Econ. 2014, 24, 1235–1248. [Google Scholar] [CrossRef]
- Lo, A.W. Long-Term Memory in Stock Market Prices. Econometrica 1991, 59, 1279–1313. [Google Scholar]
- Lo, A.W.; MacKinlay, A.C. Long-term memory in stock market prices. In A Non-Random Walk Down Wall Street; Dougherty, P., Ed.; Princeton University Press: Princeton, NJ, USA, 1999. [Google Scholar]
- Sánchez-Granero, M.A.; Trinidad-Segovia, J.E.; García-Pérez, J. Some comments on Hurst exponent and the long memory processes on capital markets. Phys. A Stat. Mech. Its Appl. 2008, 387, 5543–5551. [Google Scholar] [CrossRef]
- Gervais, S.; Odean, T. Learning to Be Overconfident. Rev. Financ. Stud. 2001, 14, 1–27. [Google Scholar] [CrossRef]
- De Bondt, W.F.M.; Thaler, R. Does the Stock Market Overreact? J. Financ. 1985, 40, 793–805. [Google Scholar] [CrossRef]
- Bell, D.E. Regret in Decision Making under Uncertainty. Oper. Res. 1982, 30, 961–981. [Google Scholar]
- Cajueiro, D.O.; Tabak, B.M. Ranking efficiency for emerging equity markets. Chaos Solitons Fractals 2005, 23, 671–675. [Google Scholar] [CrossRef]
- Oprean, C.; Tănăsescu, C. Fractality evidence and long-range dependence on capital markets: A Hurst exponent evaluation. Fractals 2014, 22, 1450010. [Google Scholar] [CrossRef]
- Oprean, C.; Tănăsescu, C.; Brătian, V. Are the capital markets efficient? A fractal market theory approach. Econ. Comput. Econ. Cybern. Stud. Res. 2014, 48, 190–205. [Google Scholar]
- Ahamed, N.; Kalita, M.; Tiwari, A. Testing the long-memory features in return and volatility of NSE index. Theor. Econ. Lett. 2015, 5, 431–440. [Google Scholar] [CrossRef][Green Version]
- Cajueiro, D.O.; Tabak, B.M. Evidence of long range dependence in Asian equity markets: The role of liquidity and market restrictions. Phys. A Stat. Mech. Its Appl. 2004, 342, 656–664. [Google Scholar]
- Hull, M.; McGroarty, F. Do emerging markets become more efficient as they develop? Long memory pedrsistence in equity indices. Emerg. Mark. Rev. 2014, 18, 45–61. [Google Scholar]
- Kale, M.; Butar, F.B. Fractal analysis of time series and distribution properties of Hurst exponent. J. Math. Sci. Math. Educ. 2011, 5, 8–19. [Google Scholar]
- Kristoufek, L.; Vosvrda, M. Measuring capital market efficiency: Global and local correlations structure. Phys. A Stat. Mech. Its Appl. 2013, 392, 184–193. [Google Scholar]
- Kristoufek, L.; Vosvrda, M. Commodity futures and market efficiency. Energy Econ. 2014, 42, 50–57. [Google Scholar]
- Kristoufek, L.; Vosvrda, M. Measuring capital market efficiency: Long-term memory, fractal, dimension and approximate entropy. Eur. Phys. J. B. 2014, 87, 34. [Google Scholar] [CrossRef]
- Necula, C.; Radu, A.N. Long memory in Eastern European financial markets returns. Econ. Res. 2012, 25, 361–378. [Google Scholar]
- Pele, D.T.; Tepus, A.M. Information–entropy and efficient market hypothesis. In Proceedings of the International Conference of Applied Economics, Perugia, Italy, 25–27 August 2011; pp. 463–473. [Google Scholar]
- Plesoianu, A.; Todea, A. Long memory and thin trading: Empirical evidence from Central and Eastern European stock markets. Oeconomica 2012, 1, 21–27. [Google Scholar]
- Risso, A.W. The informational efficiency and the financial crashes. Res. Int. Bus. Financ. 2008, 22, 396–408. [Google Scholar]
- Tan, P.P.; Chin, C.W.; Galagedera, D.U.A. A wavelet-based evaluation of time-varying long memory of equity markets: A paradigm in crisis. Physica A 2014, 410, 345–358. [Google Scholar]
- Sánchez, M.Á.; Trinidad, J.E.; García, J.; Fernández, M. The Effect of the Underlying Distribution in Hurst Exponent Estimation. PLoS ONE 2015, 10, e0127824. [Google Scholar] [CrossRef]
- Grau-Carles, P. Tests of long memory: A bootstrap approach. Comput. Econ. 2005, 25, 103–113. [Google Scholar]
- Oh, G.; Um, C.; Kim, S. Long-term memory and volatility clustering in daily and highfrequency price changes. arXiv 2006, arXiv:physics/0601174v2. [Google Scholar]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian Motions. Fractional Noises and Applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar]
- Peters, E.E. Fractal Market Analysis, Applying Chaos Theory to Investment and Economics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1994. [Google Scholar]
- Ma, H.; Li, Y. Stock Price Jump-diffusion Process Model Based on Fractional Brownian Motion Theory. In Proceedings of the 2019 3rd International Conference on Education, Economics and Management Research, Singapore, 29–30 November 2019; pp. 2352–5398. [Google Scholar] [CrossRef][Green Version]
- Osborne, M.F.M. Brownian Motion in the Stock Market. Oper. Res. 1959, 7, 145–173. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar]
- Scholes, M. Taxes and the Pricing of Options. J. Financ. 1976, 31, 319–332. [Google Scholar] [CrossRef]
- Merton, R.C. Theory of rational option pricing. Rand J. Econ. 1973, 4, 141–183. [Google Scholar] [CrossRef]
- Reddy, K.; Clinton, V. Simulating Stock Prices Using Geometric Brownian Motion: Evidence from Australian Companies. Australas. Account. Bus. Financ. J. 2016, 10, 23–47. [Google Scholar] [CrossRef]
- Rostek, S.; Schöbel, R. A note on the use of fractional Brownian motion for financial modeling. Econ. Model. 2013, 30, 30–35. [Google Scholar] [CrossRef]
- Ibrahim, S.N.I.; Misiran, M.; Laham, M.F. Geometric fractional Brownian model for commodity market simulation. Alex. Eng. 2021, 60, 955–962. [Google Scholar] [CrossRef]
- Chan, J.; Grant, A. Modeling energy price dynamics: GARCH versus stochastic volatility. Energy Econ. 2016, 54, 182–189. [Google Scholar] [CrossRef]
- Hamdan, Z.N.; Ibrahim, S.N.I.; Mustafa, M.S. Modelling Malaysian Gold Prices using Geometric Brownian Motion Model. Adv. Math. Sci. J. 2020, 9, 7463–7469. [Google Scholar] [CrossRef]
- Kolmogorov. A.N. Wienerssche Spiralen und einige andere interessante Kurven im Hilbertschen Raum.C.R. (Doklady). Acad. Sci. URSS (NS) 1940, 26, 115–118. [Google Scholar]
- Mandelbrot, B.; Wallis, J.R. Noah, Joseph, and operational hydrology. Water Resour. Res. 1968, 4, 909–918. [Google Scholar]
- Mandelbrot, B.; Wallis, J.R. Computer experiments with fractional Gaussian noises. Parts I, II, III. Water Resour. Res. 1969, 5, 228–267. [Google Scholar]
- Mandelbrot, B.; Wallis, J.R. Some long-run properties of geophysical records. Water Resour. Res. 1969, 5, 321–340. [Google Scholar]
- Mandelbrot, B.; Wallis, J.R. Robustness of the rescaled range RIS in the measurement of noncyclic long run statistical dependence. Water Resour. Res. 1969, 5, 967–988. [Google Scholar]
- Abundo, M.; Pirozzi, E. On the Integral of the Fractional Brownian Motion and Some Pseudo-Fractional Gaussian Processes. Mathematics 2019, 7, 991. [Google Scholar] [CrossRef]
- Balcerek, M.; Burnecki, K. Testing of fractional Brownian motion in a noisy environment. Chaos Solitons Fractals 2020, 140. [Google Scholar] [CrossRef]
- Alhagyan, M.; Alduais, F. Forecasting the Performance of Tadawul All Share Index (TASI) using Geometric Brownian Motion and Geometric Fractional Brownian Motion. Adv. Appl. Stat. 2020, 62, 55–65. [Google Scholar] [CrossRef]
- Rogers, L.C.G. Arbitrage with Fractional Brownian Motion. Math. Financ. 1997, 7, 95–105. [Google Scholar] [CrossRef]
- Tarnopolski, M. Modeling the price of Bitcoin with geometric fractional Brownian motion: A Monte Carlo approach. arXiv 2017, arXiv:1707.03746. [Google Scholar]
- Akinlar, M.A.; Inc, M.; Go’mez-Aguilar, J.F.; Boutarfa, B. Solutions of a disease model with fractional white noise. Chaos Solitons Fractals 2020, 137, 109840. [Google Scholar] [CrossRef]
- Li, Q.; Liu, S.; Zhou, M. Nonparametric Estimation of Fractional Option Pricing Model. Math. Probl. Eng. 2020, 8858821. [Google Scholar] [CrossRef]
- Xiao, W.L.; Zhang, W.G.; Zhang, X.L.; Wang, Y.L. Pricing currency options in a fractional Brownian motion with jumps. Econ. Model. 2010, 27. [Google Scholar] [CrossRef]
- Necula, C. Option Pricing in a Fractional Brownian Motion Environment. SSRN 2002. [Google Scholar] [CrossRef]
- Shokrollahi, F.; Kılıçman, A. The valuation of currency options by fractional Brownian motion. SpringerPlus 2016, 5, 1145. [Google Scholar] [CrossRef]
- Areerak, T. Mathematical Model of Stock Prices via a Fractional Brownian Motion Model with Adaptive Parameters. ISRN Appl. Math. 2014, 3, 1–6. [Google Scholar] [CrossRef]
- Dhesi, G.; Shakeel, B.; Ausloos, M. Modelling and forecasting the kurtosis and returns distributions of financial markets: Irrational fractional Brownian motion model approach. Ann. Oper. Res. 2021, 299, 1397–1410. [Google Scholar] [CrossRef]
- Maleki Almani, H.; Hosseini, S.M.; Tahmasebi, M. Fractional Brownian motion with two-variable Hurst exponent. J. Comput. Appl. Math. 2021, 388. [Google Scholar] [CrossRef]
- Chang, Y.; Wang, Y.; Zhang, S. Option Pricing under Double Heston Jump-Diffusion Model with Approximative Fractional Stochastic Volatility. Mathematics 2021, 9, 126. [Google Scholar] [CrossRef]
- Dittrich, L.; Srbek, P. Is Violation of the Random Walk Assumption an Exception or Rule in Capital Markets? Atl. Econ. J. 2020, 48, 491–501. [Google Scholar]
- Weron, R. Estimating long-range dependence: Finite sample properties and confidence intervals. Phys. A Stat. Mech. Its Appl. 2002, 312, 285–299. [Google Scholar]
- Mandelbrot, B.B.; Taqqu, M.S. Robust R/S analysis of long-run serial correlation. Bull. Int. Stat. Inst. 1979, 48, 59–104. [Google Scholar]
- Willinger, W.; Taqqu, M.S.; Teverovsky, V. Stock market prices and long-range dependence. Finance Stochast. 1999, 3, 1–13. [Google Scholar]
- Geweke, J.; Porter-Hudak, S. The Estimation and Application of Long Memory Time Series Models. J. Time Ser. Anal. 1983, 4, 221–238. [Google Scholar]
- Haslett, J.; Raftery, A.E. Space-Time Modelling with Long-Memory Dependence: Assessing Ireland’s Wind Power Resource. J. R. Stat. Society. Ser. C Appl. Stat. 1989, 38, 1–50. [Google Scholar] [CrossRef]
- Barabasi, A.L.; Vicsek, T. Multifractality of self-affine fractals. Phys. Rev. A 1991, 44, 2730–2733. [Google Scholar]
- Taqqu, M.S.; Teverovsky, V.; Willinger, W. Estimators for Long-Range Dependence: An Empirical Study. Fractals 1995, 3, 785–798. [Google Scholar]
- Veitch, D.; Abry, P. A wavelet based joint estimator of the parameters of long–range dependence. IEEE Trans. Inf. Theory 1999, 45, 878–897. [Google Scholar]
- Alessio, E.; Carbone, A.; Castelli, G.; Frappietro, V. Second-order moving average and scaling of stochastic time series. Eur. Phys. J. B 2002, 27, 197–200. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar]
- Fernández-Martínez, M.; Sánchez-Granero, M.A.; Trinidad Segovia, J.E.; Román-Sánchez, I.M. An accurate algorithm to calculate the Hurst exponent of self-similar processes. Phys. Lett. A 2014, 378, 2355–2362. [Google Scholar]
- Gómez-Águila, A.; Sánchez-Granero, M.A. A theoretical framework for the TTA algorithm. Phys. A Stat. Mech. Its Appl. 2021, 582, 126288. [Google Scholar]
- Razdan, A. Wavelet correlation coefficient of strongly correlated time series. Phys. A Stat. Mech. Its Appl. 2004, 333, 335–342. [Google Scholar]
- Okonkwo, U.C.; Osu, B.O.; Uchendu, K.A. Wavelet analysis of stocks in the Nigerian capital market Niger. Ann. Pure Appl. Sci. 2019, 2, 176–183. [Google Scholar]
- Gourène, G.A.; Mendy, P. Oil prices and African stock markets co-movement: A time and frequency analysis. J. Afr. Trade 2018, 5, 55–67. [Google Scholar]
- Shimotsu, K.; Phillips, P.C.B. Exact local Whittle estimation of fractional integration. Ann. Statist. 2005, 33, 1890–1933. [Google Scholar] [CrossRef]
- Wilmott, P. Paul Wilmott Introduces Quantitative Finance; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Negrea, B. Financial Assets Pricing: An Introduction to the Stochastic Process Theory; Economica Publishing House: Bucharest, Romania, 2006. (In Romanian) [Google Scholar]
- Huy, D.P. A Remark on Non-Markov Property of a Fractional Brownian Motion. Vietnam. J. Math. 2003, 31, 237–240. [Google Scholar]
- Zhao, C.; Zhai, Z.; Du, Q. Optimal control of stochastic system with Fractional Brownian Motion. MBE 2021, 18, 5625–5634. [Google Scholar] [CrossRef]
- Reyes Montes de Oca, C.C. Stochastic Volatility Models: Present, Past and Future. Master’s Thesis, University of Barcelona, Barcelona, Spain, 28 June 2018; pp. 18–29. Available online: http://hdl.handle.net/2445/129665 (accessed on 23 June 2021).
- Hu, Y.; Øksendal, B. Fractional White Noise Calculus and Applications to Finance. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 2003, 6, 1–32. [Google Scholar]
- Feng, Z. Stock-Price Modeling by the Geometric Fractional Brownian Motion: A View towards the Chinese Financial Market (Dissertation). 2018. Available online: http://urn.kb.se/resolve?urn=urn:nbn:se:lnu:diva-78375 (accessed on 19 May 2021).
- Kijima, M.; Tam, C.M. Fractional Brownian Motion in Financial Models and Their Monte Carlo Simulation, Theory and Application of Monte Carlo Simulations. Chan, W.K., Ed.; In Tech: Rijeka, Croatia, 2013; pp. 53–85. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Wang, K.; Jiang, T.; Yang, L. Modified periodogram method for estimating the Hurst exponent of fractional Gaussian noise. Phys. Rev. E 2009, 80, 066207. [Google Scholar]
- Pallikari, F.; Boller, E. A Rescaled Range Analysis of Random Events. J. Sci. Explor. 1999, 13, 25–40. [Google Scholar]
- Feng, L.; Zhou, J. Trend predictions in water resources using rescaled range (R/S) analysis. Environ Earth Sci. 2013, 68, 2359–2363. [Google Scholar]
- Tofallis, C.A. Better measure of relative prediction accuracy for model selection and model estimation. J. Oper. Res. Soc. 2015, 66, 1352–1362. [Google Scholar]
- Kim, S.; Heeyoung, K. A new metric of absolute percentage error for intermittent demand forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar]
- Vukovic, O. Analysing the Chinese Stock Market using the Hurst Exponent, Fractional Brownian Motion and Variants of a Stochastic Logistic Differential Equation. Int. J. Des. Nat. Ecodynamics 2015, 10, 300–309. [Google Scholar] [CrossRef]

| MAPE Value | Interpretation |
|---|---|
| <10% | Highly accurate forecasting |
| 10–20% | Good forecasting |
| 20–50% | Reasonable forecasting |
| >50% | Inaccurate forecasting |
| 3 Years | 5 Years | 7 Years | 10 Years | ||
|---|---|---|---|---|---|
| Hurst PE | H | 0.3734 | 0.363 | 0.4433 | 0.4136 |
| Average MAPE | 0.0995 | 0.0978 | 0.1456 | 0.1615 | |
| MAPE standard deviation | 0.043 | 0.041 | 0.071 | 0.08 | |
| Confidence interval Average MAPE * | (0.097, 0.102) | (0.095, 0.100) | (0.139, 0.148) | (0.160, 0.170) | |
| Hurst RS | H | 0.4925 | 0.4793 | 0.4715 | 0.444 |
| Average MAPE | 0.1535 | 0.1805 | 0.1708 | 0.196 | |
| MAPE standard deviation | 0.078 | 0.109 | 0.099 | 0.109 | |
| Confidence interval Average MAPE * | (0.149, 0.158) | (0.174, 0.187) | (0.170, 0.182) | (0.195, 0.209) | |
| Hurst 0.5 | Average MAPE | 0.1638 | 0.2005 | 0.2049 | 0.3059 |
| MAPE standard deviation | 0.086 | 0.129 | 0.128 | 0.212 | |
| Confidence interval Average MAPE * | (0.158, 0.169) | (0.193, 0.208) | (0.207, 0.223) | (0.291, 0.317) |
| 3 Years | 5 Years | 7 Years | 10 Years | ||
|---|---|---|---|---|---|
| Hurst PE | H | 0.3649 | 0.3996 | 0.3294 | 0.4108 |
| Average MAPE | 0.1156 | 0.1374 | 0.103 | 0.1819 | |
| MAPE standard deviation | 0.042 | 0.052 | 0.031 | 0.091 | |
| Confidence interval Average MAPE * | (0.113, 0.118) | (0.130, 0.137) | (0.100, 0.104) | (0.170, 0.182) | |
| Hurst RS | H | 0.5099 | 0.5047 | 0.5156 | 0.4989 |
| Average MAPE | 0.1822 | 0.2302 | 0.274 | 0.3206 | |
| MAPE standard deviation | 0.089 | 0.131 | 0.199 | 0.211 | |
| Confidence interval Average MAPE * | (0.176, 0.187) | (0.219, 0.235) | (0.271, 0.296) | (0.297, 0.323) | |
| Hurst 0.5 | Average MAPE | 0.1727 | 0.2158 | 0.2462 | 0.3164 |
| MAPE standard deviation | 0.083 | 0.121 | 0.175 | 0.26 | |
| Confidence interval Average MAPE * | (0.172, 0.182) | (0.212, 0.228) | (0.242, 0.264) | (0.324, 0.357) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brătian, V.; Acu, A.-M.; Oprean-Stan, C.; Dinga, E.; Ionescu, G.-M. Efficient or Fractal Market Hypothesis? A Stock Indexes Modelling Using Geometric Brownian Motion and Geometric Fractional Brownian Motion. Mathematics 2021, 9, 2983. https://doi.org/10.3390/math9222983
Brătian V, Acu A-M, Oprean-Stan C, Dinga E, Ionescu G-M. Efficient or Fractal Market Hypothesis? A Stock Indexes Modelling Using Geometric Brownian Motion and Geometric Fractional Brownian Motion. Mathematics. 2021; 9(22):2983. https://doi.org/10.3390/math9222983
Chicago/Turabian StyleBrătian, Vasile, Ana-Maria Acu, Camelia Oprean-Stan, Emil Dinga, and Gabriela-Mariana Ionescu. 2021. "Efficient or Fractal Market Hypothesis? A Stock Indexes Modelling Using Geometric Brownian Motion and Geometric Fractional Brownian Motion" Mathematics 9, no. 22: 2983. https://doi.org/10.3390/math9222983
APA StyleBrătian, V., Acu, A.-M., Oprean-Stan, C., Dinga, E., & Ionescu, G.-M. (2021). Efficient or Fractal Market Hypothesis? A Stock Indexes Modelling Using Geometric Brownian Motion and Geometric Fractional Brownian Motion. Mathematics, 9(22), 2983. https://doi.org/10.3390/math9222983







