A Note on the Boundedness of Doob Maximal Operators on a Filtered Measure Space
Abstract
1. Introduction
- 1
- Motivated by the proof of [4] (Theorem B), we get
- 2
- Using the construction of principal sets [2] and the conditional sparsity [5], we have where are the constants in the construction of principal sets (Appendix A).
- 3
- Long [1] [Theorem 6.6.3] qualitatively evaluated . Modifying Long’s proof, we have which is the same as 1.
2. Preliminaries
2.1. Filtered Measure Space
2.2. Stopping Times
2.3. Operators and Weights
3. Approaches of Theorem 1
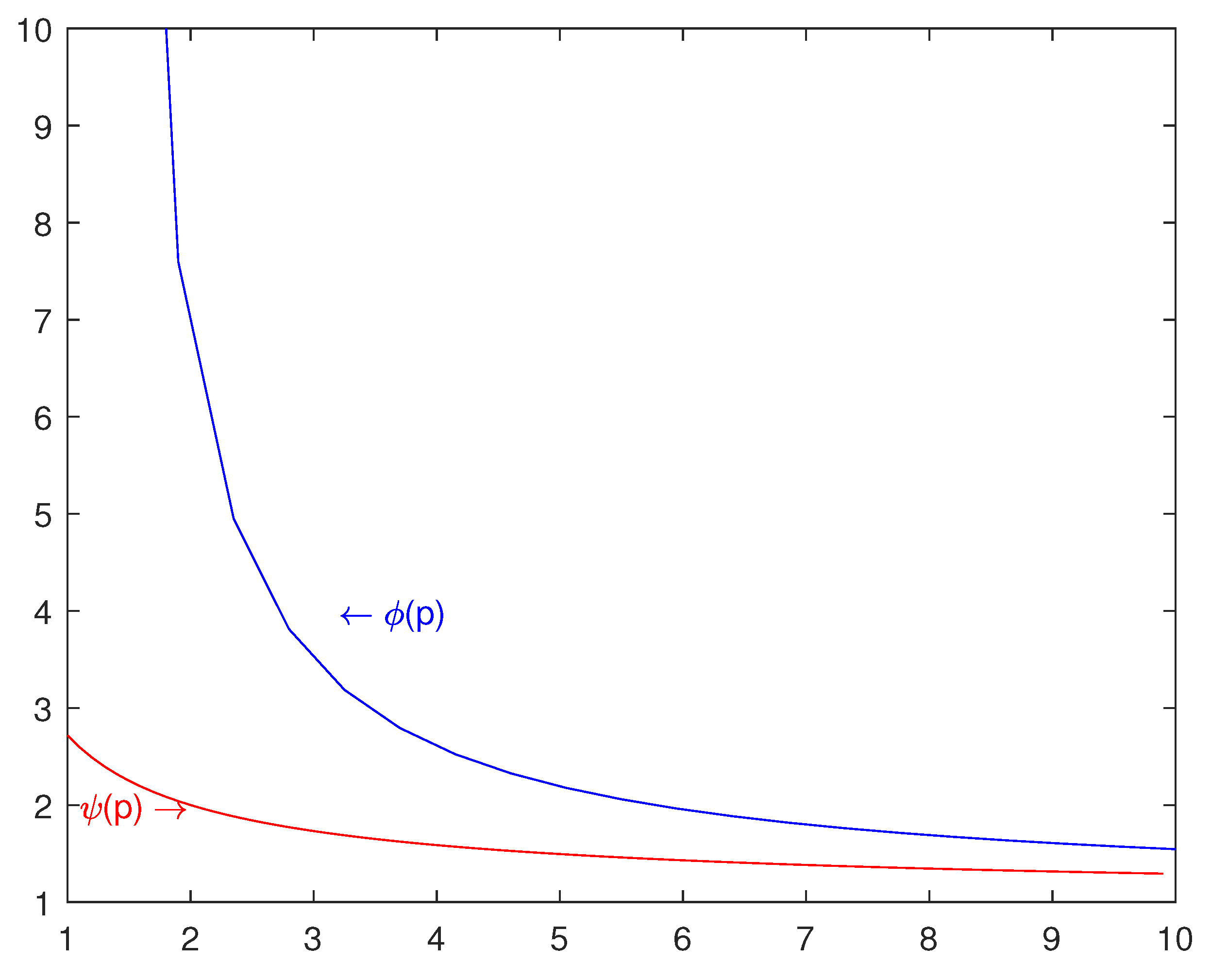
4. Comparison of and
- 1
- We claim that the function is decreasing on Writing and we will show that and are both decreasing on Combining this with and we obtain that is decreasing on We now check that and are both decreasing.For with it is clear thatThus, is decreasing onFor with considerIt is clear thatUsing the mean value theorem, we havewhere It follows thatwhich implies Thus, is decreasing on
- 2
- We claim that the function is decreasing on It suffices to show that We haveIt is clear that if and only if Let with Because of on the function is strictly increasing on It follows from that on That is, with Thus, is decreasing on
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Construction of Principal Sets
- The sets where are disjoint and
- on
- on
References
- Long, R.L. Martingale Spaces and Inequalities; Peking University Press: Beijing, China; Friedr. Vieweg & Sohn: Braunschweig, Germany, 1993; p. iv+346. [Google Scholar] [CrossRef]
- Tanaka, H.; Terasawa, Y. Positive operators and maximal operators in a filtered measure space. J. Funct. Anal. 2013, 264, 920–946. [Google Scholar] [CrossRef]
- Moen, K. Sharp one-weight and two-weight bounds for maximal operators. Stud. Math. 2009, 194, 163–180. [Google Scholar] [CrossRef][Green Version]
- Lerner, A.K. An elementary approach to several results on the Hardy-Littlewood maximal operator. Proc. Am. Math. Soc. 2008, 136, 2829–2833. [Google Scholar] [CrossRef]
- Chen, W.; Zhu, C.; Zuo, Y.; Jiao, Y. Two-weighted estimates for positive operators and Doob maximal operators on filtered measure spaces. J. Math. Soc. Jpn. 2020, 72, 795–817. [Google Scholar] [CrossRef]
- Cao, M.; Xue, Q. Characterization of two-weighted inequalities for multilinear fractional maximal operator. Nonlinear Anal. 2016, 130, 214–228. [Google Scholar] [CrossRef]
- Hytönen, T.; van Neerven, J.; Veraar, M.; Weis, L. Analysis in Banach Spaces. Volume I. Martingales and Littlewood-Paley Theory; Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge; A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series; A Series of Modern Surveys in Mathematics]; Springer: Cham, Switzerland, 2016; Volume 63, p. xvi+614. [Google Scholar]
- Hytönen, T.; Kairema, A. Systems of dyadic cubes in a doubling metric space. Colloq. Math. 2012, 126, 1–33. [Google Scholar] [CrossRef]
- Hytönen, T.P. The sharp weighted bound for general Calderón-Zygmund operators. Ann. Math. 2012, 175, 1473–1506. [Google Scholar] [CrossRef]
- Hytönen, T.; Kemppainen, M. On the relation of Carleson’s embedding and the maximal theorem in the context of Banach space geometry. Math. Scand. 2011, 109, 269–284. [Google Scholar] [CrossRef][Green Version]
- Schilling, R.L. Measures, Integrals and Martingales, 2nd ed.; Cambridge University Press: Cambridge, UK, 2017; p. xvii+476. [Google Scholar]
- Stroock, D.W. Probability Theory, an Analytic View; Cambridge University Press: Cambridge, UK, 1993; p. xvi+512. [Google Scholar]
- Lacey, M.T.; Petermichl, S.; Reguera, M.C. Sharp A2 inequality for Haar shift operators. Math. Ann. 2010, 348, 127–141. [Google Scholar] [CrossRef]
- Chen, W.; Jiao, Y. Weighted estimates for the bilinear maximal operator on filtered measure spaces. J. Geom. Anal. 2021, 31, 5309–5335. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Cui, J. A Note on the Boundedness of Doob Maximal Operators on a Filtered Measure Space. Mathematics 2021, 9, 2953. https://doi.org/10.3390/math9222953
Chen W, Cui J. A Note on the Boundedness of Doob Maximal Operators on a Filtered Measure Space. Mathematics. 2021; 9(22):2953. https://doi.org/10.3390/math9222953
Chicago/Turabian StyleChen, Wei, and Jingya Cui. 2021. "A Note on the Boundedness of Doob Maximal Operators on a Filtered Measure Space" Mathematics 9, no. 22: 2953. https://doi.org/10.3390/math9222953
APA StyleChen, W., & Cui, J. (2021). A Note on the Boundedness of Doob Maximal Operators on a Filtered Measure Space. Mathematics, 9(22), 2953. https://doi.org/10.3390/math9222953




