Figure 1.
Applying the Logistic model and LSTM model on day 5 for ongoing project F10. (a) Logistic Model. (b) LSTM Model.
Figure 1.
Applying the Logistic model and LSTM model on day 5 for ongoing project F10. (a) Logistic Model. (b) LSTM Model.
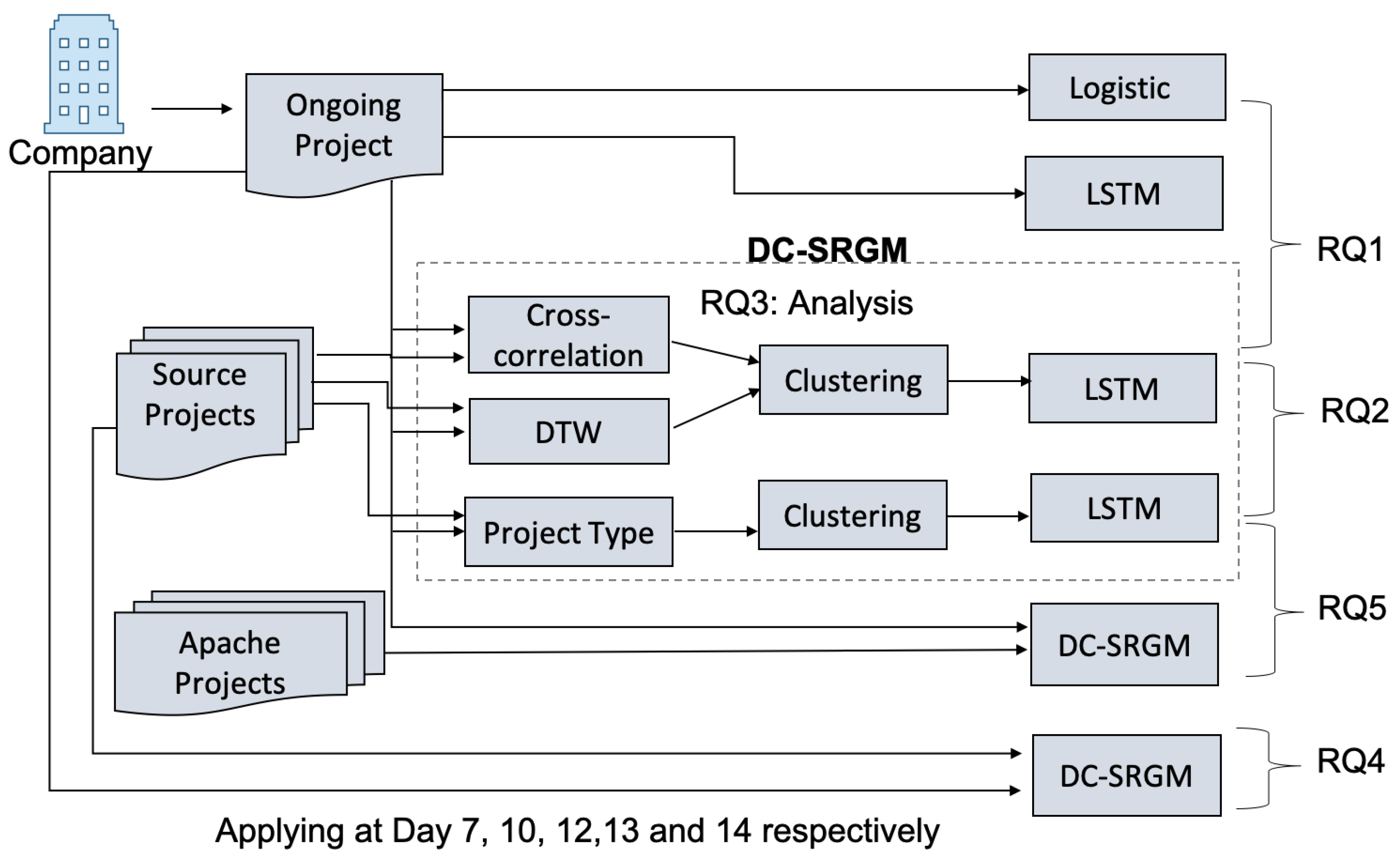
Figure 2.
Overview of the DC-SRGM model.
Figure 2.
Overview of the DC-SRGM model.
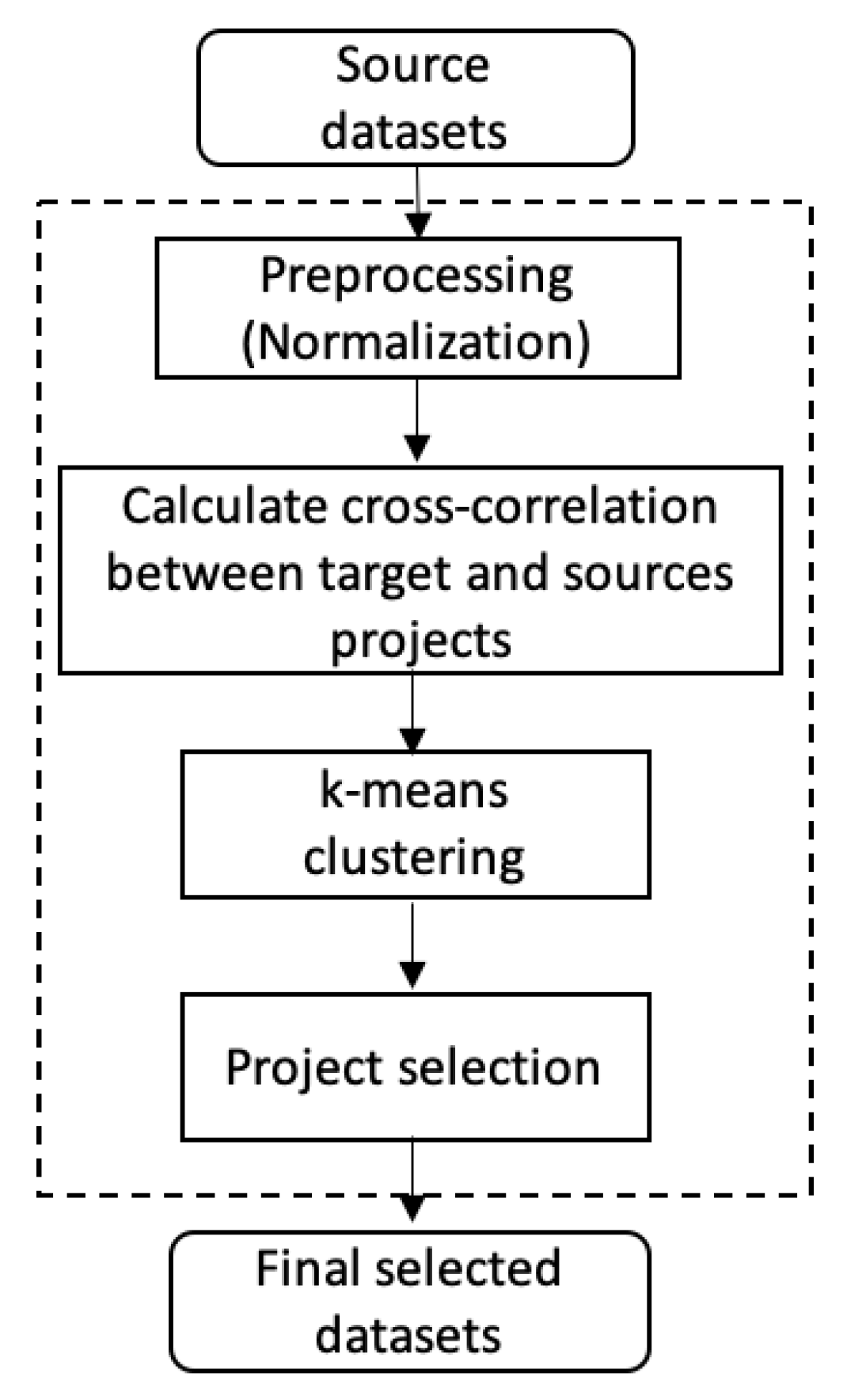
Figure 3.
Project selection process.
Figure 3.
Project selection process.
Figure 4.
Model training process.
Figure 4.
Model training process.
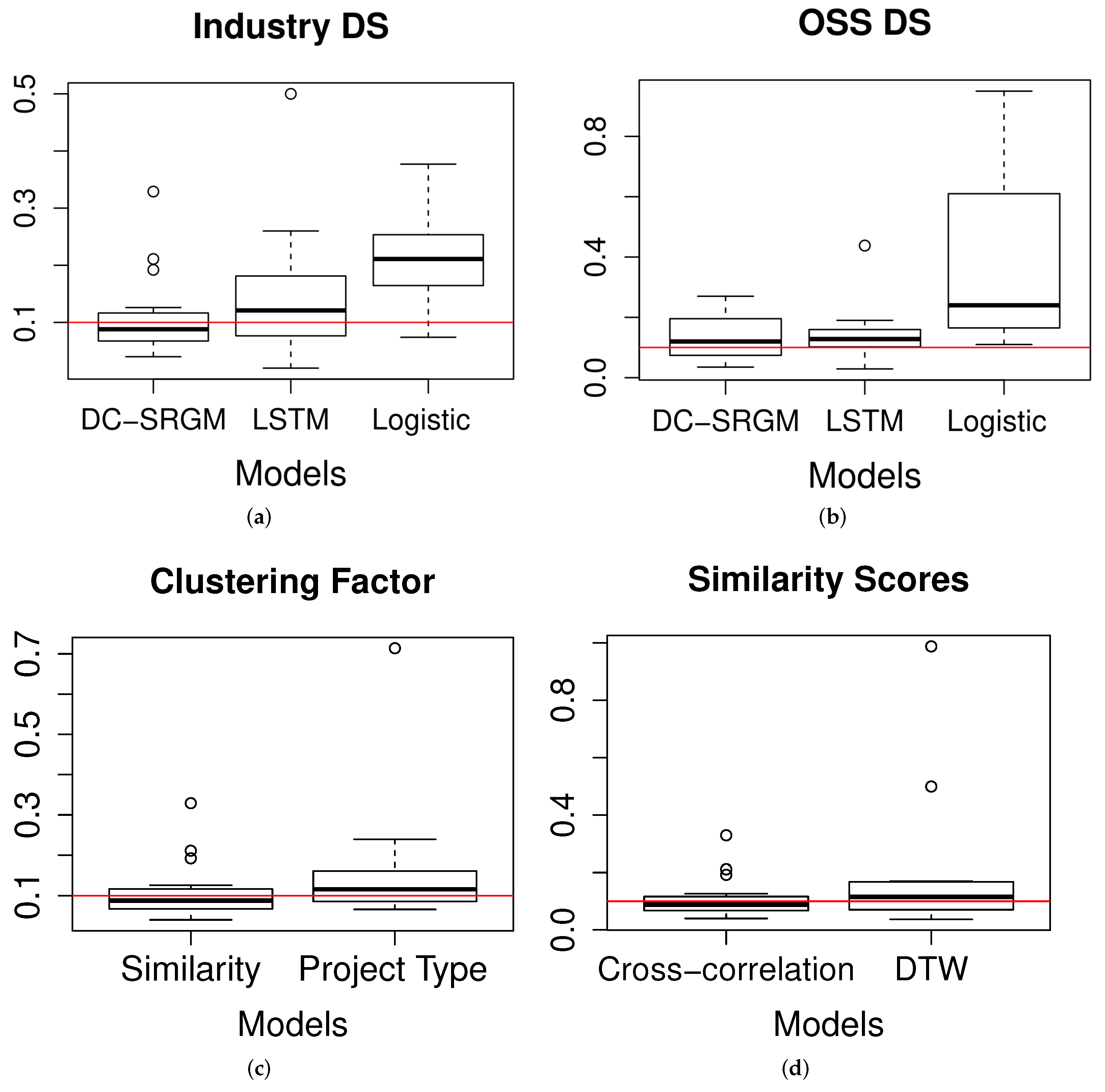
Figure 6.
Comparison of the model prediction accuracy in terms of average error, AE. (a) Performance in industrial datasets (DS), (b) Performance in OSS datasets, (c) DC-SRGM based on project similarity and project domain type, (d) DC-SRGM based on cross-correlation and DTW, (e) DC-SRGM applied at the different number of days, and (f) DC-SRGM across organizations.
Figure 6.
Comparison of the model prediction accuracy in terms of average error, AE. (a) Performance in industrial datasets (DS), (b) Performance in OSS datasets, (c) DC-SRGM based on project similarity and project domain type, (d) DC-SRGM based on cross-correlation and DTW, (e) DC-SRGM applied at the different number of days, and (f) DC-SRGM across organizations.
Figure 7.
Predicted number of bugs at the middle of the projects. Actual, DC-SRGM, LSTM, SRGM represent the actual detected number of bugs, the prediction by DC-SRGM, the LSTM model, and the Logistic SRGM model, respectively. (a) Project F02, (b) F03, (c) F04, and (d) F10.
Figure 7.
Predicted number of bugs at the middle of the projects. Actual, DC-SRGM, LSTM, SRGM represent the actual detected number of bugs, the prediction by DC-SRGM, the LSTM model, and the Logistic SRGM model, respectively. (a) Project F02, (b) F03, (c) F04, and (d) F10.
Table 1.
Industrial project details.
Table 1.
Industrial project details.
| Project | Days | # of Bugs |
|---|
| F01 | 19 | 91 |
| F02 | 22 | 137 |
| F03 | 12 | 47 |
| F04 | 17 | 259 |
| F05 | 19 | 188 |
| F06 | 26 | 263 |
| F07 | 15 | 146 |
| F08 | 17 | 97 |
| F09 | 16 | 99 |
| F10 | 18 | 184 |
| F11 | 14 | 74 |
| F12 | 25 | 351 |
| F13 | 22 | 187 |
| F14 | 34 | 331 |
| F15 | 18 | 752 |
Table 2.
OSS projects details.
Table 2.
OSS projects details.
| Project | Days | # of Bugs | Studied Version |
|---|
| Camel | 36 | 32 | 2.15.1 | 2.15.2 |
| Ignite | 48 | 149 | 2.5 | 2.6 |
| Jclouds | 175 | 25 | 2.1.0 | 2.1.1 |
| Karaf | 56 | 64 | 4.1 | 4.2 |
| Lucene | 91 | 6 | 6.6.0 | 6.6.1 |
| Maven | 160 | 22 | 3.5.1 | 3.5.2 |
| Shiro | 30 | 6 | 1.3.0 | 1.3.1 |
| Spark | 99 | 185 | 2.3.1 | 2.3.2 |
| Syncope | 80 | 36 | 2.0.2 | 2.0.3 |
| Tez | 120 | 27 | 0.6.0 | 0.6.1 |
| Zookeeper | 86 | 14 | 3.4.12 | 3.4.13 |
Table 3.
Summary of the clustering factors.
Table 3.
Summary of the clustering factors.
| Similarity | Max Bugs | Max Days |
|---|
| 0∼1 | 47∼752 | 14∼36 |
Table 4.
Summary of the clustering results. Projects are generally clustered into three groups according to similarity scores and the project scales. Grad, Expo and Grad, and Expo indicate the growth of the number of bugs is gradually increasing, exponentially increasing and gradually increasing, and exponentially increasing.
Table 4.
Summary of the clustering results. Projects are generally clustered into three groups according to similarity scores and the project scales. Grad, Expo and Grad, and Expo indicate the growth of the number of bugs is gradually increasing, exponentially increasing and gradually increasing, and exponentially increasing.
| Cluster | Clustered Projects | Max Bugs | Max Days | Growth | Type |
|---|
| C1 | F01, F02, F04, F05, F07, F08, F09, F10, F11 | 91∼188 | 14∼22 | Grad | Similarity |
| C2 | F12, F15 | 540∼752 | 18∼24 | Expo | # Bugs |
| C3 | F03, F06, F13, F14 | 47∼331 | 22∼36 | Expo and Grad | # Days |
Table 5.
Summary of the clustering results by project. Grad, Expo and Grad, Expo, and Const indicate that the number of bugs is gradually increasing, exponentially increasing and gradually increasing, exponentially increasing, and constantly increasing.
Table 5.
Summary of the clustering results by project. Grad, Expo and Grad, Expo, and Const indicate that the number of bugs is gradually increasing, exponentially increasing and gradually increasing, exponentially increasing, and constantly increasing.
| Project | Cluster | Actual Growth | Prediction Result |
|---|
| F01 | C1 | Grad | Grad |
| F02 | C1 | Grad | Grad |
| F03 | C3 | Grad | Grad |
| F04 | C1 | Grad | Grad |
| F05 | C1 | Grad | Grad |
| F06 | C3 | Expo | Expo |
| F07 | C1 | Grad and Expo | Grad |
| F08 | C2 | Grad | Grad |
| F09 | C3 | Expo and Grad | Grad |
| F10 | C4 | Grad | Grad |
| F11 | C5 | Grad | Grad |
| F12 | C2 | Expo | Expo and Grad |
| F13 | C3 | Expo and Grad | Expo and Grad |
| F14 | C3 | Expo and Grad | Const |
| F15 | C2 | Expo | Expo |
Table 6.
Comparison of DC-SRGM with the LSTM and Logistic models by the AE values. Bold denotes the best AE values. W/L is the number of datasets that each method is better and worse than. “# DS Threshold below 0.1” is the number of datasets for which each model’s performance is lower than the threshold.
Table 6.
Comparison of DC-SRGM with the LSTM and Logistic models by the AE values. Bold denotes the best AE values. W/L is the number of datasets that each method is better and worse than. “# DS Threshold below 0.1” is the number of datasets for which each model’s performance is lower than the threshold.
| Project | DC-SRGM | LSTM | Logistic |
|---|
| F01 | 0.067 | 0.040 | 0.266 |
| F02 | 0.071 | 0.080 | 0.146 |
| F03 | 0.192 | 0.130 | 0.142 |
| F04 | 0.091 | 0.260 | 0.377 |
| F05 | 0.075 | 0.127 | 0.218 |
| F06 | 0.040 | 0.090 | 0.211 |
| F07 | 0.329 | 0.500 | 0.146 |
| F08 | 0.049 | 0.104 | 0.187 |
| F09 | 0.055 | 0.048 | 0.146 |
| F10 | 0.088 | 0.121 | 0.214 |
| F11 | 0.068 | 0.073 | 0.074 |
| F12 | 0.095 | 0.161 | 0.359 |
| F13 | 0.211 | 0.243 | 0.348 |
| F14 | 0.107 | 0.020 | 0.183 |
| F15 | 0.126 | 0.201 | 0.191 |
| Average | 0.110 | 0.146 | 0.220 |
| Improved% | - | +24.6% | +50% |
| W/L | 10/5 | 4/11 | 1/14 |
| # DS Threshold below 0.1 | 10 | 6 | 1 |
Table 7.
Prediction Accuracy of the models on OSS datasets by the AE values. Bold denotes the best AE Values. W/L is the number of datasets for which each method is better and worse than. “# DS Threshold below 0.1” is the number of datasets that each model’s performance is lower than the threshold.
Table 7.
Prediction Accuracy of the models on OSS datasets by the AE values. Bold denotes the best AE Values. W/L is the number of datasets for which each method is better and worse than. “# DS Threshold below 0.1” is the number of datasets that each model’s performance is lower than the threshold.
| Project | DC-SRGM | LSTM | Logistic |
|---|
| Camel | 0.081 | 0.099 | 0.440 |
| Ignite | 0.067 | 0.063 | 0.110 |
| Jclouds | 0.190 | 0.029 | 0.260 |
| Karaf | 0.035 | 0.105 | 0.830 |
| Lucene | 0.270 | 0.438 | 0.950 |
| Maven | 0.120 | 0.122 | 0.240 |
| Shiro | 0.100 | 0.139 | 0.110 |
| Spark | 0.201 | 0.139 | 0.190 |
| Syncope | 0.240 | 0.128 | 0.220 |
| Tez | 0.037 | 0.180 | 0.780 |
| Zookeeper | 0.133 | 0.190 | 0.140 |
| Average | 0.134 | 0.148 | 0.388 |
| Improved% | - | +9.45% | +65.4% |
| W/L | 7/4 | 4/7 | 0/11 |
| # DS Threshold below 0.1 | 5 | 3 | 1 |
Table 8.
Statistic results with the Nemenyi test for the effectiveness of DC-SRGM. * and ** denote that there were significant differences in the groups as the significance levels were 0.1 and 0.01, respectively.
Table 8.
Statistic results with the Nemenyi test for the effectiveness of DC-SRGM. * and ** denote that there were significant differences in the groups as the significance levels were 0.1 and 0.01, respectively.
| | Models | p_Value |
|---|
| Industry | DC-SRGM and LSTM | 0.0710 * |
| DC-SRGM and Logistic | 0.0045 ** |
| OSS | DC-SRGM and LSTM | 0.3657 |
| DC-SRGM and Logistic | 0.0288 * |
Table 9.
Comparison of the prediction accuracy of DC-SRGM using project similarity and project domain type as clustering factors. W/L is the number of datasets that each method is better and worse than. “# DS Threshold below 0.1” is the number of datasets for which each method’s performance is lower than the threshold.
Table 9.
Comparison of the prediction accuracy of DC-SRGM using project similarity and project domain type as clustering factors. W/L is the number of datasets that each method is better and worse than. “# DS Threshold below 0.1” is the number of datasets for which each method’s performance is lower than the threshold.
| Project | Project Similarity | Project Domain Type |
|---|
| F01 | 0.067 | 0.074 |
| F02 | 0.071 | 0.091 |
| F03 | 0.192 | 0.129 |
| F04 | 0.091 | 0.137 |
| F05 | 0.075 | – |
| F06 | 0.040 | 0.119 |
| F07 | 0.329 | 0.714 |
| F08 | 0.049 | 0.186 |
| F09 | 0.055 | 0.113 |
| F10 | 0.088 | 0.096 |
| F11 | 0.068 | 0.066 |
| F12 | 0.095 | – |
| F13 | 0.211 | 0.239 |
| F14 | 0.107 | – |
| F15 | 0.126 | 0.080 |
| Average | 0.110 | 0.170 |
| W/L | 9/3 | 3/9 |
| # DS Threshold below 0.1 | 10 | 7 |
Table 10.
Comparison of the prediction accuracy DC-SRGM using cross-correlation and DTW as similarity measures. W/L is the number of datasets that each method is better and worse than. “# DS Threshold below 0.1” is the number of datasets for which each method’s performance is lower than the threshold.
Table 10.
Comparison of the prediction accuracy DC-SRGM using cross-correlation and DTW as similarity measures. W/L is the number of datasets that each method is better and worse than. “# DS Threshold below 0.1” is the number of datasets for which each method’s performance is lower than the threshold.
| Project | Cross-Correlation | DTW |
|---|
| F01 | 0.067 | 0.037 |
| F02 | 0.071 | 0.039 |
| F03 | 0.192 | 0.499 |
| F04 | 0.091 | 0.081 |
| F05 | 0.075 | 0.048 |
| F06 | 0.040 | 0.170 |
| F07 | 0.329 | 0.988 |
| F08 | 0.049 | 0.166 |
| F09 | 0.055 | 0.089 |
| F10 | 0.088 | 0.115 |
| F11 | 0.068 | 0.169 |
| F12 | 0.095 | 0.115 |
| F13 | 0.211 | 0.165 |
| F14 | 0.107 | 0.060 |
| F15 | 0.126 | 0.089 |
| Average | 0.110 | 0.188 |
| W/L | 8/7 | 7/8 |
| # DS Threshold below 0.1 | 10 | 7 |
Table 11.
Comparison of DC-SRGM for different numbers of days. “# DS Threshold below 0.1” is the number of datasets for which each model’s performance is lower than the threshold.
Table 11.
Comparison of DC-SRGM for different numbers of days. “# DS Threshold below 0.1” is the number of datasets for which each model’s performance is lower than the threshold.
| Project | Day 7 | Day 10 | Day 12 | Day 13 | Day 14 |
|---|
| F01 | 0.070 | 0.078 | 0.072 | 0.060 | 0.060 |
| F02 | 0.050 | 0.030 | 0.045 | 0.040 | 0.050 |
| F03 | 0.580 | 0.377 | 0.167 | 0.160 | 0.170 |
| F04 | 0.100 | 0.087 | 0.073 | 0.031 | 0.028 |
| F05 | 0.130 | 0.070 | 0.029 | 0.024 | 0.020 |
| F06 | 0.140 | 0.225 | 0.039 | 0.043 | 0.030 |
| F07 | 1.140 | 0.780 | 0.333 | 0.270 | 0.140 |
| F08 | 0.410 | 0.098 | 0.009 | 0.011 | 0.015 |
| F09 | 0.160 | 0.111 | 0.007 | 0.005 | 0.005 |
| F10 | 0.190 | 0.112 | 0.143 | 0.110 | 0.079 |
| F11 | 0.140 | 0.020 | 0.006 | 0.007 | 0.007 |
| F12 | 0.190 | 0.230 | 0.058 | 0.066 | 0.060 |
| F13 | 0.430 | 0.190 | 0.025 | 0.260 | 0.270 |
| F14 | 0.130 | 0.100 | 0.131 | 0.120 | 0.100 |
| F15 | 0.080 | 0.190 | 0.125 | 0.087 | 0.050 |
| Average | 0.262 | 0.179 | 0.090 | 0.092 | 0.072 |
| # DS Threshold below 0.1 | 4/15 | 7/15 | 10/15 | 10/15 | 12/15 |
Table 12.
Accuracies of DC-SRGM built with industrial datasets and cross-organization datasets (OSS) are compared with the LSTM model and Logistic model. W/L is the number of datasets that each method is better and worse than. “Threshold below 0.1” is the number of datasets for which each method’s performance is lower than the threshold.
Table 12.
Accuracies of DC-SRGM built with industrial datasets and cross-organization datasets (OSS) are compared with the LSTM model and Logistic model. W/L is the number of datasets that each method is better and worse than. “Threshold below 0.1” is the number of datasets for which each method’s performance is lower than the threshold.
| Project | DC-SRGM | LSTM | Logistic |
|---|
| Industry DS | Cross-org DS |
|---|
| F01 | 0.067 | 0.051 | 0.040 | 0.266 |
| F02 | 0.071 | 0.104 | 0.080 | 0.146 |
| F03 | 0.192 | 0.107 | 0.130 | 0.142 |
| F04 | 0.091 | 0.124 | 0.260 | 0.377 |
| F05 | 0.075 | 0.049 | 0.127 | 0.218 |
| F06 | 0.040 | 0.136 | 0.090 | 0.211 |
| F07 | 0.329 | 0.196 | 0.500 | 0.146 |
| F08 | 0.049 | 0.333 | 0.104 | 0.187 |
| F09 | 0.055 | 0.196 | 0.048 | 0.146 |
| F10 | 0.088 | 0.120 | 0.121 | 0.214 |
| F11 | 0.068 | 0.066 | 0.073 | 0.074 |
| F12 | 0.095 | 0.066 | 0.161 | 0.359 |
| F13 | 0.211 | 0.205 | 0.243 | 0.348 |
| F14 | 0.107 | 0.172 | 0.020 | 0.183 |
| F15 | 0.126 | 0.196 | 0.201 | 0.191 |
| Average | 0.110 | 0.141 | 0.146 | 0.220 |
| W/L | 6/9 | 6/9 | 2/13 | 1/14 |
| # DS Threshold below 0.1 | 10 | 4 | 6 | 1 |