An Enhanced Naked Mole Rat Algorithm for Optimal Cross-Layer Solution for Wireless Underground Sensor Networks

Abstract

Nature-inspired algorithms serve as the backbone of modern computing technology, and over the past three decades, the field has grown enormously. Many applications were solved by such algorithms and are replacing the traditional classical optimization processes. A recent naked mole-rat algorithm (NMRA) was proposed based on the mating patterns of naked mole-rats. This algorithm proved its worth in terms of competitiveness and application to various domains of research. The aim was to propose an algorithm based on NMRA, named enhanced NMRA (ENMRA), by mitigating the problems that this algorithm suffers from: slow convergence, poor exploration, and local optima stagnation. To enhance the exploration capabilities of basic NMRA, grey wolf optimization (GWO)-based search equations were employed. Exploitation was improved using population division methods based on local neighborhood search (LNS) and differential evolution (DE) equations. To avoid the local stagnation problem, a neighborhood search strategy around the best individual was utilized. Such improvements help the new variant to solve highly challenging optimization problems in contrast to existing algorithms. The efficacy of ENMRA was evaluated using CEC 2019 benchmark test suite. The results were statistically analyzed by the Wilcoxon rank-sum test and Friedman rank (f-rank) test. The resulting analysis proved that ENMRA is superior to the competitive algorithms for test functions CEC 2019 with overall effectiveness of 60.33%. Moreover, the real-world optimization problem from underground wireless sensor networks for an efficient cross-layer solution was also used to test the efficiency of ENMRA. The results of comparative study and statistical tests affirmed the efficient performance of the proposed algorithm.

1. Introduction

In the present world, there are numerous real-world applications of optimization. Currently, many scientific fields and industrial companies face many hurdles in finding an appropriate optimization tool or, more precisely, an optimization algorithm to solve real-world problems. The main reason to employ such algorithms is that the majority of the real-life applications may be expressed as potential domain optimization problems depending upon their nature and the number of objectives to be optimized. This can be estimated from the fact that these algorithms find application in almost every research domain, such as economics, engineering, mathematics, signal processing, weather forecasting, operation research, management, production planning, scheduling, routing problems, machine learning, and others. These optimization problems are highly complex and pose a challenge for researchers to solve them efficiently. In recent times, nature-inspired algorithms (NIAs) have dominated the various spheres of optimization research and are in use in almost every field [1].

NIAs are considered efficient solutions for solving various real-life issues. These algorithms include differential evolution (DE) [2], cuckoo search (CS) [3], flower pollination algorithm (FPA) [4], and others. These algorithms incorporate four major processes to simulate natural behavior: initialization, global search, local search, and selection. Although these algorithms demonstrate exceptional performance and competitiveness, many theoretical and experimental analyses proved that they are still dependent on the choice of tuning parameters [5,6]. Such parameters include scaling factor, switch probability, crossover/mutation rate, local/global search, population size, and standard randomization. Early investigation proved that these algorithms require a trial-and-error methodology to tune their parameters [6]. This method is tedious and hence is not efficient. Apart from that, these algorithms suffer from premature convergence, slow convergence, local optima stagnation, and more [5]. Such drawbacks make these algorithms vulnerable to poor solution generation, thus adding to less diversity and, hence, unable to find the desired solution.

An important factor is the local optima stagnation and slow convergence associated with the above algorithms. DE has a deficiency of premature convergence and stagnation. Also, DE sometimes stops proceeding toward the global optima, even though the population has not converged to local optima or any other point. It was found that FPA also suffers from the local optima stagnation problem and slow convergence [7,8], and hence, the requirement of a new enhanced version of such algorithms is needed. Overall, NIAs suffer from these problems, and there is a requirement to design new algorithms or improve the existing algorithms for prospective researchers. In this respect, a substantial effort was made to eradicate the issues above by introducing new enhanced versions of nature-inspired algorithms using new and novel strategies. These algorithms perform significantly better but have some inherent drawbacks. Many hybrid and improved versions of these procedures were also investigated to eradicate the flaws of basic algorithms.

The no free lunch (NFL) theorem [9] is an essential source of inspiration for investigators to propose novel algorithms that meet the problem objectives. According to the theory, no algorithm can be regarded as the single solution to all domain research tasks, and problem-based tweaks are always necessary for enhanced performance [9]. The fundamental reason for this adaptation is that each domain’s research challenge may have a variety of situations, such as complexity, dimension size, nature (constrained or unconstrained), and so on. The high peak in a problem and the local minimal solutions make it difficult for investigators to propose improved variants and deliver consistent outcomes.

A new algorithm was introduced by using the worker–breeder relationship of naked mole-rats (NMRs) [5]. This NMR algorithm (NMRA) aimed to provide an altogether new metaheuristic algorithm for prospective researchers to exploit and apply to their research domains. However, the NMRA has the disadvantage of poor exploration and was predicted to produce less consistent outcomes. The lack of randomness in the algorithm’s search equations is the primary cause of inadequate investigation. This work mainly focused on designing NMRA with improved exploration and exploitation. The authors aimed to achieve this by using randomly generated solutions inside the search space using grey wolf optimization (GWO) [10], instead of moving all the random solutions toward the best particles. For exploitation, it was required that the unexpected solutions follow the local group leader or simply the current best solution. So here, the general equation of both exploration and exploitation phases were enhanced to achieve better results.

This work dealt with the proposal to enhance the exploitation and exploration characteristics of a new algorithm, namely NMRA, to solve CEC 2019 benchmark problems and some real-world applications, such as an energy-throughput efficient, cross-layer solution for underground wireless sensor networks.

The major contributions of this work are summarized as follows:

• To improve the exploration and exploitation tendency of NMRA, a new variant of NMRA was presented.
• The exploration capability was enhanced with the implementation of GWO-inspired equations in basic NMRA.
• The local neighborhood search along with DE equations were employed for enhanced exploitation characteristics of NMRA.
• The performance of the proposed NMRA variant was evaluated using a set of CEC 2019 benchmark test functions and a real-time underground wireless sensor network problem.

The rest of the paper is structured as follows. Section 2 deals with the related work. The description of NMRA and enhanced NMRA (ENMRA) is presented in Section 3. The statistical testing of ENMRA is evaluated in Section 4. The framework of DECEN is given in Section 5 to attain optimal energy throughput as a cross-layer design and the system model for a cross-layer communication solution. Section 6 concludes the paper with possible future work.

2. Related Work

To find the best possible solutions, many real-world problems are formulated as optimization problems. Hence, many researchers work in tandem to introduce new effective methods and tools to resolve such domain-specific optimization tasks. The objective is to attain the optimal global solution for an objective function under a specific set of decision variables within a particular range. Without the loss of generality, these optimization problems are represented mathematically either as minimization of a maximization problem.

Due to various optimization problems and real-world applications in many related fields, different optimization algorithms were developed by researchers. Earlier classical methods were found to be effective [10,11,12,13,14]. These classical methods used differential mathematical calculus methods requiring two main features. The first feature was to differentiate the objective function of the optimization problem concerning X, and second, the derivative ought to be continuous. These requirements limited classical optimization techniques to a specific set of benchmark optimization problems and only a particular set of real-world applications. Apart from that, these algorithms easily got trapped into local optima and required more computational time and cost than other algorithms [14]. For millions of years, nature has continuously solved problems. Biological systems, such as immune systems, help eliminate foreign bodies; perception is used to recognize different patterns, decision-making helps design robots, etc. Such systems show high-level computational intelligence present in nature, and these algorithms are called NIAs. Such algorithms are popular in various applications, such as business management, traveling optimal paths, and others [15]. They are popular due to their flexibility, resilience, and quick response. These are population-based algorithms, which eliminate the need for an initial assumption when solving any problem. These algorithms are suitable for highly complex domain research challenges due to a smaller number of tuned parameters.

NIAs have dominated the sphere of optimization research. Because of their simple structure, the low requirement of parametric and gradient information, and simple conceptual modeling, these algorithms are found to provide highly viable solutions. Broadly, these algorithms are classified into two categories, namely evolutionary algorithms (EAs), based on Darwin’s theory of natural selection, and swarm intelligent (SI) algorithms using the concept of social and swarming behavior of animal species. All EAs and SIs algorithms are stochastic and require a certain population for generating an initial solution. Certain operators, such as crossover, mutation, and selection are used to generate new solutions. The new solutions thus found are evaluated over subsequent iterations, and over a due course of iterations or stopping criteria, the final solution is obtained. Generally, EAs were the first of their kind and used the Darwinian theory of survival of the fittest. The genetic algorithm (GA) [16], proposed in the late 1970s, can be called the mother of all EAs. This algorithm is one of the best EAs and is still in use. The first variant was a binary algorithm and was lately extended to continuous domain. At present, the algorithm is mostly used to optimize multi-objective problems with NSGA-II as one of the best variants. For single-objective optimization, the EA-based algorithms were projected, namely evolutionary strategy (ES) [17], DE [2], BBO [18], GP [19], ALO [20], PBIL [21], and others.

SI is another category of NIAs in that swarm refers to a set of species, such as bees, monkeys, wolves, ants, and birds, that work together to achieve a certain goal. SIs make use of these species’ learning abilities and adaptability to solve extremely complex problems. Beni and Wang [22] presented the first work on SI in cellular robots. It has since been used in nearly every sector, including electrical load dispatch problems, business modelling, forecasting, search optimization, structural engineering design, etc. Main algorithms under this category include ABC algorithm [23], FA [24], DA [25], FPA [4], SSA [26], CS [27], fitness-dependent optimizer (FDO) [28], GWO [10], and others.

Inspired by the collective nature of the community of interacting scientists, the Community of Scientists Optimization (CoSO) algorithm [29] was proposed. The solutions were updated based on the interactions of a group of scientists pursuing their research outcomes by raising finances to continue their research. In addition to the above-mentioned algorithms, there are some recent algorithms, such as Aquila optimizer (AO) [30], arithmetic optimization algorithm (AOA) [31], and hybridized optimization algorithms, such as adaptive SSA (ASSA) [32], adaptive FPA (AFPA) [33], CS version 1.0 (CV 1.0) [34], and NMRA version 3.0 (NMRV 3.0) [35] that are employed in every field of research, such as mathematics, medical imaging, robotics, antenna arrays, image segmentation, artificial immune systems, business management, and others. Furthermore, such algorithms are easier to implement and demonstrate a major contribution to basic optimization techniques.

However, there are certain downsides to using nature-inspired algorithms. They may be appropriate for specific problems but not for others. The NFL theorem [9] confirmed this. Many scholars are inspired by this notion to examine and develop novel algorithms for tackling optimization problems. The inherent shortcomings of existing algorithms, such as inadequacy in exploring, stagnation, and premature convergence of population-based algorithms, are another motivation to create new algorithms. As a result, one must evaluate, hybridize, and propose more powerful algorithms to address optimization issues to eliminate these flaws.

Compared to prior NIAs, such as FA, CS, GWO, and others, NMRA is a newly presented approach that offers extremely dependable results [35]. However, compared to upgraded variants or hybrid algorithms, the NMRA was proved to produce less accurate results. This is primarily due to NMRA’s inadequate exploration and exploitation capabilities. A closer examination of these notions revealed that because the worker phase contains less randomness in the search space, the algorithm was more likely to get stuck in a local optimum, resulting in lower performance. This can be addressed by introducing new potential equations in the worker and breeder phases, significantly improving the algorithm’s global and local searching capabilities.

3. Proposed Naked Mole-Rat Algorithm Variant

3.1. Naked Mole-Rat Algorithm

The NMRA was developed in response to the behavioral characteristics of NMRs [5]. Thus, NMRA is capable of simulating the mating patterns of NMRs. NMRs live in groups of about 70–80 individuals led by a female queen who is solely interested in mating, and the rest are worker NMRs and breeder NMRs. For the sake of simplicity, breeders are considered to be 20% of total NMRs [5].

Breeders are the productive NMRs, with their primary function being to mate with queens, while the remaining NMRs perform a variety of other tasks. The NMRA consists of many steps. Initially, an NMR group is created that is further divided into worker and breeder subgroups. Next, breeders select their breeding stock based on their breeding potential. The following sections discuss the steps taken by the NMRA.

Initialization. A randomly generated population of n NMRs is obtained where each NMR is denoted as a vector in a vector space (D-dimensional), initialized as follows:

$$NM{R}_{i,j}=NM{R}_{min,j}+U\left(0,1\right)\times \left(NM{R}_{min,j}-NM{R}_{max,j}\right)$$

(1)

where $i\in \left[1,2,\dots ,\dots ,n\right]$, $j\in \left[1,2,\dots ,\dots ,D\right]$, $NM{R}_{i,j}$ is the $i$th solution in the $j$th dimension, $NM{R}_{min,j}$ and $NM{R}_{max,j}$ are the lower and upper limit of the problem under study, and $U\left(0,1\right)$ is a random number between 0 and 1. The fitness of each solution is evaluated following the initialization stage. Breeder and worker NMRs are classified based on their fitness value attained, and out of these, the best NMR is determined.

Worker Phase. In this stage, the workers (W) attempt to advance their fitness to pursue work as a breeder.

The updated solution is created using the updated equation as follows:

$$w_i^{t+1}=w_i^t+\lambda (w_j^t-w_k^t)$$

(2)

where $w_i^t$ denotes the $i$th worker in the $t$th iteration, $w_i^{t+1}$ signifies the new fitness solution, and $w_j^t$ and $w_k^t$ are the randomly chosen worker NMRs. The $\lambda$ is the random variable uniformly distributed $\left[0, 1\right]$.

Breeder Phase. Breeder (B) must improve his fitness to be considered as a mating partner or to maintain his status as a breeder. The breeders are upgraded based on the breeding probability (bp initially set to 0.5). If the breeder is unable to supersede its fitness, it may be reintroduced into the worker pool:

$$b_i^{t+1}=\left(1-\lambda \right)b_i^t+\lambda \left(d-b_i^t\right)$$

(3)

where $b_i^t$ signifies the $i$th breeder in the $t$th iteration and the mating frequency is controlled by parameter $\lambda$.

The process is repeated iteratively until the termination requirements are satisfied. The best breeder from the entire population is a possible outcome to the situation under consideration. The pseudocode of NMRA is given in Algorithm 1 as follows:

Algorithm 1. Pseudocode of NMRA.

Input: Define objective function f(NMR), NMR = (NMR1, NMR2, …, NMRD)

Output: Determine current best solution $d$

Initialization: Initialize NMRs: n, breeders B: n/5, workers W: B − n

Define breeding probability: bp

while iterations$\le {\mathit{t}}_{\mathit{m}\mathit{a}\mathit{x}}$

fori = 1:w

perform worker phase:${\mathit{w}}_{\mathit{i}}^{\mathit{t}\mathbf{+}\mathbf{1}}\mathbf{=}{\mathit{w}}_{\mathit{i}}^{\mathit{t}}\mathbf{+}\mathit{\lambda }({\mathit{w}}_{\mathit{k}}^{\mathit{t}}-{\mathit{w}}_{\mathit{j}}^{\mathit{t}})$

evaluate${\mathit{w}}_{\mathit{i}}^{\mathit{t}\mathbf{+}\mathbf{1}}$

end for

fori = 1:B

if rand >bp

perform breeder phase:${\mathit{b}}_{\mathit{i}}^{\mathit{t}\mathbf{+}\mathbf{1}}\mathbf{=}\mathbf{\left(}\mathbf{1}-\mathit{\lambda }\mathbf{\right)}{\mathit{b}}_{\mathit{i}}^{\mathit{t}}\mathbf{+}\mathit{\lambda }\mathbf{\left(}\mathit{d}-{\mathit{b}}_{\mathit{i}}^{\mathit{t}}\mathbf{\right)}$

end if

evaluate${\mathit{b}}_{\mathit{i}}^{\mathit{t}+\mathbf{1}}$

end for

combine the updated worker and breeder population

evaluate the population

update the overall best d

update iteration count

end while

update final bestd

end

3.2. Enhanced Naked Mole-Rat Algorithm

Due to its simplicity and linear nature, NMRA received attention in the recent past [35]. The updated, enhanced NMRA (ENMRA) aims to improve efficiency by enhancing its fundamental exploitation and exploration capabilities. Exploration is enriched with the implementation of GWO-inspired equations [10] in basic NMRA, and local neighborhood search (LNS), along with DE equations, are used for enhanced exploitation [36]. The notion of LNS is addressed as follows.

Local Neighborhood Search (LNS). To boost the search space in the worker phase, NMRA employs the current solution and local information. In addition, the local neighborhood search (LNS) model is implemented to enhance the search functionality with increased convergence speed [37].

The key concept is to update the old solution to the new one in a small neighborhood using the best solution. The initial population $X=\left(X_1, X_2, X_3,\dots , X_n\right), X_i\left(i\in \left[1,\dots , n\right]\right)$ is a vector (D-dimensional). The neighborhood radius r (where 2r + 1 <$n$) is defined for each vector $X_i$; that is, $X_i$ neighborhood comprises of $X_{i-r}, \dots , X_i, \dots , X_{i+r}$. The vectors here are structured according to their indices into a ring topology [35]. Figure 1 represents the notion of the LNS model, which is defined as:

$$L_i=X_i+m\ast \left(X_{n\_opt}-X_i\right)+n\ast \left(X_p-X_q\right)$$

(4)

where $X_{n\_opt}$ is the optimum solution so far in the $X_i$; m, n ∈ rand () are the scaling factors and p, q ∈ [i − r, i + r] (p$\ne$ q$\ne$i). In the improved NMRA, the best solution is modified using Equation (4), and the modified solution executes the worker phase:

$$x_i^{t+1}=L_i^t+r\ast \left(x_k^t-x_m^t\right)$$

(5)

where r∈ rand( ) is a scaling factor, $L_i$ is the best solution modified using LNS, and $x_k^t and x_m^t$ are randomly selected vectors for kth and mth NMR with $k\ne m$.

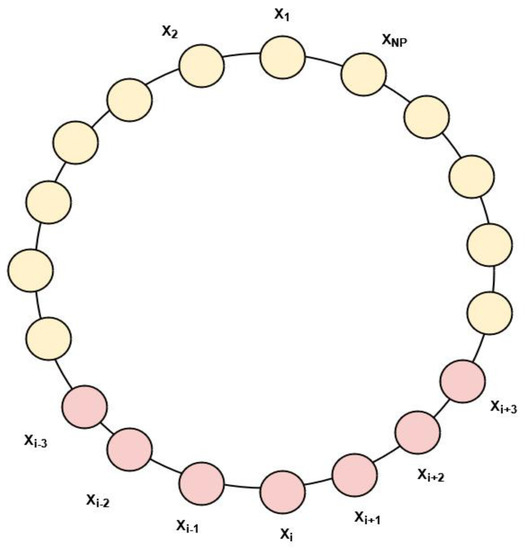
Figure 1. Neighborhood ring topology of radius 3.

Worker Phase. The worker phase is upgraded in the enhanced NMRA to improve the performance of conventional NMRA. Here, the total iterations are divided into two portions. The regular NMRA’s general Equation (2) is utilized for the latter part of the iterations, and a new search equation is introduced for the first half. This equation is supported by considering the mean of the first three solutions that are created based on the best solution available and is represented as:

$$w_1=w_i-A_1\left(C_1·d-w_i\right), w_2=w_i-A_2\left(C_2·d-w_i\right), w_3=w_i-A_3\left(C_3·d-w_i\right)$$

(6)

$$w_{new}=\frac{w_1+w_2+w_3}{3}$$

(7)

The main idea for this adjustment came from GWO search equations [10]. The solution in GWO is built by tweaking the parameters to the best search agent position. GWO search equations help to improve the randomness in the algorithm’s worker phase search equations, and hence to overcome the poor exploration of conventional NMRA. To obtain a new solution, the same definition is employed:

$$w_i^{t+1}=w_{new}^t+\lambda (w_j^t-w_k^t)$$

(8)

where $A_1$, $A_2$, $A_3$ and $C_1$, $C_2$, $C_3$ belong to $A$ and $C$, respectively, and are given as:

$$A=2a{r}_1-a, C=2· r_2$$

(9)

where $a$ is a random number that is linearly decreasing [0, 2] in relation to iterations and $r_1$ and $r_2$ are the uniformly distributed random numbers. The random number allows the agents to move around within the search space at any location, enhancing the NMRA’s exploration capabilities.

Breeder Phase. In this phase, to enhance the exploitation efficiency of NMRA, the population is separated into three sections, and the final solution is evaluated using three separate search strategies. First, the general equation similar to standard NMRA is used as follows for the first part of the population:

$$b_i^{t+1}=\{\begin{array}{c}{b}_{new}^t+\lambda (b_j^t-b_k^t), if 0\ge t\ge t_{max}/2\hfill \\ b_i^t+\lambda (b_j^t-b_k^t), if\frac{t_{max}}{2}+1\ge t\ge t_{max}\hfill \end{array}$$

(10)

For the second part of the population, an LNS-based search equation is used, inspired by Equation (4) as follows:

$$b_i^{t+1}=\{\begin{array}{c}{L}_{new}^t+\lambda \left(b_k^t-b_m^t\right), if 0\ge t\ge t_{max}/2\hfill \\ L_i^t+\lambda \left(b_k^t-b_m^t\right), if\frac{t_{max}}{2}+1\ge t\ge t_{max}\hfill \end{array}$$

(11)

where $L_i^t$ is the best solution modified using LNS and $\lambda$ is a uniformly generated scaling factor [0, 1]. Here $L_{new}=b_{new}+m\ast \left(b_{n\_opt}-b_{new}\right)+n\ast \left(b_p-b_q\right)$ using Equation (4).

For the third part of the population, the search equation inspired by DE is used and is given by:

$$b_i^{t+1}=\{\begin{array}{c}{b}_{new}^t+ \lambda \left(\left(b_j^t-b_k^t\right)+\left(b_p^t-b_q^t\right)\right), if 0\ge t\ge t_{max}/2\hfill \\ b_i^t+ \lambda \left(\left(b_j^t-b_k^t\right)+\left(b_p^t-b_q^t\right)\right), if\frac{t_{max}}{2}+1\ge t\ge t_{max}\hfill \end{array}$$

(12)

Also, in the basic NMRA breeder phase, the search directions of the new breeders are simply updating processes within the population by best-estimated NMR. However, the entire algorithm quickly gets into premature convergence if the globally optimal individuals collapse into the local optima. Therefore, the guiding function of the better individuals potentially residing near the optimum solution is to minimize the probability of the algorithm getting into the local optimum. In this work, the random individuals near the best solution are used to substitute the current optimal individuals to direct the search for the algorithm to expand the probability of deviating the algorithm from the local optima.

The updated scheme for the neighborhood search of the best individual in ENMRA is:

$$b_i^{t+1}=\left(1-\lambda \right)b_i^t+\lambda \left(d\left(1+\mu .unifrnd\left(-1, 1\right)\right)-b_i^t\right)$$

(13)

where µ is the disturbance coefficient and$unifrnd\left(-1, 1\right)$ is the uniformly distributed variable within ($-1$, 1). The current best solution is taken as the center and μ as the step size in the neighborhood quest for the optimal individual, and the algorithm searches between segment $d\left(1-\mu \right)$ and $d\left(1+\mu \right)$. This essentially extends the search direction and raises the probability of the algorithm jumping from the local optimal. The pseudocode of ENMRA is shown in Algorithm 2 as follows:

Algorithm 2. Pseudocode of Enhanced NMRA.

Input: Define objective function (NMR), NMR = (NMR1, NMR2, …, NMRD)

Output: Determine current best solution $d$

Initialization: Initialize NMRs: n, B: n/5, W: B − n

Define breeding probability: bp

whileiterations <$t_{max}$

fori = 1: workers

perform worker phase:

if$t\le t_{max}/2$

$w_1=w_i-A_1\left(C_1·d-w_i\right)$$, w_2=w_i-A_2\left(C_2·d-w_i\right)$$, w_3=w_i-A_3\left(C_3·d-w_i\right)$

$w_{new}=\frac{w_1+w_2+w_3}{3}$

$w_i^{t+1}=w_{new}^t+\lambda (w_j^t-w_k^t)$

else

$w_i^{t+1}=w_i^t+\lambda (w_j^t-w_k^t)$

evaluate${\mathit{w}}_{\mathit{i}}^{\mathit{t}+\mathbf{1}}$

end for

fori = 1: breeders

ifrand >bp

perform breeder phase: divide the whole population into three parts

For the first part of population:

$b_i^{t+1}=\{\begin{array}{c}{b}_{new}^t+\lambda (b_j^t-b_k^t), if 0\ge t\ge t_{max}/2\hfill \\ b_i^t+\lambda (b_j^t-b_k^t), if\frac{t_{max}}{2}+1\ge t\ge t_{max}\hfill \end{array}$

For the second part of population:

$b_i^{t+1}=\{\begin{array}{c}{L}_{new}^t+\lambda \left(b_k^t-b_m^t\right), if 0\ge t\ge t_{max}/2\hfill \\ L_i^t+\lambda \left(b_k^t-b_m^t\right), if\frac{t_{max}}{2}+1\ge t\ge t_{max}\hfill \end{array}$

For the third part of the population:

$b_i^{t+1}=\{\begin{array}{c}{b}_{new}^t+ \lambda \left(\left(b_j^t-b_k^t\right)+\left(b_p^t-b_q^t\right)\right), if 0\ge t\ge t_{max}/2\hfill \\ b_i^t+ \lambda \left(\left(b_j^t-b_k^t\right)+\left(b_p^t-b_q^t\right)\right), if\frac{t_{max}}{2}+1\ge t\ge t_{max}\hfill \end{array}$

end if

evaluate${\mathit{b}}_{\mathit{i}}^{\mathit{t}\mathbf{+}\mathbf{1}}$

end for

Updating strategy for the neighborhood search

$b_i^{t+1}=\left(1-\lambda \right)b_i^t+\lambda \left(d\left(1+\mu .unifrnd\left(-1,1\right)\right)-b_i^t\right)$

combine the updated worker and breeder population

evaluate the population

update the overall best d

update iteration count

end while

update final best$d$

end

4. Statistical Testing of ENMRA Algorithm

The 100-Digit Challenge [38], a set of 10 CEC 2019 benchmark functions, was nominated for ENMRA evaluation. All the test functions are scalable. Comparison with FPA [4], DA [25], SSA [26], CS [27], FDO [28], GWO [10], ASSA [32], CV 1.0 [34], NMRA [5], and NMRV 3.0 [35] was performed to test the efficacy of ENMRA. The ENMRA and competitive algorithms were coded using MATLAB version R2020a. All compared methods were run under the same configuration, an Intel^R Core^TM, 2.4 GHz (i5 CPU) with 4 GB memory to ensure a fair comparison. Each algorithm underwent 500 iterations with the help of 30 search agents. The parameter settings of competitive algorithms are given in Table 1. The findings are reported in terms of the performance metric such as best, worst, mean, and standard deviation values for 30 independent runs for each algorithm under consideration. Except in CEC02, CEC06–07, and CEC09–10 (see Table 2), ENMRA outperformed competitive algorithms. The box plots and convergence graphs of various methods for various test functions are shown in Figure 2.

Table 1. Parameter settings of competitive algorithms.

Algorithm	Parameters
FPA [3]	$p_s$ = 0.5
GWO [8]	A = linearly decreasing from 2 to 0
SSA [24]	$c_1=c_2=c_3=$ rand[0, 1]
CS [25]	probability (pa) = 0.25
DA [23]	w = [0.4–0.9], s = 0.1, a = 0.1, c = 0.7, f = 1, e = 1
FDO [26]	weight factor (Wf) = 0; r is rand[−1, 1]
ASSA [29]	$c_1=c_2=c_3=$rand[0, 1]; $\lambda =3$
CV 1.0 [31]	$A=\mathrm{linearly} \mathrm{decreasing} \mathrm{from}$2 to 0,r1 = r2 = rand[0, 1]
NMRA [4]	bp = 0.5; λ = rand[0, 1]; number of breeders B = population(n)/5
NMRV 3.0 [32]	bp = 0.5; λ = rand[0, 1]; B = n/5
ENMRA	bp = 0.5; λ = rand[0, 1]; B = n/5; ; a = linearly decreasing from 2 to 0; r1 = r2 = rand[0, 1]

Table 2. Statistical analysis of competitive algorithms for CEC 2019 test suite.

Function	Metric	FPA	GWO	SSA	CS	DA	FDO	ASSA	CV 1.0	NMRA	NMRA 3.0	ENMRA
CEC01	Best	1.37E + 08	5.15E + 04	4.18E + 08	1.00E + 10	2.03E + 09	7.32E + 07	7.55E + 04	1.00E + 10	8.91E + 05	3.86E + 04	3.68E + 04
	Median	4.41E + 08	3.46E + 07	2.68E + 09	1.00E + 10	4.09E + 10	6.37E + 08	2.74E + 05	1.00E + 10	3.07E + 09	5.24E + 06	3.94E + 04
	Worst	1.20E + 09	6.35E + 08	2.63E + 10	1.00E + 10	1.67E + 11	7.66E + 09	1.24E + 06	1.00E + 10	3.58E + 10	6.59E + 08	4.82E + 04
	Mean	5.03E + 08	1.14E + 08	5.38E + 09	1.00E + 10	4.95E + 10	1.34E + 09	5.57E + 05	1.00E + 10	6.65E + 09	6.35E + 07	4.01E + 04
	Std	2.78E + 08	1.64E + 08	6.16E + 09	0.00E + 00	4.73E + 10	1.72E + 09	4.12E + 05	0.00E + 00	9.21E + 09	1.32E + 08	2.45E + 03
	p-rank	−	−	−	−	−	−	−	−	−	−
	f-rank	5	4	7	9	11	6	2	9	8	3	1
CEC02	Best	1.81E + 01	1.73E + 01	1.73E + 01	1.73E + 01	1.74E + 01	1.73E + 01	1.75E + 01	7.36E + 03	1.74E + 01	1.73E + 01	1.73E + 01
	Median	2.16E + 01	1.73E + 01	1.73E + 01	1.73E + 01	3.77E + 01	1.73E + 01	1.77E + 01	1.61E + 04	1.75E + 01	1.73E + 01	1.73E + 01
	Worst	3.37E + 01	1.73E + 01	1.74E + 01	1.73E + 01	3.16E + 02	1.73E + 01	1.90E + 01	2.44E + 04	1.77E + 01	1.74E + 01	1.73E + 01
	Mean	2.24E + 01	1.73E + 01	1.73E + 01	1.73E + 01	6.00E + 01	1.73E + 01	1.79E + 01	1.61E + 04	1.75E + 01	1.73E + 01	1.73E + 01
	Std	3.66E + 00	2.69E-04	1.48E-02	3.44E-04	6.71E + 01	1.65E-05	4.10E-01	4.57E + 03	7.24E-02	6.40E-03	6.24E-05
	p-rank	−	−	−	−	−	+	−	−	−	−
	f-rank	9	3	6	4	10	1	8	11	7	5	2
CEC03	Best	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01
	Median	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01
	Worst	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01
	Mean	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01	1.27E + 01
	Std	1.47E-07	2.18E-07	1.93E-13	9.07E-11	5.25E-04	1.40E-11	3.14E-05	9.19E-04	4.73E-05	9.00E-15	1.53E-16
	p-rank	−	−	−	−	−	−	−	−	−	−
	f-rank	6	7	3	5	11	4	8	10	9	2	1
CEC04	Best	9.52E + 01	2.58E + 01	1.58E + 01	1.79E + 01	2.17E + 01	1.10E + 01	7.14E + 02	9.77E + 03	4.53E + 02	4.23E + 01	8.50E + 00
	Median	1.37E + 02	5.56E + 01	3.87E + 01	2.56E + 01	3.94E + 02	3.27E + 01	2.45E + 03	2.82E + 04	1.10E + 03	6.75E + 02	4.68E + 01
	Worst	1.93E + 02	9.38E + 01	7.15E + 01	3.91E + 01	9.05E + 02	8.56E + 01	4.64E + 03	5.43E + 04	2.06E + 03	1.96E + 03	6.65E + 01
	Mean	1.37E + 02	5.87E + 01	4.04E + 01	2.74E + 01	3.80E + 02	3.75E + 01	2.63E + 03	2.97E + 04	1.15E + 03	7.05E + 02	4.28E + 01
	Std	2.50E + 01	1.82E + 01	1.55E + 01	6.04E + 00	2.72E + 02	2.05E + 01	1.06E + 03	9.60E + 03	4.12E + 02	5.32E + 02	1.60E + 01
	p-rank	−	−	−	−	−	−	−	−	−	−
	f-rank	6	4	3	2	8	5	10	11	7	9	1
CEC05	Best	1.38E + 00	1.12E + 00	1.04E + 00	1.03E + 00	1.12E + 00	1.06E + 00	2.06E + 00	3.53E + 00	1.93E + 00	1.16E + 00	1.01E + 00
	Median	1.60E + 00	1.32E + 00	1.25E + 00	1.06E + 00	1.42E + 00	1.15E + 00	2.47E + 00	7.97E + 00	2.17E + 00	1.49E + 00	1.07E + 00
	Worst	1.72E + 00	1.88E + 00	1.50E + 00	1.12E + 00	2.18E + 00	1.54E + 00	3.09E + 00	1.22E + 01	2.32E + 00	2.69E + 00	1.74E + 00
	Mean	1.58E + 00	1.43E + 00	1.26E + 00	1.06E + 00	1.49E + 00	1.19E + 00	2.49E + 00	7.99E + 00	2.17E + 00	1.59E + 00	1.15E + 00
	Std	8.72E-02	2.55E-01	1.39E-01	1.68E-02	3.15E-01	1.23E-01	2.91E-01	1.71E + 00	8.31E-02	3.44E-01	2.00E-01
	p-rank	−	−	−	−	−	−	−	−	−	−
	f-rank	8	5	4	2	6	3	10	11	9	7	1
CEC06	Best	9.50E + 00	9.91E + 00	1.41E + 00	7.34E + 00	5.08E + 00	9.31E + 00	9.65E + 00	1.13E + 01	9.52E + 00	9.65E + 00	9.55E + 00
	Median	1.07E + 01	1.08E + 01	5.03E + 00	9.36E + 00	8.78E + 00	1.11E + 01	1.16E + 01	1.57E + 01	1.07E + 01	1.14E + 01	1.08E + 01
	Worst	1.15E + 01	1.18E + 01	1.02E + 01	1.01E + 01	1.11E + 01	1.23E + 01	1.30E + 01	1.75E + 01	1.17E + 01	1.25E + 01	1.19E + 01
	Mean	1.07E + 01	1.08E + 01	5.01E + 00	9.08E + 00	8.78E +00	1.10E + 01	1.14E + 01	1.56E + 01	1.08E + 01	1.13E + 01	1.09E + 01
	Std	6.07E-01	5.93E-01	2.06E + 00	7.91E-01	1.51E + 00	7.62E-01	9.15E-01	1.23E + 00	5.72E-01	7.07E-01	6.16E-01
	p-rank	+	+	+	+	+	−	−	−	+	−
	f-rank	4	6	1	3	2	8	10	11	5	9	7
CEC07	Best	5.03E + 00	2.57E + 00	3.01E + 00	4.61E + 00	5.13E + 00	3.36E + 00	3.85E + 02	1.14E + 03	4.88E + 00	2.67E + 02	6.87E + 01
	Median	5.76E + 00	4.83E + 00	5.13E + 00	5.36E + 00	5.92E + 00	5.12E + 00	9.19E + 02	2.12E + 03	5.91E + 00	8.27E + 02	5.38E + 02
	Worst	6.27E + 00	6.65E + 00	6.38E + 00	5.74E + 00	6.79E + 00	6.28E + 00	1.47E + 03	2.64E + 02	6.92E + 00	1.35E + 03	1.02E + 03
	Mean	5.70E + 00	4.86E + 00	5.08E + 00	5.34E + 00	5.85E + 00	5.05E + 00	9.08E + 02	2.07E + 03	5.85E + 00	7.75E + 02	5.11E + 02
	Std	3.40E-01	1.11E + 00	7.27E-01	2.38E-01	4.22E-01	6.27E-01	2.35E + 02	4.13E + 02	5.42E-01	2.34E + 02	2.78E + 02
	p-rank	+	+	+	+	+	+	−	−	+	−
	f-rank	5	1	2	4	6	3	10	11	7	9	8
CEC08	Best	5.11E + 00	3.45E + 00	4.05E + 00	4.82E + 00	5.16E + 00	2.69E + 00	4.68E + 00	6.74E + 00	4.42E + 00	2.86E + 00	2.14E + 00
	Median	5.77E + 00	5.27E + 00	5.37E + 00	5.33E + 00	5.72E + 00	4.86E + 00	6.34E + 00	8.45E + 00	5.87E + 00	5.76E + 00	4.96E + 00
	Worst	6.47E + 00	6.75E + 00	6.14E + 00	5.65E + 00	6.53E + 00	6.02E + 00	6.90E + 00	9.09E + 00	6.88E + 00	6.79E + 00	6.74E + 00
	Mean	5.77E + 00	5.18E + 00	5.34E + 00	5.26E + 00	5.71E + 00	4.85E + 00	6.15E + 00	8.32E + 00	5.93E + 00	5.65E + 00	4.83E + 00
	Std	3.41E-01	9.32E-01	4.67E-01	1.95E-01	4.10E-01	7.80E-01	5.84E-01	5.81E-01	5.91E-01	8.41E-01	1.83E-01
	p-rank	−	−	−	−	−	−	−	−	−	−
	f-rank	8	3	5	4	7	2	10	11	9	6	1
CEC09	Best	3.17E + 00	3.11E + 00	2.37E + 00	2.49E + 00	2.88E + 00	2.39E + 00	1.33E + 02	3.27E + 03	6.83E + 00	3.27E + 00	2.65E + 00
	Median	4.83E + 00	4.28E + 00	2.47E + 00	2.75E + 00	4.17E + 00	2.51E + 00	3.29E + 02	5.91E + 03	7.90E + 01	7.43E + 00	4.19E + 00
	Worst	7.82E + 00	6.36E + 00	2.96E + 00	2.94E + 00	6.71E + 00	3.17E + 00	7.51E + 02	1.06E + 04	3.92E + 02	1.88E + 02	5.10E + 00
	Mean	4.74E + 00	4.51E + 00	2.52E + 00	2.75E + 00	4.30E + 00	2.55E + 00	3.69E + 02	6.11E + 03	9.12E + 01	4.48E + 01	4.19E + 00
	Std	9.58E-01	9.03E-01	1.20E-01	1.34E-01	9.20E-01	1.54E-01	1.41E + 02	1.94E + 03	6.96E + 01	5.65E + 01	6.57E-01
	p-rank	−	−	+	+	−	+	−	−	−	−
	f-rank	7	6	1	3	5	2	10	11	9	8	4
CEC10	Best	2.02E + 01	2.02E + 01	2.00E + 01	2.02E + 01	2.00E + 01	2.34E-08	2.03E + 01	2.07E + 01	1.97E + 01	1.44E + 01	6.35E + 00
	Median	2.04E + 01	2.05E + 01	2.00E + 01	2.03E + 01	2.02E + 01	2.00E + 01	2.05E + 01	2.11E + 01	2.05E + 01	2.05E + 01	2.05E + 01
	Worst	2.06E + 01	2.06E + 01	2.05E + 01	2.04E + 01	2.05E + 01	2.00E + 01	2.07E + 01	2.15E + 01	2.06E + 01	2.07E + 01	2.06E + 01
	Mean	2.04E + 01	2.05E + 01	2.00E + 01	2.03E + 01	2.02E + 01	1.93E + 01	2.05E + 01	2.11E + 01	2.04E + 01	2.02E + 01	2.00E + 01
	Std	9.37E-02	9.62E-02	1.05E-01	6.07E-02	1.51E-01	3.65E + 00	7.44E-02	2.07E-01	1.55E-01	1.23E + 00	2.57E + 00
	p-rank	−	−	−	−	−	+	−	−	−	−
	f-rank	7	9	3	6	5	1	10	11	8	4	2
Average f-rank		6.5	4.8	3.5	4.2	7.1	3.5	8.8	10.7	7.8	6.2	2.8
Overall f-rank		7	5	2	4	8	2	10	11	9	6	1
win(w)|loss(l)|tie(t)		4|294|2	28|272|0	53|225|2	2|298|0	5|292|3	56|240|4	4|293|3	8|292|0	12|286|2	8|289|3	165|119|16
OE%		2%	9.33%	18.33%	0.67%	2.67%	20%	2.33%	2.67%	4.67%	3.67%	60.33%

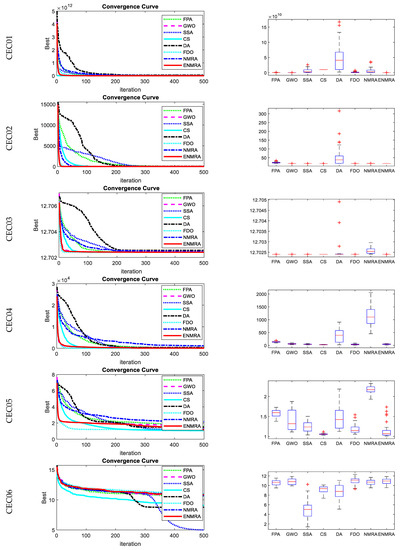
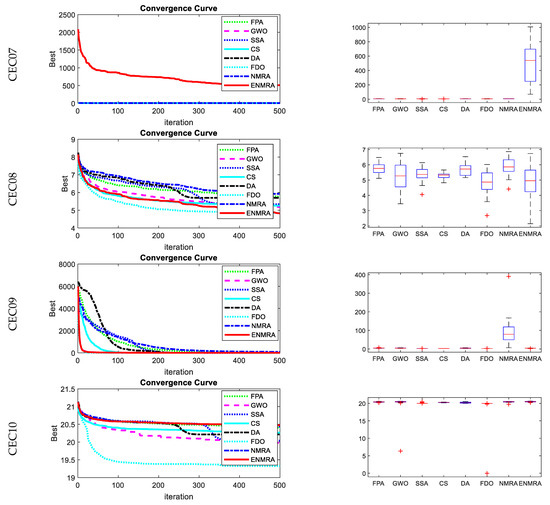
Figure 2. Convergence graphs and boxplots for CEC 2019 benchmark functions.

ENMRA’s results for CEC01 function were better in terms of the best, median, worst, and mean values obtained. For CEC02 function, ENMRA, CS, and GWO identified an optimal solution, but FDO was found to be the best. Most algorithms produced a nearly globally optimal solution for the CEC03, but ENMRA was proven to be better than other methods in terms of least standard deviation. In the case of CEC04 and CEC05, ENMRA outperformed the competition in terms of fitness performance.

When compared to competitive algorithms, ENMRA’s results for CEC06 and CEC07 functions were the worst. In terms of the best-acquired fitness performance, ENMRA’s results for function CEC08 were better. For CEC09 and CEC10 functions, ENMRA’s findings were comparable to those of other methods.

The box plots of competing algorithms for the benchmark test suite are shown in Figure 2. In this case, the box plots are utilized to assess algorithm efficiency concerning the fitness value attained. It was demonstrated that the proposed ENMRA was cost-effective in terms of fitness values in the majority of cases, as the median of fitness values for ENMRA was lower. As a result, ENMRA’s overall performance was determined to be consistent to that of other optimization techniques.

The performance of the competitive algorithms was statistically assessed using two nonparametric statistical tests, namely the Wilcoxon rank-sum test [39] and Friedman rank (f-rank) test [40], because of the stochastic nature of the above algorithms.

When the outcome of the two algorithms was compared, the Wilcoxon rank-sum test was employed to get the p-rank. In this scenario, the statistical efficiency of the suggested ENMRA was demonstrated in contrast to other methods. For each CEC function, the rank of distinct algorithms is shown in the sixth row of Table 2 and is represented in terms of win(w)/loss(l)/tie(t). The win(w) condition occurred when the tested method outperformed the suggested one and was given the + sign. The performance of the algorithm was worse in the loss(l) situation than in the proposed approach, and the - sign was utilized for this scenario. Both methods under test were statistically significant in the last tie(t) condition, as indicated by the = symbol. As one can observe from the w/l/t row in Table 2, the proposed ENMRA outperformed competitive algorithms in most cases.

The f-rank test additionally evaluated the suggested ENMRA’s performance after the Wilcoxon rank-sum test. The f-rank test assigned a unique rank to each algorithm under comparison based on its performance, and the total f-rank was generated from all the functions as shown in Table 2. The table shows that ENMRA had the best performance and was ranked first majority of cases among all the other algorithms tested.

Table 2 (last row) displays the overall effectiveness (OE) of the ENMRA and competitor algorithms based on their complete performance to summarize the performance evaluation results. Again, Equation (14) is used to calculate the OE of each method [41], where L is the total number of losing tests and N represents the total number of tests for each algorithm.

$$OE=\left(\frac{N-L}{N}\right)\times 100$$

(14)

Here, the total number of tests N is 300 as each algorithm runs 30 times for 10 CEC 2019 benchmark functions.

5. Real-Time Application: Energy-Throughput-Efficient Cross-Layer Solution for Wireless Underground Sensor Networks (WUSNs)

In the wide range of new applications, WUSNs [42,43,44] have attracted a great deal of attention that includes monitoring the soil and electricity grid, preventing/saving of mine disasters, extracting oil, predicting earthquakes and landslides, regulating border and security, and a lot more. However, as indicated in [45], these underground environments create significant wireless communication challenges through conventional electromagnetic (EM) waves. Especially, the main problems with EM communication are caused by large antenna sizes, highly unreliable channel conditions, and concise communication ranges.

The magnetic induction (MI) technique is a promising alternate wireless communications solution to deal with the underground challenges [45]. This technique uses a near magnet field of coils to spread information, thereby attaining stable channel conditions through small coil sizes. Numerous significant contributions to underground wireless sensor networks were extensively reported in the literature [46,47,48,49]. MI communication is ideal for underground environments with these great features. The majority of physical layer work has been completed to date, including signal analysis and antenna design. However, there is currently no protocol for MI-based WUSNs. This work aimed to provide a cross-layer solution for optimizing MI communication within the network via a distributed approach.

In this article, we presented a distributed cross-layer solution for WUSNs based on MI using an enhanced naked mole-rat algorithm (ENMRA), called the DECEN protocol framework. Our solution satisfied the quality requirements (i.e., packet delay and transmission reliability) of various applications while achieving optimal energy efficiency and computational complexity, resulting in increased throughput. These characteristics contribute to the practicality of our solution.

The rest of this section is arranged accordingly. Section 5.1 presents classification of MI techniques used in WUSNs. The system model is presented in Section 5.2. A cross-layer framework using ENMRA is proposed for the optimal energy-throughput performance in Section 5.3. Performance evaluation is provided in Section 5.4.

5.1. Magnetic Induction Techniques Used in WUSNs

The basic principle of mutual magnetic induction is used to transmit and receive communication signals in direct MI communication architecture [50]. As with transformers, the transmitter coil communicates the signal as sinusoidal current, which induces analogous sinusoidal current to the receiving node, completing the communication [51,52]. Due to mutual induction, the interaction between the coupled coils of the transmitter and receiver is accomplished (See Figure 3).

Figure 3. Structure of direct MI communication.

Despite the advantages of direct MI communication, such as a small coil size, low path loss, and stable communication channel, few limitations prevent it from being a viable alternate to WUSN applications.

To overcome the limitations of direct MI communication, such as limited communication range, investigators developed waveguide-based MI communication, which proved to be effective in achieving a practical bandwidth of intersensor communication. Moreover, it increased the communication range and reduced the transmission path loss in numerous applications in the underground environment (see Figure 4).

Figure 4. Structure of MI waveguide technique.

This design was made up of a succession of resonant relay nodes [52] that were deployed between underneath transceiver sensor nodes and were wirelessly coupled in MI-based WUSNs. To achieve an effective signal strength increase with a transmission range of 2 m, six or more relay coils were necessary.

The following advantages were observed when using this approach: sufficient bandwidth, fewer sensors, increased transmission range, path loss reduction, better robustness, extended system lifetime, a stable MI channel, and easier deployability and maintenance.

In practical underground communication applications, coils are not buried in a straight line due to two probable causes: the first one is the inability to deploy in exact planned positions due to rocks or pipes present inside the ground, and second, the positions of already buried coils may get changed during operation of the network due to above-ground pressure or movement of soil. Moreover, it was also well established that received signal strength at the MI transceiver end was affected by the angle between the axes of two adjacently placed coils. Therefore, the option of using multidimensional MI coils in such a complex scenario was worked on for high-quality transmission between sensing nodes [52]. More precisely, three-directional (3D) coils were designed and used, which offered omnidirectional signal coverage, as well as a minimal number of coils, leading to reduced system complexity and cost (see Figure 5).

Figure 5. Basic structure of MI waveguide with 3D coils.

In a 3D MI coil system, three individually fabricated unidirectional (UD) coils were vertically mounted on a cubical structure having each side with a length of 10 cm, such that each UD coil was perpendicularly deployed in relation to others. These three coils were meant to form a powerful beam along the three different axes of a Cartesian coordinate. Due to magnetic flux created by one surrounding coil becoming zero on another two orthogonal coils, these three coils did not interfere with each other, attributing to the field distribution structure of the coils. Like direct MI coils, the 3D MI coils were also made up of 26AWG wire, and each one of these coils was supported by a serial capacitor for detecting resonance. At the side of the receiving node, all three signals from three coils were introduced.

Depending on the channel model, after fixing MI coil parameters and transmission distance, the intersection angle between transmission and receiver nodes determined the signal strength. At least one coil achieved adequate signal strength with three orthogonal coils regardless of how the angle of intersection was changed. Even if MI coils were rotated, or the intersection angle between them changed, a high degree of communication was supposed to be kept by the system in this case [53]. It was also observed that if transmission gain was maximized using optimal power allocation and adoption of spatial-temporal code, good system performance was achieved by combining the received signals at three orthogonally placed coils [44].

In underwater sensor networks, it was found through modeling and analysis that the transmission range of an MI system achieved was a 20 m range using small-sized coils of 5 cm radius with high value of water conductivity. Therefore, using 3D coils rebut, MU links were established, which remained unaffected by the dynamical rotation of underground sensor nodes [54].

5.2. System Model

5.2.1. Modulation

As observed in [55], fewer variations of the channel were faced by MI communication than EM waves. Advanced modulation techniques may result in more energy consumption with energy-restricted MI-USNs [44]. For underground communication, many easy and suitable modulation techniques can be picked up, e.g., BFSK, BPSK, QPSK, and 16-QAM. Given the connection $i-j$, $m_{ij }\in ℳ$ represents the adopted modulation technique and $\eta (m_{ij})$ signifies the modulation spectrum efficiency. The bit error rate (BER) ψ can be obtained for the modulation scheme $m_{ij}$ over link $i-j$, called the received SNR, ${\psi }_{ij}^{m_{ij }}$.

5.2.2. FEC Schemes

In comparison to the automatic repeat request (ARQ), when addressing channel coding systems, FEC improved the reliability of transmission lines without adding overhead or retransmission cost. Furthermore, compared to the energy-efficient convolutional codes, the multilevel cyclic BCH code for WSNs achieved roughly 15% better [56]. Thus, it was necessary to strike a balance between transmission quality and energy consumption, and the presented cross-layer approach enabled such a compromise for maximum energy-throughput efficiency.

5.2.3. DS-CDMA Design

The DS-CDMA system delivered low-packet retransmissions and high-channel reuse and thereby offset the multipath effect in WUSNs. It lessened the use of energy and thereby increased the network throughput. The multiuser access interference (MAI) [57] must be reduced if this technique is used in MI-USNs.

5.2.4. Geographical Routing Algorithm

The notion of geographical routing protocol [58] was promising with a required limited signaling and limited scalability for underground environments. A source $i$ was selected among the neighbors of node $i$, the best forwarder was $j^{*}$, i.e., $S_i{{\displaystyle \cap }}^{ }{F}_i^D$ corresponded to the specified objective function.

5.2.5. Statistical QoS Guarantees

The statistical QoS to reaffirm end-to-end data traffic reliably in MI-USNs was analyzed. The reliability of the upsurged transmission was particularly crucial in nearly all underground sensing applications with lower packet loss [44]. The bounded delay was also significant in the setting of timing constraints and real-time monitoring [59]. The communications link $i-j$ is given for the packet delay and link reliability with the aim of distributed functionality between sensors.

5.3. Distributed Cross-Layer Energy-Throughput-Efficient Protocol Using ENMRA for WUSNs

Because of the significant differences in communication media (for example, between the air and the soil), it was discovered that the methodologies for terrestrial WSNs were not appropriate to WUSNs. In addition, the majority of the study centered around the physical layer, such as receiving signal analysis and antenna design. As a result, a wholly distributed cross-layer solution was proposed rather than the traditional layered protocol approach, resulting in well-organized resource usage and high system performance (the OSI model).

In WUSNs, viable throughput of link transmissions and energy consumption were the main challenges to be addressed. To obtain the packet successfully for link $i-j$, the objective was to reduce average packet energy and make the most of the average transmitted packet rate, characterized by the acceptable link throughput, given by:

$$\begin{array}{c}\mathit{M}\mathit{i}\mathit{n}\mathit{i}\mathit{m}\mathit{i}\mathit{z}\mathit{e} E_{ij}=L(P_{ij}/R_{ij}(T,\sigma )R_C^{ij}+2E_{elec}^b)\hfill \\ \mathit{M}\mathit{a}\mathit{x}\mathit{i}\mathit{m}\mathit{i}\mathit{z}\mathit{e} Q_{ij}\hfill \end{array}$$

(15)

The energy dissipation per bit for transfer data from the node $i$ to $j$ is expressed as $P_{ij}/R_{ij}\left(T,\sigma \right)R_C^{ij}+2E_{elec}^b$. $P_{ij}/R_{ij}\left(T,\sigma \right)R_C^{ij}$ is the energy consumption as a function of distance. $E_{elec}^b=E_{elec}^{trans}=E_{elec}^{rec} \left[J/bit\right]$ represents the energy dissipation independent of transmitter-receiver separation. $E_{elec}^{trans}$ and $E_{elec}^{rec}$ denote the energy consumed per bit by the transmitter and receiver circuit, respectively.

The above objective functions were transformed to a single one using the vector sum method, and the optimization problem (i.e., energy and throughput$\left(EaT\right)$) is expressed as:

$$\begin{array}{c}\mathit{M}\mathit{i}\mathit{n}\mathit{i}\mathit{m}\mathit{i}\mathit{z}\mathit{e} Ea{T}_{ij}\left(T,\sigma \right)=w_1\ast L(P_{ij}/R_{ij}(T,\sigma )R_C^{ij}+2E_{elec}^b)-w_2\ast Q_{ij}\hfill \\ \mathit{F}\mathit{i}\mathit{n}\mathit{d} T,\sigma ,j\in S_i{{\displaystyle \cap }}^{ }{F}_i^D, m_{ij }\in ℳ, c_{ij }\in ℂ,\hfill \\ P_{ij}\in \left[0,P_i^{max}\right], Q_{ij}, l_{ij}\in ℒ\hfill \\ \mathit{S}\mathit{u}\mathit{b}\mathit{j}\mathit{e}\mathit{c}\mathit{t} \mathit{t}\mathit{o} \mathrm{power}, \mathrm{link}, \mathrm{average} \mathrm{delay}, \mathrm{delay} \mathrm{variance} \mathrm{constraints}\hfill \end{array}$$

(16)

The decision variables for node $i$ are the allowed link throughput, DS-CDMA code length, operating temperature, modulation scheme, forwarder, soil conductivity, power level, and channel coding scheme.

For the best support in actual applications of WUSNs, cross-layer frameworks should have environmentally aware and distributive properties. DECEN’s main concerns were that: (i) it calculate the relationship between link throughput and chaotic code, (ii) it achieve sensing and information exchange, (iii) it measure two environment-dependent parameters (electrical conductivity and temperature), (iv) it employ a two-phase decision strategy, and (v) it implement a loss-tolerance random-access scheme.

DECEN was intended to solve the initial cross-layer design’s application-driven objective optimization problem. DECEN employed non-cooperative game theory to solve a near-far dilemma in DS-CDMA and examined the relationship between link throughput and chaotic code length using distributed power management. The goal was to determine the relationship between DS-CDMA code lengths and link throughput. A two-phase technique was used to determine which geographic routes can be favored by low signaling overhead and their scalability, which is ideal for oil reservoirs. As a result, we presented a distributed two-stage framework with a cross-layer design.

The sender divided the cross-layer optimization into two sequentially solved subproblems, taking inspiration from the geographical routing algorithm as follows:

(i)

Minimize link metric $Ea{T}_{ij}$ using ENMRA, concerning power level $P_{ij}$, acceptable link throughput $Q_{ij}$, DS-CDMA code length $l_{ij}$, and possible modulation function and channel coding combinations, i.e., $j, m_{ij}$, and $c_{ij}$, and each of its possible next-hop neighbors.

(ii)

Select the appropriate next-hop $j^{*}$ and optimum link metric physical functionalities ($m_{ij}^{*}; c_{ij}^{*}$).

5.4. Performance Evaluation

This section examines DECEN’s performance in comparison to other algorithms. The DECEN algorithm was modeled in MATLAB version R2020a with the same system and resource characteristics. DECEN’s performance (for MI communication, MI waveguide, and MI waveguide with 3D coil) was compared to DEAP and DECN [55], two traditional layered protocol systems. The population size (NP = 20), number of iterations ($t_{max}$ = 100), and problem dimension (D = 2) were the simulation parameters employed by DECEN and DECN algorithms. The simulation results revealed that DECEN saved substantial energy while also providing higher throughput, ideal for use in WUSNs.

Figure 6 and Figure 7 illustrate the results for a successfully decoded payload bit on the receiver. Because centrally regulated power gives more network information, it uses less energy and power than the proposed distributed method. Such assumptions can only be reached theoretically with a massive interchange of control signals, untenable in real-world settings, such as WUSNs. DECEN enabled the MAI power level, and the received noise at the receivers became the transmitter’s only required information. It allowed for practically centralized energy usage and even achieved efficiency over extended transmission distances. The effect of the coil angle inaccuracy on the DECEN was not considered, and actual applications did not permit the use of multilayer arrangements. In this setting, DECEN and the central design required about the same amount of energy even over small transmission distances. Huge antenna size, dynamic channel conditions, and small communication range were addressed by MI-based WUSNs using MI waveguide and 3D MI coils, making them better for underground communication. Cross-layered architecture proved superior to traditional layered protocol architecture in terms of energy savings and link reliability.

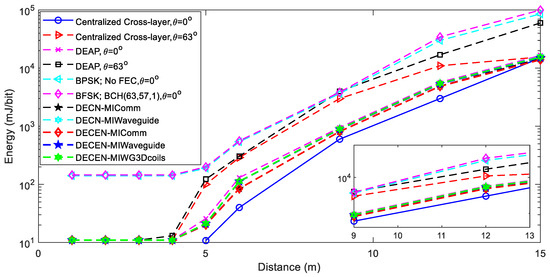
Figure 6. Comparison graph for transmitted energy as a function of distance.

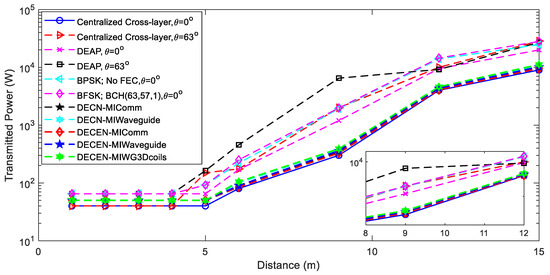
Figure 7. Comparison graph for transmitted power as a function of distance.

Figure 8 depicts the average bit rates of layered and cross-layered systems (i.e., DECEN, DECN, DEAP, and centralized). Cross-layer design is preferable over layered design because of its higher bit rate. On the other hand, the proposed DECEN outperformed the centralized system for almost all transmission lengths and allowed for a much greater bit rate, especially over medium communication ranges. This was because our distributed method was not constrained by the severe power limits of two-hop neighbors, like a centralized system, which is always the worst-case situation. Instead, DECEN employed the ENMRA optimization algorithm to manage each sensor’s transmission power distribution better and increase its performance.

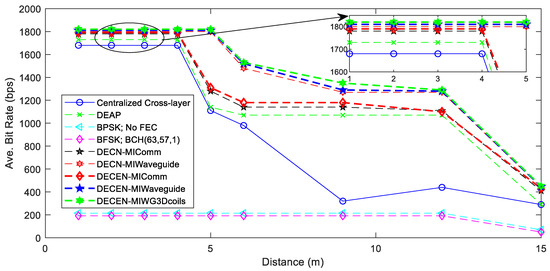
Figure 8. Comparison graph for average bit rate as a function of distance.

DECEN achieved an energy level that was nearly identical to that of the centralized technique. It also enabled exceptional connectivity via bandwidth-constrained MI routes and significantly reduced the computational complexity of highly viable WUSNs.

Figure 9 and Figure 10 depict the normalized energy usage and packet rate for the successfully received end-to-end data flow, respectively. As the number of sensor nodes grew, better routes became available, and a wider variety of cooperatives emerged. In all of the simulated procedures, these benefits were demonstrated by lower energy usage and higher throughput. Without interchanging data between the multiple layer functionalities and employing a layered strategy, GEO precisely picked the set of nodes that advance successively closest to their target, principally in terms of geographical progress and the poorest performance. TPL reduced the amount of transmitted power required in multihop scenarios, resulting in improved energy savings, more connections, and longer routes. Our solutions delivered the best energy and performance by overcoming GEO, TPL, DEAP, and DECN solutions with higher throughput gain and more energy savings. It is because combining the optimization of several layers’ communication features yielded significant synergy in terms of boosting system performance from one end to the other. The suggested DECEN’s appropriateness for underground conditions was confirmed by its outstanding spectral and energy efficiency, as well as its lower computational complexity. As a result, we propose a novel protocol for efficient and dependable MI communication, as well as a new cross-layer approach in WUSNs.

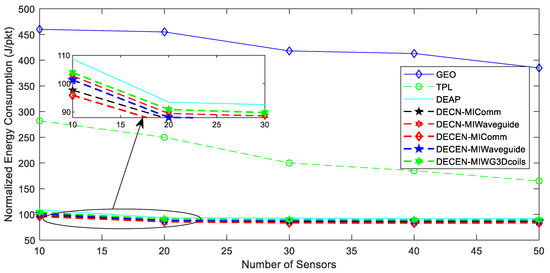
Figure 9. Comparison graph for energy consumption with the varying number of sensors.

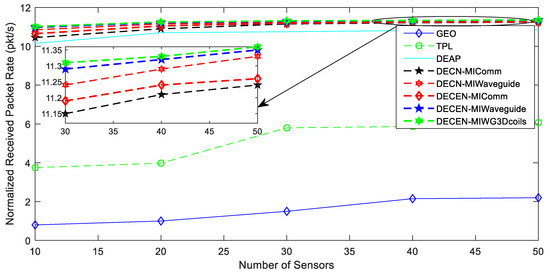
Figure 10. Comparison graph for received packet rate with the varying number of sensors.

6. Conclusions

This work enhanced the performance of the optimization algorithm based on the mating behavior of NMRs. The proposed ENMRA used enhanced exploration and exploitation properties, concepts of hybridization, and a division of population strategy to improve the performance of a basic NMRA optimizer. A GWO-based exploration strategy and LNS- and DE-based exploitation characteristics helped attain good results compared to competitive algorithms. The neighborhood search around the best solution caused the algorithm to converge to the global optimum faster than the competitive algorithms. The effectiveness of the proposed algorithm was evaluated using a CEC 2019 benchmark test suite. The superiority of ENMRA was confirmed using the Wilcoxon rank-sum test and Friedman rank (f-rank) test. The overall effectiveness (OE) summarized the performance of ENMRA over compared algorithms.

The interaction of essential underground communications functions was also addressed in this study, and a distributed cross-layer framework called DECEN for the effective utilization of bandwidth-limited MI channels was presented. The DS-CDMA technique provided reliable transmissions links with little network information by leveraging ENMRA. Furthermore, statistical delay constraints were guaranteed, and the best link performance was realized through analytical cross-layer design resolution for the given code length. According to simulation outcomes, the DECEN had lower latency, higher throughput, and lower energy usage.

Other modified variants of the suggested ENMRA can also be proposed to tackle optimization issues with binary, discrete, or multi-objective problems. The suggested method can also be integrated with opposition-based learning, mutation, disruption, and Levy flight for improved performance. Finally, research into the use of ENMRA in other disciplines, such as industry and engineering applications, signal denoising, cloud computing task scheduling, image-processing applications, resource management applications, big data applications, feature selection, neural networks, and other real-world applications, would be a valuable contribution.