Induced Matchings and the v-Number of Graded Ideals ^†

Abstract

We give a formula for the v-number of a graded ideal that can be used to compute this number. Then, we show that for the edge ideal $I\left(G\right)$ of a graph G, the induced matching number of G is an upper bound for the v-number of $I\left(G\right)$ when G is very well-covered, or G has a simplicial partition, or G is well-covered connected and contains neither four, nor five cycles. In all these cases, the v-number of $I\left(G\right)$ is a lower bound for the regularity of the edge ring of G. We classify when the induced matching number of G is an upper bound for the v-number of $I\left(G\right)$ when G is a cycle and classify when all vertices of a graph are shedding vertices to gain insight into the family of $W_2$-graphs.

1. Introduction

Let $S=K[t_1,\dots ,t_s]={⨁}_{d=0}^{\infty }{S}_d$ be a polynomial ring over a field K with the standard grading, and let I be a graded ideal of S. A prime ideal $\mathfrak{p}$ of S is an associated prime of $S/I$ if $(I:f)=\mathfrak{p}$ for some $f\in S_d$, where $(I:f)$ is the set of all $g\in S$ such that $gf\in I$. The set of associated primes of $S/I$ is denoted by $\mathrm{Ass}\left(I\right)$, and the set of maximal elements of $\mathrm{Ass}\left(I\right)$ with respect to inclusion is denoted by $\mathrm{Max}\left(I\right)$. The v-number of I, denoted $\mathrm{v}\left(I\right)$, is the following invariant of I that was introduced in [1] to study the asymptotic behavior of the minimum distance of projective Reed–Muller-type codes, Corollary 4.7 in [1]:

$$\mathrm{v}\left(I\right):=min\{d\ge 0\mid \exists f\in S_d \mathrm{and} \mathfrak{p}\in \mathrm{Ass}\left(I\right) \mathrm{with} (I:f)=\mathfrak{p}\}.$$

One can define the v-number of I locally at each associated prime $\mathfrak{p}$ of I:

$${\mathrm{v}}_{\mathfrak{p}}\left(I\right):=\min \{d\ge 0\mid \exists f\in S_d \mathrm{with} (I:f)=\mathfrak{p}\}.$$

For a graded module $M\ne 0$, we define $\alpha \left(M\right):=min\{deg(f)\mid f\in M\setminus \{0\left\}\right\}$. By convention, we set $\alpha \left(0\right):=0$. Part (d) of the next result was shown in Proposition 4.2 in [1] for unmixed graded ideals. The next result gives a formula for the v-number of any graded ideal.

Theorem 1.

Let $I\subset S$ be a graded ideal, and let $\mathfrak{p}\in \mathrm{Ass}\left(I\right)$. The following hold:

(a) 

If $\mathcal{G}=\{{\overline{g}}_1,\dots ,{\overline{g}}_r\}$ is a homogeneous minimal generating set of $(I:\mathfrak{p})/I$, then:

$${\mathrm{v}}_{\mathfrak{p}}\left(I\right)=min\{deg\left(g_i\right)\mid 1\le i\le r \mathrm{and} (I:g_i)=\mathfrak{p}\};$$

(b) 

$\mathrm{v}\left(I\right)=min\{{\mathrm{v}}_{\mathfrak{q}}\left(I\right)\mid \mathfrak{q}\in \mathrm{Ass}\left(I\right)\}$;

(c) 

${\mathrm{v}}_{\mathfrak{p}}\left(I\right)\ge \alpha ((I:\mathfrak{p})/I)$ with equality if $\mathfrak{p}\in \mathrm{Max}\left(I\right)$;

(d) 

If I has no embedded primes, then $\mathrm{v}\left(I\right)=min\left\{\alpha \left((I:\mathfrak{q})/I\right)\right|\mathfrak{q}\in \mathrm{Ass}\left(I\right)\}.$

The formulas of Parts (a) and (b) give an algorithm to compute the v-number using Macaulay2 [2] (Example 1, Procedure A1 in Appendix A).

The v-number of nongraded ideals was used in [3] to compute the regularity index of the minimum distance function of affine Reed–Muller-type codes, Proposition 6.2 in [3]. In this case, one considers the vanishing ideal of a set of affine points over a finite field.

For certain classes of graded ideals, $\mathrm{v}\left(I\right)$ is a lower bound for $\mathrm{reg}(S/I)$, the regularity of the quotient ring $S/I$ (Definition 1); see [1,4,5]. There are examples of ideals where $\mathrm{v}\left(I\right)>\mathrm{reg}(S/I)$ [4]. It is an open problem whether $\mathrm{v}\left(I\right)\le \mathrm{reg}(S/I)+1$ holds for any squarefree monomial ideal. Upper and lower bounds for the regularity of edge ideals and their powers were given in [6,7,8,9,10,11,12,13,14,15]; see Section 2. Using the polarization technique of Fröberg [16], we give an upper bound for the regularity of a monomial ideal I in terms of the dimension of $S/I$ and the exponents of the monomials that generate I (Proposition 2).

Let G be a graph with vertex set $V\left(G\right)$ and edge set $E\left(G\right)$. If $V\left(G\right)=\{t_1,\dots ,t_s\}$, we can regard each vertex $t_i$ as a variable of the polynomial ring $S=K[t_1,\dots ,t_s]$ and think of each edge $\{t_i,t_j\}$ of G as the quadratic monomial $t_i{t}_j$ of S. The edge ideal of G is the squarefree monomial ideal of S, defined as:

$$I\left(G\right):=(t_i{t}_j\mid \{t_i,t_j\}\in E\left(G\right)).$$

This ideal, introduced in [17], has been studied in the literature from different perspectives; see [18,19,20,21,22,23,24,25,26] and the references therein. We use induced matchings of G to compare the v-number of $I\left(G\right)$ with the regularity of $S/I\left(G\right)$ for certain families of graphs.

A subset C of $V\left(G\right)$ is a vertex cover of G if every edge of G is incident with at least one vertex in C. A vertex cover C of G is minimal if each proper subset of C is not a vertex cover of G. A subset A of $V\left(G\right)$ is called stable if no two points in A are joined by an edge. Note that a set of vertices A is a (maximal) stable set of G if and only if $V\left(G\right)\setminus A$ is a (minimal) vertex cover of G. The stability number of G, denoted by ${\beta }_0\left(G\right)$, is the cardinality of a maximum stable set of G, and the covering number of G, denoted ${\alpha }_0\left(G\right)$, is the cardinality of a minimum vertex cover of G. We introduce the following two families of stable sets:

$$\begin{array}{cc}\hfill {\mathcal{F}}_G& :=\{A\mid A \mathrm{is\; a\; maximal\; stable\; set\; of} G\};\hfill \\ \hfill {\mathcal{A}}_G& :=\{A\mid A \mathrm{is\; a\; stable\; set\; of} G,\mathrm{and}{N}_G\left(A\right) \mathrm{is\; a\; minimal\; vertex\; cover\; of} G\}.\hfill \end{array}$$

According to Theorem 3.5 in [4], ${\mathcal{F}}_G\subset {\mathcal{A}}_G$ and the $\mathrm{v}$-number of $I\left(G\right)$ is given by:

$$\mathrm{v}\left(I\left(G\right)\right)=min\left\{\right|A|:A\in {\mathcal{A}}_G\}.$$

The v-number of $I\left(G\right)$ is a combinatorial invariant of G that has been used to characterize the family of $W_2$-graphs (see the discussion below after Corollary 1). We can define the v-number of a graph G as $\mathrm{v}\left(G\right):=\mathrm{v}\left(I\right(G\left)\right)$ and study $\mathrm{v}\left(G\right)$ from the viewpoint of graph theory.

A set P of pairwise disjoint edges of G is called a matching. A matching $P=\{e_1,\dots ,e_r\}$ is perfect if $V\left(G\right)={\bigcup }_{i=1}^r{e}_i$. An induced matching of a graph G is a matching $P=\{e_1,\dots ,e_r\}$ of G such that the only edges of G contained in ${\bigcup }_{i=1}^r{e}_i$ are $e_1,\dots ,e_r$. The matching number of G, denoted ${\beta }_1\left(G\right)$, is the maximum cardinality of a matching of G, and the induced matching number of G, denoted $\mathrm{im}\left(G\right)$, is the number of edges in the largest induced matching.

The graph G is well-covered if every maximal stable set of G is of the same size, and G is very well-covered if G is well-covered, has no isolated vertices, and $\left|V\left(G\right)\right|=2{\alpha }_0\left(G\right)$. The class of very well-covered graphs includes the bipartite well-covered graphs without isolated vertices [27,28] and the whisker graphs [24] (p. 392) (Lemma 1). A graph without isolated vertices is very well-covered if and only if G is well-covered and ${\beta }_1\left(G\right)={\alpha }_0\left(G\right)$ (Proposition 1). One of the properties of very well-covered graphs that will be used to show the following theorem is that they can be classified using combinatorial properties of a perfect matching, as was shown by Favaron, Theorem 1.2 in [29] (Theorem 7, cf. Theorem 6).

We come to one of our main results.

Theorem 2.

Let G be a very well-covered graph, and let $P=\{e_1,\dots ,e_r\}$ be a perfect matching of G. Then, there is an induced submatching $P^{\prime }$ of P and $D\in {\mathcal{A}}_G$ such that $D\subset V\left(P^{\prime }\right)$ and $|e\bigcap D|=1$ for each $e\in P^{\prime }$. Furthermore, $\mathrm{v}\left(I\left(G\right)\right)\le |P^{\prime }|=|D|\le \mathrm{im}\left(G\right)\le \mathrm{reg}(S/I\left(G\right))$.

Let G be a graph, and let $W_G$ be its whisker graph (Section 2). As a consequence, we recover a result of [4] showing that the v-number of $I\left(W_G\right)$ is bounded from above by the regularity of the quotient ring $K\left[V\left(W_G\right)\right]/I\left(W_G\right)$ (Corollary 3). The independent domination number of G, denoted by $i\left(G\right)$, is the minimum size of a maximal stable set, Proposition 2 in [30]:

$$i\left(G\right):=min\left\{\right|A|:A\in {\mathcal{F}}_G\},$$

and $i\left(G\right)$ is equal to the v-number of the whisker graph $W_G$ of G, Theorem 3.19(a) in [4].

A cycle of length s is denoted by $C_s$. The inequality $\mathrm{v}\left(I\right(G\left)\right)\le \mathrm{reg}(S/I(G\left)\right)$ of Theorem 2 is false if we only assume that G is a well-covered graph, since the cycle $C_5$ is a well-covered graph, but one has $\mathrm{im}\left(C_5\right)=1<2=\mathrm{v}\left(I\left(C_5\right)\right)$. We prove that $C_5$ is the only cycle where the inequality $\mathrm{v}\left(I\left(C_s\right)\right)\le \mathrm{im}\left(C_s\right)$ fails.

Theorem 3.

Let $C_s$ be an s-cycle, and let $I\left(C_s\right)$ be its edge ideal. Then, $\mathrm{v}\left(I\left(C_s\right)\right)\le \mathrm{im}\left(C_s\right)$ if and only if $s\ne 5$.

If $v\in V\left(G\right)$, we denote the closed neighborhood of v by $N_G\left[v\right]$. A vertex v of G is called simplicial if the induced subgraph $H=G\left[N_G\left[v\right]\right]$ on the vertex set $N_G\left[v\right]$ is a complete graph. A subgraph H of G is called a simplex if $H=G\left[N_G\left[v\right]\right]$ for some simplicial vertex v. A graph G is simplicial if every vertex of G is either simplicial or is adjacent to a simplicial vertex of G.

If A is a stable set of a graph G, $H_i$ is a complete subgraph of G for $i=1,\dots ,r$, and $A\bigcup {\left\{V\left(H_i\right)\right\}}_{i=1}^r$ is a partition of $V\left(G\right)$, then $\mathrm{reg}(S/I(G\left)\right)\le r$, Theorem 2 in [15]. We consider a special type of partition of $V\left(G\right)$ that allows us to link ${\mathcal{A}}_G$ with induced matchings of G. A graph G has a simplicial partition if G has simplexes $H_1,\dots ,H_r$, such that ${\left\{V\left(H_i\right)\right\}}_{i=1}^r$ is a partition of $V\left(G\right)$. Our next result shows that $\mathrm{v}\left(I\right(G\left)\right)\le \mathrm{im}\left(G\right)$ if G has a simplicial partition.

Theorem 4.

Let G be a graph with simplexes $H_1,\dots ,H_r$, such that ${\left\{V\left(H_i\right)\right\}}_{i=1}^r$ is a partition of $V\left(G\right)$. If G has no isolated vertices, then there is $D=\{y_1,\dots ,y_k\}\in {\mathcal{A}}_G$, and there are simplicial vertices $x_1,\dots ,x_k$ of G and integers $1\le j_1<\cdots <j_k\le r$ such that $P={\left\{\{x_i,y_i\}\right\}}_{i=1}^k$ is an induced matching of G and $H_{j_i}$ is the induced subgraph $G\left[N_G\left[x_i\right]\right]$ on $N_G\left[x_i\right]$ for $i=1,\dots ,k$. Furthermore, $\mathrm{v}\left(I\right(G\left)\right)\le \left|D\right|=\left|P\right|\le \mathrm{im}\left(G\right)\le \mathrm{reg}(S/I(G\left)\right)$.

As a consequence, using a result of Finbow, Hartnell, and Nowakowski that classifies the connected well-covered graphs without four and five cycles, Theorem 1.1 in [31] (Theorem 8), we show other families of graphs where the induced matching number of G is an upper bound for the v-number of $I\left(G\right)$.

Corollary 1.

Let G be a well-covered graph, and let $I\left(G\right)$ be its edge ideal. If G is simplicial or G is connected and contains neither four, nor five cycles, then:

$$\mathrm{v}\left(I\left(G\right)\right)\le \mathrm{im}\left(G\right)\le \mathrm{reg}(S/I\left(G\right))\le {\beta }_0\left(G\right).$$

A vertex v of a graph G is called a shedding vertex if each stable set of $G\setminus N_G\left[v\right]$ is not a maximal stable set of $G\setminus v$. We prove that every vertex of G is a shedding vertex if and only if ${\mathcal{A}}_G={\mathcal{F}}_G$ (Proposition 4).

A graph G belongs to class $W_2$ if $\left|V\right(G\left)\right|\ge 2$ and any two disjoint stable sets $A_1,A_2$ are contained in two disjoint maximum stable sets $B_1,B_2$ with $|B_i|={\beta }_0\left(G\right)$ for $i=1,2$. A graph G is in $W_2$ if and only if G is well-covered, $G\setminus v$ is well-covered for all $v\in V\left(G\right)$, and G has no isolated vertices, Theorem 2.2 in [32]. A graph G without isolated vertices is in $W_2$ if and only if $\mathrm{v}\left(I\left(G\right)\right)={\beta }_0\left(G\right)$, Theorem 4.5 in [4]. As an application we recover the only if implication of this result (Corollary 5). Using the fact that a graph G without isolated vertices is in $W_2$ if and only if G is well-covered and ${\mathcal{A}}_G={\mathcal{F}}_G$, Theorem 4.3 in [4], by Proposition 4, we recover the fact that a graph G without isolated vertices is in $W_2$ if and only if G is well-covered and every $v\in V\left(G\right)$ is a shedding vertex, Theorem 3.9 in [32]. For other characterizations of graphs in $W_2$, see [32,33] and the references therein.

In Section 5, we show examples illustrating some of our results. In particular, in Example 3, we compute the combinatorial and algebraic invariants of the well-covered graphs $C_7$ and $T_{10}$ that are depicted in Figure 1. These two graphs occur in the classification of connected well-covered graphs without four and five cycles, Theorem 1.1 in [31] (Theorem 8). A related result is the characterization of well-covered graphs of girth at least five given in [34].

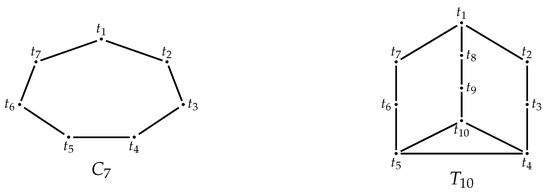
Figure 1. Two well-covered graphs with no 4 or 5 cycles.

For all unexplained terminology and additional information, we refer to [35,36] for the theory of graphs and [19,21,25] for the theory of edge ideals and monomial ideals.

2. Preliminaries

In this section, we give some definitions and present some well-known results that will be used in the following sections. To avoid repetition, we continue to employ the notations and definitions used in Section 1.

Definition 1

([37]). Let $I\subset S$ be a graded ideal, and let $\mathbf{F}$ be the minimal graded free resolution of $S/I$ as an S-module:

$$\mathbf{F}:0\to \underset{j}{⨁}S{(-j)}^{b_{g,j}}\stackrel{}{\to }\cdots \to \underset{j}{⨁}S{(-j)}^{b_{1,j}}\stackrel{}{\to }S\to S/I\to 0.$$

The Castelnuovo–Mumford regularity of $S/I$ (regularity of $S/I$) is defined as:

$$\mathrm{reg}(S/I):=max\{j-i\mid b_{i,j}\ne 0\}.$$

The integer g, denoted $\mathrm{pd}(S/I)$, is the projective dimension of $S/I$.

Let G be a graph with vertex set $V\left(G\right)$. Given $A\subset V\left(G\right)$, the induced subgraph on A, denoted $G\left[A\right]$, is the maximal subgraph of G with vertex set A. The edges of $G\left[A\right]$ are all the edges of G that are contained in A. The induced subgraph $G\left[V\right(G)\setminus A]$ of G on the vertex set $V\left(G\right)\setminus A$ is denoted by $G\setminus A$. If v is a vertex of G, then we denote the neighborhood of v by $N_G\left(v\right)$ and the closed neighborhood $N_G\left(v\right)\bigcup \left\{v\right\}$ of v by $N_G\left[v\right]$. Recall that $N_G\left(v\right)$ is the set of all vertices of G that are adjacent to v. If $A\subset V\left(G\right)$, we set $N_G\left(A\right):={\bigcup }_{a\in A}{N}_G\left(a\right)$.

Theorem 5

([38]). If a graph G is well-covered and is not complete, then $G_v:=G\setminus N_G\left[v\right]$ is well-covered for all v in $V\left(G\right)$. Moreover, ${\beta }_0\left(G_v\right)={\beta }_0\left(G\right)-1$.

If G is a graph, then ${\beta }_1\left(G\right)\le {\alpha }_0\left(G\right)$. We say that G is a König graph if ${\beta }_1\left(G\right)={\alpha }_0\left(G\right)$. This notion can be used to classify very well-covered graphs (Proposition 1).

Theorem 6

([39], Theorem 5, and [40], Lemma 2.3). Let G be a graph without isolated vertices. If G is a graph without 3, 5, and 7 cycles or G is a König graph, then G is well-covered if and only if G is very well-covered.

Definition 2.

A perfect matching P of a graph G is said to have Property (P) if for all $\{a,b\}$, $\{a^{\prime },b^{\prime }\}\in E\left(G\right)$, and $\{b,b^{\prime }\}\in P$, one has $\{a,a^{\prime }\}\in E\left(G\right)$.

Remark 1.

Let P be a perfect matching of a graph G with Property(P). Note that if $\{b,b^{\prime }\}\in P$ and $a\in V\left(G\right)$, then $\{a,b\}$ and $\{a,b^{\prime }\}$ cannot be both in $E\left(G\right)$ because G has no loops. In other words, G has no triangle containing an edge in P.

Theorem 7

([29], Theorem 1.2). The following conditions are equivalent for a graph G:

1. 

G is very well-covered;

2. 

G has a perfect matching with Property (P);

3. 

G has a perfect matching, and each perfect matching of G has Property (P).

Let G be a graph with vertex set $V\left(G\right)=\{t_1,\dots ,t_s\}$, and let $U=\{u_1,\dots ,u_s\}$ be a new set of vertices. The whisker graph or suspension of G, denoted by $W_G$, is the graph obtained from G by attaching to each vertex $t_i$ a new vertex $u_i$ and a new edge $\{t_i,u_i\}$. The edge $\{t_i,u_i\}$ is called a whisker or pendant edge. The graph $W_G$ was introduced in [24] as a device to study the numerical invariants and properties of graphs and edge ideals.

Lemma 1.

Let G be a graph without isolated vertices. The following hold:

(a) 

If G is a bipartite well-covered graph, then G is very well-covered;

(b) 

The whisker graph $W_G$ of G is very well-covered.

Proof. (a) A bipartite well-covered graph without isolated vertices has a perfect matching P that satisfies Property (P), Theorem 1.1 in [28]. Thus, by Theorem 7, G is very well-covered;

(b) The perfect matching $P={\left\{\{t_i,u_i\}\right\}}_{i=1}^n$ of the whisker graph $W_G$ satisfies Property (P) and, by Theorem 7, G is very well-covered. □

Proposition 1

([41], Lemma 17). Let G be a graph without isolated vertices. Then, G is a very well-covered graph if and only if G is well-covered and ${\beta }_1\left(G\right)={\alpha }_0\left(G\right)$.

Proof. 

⇒) Assume that G is very well-covered. Then, $\left|V\left(G\right)\right|=2{\alpha }_0\left(G\right)$. It suffices to show that ${\beta }_1\left(G\right)={\alpha }_0\left(G\right)$. In general, ${\beta }_1\left(G\right)\le {\alpha }_0\left(G\right)$. By Theorem 7, G has a perfect matching $P=\{e_1,\dots ,e_r\}$. Then, $\left|V\left(G\right)\right|=2r=2{\alpha }_0\left(G\right)$ and $r={\alpha }_0\left(G\right)$. Thus, ${\alpha }_0\left(G\right)=\left|P\right|\le {\beta }_1\left(G\right)$, and one has ${\alpha }_0\left(G\right)={\beta }_1\left(G\right)$.

⇐) Assume that G is well-covered and ${\beta }_1\left(G\right)={\alpha }_0\left(G\right)$. Let $P=\{e_1,\dots ,e_r\}$ be a matching of G with $r={\beta }_1\left(G\right)$. We need only to show that $\left|V\left(G\right)\right|=2{\alpha }_0\left(G\right)$. Clearly, $\left|V\right(G\left)\right|$ is greater than or equal to $2{\alpha }_0\left(G\right)$ because ${\bigcup }_{i=1}^r{e}_i\subset V\left(G\right)$. We argue by contradiction assuming that ${\bigcup }_{i=1}^r{e}_i⊊V\left(G\right)$. Pick $v\in V\left(G\right)\setminus {\bigcup }_{i=1}^r{e}_i$. As v is not an isolated vertex of G, there is a minimal vertex cover C of G that contains v. As G is well-covered, one has that $\left|C\right|={\alpha }_0\left(G\right)=r$. Since $e_i\bigcap C\ne \varnothing$ for $i=1,\dots ,r$ and $v\in C$, we obtain $\left|C\right|\ge r+1$, a contradiction. □

We say that a graph G is in the family $\mathcal{F}$ if there exists $\{x_1,\dots ,x_k\}\subset V\left(G\right)$ where for each i, $x_i$ is simplicial, $|N_G\left[x_i\right]|\le 3$, and $\{N_G\left[x_i\right]\mid i=1,\dots ,k\}$ is a partition of $V\left(G\right)$.

Theorem 8

([31], Theorem 1.1). Let G be a connected graph that contains neither four, nor five cycles, and let $C_7$ and $T_{10}$ be the two graphs in Figure 1. Then, G is a well-covered graph if and only if $G\in \{C_7,T_{10}\}$ or $G\in \mathcal{F}$.

Theorem 9.

Let G be a graph. The following hold:

(a) 

([7], Theorem 4.5, [42]) $2(n-1)+\mathrm{im}\left(G\right)\le \mathrm{reg}(S/I{\left(G\right)}^n)$ for all $n\ge 1$;

(b) 

([7], Theorem 4.7, [43]) If G is a forest or G is very well-covered, then:

$$\mathrm{reg}(S/I{\left(G\right)}^n)=2(n-1)+\mathrm{im}\left(G\right)\mathrm{for}\mathrm{all}n\ge 1;$$

(c) 

([44], Theorem 1.3) If G is very well-covered, then $\mathrm{reg}(S/I(G\left)\right)=\mathrm{im}\left(G\right)$.

The projective dimension of the edge ideal of a graph, the Wiener index, the independence polynomial, the h-vector, and the symbolic powers of cover ideals of graphs have been studied for very well-covered graphs [45,46,47,48,49,50,51].

3. The v-Number of a Graded Ideal

Let $S=K[t_1,\dots ,t_s]={⨁}_{d=0}^{\infty }{S}_d$ be a polynomial ring over a field K with the standard grading, and let I be a graded ideal of S. In this section, we prove a formula for the v-number of I that can be used to compute this number using Macaulay2 [2]. To avoid repetition, we continue to employ the notations and definitions used in Section 1 and Section 2.

Lemma 2.

Let $I\subset S$ be a graded ideal. If $(I:f)=\mathfrak{p}$ for some prime ideal $\mathfrak{p}$ and some $f\in S_d$, $d\ge 0$, then $I⊊(I:\mathfrak{p})$, and there is a minimal homogeneous generator $\overline{g}:=g+I$ of $(I:\mathfrak{p})/I$ such that $deg\left(f\right)\ge deg\left(g\right)$ and $(I:g)=\mathfrak{p}$.

Proof. 

The strict inclusion $I⊊(I:\mathfrak{p})$ is clear because $f\in (I:\mathfrak{p})\setminus I$. Let $\mathcal{G}=\{{\overline{g}}_1,\dots ,{\overline{g}}_r\}$ be a minimal generating set of $(I:\mathfrak{p})/I$ such that $g_i$ is a homogeneous polynomial for all i. As $(I:f)=\mathfrak{p}$, one has $\overline{f}\ne \overline{0}$ and $f\in (I:\mathfrak{p})$. Then, we can choose homogeneous polynomials $h_1,\dots ,h_r$ in S, p in I, such that $f={\sum }_{i=1}^r{h}_i{g}_i+p$ and $d=deg\left(h_i{g}_i\right)$ for all i with $h_i\ne 0$. One has the inclusion ${\bigcap }_{i=1}^r(I:g_i{h}_i)\subset (I:f)$. Indeed, if we take h in ${\bigcap }_{i=1}^r(I:g_i{h}_i)$, then $h{h}_i{g}_i\in I$ for all i and $hf={\sum }_{i=1}^{r}h{h}_i{g}_i+hp\in I$, thus $h\in (I:f)$. Therefore, using the fact that all $g_i$’s are in $(I:\mathfrak{p})$, one has the inclusions:

$$\mathfrak{p}\subset \bigcap _{i=1}^r(I:g_i)\subset \bigcap _{i=1}^r(I:g_i{h}_i)\subset (I:f)=\mathfrak{p},$$

and consequently, $\mathfrak{p}={\bigcap }_{i=1}^r(I:g_i{h}_i)$. Hence, by [25] (p. 74, 2.1.48), we obtain $(I:g_i{h}_i)=\mathfrak{p}$ for some $1\le i\le r$. As $g_i\in (I:\mathfrak{p})$, we obtain:

$$\mathfrak{p}\subset (I:g_i)\subset (I:g_i{h}_i)=\mathfrak{p}.$$

Hence, $\mathfrak{p}=(I:g_i)$ and $d=deg\left(f\right)=deg\left(g_i{h}_i\right)\ge deg\left(g_i\right)$. □

Theorem 10

(The same as Theorem 1). Let $I\subset S$ be a graded ideal, and let $\mathfrak{p}\in \mathrm{Ass}\left(I\right)$. The following hold:

(a) 

If $\mathcal{G}=\{{\overline{g}}_1,\dots ,{\overline{g}}_r\}$ is a homogeneous minimal generating set of $(I:\mathfrak{p})/I$, then:

$${\mathrm{v}}_{\mathfrak{p}}\left(I\right)=min\{deg\left(g_i\right)\mid 1\le i\le r \mathrm{and} (I:g_i)=\mathfrak{p}\};$$

(b) 

$\mathrm{v}\left(I\right)=min\{{\mathrm{v}}_{\mathfrak{q}}\left(I\right)\mid \mathfrak{q}\in \mathrm{Ass}\left(I\right)\}$;

(c) 

${\mathrm{v}}_{\mathfrak{p}}\left(I\right)\ge \alpha ((I:\mathfrak{p})/I)$ with equality if $\mathfrak{p}\in \mathrm{Max}\left(I\right)$;

(d) 

If I has no embedded primes, then $\mathrm{v}\left(I\right)=min\left\{\alpha \left((I:\mathfrak{q})/I\right)\right|\mathfrak{q}\in \mathrm{Ass}\left(I\right)\}.$

Proof. (a) Take any homogeneous polynomial f in S such that $(I:f)=\mathfrak{p}$. Then, by Lemma 2, there is $g_j\in \mathcal{G}$ such that $deg\left(f\right)\ge deg\left(g_j\right)$ and $(I:g_j)=\mathfrak{p}$. Thus, the set $\{g_i\mid (I:g_i)=\mathfrak{p}\}$ is not empty and the inequality:

$${\mathrm{v}}_{\mathfrak{p}}\left(I\right)\le min\{deg\left(g_i\right)\mid 1\le i\le r \mathrm{and} (I:g_i)=\mathfrak{p}\}$$

follows by the definition of ${\mathrm{v}}_{\mathfrak{p}}\left(I\right)$. Now, we can pick a homogeneous polynomial f in S such that $deg\left(f\right)={\mathrm{v}}_{\mathfrak{p}}\left(I\right)$ and $(I:f)=\mathfrak{p}$. Then, by Lemma 2, there is $g_j\in \mathcal{G}$ such that $deg\left(f\right)\ge deg\left(g_j\right)$ and $(I:g_j)=\mathfrak{p}$. Thus, $deg\left(f\right)=deg\left(g_j\right)$ and the inequality “≥” holds;

(b) This follows at once from the definitions of $\mathrm{v}\left(I\right)$ and ${\mathrm{v}}_{\mathfrak{q}}\left(I\right)$;

(c) Pick a homogeneous polynomial g in S such that $deg\left(g\right)={\mathrm{v}}_{\mathfrak{p}}\left(I\right)$ and $(I:g)=\mathfrak{p}$. Then, $g\notin I$ and $g\mathfrak{p}\subset I$, that is $g\in (I:\mathfrak{p})\setminus I$. Thus, ${\mathrm{v}}_{\mathfrak{p}}\left(I\right)\ge \alpha ((I:\mathfrak{p})/I)$. Now, assume that $\mathfrak{p}\in \mathrm{Max}\left(I\right)$. To show the reverse inequality, take any homogeneous polynomial f in $(I:\mathfrak{p})\setminus I$. Then, $f\mathfrak{p}\subset I$ and $\mathfrak{p}\subset (I:f)$. Since $\mathrm{Ass}(I:f)$ is contained in $\mathrm{Ass}\left(I\right)$, there is $\mathfrak{q}\in \mathrm{Ass}\left(I\right)$ such that $\mathfrak{p}\subset (I:f)\subset \mathfrak{q}$. Hence, $\mathfrak{p}=\mathfrak{q}$ and $\mathfrak{p}=(I:f)$. Thus, ${\mathrm{v}}_{\mathfrak{p}}\left(I\right)\le deg\left(f\right)$ and ${\mathrm{v}}_{\mathfrak{p}}\left(I\right)\le \alpha ((I:\mathfrak{p})/I)$;

(d) This follows immediately from (b) and (c). □

We give a direct proof of the next result, which in particular relates the v-number of a Cohen–Macaulay monomial ideal $I\subset S$ to that of $(I,h)$, where $h\in S_1$ and $(I:h)=I$.

Corollary 2

([4], Proposition 4.9). Let $I\subset S$ be a Cohen–Macaulay nonprime graded ideal whose associated primes are generated by linear forms, and let $h\in S_1$ be a regular element on $S/I$. Then, $\mathrm{v}(I,h)\le \mathrm{v}\left(I\right)$.

Proof. 

Since the ideal I has no embedded primes, by Theorem 10d, there are $\mathfrak{p}\in \mathrm{Ass}\left(I\right)$ and $f\in (I:\mathfrak{p})\setminus I$ such that $\overline{f}=f+I$ is a minimal generator of $M_{\mathfrak{p}}=(I:\mathfrak{p})/I$ and $deg\left(f\right)=\mathrm{v}\left(I\right)$. The associated primes of $(I:f)$ are contained in $\mathrm{Ass}\left(I\right)$; thus, there is $\mathfrak{q}\in \mathrm{Ass}\left(I\right)$ such that $\mathfrak{p}\subset (I:f)\subset \mathfrak{q}$. Hence, $\mathfrak{p}=\mathfrak{q}$ because I has no embedded associated primes, and one has the equality $(I:f)=\mathfrak{p}$. We claim that f is not in $(I,h)$. We assume, by contradiction, that $f\in (I,h)$. Then, we can write $f=f_1+h{f}_2$, with $f_i$ a homogeneous polynomial for $i=1,2$, $f_1\in I$, $f_2\in S$. Hence, one has:

$$\mathfrak{p}=(I:f)=(I:h{f}_2)=(I:f_2).$$

Therefore, $f_2\in (I:\mathfrak{p})\setminus I$ and $\overline{f}=\overline{h}\overline{f_2}$, a contradiction because $\overline{f}$ is a minimal generator of $M_{\mathfrak{p}}$. This proves that $f\notin (I,h)$. Next, we show the equality $(\mathfrak{p},h)=\left(\right(I,h):f)$. The inclusion “⊂” is clear because $(I:f)=\mathfrak{p}$. Take an associated prime ${\mathfrak{p}}^{\prime }$ of $\left(\right(I,h):f)$. The height of ${\mathfrak{p}}^{\prime }$ is equal to $\mathrm{ht}\left(I\right)+1$ because $(I,h)$ is Cohen–Macaulay and the associated primes of $\left(\right(I,h):f)$ are contained in $\mathrm{Ass}(I,h)$. Then:

$$\mathfrak{p}=(I:f)\subset ((I,h):f)\subset {\mathfrak{p}}^{\prime },$$

and consequently, $(\mathfrak{p},h)\subset ((I,h):f)\subset {\mathfrak{p}}^{\prime }$. Now, $(\mathfrak{p},h)$ is prime because $\mathfrak{p}$ is generated by linear forms, and $\mathrm{ht}(\mathfrak{p},h)=\mathrm{ht}\left(\mathfrak{p}\right)+1=\mathrm{ht}\left(I\right)+1$ because I is Cohen–Macaulay and h is a regular element on $S/I$. Thus, $(\mathfrak{p},h)={\mathfrak{p}}^{\prime }$, $(\mathfrak{p},h)=\left(\right(I,h):f)$, and $\mathrm{v}(I,h)\le \mathrm{v}\left(I\right)$. □

Proposition 2.

Let $I\subset S$ be a monomial ideal minimally generated by $G\left(I\right)$, and for each $t_i$ that occurs in a monomial of $G\left(I\right)$, let ${\gamma }_i:=max\left\{{deg}_{t_i}\left(g\right)\right|g\in G\left(I\right)\}$. Then:

$$\mathrm{reg}(S/I)\le dim(S/I)+{\sum }_i({\gamma }_i-1).$$

Proof. 

To show the inequality, we use the polarization technique due to Fröberg (see [52] and [25] (p. 203)). To polarize I we use the set of new variables:

$$T_I={\bigcup }_{i=1}^n\{t_{i,2},\dots ,t_{i,{\gamma }_i}\},$$

where $\{t_{i,2},\dots ,t_{i,{\gamma }_i}\}$ is empty if ${\gamma }_i=1$. Note that $|T_I|={\sum }_i({\gamma }_i-1)$. A power $t_i^{c_i}$ of a variable $t_i$, $1\le c_i\le {\gamma }_i$, polarizes to ${\left(t_i^{c_i}\right)}^{\mathrm{pol}}=t_i$ if ${\gamma }_i=1$, to ${\left(t_i^{c_i}\right)}^{\mathrm{pol}}=t_{i,2}\cdots t_{i,c_i+1}$ if $c_i<{\gamma }_i$, and to ${\left(t_i^{c_i}\right)}^{\mathrm{pol}}=t_{i,2}\cdots t_{i,{\gamma }_i}{t}_i$ if $c_i={\gamma }_i$. Setting $G\left(I\right)=\{g_1,\dots ,g_r\}$, the polarization $I^{\mathrm{pol}}$ of I is the ideal of $S\left[T_I\right]$ generated by $g_1^{\mathrm{pol}},\dots ,g_r^{\mathrm{pol}}$. According to Corollary 1.6.3 in [21], one has:

$$\mathrm{reg}(S/I)=\mathrm{reg}(S\left[T_I\right]/I^{\mathrm{pol}})and\mathrm{ht}\left(I\right)=\mathrm{ht}\left(I^{\mathrm{pol}}\right).$$

As $I^{\mathrm{pol}}$ is squarefree, by Proposition 3.2 in [4], one has $\mathrm{reg}(S\left[T_I\right]/I^{\mathrm{pol}})\le dim(S\left[T_I\right]/I^{\mathrm{pol}})$. Hence, we obtain:

$$\mathrm{reg}(S/I)=\mathrm{reg}(S\left[T_I\right]/I^{\mathrm{pol}})\le dim(S\left[T_I\right]/I^{\mathrm{pol}})=dim\left(S\left[T_I\right]\right)-\mathrm{ht}\left(I\right).$$

To complete the proof, notice that $dim\left(S\left[T_I\right]\right)-\mathrm{ht}\left(I\right)=dim(S/I)+\left|T_I\right|$. □

Given $a=(a_1,\cdots ,a_s)\in {\mathbb{N}}^s$, where $\mathbb{N}=\{0,1,\dots \}$, the monomial $t_1^{a_1}\cdots t_s^{a_s}$ is denoted by $t^a$. A result of Beintema [53] shows that a zero-dimensional monomial ideal is Gorenstein if and only if it is a complete intersection. (This is also true in dimension one; see Exercise 4.4.19 in [54].) The next result classifies the complete intersection property using regularity.

Proposition 3.

Let I be a monomial ideal of S of dimension zero minimally generated by $G\left(I\right)=\{t_1^{d_1},\dots ,t_s^{d_s},t^{d_{s+1}},\dots ,t^{d_m}\}$, where $d_i\ge 1$ for $i=1,\dots ,s$ and $d_i\in {\mathbb{N}}^s\setminus \left\{0\right\}$ for $i>s$. Then, $\mathrm{reg}(S/I)\le {\sum }_{i=1}^s(d_i-1)$, with equality if and only if I is a complete intersection.

Proof. 

The inequality $\mathrm{reg}(S/I)\le {\sum }_{i=1}^s(d_i-1)$ follows directly from Proposition 2 because $dim(S/I)=0$. If I is a complete intersection, then $I=(t_1^{d_1},\dots ,t_s^{d_s})$, and by Lemma 3.5 in [55], we obtain $\mathrm{reg}(S/I)={\sum }_{i=1}^s(d_i-1)$. Conversely, assume that $\mathrm{reg}(S/I)$ is equal to ${\sum }_{i=1}^s(d_i-1)$. We argue by contradiction assuming that $m>s$. Then, the exponents of the monomial $t^{d_m}=t_1^{c_1}\cdots t_s^{c_s}$ satisfy $c_i\le d_i-1$ for $i=1,\dots ,s$ because $t^{d_m}\in G\left(I\right)$. The regularity of $S/I$ is the largest integer $d\ge 0$ such that ${(S/I)}_d\ne \left(0\right)$, Proposition 4.14 in [37]. Pick a monomial $t^a=t_1^{a_1}\cdots t_s^{a_s}$ such that $t^a\in S_d\setminus I$ and $d={\sum }_{i=1}^s(d_i-1)$. Then, $a_i\le d_i-1$ for $i=1,\dots ,s$ because $t^a$ is not in I, and consequently, $a_i=d_i-1$ for $i=1,\dots ,s$. Hence, $t^a=t^{\delta }{t}^{d_m}$ for some $\delta \in {\mathbb{N}}^s$, a contradiction. □

Remark 2.

Note that Proposition 3 follows also from Corollary 3.17 in [56]. Indeed, assume that $\mathrm{reg}(S/I)$ is equal to ${\sum }_{i=1}^s(d_i-1)$. Let $I={\bigcap }_{k=1}^r{\mathfrak{q}}_k$ be the irreducible decomposition of I, where the ${\mathfrak{q}}_k$’s are irreducible monomial ideals of S, i.e., ideals generated by powers of variables in S. We argue by contradiction assuming that I is not a complete intersection. Then, I is not irreducible and $\mathrm{reg}(S/{\mathfrak{q}}_k)<{\sum }_{i=1}^s(d_i-1)$ for all k because $(t_1^{d_1},\dots ,t_s^{d_s})⊊{\mathfrak{q}}_k$ for all k. Therefore, by Corollary 3.17 in [56], it follows that $\mathrm{reg}(S/I)<{\sum }_{i=1}^s(d_i-1)$ because I is $\mathfrak{m}$-primary, $\mathfrak{m}=(t_1,\dots ,t_s)$, and $\mathrm{reg}(S/I)=max{\left\{\mathrm{reg}(S/{\mathfrak{q}}_k)\right\}}_{k=1}^r$, a contradiction.

4. Induced Matchings and the v-Number

In this section, we show that the induced matching number of a graph G is an upper bound for the v-number of $I\left(G\right)$ when G is very well-covered, or G has a simplicial partition, or G is well-covered connected and contains neither four, nor five cycles. We classify when the induced matching number of G is an upper bound for the v-number of $I\left(G\right)$ when G is a cycle and classify when all vertices of a graph are shedding vertices to gain insight into the family of $W_2$-graphs. To avoid repetition, we continue to employ the notations and definitions used in Section 1 and Section 2.

Theorem 11

([4], Theorem 3.5). If $I=I\left(G\right)$ is the edge ideal of a graph G, then ${\mathcal{F}}_G\subset {\mathcal{A}}_G$ and the $\mathrm{v}$-number of I is:

$$\mathrm{v}\left(I\right)=min\left\{\right|A|:A\in {\mathcal{A}}_G\}.$$

Lemma 3.

Let A be a stable set of a graph G. If $N_G\left(A\right)$ is a vertex cover of G, then $A\in {\mathcal{A}}_G$.

Proof. 

We take any $b\in N_G\left(A\right)$, then there is $e\in E\left(G\right)$ such that $e\subset A\bigcup \left\{b\right\}$. Furthermore, $N_G\left(A\right)\bigcap A=\varnothing$, since A is a stable set of G. Thus,

$$e\bigcap N_G\left(A\right)\subset (A\bigcup \left\{b\right\})\bigcap N_G\left(A\right)\subset \left\{b\right\},$$

and consequently, $e\bigcap (N_G\left(A\right)\setminus \left\{b\right\})=\varnothing$. Hence, $N_G\left(A\right)\setminus \left\{b\right\}$ is not a vertex cover of G, since $e\in E\left(G\right)$. Therefore, $N_G\left(A\right)$ is a minimal vertex cover of G and $A\in {\mathcal{A}}_G$ □

Theorem 12

(The same as Theorem 2). Let G be a very well-covered graph, and let $P=\{e_1,\dots ,e_r\}$ be a perfect matching of G. Then, there is an induced submatching $P^{\prime }$ of P and $D\in {\mathcal{A}}_G$ such that $D\subset V\left(P^{\prime }\right)$ and $|e\bigcap D|=1$ for each $e\in P^{\prime }$. Furthermore, $\mathrm{v}\left(I\left(G\right)\right)\le |P^{\prime }|=|D|\le \mathrm{im}\left(G\right)\le \mathrm{reg}(S/I\left(G\right))$.

Proof. 

To show the first part, we use induction on $\left|P\right|$. If $r=1$, we set $P^{\prime }=P=\left\{e_1\right\}$ and $D=\left\{x_1\right\}$, where $e_1=\{x_1,y_1\}$. Assume $r>1$. We set $e_r=\{x,x^{\prime }\}$, $G_1:=G\setminus \{x,x^{\prime }\}$ and $P_1:=P\setminus \left\{e_r\right\}$. By Theorem 7, P satisfies Property (P). Then, $P_1$ satisfies Property (P) as well. Thus, by Theorem 7, $G_1$ is very well-covered with a perfect matching $P_1$. Hence, by the induction hypothesis, there is an induced submatching $P_1^{\prime }$ of $P_1$ and $D_1\in {\mathcal{A}}_{G_1}$ such that $D_1\subset V\left(P_1^{\prime }\right)$ and $|e\bigcap D_1|=1$ for each $e\in P_1^{\prime }$. Consequently, $N_{G_1}\left(D_1\right)$ is a minimal vertex cover of $G_1$. We consider two cases: $e_r\bigcap N_G\left(D_1\right)\ne \varnothing$ and $e_r\bigcap N_G\left(D_1\right)=\varnothing$:

Case (I). Assume that $e_r\bigcap N_G\left(D_1\right)\ne \varnothing$. Thus, we may assume that there is $\{x,d\}\in E\left(G\right)$ with $d\in D_1$. Then, $N_G\left(x^{\prime }\right)\subset N_G\left(d\right)\subset N_G\left(D_1\right)$, since P satisfies Property (P). Hence, $N_G\left(D_1\right)$ is a vertex cover of G, since $N_{G_1}\left(D_1\right)$ is a vertex cover of $G_1$ and $\left\{x\right\}\subset N_G\left(x^{\prime }\right)\subset N_G\left(D_1\right)$. Therefore, by Lemma 3, $D_1\in {\mathcal{A}}_G$, so this case follows by making $D=D_1$ and $P^{\prime }=P_1^{\prime }$;

Case (II). Assume that $e_r\bigcap N_G\left(D_1\right)=\varnothing$. We set $D_2:=V\left(P_1^{\prime }\right)\setminus D_1$, then $D_2$ is a stable set of $G_1$ and also of G, since $P_1^{\prime }$ is an induced matching of $G_1$ and also of G. One has the inclusion:

$$V\left(P_1^{\prime }\right)\bigcap (N_G\left(x\right)\bigcup N_G\left(x^{\prime }\right))\subset D_2,$$

(1)

indeed taking $z\in V\left(P_1^{\prime }\right)\bigcap N_G\left(x\right)$ (the case $z\in V\left(P_1^{\prime }\right)\bigcap N_G\left(x^{\prime }\right)$ is similar). If $z\notin D_2$, then $z\in D_1\bigcap N_G\left(x\right)$, $\{z,x\}\in E\left(G\right)$, and $x\in e_r\bigcap N_G\left(D_1\right)$, a contradiction. We claim that $|e_r\bigcap N_G\left(D_2\right)|\le 1$. We assume, by contradiction, that $x,x^{\prime }\in N_G\left(D_2\right)$. Then, there are $d_1,d_2\in D_2$ such that $\{x,d_1\},\{x^{\prime },d_2\}\in E\left(G\right)$. Thus, $\{d_1,d_2\}\in E\left(G\right)$, since P satisfies Property (P), a contradiction, since $D_2$ is a stable set of G. Hence, $|e_r\bigcap N_G\left(D_2\right)|\le 1$, and we may assume:

$$e_r\bigcap N_G\left(D_2\right)\subset \left\{x\right\}.$$

(2)

Next we show that $V\left(P_1^{\prime }\right)\bigcap N_G\left(x^{\prime }\right)=\varnothing$. If the intersection is nonempty, by Equation (1), we can pick z in $D_2\bigcap N_G\left(x^{\prime }\right)$, then $\{z,x^{\prime }\}\in E\left(G\right)$ and $x^{\prime }\in N_G\left(D_2\right)$, a contradiction to Equation (2). Therefore, by Equation (1), we obtain the inclusion:

$$V\left(P_1^{\prime }\right)\bigcap (N_G\left(x\right)\bigcup N_G\left(x^{\prime }\right))\subset D_2\bigcap N_G\left(x\right)=:A_2,$$

Thus, the edge set $Q:=\{e\in P_1^{\prime }\mid e\bigcap A_2=\varnothing \}\bigcup \left\{e_r\right\}$ is an induced matching, since $P_1^{\prime }$ is an induced matching. Setting:

$$D_3:=\{y\in D_1\mid \{y,y^{\prime }\}\in P_1^{\prime } \mathrm{with} y^{\prime }\notin A_2\}\bigcup \left\{x\right\},$$

(3)

i.e., $D_3=(D_1\bigcap V\left(Q\right))\bigcup \left\{x\right\}$, we obtain $|f\bigcap D_3|=1$ for each $f\in Q$, since $|e\bigcap D_1|=1$ for each $e\in P_1^{\prime }$. Note that $D_3$ is a stable set of G, since $D_1$ is a stable set and $\left\{x\right\}\bigcap N_G\left(D_1\right)=\varnothing$. Now, take $e\in E\left(G\right)$. We prove that $e\bigcap N_G\left(D_3\right)\ne \varnothing$. Clearly, $N_G\left(x\right)\subset N_G\left(D_3\right)$ because $x\in D_3$. If $x^{\prime }\in e$, then $x^{\prime }\in e\bigcap N_G\left(x\right)\subset e\bigcap N_G\left(D_3\right)$. Now, if $x\in e$, then $e=\{x,y\}$ for some y in $V\left(G\right)$, and $y\in e\bigcap N_G\left(x\right)\subset e\bigcap N_G\left(D_3\right)$. Therefore, we may assume $e\bigcap \{x,x^{\prime }\}=\varnothing$, then $e\in E\left(G_1\right)$. Thus, there is $z\in e\bigcap N_{G_1}\left(D_1\right)$, since $N_{G_1}\left(D_1\right)$ is a vertex cover of $G_1$. Then, there is $d\in D_1$, such that $z\in N_{G_1}\left(d\right)$. If $d\in D_3$, then $z\in N_G\left(D_3\right)\bigcap e$. Finally, if $d\notin D_3$, then by Equation (3) and the inclusion $D_1\subset V\left(P_1^{\prime }\right)$, there is $d^{\prime }\in A_2$ such that $\{d,d^{\prime }\}\in P_1^{\prime }$. Therefore, $\{x,d^{\prime }\}\in E\left(G\right)$, since $d^{\prime }\in A_2$. This implies, $\{x,z\}\in E\left(G\right)$, since $\{d,z\}\in E\left(G\right)$, $\{x,d^{\prime }\}\in E\left(G\right)$, $\{d,d^{\prime }\}\in P$, and P satisfies Property (P). Thus, $z\in e\bigcap N_G\left(x\right)\subset e\bigcap N_G\left(D_3\right)$. Hence, $N_G\left(D_3\right)$ is a vertex cover, and by Lemma 3, $D_3\in {\mathcal{A}}_G$. Therefore, this case follows by making $P^{\prime }=Q$ and $D=D_3$. This completes the induction process.

Next, we show the equality $|P^{\prime }|=|D|$. By the first part, we may assume that $P^{\prime }=\{e_1,\dots ,e_{\ell }\}$, $1\le \ell \le r$, $e_i=\{x_i,y_i\}$ for $i=1,\dots ,\ell$, and $x_1,\dots ,x_{\ell }\in D$. Thus, $\ell =|P^{\prime }|\le |D|$, and since $D\subset V\left(P^{\prime }\right)$, we obtain $2\left|D\right|\le 2|P^{\prime }|$. Then, $|P^{\prime }|=|D|$. The inequality $\mathrm{v}\left(I\right(G\left)\right)\le \left|D\right|$ follows by Theorem 11, and $|P^{\prime }|\le \mathrm{im}\left(G\right)$ is clear by the definition of $\mathrm{im}\left(G\right)$. Finally, the inequality $\mathrm{im}\left(G\right)\le \mathrm{reg}(S/I(G\left)\right)$ follows directly from Theorem 9. □

Corollary 3

([4], Theorem 3.19(b)). Let G be a graph, and let $W_G$ be its whisker graph. Then:

$$\mathrm{v}\left(I\left(W_G\right)\right)\le \mathrm{reg}(K\left[V\left(W_G\right)\right]/I\left(W_G\right)).$$

Proof. 

By Lemma 1, $W_G$ is very well-covered. Thus, by Theorem 12, the v-number of $I\left(W_G\right)$ is bounded from above by the regularity of $K\left[V\left(W_G\right)\right]/I\left(W_G\right)$. □

Lemma 4.

Let $\ell \ge 0$ and $s=4\ell +r$ be integers with $r\in \{0,1,2,3\}$. If $s\ge 3$ and $s\ne 5$, then:

$$⌊\frac{s}{3}⌋\ge \ell if r=0 and ⌊\frac{s}{3}⌋\ge \ell +1 otherwise.$$

Proof. 

By the division algorithm, $s\equiv r^{\prime }(mod3)$, where $r^{\prime }\in \{0,1,2\}$. Then:

$$⌊\frac{s}{3}⌋=\frac{4\ell +r-r^{\prime }}{3}=\ell +\frac{\ell +r-r^{\prime }}{3}\in \mathbb{Z}.$$

Thus, $a:=\frac{\ell +r-r^{\prime }}{3}\in \mathbb{Z}$. If $r=0$, then $a\ge 0$. This follows using the fact that $0\le r^{\prime }\le 2$ and $\ell \ge 0$. Hence, $⌊\frac{s}{3}⌋\ge \ell$. Now, assume $r\in \{1,2,3\}$. We claim that $a\ge 1$. We assume, by contradiction, that $a\le 0$, then $\ell +r\le r^{\prime }$. If $\ell =0$, then $s=r=3$, since $s\ge 3$, a contradiction, since $3=\ell +r\le r^{\prime }$ and $r^{\prime }\le 2$. Thus, $\ell \ge 1$, and we have $2\le \ell +1\le \ell +r\le r^{\prime }\le 2$. This implies $\ell =1=r$ and $r^{\prime }=2$. Consequently $s=5$, a contradiction. Therefore, $a\ge 1$ and $⌊\frac{s}{3}⌋\ge \ell +1$. □

Theorem 13

(The same as Theorem 3). Let $C_s$ be an s-cycle, and let $I\left(C_s\right)$ be its edge ideal. Then, $\mathrm{v}\left(I\left(C_s\right)\right)\le \mathrm{im}\left(C_s\right)$ if and only if $s\ne 5$.

Proof. 

⇒) Assume that $\mathrm{v}\left(I\left(C_s\right)\right)\le \mathrm{im}\left(C_s\right)$. If $s=5$, then $\mathrm{v}\left(I\left(C_s\right)\right)=2$ and $\mathrm{im}\left(C_s\right)=1$, a contradiction. Thus, $s\ne 5$.

⇐) Assume that $s\ne 5$. We can write $C_s=(t_1,e_1,t_2,\dots ,t_i,e_i,t_{i+1},\dots ,t_s,e_s,t_1)$. The matching $P=\{e_1,e_4,\dots ,e_{3q-2}\}$, where $q:=\lfloor \frac{s}{3}\rfloor$, is an induced matching of $C_s$ and $\left|P\right|=q$. Now, we choose a stable set A of $C_s$, for each one of the following cases:

Case $s=4\ell$. If $A=\{t_2,t_6,\dots ,t_{4\ell -2}\}$, then $N_{C_s}\left(A\right)=\{t_1,t_3,t_5,t_7,\dots ,t_{s-3},t_{s-1}\}$ is a vertex cover of G and $\left|A\right|=\ell$;

Case $s=4\ell +1$. If $A=\{t_2,t_6,\dots ,t_{4\ell -2}\}\bigcup \left\{t_{4\ell }\right\}$, then $N_{C_s}\left(A\right)=\{t_1,t_3,\dots ,t_{s-4},t_{s-2}\}\bigcup \left\{t_s\right\}$ is a vertex cover of G and $\left|A\right|=\ell +1$;

Case $s=4\ell +2$. If $A=\{t_2,t_6,\dots ,t_{4\ell +2}\}$, then $N_{C_s}\left(A\right)=\{t_1,t_3,t_5,t_7,\dots ,t_{s-3},t_{s-1}\}$ is a vertex cover of G and $\left|A\right|=\ell +1$;

Case $s=4\ell +3$. If $A=\{t_2,t_6,\dots ,t_{4\ell +2}\}$, then $N_{C_s}\left(A\right)=\{t_1,t_3,t_5,t_7,\dots ,t_{s-2},t_s\}$ is a vertex cover of G and $\left|A\right|=\ell +1$.

In each case, $N_{C_s}\left(A\right)=\left\{t_i\right|iisodd\}$ and $N_{C_s}\left(A\right)$ is a vertex cover of G. Therefore, by Lemma 3, $A\in {\mathcal{A}}_{C_s}$. Now, assume $s=4\ell +r$, with $r\in \{0,1,2,3\}$ and $\ell \ge 0$ an integer. Then, by Lemma 4, $\lfloor \frac{s}{3}\rfloor \ge \ell$ if $r=0$ and $\lfloor \frac{s}{3}\rfloor \ge \ell +1$ otherwise. Hence, $\left|P\right|=\lfloor \frac{s}{3}\rfloor \ge \left|A\right|$. Therefore, $\mathrm{im}\left(C_s\right)\ge \mathrm{v}\left(I\left(C_s\right)\right)$, since $\mathrm{im}\left(C_s\right)\ge \left|P\right|$ and $\left|A\right|\ge \mathrm{v}\left(I\left(C_s\right)\right)$. □

Remark 3.

The induced matching number of the cycle $C_s$ is equal to $\lfloor \frac{s}{3}\rfloor$. The regularity of $S/I\left(C_s\right)$ is equal to $\lfloor (s+1)/3\rfloor$, Proposition 10 in [15].

Lemma 5.

Let G be a graph without isolated vertices, and let $z_1,\dots ,z_m$ be vertices of G such that ${\left\{N_G\left[z_i\right]\right\}}_{i=1}^m$ is a partition of $V\left(G\right)$. If $G_1=G\setminus N_G\left[z_m\right]$, then:

(i) 

$N_{G_1}\left[z_i\right]=N_G\left[z_i\right]$ for $i<m$;

(ii) 

$G_1\left[N_{G_1}\left[z_i\right]\right]=G\left[N_G\left[z_i\right]\right]$ for $i<m$.

Proof. (i) Assume that $1\le i\le m-1$. Clearly, $N_{G_1}\left[z_i\right]\subset N_G\left[z_i\right]$ because $G_1$ is a subgraph of G. To show the inclusion “⊃”, take $z\in N_G\left[z_i\right]$. Then, $z=z_i$ or $\{z,z_i\}\in E\left(G\right)$. If $z\in N_G\left[z_m\right]$, then $z\in N_G\left[z_m\right]\bigcap N_G\left[z_i\right]$, a contradiction. Thus, $z\notin N_G\left[z_m\right]$, and since $G_1$ is an induced subgraph of G, we obtain $z=z_i$ or $\{z,z_i\}\in E\left(G_1\right)$. Thus, $z\in N_{G_1}\left[z_i\right]$;

(ii) By Part (i), one has $N_G\left[z_i\right]=N_{G_1}\left[z_i\right]\subset V\left(G\right)\setminus N_G\left[z_m\right]=V\left(G_1\right)$. Then:

$$\begin{array}{cc}\hfill E\left(G\left[N_G\left[z_i\right]\right]\right)& =\{e\in E\left(G\right)\mid e\subset N_G\left[z_i\right]\}=\{e\in E\left(G\right)\mid e\subset N_{G_1}\left[z_i\right]\}\hfill \\ \hfill & =\{e\in E\left(G_1\right)\mid e\subset N_{G_1}\left[z_i\right]\}=E\left(G_1\left[N_{G_1}\left[z_i\right]\right]\right).\hfill \end{array}$$

Thus, $E\left(G\left[N_G\left[z_i\right]\right]\right)=E\left(G_1\left[N_{G_1}\left[z_i\right]\right]\right)$. □

Theorem 14

(The same as Theorem 4). Let G be a graph with simplexes $H_1,\dots ,H_r$, such that ${\left\{V\left(H_i\right)\right\}}_{i=1}^r$ is a partition of $V\left(G\right)$. If G has no isolated vertices, then there is $D=\{y_1,\dots ,y_k\}\in {\mathcal{A}}_G$, and there are simplicial vertices $x_1,\dots ,x_k$ of G and integers $1\le j_1<\cdots <j_k\le r$ such that $P={\left\{\{x_i,y_i\}\right\}}_{i=1}^k$ is an induced matching of G and $H_{j_i}$ is the induced subgraph $G\left[N_G\left[x_i\right]\right]$ on $N_G\left[x_i\right]$ for $i=1,\dots ,k$. Furthermore, $\mathrm{v}\left(I\right(G\left)\right)\le \left|D\right|=\left|P\right|\le \mathrm{im}\left(G\right)\le \mathrm{reg}(S/I(G\left)\right)$.

Proof. 

We proceed by induction on r. If $r=1$, then $V\left(H_1\right)=V\left(G\right)$, and there is a simplicial vertex $x_1$ of G such that $H_1=G\left[N_G\left[x_1\right]\right]$ is a complete graph with at least two vertices. Picking $y_1\in N_G\left[x_1\right]$, $y_1\ne x_1$, one has $\left\{x_1\right\}\in {\mathcal{A}}_G$ and $\{x_1,y_1\}$ is an induced matching. Now, assume that $r>1$. We set $G_1:=G\setminus V\left(H_r\right)$. Note that $H_1,\dots ,H_{r-1}$ are simplexes of $G_1$ (Lemma 5) and ${\left\{V\left(H_i\right)\right\}}_{i=1}^{r-1}$ is a partition of $V\left(G_1\right)$. Then, by the induction hypothesis, there is $D_1=\{y_1,\dots ,y_{k^{\prime }}\}\in {\mathcal{A}}_{G_1}$, and there are simplicial vertices $x_1,\dots ,x_{k^{\prime }}$ of $G_1$ and integers $1\le j_1<\cdots <j_{k^{\prime }}\le r-1$, such that $P_1=\{\{x_1,y_1\},\dots ,\{x_{k^{\prime }},y_{k^{\prime }}\}\}$ is an induced matching of $G_1$ and $H_{j_i}=G_1\left[N_{G_1}\left[x_i\right]\right]$ for $i=1,\dots ,k^{\prime }$. By Lemma 5, one has $G_1\left[N_{G_1}\left[x_i\right]\right]=G\left[N_G\left[x_i\right]\right]$ for $i=1,\dots ,k^{\prime }$. We can write $H_r=G\left[N_G\left[x\right]\right]$ for some simplicial vertex x of G.

Case (I). Assume that $V\left(H_r\right)\setminus \left\{x\right\}\subset N_G\left(D_1\right)$. Then, $N_G\left(D_1\right)$ is a vertex cover of G. Indeed, take any edge e of G. If $e\bigcap V\left(H_r\right)=\varnothing$, then e is an edge of $G_1$ and is covered by $N_{G_1}\left(D_1\right)$. Assume that $e\cap V\left(H_r\right)\ne \varnothing$. If $x\notin e$, then there is $z\in e$ with $z\in V\left(H_r\right)\setminus \left\{x\right\}\subset N_G\left(D_1\right)$. Now, if $x\in e$, then $e=\{x,z\}$ with $z\in N_G\left[x\right]\setminus \left\{x\right\}=V\left(H_r\right)\setminus \left\{x\right\}\subset N_G\left(D_1\right)$. This proves that $N_G\left(D_1\right)$ is a vertex cover of G. Hence, by Lemma 3, $D_1\in {\mathcal{A}}_G$, and, noticing that $P_1$ is an induced matching of G, this case follows by making $D=D_1$ and $P=P_1$;

Case (II) Assume that there is $y\in V\left(H_r\right)\setminus \left\{x\right\}$ such that $y\notin N_G\left(D_1\right)$. Then, $D_2:=D_1\bigcup \left\{y\right\}$ is a stable set of G. Furthermore, $N_G\left(D_2\right)$ is a vertex cover of G, since $N_{G_1}\left(D_1\right)$ is a vertex cover of $G_1$, $H_r$ is a complete subgraph of G, and $V\left(H_r\right)\subset N_G\left[y\right]$. Thus, by Lemma 3, $D_2$ is in ${\mathcal{A}}_G$. We set $x_{k^{\prime }+1}:=x$, $y_{k^{\prime }+1}:=y$, and $H_{j_{k^{\prime }+1}}:=H_r$. Then, $\{x_{k^{\prime }+1},y_{k^{\prime }+1}\}\in E\left(H_r\right)$ and $P_2:=P_1\bigcup \left\{\{x_{k^{\prime }+1},y_{k^{\prime }+1}\}\right\}$ is an induced matching of G, since $P_1$ is an induced matching of $G_1$, $y\in V\left(H_r\right)\setminus N_G\left(D_1\right)$ and $H_{j_i}=G\left[N_G\left[x_i\right]\right]$, for $i=1,\dots ,k^{\prime }+1$. Therefore, this case follows by making $D=D_2$ and $P=P_2$.

The equality $\left|D\right|=\left|P\right|$ is clear. The inequality $\mathrm{v}\left(I\right(G\left)\right)\le \left|D\right|$ follows from Theorem 11, and $\left|P\right|\le \mathrm{im}\left(G\right)$ is clear by the definition of $\mathrm{im}\left(G\right)$. Finally, the inequality $\mathrm{im}\left(G\right)\le \mathrm{reg}(S/I(G\left)\right)$ follows directly from Theorem 9. □

Corollary 4

(The same as Corollary 1). Let G be a well-covered graph, and let $I\left(G\right)$ be its edge ideal. If G is simplicial or G is connected and contains neither four, nor five cycles, then:

$$\mathrm{v}\left(I\left(G\right)\right)\le \mathrm{im}\left(G\right)\le \mathrm{reg}(S/I\left(G\right))\le {\beta }_0\left(G\right).$$

Proof. 

Assume that G is simplicial. Let $\{z_1,\dots ,z_{\ell }\}$ be the set of all simplicial vertices of G. Then, $V\left(G\right)={\bigcup }_{i=1}^{\ell }{N}_G\left[z_i\right]$. As G is well-covered, by Lemma 2.4 in [31], for $1\le i<j\le \ell$, either $N_G\left[z_i\right]=N_G\left[z_j\right]$ or $N_G\left[z_i\right]\bigcap N_G\left[z_j\right]=\varnothing$. Thus, there are simplicial vertices $x_1,\dots ,x_k$ of G such that ${\left\{N_G\left[x_i\right]\right\}}_{i=1}^k$ is a partition of $V\left(G\right)$. Setting $H_i=G\left[N_G\left[x_i\right]\right]$ for $i=1,\dots ,k$ and applying Theorem 14, we obtain that $\mathrm{v}\left(I\right(G\left)\right)\le \mathrm{im}\left(G\right)\le \mathrm{reg}(S/I(G\left)\right)$. Noticing that $dim(S/I\left(G\right))={\beta }_0\left(G\right)$, the inequality $\mathrm{reg}(S/I\left(G\right))\le {\beta }_0\left(G\right)$ follows from Proposition 2.

Next, assume that G is connected and contains neither four, nor five cycles. Then, by Theorem 8, $G\in \{C_7,T_{10}\}$ or $G\in \mathcal{F}$. The cases $G=C_7$ or $G=T_{10}$ are treated in Example 3 (cf. Theorem 13). If $G\in \mathcal{F}$, then there exists $\{x_1,\dots ,x_k\}\subset V\left(G\right)$ where for each i, $x_i$ is simplicial, $|N_G\left[x_i\right]|\le 3$, and $\{N_G\left[x_i\right]\mid i=1,\dots ,k\}$ is a partition of $V\left(G\right)$. In particular, G is simplicial, and the asserted inequalities follow from the first part of the proof. □

Proposition 4.

Let G be a graph. The following conditions are equivalent:

1. 

Every vertex of G is a shedding vertex;

2. 

${\mathcal{A}}_G={\mathcal{F}}_G$.

Proof. (1) ⇒ (2) The inclusion ${\mathcal{A}}_G\supset {\mathcal{F}}_G$ follows from Theorem 11. To show the inclusion ${\mathcal{A}}_G\subset {\mathcal{F}}_G$, we argue by contradiction assuming that there is $D\in {\mathcal{A}}_G\setminus {\mathcal{F}}_G$. Then, D is a stable set of G and $N_G\left(D\right)$ is a vertex cover of G. Thus, $D\bigcap N_G\left(D\right)=\varnothing$. Furthermore, since $D\notin {\mathcal{F}}_G$, there is $x\in V\left(G\right)\setminus D$ such that $D\bigcup \left\{x\right\}$ is a stable set of G. Then, $x\notin N_G\left(D\right)$. However, $N_G\left(D\right)$ is a vertex cover of G, then $N_G\left(x\right)\subset N_G\left(D\right)$ and $A:=V\left(G\right)\setminus N_G\left(D\right)$ is a stable set of G. Therefore, $A\subset V\left(G\right)\setminus N_G\left(x\right)$ and $A^{\prime }:=A\setminus x$ is a stable set of $V\left(G\right)\setminus N_G\left[x\right]$. Now, we prove that $A^{\prime }$ is a maximal stable set of $G\setminus x$. We argue by contradiction assuming that there is $a\in V(G\setminus x)\setminus A^{\prime }$, such that $A^{\prime }\bigcup \left\{a\right\}$ is a stable set. Then, $a\in N_G\left(D\right)$, since $V\left(G\right)=A\bigcup N_G\left(D\right)$. Furthermore, $D\subset A^{\prime }$, since $D\bigcap N_G\left(D\right)=\varnothing$ and $x\notin D$, a contradiction, since $a\in N_G\left(D\right)$ and $A^{\prime }\bigcup \left\{a\right\}$ is a stable set. Hence, $A^{\prime }$ is a maximal stable set of $G\setminus x$. Therefore, x is not a shedding vertex of G, a contradiction.

(2) ⇒ (1) We assume, by contradiction, that there is $x\in V\left(G\right)$ such that x is not a shedding vertex. Thus, there is a maximal stable set A of $G\setminus x$ such that $A\subset V\left(G\right)\setminus N_G\left[x\right]$. Then, $C:=V(G\setminus x)\setminus A$ is a minimal vertex cover of $G\setminus x$ and $A\bigcup \left\{x\right\}$ is a stable set of G. Therefore, $A\notin {\mathcal{F}}_G$. Since C is a minimal vertex cover of $G\setminus x$, we have that for each $z\in C$, there is $z^{\prime }\in V(G\setminus x)\setminus C=A$ such that $\{z,z^{\prime }\}\in E\left(G\right)$. Consequently, $C\subset N_G\left(A\right)$. Furthermore, if $a\in N_G\left(x\right)$, then $a\in G\setminus x$ and $a\notin A$. Thus, $a\in N_G\left(A\right)$, since A is a maximal stable set of $G\setminus x$. Hence, $N_G\left(x\right)\subset N_G\left(A\right)$. This implies that $N_G\left(A\right)$ is a vertex cover of G, since $C\subset N_G\left(A\right)$. Therefore, by Lemma 3, $A\in {\mathcal{A}}_G$, a contradiction since $A\notin {\mathcal{F}}_G$. □

Lemma 6

([32], cf. Corollary 3.3). If $G\in W_2$, then every $v\in V\left(G\right)$ is a shedding vertex.

Proof. 

Let v be a vertex of G. We may assume that G is not a complete graph. Let A be a stable set of $G_v:=G\setminus N_G\left[v\right]$. We argue by contradiction assuming that A is a maximal stable set of $G\setminus v$. Then, as G and $G\setminus v$ are well-covered, we obtain:

$${\beta }_0\left(G\right)={\beta }_0(G\setminus v)=\left|A\right|.$$

According to [57], Theorem 5, the graph $G_v$ is in $W_2$ and ${\beta }_0\left(G_v\right)={\beta }_0\left(G\right)-1$. In particular, $G_v$ is well-covered and ${\beta }_0\left(G_v\right)={\beta }_0\left(G\right)-1$ (cf. Theorem 5). However, A is a stable set of $G_v$ and $\left|A\right|={\beta }_0\left(G\right)$, a contradiction. □

Corollary 5

([4], Theorem 4.5). If G is a $W_2$-graph and $I=I\left(G\right)$, then $\mathrm{v}\left(I\right)={\beta }_0\left(G\right)$.

Proof. 

By Theorem 11, there is $D\in {\mathcal{A}}_G$ such that $\mathrm{v}\left(I\right)=\left|D\right|$. Since G is a $W_2$-graph, by Lemma 6, every vertex of G is a shedding vertex. Thus, by Proposition 4, $D\in {\mathcal{F}}_G$, i.e., D is a maximal stable set of G. Furthermore, G is well-covered, since G is a $W_2$-graph. Hence, $\left|D\right|={\beta }_0\left(G\right)$. Therefore, $\mathrm{v}\left(I\right)={\beta }_0\left(G\right)$. □

5. Examples

Example 1.

Let $S=\mathbb{Q}[t_1,t_2,t_3]$ be a polynomial ring and $I=(t_1^5,t_2^5,t_2^4{t}_3^5,t_1^4{t}_3^5)$. Then, an irredundant primary decomposition of I is given by:

$$I=(t_1^4,t_2^4)\bigcap (t_1^5,t_2^5,t_3^5).$$

The associated primes of I are ${\mathfrak{p}}_1=(t_1,t_2)$ and ${\mathfrak{p}}_2=(t_1,t_2,t_3)$. Setting $g_1=t_1^4{t}_2^4$, $g_2=t_1^3{t}_2^3{t}_3^5$, and $g_3=t_1^4{t}_2^4{t}_3^4$ and using Procedure A1 in Appendix A, we obtain that $(I:{\mathfrak{p}}_1)/I$ and $(I:{\mathfrak{p}}_2)/I$ are minimally generated by $\{{\overline{g}}_1,{\overline{g}}_2\}$ and $\left\{{\overline{g}}_3\right\}$, respectively. Using Theorem 10 and the equalities:

$$(I:g_1)=(t_1,t_2,t_3^5),(I:g_2)={\mathfrak{p}}_1,(I:g_3)={\mathfrak{p}}_2,$$

we obtain that $\mathrm{v}\left(I\right)=11$. The regularity of the quotient ring $S/I$ is equal to 12.

Example 2.

Let $S=\mathbb{Q}[t_1,\dots ,t_6]$ be a polynomial ring; let I be the ideal:

$$I=(t_1{t}_2,t_2{t}_3,t_3{t}_4,t_1{t}_4,t_1{t}_5,t_2{t}_5,t_3{t}_5,t_4{t}_5,t_1{t}_6,t_2{t}_6,t_3{t}_6,t_4{t}_6);$$

let G be the graph defined by the generators of I. The associated primes of I are:

$${\mathfrak{p}}_1=(t_1,t_2,t_3,t_4),{\mathfrak{p}}_2=(t_1,t_3,t_5,t_6),{\mathfrak{p}}_3=(t_2,t_4,t_5,t_6).$$

Thus, $I\left(G\right)$ is unmixed, G is well-covered, and ${\alpha }_0\left(G\right)=4$. The graph G is not very well-covered because $\left|V\left(G\right)\right|\ne 2{\alpha }_0\left(G\right)$. The v-number of I is one because $N_G\left(t_6\right)=\{t_1,t_2,t_3,t_4\}$ is a vertex cover of G. Using Macaulay2 [2], we obtain that $\mathrm{reg}(S/I)=1$. Note that $\mathrm{im}\left(G\right)=1$.

Example 3.

Let $C_7$ and $T_{10}$ be the well-covered graphs of Figure 1. Let R and S be polynomial rings over the field $\mathbb{Q}$ in the variables $\{t_1,\dots ,t_7\}$ and $\{t_1,\dots ,t_{10}\}$, respectively. Using Macaulay2 [2] and Procedure A1 in Appendix A, we obtain $\mathrm{ht}\left(I\left(C_7\right)\right)={\alpha }_0\left(C_7\right)=4$, $\mathrm{pd}(R/I\left(C_7\right))=5$, and:

$$\mathrm{v}\left(I\left(C_7\right)\right)=2=\mathrm{im}\left(C_7\right)=\mathrm{reg}(R/I\left(C_7\right))\le dim(R/I\left(C_7\right))={\beta }_0\left(C_7\right)=3.$$

The neighbor set of $A=\{t_1,t_4\}$ in $C_7$ is $N_{C_7}\left(A\right)=\{t_2,t_3,t_5,t_7\}$, and $N_{C_7}\left(A\right)$ is a minimal vertex cover of $C_7$, that is $A\in {\mathcal{A}}_{C_7}$. Using Macaulay2 [2] and Procedure A1 in Appendix A, we obtain $\mathrm{ht}\left(I\left(T_{10}\right)\right)={\alpha }_0\left(G\right)=6$, $\mathrm{pd}(S/I\left(T_{10}\right))=7$, and:

$$\mathrm{v}\left(I\left(T_{10}\right)\right)=2=\mathrm{im}\left(T_{10}\right)\le \mathrm{reg}(S/I\left(T_{10}\right))=3\le dim(S/I\left(T_{10}\right))={\beta }_0\left(T_{10}\right)=4.$$

The neighbor set of $A=\{t_1,t_4\}$ in $T_{10}$ is $N_{T_{10}}\left(A\right)=\{t_2,t_3,t_5,t_7,t_8,t_{10}\}$, and $N_{T_{10}}\left(A\right)$ is a minimal vertex cover of $T_{10}$, that is $A\in {\mathcal{A}}_{T_{10}}$.

Example 4.

Let G be the graph consisting of two disjoint three cycles with vertices $x_1,x_2,x_3$ and $y_1,y_2,y_3$. Take two disjoint independent sets of G, say $A_1=\left\{x_1\right\}$ and $A_2=\left\{y_1\right\}$. To verify that G is a graph in $W_2$, note that $B_1=\{x_1,y_2\}$ and $B_2=\{y_1,x_2\}$ are maximum independent sets of G containing $A_1$ and $A_2$, and that $|B_i|={\beta }_0\left(G\right)=2$ for $i=1,2$.