Evaluation of Multivariate Adaptive Regression Splines and Artificial Neural Network for Prediction of Mean Sea Level Trend around Northern Australian Coastlines
Abstract
1. Introduction
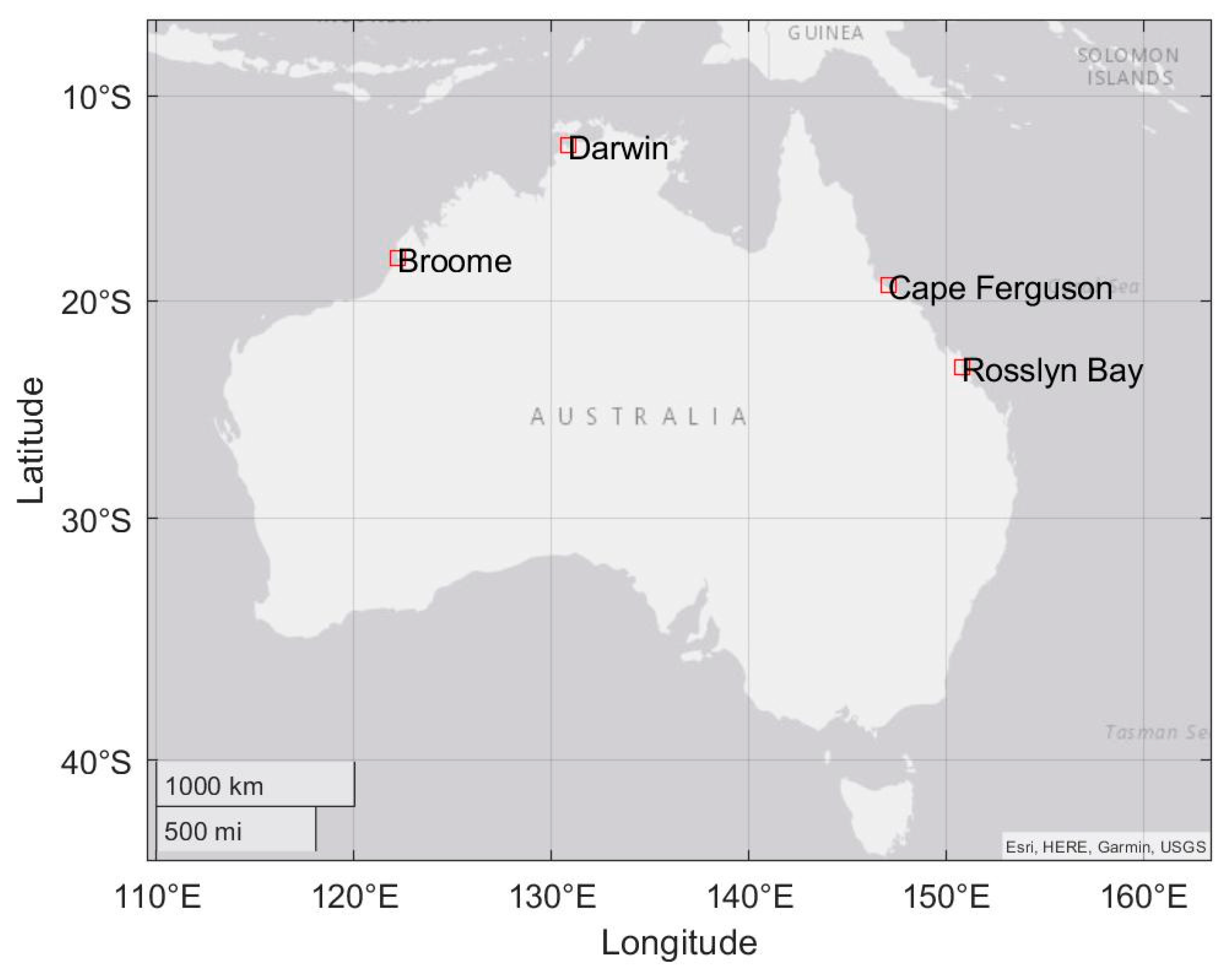
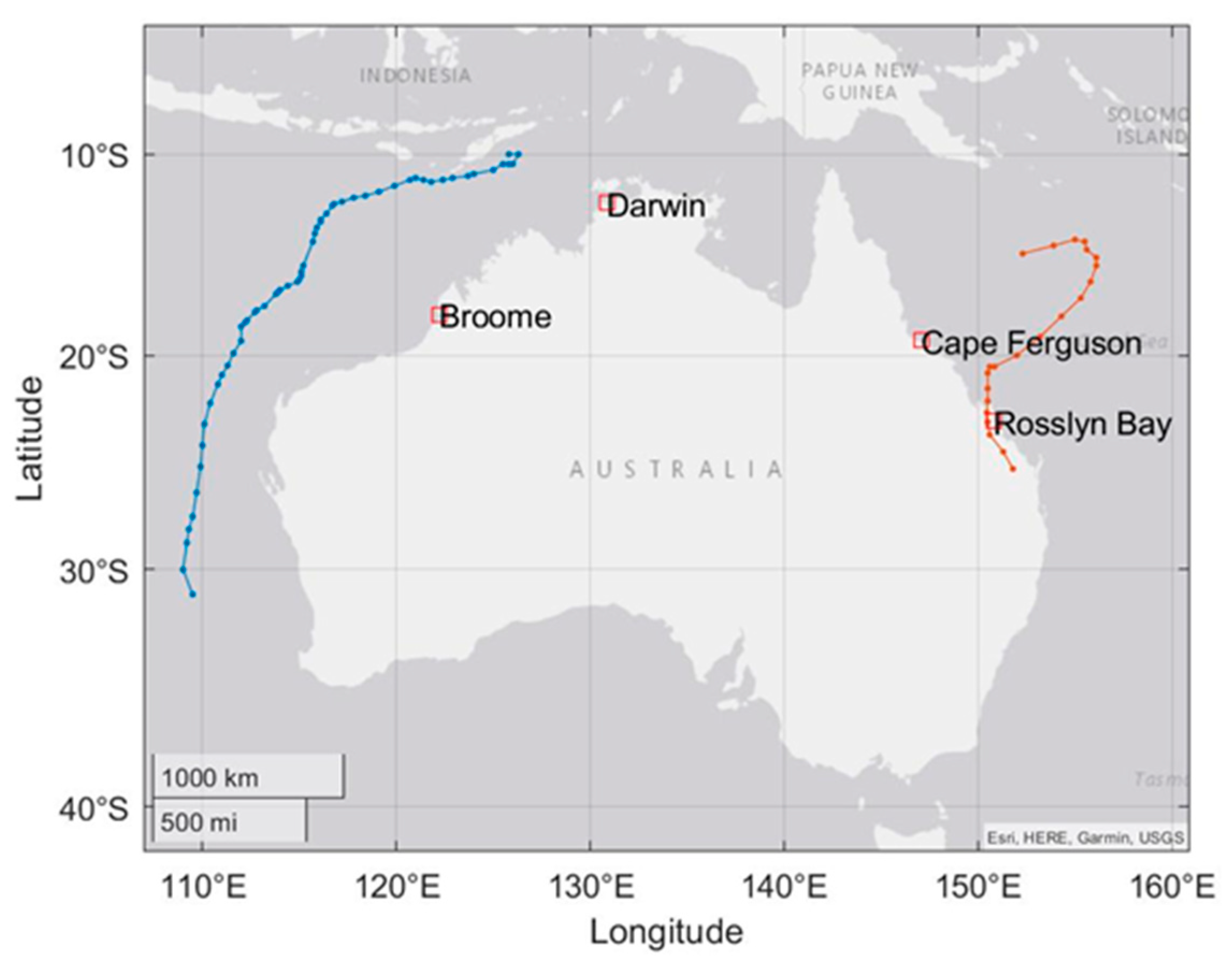
2. Data and Study Area
3. Methodology
3.1. Theoretical Background
3.1.1. Multivariate Adaptive Regression Splines (MARS) Model
3.1.2. Artificial Neural Network (ANN) Model
3.2. Data Preparation
3.3. Data Normalisation
3.4. Model Development
3.4.1. MARS Model Development
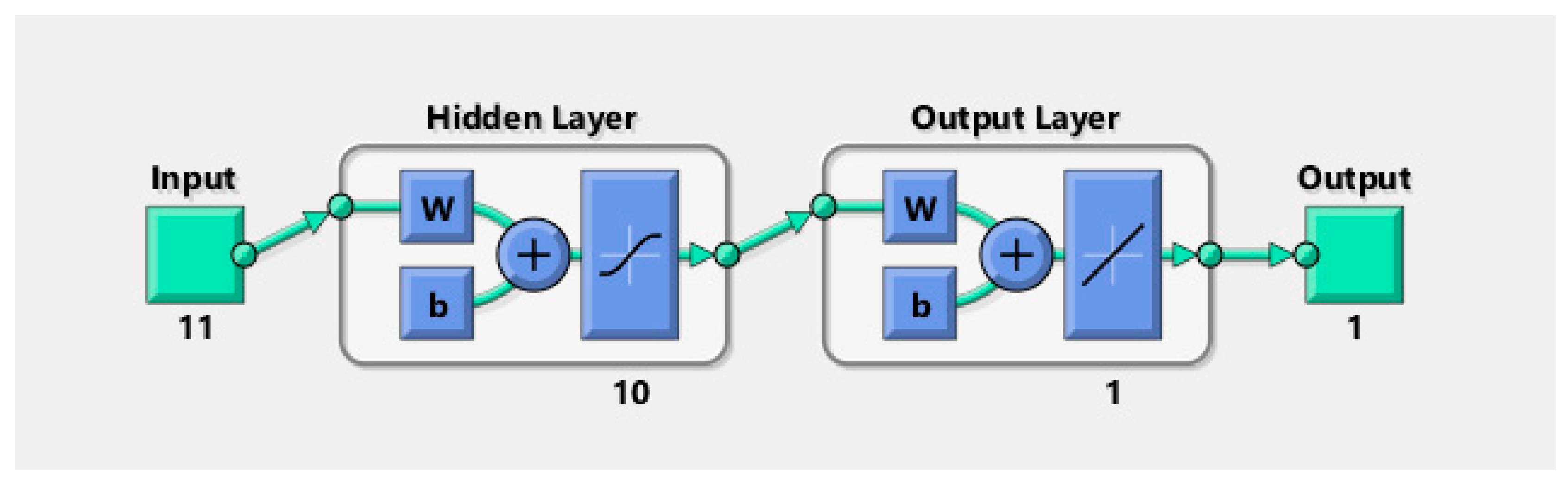
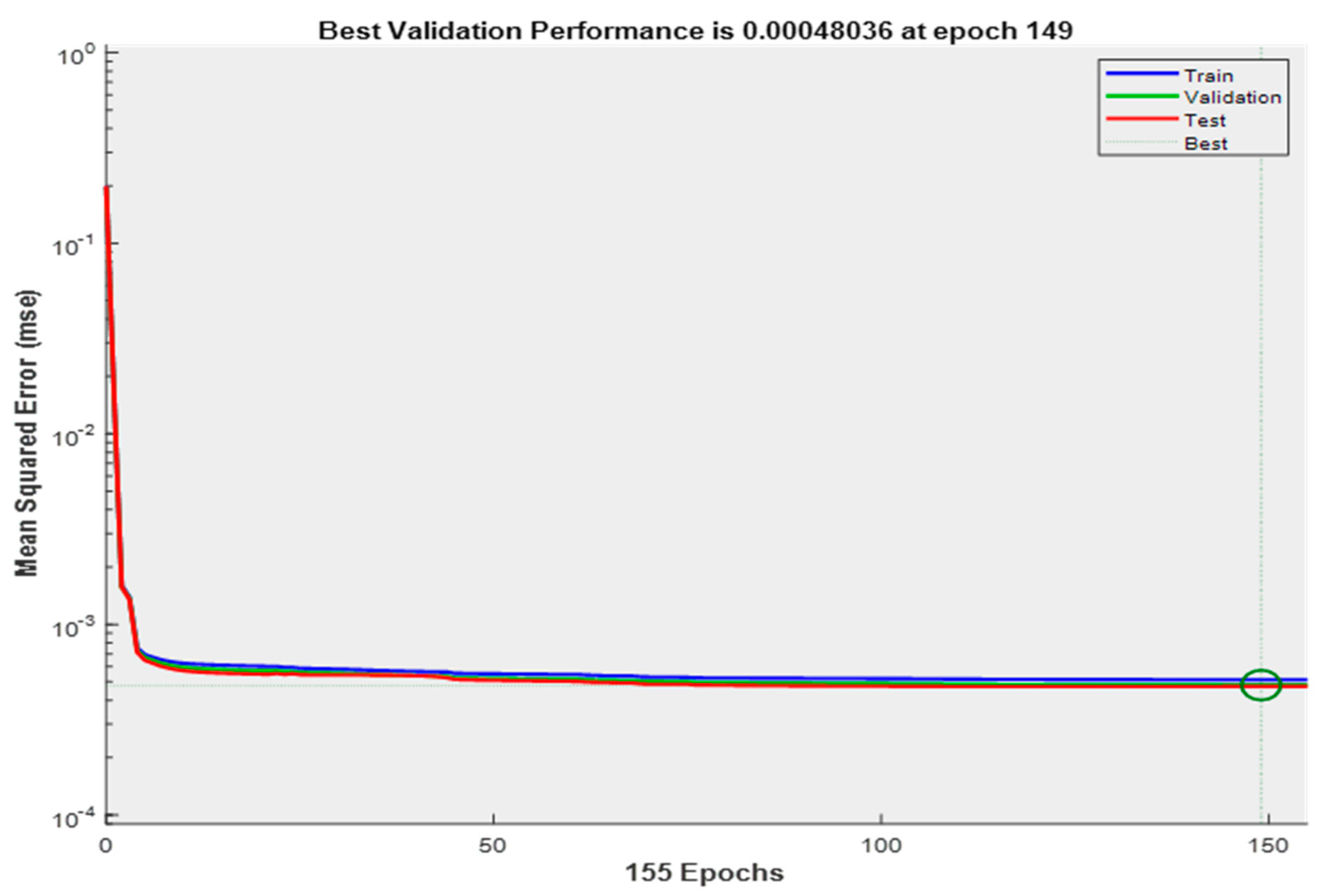
3.4.2. Artificial Neural Network (ANN) Model Development
3.5. Model Performance Criteria
- Correlation coefficient (R)where:
- Nash–Sutcliffe Coefficient (ENS)
- Willmott’s Index of agreement (d)
- Root Mean Square Error (RMSE)
- Mean Absolute Error (MAE)
- Relative Root Mean Square Error (RRMSE)
- Legates and McCabes index (L)
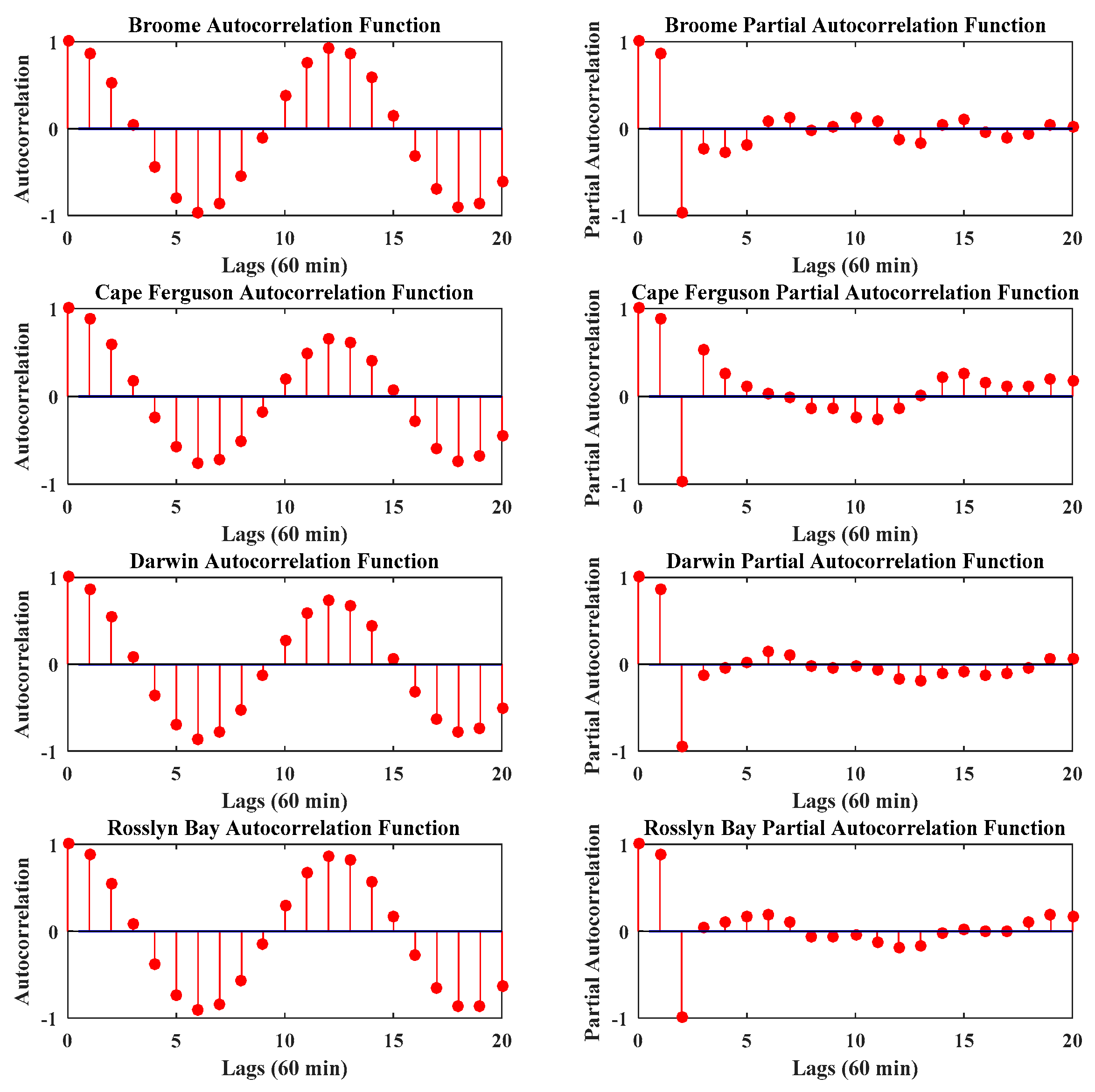
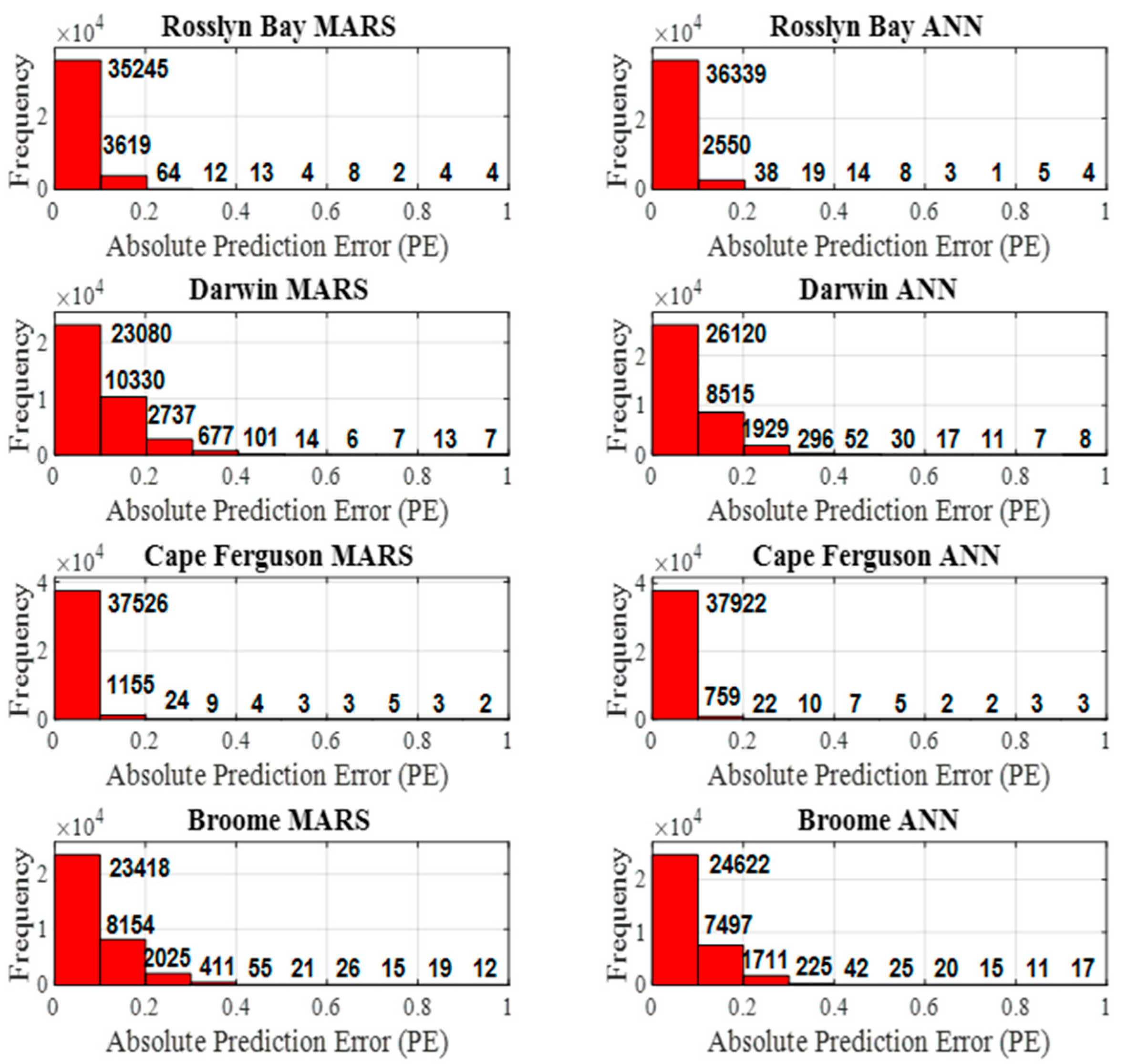
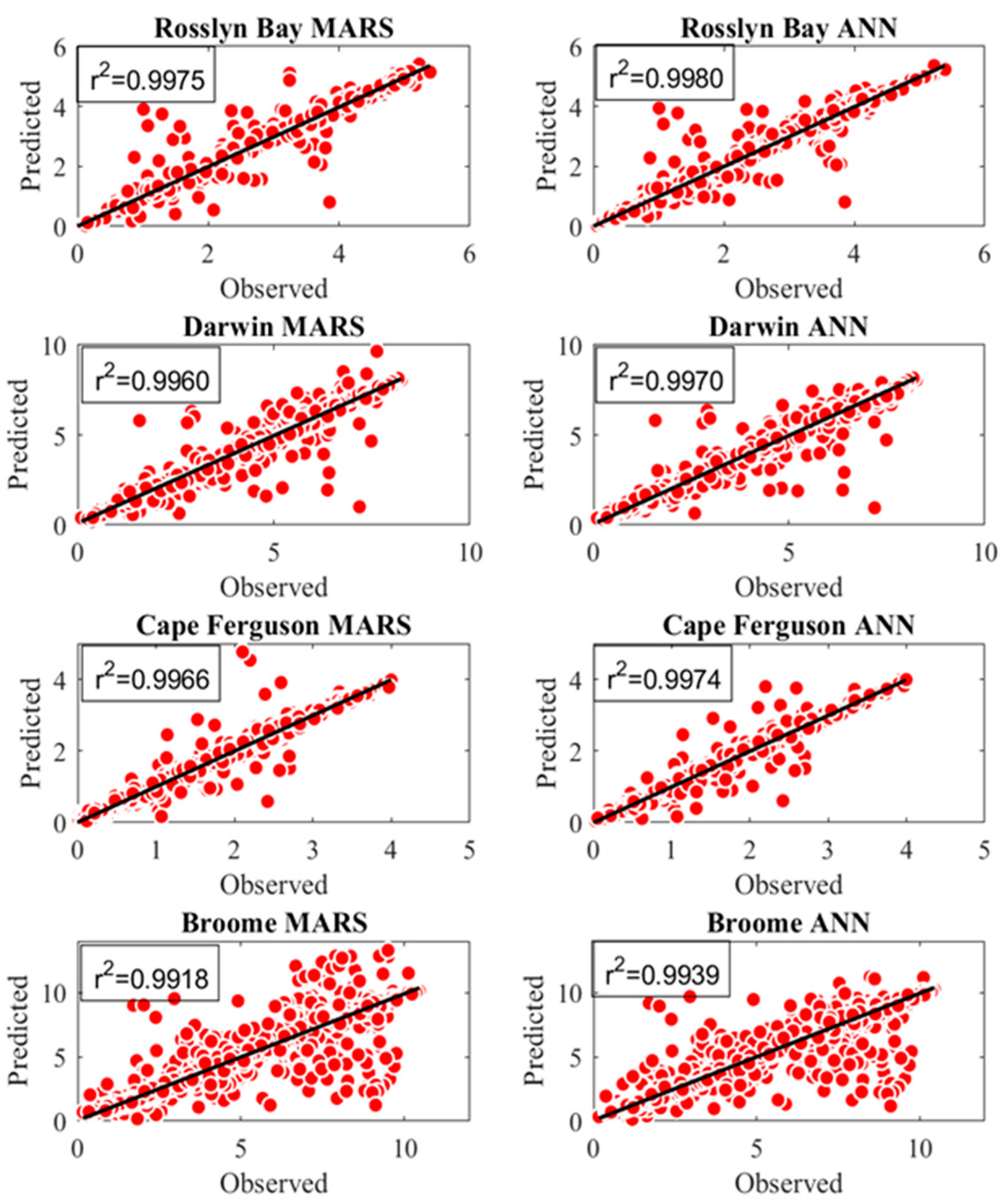
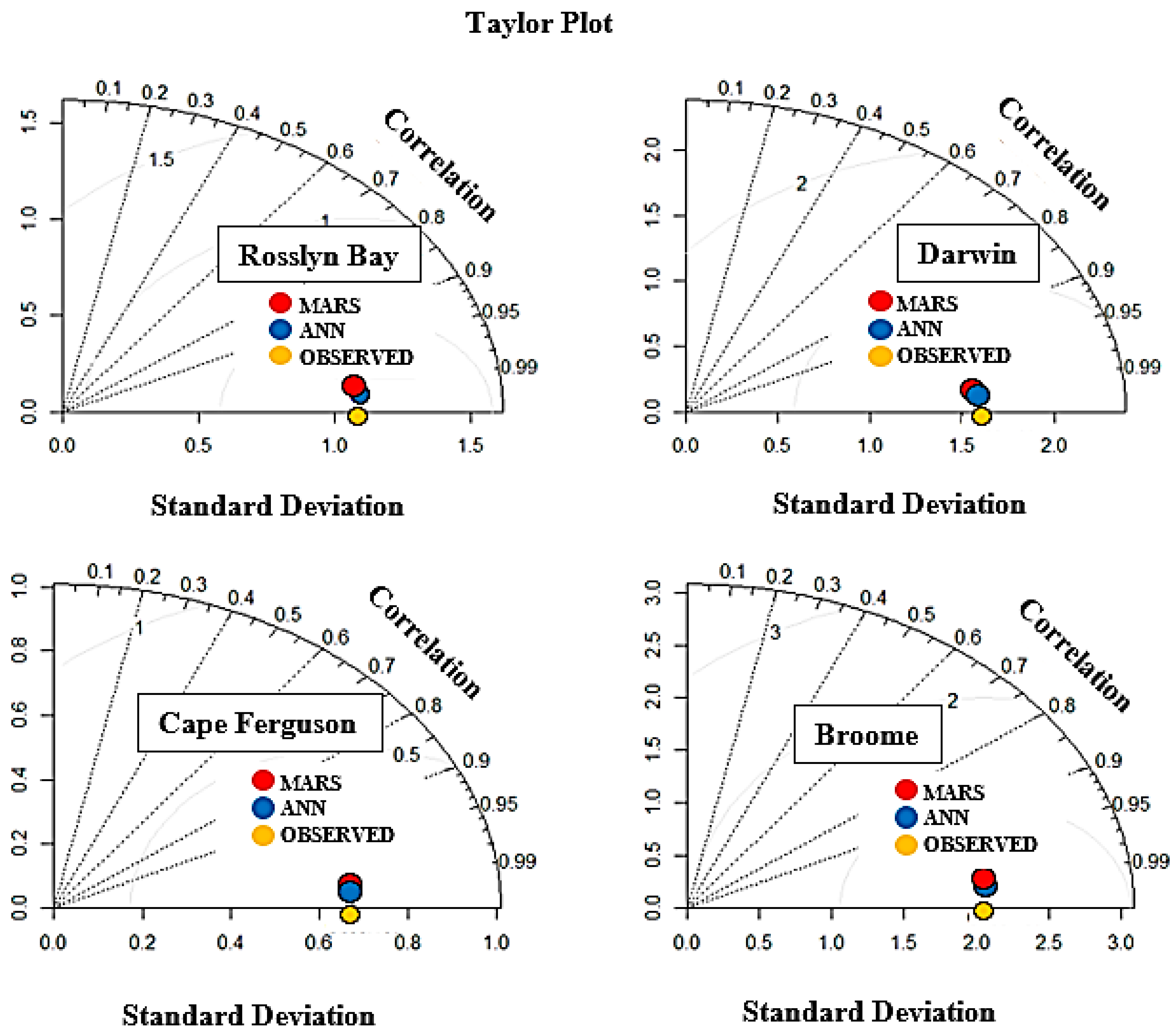
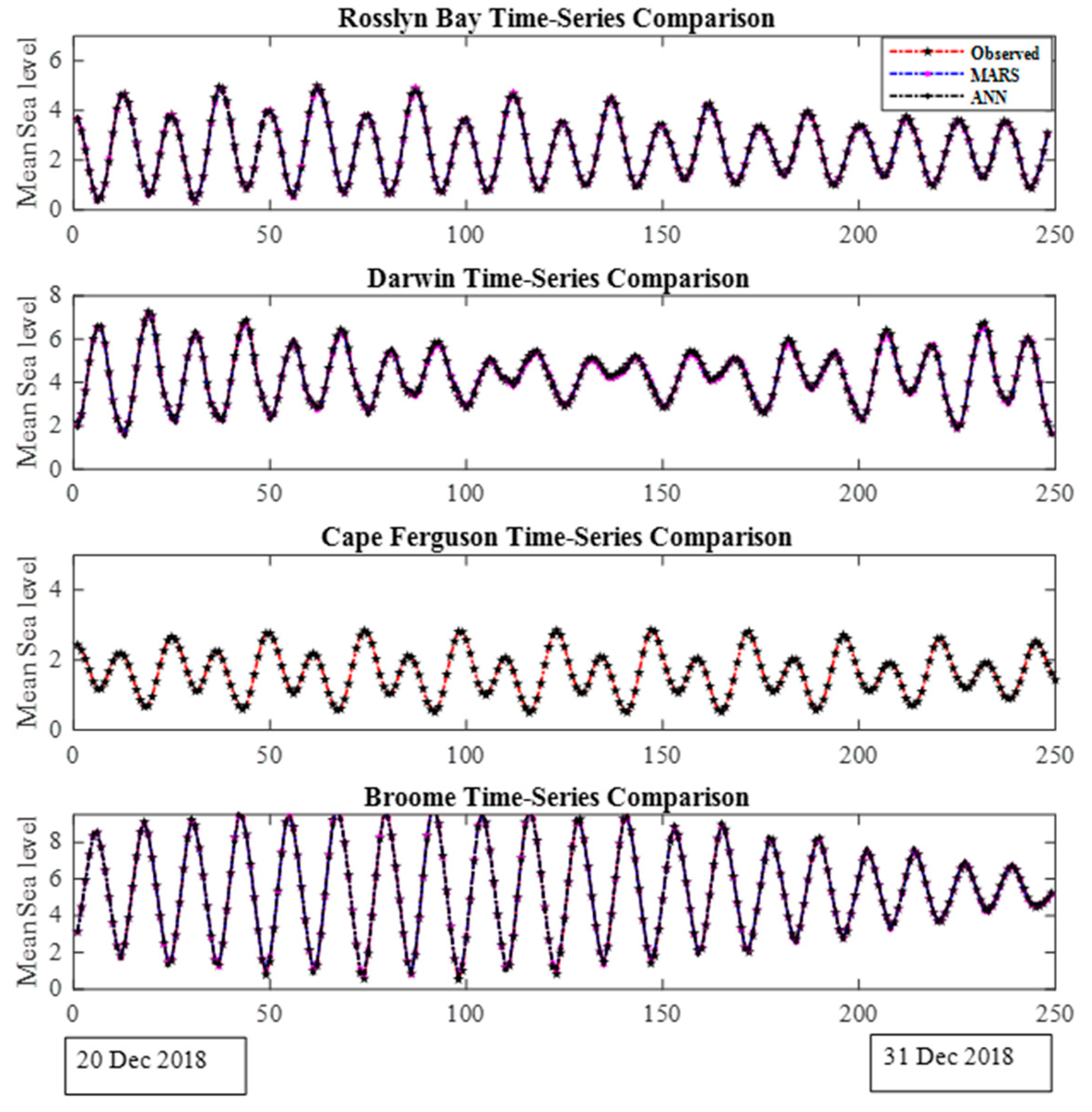
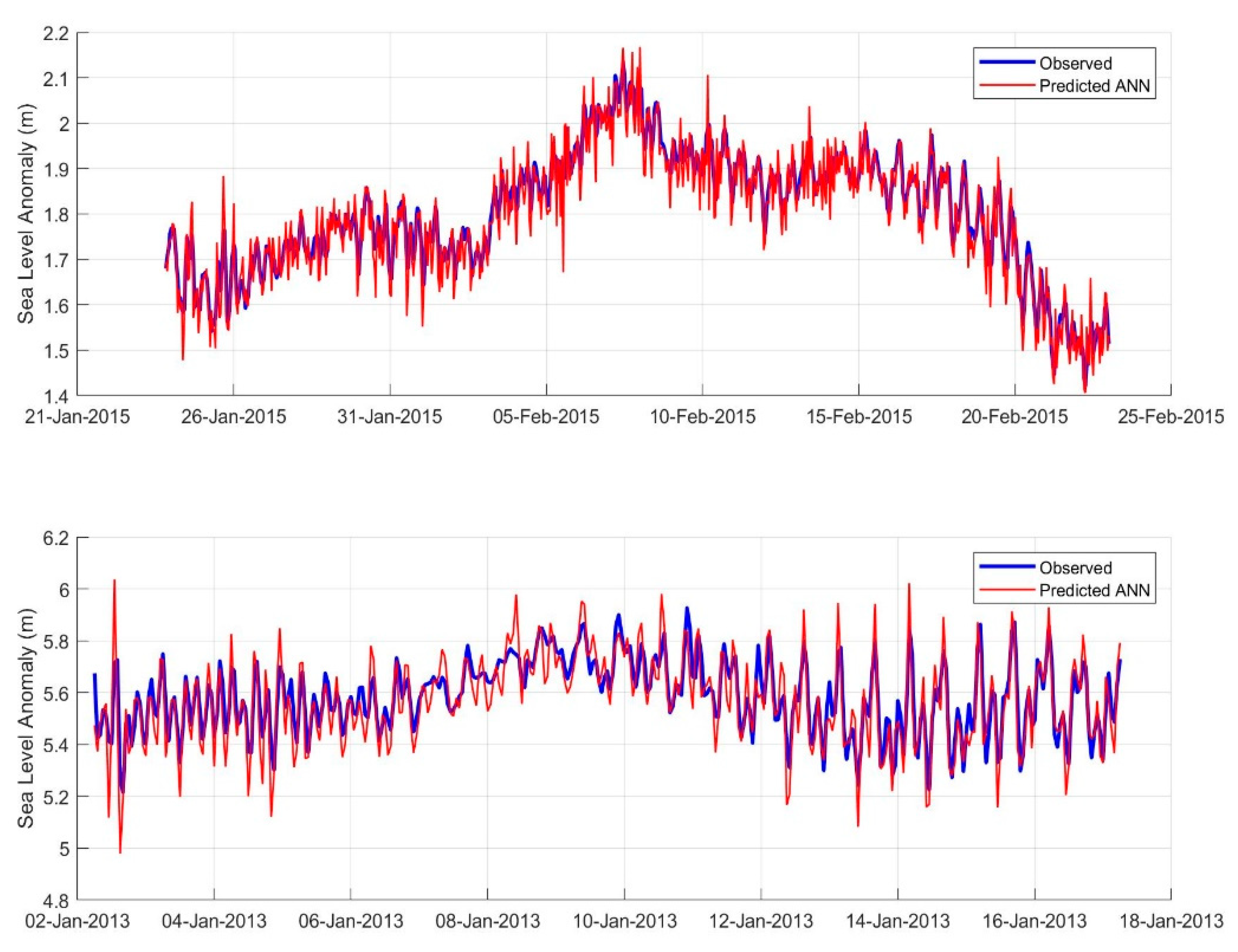
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Church, J.A.; White, N.J. Sea-Level Rise from the Late 19th to the Early 21st Century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef]
- White, N.J.; Haigh, I.D.; Church, J.A.; Koen, T.; Watson, C.; Pritchard, T.R.; Watson, P.J.; Burgette, R.J.; McInnes, K.L.; You, Z.-J.; et al. Australian sea levels—Trends, regional variability and influencing factors. Earth-Sci. Rev. 2014, 136, 155–174. [Google Scholar] [CrossRef]
- Watson, P.J. An Assessment of the Utility of Satellite Altimetry and Tide Gauge Data (ALT-TG) as a Proxy for Estimating Vertical Land Motion. J. Coast. Res. 2019, 35, 1131–1144. [Google Scholar] [CrossRef]
- Gharineiat, Z.; Deng, X. Description and assessment of regional sea-level trends and variability from altimetry and tide gauges at the northern Australian coast. Adv. Space Res. 2018, 61, 2540–2554. [Google Scholar] [CrossRef]
- Deng, X.; Gharineiat, Z.; Andersen, O.B.; Stewart, M.G. Observing and modelling the high water level from satellite radar altimetry during tropical cyclones. In IAG 150 Years; Springer: Cham, Switzerland, 2015; pp. 491–500. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Grinsted, A.; Moore, J.; Holgate, S. Nonlinear trends and multiyear cycles in sea level records. J. Geophys. Res. Space Phys. 2006, 111. [Google Scholar] [CrossRef]
- Watson, P.J. Acceleration in European Mean Sea Level? A New Insight Using Improved Tools. J. Coast. Res. 2017, 331, 23–38. [Google Scholar] [CrossRef]
- Watson, P.J. Acceleration in U.S. Mean Sea Level? A New Insight using Improved Tools. J. Coast. Res. 2016, 322, 1247–1261. [Google Scholar] [CrossRef]
- Gharineiat, Z.; Deng, X. Application of the Multi-Adaptive Regression Splines to Integrate Sea Level Data from Altimetry and Tide Gauges for Monitoring Extreme Sea Level Events. Mar. Geodesy 2014, 38, 261–276. [Google Scholar] [CrossRef]
- Quirós, E.; Felicísimo, M.; Cuartero, A. Testing Multivariate Adaptive Regression Splines (MARS) as a Method of Land Cover Classification of TERRA-ASTER Satellite Images. Sensors 2009, 9, 9011–9028. [Google Scholar] [CrossRef]
- Boye, C.B.; Amoah, V.I. Performance Evaluation for Mean Sea Level Prediction using Multivariate Adaptive Regression Spline and Artificial Neural Network. Ghana Min. J. 2018, 18, 1–8. [Google Scholar] [CrossRef]
- Pashova, L.; Popova, S. Daily sea level forecast at tide gauge Burgas, Bulgaria using artificial neural networks. J. Sea Res. 2011, 66, 154–161. [Google Scholar] [CrossRef]
- Conyers, Z.A.; Grant, R.; Roy, S.S. Sea Level Rise in Miami Beach: Vulnerability and Real Estate Exposure. Prof. Geogr. 2019, 71, 278–291. [Google Scholar] [CrossRef]
- Meena, B.; Agrawal, J. Tidal Level Forecasting Using ANN. Procedia Eng. 2015, 116, 607–614. [Google Scholar] [CrossRef][Green Version]
- Lee, H.S.; Kim, S. Sea-Level Records Analysis with Improved Empirical Mode Decomposition (EMD) and Artificial Neural Networks (ANN). In Proceedings of the 27th International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25 June 2017. [Google Scholar]
- Gharineiat, Z.; Deng, X. Spectral Analysis of Satellite Altimeter and Tide Gauge Data around the Northern Australian Coast. Remote Sens. 2020, 12, 161. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Mansouri, I.; Ozbakkaloglu, T.; Kisi, O.; Xie, T. Predicting behavior of FRP-confined concrete using neuro fuzzy, neural network, multivariate adaptive regres-sion splines and M5 model tree techniques. Mater. Struct. 2016, 49, 4319–4334. [Google Scholar] [CrossRef]
- Keshtegar, B.; Mert, C.; Kisi, O. Comparison of four heuristic regression techniques in solar radiation modeling: Kriging method vs RSM, MARS and M5 model tree. Renew. Sustain. Energy Rev. 2018, 81, 330–341. [Google Scholar] [CrossRef]
- Kisi, O. Pan evaporation modeling using least square support vector machine, multivariate adaptive regression splines and M5 model tree. J. Hydrol. 2015, 528, 312–320. [Google Scholar] [CrossRef]
- Yang, C.-C.; Prasher, S.O.; Lacroix, R.; Kim, S.H. Application of multivariate adaptive regression splines (mars) to simulate soil temperature. Trans. ASAE 2004, 47, 881–887. [Google Scholar] [CrossRef]
- Deo, R.C.; Kisi, O.; Singh, V.P. Drought forecasting in eastern Australia using multivariate adaptive regression spline, least square support vector machine and M5Tree model. Atmos. Res. 2017, 184, 149–175. [Google Scholar] [CrossRef]
- Kourou, K.; Exarchos, T.P.; Exarchos, K.P.; Karamouzis, M.V.; Fotiadis, D.I. Machine learning applications in cancer prognosis and prediction. Comput. Struct. Biotechnol. J. 2014, 13, 8–17. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, B.; Solomatine, D. Neural networks and M5 model trees in modelling water level–discharge relationship. Neurocomputing 2005, 63, 381–396. [Google Scholar] [CrossRef]
- Nazari, A.; Khalaj, G.; Riahi, S.; Bohlooli, H.; Kaykha, M.M. RETRACTED: Prediction total specific pore volume of geopolymers produced from waste ashes by ANFIS. Ceram. Int. 2012, 38, 3111–3120. [Google Scholar] [CrossRef]
- Topçu, I.B.; Sarıdemir, M. Prediction of compressive strength of concrete containing fly ash using artificial neural networks and fuzzy logic. Comput. Mater. Sci. 2008, 41, 305–311. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Olmo, M.C.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Abdullah, S.N.; Zeng, X. Machine learning approach for crude oil price prediction with Artificial Neural Networks-Quantitative (ANN-Q) model. In Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Kankar, P.; Sharma, S.C.; Harsha, S. Fault diagnosis of ball bearings using machine learning methods. Expert Syst. Appl. 2011, 38, 1876–1886. [Google Scholar] [CrossRef]
- Agatonovic-Kustrin, S.; Beresford, R. Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research. J. Pharm. Biomed. Anal. 2000, 22, 717–727. [Google Scholar] [CrossRef]
- Nwankpa, C.; Ijomah, W.; Gachagan, A.; Marshall, S. Activation functions: Comparison of trends in practice and research for deep learning. arXiv 2018, arXiv:1811.03378. [Google Scholar]
- Ghimire, S.; Deo, R.C.; Downs, N.J.; Raj, N. Global solar radiation prediction by ANN integrated with European Centre for medium range weather forecast fields in solar rich cities of Queensland Australia. J. Clean. Prod. 2019, 216, 288–310. [Google Scholar] [CrossRef]
- Cook, R.D. Detection of Influential Observation in Linear Regression. Technometrics 1977, 19, 15–18. [Google Scholar]
- Metcalfe, A.V.; Cowpertwait, P.S. Introductory Time Series with R; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Jiang, X.; Adeli, H. Wavelet Packet-Autocorrelation Function Method for Traffic Flow Pattern Analysis. Comput. Civ. Infrastruct. Eng. 2004, 19, 324–337. [Google Scholar] [CrossRef]
- Shimamura, T.; Kobayashi, H. Weighted autocorrelation for pitch extraction of noisy speech. In IEEE Transactions on Speech and Audio Processing; IEEE: New York, NY, USA, 2001; Volume 9, pp. 727–730. [Google Scholar]
- Muhtarov, P.; Kutiev, I. Autocorrelation method for temporal interpolation and short-term prediction of ionospheric data. Radio Sci. 1999, 34, 459–464. [Google Scholar] [CrossRef]
- Morf, M.; Vieira, A.; Kailath, T. Covariance Characterization by Partial Autocorrelation Matrices. Ann. Stat. 1978, 6, 643–648. [Google Scholar] [CrossRef]
- Dégerine, S.; Lambert-Lacroix, S. Characterization of the partial autocorrelation function of nonstationary time series. J. Multivar. Anal. 2003, 87, 46–59. [Google Scholar] [CrossRef]
- Dean, R.T.; Dunsmuir, W.T.M. Dangers and uses of cross-correlation in analyzing time series in perception, performance, movement, and neuroscience: The importance of constructing transfer function autoregressive models. Behav. Res. Methods 2015, 48, 783–802. [Google Scholar] [CrossRef]
- Mouatadid, S.; Raj, N.; Deo, R.C.; Adamowski, J.F. Input selection and data-driven model performance optimization to predict the Standardized Precipitation and Evaporation Index in a drought-prone region. Atmos. Res. 2018, 212, 130–149. [Google Scholar] [CrossRef]
- Kotsiantis, S.B.; Kanellopoulos, D.; Pintelas, P.E. Data preprocessing for supervised leaning. Int. J. Comput. Sci. 2006, 1, 111–117. [Google Scholar]
- Deo, R.C.; Ghimire, S.; Downs, N.J.; Raj, N. Optimization of windspeed prediction using an artificial neural network compared with a genetic programming model. In Handbook of Research on Predictive Modeling and Optimization Methods in Science and Engineering; IGI Global: Hershey, PA, USA, 2018; pp. 328–359. [Google Scholar]
- Ghimire, S.; Deo, R.C.; Downs, N.J.; Raj, N. Self-adaptive differential evolutionary extreme learning machines for long-term solar radiation prediction with remotely-sensed MODIS satellite and Reanalysis atmospheric products in solar-rich cities. Remote Sens. Environ. 2018, 212, 176–198. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar] [CrossRef]
- Williamson, D.F.; Parker, R.A.; Kendrick, J.S. The Box Plot: A Simple Visual Method to Interpret Data. Ann. Intern. Med. 1989, 110, 916–921. [Google Scholar] [CrossRef] [PubMed]
- Schwertman, N.C.; Owens, M.A.; Adnan, R. A simple more general boxplot method for identifying outliers. Comput. Stat. Data Anal. 2004, 47, 165–174. [Google Scholar] [CrossRef]
- Cleveland, W.S.; McGill, R. Graphical perception: Theory, experimentation, and application to the development of graphical methods. J. Am. Stat. Assoc. 1984, 79, 531–554. [Google Scholar] [CrossRef]
- Keim, D.A.; Hao, M.C.; Dayal, U.; Janetzko, H.; Bak, P. Generalized Scatter Plots. Inf. Vis. 2009, 9, 301–311. [Google Scholar] [CrossRef]
- Burston, J.; Symonds, A.; Scheel, F. Application of D-Flow FM for Storm Surge Modelling: Case Study of TC Yasi. Available online: https://www.griffith.edu.au/__data/assets/pdf_file/0014/107312/Burston_DFlow_OCEANSCIENCES14_poster.pdf (accessed on 20 October 2021).
- Høyer, J.L.; Andersen, O.B. Improved description of sea level in the North Sea. J. Geophys. Res. Space Phys. 2003, 108. [Google Scholar] [CrossRef]
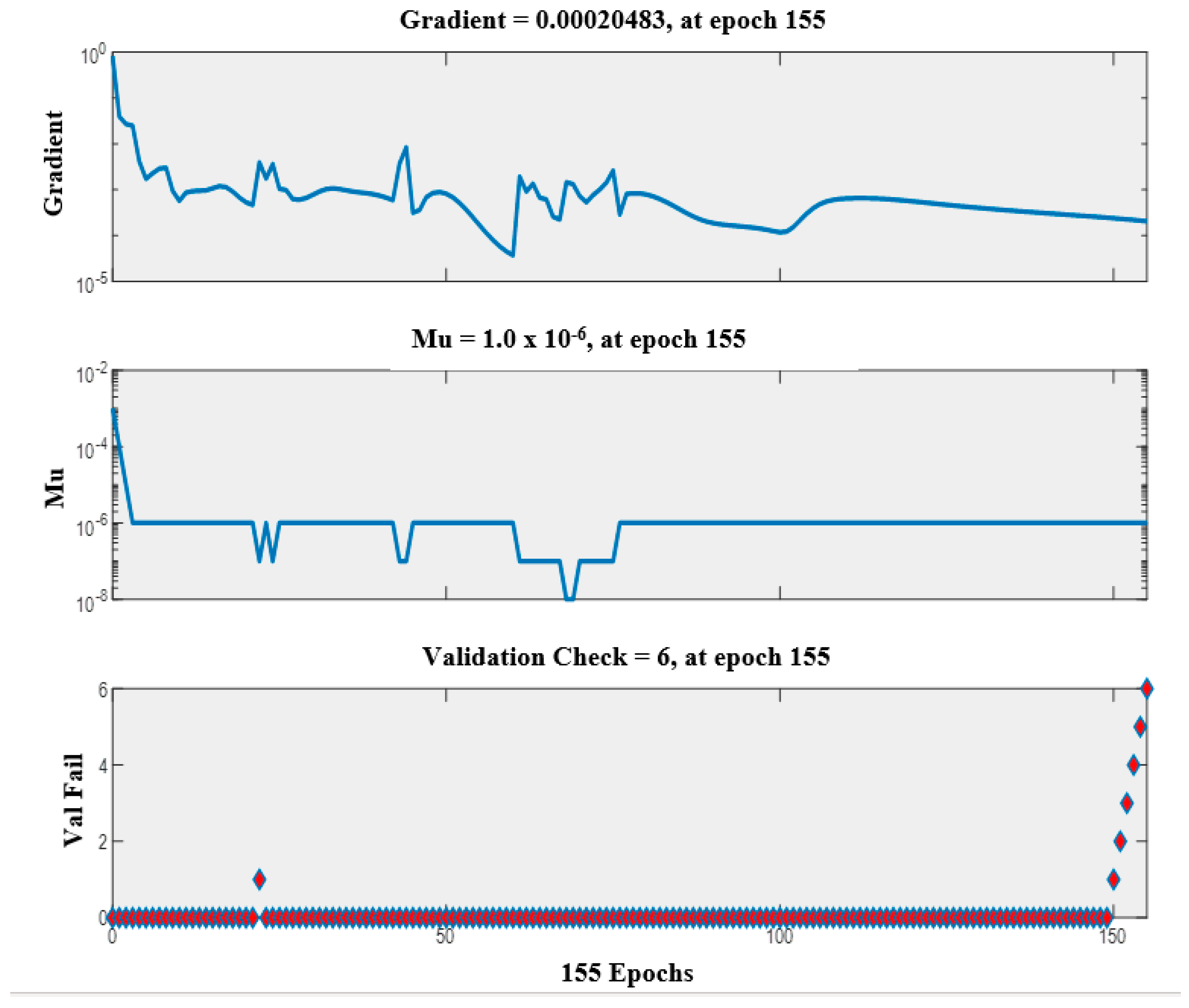
| ADF Statistic: −16.195319 | |
|---|---|
| Results of the Test: | |
| Test Statistic | −16.19532 |
| p-value | 4.130155 × 10−29 |
| #Lags Used | 74.00000 |
| Observations Used | 1.373840 × 105 |
| Critical Value (1%) | −3.430398 |
| Critical Value (5%) | −2.861561 |
| Critical Value (10%) | −2.566781 |
| Broome | Water Temp | Air Temp | Barometric Pressure | Residuals | Adjusted Residuals | Wind Direction | Wind Gust | Wind Speed | Sea Level |
|---|---|---|---|---|---|---|---|---|---|
| Water Temp | 1 | 0.8 | −0.74 | 0.034 | −0.29 | 0.29 | 0.13 | 0.078 | 0.025 |
| Air Temp | 0.8 | 1 | -0.63 | 0.028 | −0.24 | 0.33 | 0.002 | −0.021 | 0.07 |
| Barometric Pressure | −0.74 | −0.63 | 1 | −0.22 | 0.21 | −0.32 | −0.24 | −0.19 | −0.029 |
| Residuals | 0.034 | 0.028 | −0.22 | 1 | 0.91 | 0.0023 | −0.089 | −0.098 | 0.066 |
| Adjusted Residuals | −0.29 | −0.24 | 0.21 | 0.91 | 1 | −0.13 | −0.2 | −0.18 | 0.072 |
| Wind Direction | 0.29 | 0.33 | −0.32 | 0.0023 | −0.13 | 1 | 0.031 | 0.043 | 0.024 |
| Wind Gust | 0.13 | 0.002 | −0.24 | −0.089 | −0.2 | 0.031 | 1 | 0.92 | −0.03 |
| Wind Speed | 0.078 | −0.021 | −0.19 | −0.098 | −0.18 | 0.043 | 0.92 | 1 | −0.024 |
| Sea Level | 0.025 | 0.07 | −0.029 | 0.066 | 0.072 | 0.024 | −0.03 | −0.024 | 1 |
| maxFuncs | c | maxInteractions | Cubic |
|---|---|---|---|
| 20 | 0 | 2 | piecewise-cubic |
| Algorithm | Performance Criteria | Inputs | Hidden Layers | Output Layer |
|---|---|---|---|---|
| Levenberq-Marquardt (trainlm) | Mean Squared Error (mse) | 11 | 10 | 1 |
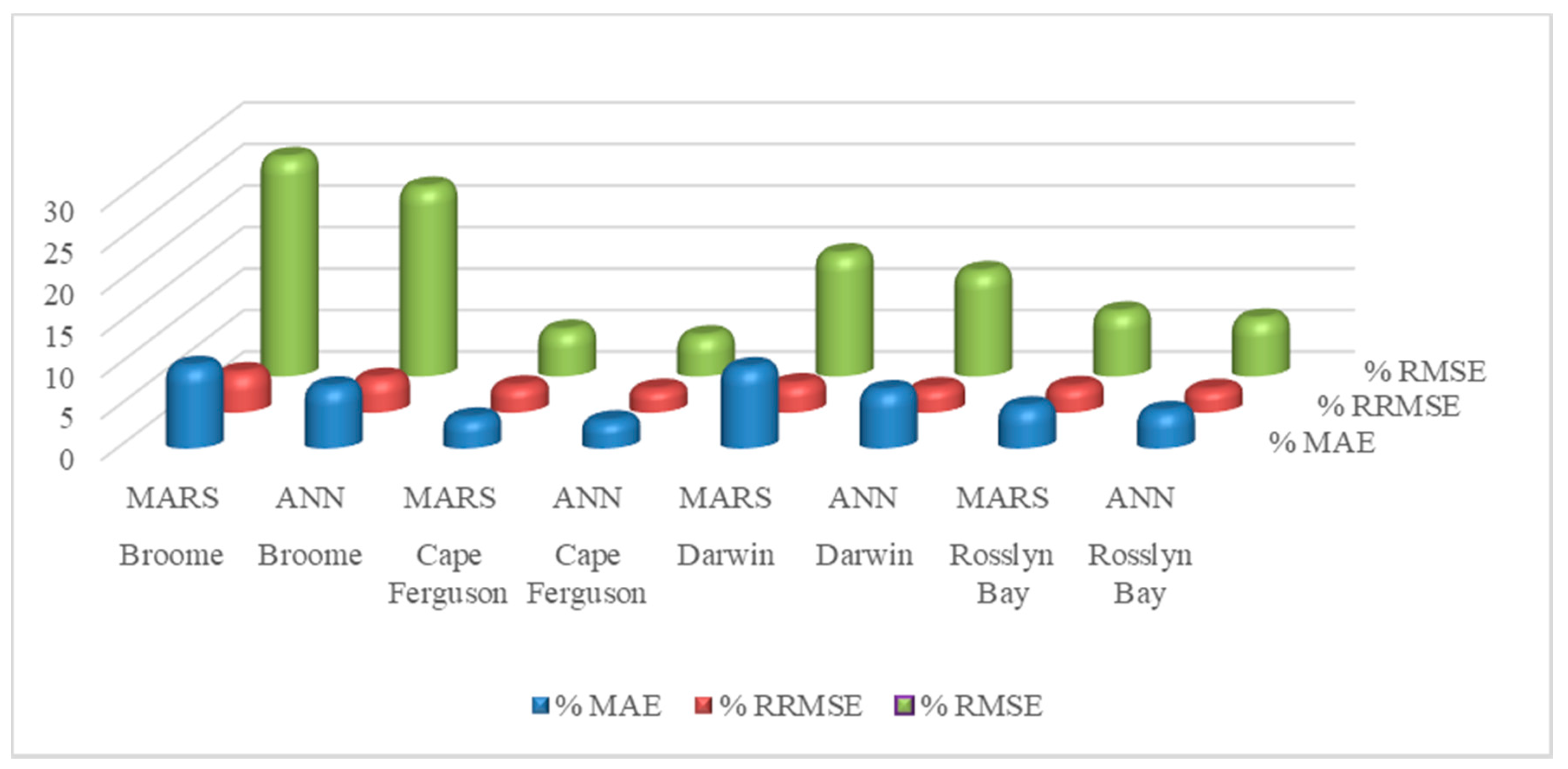
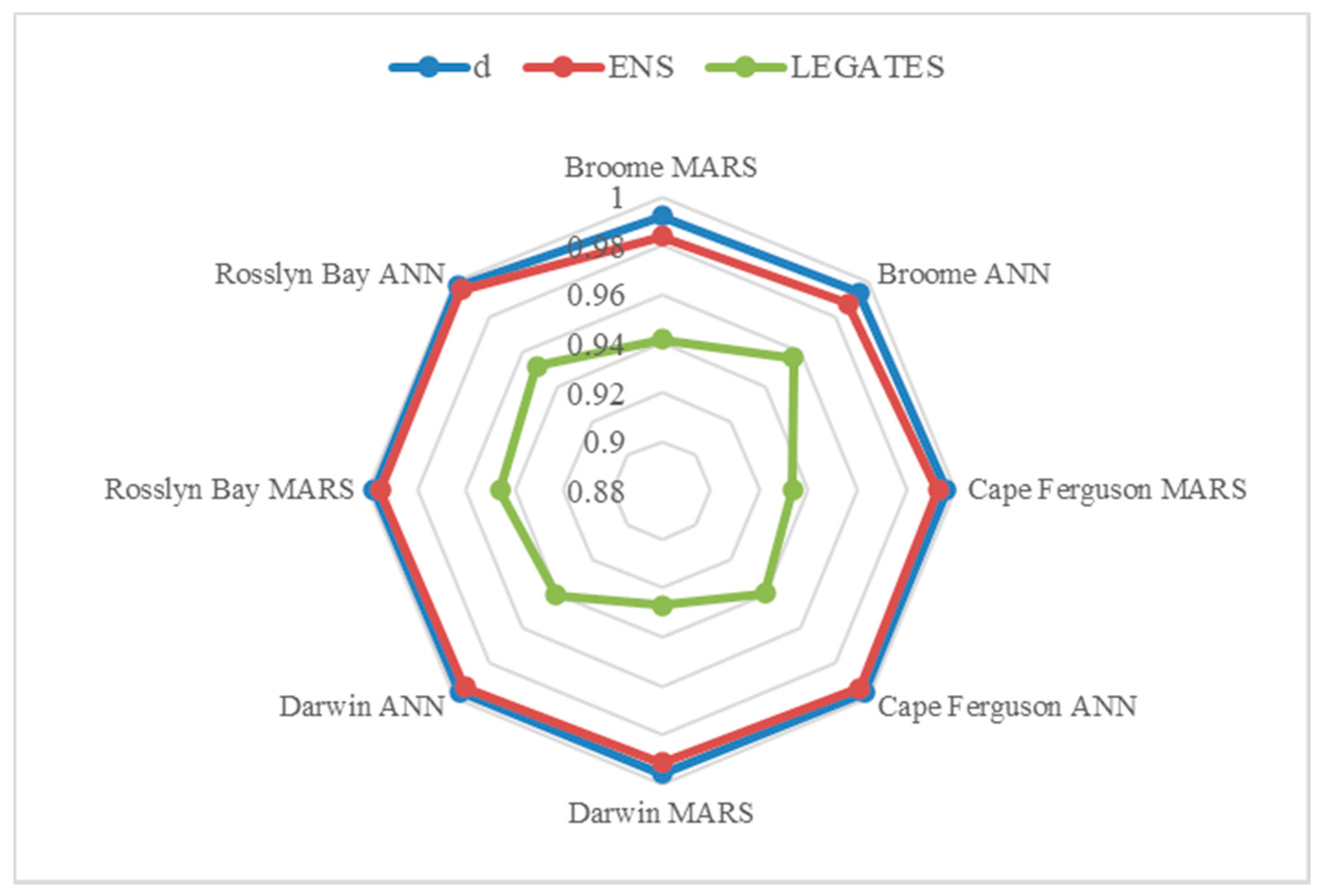
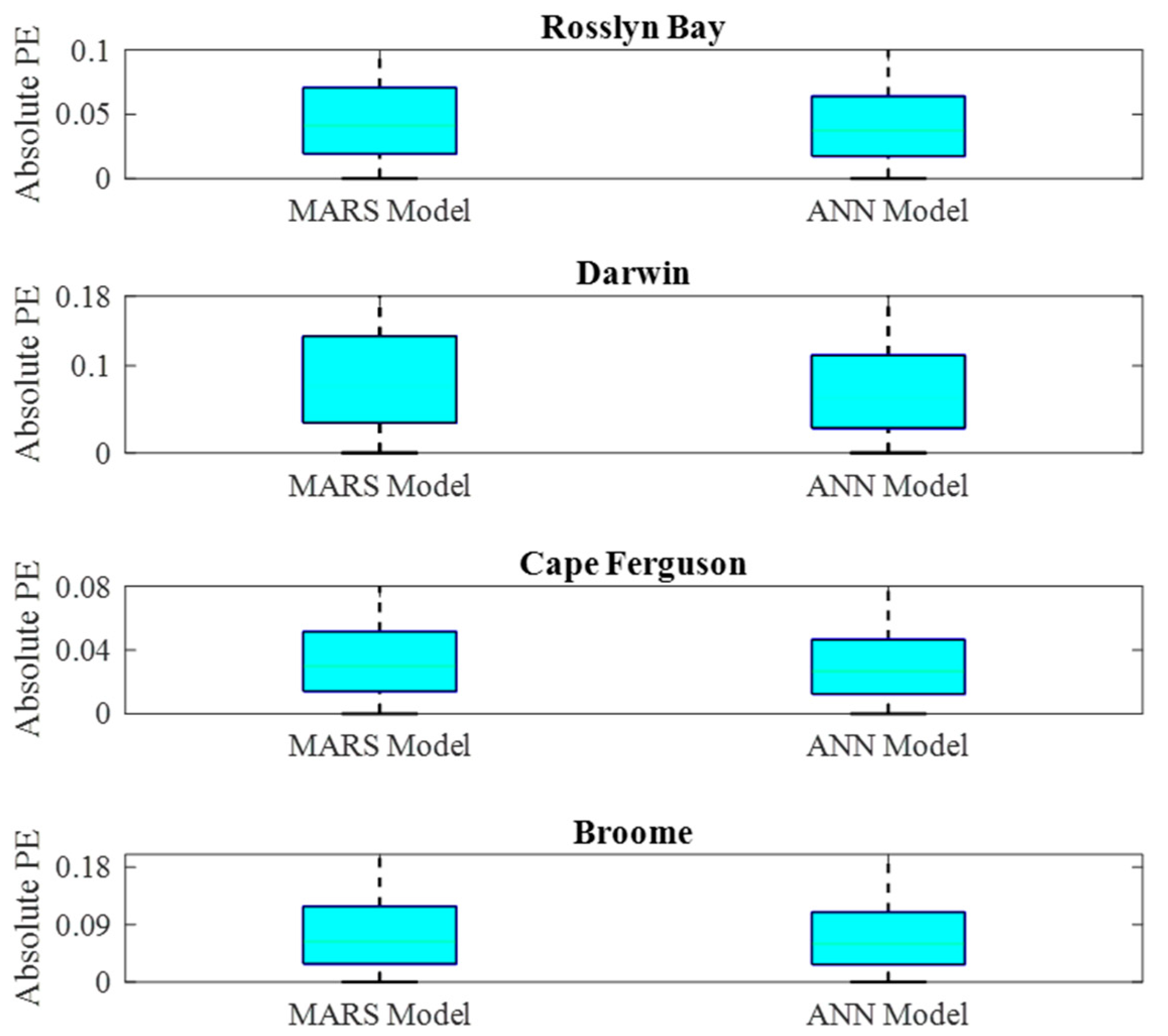
| Location | Model | R2 | RMSE | MAE | RRMSE | d | ENS | LEGATES |
|---|---|---|---|---|---|---|---|---|
| Broome | MARS | 0.9944 | 0.2185 | 0.0931 | 4.0375 | 0.9944 | 0.9888 | 0.9455 |
| Broome | ANN | 0.9959 | 0.1873 | 0.0698 | 3.4607 | 0.9959 | 0.9918 | 0.9591 |
| Cape Ferguson | MARS | 0.9958 | 0.0621 | 0.0393 | 3.5402 | 0.9955 | 0.9915 | 0.9290 |
| Cape Ferguson | ANN | 0.9973 | 0.0489 | 0.0337 | 2.9032 | 0.9972 | 0.9947 | 0.9386 |
| Darwin | MARS | 0.9862 | 0.2663 | 0.1227 | 6.4002 | 0.9862 | 0.9726 | 0.9091 |
| Darwin | ANN | 0.9892 | 0.2360 | 0.1071 | 5.6718 | 0.9891 | 0.9785 | 0.9206 |
| Rosslyn Bay | MARS | 0.9952 | 0.1032 | 0.0564 | 4.2664 | 0.9951 | 0.9905 | 0.9378 |
| Rosslyn Bay | ANN | 0.9961 | 0.0931 | 0.0502 | 3.8511 | 0.9960 | 0.9923 | 0.9447 |
| Location | Model | R2 | RMSE | MAE | RRMSE | d | ENS | LEGATES |
|---|---|---|---|---|---|---|---|---|
| Broome | MARS | 0.9918 | 0.2636 | 0.0990 | 4.7889 | 0.9919 | 0.9836 | 0.9417 |
| Broome | ANN | 0.9939 | 0.2278 | 0.0743 | 4.1397 | 0.9940 | 0.9877 | 0.9563 |
| Cape Ferguson | MARS | 0.9966 | 0.0558 | 0.0368 | 3.1877 | 0.9964 | 0.9931 | 0.9337 |
| Cape Ferguson | ANN | 0.9974 | 0.0488 | 0.0333 | 2.7919 | 0.9973 | 0.9947 | 0.9399 |
| Darwin | MARS | 0.9960 | 0.1478 | 0.0974 | 3.4788 | 0.9957 | 0.9914 | 0.9270 |
| Darwin | ANN | 0.9970 | 0.1262 | 0.07 | 2.9703 | 0.9968 | 0.9937 | 0.9409 |
| Rosslyn Bay | MARS | 0.9975 | 0.0777 | 0.0503 | 3.1130 | 0.9974 | 0.9948 | 0.9459 |
| Rosslyn Bay | ANN | 0.9980 | 0.0692 | 0.0448 | 2.7736 | 0.9979 | 0.9959 | 0.9519 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raj, N.; Gharineiat, Z. Evaluation of Multivariate Adaptive Regression Splines and Artificial Neural Network for Prediction of Mean Sea Level Trend around Northern Australian Coastlines. Mathematics 2021, 9, 2696. https://doi.org/10.3390/math9212696
Raj N, Gharineiat Z. Evaluation of Multivariate Adaptive Regression Splines and Artificial Neural Network for Prediction of Mean Sea Level Trend around Northern Australian Coastlines. Mathematics. 2021; 9(21):2696. https://doi.org/10.3390/math9212696
Chicago/Turabian StyleRaj, Nawin, and Zahra Gharineiat. 2021. "Evaluation of Multivariate Adaptive Regression Splines and Artificial Neural Network for Prediction of Mean Sea Level Trend around Northern Australian Coastlines" Mathematics 9, no. 21: 2696. https://doi.org/10.3390/math9212696
APA StyleRaj, N., & Gharineiat, Z. (2021). Evaluation of Multivariate Adaptive Regression Splines and Artificial Neural Network for Prediction of Mean Sea Level Trend around Northern Australian Coastlines. Mathematics, 9(21), 2696. https://doi.org/10.3390/math9212696







