The Log Exponential-Power Distribution: Properties, Estimations and Quantile Regression Model

Abstract

Recently, bounded distributions have attracted attention. These distributions are frequently used in modeling rate and proportion data sets. In this study, a new alternative model is proposed for modeling bounded data sets. Parameter estimations of the proposed distribution are obtained via maximum likelihood method. In addition, a new regression model is defined under the proposed distribution and its residual analysis is examined. As a result of the empirical studies on real data sets, it is observed that the proposed regression model gives better results than the unit-Weibull and Kumaraswamy regression models.

1. Introduction

The exponential-power (EP) distribution has been proposed by [1]. If T random variable has EP distribution then its cumulative distribution function (cdf) and probability density function (pdf) are respectively given by

$$K(t,\alpha ,\beta )=1-e^{1-exp\left\{\alpha t^{\beta }\right\}}$$

(1)

and

$$k(t,\alpha ,\beta )=\alpha \beta e^{\alpha t^{\beta }}{e}^{\alpha {\left(-logx\right)}^{\beta }}{t}^{\beta -1}{e}^{1-exp\left\{\alpha t^{\beta }\right\}},$$

(2)

where $t\ge 0$, $\alpha >0$ is the scale parameter and $\beta >0$ is the shape parameter. This distribution is well-known in the literature because of its hazard rate function (hrf) with bathtub shaped. It can be noticed that for $\beta \in (0,1)$, it has hrf with bathtub shaped. Characterizations of the EP distribution was studied by [2].

Several generalizations of the EP distributions have been proposed. For instance, [3] introduced the transmuted-EP (TEP) distribution with applications on the holes operation on jobs made of iron sheet and breaking stress data sets. [4] introduced the generalization of the complementary EP distribution and compared it with other transmuted generalized distributions. [5] introduced the four-parameter generalized EP distribution which has bimodal right-skewed and nearly symmetric pdf shapes.

In the recent years, many lifetime distributions are tranformed to bounded distributions, defined on (0, 1) interval. Two transformation methods are commonly prefered for this goal. These are $X=exp\left(-T\right)$ and $X=T/\left(T+1\right)$ transformations. When the random variable is defined on $T\in \mathbb{R}$, the transformed random variable will be $T\in (0,1)$. As an example, [6] used $X=exp\left(-T\right)$ transformation on the weighted-exponential (WE) distribution and resulting distribution was called as log-WE distribution. Again, [7] used the same transformation for the Bilal distribution and proposed the log-Bilal distribution for extremely left/right skewed data sets defined on the interval $(0,1)$. Similarly, [8] used $X=T/\left(T+1\right)$ transformation on the improved second-degree Lindley (ISDL) distribution and resulting distribution was called as unit-ISDL distribution. These approaches have been used many authors such as 9,10,11,12,13,14,15,16,17,18,19] and so on.

The presented work aims to develop a new sophisticated statistical model for bounded data sets in (0, 1) interval. For this aim, we use $X=exp\left(-T\right)$ transformation on the EP distribution. The resulting cdf and pdf of the log-exponential-power (LEP) distribution are given as

$$F(x,\alpha ,\beta )=e^{1-exp\left\{\alpha {\left(-logx\right)}^{\beta }\right\}},x\in (0,1)$$

(3)

and

$$f(x,\alpha ,\beta )=\frac{\alpha \beta }{x}{e}^{\alpha {\left(-logx\right)}^{\beta }}{\left(-logx\right)}^{\beta -1}{e}^{1-exp\left\{\alpha {\left(-logx\right)}^{\beta }\right\}},x\in (0,1)$$

(4)

respectively, where $\alpha >0$ and $\beta >0$ are the model parameters. This new unit model is called as LEP distribution and after here, a random variable X is denoted as $X\sim LEP\left(\alpha ,\beta \right)$. The associated hrf is given by

$$h\left(x,\alpha ,\beta \right)=\frac{\alpha \beta }{x\left(e^{exp\left\{\alpha {\left(-logx\right)}^{\beta }\right\}-1}-1\right)}{e}^{\alpha {\left(-logx\right)}^{\beta }}{\left(-logx\right)}^{\beta -1},x\in (0,1).$$

(5)

If the $\beta$ parameter is equal to one, then we have following simple cdf and pdf $F\left(x,\alpha ,1\right)=e^{1-x^{-\alpha }}$ and $f\left(x,\alpha ,1\right)=\alpha x^{-\alpha -1}{e}^{1-x^{-\alpha }}$ for $x\in (0,1)$ respectively. The possible shapes of the pdf and hrf have been sketched by Figure 1. According to this Figure 1, the shapes of the pdf can be seen as various shapes such as U-shaped, increasing, decreasing and unimodal as well as its hrf shapes can be bathtub, increasing and N-shaped.

Other parts of the study are as follows. Statistical properties of the LEP distribution are given in Section 2. Parameter estimation method is presented in Section 3. Section 4 is devoted to the LEP quantile regression model. Section 5 contains two simulation studies for LEP distribution and the LEP quantile regression model. Empirical results of the study are given in Section 6. The study is concluded with Section 7.

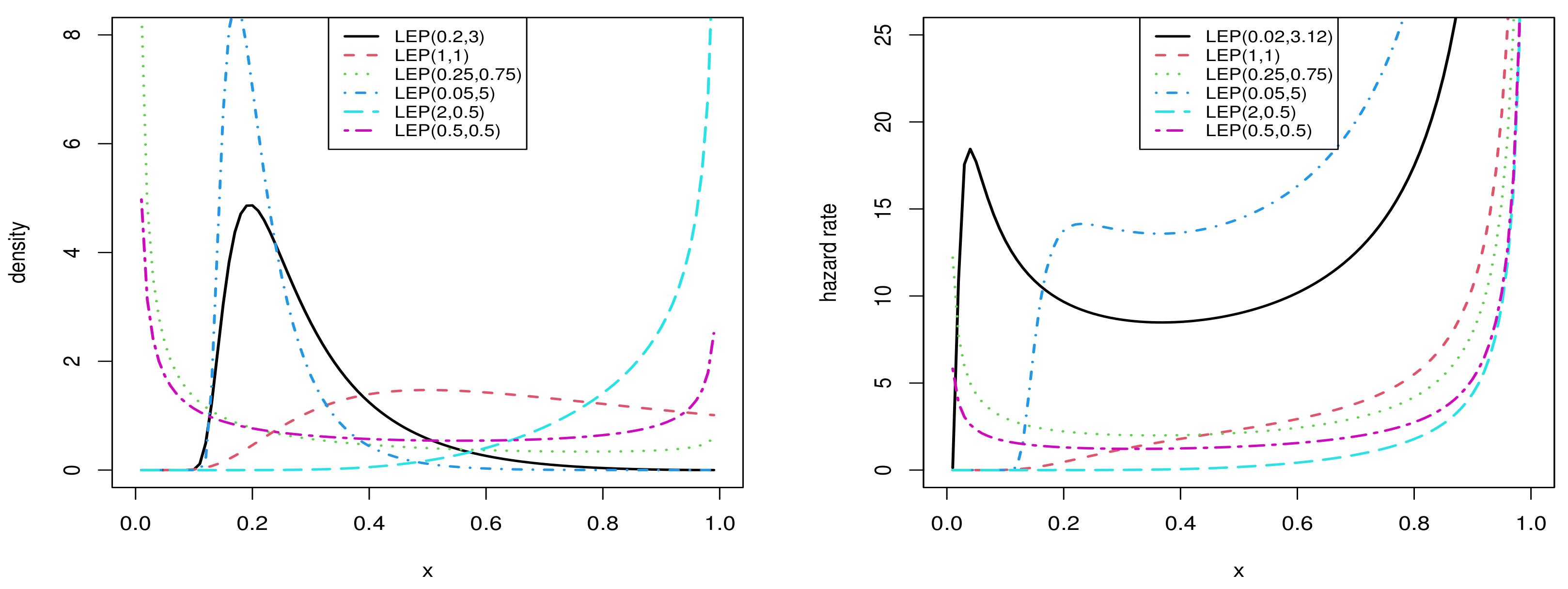
2. Some Distributional Properties of the LEP Distribution

The moments, order statistics, entropy and quantile function of the LEP distribution are studied.

2.1. Moments

The n-th non-central moment of the LEP distribution is denoted by $\mathrm{E}\left(X^n\right)$ which is defined as

$$\begin{array}{ccc}\hfill E\left(X^n\right)& =& n{\int }_0^1{x}^{n-1}\left[1-F\left(x\right)\right]dx=1-n{\int }_0^1{x}^{n-1}{e}^{1-exp\left(\alpha {(-log\left(x\right))}^{\beta }\right)}dx\hfill \end{array}$$

By changing $-log\left(x\right)=u$ transform we obtain

$$\begin{array}{ccc}\hfill E\left(X^n\right)& =& 1+ne{\int }_0^{\infty }{e}^{-nu}{e}^{-exp\left(\alpha u^{\beta }\right)}du=1+ne\left\{{\int }_0^{\infty }{e}^{-nu}\left[1+\sum _{i=1}^{\infty }\frac{{(-1)}^i}{i!}exp\left(i\alpha u^{\beta }\right)\right]du\right\}\hfill \\ & =& 1+ne\frac{1}{n}+\sum _{i=1}^{\infty }\frac{{(-1)}^i}{i!}{\int }_0^{\infty }{e}^{-nu}exp\left(i\alpha u^{\beta }\right)du\hfill \\ & =& 1+e+ne\sum _{i=1}^{\infty }\sum _{j=0}^{\infty }\frac{{(-1)}^i{\left(\alpha i\right)}^j}{i!j!}{\int }_0^{\infty }{u}^{\beta j}{e}^{-nu}du\hfill \\ & =& 1+e+e\sum _{i=1}^{\infty }\sum _{j=0}^{\infty }\frac{{(-1)}^i{\left(\alpha i\right)}^j}{i!j!}{n}^{-\beta j}\Gamma (\beta j+1)\hfill \end{array}$$

Based on the first four non-central moments of the LEP distribution, we calculate the skewness and kurtosis values of the LEP distributions. These measures are plotted in Figure 2 against the parameters $\alpha$ and $\beta$.

2.2. Order Statistics

The cdf of i-th order statistics of the LEP distribution is given by

$$\begin{array}{c}\hfill F_{i:n}\left(x\right)=\sum _{k=0}^n\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)F{\left(x\right)}^k{(1-F\left(x\right))}^{n-k}=\sum _{k=0}^n\sum _{j=0}^{n-k}{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{n-k}{j}}\right)F{\left(x\right)}^{k+j}\end{array}$$

Then

$$\begin{array}{ccc}\hfill \mathrm{E}\left(X_{i:n}^r\right)& =& r{\int }_0^1{x}^{r-1}\left[1-F_{i:n}\left(x\right)\right]dx\hfill \\ & =& 1-r\sum _{k=0}^n\sum _{j=0}^{n-k}{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{n-k}{j}}\right){\int }_0^1{x}^{r-1}{e}^{(k+j)\left[1-exp\left(\alpha {(-log\left(x\right))}^{\beta }\right)\right]}dx\hfill \end{array}$$

By changing $-log\left(x\right)=u$ transform we obtain

$$\begin{array}{ccc}& & \mathrm{E}\left(X_{i:n}^r\right)=1+r\sum _{k=0}^n\sum _{j=0}^{n-k}{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{n-k}{j}}\right)e^{k+j}{\int }_0^{\infty }{e}^{-ru}{e}^{-(k+j)exp\left(\alpha u^{\beta }\right)}du\hfill \\ & =& 1+r\sum _{k=0}^n\sum _{j=0}^{n-k}{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{n-k}{j}}\right)e^{k+j}{\int }_0^{\infty }{e}^{-ru}\left[1+\sum _{l=1}^{\infty }\frac{{(-1)}^l{(k+j)}^l}{l!}exp\left(l\alpha u^{\beta }\right)\right]du\hfill \\ & =& 1+r\sum _{k=0}^n\sum _{j=0}^{n-k}{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{n-k}{j}}\right)e^{k+j}\left[\frac{1}{r}+\sum _{l=1}^{\infty }\sum _{s=0}^{\infty }\frac{{(-1)}^l{(k+j)}^l{\left(l\alpha \right)}^s}{l!s!}{\int }_0^{\infty }{e}^{-ru}{u}^{\beta s}du\right]\hfill \\ & =& 1+r\sum _{k=0}^n\sum _{j=0}^{n-k}{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{n-k}{j}}\right)e^{k+j}\left[\frac{1}{r}+\sum _{l=1}^{\infty }\sum _{s=0}^{\infty }\frac{{(-1)}^l{(k+j)}^l{\left(l\alpha \right)}^s}{l!s!}\times \frac{\Gamma (\beta s+1)}{r^{\beta s+1}}\right]\hfill \end{array}$$

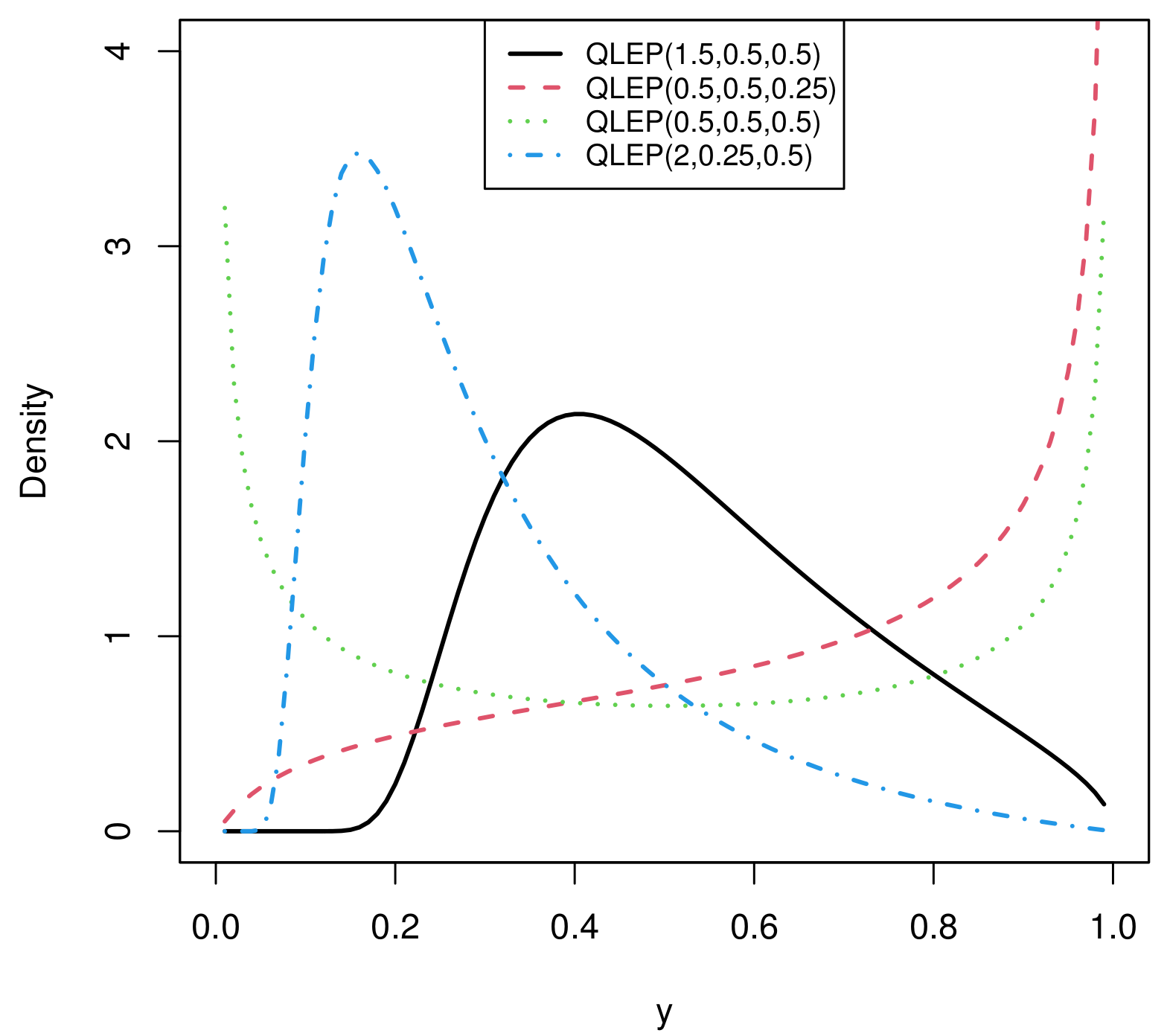
2.3. Quantile Function and Quantile LEP Distribution

Inverting Equation (3), the quantile function of the $LEP$ distribution is given, we obtain

$$\begin{array}{c}\hfill x_{\tau }\left(\alpha ,\beta \right)=e^{-{\left(\frac{log\left(1-log\tau \right)}{\alpha }\right)}^{1/\beta }},\end{array}$$

(6)

where $\tau \in (0,1)$. For the special case $\beta =1$, we have $x_{\tau }\left(\alpha ,1\right)={\left(1-log\tau \right)}^{-1/\alpha }$. The median of the $LEP$ distribution has been derived as $x_{0.5}\left(\alpha ,\beta \right)=exp\left\{{\left(\frac{0.5266}{\alpha }\right)}^{1/\beta }\right\}$. Furthermore, if random variable U follows the uniform distribution, the rv $X_U(\alpha ,\beta )\sim LEP(\alpha ,\beta )$.

On the other hand, since the model has manageable quantile function, its pdf and cdf can be re-parameterized easily. Let define $\mu =x_{\tau }\left(\alpha ,\beta \right)$ and $\alpha =log\left(1-log\tau \right){\left(-log\mu \right)}^{-\beta }$. Then the re-parameterized cdf and pdf are obtained as

$$G\left(y,\beta ,\mu ,\tau \right)=e^{1-{\left(1-log\tau \right)}^{{\left(logy/log\mu \right)}^{\beta }}}$$

(7)

and

$$\begin{array}{c}\hfill g\left(y,\beta ,\mu ,\tau \right)=\frac{\beta log\left(1-log\tau \right){\left(1-log\tau \right)}^{{\left(logy/log\mu \right)}^{\beta }}{\left(-logy\right)}^{\beta -1}{e}^{1-{\left(1-log\tau \right)}^{{\left(logy/log\mu \right)}^{\beta }}}}{y{\left(-log\mu \right)}^{\beta }}\end{array}$$

(8)

respectively, where $y\in (0,1)$, the $\mu \in (0,1)$ is the quantile parameter, $\beta >0$ is the shape parameter and $\tau \in (0,1)$ is known. Hereafter, the random variable Y will be called quantile LEP (QLEP) random variable and we denote it with $Y\sim QLEP(\beta ,\mu ,\tau )$. For some selected parameters values, the pdf shapes of the QLEP distribution are displayed in Figure 3. The QLEP distribution has U-shaped, increasing and unimodal shapes.

2.4. Residual Entropy and Cumulative Residual Entropy

Entropy is used to measure uncertainty in different fields such as engineering and natural sciences. The definition of the residual entropy is given by

$$\begin{array}{c}\hfill \mathcal{E}\left(X\right)=-{\int }_0^{\infty }F\left(x\right)log\left(F\left(x\right)\right)dx.\end{array}$$

(9)

The another entropy measure, cumulative residual entropy is defined by

$$\begin{array}{c}\hfill \mathcal{CE}\left(X\right)=-{\int }_0^{\infty }\overline{F}\left(x\right)log\left(\overline{F}\left(x\right)\right)dx.\end{array}$$

(10)

After some simple algebra, using $u=-log\left(x\right)$ transformation and Taylor expansion for LEP($\alpha ,\beta$) we have

$$\begin{array}{c}\hfill \mathcal{E}\left(X\right)=\sum _{i,j=0}^{\infty }\frac{{\left(-1\right)}^i\alpha {\left(i+1\right)}^j\mathsf{\Gamma }\left(\beta j+1\right)}{i!j!}\end{array}$$

(11)

and

$$\begin{array}{c}\hfill \mathcal{CE}\left(X\right)=\sum _{i,j=0}^{\infty }\frac{{\mathrm{e}}^{\mathrm{i}+1}{(\mathrm{i}+1)}^{\mathrm{j}}-{\mathrm{e}}^{\mathrm{i}+2}{(\mathrm{i}+2)}^{\mathrm{j}}}{j!(i+1)}\left[1+\sum _{k=1}^{\infty }\frac{{\left(j\alpha \right)}^k\Gamma (\beta k+1)}{k!}\right]\end{array}$$

(12)

3. Procedure of the Maximum Likelihood for the Parameter Estimation

The maximum likelihood estimators (MLEs) of the LEP distribution has been derived. It has been worked on the case when both $\alpha$ and $\beta$ are unknown.

Let $x_1,x_2,\dots ,x_n$ random sample of size n from the LEP distribution and let $\Theta ={\left(\alpha ,\beta \right)}^T$ be the parameter vector. Then, the log-likelihood function is given by

$$\begin{array}{cc}\hfill \ell \left(\Theta \right)& =n+nlog\alpha +nlog\beta +\alpha \sum _{i=1}^n{\left(-log{x}_i\right)}^{\beta }+\left(\beta -1\right)\sum _{i=1}^{n}log\left(-log{x}_i\right)-\sum _{i=1}^n{e}^{\alpha {\left(-log{x}_i\right)}^{\beta }}.\hfill \end{array}$$

(13)

Then, differentiating (13), the normal equations are obtained by

$$\frac{\partial \ell (\Theta )}{\partial \alpha }=\frac{n}{\alpha }+\sum _{i=1}^n{\left(-log{x}_i\right)}^{\beta }-\sum _{i=1}^n{\left(-log{x}_i\right)}^{\beta }{e}^{\alpha {\left(-log{x}_i\right)}^{\beta }}=0$$

and

$$\frac{\partial \ell (\Theta )}{\partial \beta }=\frac{n}{\beta }+\alpha \sum _{i=1}^{n}log\left(-log{x}_i\right){\left(-log{x}_i\right)}^{\beta }-\alpha \sum _{i=1}^{n}log\left(-log{x}_i\right){\left(-log{x}_i\right)}^{\beta }{e}^{\alpha {\left(-log{x}_i\right)}^{\beta }}=0.$$

Above equation systems have no explicit solutions. To obtain the $\widehat{\alpha }$ and $\widehat{\beta }$, the numerical approaching should be needed and they have to be solved via numerical methods. The Newton-Raphson and quasi-Newton algorithms can be used for this purpose. However, Equation (13) can be also optimized directly by the special functions in some well-known software such as R (constrOptim and optim and maxLik functions), S-Plus and Matlab. These functions use the numerical optimization methods for solving them. When the log-likelihood is directly optimized, one should carefully choose the initial values and remove the constraints of parameters [20].

The observed information matrix plays an important role in order to obtain the standard errors and asymptotic confidence interval of the MLEs. Based on the regularity conditions, the $\widehat{\Theta }$ MLEs have approximately the bivariate normal distribution with mean $M=(\alpha ,\beta )$ and covariance matrix $I^{-1}$, where I is the observed information matrix with the following elements

$$I=-{\left.\left(\begin{array}{cc}{\displaystyle \frac{{\partial }^2}{\partial {\alpha }^2}\ell (\Theta )}& {\displaystyle \frac{{\partial }^2}{\partial \alpha \partial \beta }\ell (\Theta )}\\ {\displaystyle \frac{{\partial }^2}{\partial \alpha \partial \beta }\ell (\Theta )}& {\displaystyle \frac{{\partial }^2}{\partial {\beta }^2}\ell (\Theta )}\end{array}\right)\right|}_{\Theta =(\widehat{\alpha },\widehat{\beta })}.$$

The components of the I can be given by the following derivations

$$\frac{{\partial }^2}{\partial {\alpha }^2}\ell (\Theta )=-\frac{n}{{\alpha }^2}-\sum _{i=1}^n{\left(-log{x}_i\right)}^{2\beta }{e}^{\alpha {\left(-log{x}_i\right)}^{\beta }},$$

$$\begin{array}{ccc}\hfill \frac{{\partial }^2}{\partial \alpha \partial \beta }\ell (\Theta )& =& \sum _{i=1}^{n}log\left(-log{x}_i\right){\left(-log{x}_i\right)}^{\beta }\hfill \\ & -& \sum _{i=1}^{n}log\left(-log{x}_i\right){\left(-log{x}_i\right)}^{\beta }{e}^{\alpha {\left(-log{x}_i\right)}^{\beta }}\left[1+\alpha {\left(-log{x}_i\right)}^{\beta }\right]\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \frac{{\partial }^2}{\partial {\beta }^2}\ell (\Theta )& =& -\frac{n}{{\beta }^2}+\alpha \sum _{i=1}^n{log}^2\left(-log{x}_i\right){\left(-log{x}_i\right)}^{\beta }\hfill \\ & -& \alpha \sum _{i=1}^{n}log\left(-log{x}_i\right)\left[log\left(-log{x}_i\right){\left(-log{x}_i\right)}^{\beta }{e}^{\alpha {\left(-log{x}_i\right)}^{\beta }}\left(1+\alpha {\left(-log{x}_i\right)}^{\beta }\right)\right].\hfill \end{array}$$

The standard errors of the estimated parameters are obtained by the inverse of I, say $I^{-1}$. So, the asymptotic confidence intervals of the parameters can be easily constructed by

$$\widehat{\alpha }\pm z_{\zeta /2}{s}_{\widehat{\alpha }}\mathrm{and}\widehat{\beta }\pm z_{\zeta /2}{s}_{\widehat{\beta }},$$

where $s_{\alpha }=\sqrt{I_{11}^{-1}}$, $s_{\beta }=\sqrt{I_{22}^{-1}}$ and $z_{\zeta /2}$ is the upper $\zeta /2$ th percentile of $\mathrm{N}\left(0,1\right)$ distribution.

4. The New Quantile Regression Model Based on the QLEP Distribution for the Unit Response

The regression models are used to explain the relation between dependent and independent variables. When the dependent variable is on $(0,1)$ interval, the beta regression model by [21] is usually used. The idea of the beta regression model is based on the re-parameterization of the mean and variance functions. Similar idea has been used by several authors such as [6,8,17,22,23]. These studies are constructed on the conditional mean modeling.

The other possible idea is to model the dependent variable with conditional quantile function as in the quantile regression model pioneered by [24]. Ref. [25] introduced the Kumaraswamy quantile regression model for the dependent variables on the $(0,1)$ interval. The presented idea in the study of [25] has been applied to different probability distributions by [9,11,12,14,26,27,28,29].

Following the idea of [25], we propose QLEP quantile regression model. Let $Y_1,Y_2,\dots ,$$Y_n$ be n random variables from the QLEP distribution denoted by $Y\sim QLEP\left(\beta ,{\mu }_i,\tau \right)$ where ${\mu }_i$ and $\beta$ unknown parameters and $\tau$ is known. Assume that $y_1,y_2,\dots ,y_n$ are the realizations of the random variables, $Y_1,Y_2,\dots ,Y_n$. Then, the QLEP regression model is given as follows

$$g\left({\mu }_i\right)={\mathbf{x}}_i{\mathbf{\beta }}^T,$$

where $\mathbf{\beta }={\left({\beta }_0,{\beta }_1,{\beta }_2,\dots ,{\beta }_p\right)}^T$ is the unknown regression parameter vector, ${\mathrm{x}}_i=\left(1,x_{i1},x_{i2},x_{i3},\dots ,x_{ip}\right)$ is the known $i^{th}$ vector of the covariates, and $g(·)$ is the link function which connects covariates with conditional quantile of the response variable. The logit link function is preferred by the reason that the response variable is on $(0,1)$ interval. The definition of the logit link function is

$$g\left({\mu }_i\right)=log\left(\frac{{\mu }_i}{1-{\mu }_i}\right).$$

If the parameter $\tau =0.5$, we model the median of the dependent variable with known independent variables which is called as QLEP median regression model.

4.1. The MLEs of the Model Parameters

Let $Y_1,Y_2,\dots ,Y_n$ be n independent random variables from $Y_i\sim QLEP\left(\beta ,{\mu }_i,\tau \right)$ where

$${\mu }_i=\frac{e^{{\mathrm{x}}_i{\beta }^T}}{1+e^{{\mathrm{x}}_i{\beta }^T}}$$

(14)

is the inverse of the logit link function and $\tau$ is the known. The $\mathbf{\Phi }={\left(\beta ,{\mathit{\beta }}^T\right)}^T$ be unknown parameter vector with $p+2$. Then, putting (14) in (8), the log-likelihood function of the QLEP regression model is obtained as

$$\begin{array}{cc}\hfill \ell \left(\mathbf{\Phi }\right)& =n+nlog\beta +nlog\left[log\left(1-log\tau \right)\right]+log\left[\left(1-log\tau \right)\right]\sum _{i=1}^n{\left(\frac{log{y}_i}{log{\mu }_i}\right)}^{\beta }\hfill \\ \hfill & +\left(\beta -1\right)\sum _{i=1}^{n}log\left(-log{y}_i\right)-\sum _{i=1}^{n}log{y}_i-\beta \sum _{i=1}^{n}log\left(-log{\mu }_i\right)-\sum _{i=1}^n{\left(1-log\tau \right)}^{{\left(\frac{log{y}_i}{log{\mu }_i}\right)}^{\beta }}.\hfill \end{array}$$

(15)

The score equations of the Equation (15) are given by

$$\begin{array}{cc}\hfill \frac{\partial \ell \left(\mathbf{\Phi }\right)}{\partial \beta }& =\frac{n}{\beta }+log\left[\left(1-log\tau \right)\right]\sum _{i=1}^n{\left(\frac{log{y}_i}{log{\mu }_i}\right)}^{\beta }log\left(\frac{log{y}_i}{log{\mu }_i}\right)+\sum _{i=1}^{n}log\left(-log{y}_i\right)-\sum _{i=1}^{n}log\left(-log{\mu }_i\right)\hfill \\ \hfill & -log\left[\left(1-log\tau \right)\right]\sum _{i=1}^n{\left(\frac{log{y}_i}{log{\mu }_i}\right)}^{\beta }log\left(\frac{log{y}_i}{log{\mu }_i}\right){\left(1-log\tau \right)}^{{\left(\frac{log{y}_i}{log{\mu }_i}\right)}^{\beta }}\hfill \end{array}$$

(16)

and

$$\begin{array}{cc}\hfill \frac{\partial \ell \left(\mathbf{\Phi }\right)}{\partial {\beta }_r}& =-\beta log\left[\left(1-log\tau \right)\right]\sum _{i=1}^n{\left(\frac{log{y}_i}{log{\mu }_i}\right)}^{\beta }\frac{1}{{\mu }_{i}log{\mu }_i}\frac{\partial {\mu }_i}{\partial {\beta }_r}-\beta \sum _{i=1}^n\frac{1}{{\mu }_{i}log{\mu }_i}\frac{\partial {\mu }_i}{\partial {\beta }_r}\hfill \\ \hfill & +\beta log\left(1-log\tau \right)\sum _{i=1}^n{\left(\frac{log{y}_i}{log{\mu }_i}\right)}^{\beta }{\left(1-log\tau \right)}^{{\left(\frac{log{y}_i}{log{\mu }_i}\right)}^{\beta }}\frac{1}{{\mu }_{i}log{\mu }_i}\frac{\partial {\mu }_i}{\partial {\beta }_r},\hfill \end{array}$$

(17)

where $\partial {\mu }_i/\partial {\beta }_r={\mu }_i\left(1-{\mu }_i\right)x_{ir}$, $i=1,2,\dots ,n,r=1,\dots ,p$. Above score function consist of the nonlinear function according to model parameters. Therefore, they should be solved by the numerical methods. One may find these solutions via direct maximization of the (15) using software such as R software. The asymptotic distribution of the $\left(\widehat{\mathbf{\Phi }}-\mathbf{\Phi }\right)$ is multivariate normal $N_{p+2}\left(0,I^{-1}\left(\mathbf{\Phi }\right)\right)$, where $I^{-1}\left(\mathbf{\Phi }\right)$ is the expected information matrix. The $\left(p+2\times p+2\right)$ observed information matrix can be used for the $I^{-1}\left(\widehat{\mathbf{\Phi }}\right)$.

4.2. Model Validity for the Fitting

The model validity is examined via the residual analysis. The randomized quantile residual (rqr) was proposed by [30]. The $i^{th}$ rqr is calculated by

$${\widehat{r}}_i={\mathbf{\Phi }}^{-1}\left[G(y_i,\widehat{\beta },{\widehat{\mu }}_i,\tau )\right],$$

where $G(y,\beta ,\mu ,\tau )$ is the cdf of the QLEP distribution given by (7), ${\mathbf{\Phi }}^{-1}\left(x\right)$ is the qf of $N(0,1)$, and ${\widehat{\mu }}_i$ is defined by (14). If the model has good explanatory power, the the rqrs are distributed as the $N(0,1)$ model. The second residual is Cox-Snell residual [31] which is calculated by

$${\widehat{e}}_i=-log\left[1-G(y_i,\widehat{\beta },{\widehat{\mu }}_i,\tau )\right].$$

As in rqr, the model is valid, once the ${\widehat{e}}_i$ follows the standard exponential model.

5. Simulation Studies

In this section, we discuss on the simulation studies to see the efficiency of the MLEs of the LEP distribution under different simulation scenarios. Also, we perform another simulation study for the proposed regression model to discuss the asymptotic behaviours of the MLEs of the QLEP quantile regression model. The R software is used to implement the simulation studies.

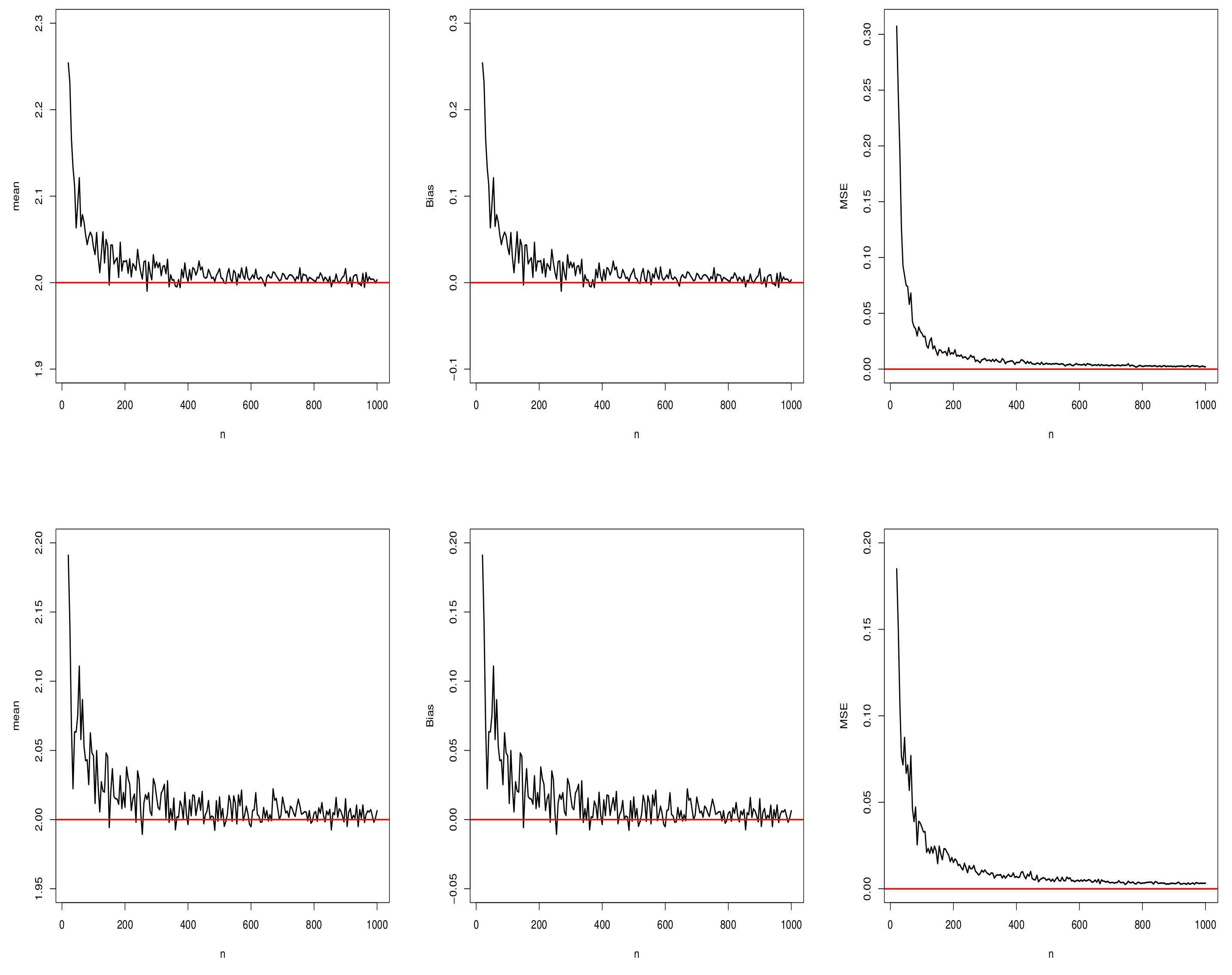
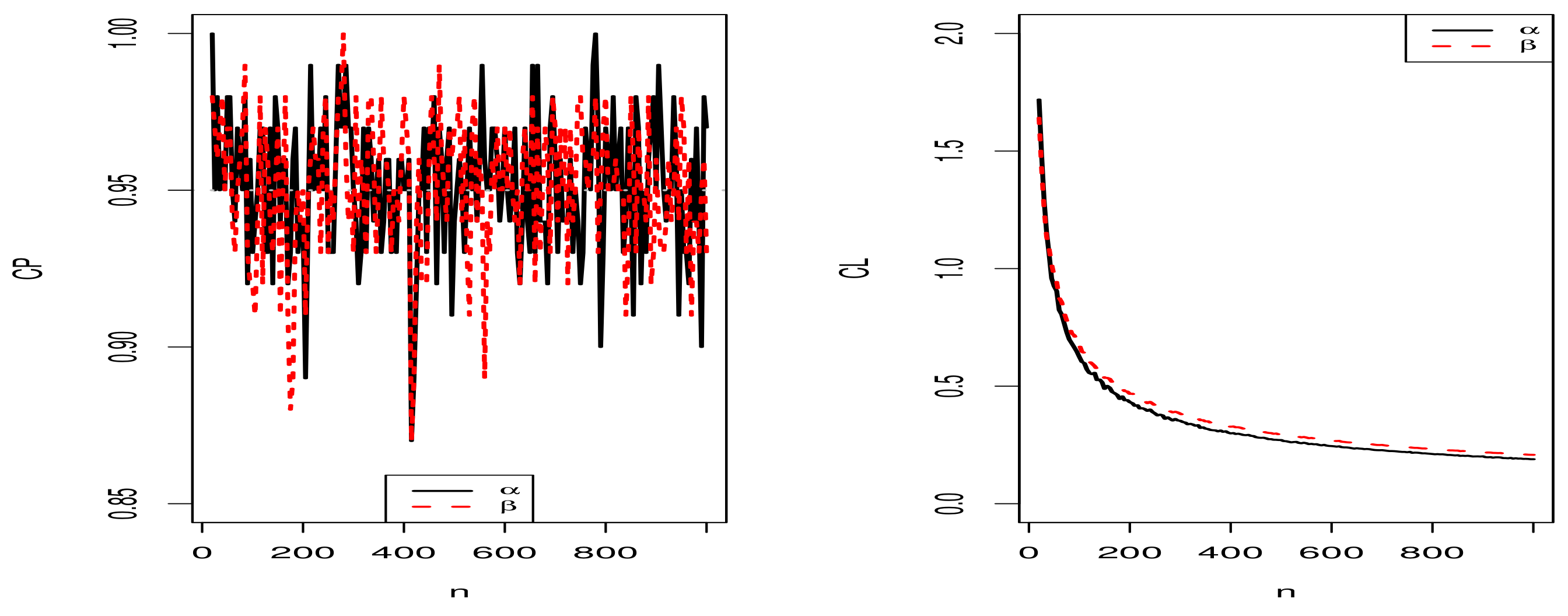
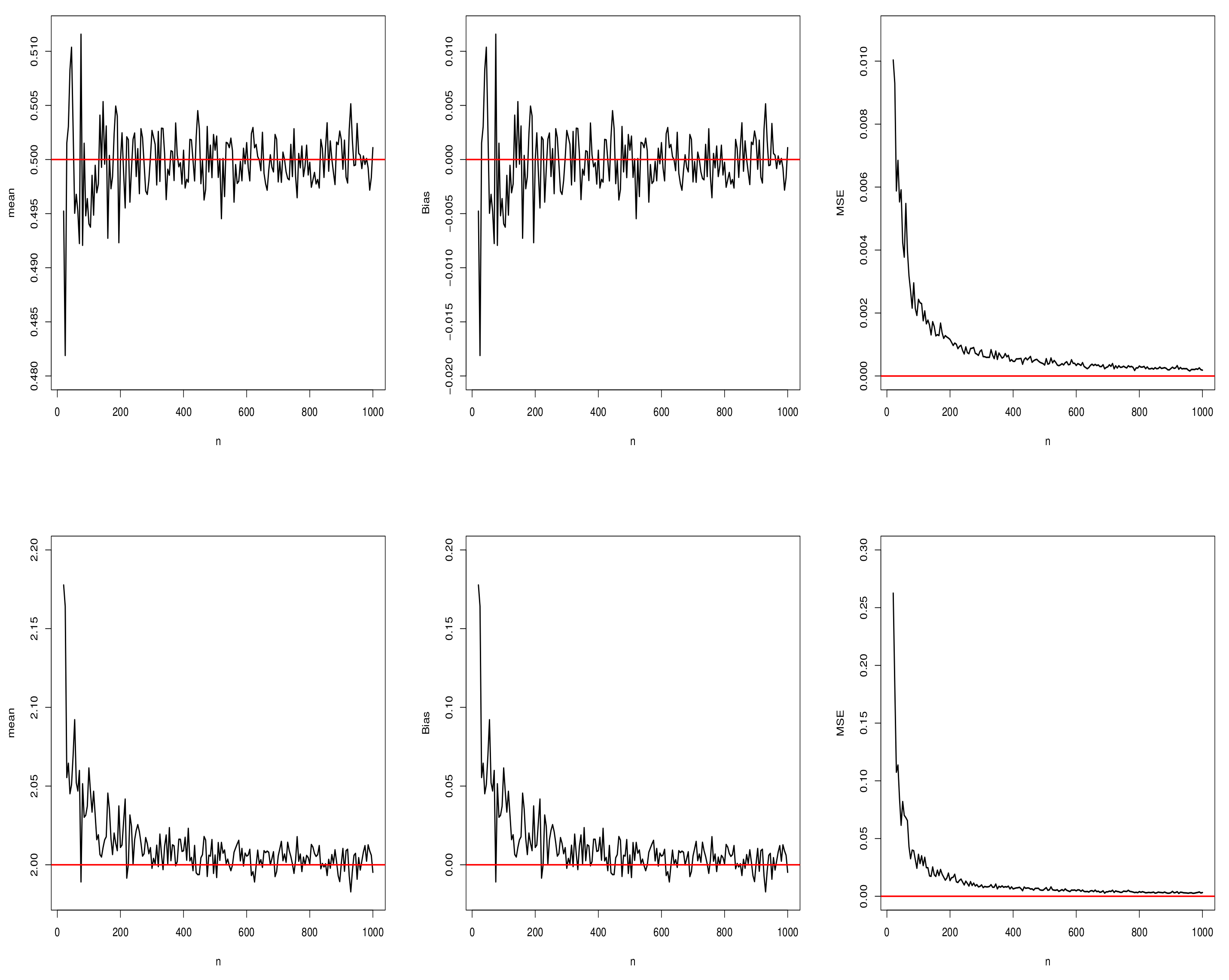
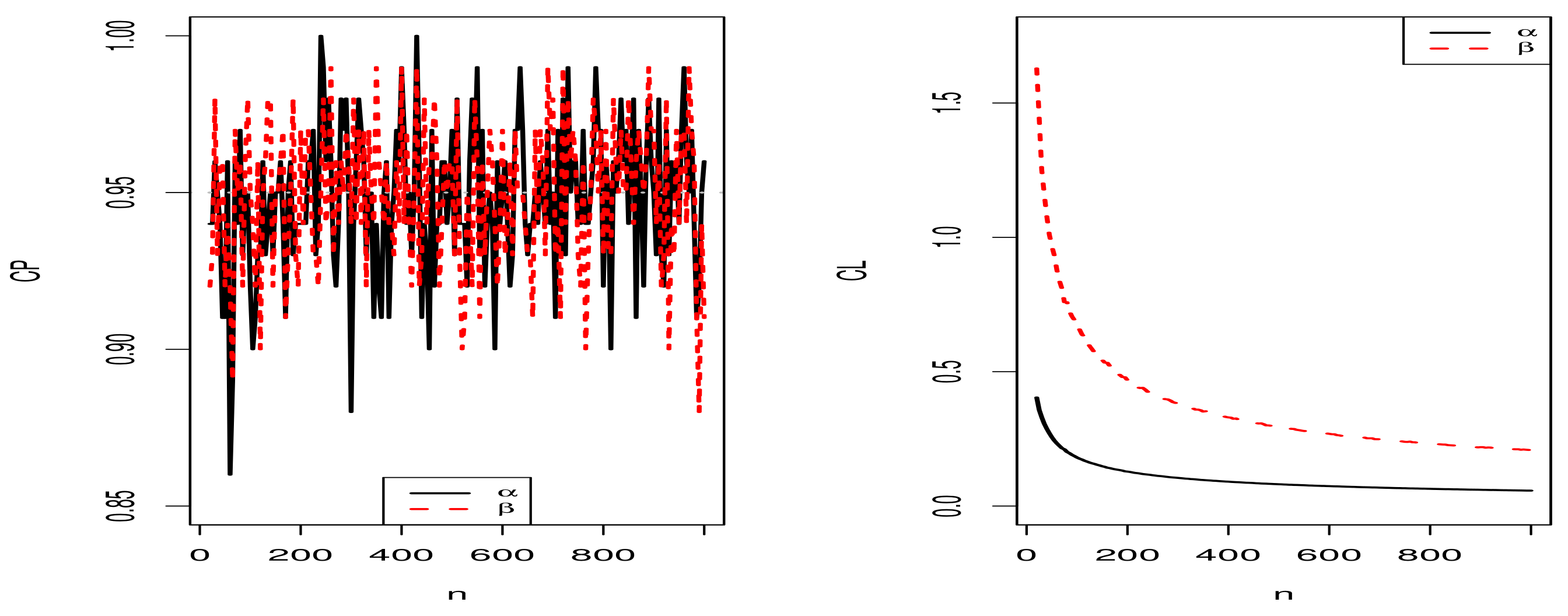
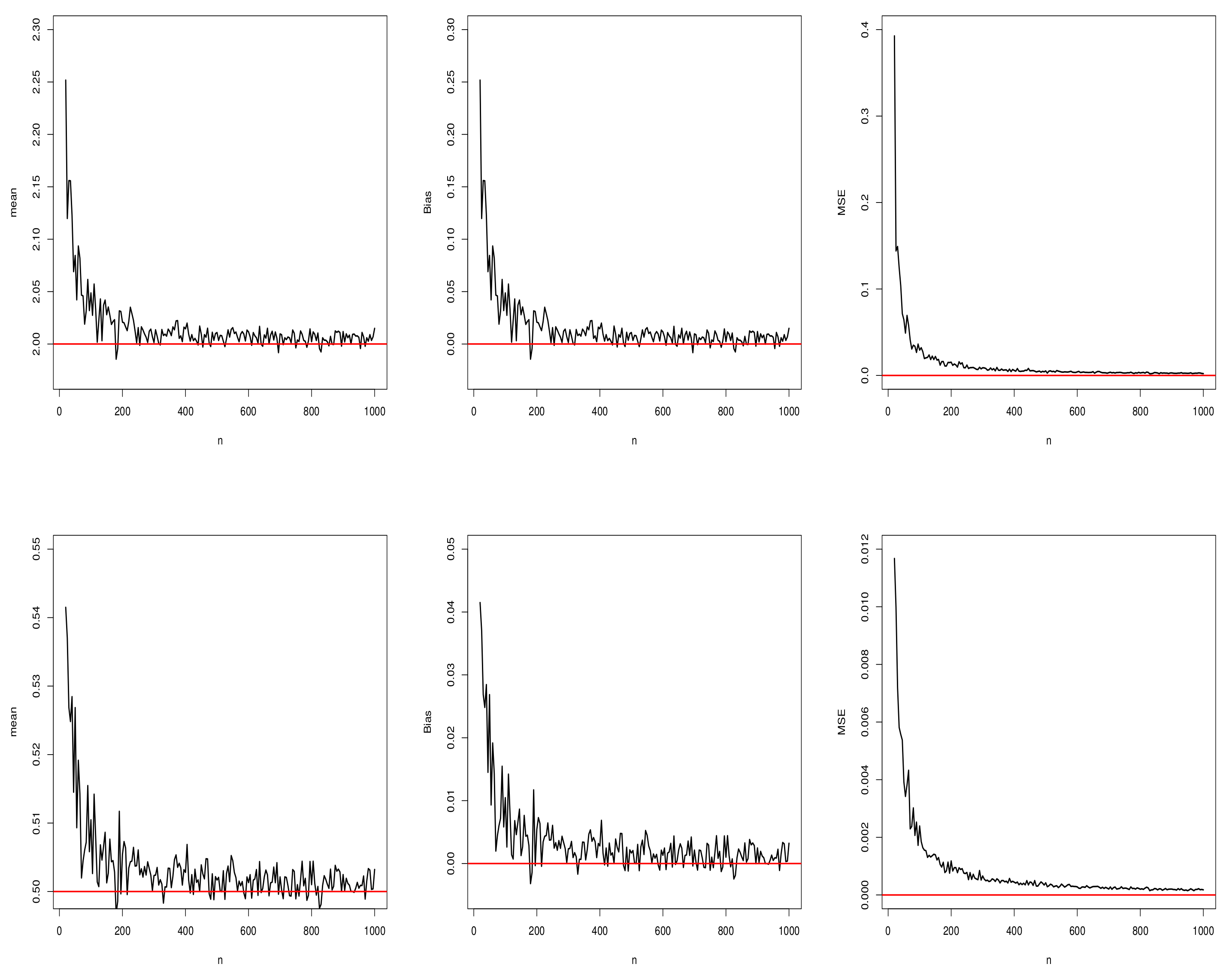
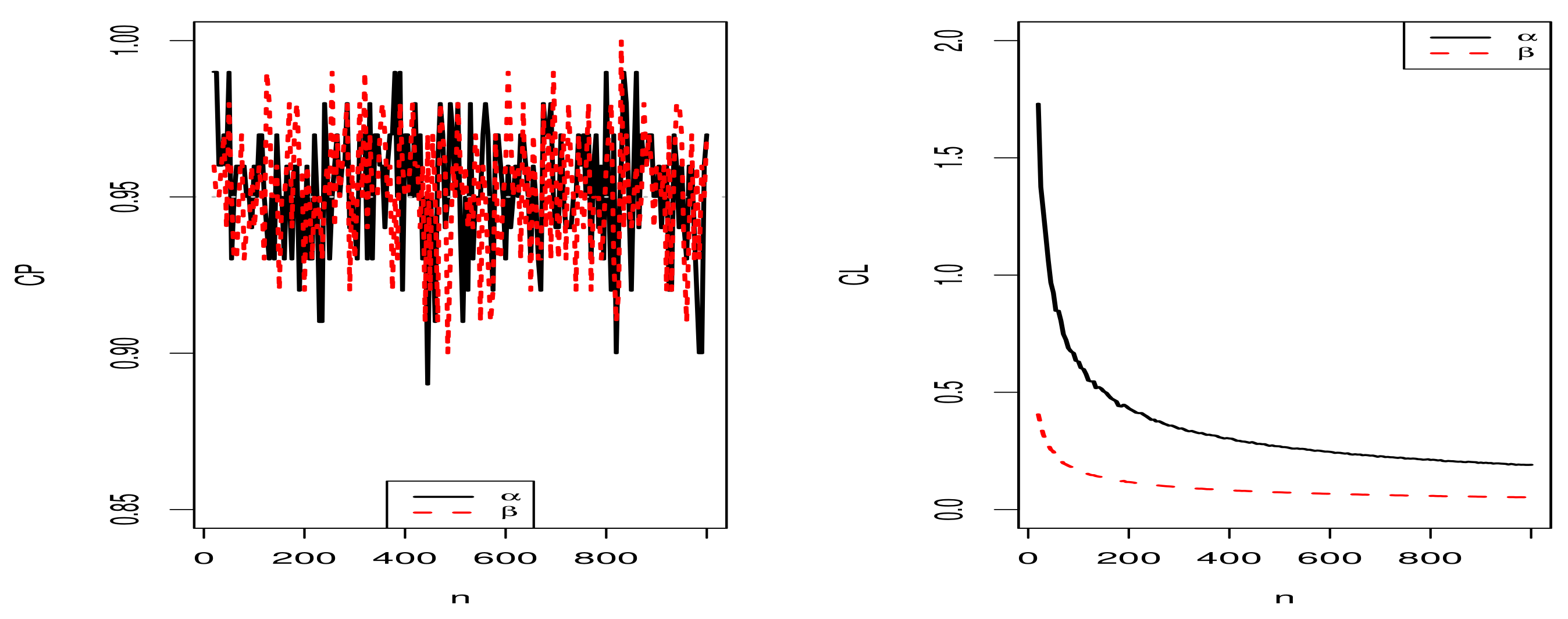
5.1. Simulation Results for the MLEs of the Proposed Distribution

We focus on the behaviours of the MLEs of the LEP distribution. For this aim, four simulation studies are conducted and the results of these simulation studies are summarized graphically. We have the following settings for the simulation studies. The $N=1000$ samples of size $n=20,25,\dots ,1000$ from a random variable following the LEP distribution are generated. Four scenarios are considered. The (6) has been used for the random numbers. By setting $ϵ=\alpha$ or $\beta$, the related bias and mean square error (MSE) are calculated by

$$\begin{array}{c}\hfill Bia{s}_{ϵ}\left(n\right)=\frac{1}{N}{\sum }_{i=1}^N\left({ϵ}_i-{\widehat{ϵ}}_i\right),MS{E}_{ϵ}\left(n\right)=\frac{1}{N}{\sum }_{i=1}^N{\left({ϵ}_i-{\widehat{ϵ}}_i\right)}^2,\end{array}$$

respectively. In addition, for the behaviours of the 95% confidence intervals of the MLEs, we calculate the empirical coverage length (CL) and coverage probability (CP) which are defined by

$$\begin{array}{c}\hfill C{L}_{ϵ}\left(n\right)=\frac{1}{N}{\sum }_{i=1}^{N}3.9198s_{{\widehat{ϵ}}_i},\end{array}$$

and

$$\begin{array}{c}\hfill C{P}_h\left(n\right)=\frac{1}{N}{\sum }_{i=1}^{N}I\left({\widehat{h}}_i-1.9599s_{{\widehat{h}}_i}<h<{\widehat{h}}_i+1.9599s_{{\widehat{h}}_i}\right)\end{array}$$

respectively, where $I\left(·\right)$ is the indicator function and the $s_{{\widehat{ϵ}}_i}=\left(s_{{\widehat{\alpha }}_i},s_{{\widehat{\beta }}_i}\right)$ are the standard errors of the MLEs which are calculated by the inverse of the observed information matrix.

5.1.1. Scenario I

The true parameter values for the scenario-I is determined as $\alpha =0.5$ and $\beta =0.5$. The estimated means, MSEs and biases for each sample size are displayed in Figure 4. The estimated CLs and CPs are also displayed in Figure 5. From these results, we conclude that the estimated biases and MSEs are near the zero. The estimated means approach the true values of each parameters. As expected, the CPs are near the desired value, $0.95$ for all sample sizes. The CLs decrease when the sample sizes increase. In the light of these results, it is verified that the consistency property of the MLE is valid for the LEP distribution.

5.1.2. Scenario II

The true parameters are determined as $\alpha =2$ and $\beta =2$ for the scenario-II and the results are summarized in Figure 6 and Figure 7. Since the results of the scenario-II is the same with scenario-I, the interpretation of the simulation results are omitted. These results also verify the suitability of the MLE method for the LEP distribution.

5.1.3. Scenario III

The true parameter values for the scenario-III is determined as $\alpha =0.5$ and $\beta =2$. The simulation results are displayed in Figure 8 and Figure 9. The results are similar with the results of the scenario-I. Therefore, the interpretation of the results are omitted. As in previous simulation studies, these results verify the suitability of the MLE method for the proposed distribution.

5.1.4. Scenario IV

For the last scenario, the true values of the parameters are determined as $\alpha =2$ and $\beta =0.5$. Figure 10 and Figure 11 give the results of the simulation study graphically. General result of these simulation studies is that the MLE method works well to estimate the unknown parameter of the LEP distribution.

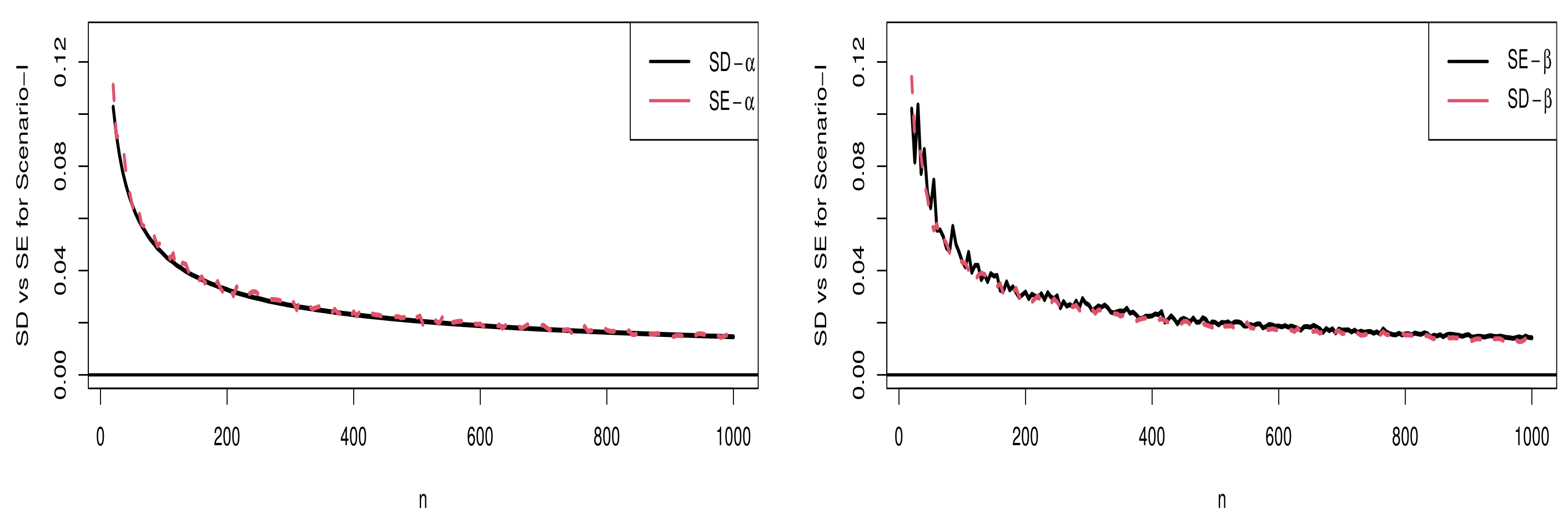
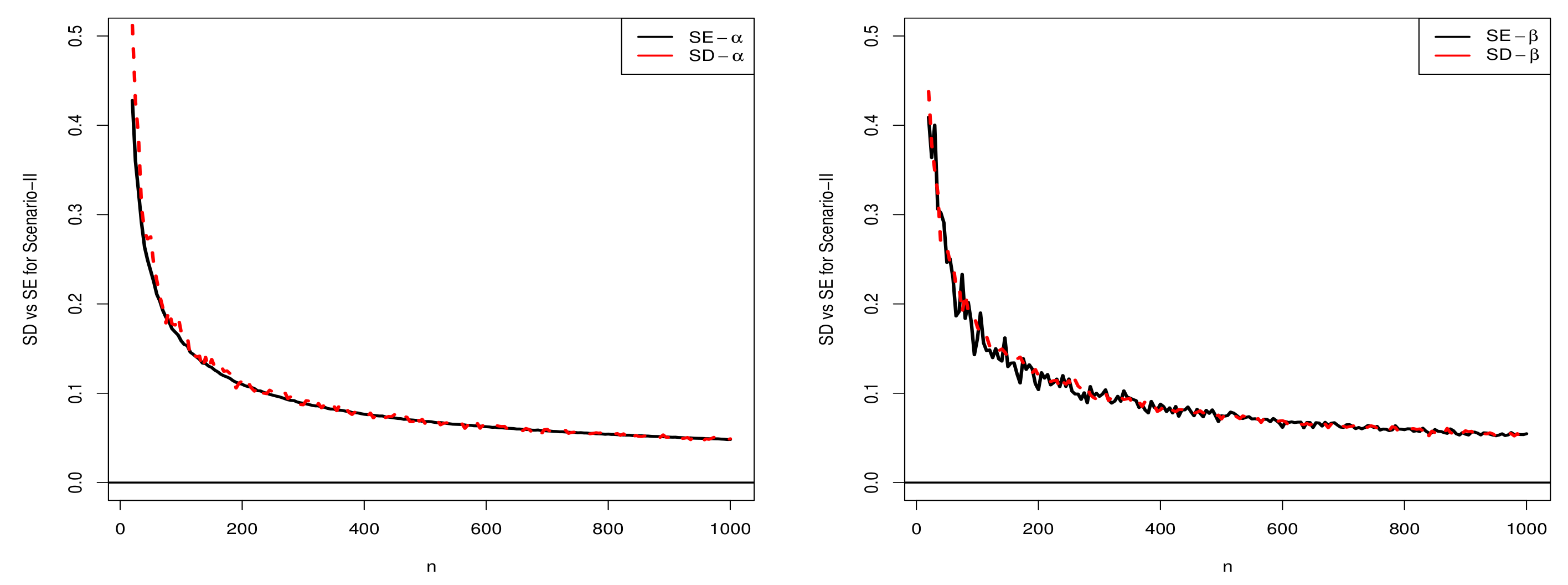
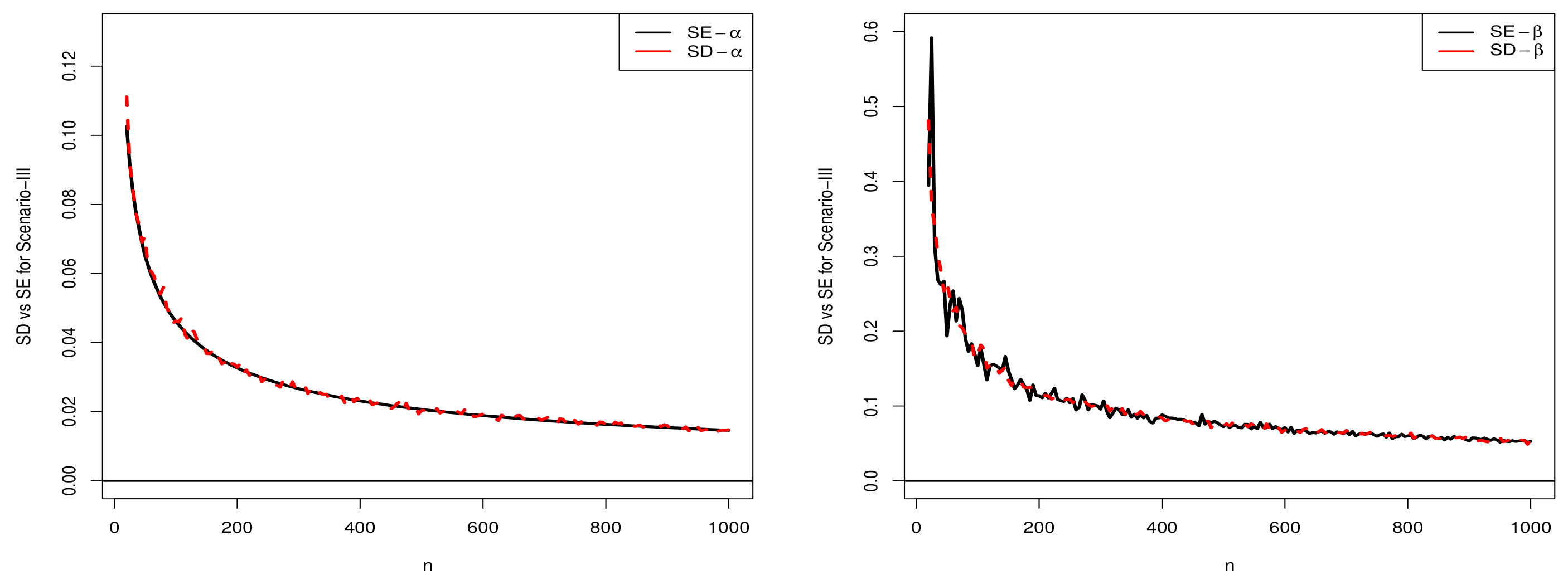
5.2. Comparison of SD and SE

Here, we compare the average of the standard errors (SEs) and standard deviations (SDs) of the estimated parameters to evaluate the unbiasedness of the SEs. For this aim, the SDs and SEs are calculated for four different scenarios and the results are graphically summarized in Figure 12, Figure 13, Figure 14 and Figure 15. If the SEs are unbiased, we expect to see that SDs and SEs should be near to each other. As seen from Figure 12, Figure 13, Figure 14 and Figure 15, the values of the SDs and SEs are near to each other. The simulation results verify the unbiasedness of the SEs.

5.3. Simulation Studies for the Proposed Regression Model

We give the simulation study in order to evaluate MLEs of the parameters of the QLEP regression model based on the bias and MSE calculations. For the varying sample size n, known $\tau$, true $\beta$, and generated covariates values, the values of the unit response variable have been obtained with

$$y_i=exp{\left(-\frac{log\left(1-log{u}_i\right)}{{\alpha }_i}\right)}^{1/\beta },$$

where $u_i\sim U(0,1)$ and ${\alpha }_i=log\left(1-log\tau \right){\left(-log{\mu }_i\right)}^{-\beta }$ for $i=1,2,\dots ,n$.

In this simulation study, it has been considered as replication number $N=1000$, sample sizes $n=25,50,100,250,500$, $\tau =0.25,0.50,0.75$, $\beta =5$ with the following regression structure

$$\mathrm{logit}\left({\mu }_i\right)={\beta }_0+{\beta }_1{z}_{i1},i=1,2,\dots ,n,$$

where ${\beta }_0=0.5$, ${\beta }_1=1$ and $z_{i1}\sim \mathrm{N}(0,1)$.

Table 1. The empirical biases, MSE, $95\%$ CP, and $95\%$ CL for the QLEP regression model with $\tau =0.25,0.50$ and $0.75$.

$\tau =0.25$
n	Bias-${\beta }_0$	Bias-${\beta }_1$	Bias-$\beta$	MSE-${\beta }_0$	MSE-${\beta }_1$	MSE-$\beta$	CL-${\beta }_0$	CL-${\beta }_1$	CL-$\beta$	CP-${\beta }_0$	CP-${\beta }_1$	CP-$\beta$
25	$0.0100$	$0.0020$	$0.4837$	$0.0013$	$0.0021$	$1.3551$	$0.1255$	$0.1636$	$3.7139$	$0.8900$	$0.9250$	$0.9440$
50	$0.0030$	$0.0023$	$0.2659$	$0.0007$	$0.0006$	$0.5236$	$0.0957$	$0.0894$	$2.4852$	$0.9300$	$0.9290$	$0.9430$
100	$0.0028$	$0.0017$	$0.0914$	$0.0003$	$0.0003$	$0.1972$	$0.0671$	$0.0614$	$1.6859$	$0.9420$	$0.9440$	$0.9560$
250	$0.0003$	$0.0007$	$0.0360$	$0.0001$	$0.0001$	$0.0728$	$0.0430$	$0.0401$	$1.0470$	$0.9470$	$0.9460$	$0.9530$
500	$0.0001$	$0.0005$	$0.0227$	$0.0001$	$0.0001$	$0.0385$	$0.0303$	$0.0293$	$0.7375$	$0.9480$	$0.9390$	$0.9460$
$\tau =0.5$
n	Bias-${\beta }_0$	Bias-${\beta }_1$	Bias-$\beta$	MSE-${\beta }_0$	MSE-${\beta }_1$	MSE-$\beta$	CL-${\beta }_0$	CL-${\beta }_1$	CL-$\beta$	CP-${\beta }_0$	CP-${\beta }_1$	CP-$\beta$
25	$0.0007$	$0.0066$	$0.4996$	$0.0020$	$0.0020$	$1.2113$	$0.1713$	$0.1595$	$3.7157$	$0.9350$	$0.9100$	$0.9610$
50	$0.0003$	$0.0015$	$0.2131$	$0.0011$	$0.0008$	$0.4604$	$0.1264$	$0.1134$	$2.4639$	$0.9410$	$0.9450$	$0.9550$
100	-$0.0011$	$0.0013$	$0.1285$	$0.0006$	$0.0003$	$0.2129$	$0.0920$	$0.0696$	$1.6977$	$0.9440$	$0.9280$	$0.9530$
250	-$0.0008$	$0.0006$	$0.0531$	$0.0002$	$0.0001$	$0.0742$	$0.0582$	$0.0439$	$1.0503$	$0.9490$	$0.9610$	$0.9570$
500	$-0.0003$	$0.0002$	$0.0273$	$0.0001$	$0.0001$	$0.0363$	$0.0413$	$0.0301$	$0.7368$	$0.9400$	$0.9500$	$0.9470$
$\tau =0.75$
n	Bias-${\beta }_0$	Bias-${\beta }_1$	Bias-$\beta$	MSE-${\beta }_0$	MSE-${\beta }_1$	MSE-$\beta$	CL-${\beta }_0$	CL-${\beta }_1$	CL-$\beta$	CP-${\beta }_0$	CP-${\beta }_1$	CP-$\beta$
25	-$0.0117$	$0.0038$	$0.5318$	$0.0057$	$0.0016$	$1.4534$	$0.2782$	$0.1340$	$3.7260$	$0.8990$	$0.9050$	$0.9430$
50	$-0.0069$	$0.0050$	$0.2627$	$0.0026$	$0.0008$	$0.5056$	$0.1984$	$0.1017$	$2.4788$	$0.9340$	$0.9010$	$0.9440$
100	− .0025	$0.0018$	$0.0973$	$0.0013$	$0.0003$	$0.1987$	$0.1440$	$0.0700$	$1.6731$	$0.9430$	$0.9450$	$0.9480$
250	− .0018	$0.0009$	$0.0533$	$0.0005$	$0.0001$	$0.0714$	$0.0913$	$0.0406$	$1.0400$	$0.9500$	$0.9470$	$0.9510$
500	$-0.0015$	$0.0003$	$0.0310$	$0.0003$	$0.0001$	$0.0378$	$0.0644$	$0.0317$	$0.7336$	$0.9400$	$0.9480$	$0.9460$

shows the simulation results for the QLEP regression model. As seen from these results, the empirical CLs decrease while the sample size increases as well as the empirical CPs are around the $0.95$ value. All biases are close zero value as wel as all MSEs tend to zero value at the same time.

6. Applications

The presented section aims to show the importance of the modeling ability of both LEP distribution and QLEP regression model, based on the real data sets. The maximized log-likelihood value $\widehat{\ell }$, Akaike Information Criteria (AIC), Bayesian information criterion (BIC), Cramer-von-Mises, ($W^{*}$), Anderson-Darling ($A^{*}$) and Kolmogorov-Smirnov (KS) goodness of-fit statistics have been calculated based on all distribution models to choose the optimum model. It is chosen as the optimum model the one which has the smaller the values of the AIC, BIC, $W^{*}$ and $A^{*}$ statistics and the larger the values of $\widehat{\ell }$. The calculations have been obtained by the maxLik and goftest functions of the R software. The details are in the following subsections.

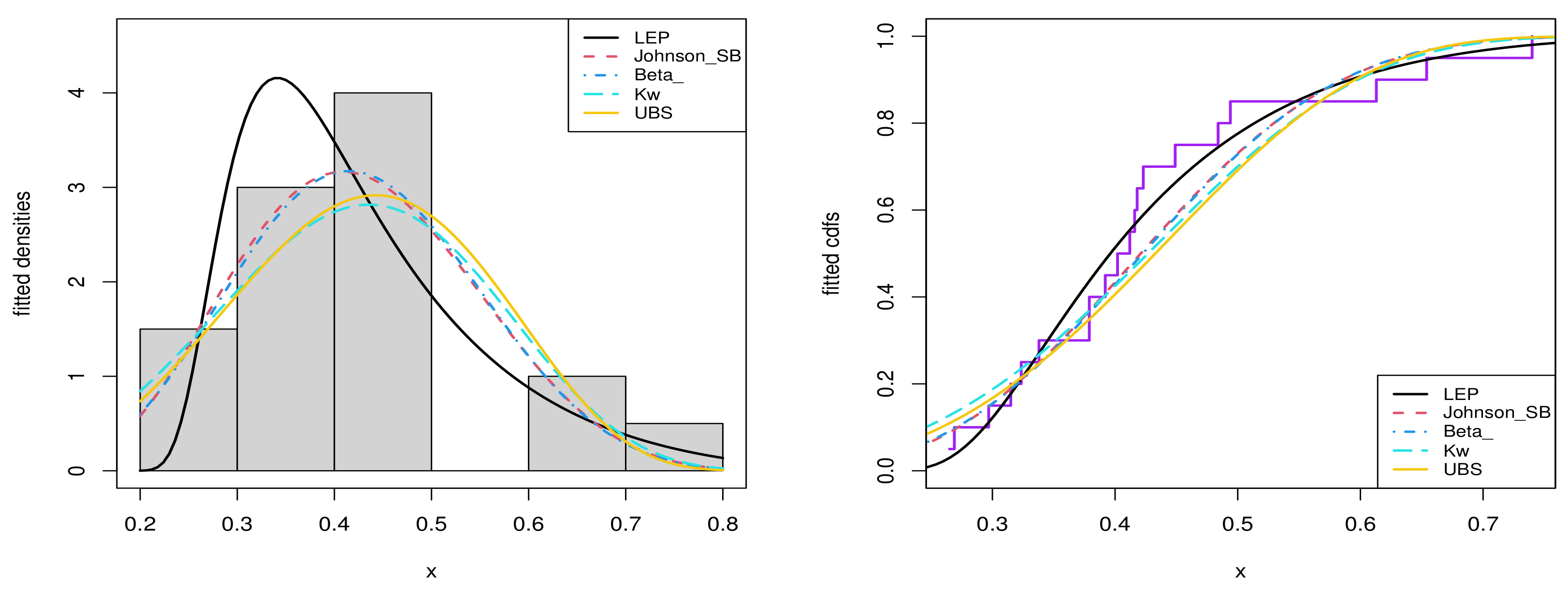
6.1. Real Data Application for the Univariate Data Modeling

The data includes in the flood levels for the Susquehanna River at Harrisburg, Pennsylvania, and represents the maximum flood level (in millions of cubic feet per second). These data are: 0.654, 0.613, 0.315, 0.449, 0.297, 0.402, 0.379, 0.423, 0.379, 0.3235, 0.269, 0.740, 0.418, 0.412, 0.494, 0.416, 0.338, 0.392, 0.484, 0.265. Recenly, this data set has been analyzed by [32,33].

Well known unit distributions in the literature have been compared with our distribution under the MLE method. Their densities have been given as follows.

• Beta distribution:

  $$f_{Beta}(x,\alpha ,\beta )=\frac{1}{B(\alpha ,\beta )}{x}^{\alpha -1}\left(1-x\right){}^{\beta -1},x\in (0,1),$$

  and $f_{Beta}(x,\alpha ,\beta )=0$ for $x\notin (0,1)$, where $\alpha >0$, $\beta >0$, and $B(\alpha ,\beta )$ is the standard beta function.
• Kumaraswamy (Kw) distribution [34]:

  $$f_{Kw}(x,\alpha ,\beta )=\alpha \beta x^{\alpha -1}{\left(1-x^{\alpha }\right)}^{\beta -1},x\in (0,1),$$

  and $f_{Kw}(x,\alpha ,\beta )=0$ for $x\notin (0,1)$, where $\alpha >0$ and $\beta >0$.
• Johnson $S_B$ distribution [35]:

  $$f_{S_B}(x,\alpha ,\beta )=\frac{\beta }{x\left(1-x\right)}\varphi \left[\beta log\left(\frac{x}{1-x}\right)+\alpha \right],x\in (0,1),$$

  and $f_{S_B}(x,\alpha ,\beta )=0$ for $x\notin (0,1)$, where $\alpha \in \mathbb{R}$, $\beta >0$, and the $\varphi \left(x\right)$ is the pdf of the standard normal distribution.
• Unit Birnbaum Saunders ($UBS$) distribution [36]:

  $$f_{UBS}\left(x,\alpha ,\beta \right)=\frac{1}{2x\alpha \beta \sqrt{2\pi }}\left[\sqrt{-\frac{\beta }{logx}}+\sqrt{{\left(-\frac{\beta }{logx}\right)}^3}\right]e^{\frac{1}{2{\alpha }^2}\left(\frac{logx}{\beta }+\frac{\beta }{logx}+2\right)},$$

  and $f_{UBS}(x,\alpha ,\beta )=0$ for $x\notin (0,1)$, where $\alpha >0$ and $\beta >0$.

Table 2. The results of the fitted models for the maximum flood level data.

Model	$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\beta }}$	$\widehat{\mathit{\ell }}$	$\mathbf{AIC}$	$\mathbf{BIC}$	${\mathit{A}}^{*}$	${\mathit{W}}^{*}$	$\mathit{KS}\left[\mathit{p}-\mathbf{Value}\right]$
LEP	0.6593	2.9194	16.5800	−29.1593	−28.4534	0.2923	0.0498	0.1366 $\left[0.8494\right]$
	(0.1128)	(0.5537)
Johnson $S_B$	0.6143	1.9261	14.2629	−24.5257	−22.5342	0.6932	0.1154	0.1935 $\left[0.4421\right]$
	(0.2438)	(0.3035)
Beta	6.7568	9.1114	14.0622	−24.1244	−22.1330	0.7327	0.1236	0.1988 $\left[0.4082\right]$
	(2.7299)	(3.4697)
$UBS$	0.3783	0.8374	12.6784	−21.3568	−19.3653	1.0516	0.1898	0.2286 $\left[0.2470\right]$
	(0.0598)	0.0696
Kw	3.3632	11.7892	12.8662	−21.7324	−19.7409	0.9322	0.1636	0.2109 $\left[0.3359\right]$
	(0.6143)	(5.4906)

shows the results of data analysis. The standard errors are in $\left(·\right)$ and p-values of the KS tests are in $\left[·\right]$ From this Table, we can say that the LEP distribution is the best model based on above comparison criteria.

Figure 16 displays the estimated pdfs and cdfs of all distributions according to results of the fitted models. The probability-probability (PP) Quantile-Quantile (QQ) plots of the fitted LEP distribution have been given by Figure 17. All these plots indicates the acceptable fitting of the LEP distribution for the data set.

The profile log-likelihood (PLL) functions are plotted in Figure 18 for the parameters of the QLEP distribution. According to Figure 18, the estimated parameters are maximizers of the function in (13).

6.2. Quantile Regression Application

We use the Better Life Index (BLI) data set measured in the year of 2017, available at https://stats.oecd.org/index.aspx?DataSetCode=BLI (accessed on 7 June 2021), to demonstrate the practicality of the QLEP regression model. We compare the QLEP model with two quantile regression models: Kumaraswamy and unit-Weibull. Homicide rate, $y_i$, is considered as dependent variable. The covariates are: employment rate $x_{i1}$, personal earnings $x_{i2}$ and labour market insecurity $x_{i3}$. The goal of the presented application is to explain the variability of the homicide rate with these covariates.

The estimated parameters as well as model selection criteria of the quantile regression models for $\tau =0.5$ are given in

Table 3. Estimated parameters and model selection criteria of the fitted quantile regression models.

Parameters	QLEP			Kumaraswamy			Unit-Weibull
	Estimates	SEs	p-Values	Estimates	SEs	p-Values	Estimates	SEs	p-Values
${\beta }_0$	−1.794	2.097	0.196	0.149	2.484	0.476	-2.938	2.351	0.106
${\beta }_1$	−0.025	0.031	0.208	−0.034	0.035	0.167	-0.004	0.034	0.456
${\beta }_2$	−0.026	0.014	0.031	−0.048	0.011	<0.001	-0.034	0.015	0.010
${\beta }_3$	−0.004	0.040	0.463	−0.048	0.051	0.174	0.015	0.046	0.369
$\beta$	4.426	0.661	-	1.004	0.121	-	5.625	0.778	-
AIC	−223.970			−209.571			−219.351
BIC	−215.782			−201.383			−211.163

. The calculated AIC and BIC values show that the QLEP regression model is better than the Kumaraswamy and unit-Weibull regression models for the considered data set since the proposed model has the lowest value of these statistics. According to estimated regression parameters, ${\beta }_2$ is found statistically significant at % 5 level for three regression models. It means that when the personal earnings increase, the homicide rate decreases. It is an expected outcome. Because, the countries having high earnings provide better life conditions and it decreases the homicide rate. It is widely documented that the income inequality leads to increased homicide rate [37].

Accuracy of the fitted regression models are evaluated by means of the rqrs. As mentioned before, when the fitted model is preferable, the rqrs should be distributed as $N\left(0,1\right)$. Figure 19 shows the QQ plots of the rqrs for all fitted regression models. From these figures, one can conclude that the QLEP model is more appropriate model than others because the plotted points for the LEP regression models is more closer the diagonal line than those of others.

Also,

Table 4. KS test results for the rqrs of the models.

KS	QLEP	Kumaraswamy	Unit-Weibull
Test statistic	0.097	0.148	0.102
p-value	0.824	0.335	0.782

lists the KS test results to verify that whether the randomized quantile residuals are distributed as standard normal distribution. Obviously, all p-values are higher than $0.05$. So, randomized quantile residuals are normally distributed for all regression models. However, the p-value of the QLEP regression model is higher than those of other models. It is also evidence for the superiority of the QLEP regression model over two other models.

7. Conclusions

In this study, a quantile regression model is defined under the proposed distribution. The parameter estimates of the proposed regression model are obtained by the maximum likelihood estimation method, and the efficiency of the estimation method is examined via simulation study. Homicide rate of the OECD countries are analyzed by the proposed approach as well as unit-Weibull and Kumaraswamy regression models. The residual analysis of the fitted regression models are performed with the randomized quantile residuals. Based on the residual analysis and model selection criteria, the proposed approach is selected as a best model among others. Additionally, the distance-based model selection criteria is used in the study. However, the likelihood-based model selection methods are more effective than the distance-based methods [38]. So, the comparison of the LEP model with existing bounded distributions can be performed under the likelihood-based model selection approaches. We plan this issue as a future work of the presented study. Moreover, we plan to develop an extension of the proposed model when the response variable is time-dependent such as monthly incidence ratio of the corona-virus disease or weekly car accident involving death ratio.