1. Introduction
This paper provides a proof for the following theorem:
Theorem 1. Given two real valued polynomials and , where the latter polynomial has roots which may be real or complex conjugate pairs, thenwhere ; N and M denote the order of the numerator and denominator polynomials, respectively; are again the roots of the denominator polynomial; is the Gauss Hypergeometric function; and are the coefficients of the partial fraction decomposition of the denominator, which require an algorithmic approach to determine (to be explained soon). Such an integral is useful if one needs to integrate a complicated ratio of functions, and can expand the numerator and denominator into their Taylor series representations. Integrals of this form also appear in physics and engineering, some examples being the calculation of the Petzval curvature in gradient index optics [
1,
2], and inverse square law theories. Furthermore, the result of this integration condenses perhaps hundreds of solutions showcased in integral tables involving ratios of various types of polynomials, into one generalized result. Such a result does not appear to be found in integral table resources [
3,
4,
5,
6,
7]. References [
6,
7] come close, following a similar approach initially, but fall short by (i) not writing the results in a generalized closed form, and (ii) not allowing the denominator polynomial be raised to arbitrary integer exponent.
The development of the proof will be pedagogical, starting with , then , and finally general . This is to very clearly show the logical progression of starting with the simplest case, and then generalizing. Note that for simplicity, the proceeding analysis does not include denominator polynomials with degenerate roots. Such an analysis will be left for future work.
2. Denominator of Linear Total Exponentiation
We begin by writing down the generalized ratio of polynomials with
, as an integrand:
where we have written
to be equal to the integral in question. The subscript 1 refers to the total exponentiation of the denominator. This notation will continue throughout this article as we analyze different values of
r.
By the fundamental theorem of algebra, the denominator can be factored into a product of binomials consisting of the roots
.
where the integration and summation operations have been swapped due to their linearity.
Remark 1. Note how this indicates that the roots can be complex in nature, meaning the approach at this point is valid for all polynomials.
Isolating, for a moment, the term involving the denominator, one realizes that it can be decomposed via partial fraction decomposition: To find any particular , one simply multiplies both sides by and then substitutes in —namely:where the substitution of kills all of the terms except . Knowing that the A coefficients are now known, we can proceed with the integration: To continue with this and the following proofs, we make use of the following Lemma:
Proof. The Taylor expansion of the integrand can be found as:
where we have utilized the rising factorial (sometimes referred to as the Pochhammer symbol)
. Integrating term-wise gives:
Multiplying by 1 in a judicious manner yields:
where we have used the definition of the Gauss Hypergeometric function, namely:
Returning back to Equation (
6), using Lemma 1 for
gives:
where we have absorbed the
m and
n summation into the constant
C. □
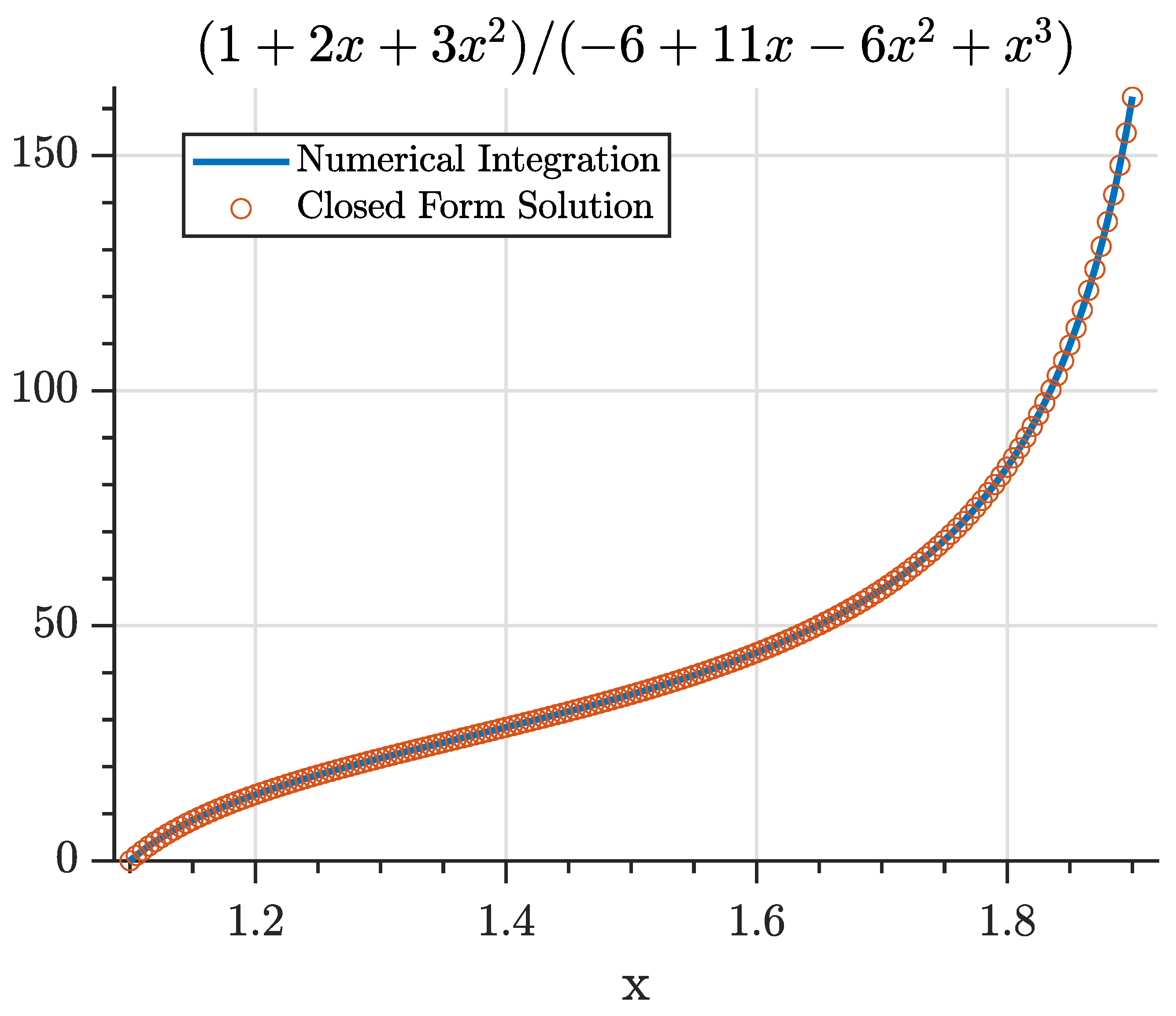
An example of the agreement between the analytical solution and the numerical calculation is shown in
Figure 1 for a denominator polynomial with one real root and two complex roots. In all numerical examples, the integration was performed via the MATLAB function
cumtrapz, which utilizes the cumulative trapezoidal technique. The
cumtrapz function simply has inputs of (i) the independent variable
x defined by a vector and (ii) the integrand function, also defined by a vector, evaluated at the points
x. After the integration, an arbitrary constant is generated and offsets the curve. Therefore, in all of the presented results the integration constants from both the numerical calculation and the closed-form solution are both set to zero.
3. Denominator of Squared Total Exponentiation
Next, we extend this analysis to the condition such that the denominator is squared. Much of the procedure is the same as shown above, so these steps will not be shown in such detail. We begin by rewriting the integral:
Again, by the fundamental theorem of algebra, the denominator can be factored into a product of binomials consisting of the roots
.
Again isolating, for a moment, the term involving the denominator, one again decomposes via partial fraction decomposition:
Note the extra term on the right-hand side due to the squared binomials in the denominator. We initially begin much the same way as shown in the previous section, the difference this time being that we are solving for the coefficients on the squared binomial term first by multiplying on both sides by
and then substituting in
. This yields:
The same trick cannot be done to the linear binomial term; namely, multiplying on both sides by
and substituting
. Doing so would cause a divergent term on the lefthhand side of the equation. Thus, we choose instead to multiply both sides by the entire denominator term, yielding:
where we have changed the dummy index on the product to not be ambiguous. Next we isolate the term involving
:
From this equation, all of the constants
can be found by realizing this expression is valid for all values of
x (where
so as not to cause singularities). Thus, one can choose arbitrary values of
x and create the necessary number of equations to form a well-defined system. This system can be solved by conventional matrix methods. Indeed, the right-hand side when
is simply a constant, and the left-hand side forms the equation with all
variables. In other words:
where
where again the
are arbitrary values that are not equal to the zeros of the denominator polynomial. We can now return to Equation (
14) knowing now that the
A constants are all known.
The first term is the identical integral to the previous section. The second integral is again obtained by Lemma 1, but this time for
. Doing this gives the final result:
Figure 2 shows one particular numerical example validating the partial fraction coefficient calculation algorithm, by showing agreement between the numerical integration and the overall closed-form solution. The particular choices of numerator and denominator polynomials are the same as those of
Figure 1, though in this case, the denominator is squared. The figure shows only the range of
x that is between two singularities. The reason for this will be explained more thoroughly in
Section 5. In short, for
, integrating through multiple poles causes the resultant area under the curve to diverge.
4. Denominator of Arbitrary Total Exponentiation
The above process, along with Lemma 1, can be easily extended to any denominator order
r. Namely, extending the analysis to solve the integral:
The critical step is the partial fraction decomposition. For
, this amounts to one term for each root, shown in Equation (
4). For
it amounts to two terms for each root, one with a linear denominator, and one squared, shown in Equation (
15). This trend continues for arbitrary order
r. Namely, for denominator order
r, each binomial will yield
r terms of increasing denominator order:
The integration can proceed in an identical fashion as the previous section, with continued use of Lemma 1 for each value of
k. Thus, the total generalized result is:
Finding the coefficients
can be done in an identical manner as the order 2 case. The final coefficient
can be determined by first multiplying both sides of Equation (
26) by
:
and then substituting
. Doing so causes the right-most term to vanish and allows
to be easily found:
To obtain all of the other coefficients
, we again multiply both sides of Equation (
26) by the entire denominator on the left-hand side (changing the dummy index again on the product):
Inserting arbitrary values
gives a system of equations of
. Using the same notation as the previous section:
where:
5. Spanning Multiple Poles in the Integration Range
When integrating over a pole, the underlying hypergeometric functions reach one of their singular points (argument equal to 1) at the pole itself and must be analytically continued for values of
. These analytic continuations occur in the complex plane, and a question arises of how these complex outputs contribute to the overall integration result, as it must be purely real since it represents an area under the curve of the integrand. We investigate this behavior by expanding the hypergeometric function:
Performing an index shift, such that
, and then renaming
to
k gives:
We now investigate the behavior of this expression for different values of
r, starting with
:
By realizing that the Taylor expansion for the natural logarithm is given by
one can then add and subtract the quantity
to Equation (
38) and obtain:
Recall that
, and as such, when
x approaches the value of the root
, then
z becomes equal to 1. As
x continues (either positively or negatively, depending on the location of
and the domain of interest), the value of this ratio becomes larger than 1. In this circumstance, the second term in Equation (
39) must converge since the sum is finite. The argument for the first term then becomes negative. To allow for computation, one must extend the input values into the complex plane. For purely real inputs, the phase is simply equal to odd integer multiples of
, where we restrict the domain of values to be just
, which accounts for the negative sign. In this case, one can simply define
, and then write it in polar form with phase equal to
, namely,
. Substituting this into Equation (
39) gives:
We can now substitute it into Equation (
12) with
, and see that the prefactor term
cancels. Upon summing, there will be a constant imaginary component. The consequence of this result is that the constant imaginary part can be subtracted away by the integration constant
C if one imposes that
, and the result becomes purely real.
If there exist complex roots, then Equation (
39) must be treated differently. The complex roots will cause
to be complex, and therefore yield some non-trivial phase value
. Thus, we can write the argument of the logarithm as:
The last step allows one to use the same procedure as the purely real zero case in regards to the complex logarithm. We must determine how the phase changes as
z changes value. This is most easily done by first equating imaginary parts:
and then solving for
:
Realizing that since
and
, where
and
denote the real and imaginary parts of
z, respectively, one can solve for
in the expression for
R to get:
This expression can then be substituted into the
expression and simplified to yield:
Thus, we see from Equation (
45), the imaginary part (dictated by the phase) will not remain constant, as was the previous case. However, because complex roots in real polynomials always come in conjugate pairs, the term corresponding to the conjugate root will have a phase of
. Substituting
into Equation (
45) and using the fact that both sine and arcsin are odd functions results in an equal and opposite phase. Therefore, when summing the total contributions from both roots, the imaginary portions will cancel out completely and the resulting integration result will be purely real. Note that this analytic continuation choice does not include
, and the divergence at this point (corresponding to
) cannot be removed, and thus, integration ranges should exclude these points.
In summary, these results indicate that for the case, as long as one does not include the exact singular points, there is no need to worry about divergence. Furthermore, there will be no complex output, even though the complex nature of the analytic continuation is a necessity. Next we examine the case:
Referring back to Equation (
36), if
, the expression becomes:
This can be simplified by using the rising factorial:
The
term will produce, after cancellation/simplification, a multiplication of many polynomials in terms of
, and
r. Since there is only a linear
k term in the denominator of Equation (
47), any term with linear or larger
k factors in the numerator will cause a divergent sum. The terms only involving
n and
r will yield identical behavior has described earlier with the complex logarithm. Consider the
case:
As mentioned, one can manipulate the second term as done earlier into the natural logarithm. The first term, however, is divergent once a pole is crossed and
. This can be circumvented by analytically continuing the hypergeometric function to accept the domain
. This topic has been extensively studied, and formulas have been derived to allow convergence over the entire complex plane except at a few points [
8], and of course the three usual divergence points of the hypergeometric function: 0, 1, and
∞. Continued study on crossing the poles for every
r and for all possible values of
z is beyond the scope of this paper. It suffices to say that in all cases, it must be the case that the output can be made to be purely real, as it represents the area under the curve of the integrand. The computational implementation of the hypergeometric function for this article applies some but not all of these formulas automatically, and restricts the divergent nature to just the usual three points when possible.
6. Closing Remarks
This paper showcased how to integrate a generalized ratio of polynomials, where the denominator as a whole is raised to the general integer order . The results were then studied to investigate the possible complex output due to the analytic continuation of the hypergeometric function. Examples for r = 1 and r = 2 were considered and validated using numerical integration. For all cases, poles will cause divergence, but only at the value of the pole itself with the proper choice of analytic continuation. This issue can be circumvented if one omits the exact location of the poles in the integration region.
The methods described here are valid for any numerator or denominator polynomials, except in cases where the denominator has degenerate roots. In such a case, however, the same methodology presented here can be used, the only difference being the particular form of the partial fraction decomposition. The generalized approached to include denominator polynomials with degenerate roots is left as future work.
In regard to the exponent r, as mentioned previously, the analysis is limited to . However, it may be possible to extend this work to non-integer values of r. Whether or not the above techniques, namely, partial fraction decomposition, can be generalized to include this scenario, remains an open question left for future work.
Finally, it is important to mention the sensitivity of the closed-form solution with respect to calculating the roots of the denominator polynomial.
Figure 3 shows one particular choice of numerator and denominator polynomial for differing amounts of error with respect to the location of the zeros. The image shows a domain between two roots
and
. As can be seen, the error is minimal as one gets further from the poles. However, the error is substantial close to the poles. Considerations such as these should be taken into account over the required integration domain of the problem at hand.