Multiplicatively Exact Algorithms for Transformation and Reconstruction of Directed Path-Cycle Graphs with Repeated Edges

Abstract

For any weighted directed path-cycle graphs, a and b (referred to as structures), and any equal costs of operations (intermergings and duplication), we obtain an algorithm which, by successively applying these operations to a, outputs b if the first structure contains no paralogs (i.e., edges with a repeated name) and the second has no more than two paralogs for each edge. In finding the shortest sequence of operations to be applied to pass from a to b, the algorithm has a multiplicative error of at most 13/9 + ε, where ε is any strictly positive number, and its runtime is of the order of $n^{O({\epsilon }^{-2.6})}$, where n is the size of the input pair of graphs. In the case of no paralogs, equal sets of names in the structures, and equal operation costs, we have considered the following conditions on the transformation of a into b: all structures in them are from one cycle; all structures are from one path; all structures are from paths. For each of the conditions, we have obtained an exact (i.e., zero-error) quadratic time algorithm for finding the shortest transformation of a into b. For another list of operations (join and cut of a vertex, and deletion and insertion of an edge) over structures and for arbitrary costs of these operations, we have obtained an algorithm for the extension of structures specified at the leaves of a tree onto its interior vertices. The algorithm is exact if the tree is a star—in this case, structures in the leaves may even have unequal sets of names or paralogs. The runtime of the algorithm is of the order of nΧ + n²log(n), where n is the number of names in the leaves, and Χ is an easily computable characteristic of the structures in the leaves. In the general case, a cubic time algorithm finds a locally minimal solution.

1. Introduction: Directed Structures

Any discrete optimization algorithm (minimizing a function or a functional) is said to be exact if its output exactly coincides with one of the minima of that functional. Otherwise (“algorithm with guaranteed accuracy”), it is required to estimate the worst-case error of the algorithm. Exhaustive (or brute-force) search is always an exact algorithm. Therefore, it is nontrivial to find a simple algorithm (e.g., of linear, quadratic, or near computation complexity) that is at the same time accurate and has good guaranteed accuracy.

A structure is any directed graph in which components are paths and cycles, and edges are assigned with names (in this respect, the graph is weighted) (see figures and examples in [1,2]). An edge is always considered in a pair with its name (but not with a direction). A repetition of an edge consists in the occurrence of another edge with the same name in the structure—the number of allowed repetitions strongly influences the complexity of the problems. We consider the problems of transformation and reconstruction of structures, which consist of: (1) finding the shortest transformation of one structure, a, into another, b, using pre-fixed operations over structures; and (2) finding the shortest reconstruction of structures specified at the leaves of a tree onto its interior vertices. Problem (2) is sometimes described as finding the shortest arrangement of structures specified at the leaves of a tree over its interior vertices. In these problems, “the shortest” means the minimum of the corresponding functional. In the first case, the functional is the total cost of the transformation of a into b, and in the second, the total cost of arrangement of structures over interior vertices of the tree. At the minimum point, the terms “shortest cost” of a transformation/arrangement and, respectively, the “shortest transformation” or “shortest arrangement” are used.

References to preceding works on these problems can be found in the first of the above-mentioned papers. Here, we only note that studying them in the applied aspect was apparently started in [3], and a systematic overview in the applied aspect is presented (see example in [4]). In the present paper, they are considered from a purely mathematical point of view and provide examples of, seemingly, very hard algorithmic problems which are solved by an algorithm with guaranteed estimates of accuracy and computational complexity—the second of them is a low-degree polynomial. One may regard these problems as lying on the verge between problems almost exactly solvable by linear or close to linear complexity algorithms and exhaustive search (NP-hard) problems.

An edge with a repeated name in a structure is said to be paralogic, and each of its repetitions is called a paralog (of the corresponding edge). A star is a tree consisting of a root and edges leading from the root to the leaves. A reconstruction (arrangement) is an assignment of a structure to each interior vertex of a given tree—structures at its leaves are fixed. It is said to be locally shortest if, for any vertex of the tree, changing the structure at this vertex into any other does not reduce the value of the functional. If two or more structures contain no paralogs and if sets of edge names in them are equal, these structures are said to be of equal content, and if they have no paralogs, but sets of edge names are not necessarily the same, they have unequal content. Structures in which paralogs may occur but sets of names are the same, will be called structures with quasi-equal content.

Operations allowed to be used to transform a structure a into b can be repeated unlimitedly many times in a sequence of intermediate structures from a to b. Each operation has its own cost, a strictly positive rational number. Here, two cases are again distinguished: costs of all operations are equal (in this case, we may assume them to be equal to 1), or they are not (unequal costs).

Recall the definitions of the first list of operations over a structure, called DCJ operations, illustrated in figures presented in [1]. This list will be kept unchanged until Section 7, where we consider a simplified list of operations (so-called SCJ operations). The operations from the first list were proposed in [5], and those from the second, in [6].

(1) Double intermerging (DM). Cut two vertices in a structure, and pairwise identify (the term join is used) the four thus formed ends. Formally, the vertex set of a structure does not change under this operation or under the next one. Under this operation, for vertices v₁ and v₂ of degree 2, edges with names k = (u₁,v₁) and l = (u₂,v₂) are replaced with either edges k = (u₁,v₂) and l = (u₂,v₁) or, if l has the opposite orientation, with k = (u₁,v₂) and l = (v₁,u₂) or, if both k and l have the opposite orientation, with k = (v₂,u₁) and l = (v₁,u₂).

(2) Sesquialteral intermerging (SM). Cut (unjoin) a vertex (i.e., ends of the adjacent edges joined at this vertex) in a structure and join one of the thus formed ends with one already free (i.e., not joined) end in the structure. Formally, for vertices v₁ of degree 2 and v₂ of degree 1, an edge with name k = (u₁,v₁) is replaced with either k = (u₁,v₂) or, if k has the opposite orientation, with k = (v₂,u₁).

(3, 4) Single mergings: cut and join (Cut and OM). Cut a vertex in the structure or, vice versa, join two free ends. Formally, under a Cut, a vertex v of degree 2 incident to edges e₁ and e₂ is replaced with two vertices v₁ and v₂, where v₁ is incident to e₁ and v₂ is incident to e₂. Under an OM, vertices v₁ and v₂ where v₁ is incident to an edge e₁ only and v₂ is incident to e₂ only are replaced with a vertex v incident to both e₁ and e₂.

Recall the definition of a breakpoint (sometimes referred to as common) graph a + b for structures a and b with equal content. This is an undirected graph consisting of paths and cycles (not loops) whose edges are labeled with symbols a or b. Specifically, vertices in a + b are names of the endpoints of all edges in a and in b—the tail of an edge with the name k is denoted by k₁, and its head, by k₂ (thus, a vertex of a structure may have two names). An edge in a + b connects two ends whenever they are joined in a or in b—this edge is labeled with either a or b, respectively. Formally, the vertex set of a + b consists of names of the form k_i, where k runs over all names of edges in a, and i is either 1 or 2—the set of its edges consists of pairs (k_i,l_j) for each vertex in structure a or b incident to edges k and l. The degree of a vertex of the breakpoint graph a + b is at most 2, and edges incident to it have different symbols, one having a, and the other b.

A final graph (or a graph of a final form) is a graph consisting of isolated vertices and of cycles of length 2 (one edge which is labeled with a, and the other with b). In [2], this definition was extended to the case of unequal content without paralogs, but here we do not need this. Even in the general case, the transformation problem is equivalent (through a linear algorithm) to the problem of minimum reduction of a + b to a final form. This equivalence is used in Section 6.

Two cases of the transformation problem are distinguished: all structures have no paralogs, or paralogs are allowed. Accordingly, we speak about transformation/reconstruction problems without or with paralogs. Problems with paralogs are reduced by a linear complexity algorithm to an integer linear programming problem [7,8].

When paralogs are present, the transformation problem is NP-hard. Therefore, its direct (i.e., without using a reduction of this problem to another) solution via a polynomial complexity algorithm assumes some constraints on initial structures and/or the list of operations over structures. In [9], paralogs are not allowed in structure a, but are allowed in b. Sets of names in a and b are the same (i.e., the structures have quasi-equal content), and only Cut and OM out of the four DCJ operations are allowed, together with an additional operation D of edge duplication, i.e., insertion of a new edge next to a given one, with the same name and direction (linear duplication), or adding an edge with the same name as a loop, a separate component of the structure (cyclic duplication). Formally, under a linear duplication, an edge (u,v) is replaced with two edges (u,v’ and v’,v) with the same name, where v’ is a new vertex. Under a cyclic duplication, a new vertex with a loop with the same name is added to the graph. Furthermore, for given structures a (starting point of the transformation) and b (final point), the duplication transforms each structure in such a way that a duplicated edge is not paralogic in a, but is paralogic in b. Note that in [9], any edge that occurs in a also occurs in b.

We will consider another constraint on structures a and b with quasi-equal content: as above, a contains no paralogs, and in b, there are at most two paralogs for each edge, but all DCJ operations over a structure are allowed, together with again the duplication D and also with deletion D’, i.e., deletion of one edge in a pair kk of neighboring codirectional edges, or deletion of a loop k when another edge k exists in the structure (i.e., D’ is inverse to D). The problem of finding the shortest (in the number of used operations) transformation of b into a by DCJ operations and operations D and D’ is trivially equivalent to the same problem without using the operation D. Note: this problem is already NP-hard, since the NP-hard problem of transformation of undirected structures with equal content can be reduced to it (even if each of the structures consists of a single path). The problems of improving the below given upper bound on the accuracy of the algorithm (i.e., proximity of the algorithm output to the exact minimum), as well as of passing to three or more allowed paralogs of an edge in b, are open and apparently hard.

2. Common Graph and Operations over It

In this section, and in the next ones, a structure is considered together with a numbering of all its paralogs: paralogs of an edge k are given names k.1 and k.2 from left to right (in a path) or clockwise (in a cycle). The numbering does not change in the course of our algorithm (unlike [7,8]). For solving the transformation problem under these new constraints on a, b, and the list of operations, we have to change the definition of the graph a + b against the definition given above. 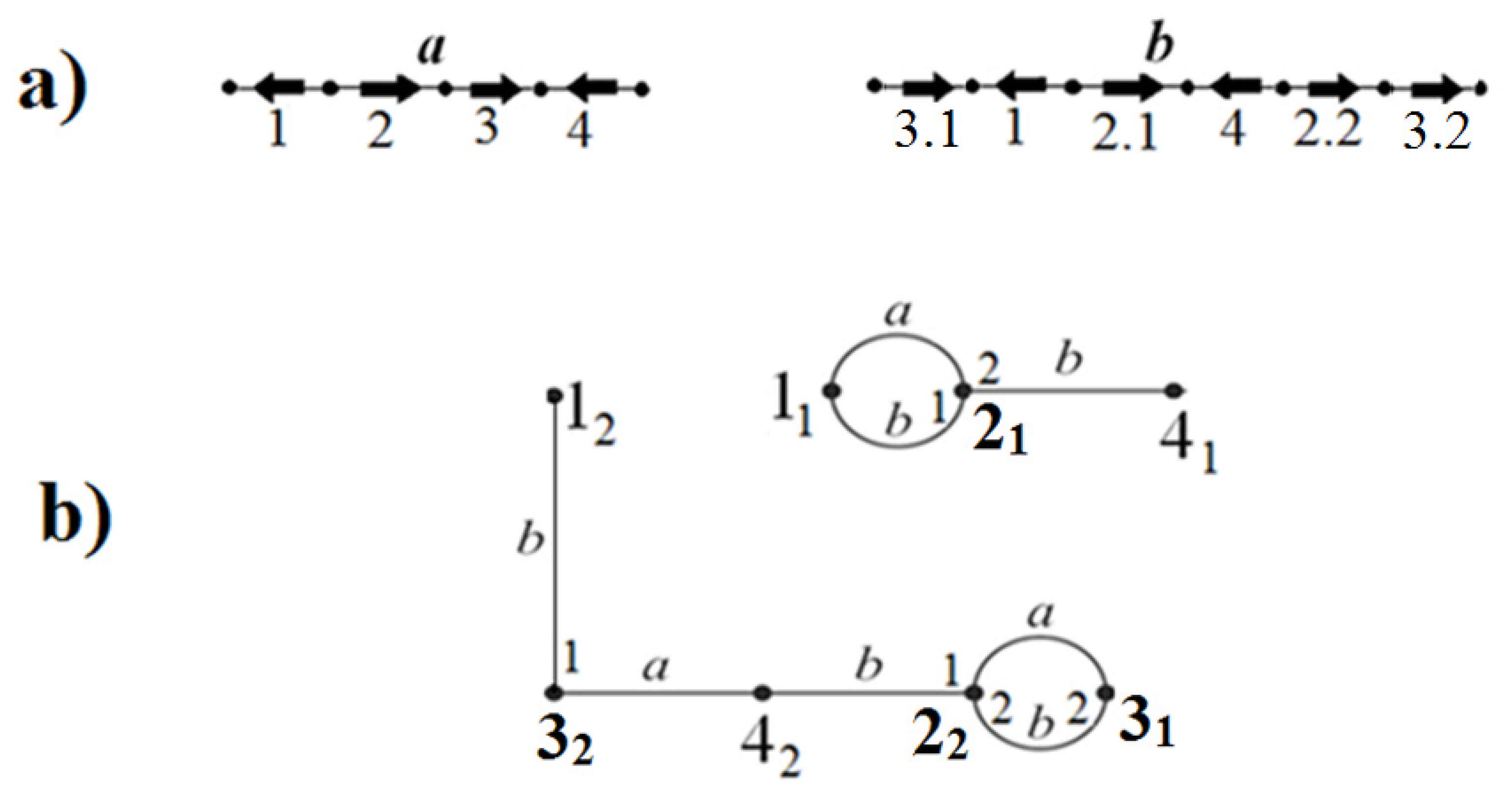Figure 1 illustrates this new definition of a + b—there, paralogs 2 and 3 in b after the enumeration, have been given the numbers, from left to right, 2.1 and 2.2, and 3.1 and 3.2. A paralogic vertex is an endpoint of a paralogic edge. In the figures, names of paralogic vertices before enumeration of paralogs are displayed in bold, i.e., are of the form k₁ and k₂. For a paralogic edge with the name k, the notation k₁ corresponds to two tails, and k₂, to two heads. In a + b, the degree of a vertex k_i is defined to be the number of a- or b-edges incident to this vertex, and it is called the a-degree and b-degree of the vertex. For a paralogic vertex, these degrees take values 0, 1, or 2, and for a nonparalogic vertex, 0 or 1.

Thus, vertices of a + b are still endpoints of all edges in a and in b before the enumeration of paralogs. Edges in a + b still indicate joins of endpoints in a or in b, and are labeled with the corresponding letter. The numbering is translated to a + b in the following way: besides the alphabetic label, an edge bears also a digit, 1 or 2, at its paralogic endpoint (digits at different ends of an edge may be different—for a loop, they must be different). Specifically, 1 or 2 at a vertex k_i indicates the number of the paralog k whose endpoint is joined in b. The difference between this new definition of a + b and the former one is only the following: now two b-edges may be incident to the same vertex, and to specify the correspondence between b-edges incident to vertices k₁ and k₂, we introduce numbering of endpoints of such edges. The latter makes it possible to recover structures a and b given a + b.

We say that vertices in a + b that correspond to a tail k₁ and head k₂ of a paralogic edge k in b are cognate. Each of these vertices is said to be b-paralogic. Similarly, an a-paralogic vertex is defined.

Operations o’ over a + b are defined as o’(a + b) = o(a) + b, where o is an operation over a structure, or by a similar equality o’(a + b) = a + o(b). Accordingly, o’ is called an a- or b-operation. Thus, operations over a + b are uniquely determined by operations over the structure. Let us explicitly define operations o’.

Double intermerging (DMb): deletion of two b-edges, and joining the four thus formed endpoints by two new b-edges with the same digital labels. DMa is defined similarly, with b changed to a. If a DM involves a loop (or loops), its (or their) vertices are regarded as having two endpoints.

Sesquialteral intermerging (SMb): deletion of a b-edge (v,w), and connecting one of the thus formed endpoints (say v) by a b-edge with a vertex not incident to a b-edge or with a b-paralogic vertex of b-degree 1. At v, digital labels of edge endpoints are not changed. SMa is defined similarly.

Single join (OMb): adding a b-edge between two vertices such that each of them is not incident to a b-edge or is b-paralogic with b-degree 1. OMa is defined similarly.

Cut (Cutb): deletion of any b-edge. Cuta is defined similarly.

Duplication (D): connecting cognate a-nonparalogic vertices k₁ and k₂ by an a-edge. For a linear duplication, endpoints of a new edge are labeled with different digits in accordance with the change of the structure, and alternative digits are put at the end of the a-edge adjacent to the new edge. For a cyclic duplication, both ends of a new edge have digit 2, and adjacent ends are labeled with 1.

Deletion (D’): deleting a b-edge between cognate b-paralogic vertices k₁ and k₂. Digits at endpoints of b-edges adjacent to k₁ and k₂ are deleted. For a linear duplication, enumeration of paralogs is performed from left to right: k.1, k.2. For a cyclic duplication, the new (looped) edge gets number k.2, and the old edge, k.1.

Each of these operations has an inverse: DMa and SMa are inverse to themselves, OMa and Cuta are inverse to each other, and the same for index b. DCJ operations are divided into a- and b-operations.

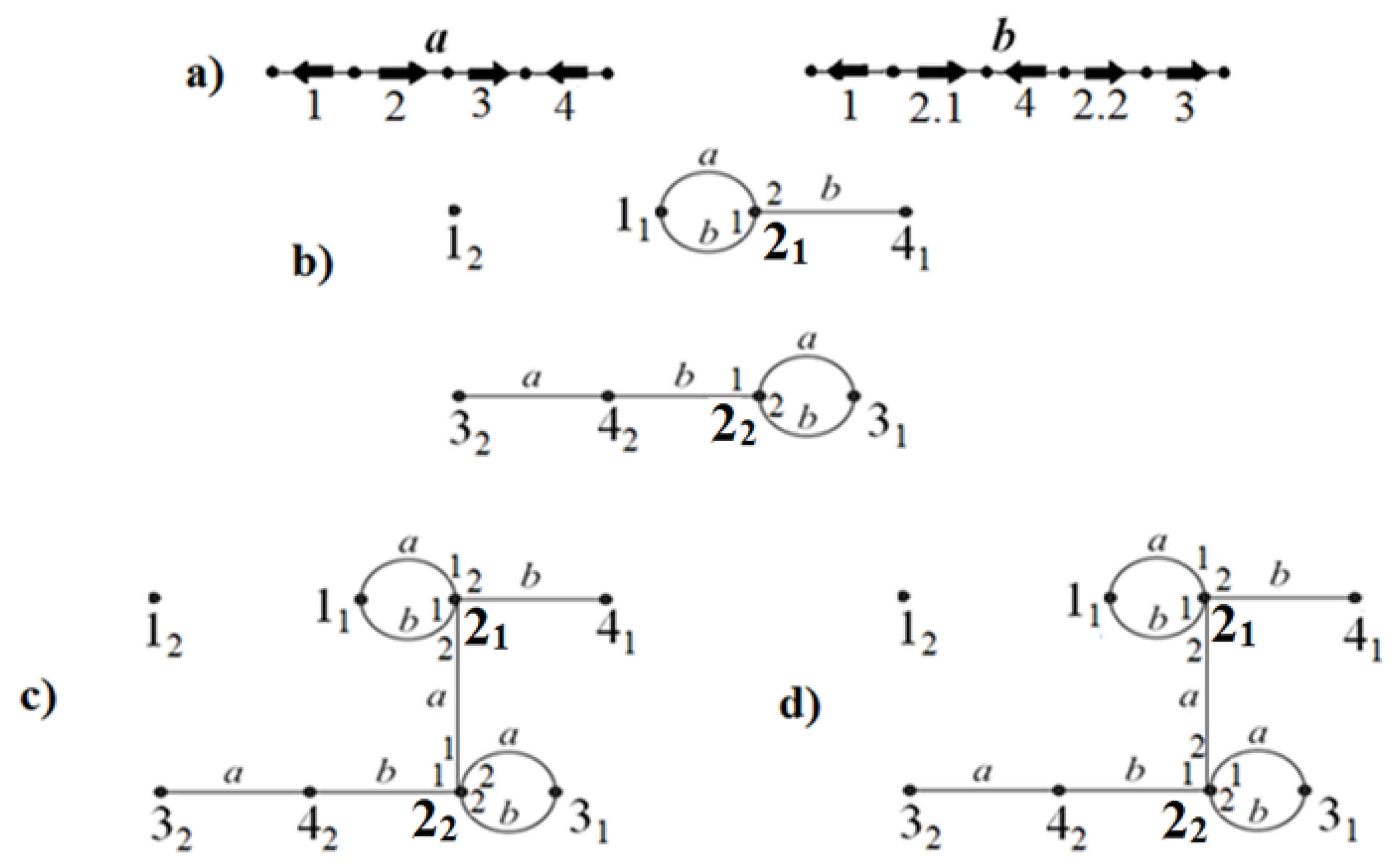
Figure 2 shows structures <a,b>, their breakpoint graph a + b, and then two variants of changing a + b: after a linear duplication D of edge 2 in a, and after a cyclic duplication D of the same edge.

A final graph (or graph of a final form) for this new definition of a + b is the same as above: it consists of cycles of length 2 (one edge is labeled with a, the other with b) and isolated vertices. The reduction problem for a + b consists in finding the minimal (in the total cost) sequence of operations that brings a + b to a final form (finalizes a + b).

We will solve the problem of transformation of b into a, which solves that of transformation of a into b due to Lemma 1B. Problems of transformation of a into b, and of b into a, require different final forms for the reduction of a + b (to ensure that Lemma 1A is fulfilled), and above we have specified the final form for precisely the transformation of b into a. This final form is simpler than the final form (which we do not specify here) for the first transformation. This is because the conditions for a and b are not symmetric. Thus, we consider precisely a transformation of b into a, which can be transformed by inverse operations into a transformation of a into b (Lemma 1B).

Throughout what follows (except for Theorem 4A,B), we consider structures with quasi-equal content.

Lemma 1.

Let all operations have equal costs.

• A.Assume that structure a contains no paralogs, and in structure b, there are at most two paralogs for each edge, both with quasi-equal content, and all DCJ operations and also duplication, D, and deletion, D’, are allowed for structures. The problem of finding the shortest transformation of b into a by DCJ operations and operation D’ is equivalent, through a linear algorithm, to the problem of minimal reduction of a + b to a final form (with the same minimum value of the functional) by using b-operations, i.e., DMb, SMb, OMb, Cutb, and D’.
• The total cost of any transformation of b into a is equal to the total cost of the corresponding reduction of a + b to a final form, and vice versa.
• B.The problems of the shortest transformation of b into a by DCJ operations and the D’-operation, and that of the shortest transformation of a into b by DCJ operations and the D-operation are linearly equivalent (with the same minimum value).

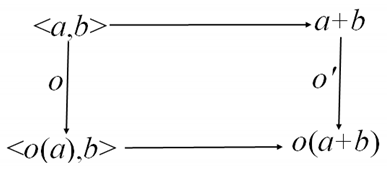
Proof. 

Operations over a + b are defined through operations over <a,b> with preserving commutativity in the following diagram: . □

3. Undirected Structures

An undirected structure is a structure with all directions of edges eliminated—it can be defined directly, without using directed structures. In [10], for equal content of undirected structures and DCJ operations, the problem of finding the shortest transformation (in the number of used operations) of one such structure into another by an algorithm with good estimates of the accuracy and runtime was solved. In [10], a breakpoint graph A * B for two undirected structures A and B was defined. Specifically, its vertices are names of edges from A and B, and its edges connect names if they are assigned to adjacent edges in A or in B, and these edges are labeled, respectively, with the names A or B (see Figure 3). The A-degree of a vertex is defined in the same way as the a-degree, and is defined analogously for the B-degree. DCJ operations over undirected structures are similarly extended to A * B, and are also divided into A- and B-operations. Namely, the following operations over A * B are considered. Double intermerging literally repeats the definition of this operation over a + b with replacing a and b by, respectively, A and B. Sesquialteral intermerging (SMA): deletion of a A-edge, and connecting one of the thus formed endpoints by a A-edge with a vertex of A-degree 0 or 1. SMB is defined similarly. Single join (OMA): adding an A-edge between two vertices of A-degree 0 or 1. OMB is defined similarly. Cut (CutA): deletion of any A-edge. CutB is defined similarly. Formal descriptions of these operations are similar to those for a + b given above.

In ref. [10], a ch-final graph (ch-final form) is defined. It consists of isolated vertices, vertices where an A-loop and a B-loop are joined, two different vertices connected by two pairs of A- and B-edges, and cycles AB of length 2 which are successively joined into a path or cycle of any length (see Figure 4). Formally, this is a graph with every edge labeled by symbol A or B, where A- and B-degrees of any vertex are from 0 to 2, A- and B-edges are bijective, and bijective edges are parallel. We exploit an algorithm from that paper which reduces A * B to a ch-final form by a chain of operations involving A-operations only. In fact, we use only part of this algorithm which finds a partition of the set of edges in A * B into cycles and paths where A- and B-edges alternate. In ref. [10], a multiplicative error of at most 13/9 + ε was proved for this algorithm, where n is the size of the initial pair of graphs, and ε is any strictly positive number, the algorithm runtime being of the order of $n^{O({\epsilon }^{-2.6})}$.

Operations over A * B satisfy the following condition: there is no vertex for which, after executing a DCJ operation, the A- or B-degree (i.e., the degree with respect to correspondingly labeled edges) is strictly greater than 2.

Theorem 1.

Assume that structure a contains no paralogs and structure b contains at most two paralogs for each edge, both being of quasi-equal content. The described algorithm outputs the shortest reduction of b into a, and has a multiplicative error of at most 13/9 + ε, where ε is any strictly positive number, its runtime being of the order of $n^{O({\epsilon }^{-2.6})}$, where n is the size of the original pair of graphs a,b.

4. Plan of the Proof of Theorem 1

(1) Given structures a without paralogs and b with paralogs (which are described in Lemma 1), construct a graph A * B for undirected equal-content structures A and B, now both without paralogs, where A and B will be obtained from a and b. It is possible to construct A * B using an auxiliary graph a + b’ = b + a’ without addressing to A and B themselves, and this is precisely what will be done.

(2) Using the above-mentioned algorithm from [10], construct a minimal reduction of A * B to the above-described ch-final form applying A-operations only.

(3) Given this minimal reduction, construct a reduction of a + b to a final form by b-operations and the D’-operation, as listed in Lemma 1A. We will prove that the second reduction is minimal. An important role will be played here by nonparalogic vertices in A * B with the A-degree 1 at most. This reduction yields the shortest transformation of initial structures, b into a, by DCJ operations and the D’-operation.

We define a quasi-final graph to be a final graph complemented by b-edges, one b-edge between each pair of cognate vertices. The nonsymmetry of conditions on a and b has the effect that when passing from a ch-final form to a corresponding breakpoint graph c + d (in a chain from a + b to a final form), the quasi-finality of c + d is achieved by using b-operations only. To this quasi-final graph c + d, only D’-operations are applied. □

Here, the role of paralog numbering is quite different than in [7,8]: the numbering is present in the initial directed structures <a,b>, and then in the breakpoint graph a + b (as digital labels at edge ends). After that, in Stages 2–4 of the algorithm presented in the next section, the numbering is not used, and we do not discriminate between paralogic and nonparalogic vertices. The numbering is recalled only at the final stage of the algorithm (Stage 5) when passing from the already found reduction of a + b to the desired transformation of b into a. □

5. Transformation of Structures with Duplications

Structures a and b with quasi-equal content are given, the first having no paralogs, and the second having at most two paralogs for each edge. The problem is to find the shortest transformation of b into a. It yields a transformation of a into b by inverse operations. The idea of our algorithm is as follows: we represent each vertex of a + b by an edge in A and an edge in B, in two specially chosen undirected structures A and B. Then, b-edges in a + b will determine adjacency of edges in A, and a-edges together with r-edges (added at Stage 2 of the algorithm) will determine edge adjacency in B. After that, a transformation of A into B will be a transformation of b into a, provided that we delete all b-edges parallel to the corresponding r-edges in a ch-final graph using a D’-operation. The solution algorithm consists of five stages.

Stage 1. Fix an arbitrary numbering of paralogs. Given that, construct a breakpoint graph a + b defined above.

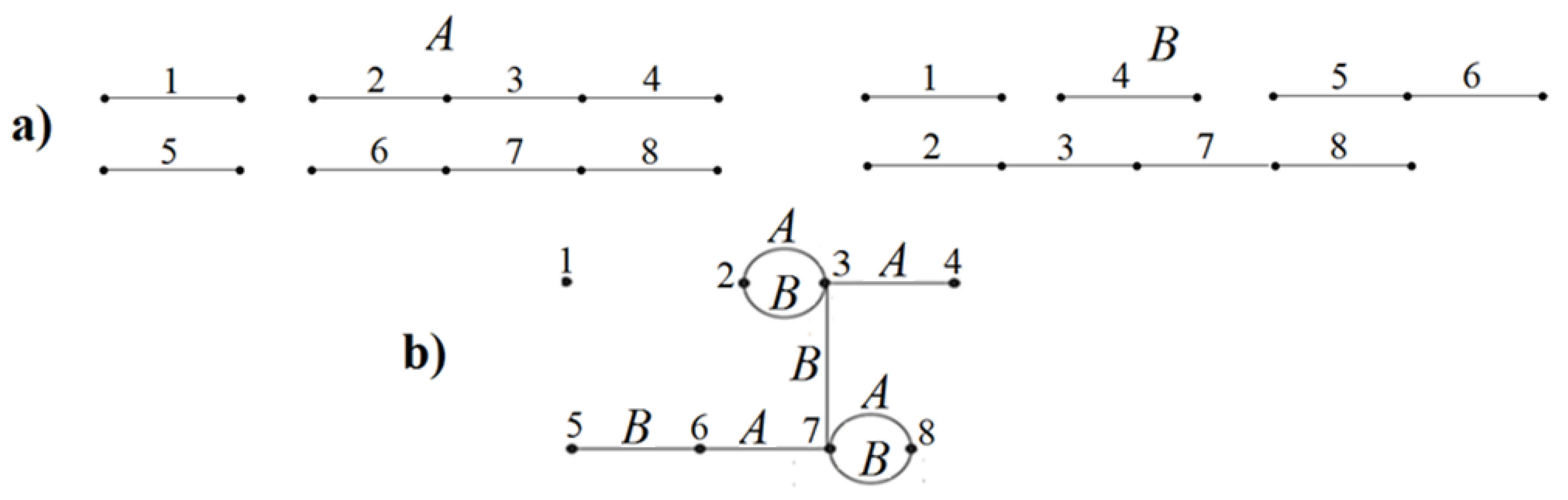
Stage 2. In a + b, join cognate vertices (i.e., a paralogic tail with a paralogic head which has the same name) by edges, labeling them by symbol r (we call them r-edges). Then, arbitrarily, but bijectively, enumerate vertices of the new graph (these numbers will be called structural), and denote the graph by a + b’, deleting all b-edges in it. Connected components in the resulting graph (paths and cycles) will be referred to as a-r-fragments. To their edges, instead of labels a and r, assign symbol B, though keep the former labels to be used later. They form a graph B’, and with that, one can easily compose an undirected structure B (though it is not involved in the algorithm directly). Similarly, delete all a- and r-edges in a + b’. Connected components in the resulting graph (paths and cycles) will be referred to as b-fragments. These edges are assigned with symbol A instead of labels b, though keeping the latter. They form a graph A’, and given this graph, one can easily compose an undirected structure A (which will not be used either). The graph A’ * B’ is defined to be the union of graphs A’ and B’ with identification of vertices having the same structural number. This A’ * B’ coincides with A * B obtained by using the corresponding undirected structures A and B, and will be denoted by A * B in what follows (see Example 1).

Stage 3. Apply to A * B the above-mentioned algorithm from [10], using A-operations only to obtain a chain of operations for the reduction of A * B to a ch-final form.

Stage 4. Throughout this chain, replace A with b, and replace B with a and r (as originally). In the ch-final graph of this chain, for each r-edge, delete a b-edge x parallel to it using operation D’ (by the definition of a ch-final form, where such an x exists). Then, delete all r-edges throughout this chain. We obtain a reducing chain for a + b in which only b-operations are used, followed by several operations D’. It is important here that, in this chain for the reduction of A*B, the A-degree of every nonparalogic vertex is not greater than 1. We will prove that the length of this chain differs from that of the minimal reduction of a + b by a factor of 13/9 + ε at most.

Stage 5. Given the thus obtained reducing chain for a + b and the original numbering, transform b into a. This transformation differs from the shortest one due to the above-mentioned difference from the minimal reduction of a + b. By applying this transformation in the reverse order to a, we obtain a transformation of a into b.

End of the algorithm.

Remark 1.

Given a graph A * B, one can easily compose the corresponding undirected equal-content structures, denoted above by A and B (see Example 1 below). Then, note the following, where n is the number of edges in a. In real computations using a distributed computing device, instead of applying the time-consuming Stage 3 of the algorithm, we may fix an arbitrary orientation in A, and exhaustively examine, in parallel, all the 2²ⁿ orientations in B. For the obtained directed structures A ⁺ and B ⁺ with equal content, find their shortest (in the number of operations) transformation, and among those, choose the shortest transformation of undirected structures A into B. The first can be done, for example, by a very particular case of the algorithm from [2] or by the algorithm from [11]. From this, obtain a minimal reduction of A * B to a ch-final form, and then execute Stages 4–5 of the algorithm.

Remark 2.

For the problem in question, the algorithm from [12] can be used instead of the algorithm from [10]. However, it is applicable only in the case where all components of undirected structures A and B are linear, which is not always the case even if all components in a and b are linear. On the other hand, the multiplicative error of the algorithm from [12] is at most 1.5, but the runtime is larger than in [10]—it amounts to O(2^2kn), where k is the minimum number of DCJ operations required to transform A into B.

Lemma 2.

Under the conditions of Theorem 1, among the shortest sequences transforming b into a, there exists a sequence in which all DCJ operations are executed before all D’-operations. Therefore, among minimal chains reducing a + b to a final form, there exists a chain in which all DCJ operations are executed before all D’-operations.

Proof. 

Let us transform any sequence into a sequence of the same length for which the conclusion holds. Assume that some DCJ operation in the initial sequence occurs immediately after D’. This D’ deletes either one of two neighboring codirectional paralogs or a looped paralog. Let us interchange these operations D’ and DCJ: first execute the DCJ on the same edges, and then D’. The structures obtained after the first and second pair of operations coincide. In this way, successively move all D’ to the end of the sequence. □

Proof of Theorem 1.

Every DCJ operation over b-edges (or a b-edge) in a + b is carried over as a similar operation over A-edges (or an A-edge) in A * B. Thus, a reduction of a + b to a quasi-final form is carried over, keeping the same length, to a reduction of A * B to a ch-final form.

Conversely, a chain of operations over A * B constructed by the algorithm from [10] possesses the following property: any vertex in A * B with the A-degree at most 1 remains the same throughout the chain. Furthermore, there exists a minimal chain reducing A * B, which possesses the same property. In the initial A * B, this property is satisfied for all nonparalogic vertices. Therefore, in these reducing chains, A-degrees of nonparalogic vertices are not greater than 1, which ensures the desired property: every SM- and OM-operation over an A-edge in A * B is carried over as a similar operation over a b-edge in a + b (and the same for all members of the reducing chain). Indeed, the only obstacle for performing an SM-operation over a b-edge in a + b for a nonparalogic vertex consists in forming a nonparalogic vertex with b-degree 2, which is, generally speaking, possible when passing from an SM-operation over an A-edge in A * B to an SM-operation over a b edge in a + b. However, the latter is impossible for Chen’s reduction of A * B. The same holds for OM. For DM and Cut, such a carryover of an operation from A * B to a + b is made without any limitations. 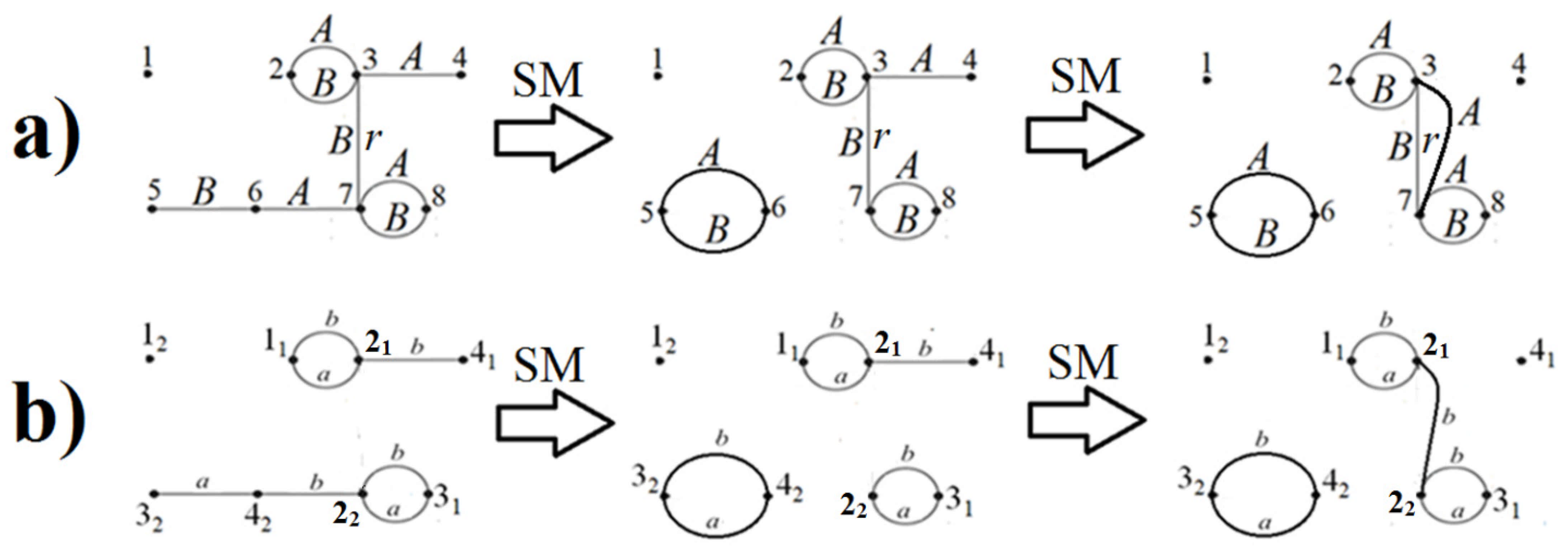Thus, the reduction of A * B with the use of one of the above-described chains is carried over, keeping the same length, to a + b, and becomes its reduction to some quasi-final graph (see Figure 5).

Now, we proceed with the proof itself. Let X be a minimal DCJ-reducing chain for A * B, ending with a ch-final graph G. Carry it over to a + b—the obtained chain X’ of the same length ends with some G’. Stage 3 applied to A * B outputs a chain Y, which consists of A-DCJ operations, and ends with its ch-final graph S—the length of this Y differs from that of X in a known way. Carry over Y to a + b—the obtained chain Y’ of b-DCJ operations ends with some S’. Stage 4 continues the chain from S by successively deleting a b-edge parallel to an r-edge, and its carryover continues S’ to a final graph fg. The length of the chain from S’ to fg equals the number r of paralogic edges in b. After completing Stage 4 over G’, we obtain our final graph fg1—the length of this continuation is also r. Thus, in the chain from a + b to G’, and then to fg1, all D’ occur after all DCJ. The length of the chain from a + b to S’, and then to fg, is |Y’| + r ≤ t|X’| + r ≤ t(|X’| + r), i.e., the multiplicative error t in the chain to fg, as compared with the chain to fg1, is as required. It remains to be verified that the chain to fg1 is minimal. To this end, compare it with the minimal reduction of a + b in Lemma 2 (let this chain X’’ end with fg2, and all D’ in it be preceded by a graph G’’). The part X’’ from G’’ to fg2 has the same length r. Its part from a + b to G’’ is no longer than the part from a + b to G’, and if it is strictly shorter, then the first part can be carried over to A * B, which contradicts the minimality of the chain X. □

Example 1 (for transformation of a into b). 

Consider structures a and b (Figure 2a) and their breakpoint graph a + b (Figure 2b), where paralog numbering and labels of edge endponts play no role until executing Stage 5. We add to a + b an r-edge and structural numbers of vertices to obtain the graph a + b’. From it, the graph A * B is obtained (without label r), as seen in Figure 3b (together with label r, it is shown in Figure 5a). We obtain a reduction to a ch-final form (Figure 5a) and the corresponding reduction of a + b to a quasi-final from (Figure 5b). Let us describe the operation of the algorithm on these structures <a,b> in more detail.

Stage 1. Using the given numeration of paralogs, construct the graph a + b (Figure 2b).

Stage 2. Add to a + b an r-edge and structural numbering of vertices. We obtain a graph of a-r-fragments consisting of the paths 1, 2-3-4, 5, 6-7-8 (according to the structural numbering), and a graph of b-fragments consisting of the paths 1, 2-3-7-8, 4, 5-6. These are graphs A’ and B’ of the structures A and B shown in Figure 3a. From them, we form the graph A * B (see Figure 3b).

Stage 3. Apply to A * B the algorithm from [10], which finds a partition of the set of edges in A * B into cycles and paths where A- and B-edges alternate: in this example, this algorithm outputs the cycles 2-3 and 7-8 (already of a final form), and the path 4-3-7-6-5. We decompose it using two SM-operations: the first deletes the edge 7-6, and the second deletes the edge 4-3 (see Figure 5a).

This reduction to a final form is similar to the reduction of the graph a + b for directed structures with equal content (see example in [11]), i.e., all operations that increase the number of cycles by 1 or the number of even-length paths by 2 are allowed.

Stage 4. Carry over these two SM-operations to the graph a + b (Figure 5b), and perform the operation D’ to delete the b-edge parallel to the former r-edge between the cognate vertices 3 and 7. Thus, our algorithm has reduced a + b to a final form in three operations.

Stage 5. Recall that enumeration of paralogs is always performed from left to right. From this reduction of a + b, we obtain a transformation of the structure b into a. The operations are as follows: perform SM with a cut between edges 2 and 4, and join the heads of edges 4 and 3. We obtain the cycle 2,3,−4 (the minus indicates the opposite direction), and the path −1,2. Then, perform SM with a cut between edges 4 and 2, and join the endpoints of two paralogs (the tail with the head). We obtain the path −1,2,2,3,−4. Then, carry out D’, the deletion of the paralog. We obtain the structure a.

By applying these operations in the reverse order to a, we obtain a transformation of a into b. Through a linear duplication of the edge 2, we obtain the structure −1,2,2,3,−4. Then, perform SM with a cut between the paralogs, and circularize the right-hand part of the path. We obtain the path −1,2 and the cycle 2,3,−4. Then, perform SM with a cut in the cycle between edges 3 and 4, and join of the head of the edge 4 with the right-hand end of the path. We obtain b. □

Remark 3.

If, instead of Stage 3, we exhaustively examine directions in B, then for the example given in Figure 3a, we obtain the following: directions of isolated edges 1 and 4 in the B result in identical structures, i.e., it suffices to examine 2⁶ variants. If the direction of edges in A is from left to right, then the minimum in B is attained when the direction of all edges except for edge 6 is from left to right.

6. Transformations of Structures Consisting of Cycles, of a Single Path, of Many Paths

If directed structures a and b with equal content are imposed by a graph topology condition, the following question arises: does there exist a shortest transformation of a into b, for which all intermediate structures satisfy this condition? We analyze this complicated question for several particular cases important in applications.

Remark 4.

The condition of equal content includes the absence of paralogs, so a breakpoint graph a + b is defined in Section 6 and in Section 7, in the same way as in Section 1 (see also [2] or a simpler version in [11]), but not the same as Section 2 or Section 5.

If structures a and b have equal content, then any shortest transformation of a into b consists of DCJ operations that increase the quality of the breakpoint graph a + b by 1, where the quality is the number of cycles plus half the number (which is even) of paths of even length, including isolated vertices, and vice versa. A proof is given for example in [11].

One can easily see the following: if structures a and b contain only cycles, the same holds for a + b too, whereas if a and b consist of cycles, then any shortest transformation of a into b consists of cycles, and involves only DM-operations. An extreme vertex (e.g., of degree 1) in a or in b remains extreme in a + b, and vice versa.

In the paper [13], the following statement (Theorem 2) is proved:

Statement 1

. Let structures a and b have equal content, and let each of them consist of a single cycle. There exists a quadratic time algorithm which outputs a shortest transformation of a into b such that every intermediate structure in it consists of at most two cycles. If the second cycle appears at some step, then at the next step, there remains a single cycle again. This algorithm possesses the following property: if there exists a DM that increases the quality of the graph a + b and does not create the second cycle, then precisely this DM is performed.

The authors do not know whether linear complexity algorithms that solve problems described in Statement 1, and Theorems 2 and 3 are possible.

If structures a and b consist of paths, then the shortest transformation of a into b, such that all intermediate structures consist of paths, does not always exist. However, the algorithm of Theorem 2 possesses the following property: if a cycle occurs in a shortest transformation, then at the next step, a DM or SM operation inserts this cycle into a path (such “short-living” cycles have an important meaning in applications).

Theorem 2.

Let structures a and b have equal content, and let each of them consist of a single path. There exists a quadratic time algorithm which outputs a shortest transformation of a into b such that any intermediate structure in it consists of at most one path and one cycle—if a cycle appears, then at the next step there remains a single path again.

Proof. 

Recall the following: paths of odd length in a + b are referred to as odd, and paths of even length, as even. A b-path in a + b is a path with extreme edges labeled with b (it is odd), and an a-path is defined similarly. An ab-path is a path where one extreme edge is labeled with a, and the second with b (it is even). An isolated vertex is considered to be an ab-path. The conditions of Theorem 2 imply that a + b contains exactly two paths: either one a-path and one b-path; or two ab-paths, and also some number of cycles.

Each iteration of our algorithm simultaneously constructs the next step of the transformation of a into b starting with a, and the next step of a reducing chain starting with a + b. Let us describe the first iteration of the algorithm, during which a is transformed into a structure c, and a + b is reduced to the graph c + b. This iteration is repeated until, respectively, the structure b and a final graph are obtained.

A. Let a + b contain no b-paths. Using Remark 4, find an a-DCJ operation (not a Cut) which increases the quality of a + b, reducing it to some c + b, which still contains no b-paths, since when the quality increases, either a cycle or two even paths appear, but a b-path does not. Denote the result of this operation over a by c. The number of paths in it is at most 1. (This c enters the preceding c + b).

B. Let a + b contain a b-path. Using an OMa operation, circularize it and obtain some c + b, which now has no b-paths (though it does have an a-path). The result of the OM over a is a cycle, denote it by c.

Thus, after steps A–B, there are no b-paths in c + b. In case B, and possibly in case A, a cycle has appeared in c, which we denote by H. For this c, which contains H, three cases are possible.

(1) Let c contain no paths. Then, in c + b there is a c-path, since there is a path in b. Apply a Cut to it, deleting an extreme edge and thereby cutting off an extreme vertex—the quality of the obtained c + b increases. In c, this Cut operation cuts a vertex in the cycle H, resulting in a structure c₁ consisting of a single path.

(2) Let c contain a path X, and let, in c + b, there exist a component containing a c-edge e₁ between endpoints of edges of this X and a c-edge e₂ between endpoints of edges in H. To the pair (e₁,e₂), apply the DM, increasing the number of cycles in c + b and increasing the quality of c + b, and denote the result by c₁ + b. This DM applied to c produces a c₁, in which H together with the former path forms a new path, which is unique.

(3) Let c contain a path, and assume that in c + b, there is no such component as in case 2, but there exists a path X containing a c-edge e between endpoints of edges in H. Since c + b contains no b-paths, it contains no c-paths either. This X is a cb-path, and the exterior end v of its extreme b-edge is an extremity of the path Y in c. Apply to the pair (e,v) the SM operation, thus increasing the number of cycles in c + b and its quality—in doing so, we obtain c₁ + b. This SM applied to c produces a c₁, in which the cycle H is merged with the path Y, and there remains a single path. Thus, in all the cases, we obtain the next structure consisting of a single path and the next breakpoint graph whose quality strictly increases after each iteration.

If the conditions in (1)–(3) are not fulfilled, then each component in c + b contains either only endpoints of edges from a path Z in c, or only endpoints of edges from H, i.e., in c + b, there is no b-edge connecting an endpoint of an edge from Z with an endpoint of an edge from H, which contradicts the fact that b consists of a single path Y. Indeed, every name of an edge in Y occurs in Z or in H, so there exist neighboring edges in Y: one in Z, and the other in H.

Thus, we have presented an obviously quadratic time algorithm that constructs a shortest sequence, as described in Theorem 2. □

Example 2 (for transformation of a into b). 

Consider two structures, each consisting of a single path: a = 1,2,3 and b = 3,2,1, with directions from left to right. The graph a + b consists of two ab-paths: 3₂b2₁a1₂ and 1₁b2₂a3₁. In a + b, there is no b-path (item A). Let us find a DCJ operation (not a Cut) which increases its quality. SM operations circularizing one of the ab-paths (for instance, the upper one) are suitable. This SM cuts the vertex in between edges 1 and 2. We obtain a structure c consisting of the cycle 2,3 (cycle H), and the path 1. Apply case (3): in c, there is a path, but c + b contains no component from case (2), and in c + b, there is a path (the second of those listed above) containing a c-edge e between endpoints of edges in H. The vertex v is the left-hand endpoint of the path e. The SM operation applied to the pair (e,v) circularizes the considered path in c + b, and transforms c into b. The transformation is completed.

Now consider the case where original structures a and b contain only (arbitrarily many) paths.

Theorem 3.

Let structures a and b have equal content, and let each of them consist of paths. There exists a quadratic time algorithm which outputs the shortest transformation of a into b such that any intermediate structure in it consists of at most one cycle—if a cycle appears, then at the next step, there remains only paths again.

Proof. 

As in the proof of Theorem 2, each iteration of our algorithm simultaneously constructs the next step of the transformation of a into b starting with a, and the next step of a reducing chain starting with a + b. Let us describe the first iteration of the algorithm, which will then be repeated.

A. Let a + b contain no a-paths. Find an a-DCJ operation which increases the quality of a + b, reducing it to some c + b, which still contains no c-paths, as when the quality increases, an odd path does not appear. Accordingly, transform a into c.

B. Let a + b contain a-paths. In each of them, apply the Cut operation to delete one extreme edge and thereby cut off an extreme vertex. We obtain a graph c + b with no c-paths. Apply step A to it.

If, after steps A or B, a cycle H has appeared in c, three cases are possible.

(1) There are no paths in c. Then, in c + b, there is a c-path, since b contains a path. This contradicts the description of this c + b.

(2), (3) The same as in the proof of Theorem 2.

If the conditions in (1)–(3) are not fulfilled, then each cycle in c + b contains either only endpoints of edges from paths in c or only endpoints of edges in H, and any path in c + b contains only endpoints of edges from paths in c. Then, in c + b, for any endpoint of an edge in H, there exists a b-edge connecting it with an endpoint of an edge in H. Therefore, edges from H form a cycle in b—this contradicts the fact that b contains only paths.

Thus, we have presented an obviously quadratic time algorithm that constructs a shortest sequence, as described in Theorem 3. □

7. Reconstructions of Structures along a Tree by SCJ Operations

Consider other operations than the DCJ, which were considered up to now. List of operations over a structure: joining two free ends of an edge (OM); cutting a vertex, i.e., joined ends of edges (Cut); deleting an isolated edge; and adding an edge from among the edges specified at the leaves of a tree. These operations are referred to as SCJ operations [6]. As above, each SCJ operation is assigned with a cost, a strictly positive rational number. The SCJ distance between structures a and b is defined to be the total cost of the shortest sequence of SCJ operations that transform a into b. As usual, “the shortest” means the minimum value of the total cost of a sequence consisting now of SCJ operations. Such a shortest transformation of a into b can easily be described: it consists in cutting all joins from a\b, deleting all isolated edges from a\b, adding all isolated edges from b\a, and adding all joins from b\a (these operations are executed in the order of listing above). Here, X\Y is the set of joins or edges in X that do not belong to Y. Therefore, the SCJ distance between a and b is known in advance, and equals the weighted sum (i.e., the sum accounting the operation costs) of the number of joins in a\b, number of edges in a\b and in b\a, and the number of joins in b\a.

Consider a rooted (possibly nonbinary) tree whose leaves are assigned with structures without paralogs, but not necessarily with equal sets of names. The problem of reconstruction of structures specified at the leaves onto the whole tree (i.e., extending the structures specified at the leaves onto interior vertices) consists in the following: arrange structures at all interior vertices of the tree in such a way that the sum, over all edges of the tree, of SCJ distances between structures at their endpoints is minimal. We will call this sum the total sum of the arrangement. In interior vertices, structures may include only edges occurring in one of the structures at the leaves (we call them allowed edges). An arrangement on which the minimum is attained will be called the shortest, and its total cost, the shortest cost. In Theorem 5, the reconstruction problem is considered in another situation, where paralogs at the leaves are allowed.

In each edge of a tree, its tail a is the end that is nearer to the root of the tree, and its head b is the end that is farther from the root. A structure at vertex v will also be denoted by v; i.e., a vertex and a structure assigned to it are not discriminated, which does not prevent different vertices from having identical structures.

It is also important to be able to solve the reconstruction problem under a condition similar to the one considered in Section 6: structures defined at the leaves are imposed by a graph topology condition (for instance, they all consist of cycles or all have no loops), and structures at interior vertices of the tree are required to satisfy the same condition. A structure that has no loops (i.e., cycles consisting of a single edge) will be called loopless, as well as the corresponding variant of the reconstruction problem. A structure consisting of cycles will be called cyclic, as well as the corresponding variant of the reconstruction problem. In applications, it is often required that all structures in an arrangement are cyclic or loopless.

Recall that a star is a tree consisting of a root and leaves, where the root is connected with every leaf.

An (undirected) graph is said to be complete if any pair of distinct vertices in it is connected by an edge. Let each edge in such a graph be assigned with a rational number (“edge length”). A matching is a subgraph of such a graph in which no two edges are incident (i.e., the subgraph has no vertex of a degree at 2 or more). A maximal matching is a matching at which the maximum value of the sum of lengths of its edges is attained.

Theorem 4.

Let us be given a tree, which is a star, such that all of its leaves are assigned with a structure without paralogs, but with sets of names which may be different (i.e., the structures need not be quasi-equal). Costs may be arbitrary.

• A. Let the structures be loopless. Then, the problem of loopless reconstruction can be reduced by a quadratic algorithm to the problem of construction of a maximal weighted matching in a complete graph consisting of ends of all edges in all the structures at the leaves.
• B. Let the structures be of equal content. Then, the reconstruction problem (also with equal content of all structures in an arrangement) can be reduced by a quadratic algorithm to the problem of construction of a maximal weighted matching in a complete graph consisting of ends of all edges in one of the original structures.
• C. Let the structures be either cyclic and loopless, or cyclic and with equal content. Then, the conclusion of part A is valid with the corresponding reconstruction being cyclic and loopless, or cyclic, respectively.

Proof. A.

In each leaf of the tree, add a k-loop for every allowed edge k that does not occur in this leaf. Thus, the original problem is reduced to the case of equal-content structures at the leaves, provided that cutting a loop (and forming an edge) has the cost of adding an edge, and joining ends of an edge has the cost of edge deletion. Indeed, for any arrangement, in its interior vertex v of the tree, add to v, as loops, the allowed edges that do not occur in it. Therefore, in the reconstruction (without the restriction on loops), we may use only joins and cuts in such structures, since this does not change the shortest cost of the arrangement.

Thus, in each vertex of any arrangement, the structure contains all ends of all allowed edges, some of them being joined, i.e., it is a matching on the set of ends of all allowed edges. Therefore, the original problem is equivalent to the following: at each leaf, we are given a matching, and in each interior vertex (which is unique in the case of a star), it is required to find a matching (on the same set) for which the sum, over all edges of the tree, of SCJ distances between matchings at their endpoints is minimal.

For any arrangement and any (unordered) pair p of different endpoints of allowed edges, denote by p_no the sum of costs of joins of this p over all leaves of the tree, and by p_yes the sum of costs of cuts of this p at the leaves of the tree—the numbers p_no and p_yes depend only on the structures at the leaves. If no pair of endpoints is joined at the root, then the arrangement cost equals the sum S of the numbers p_no over all pairs p. Any join of some p at the root adds p_yes − p_no to S. Therefore, we should minimize the sum S’ of the differences p_yes − p_no over all pairs p of the desired matching at the root, which is equivalent to maximization of −S’. By assigning each pair p with the number p_no − p_yes, we reduce the original problem, by a quadratic time algorithm, to the problem on the maximal weighted matching in a complete graph. Now, retain in this graph the edges for which p_no − p_yes > 0. Denote the number of such edges (pairs of endpoints) by Χ (it depends on the data at the leaves).

This problem on matchings can be solved in time of the order of nΧ + n²log(n), where n is the number of names at leaves [14] (Chapter 11). This estimate is also valid in the other parts of Theorem 4, as well as in Theorem 5. In the cyclic case, the sought-for matching should be required to be complete, i.e., to include all endpoints. This problem on matchings is equivalent to the problem of the minimal weighted complete matching, which is solved by a known algorithm with the same time estimation, with Χ going up to the number of all pairs of distinct ends at the leaves.

B–C. Repeat the arguments in the proof of part A. □

In ref. [15], an algorithm was proposed for solving the reconstruction problem for a star tree under equal costs of SCJ operations and equal content of all structures over the tree. In the case of a constant set of names in structures of any arrangement, the operations of deletion and insertion of an edge do not affect the shortest cost, and can be eliminated from the list of operations. Then, among the SCJ operations, there remains only OM and Cut. In ref. [9], Tannier’s algorithm from [15], also under equal costs, was extended to the case of quasi-equal content (if the root contains no paralogs) and the operations OM, Cut, and duplication D. The definitions of D and D’ are given in Section 1. The following theorem extends the result of [9] to the case of unequal costs of operations.

Theorem 5.

Let us be given a tree, which is a star, in which the structures at its leaves have quasi-equal content (i.e., paralogs are allowed). At the root, it is required to find a structure with the same content and without paralogs, and operations over the structures are OM, Cut, duplication D (linear and cyclic) from the root to the leaves, and D’ from the leaves to the root. Then, the reconstruction problem can be reduced by a quadratic algorithm to the problem of construction of a maximal weighted matching in the complete graph consisting of ends of all edges in one of the initial structures.

Proof. 

As in Section 5, we first consider the inverse transformation problem from structures b with paralogs (at the leaves) to a structure a without paralogs (at the root—both have quasi-equal content, and D’ is used). An inclusion-maximal sequence of codirectional k-edges in a structure will be called a k-block. Blocks can be linear or cyclic. Denote by B_k the number of linear k-blocks in b. For structures a and b, we describe an SCJ + D’-transformation L of b into a, which consists of the following steps executed in the order of listing. Below, by b, we denote a current structure in this transformation.

1. Cut joins of two tails and two heads of all similar paralogic edges.

2. Cut joins in b\a.

3. For each join in a, cut all similar joins except for an arbitrary one.

4. For each name k, if B_k = 0 and a k-edge is not a loop in a, cut an arbitrary cyclic k-block by the Cut operation.

5. For each join k_il_j in a\b, join any free k_i with any free l_j.

6. For each name k, if a k-edge in a is joined with any other or looped, join k-heads with k-tails where possible (the number of OM-operations to be applied is max(0, B_k − 1) if the k-edge is not a loop in a, and B_k otherwise).

7. For each name k, if a k-edge in a is neither joined nor looped, join k-heads with k-tails until there remains one linear k-block (the number of OM operations to be applied is max(0, B_k − 1)).

8. Apply operations D’ in all blocks. This results in the structure a.

Lemma 3.

The described transformation L is the shortest.

Proof. 

Under the conditions of Theorem 5, one can formulate and prove the following easy statement, similar to Lemma 2, with an additional requirement that not only all operations D’ are applied at the very end, but also all Cut operations precede all OM.

Statement 2.

Under the conditions of Theorem 5, among the shortest sequences transforming b into a, there exists a sequence in which all DCJ operations are executed before all D’-operations, and all Cut operations are executed before all OM. □

Therefore, consider the shortest transformation L’ from Statement 2. We will show that any element in L occurs also in L’, which will prove Lemma 3. For Steps 1–4 (Cut operation), Step 5 (OM over noncognate ends), and Step 8 (operation D’), this is obvious.

Consider Steps 6 and 7 (OM over cognate ends). If a k-edge is not a loop in a, from max(1,B_k) linear k-blocks, we obtain one linear block and several cyclic ones, which requires max(0, B_k − 1) operations OM. If a k-edge in a is a loop, we need to obtain from B_k, linear k-blocks cyclic blocks only, which requires B_k operations OM. After Cut operations in L’, all tails and heads of linear k-blocks are free, except for one if it is joined in a. □

The number of elements in L formed at Steps 1 and 8 is independent of a. To each element in L formed at Steps 2–7, we assign the pair p of edge ends to which it is applied (for instance, at Steps 6–7, this is a pair (k₁, k₂) with the corresponding k). Define p_no to be the sum of costs of operations assigned with p over all edges of the tree provided that p is cut at the root, and let p_yes be a similar sum provided that p is joined at the root. After that, repeat the proof of Theorem 4. □

In the case of an arbitrary tree, the reconstruction problem can be solved by the following algorithm, which is of interest since it outputs a locally minimal solution. Specifically, we say that an arrangement over a tree is locally minimal if changing a structure in it into any other at any single vertex of the tree does not reduce the total cost of the arrangement.

Consider the case of equal-content structures at the leaves: if the structures are loopless, then the case of unequal content reduces to that of equal content, as is described in the proof of Theorem 4A. From any initial arrangement, descend to a local minimum, i.e., to an arrangement with the local minimum property. A vertex satisfying this property is said to be stable. For the descent, we exhaustively check all vertices v of the tree. In each of them, we solve the problem of the maximal weighted matching with weights of pairs of different ends of edges being determined from current matchings at adjacent vertices, as is described above for the case of a star. If a new matching in v reduces the arrangement cost, we replace the former matching with the new one. The number of such step-downs in making descents from all vertices of the tree is not greater than the cost of the initial arrangement if labels of pairs are assumed to be integer (which does not lose the generality). Therefore, the runtime of the descent algorithm is of the order of the cubed number of names of all allowed edges multiplied by the number of leaves, which leads to the following result.

Claim 1.

The described algorithm outputs a locally minimal arrangement. In the case of cyclic loopless structures or cyclic structures with equal content, the algorithm outputs a locally minimal arrangement of structures with the same properties.

Reconstruction with the use of the described descent depends on the choice of an initial arrangement. In simulation of random trees labeled by random structures at the leaves (all distributions being uniform), the following algorithm for choosing an initial arrangement showed results close to the shortest arrangement (data are not presented). Specifically, to each (unordered) pair p of different ends of edges at a vertex v of a tree, we assign a real-valued variable x_vp with constraints 0 ≤ x_vp ≤ 1. At a leaf, these variables take fixed values: 1 at a joined p, and 0 at a nonjoined p. At each interior vertex v, and for each end k_i of an allowed edge, we impose the constraint ${\displaystyle \sum _{lj\ne ki}{x}_{v,ki,lj}\le 1}$ (if we seek for a complete matching, the sum is equal to 1). A pair p = k_i,l_j of ends related to adjacent vertices v and v’ of the tree (and also the corresponding pair of variables x_vp and x_v’p) will be called neighboring. The objective function F is defined as ${\displaystyle \sum _{v,v^{\prime },p}{(x_{vp}-x_{v^{\prime }p})}^2}$. Minimization of F under these constraints is a convex quadratic programming problem. Its solution {x_vp} approximately describes the probability of the event that ‘‘pair p enters the desired matching at vertex v’’. For each interior vertex v (independently of other vertices), solve the problem of construction of a maximal weighted matching with weights {x_vp}. Their solutions form an initial arrangement.

In practical computations for a binary tree, it is more efficient to make descents from two initial arrangements, then choosing the best final result. One of the initial arrangements is described above. Choose the second using the following algorithm [2] for construction of the shortest transformation of structures. Moving from the leaves to the root, consider a current vertex v and its brother v’. In the children v₁, v₂, and v’₁, v’₂ of v and v’, structures are already constructed, so find the shortest transformations between the structures v₁ and v₂, and, respectively, v’₁ and v’₂. Then, choose one structure in each transformation so that the distance between these two is minimal, and assign these structures to v and v’, respectively.

8. Discussion

Theorem 1 solves the problem on the shortest transformation of one directed structure a with paralogs into another structure b. The proof of Theorem 1 exploits a result from [10] about the shortest transformation of an undirected structure A into another structure B, both having no paralogs. The case of structures with paralogs is much more complicated than that without paralogs. Also, a genome is described by exactly a directed structure with paralogs. Reducing the problem on transformations with paralogs to the case without paralogs is nontrivial in the method and in regard to possible applications.

For NP-hard problems, designing efficient though approximate algorithms with proved accuracy is of importance. The efficiency assumes that the algorithm runtime is described by a low-degree polynomial, usually, of degree 1 or 2 in the size of the input data. We have described such an algorithm for the problem of DCJ transformation of a structure a without paralogs into a structure b with at most two paralogs for each edge. The algorithm from Theorem 1 has a multiplicative error of at most 13/9 + ε, where ε is any strictly positive number, and its runtime is of the order of $n^{O({\epsilon }^{-2.6})}$, where n is the size of the input pair of structures. If the algorithm output error is, as usual, assumed to be near 2.2, then its runtime is estimated by a second-degree polynomial in the size of input data, which is quite acceptable for modern supercomputers. The algorithm runtime depends on the computing device used (for instance, on input data of the order of several dozen thousand edges, a distributed computing system solves the problem in a few hours). Further research can be aimed at designing algorithms for cases where a also contains paralogs, or if in b, there are more than two paralogs for an edge.

Another important direction consists of finding efficient algorithms that output the shortest transformation of structures, a into b, under graph topology constraints on a, b, and all intermediate structures from a to b. We have described such algorithms for linear structures, i.e., structures consisting of a single path or several paths, and for cyclic structures, i.e., those consisting of cycles. In a transformation produced by these two algorithms, the linearity condition can be violated only transiently: a cycle appears for no longer than one step. Similarly, the second of them may transiently output two cycles. Further research can be aimed at finding algorithms for which such violations do not occur, and also at improving the accuracy and runtime of algorithms solving all the above-mentioned problems.

One more important direction is designing efficient algorithms for reconstruction of structures specified at the leaves of a tree over the whole tree. We have described an efficient reconstruction algorithm for a simple tree (star). Claim 1 and the subsequent discussion of local optimality is, in essence, setting the problem of such an algorithm for trees of a more general form.

Another way of dealing with NP-hardness consists of designing efficient algorithms for reduction of the original problem to some variant of a standard problem (for instance, a (usually integer) linear programming problem).

One of applications of the obtained results is genomics, namely the shortest transformations of genomes described as chromosome structures into each other, which corresponds to computing an evolutionary track between the genomes. A genome consists of chromosomes, each chromosome being a two-chain linear or circular sequence of genes and regulatory fragments. A genome almost always contains paralogic genes. Therefore, exact algorithms for directed structures with paralogs are important here. Another example of a possible application of these results is robotics, namely optimal motion of an object within fixed boundaries.