Improved Constrained k-Means Algorithm for Clustering with Domain Knowledge

Abstract

Witnessing the tremendous development of machine learning technology, emerging machine learning applications impose challenges of using domain knowledge to improve the accuracy of clustering provided that clustering suffers a compromising accuracy rate despite its advantage of fast procession. In this paper, we model domain knowledge (i.e., background knowledge or side information), respecting some applications as must-link and cannot-link sets, for the sake of collaborating with k-means for better accuracy. We first propose an algorithm for constrained k-means, considering only must-links. The key idea is to consider a set of data points constrained by the must-links as a single data point with a weight equal to the weight sum of the constrained points. Then, for clustering the data points set with cannot-link, we employ minimum-weight matching to assign the data points to the existing clusters. At last, we carried out a numerical simulation to evaluate the proposed algorithms against the UCI datasets, demonstrating that our method outperforms the previous algorithms for constrained k-means as well as the traditional k-means regarding the clustering accuracy rate although with a slightly compromised practical runtime.

1. Introduction

As one of the most renowned unsupervised machine learning methods, clustering has been widely used in many research areas, including data science and natural language processing, etc. Hence, it is attracting numerous research interests from both academic and industrial communities. For many applications in machine learning and data mining involving procession of large amounts of data, there might exist a lot of unlabeled data. It would consume a lot of time and resources to manually label these data in most cases. In this context, clustering arises as it does not need labels and could appropriately preprocess the data for further usage. Moreover, researchers found that some relevant domain knowledge is useful to improve the accuracy of clustering. More generally, using the background information including domain knowledge, Wagstaff and Cardie [1] proposed semi-supervised clustering to improve the clustering performance against unlabeled data, improving the state-of-the-art accuracy rate at that time. The domain information is given in the form of must-link and cannot-link constraints in many scenarios, where the must-link constraints mean that two involved sample points must be in the same cluster during the procession of clustering; in contrast, the cannot-link constraints indicate that the two involved sample points must be in different clusters after the procession of clustering. Formally, we define must-link and cannot-link as in the following:

• Must-link: constraints specifying two sample points must be in the same cluster.
• Cannot-link: constraints specifying a set of sample points that must not be placed in the same cluster, i.e., must be placed in a manner that each of them is in a distinct cluster.

For example, assume there exist two sample points $x_1,x_2$. If the two sample points are with a must-link constraint, then $x_1$ and $x_2$ must be clustered into a cluster; in contrast, if they satisfy a cannot-link then they cannot be clustered into the same cluster. Then we can formally define the constrained k-means problem as follows:

Definition 1

(The constrained k-means problem). Let $D=\{x_1,x_2,\dots ,x_n\}$ be a data set in which each point is a d-dimensional real vector. In addition, we are also given a collection of must-links $E_m$ and a set of cannot-links $E_c$. For a given integer k, the constrained k-means problem aims to divide the given data set D into k disjoint subsets $\mathcal{C}=\{C_1,C_2,\dots ,C_k\}$ such that for each must-link $(u,v)$, u is in $C_i$ if and only if v is in $C_i$, while for each cannot-link $\left(u,v\right)$, u is in $C_i$ if and only if v is not in $C_i$. Moreover, the within-cluster sum of squares is minimized as in the following:

$$\sum _{i=1}^k\sum _{x\in C_i}{∥x-{\mu }_i∥}^2,$$

where ${\mu }_i$ is the mass center of $C_i$ that ${\mu }_i=\frac{{\sum }_{x_j\in C_i}{x}_j}{|C_i|}$.

1.1. Related Work

Due to the numerous applications of clustering, there exist a large number of clustering methods, such as the famous k-means algorithm based on partitioning clustering; the well-known DBSCAN algorithm based on density clustering [2] and the AGNES algorithm derived from level clustering [3]. Among the rich literature, the k-means algorithm proposed by MacQueen [4] in 1967 is one of the most prevalent clustering method. In recent years, many variants of k-means have been studied. Li et al. [5] designed approximation algorithms for the k-means problem with penalties based on seeding algorithms, and their result was demonstrated and can be extended to the k-means++ problem with the penalty version. Bi-criteria seeding algorithms were devised by Li [6] for solving the k-means problem with penalties and spherical k-means problems, improving the performance guarantees of the k-means++ algorithm for these two problems. In the more-than-50-years history after its invention, the k-means algorithm was dominantly used in many fields, such as data mining, image segmentation and information retrieval.

Observing the fact that the performance of the k-means algorithm depends on the selection of the initial centers, many k-means seeding methods have been proposed for various of k-means algorithms [7,8,9]. The k-means++ algorithm by Arthur and Vassilvitskii [7] augmented the traditional k-means algorithm with a simple randomized seeding technique, and was shown to deserve an approximation ratio of $O\left(\ln k\right)$. For further improving the initial clustering centers of the k-means algorithm, Lai and Liu proposed a density-based method to determine the initial centers [9]. Later, the k-means$\left|\right|$ algorithm was proposed by Bahmani et al. and was shown to perform better than k-means++ in both sequential and parallel settings [8]. In the heuristic algorithm’s side, a deterministic initialization algorithm for k-means (Dk-means) was proposed by Jothi et al., which explored a set of probable centers based on a constrained bi-partitioning approach, and achieved a remarkable convergence speed and stability [10].

The k-means algorithm is of vital importance and has a wide range of applications in many different fields. In the last century, the k-means algorithm was used by Marroquin and Girosi to solve tasks including image segmentation and the pattern classification problem [11]. More recently, the k-means algorithm was employed by Chehreghan and Abbaspour to propose a hybrid clustering algorithm that can be used to cluster high-resolution satellite images by combining with the artificial bee colony optimization method [12]. Later, the k-means algorithm was applied in multi-dimensional time series analysis, and significant progress has been made by Mashtalir et al., who combined iterative deepening time-warping technology with matrix harmonic k-means to cluster video sequences [13]. Recently, the k-means algorithm was extended by Melnykov and Zhu to cluster the skewed data [14]. For a remote sensing analysis of a canopy system, Kuo et al. [15] used the k-means algorithm and an ochre structure to demonstrate a leaf segmentation approach and the subsequent application of plane-fitting to estimate the leaf angle, demonstrating a high potential to make a significant contribution to future plant and forest research. Yuan et al. [16] analyzed the impact of four k-value selection algorithms on the convergence results of the k-means clustering algorithm and used the standard data set Iris to verify the experimental results. Ahmed et al. [17] gave a structured and synoptic overview of the k-means algorithm to overcome the shortcomings of the algorithm, and studied the latest development and effectiveness of variants of k-means algorithms. The k-means algorithm was also used in agriculture [18] and water cleaning [19].

In the above problems, the traditional k-means algorithm only paid attention to the data of the given dataset. However, in practical problems, we could have some additional domain knowledge besides the given data set itself. Such information is also useful for clustering, because they could be used to significantly improve the accuracy of clustering. This brings about the concept of constrained k-means clustering, which, to the best of our knowledge, was first addressed by Wagstaff [20]. The proposed constrained semi-supervised clustering method used background information (including domain knowledge) as constraints, such that the clustering accuracy of their algorithm outperforms the traditional k-means algorithm. Constrained k-means clustering has applications in many fields and has brought many important achievements. Cao et al. [21] incorporated constraints into k-means, such that the effectiveness of multi-view video data clustering was improved. In social media, Tang et al. [22] used constrained k-means for the classification and reviewing tasks of signed network mining for better accuracy. Later, the constrained k-means algorithm was utilized by Liu et al. [23] to solve the problem of domain adaptation, which was the first time the domain adaptation problem was re-formulated as a semi-supervised clustering problem where target labels have missing values. More recently, constrained k-means algorithm was employed by Zhang and Jin [24] to construct a blind detector for spatial modulation.

Recently, Qian et al. [25] proposed an online constrained k-means algorithm based on the novel clustering pretext task such that some instances can be learned simultaneously respecting the representations and relations. Baumann [26] proposed a binary linear programming based on the k-means approach for the constrained k-means algorithm that is better at clustering than the dual iterative local search algorithm in much shorter running time. However, it is well known that the binary linear programming cannot be used to solve large-scale problems. Therefore, we proposed an algorithm to solve the problem by employing minimum weight matching.

1.2. Our Results

In this paper, we proposed an algorithm for the constrained k-means clustering problem regarding must-link and cannot-link constraints. The contribution can be summarized as follows:

• Propose a framework to incorporate must-link and cannot-link constraints with the k-means++ algorithm;
• Devise a method to cluster the points of cannot-link via novelly employing minimum weight matching and to merge the set of data points confined by must-links as a single point;
• Carry out experiments to evaluate the practical performance of the proposed algorithms against the UCI datasets, demonstrating that our algorithms outperform the previous algorithm at a rate of 65% regarding the accuracy rate.

Note that our method deserves the advantage that it produces the clustering result with a higher accuracy, and as a price, it consumes a higher runtime than the traditional k-means algorithm.

1.3. Organization

The remainder of the paper is organized as in the following: Section 2 introduces the preliminaries and problem model; Section 3 proposes the constrained k-means clustering algorithm regarding domain knowledge as side information; Section 4 introduces the method for evaluating the performance of the algorithm, and demonstrates experimental results comparing our constrained k-means with other baselines including the traditional k-means algorithm; Section 5 concludes this paper.

2. Preliminaries and Problem Statement

In this section, we mainly introduce the definition of pair-wise constraints. Then we give a figure to show the shortcomings of the constrained k-means clustering algorithm that is proposed by Wagstaff [20]. After that, we propose an improved method to improve the result of clustering.

We use Figure 1 to demonstrate the procession of the previous constrained k-means algorithm [20], and our algorithm deald with must-link and cannot-link constraints, in which Figure 1a shows the must-link constraint and Figure 1b is the cannot-link constraint.

In Figure 1a, there are a set of clustering centers $U=\left\{{\mu }_1,{\mu }_2\right\}$ and a set of sample points $V=\left\{x_1,x_2,x_3\right\}$. Since the four simple points in V must satisfy the must-link constraints, then if $x_1$ is assigned to ${\mu }_1$, $x_2,x_3$ must also be allocated to ${\mu }_1$; otherwise, if $x_1$ is assigned to ${\mu }_2$, then it means $x_2,x_3$ will be allotted to ${\mu }_2$. Therefore, the four sample points can be assigned to ${\mu }_1$ (or ${\mu }_2$) at the same time. Let $d_{ij}$ be the distance between a sample point $x_i$ and a clustering ${\mu }_j$. Let ${\sum }_{i=1}^n{d}_{ij}$ be the sum distance between a clustering ${\mu }_i$ and a set of sample points $V=\left\{x_1,\dots ,x_n\right\}$. When using the constrained k-means in [20], the four points must be allotted to ${\mu }_1$ if $x_1$ is firstly selected [20], since $d_{11}<d_{21}$. However, that is not the best result of clustering. Due to ${\sum }_{i=1}^3{d}_{1j}<{\sum }_{i=1}^3{d}_{2j}$, the four points should be assigned to ${\mu }_2$ to incorporate an optimum solution. Therefore, we propose a new method to deal with a must-link set to prevent the above inaccuracy. In our algorithm, we first calculate the center point x of the set of sample points V, and then determine whether the center x is assigned to ${\mu }_1$ or ${\mu }_2$ according to the distance between the center x and ${\mu }_1$ or ${\mu }_2$.

Figure 1b has a set of clustering mass centers $U=\left\{{\mu }_1,{\mu }_2,{\mu }_3,{\mu }_4,{\mu }_5\right\}$ and a set of sample points $V=\left\{x_1,x_2,x_3,x_4\right\}$, in which each pair of sample points in V must satisfy the cannot-link constraints. Hence, there must exist at least four clusters, so that the sample points can be divided into different clustering centers. Let $d_{ij}$ be the distance between a clustering ${\mu }_i$ and a sample point $x_j$. Then obviously $d_{ij}$ can be calculated for any pair ${\mu }_i\in U$ and $x_j\in V$. Thus, we can use the bipartite minimum weight matching between the two vertex sets U and V to solve the cannot-link constraint. The definition ofthe minimum-weight matching can be described as follows:

Definition 2

([27])). Let $G=\left(U,V;E\right)$ be a bipartite graph and let $w:E\to {\mathbb{R}}_{+}$ be the weight of the edges. For any subset F of E, denote $w\left(F\right):={\sum }_{e\in F}w\left(e\right)$ as the weight of F. We say M is a match if and only if M is a set of disjoint edges subset of E. The aim of minimum-weight matching is to find a matching M covering all vertices of U or V, such that $w\left(M\right)$ attains the minimum.

Figure 2 gives a more detailed explanation about Definition 2, in which there exist two types of sample point sets $\left\{{\mu }_1,{\mu }_2,{\mu }_3\right\}$ and $\left\{x_1,x_2,x_3,x_4\right\}$. Then we can find that $\left\{\left({\mu }_1,x_1\right),\left({\mu }_2,,x_3\right),\left({\mu }_3,x_4\right)\right\}$ is a matching and $\left\{\left({\mu }_1,x_1\right),\left({\mu }_2,,x_3\right),\left({\mu }_3,x_3\right)\right\}$ is not matching.

Let $V=\left\{x_1,\dots ,x_m\right\}$ and $U=\left\{{\mu }_1,\dots ,{\mu }_n\right\}$ be a set of sample points and a family of cluster centers, respectively. Let $d_{ij}$ be the distance between cluster ${\mu }_i\in U$ and sample point $x_j\in V$. Let $x_{ij}=1$ if $x_j$ be assigned to ${\mu }_i$, otherwise set $x_{ij}=0$ for $x_j$ is not clustered to ${\mu }_i$. Then the integer linear programming for the minimum weight matching can be described as follows:

$$\begin{array}{cc}\hfill & min\sum _i\sum _j{x}_{ij}{d}_{ij}\hfill \end{array}$$

$$\begin{array}{cccc}\hfill & s.t\sum _i{x}_{ij}\le 1\hfill & \hfill & \forall x_j\in V\hfill \end{array}$$

(1)

$$\begin{array}{cccc}\hfill & \sum _j{x}_{ij}=1\hfill & \hfill & \forall {\mu }_i\in U\hfill \end{array}$$

(2)

$$\begin{array}{cccc}\hfill & x_{ij}\in \left\{0,1\right\}\hfill & \hfill & \forall {\mu }_i\in U,x_j\in V\hfill \end{array}$$

The first constraint means each cluster contains at most one sample point; the second means each sample point must be clustered to a cluster.

As a well-known combinatorial optimization problem, the minimum weight unbalance perfect matching problem already has known efficient algorithms in the existing literature:

Lemma 1

([28]). Let G be a given graph with two partitions U and V. Assume that $n=\left|U\right|+\left|V\right|$ and there are m edges in G. Then the minimum weight unbalance perfect matching of G can be found within a runtime of $O\left(mn+n^{2}logn\right)$.

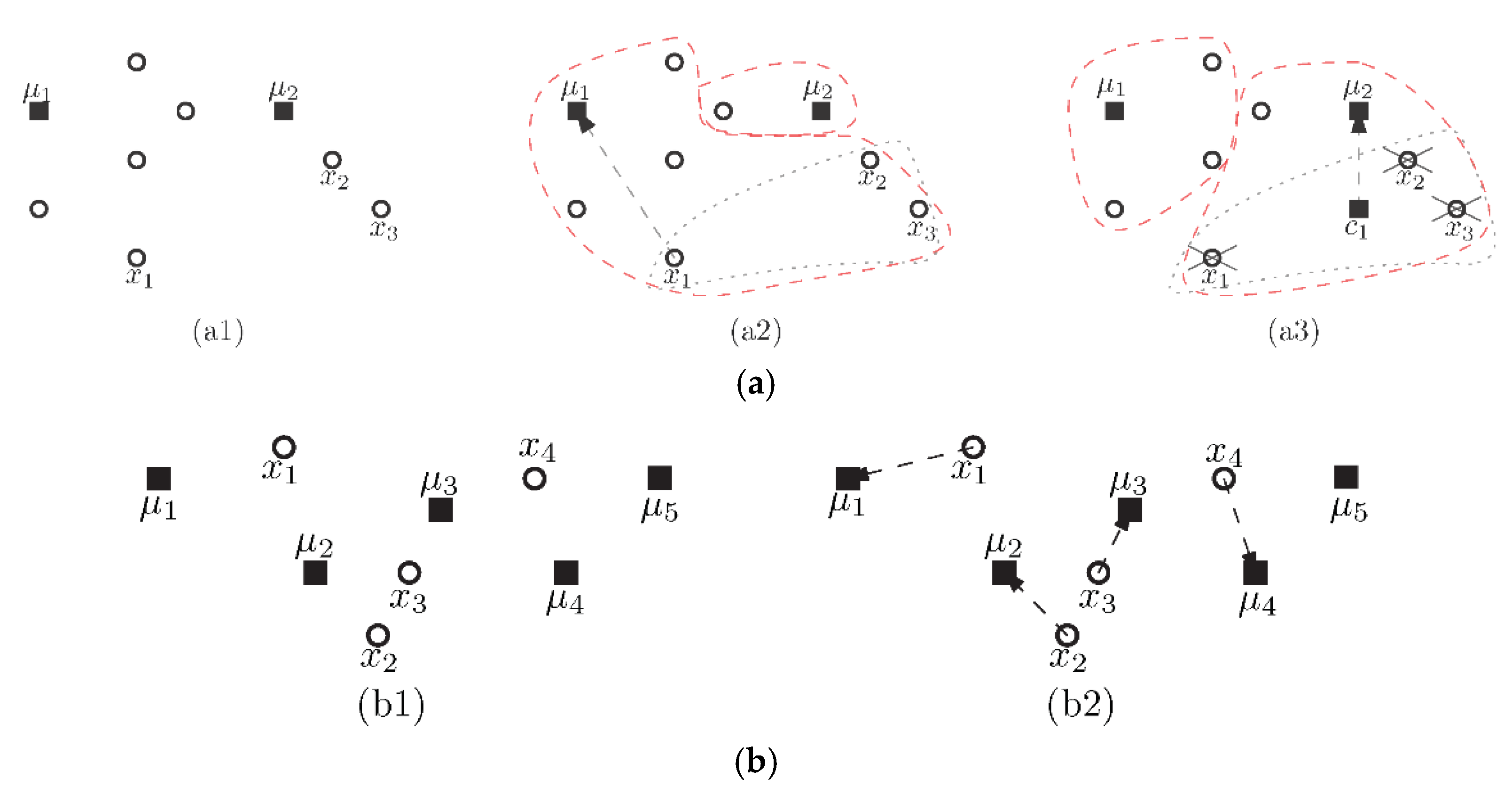
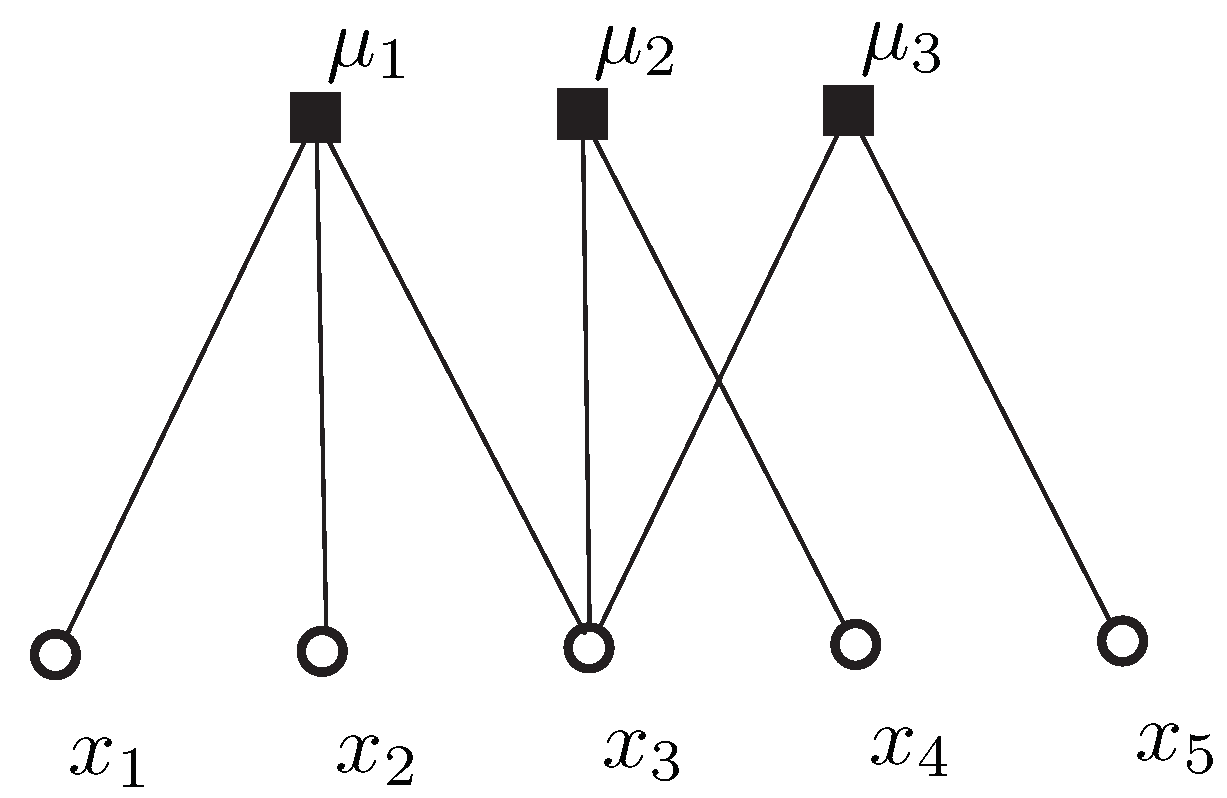
3. Constrained k-Means Clustering Algorithm with Incidental Information

In this section, for the constrained k-means problem (CKM) that is proposed by Wagstaff et al. [20], we propose an algorithm to solve this problem. Though there exists an algorithm that has been proposed in [20], a bad cluster may be found for some sample points, which satisfies the must-link constraints since the algorithm does not consider the domain knowledge of the given dataset. Therefore, we propose an algorithm to deal with the must-link constraint based on known domain knowledge. For a set of sample points with the cannot-link constraints, we solve it by using the minimum weight matching that is different to [20].

Given a set of sample points $V=\left\{x_1,\cdots ,x_n\right\}$. Let $U=\left\{{\mu }_1,\cdots ,{\mu }_m\right\}$ be the initial set of clusters. If a few sample points in V satisfy the must-link constraints, then these sample points must be divided into a group based on the transitivity of all constraints. Based on the above fact, we can compute the center of the set to replace the attribute value for all sample points of the set. Note that, when the sample point is allocated to a cluster, each sample point is allocated to the same cluster for the set. When a few sample points are with the cannot-link constraints, we can put these sample points into a set $V_1$, then all sample points of $V_1$ must be divided into different clusters based on the definition of cannot-link. Hence, there must exist $\left|V_1\right|\le k$, such that the distance between sample points $x_i\in V_1$ and cluster ${\mu }_i\in U$ can be employed as the attribute value of $x_i$. Before executing the main algorithm, we shall firstly preprocess the data points incident to the must-link and cannot-link constraints.

The key idea of our algorithm is to incorporate must-link and cannot-link constraints to the k-means++ framework. In general, we shall merge the set of data points confined by must-links as a single point and cluster the points of cannot-link separately after clustering other data points via employing minimum weight matching. Therefore, the algorithm mainly consists of iterations, where each iteration is composed of the three steps as follows: (1) embed the must-link constraints into the data points by merging the set of points confined by must-links as one point but with a weight equal to their weight sum; (2) employ the traditional k-means++ algorithm against the remaining data points, including the merged data points for must-link but excluding the points incident to cannot-links; (3) use the bipartite minimum-weight matching method to assign data points incident to cannot-link constraints to the clusters. The above steps will be repeated until the within-cluster sum of squares only decrease smaller than a given threshold $ϵ>0$. Then the formal layout of the algorithm is as described in Algorithm 1.

We illustrate an example of executing Algorithm 1 as in Figure 3. Figure 3a is the given data set $V=\left\{x_1,\cdots ,x_9\right\}$, in which the must-link constraint set is $\left\{x_1,x_2,x_3\right\}$ and the cannot-link constraint sets are $\left\{x_4,x_5\right\}$ and $\left\{x_6,x_9\right\}$. The first step is to compute the mass center for the data points incident to must-link constraints as in Figure 3b, in which $c_1$ is the center between $x_1,x_2$ and $x_3$ and we use $c_1$ to replace $x_1,x_2$ and $x_3$ as in Figure 3c. After that, we randomly select $k=2$ clusters (Figure 3d) that are $c_1$ and $x_9$. The clustering results are as shown in Figure 3e in which $C_1=\left\{c_1,x_4,x_6\right\}$ and $C_2=\left\{x_5,x_7,x_8,x_9\right\}$, where $c_1=\left\{x_1,x_2,x_3\right\}$. Later, recalculate a center for each $C_i$, obtaining the centers ${\mu }_1$ and ${\mu }_2$ for $C_1$ and $C_2$, respectively (Figure 3f). Then by the termination criteria, the clusters remain unchanged after re-assignment of the points to their nearest centers. Hence, the $k=2$ clusters are $C_1=\left\{x_1,x_2,x_3,x_4,x_6\right\}$ and $C_2=\left\{x_5,x_7,x_8,x_9\right\}$.

Algorithm 1 Constrained k-means clustering using domain information.

Input: A data set $V=\{x_1,x_2,\dots ,x_n\}$, must-link constraints $Co{n}_{=}\subseteq D\times D$, cannot-link constraints $Co{n}_{\ne }\subseteq D\times D$, a positive integer k; Output: A collection of k clusters $\mathcal{C}=\{C_1,C_2,\dots ,C_k\}$.  1: Use the k-center algorithm to select $c_1,c_2,\dots ,c_k$ as the initial cluster centers;  2: Set$C_i:=\varnothing ,(1\le i\le k)$;  3: While cluster centers change do  4:    For each set of must-link constraints do  5:        Compute mass center sample of the set;  6:        Assign all samples of the set to the nearest $c_i$;              /* Adding all samples of the set to $C_i$*/  7:    EndFor  8:    For $j=1,2,\dots ,n$ do  9:        Compute the distance $d_{ij}$ between point $x_i$ and cluster center $c_j$; 10:    EndFor 11:    Assign remaining points to their nearest $c_i$, except those incident to cannot-links; 12:    For each set of cannot-link constraint do 13:           Assign each point to the appropriate cluster via minimum weight matching; 14:    EndFor 15:    Compute the cluster center $c_i$ of $C_i$; 16: EndWhile 17: Return $\mathcal{C}=\{C_1,C_2,\dots ,C_k\}$.

4. Experimental Evaluation

In this section, we evaluate our improved constrained k-means algorithm (ICM) via comparing to baselines, including traditional k-means (TM) and constrained k-means (CM), respecting the external indicator’s Adjusted Rand Index (ARI). The experiments were run against datasets from the public UCI datasets. All the algorithms were implemented with Python 3.7, and the figures were drawn using matplotlib. For the external indicators ARI, we directly use the metrics.adjusted_rand_score method within sklearn library in Python to automatically calculate the clustering result. The experiments were carried out on a Win 10 platform with Intel Core i5-6200U CPU, 8.0G RAM.

4.1. Evaluation Approaches

In this subsection, we propose a method to evaluate the performance of our algorithm via comparing to other baselines. We adopt the performance metrics of clustering, which is known as validity metrics and is similar to the metrics of measuring the performance of supervised learning, to measure the quality of clustering results for our algorithm and the baseline algorithms in comparison.

For evaluating the clustering results, we use the following metrics for measurement: (1) the similarity for all sample points in the same cluster; (2) the difference among all sample points located in different clusters. The aim is such that higher similarity within cluster and higher difference among clusters indicate better clustering results. For the performance metric of clustering, there exists two types as follows: the first is an external indicator, which is obtained by comparing the experimental results of the cluster with a reference model; the other is an internal indicator that directly uses the clustering results to examine and without any other reference models. In this paper, the external indicators are used to evaluate the performance metric of clustering of our algorithm in a similar manner as in paper [20].

When the external indicators are used to evaluate our algorithm, an external reference model needs to be determined in advance. Let $V=\{x_1,x_2,\dots ,x_n\}$ be the given dataset, and $U^{*}=\{{\mu }_1^{*},{\mu }_2^{*},\dots ,{\mu }_k^{*}\}$ be the set of cluster centers that are produced by using the external reference model and $U=\{{\mu }_1,{\mu }_2,\dots ,{\mu }_k\}$ be also a set of clusters produced by an algorithm. We use $\lambda$ as the cluster center of U and ${\lambda }^{*}$ as $U^{*}$. Then each element of $U^{*}$ and each element of U can be matched as shown in the following:

$$\begin{array}{c}a=\left|SS\right|,SS=\left\{\left.\left(x_i,x_j\right)\right|{\lambda }_i={\lambda }_j,{\lambda }_i^{*}={\lambda }_j^{*},i<j\right\}\\ b=\left|SD\right|,SD=\left\{\left.\left(x_i,x_j\right)\right|{\lambda }_i={\lambda }_j,{\lambda }_i^{*}\ne {\lambda }_j^{*},i<j\right\}\\ c=\left|DS\right|,DS=\left\{\left.\left(x_i,x_j\right)\right|{\lambda }_i\ne {\lambda }_j,{\lambda }_i^{*}\doteq {\lambda }_j^{*},i<j\right\}\\ d=\left|DD\right|,DD=\left\{\left.\left(x_i,x_j\right)\right|{\lambda }_i\ne {\lambda }_j,{\lambda }_i^{*}\ne {\lambda }_j^{*},i<j\right\}\end{array}$$

where a is the length of $SS$, where $SS$ is a set of paired sample points, and $x_i$ and $x_j$ are clustered to the same cluster class in U and $U^{*}$ for each paired sample points $\left(x_i,x_j\right)\in SS$; Then b is also the length of a set of paired sample points $SD$, in which each paired sample points $\left(x_i,x_j\right)\in SD$ satisfies $x_i$ and $x_j$ are classified into the same cluster class in U while into different clusters in $U^{*}$. Similarly, c and d are respectively the lengths of $DS$ and $DD$. Furthermore, $\left(x_i,x_j\right)\in DS$ means $x_i$ and $x_j$ belong to two clusters for U and one cluster for $U^{*}$. $\left(x_i,x_j\right) \in DD$ shows that $x_i$ and $x_j$ must locate in different clusters of U and $U^{*}$. Hence, for each paired sample points, it only belongs to one of $SS,SD,DS$ and $DD$, such that we have the following formulation:

$$2(a+b+c+d)=m(m-1).$$

The Rand Index (RI) has been an indicator to evaluate the clustering results since 1997 due to Milligan and Cooper [29,30]. For a given dataset, we can use the RI to measure the consistency between the clustering results and the external reference model. Note that the value range of the RI is $[0,1]$. When $RI=1$, we obtain possibly the best clustering effect. In contrast, if $RI=0$, the clustering effect reaches the worst bottom. Formally, the RI can be defined as follows:

$$RI=\frac{2(a+b)}{m(m-1)}.$$

However, the coefficient value of the RI is obviously not a constant tending to zero. Therefore, we need the coefficient value of the RI such that the RI can also work when the coefficient value of the RI tends to zero. Hence, the Adjusted Rand Index (ARI) was proposed and its range is $[-1,1]$ [31]. Meanwhile, the clustering effect is more consistent with the reference model when the value is larger. In our paper, ARI is used to calculate accuracy for all of our experiments, which is formally defined as follows:

$$ARI=\frac{RI-E\left(RI\right)}{max\left(RI\right)-E\left(RI\right)}.$$

4.2. Experimental Dataset and Statistics Information

For each dataset, we use the result of 20 iterations as the final value in our experiments, which is obtained through the following steps: (1) Use Python to compute a value in each iteration; (2) calculate the ARI of each value; (3) take the average of all ARIs. Note that there exist a certain number of new constraints that are obtained after each iterate and will be added to the subsequent algorithm process for further procession.

In this paper, all datasets were selected from the UCI datasets, where each dataset contains at least one sample. Each sample contains a number of attributes, one of which may be a decision attribute. First of all, note that there may be some same or different decision attributes for different samples in one dataset. Second, the number of decision attributes is the same as the number of cluster classes in the dataset. In our algorithm, the must-link and cannot-link constraints are crucial, and they can be generated by the decision attributes, in which each must-link constraint comes from two samples that are with the same decision attribute; while each cannot-link constraint is also generated by two samples that have different decision attributes.

4.3. Comparison of Practical Performance

The first data set selected was Iris, which has 150 samples and 5 attributes, and will finally form 3 clusters. The results were demonstrated in

Table 1. Comparison of Adjusted Rand Index on dataset Iris.

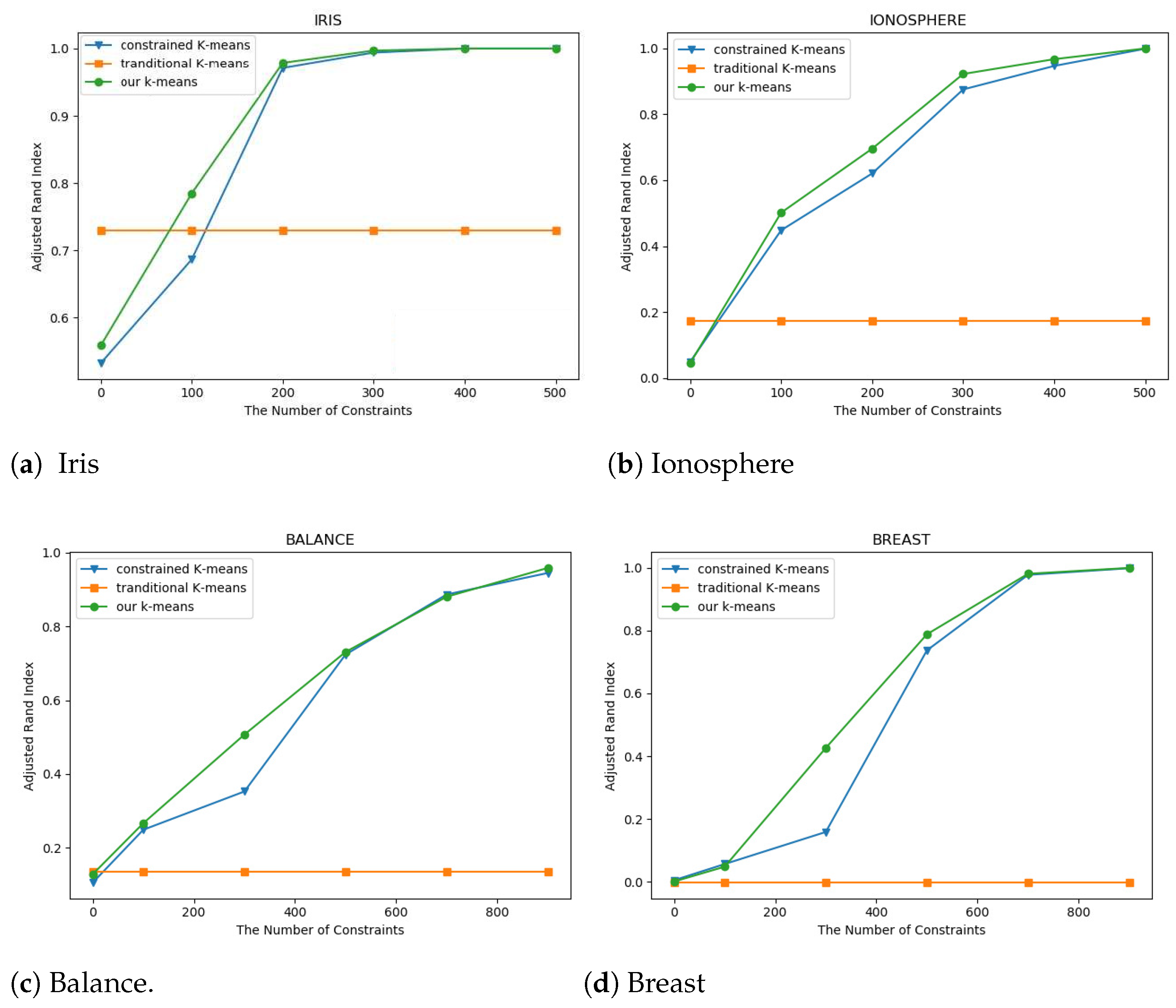
The Number of Constraints	100	200	300	400	500
CM	0.68669	0.97119	0.99399	1.00000	1.00000
TM	0.73023	0.73023	0.73023	0.73023	0.73023
ICM	0.78485	0.97860	0.99699	1.00000	1.00000

and Figure 4a. The number of constraints in the experiments increased from 100 to 500 by 100 at one step. For the constrained k-means algorithm and the improved constrained k-means algorithm, the accuracy of clustering is gradually increasing along the increment of the number of constraints. The reason is that more constraints indicate more information, which leads to better accuracy. The ARI of constrained k-means is always no more than the ARI of the improved constrained k-means when the number of constraints is less than 400. When the number of constraints is larger than 400, the ARI is identically 1 for both the constrained k-means algorithm and our improved constrained k-means algorithm. Hence, the accuracy of clustering attains 1 for both the two algorithms when the number of constraints is larger than 400 and enough domain knowledge is provided. The ARI of the traditional k-means algorithm is always 0.73023, which does not change with the number of constraints.

In the second dataset, Ionosphere, as illustrated in

Table 2. Comparison of Adjusted Rand Index on dataset Ionosphere.

The Number of Constraints	100	200	300	400	500
CM	0.44799	0.62021	0.87489	0.94606	0.99817
TM	0.17284	0.17284	0.17284	0.17284	0.17284
ICM	0.50131	0.69528	0.92172	0.96657	0.99908

and Figure 4b, the number of samples and the number of attributes are fixed at 351 and 34, respectively. After clustering, two cluster classes are eventually formed. The number of constraints of each group of Ionosphere is the same as that of Iris. It is very obvious that the ARI of the k-means algorithm is also always 0.17284. When the number of constraints is 100, the ARI of the constrained k-means is 0.44799 and it is 0.50131 for the improved constrained k-means. The ARIs are 0.99817 and 0.99908 for the constrained k-means and the improved constrained k-means, receptively. The accuracy of clustering for the improved constrained k-means is always larger than the constrained k-means that accords with our theoretical analysis.

The Balance dataset is our third selection dataset with 625 samples and 5 attributes, and eventually, 3 clusters will be found.

Table 3. Comparison of Adjusted Rand Index on dataset Balance.

The Number of Constraints	100	300	500	700	900
CM	0.24879	0.35256	0.72374	0.88657	0.94483
TM	0.13234	0.13234	0.13234	0.13234	0.13234
ICM	0.26650	0.50679	0.73070	0.88045	0.95854

and Figure 4c show the experimental results. The minimum number of constraints is 100 and the maximum is 900, and there exist five groups in our experiments. For the k-means algorithm, 0.13234 is its ARI value regardless of the number of constraints. When the number of constraints is 100, the ARI value of the constrained k-means is 0.24879 and the ARI value is 0.26650 for the improved constrained k-means, $0.24879<0.26650$ is true. When the number of constraints increases to 900, the ARI of the constrained k-means (0.94483) is also less than the improved constrained k-means (0.95854).

The fourth dataset we picked is Breast (

Table 4. Comparison of Adjusted Rand Index on dataset Breast.

The Number of Constraints	100	300	500	700	900
CM	0.05636	0.15859	0.73693	0.97761	0.99873
TM	−0.00268	−0.00268	−0.00268	−0.00268	−0.00268
ICM	0.04795	0.42613	0.78812	0.98097	0.99970

and Figure 4d). For the dataset, the numbers of samples and attributes are, respectively, 682 and 11 in our experiments, and there exist five cluster classes in total. The number of constraints for the Breast dataset is the same as the Balance dataset in each group experiment. The ARI of the traditional k-means is always less than 0, which is −0.00268, which means the clustering effect is very poor. When the number of constraints is 100, the ARI of the constrained k-means is 0.05636 and larger than the ARI of the improved constrained k-means (0.04795). The ARI of the constrained k-means is always less than the improved constrained k-means when the number of constraints is not less than 300. Importantly, the ART of the improved constrained k-means is very close to 1, with only a 0.0003 difference.

From the above four tables and four figures, we find that the ARI value increases with the number of constraints for the constrained k-means and the improved constrained k-means. That is, the clustering effect becomes better with the increase in constraints. The ARI of the improved constrained k-means algorithm is larger than the constrained k-means algorithm, so our algorithm can obtain better clustering results. Hence, the improved constrained k-means algorithm that we propose in this paper is successful.

4.4. Comparison of Runtime

Figure 5a demonstrates the runtimes of CM, TM, and ICM on Iris. When the number of constraints is not more than 320, the runtime of ICM is less than CM. Contrarily, the runtime of CM is smaller than ICM if the number of constraints is larger than 320. The runtime of TM is almost a straight line, which means the number of constraints has little effect on the runtime of TM, and the difference between the maximum and the minimum runtimes is 0.0018.

The runtimes of CM, TM, and ICM on Ionosphere are shown in Figure 5b. The runtimes of CM and ICM growth are slow when the number of constraints is not larger than 200, and after that, the runtime grows faster as the number of constraints increases. What is more, the runtime of CM is smaller than ICM when the number of constraints is less than 450. When the number of constraints increases to more than 450, the runtime of CM is larger than ICM. This means that our algorithm can be used to solve large-scale problems with more accurate results and a shorter time.

For Balance, the runtimes of CM, TM, and ICM are shown in Figure 5c. When the number of constraints is not larger than 500, the runtime of CM is smaller than ICM, and the difference between the runtimes of CM and ICM increases with the number of constraints. However, the difference is very small and is less than 1. Once the number of constraints exceeds 700, the runtime of ICM is smaller than CM, and the difference grows as the number of constraints increases, and the difference is 2.4629 when the number of constraints is 700.

The runtimes of CM, TM, and ICM on the Breast are shown in Figure 5d. When the number of constraints is less than 700, the gap between the runtimes of CM and ICM is very small and is less than 1. When the number of constraints exceeds 700, the runtime of CM is larger than ICM, and the gap between the two runtimes increases with the increase in the number of constraints.

5. Conclusions

In this paper, we first proposed a model for clustering with must-link and cannot-link constraints. Then, an algorithm incorporating side information were proposed to solve the constrained k-means clustering problem. The key idea of the algorithm is to repeat the following procession until satisfactory clustering of the data points is obtained: firstly, compute a mass center for the data points that are constrained by the must-links; secondly, collaborate the clustering against the unconstrained data as well as the must-link constrained data, while ignoring the data points involved by the cannot-links; and thirdly, to transform the task into the problem of finding a minimum weight matching in a bipartite graph regarding the cannot-link constraints. Lastly, we carried out numerical experiments against four UCI datasets: Iris, Ionosphere, Balance and Breast, demonstrating the practical gain of our algorithm compared with traditional k-means as well as the constrained k-means proposed by Wagstaff [20].