Combined Influence of Nutrient Supply Level and Tissue Mechanical Properties on Benign Tumor Growth as Revealed by Mathematical Modeling
Abstract
:1. Introduction
2. Model
2.1. Full System
2.2. Infinite Hydraulic Conductivity Limit
2.3. Parameters
| Parameter | Description | Estimated Value | Model Value | Based On |
|---|---|---|---|---|
| For the full model and the limit: | ||||
| B | tumor cells proliferation rate | 0.03 h−1 | 0.03 | [36] |
| M | tumor cells death rate | 0.003 h−1 | 0.003 | [37] + see text |
| P | nutrient supply level | s−1 | 4 & varied | [29] + see text |
| glucose diffusion coefficient | cm2/s | 100 | [39] | |
| rate of glucose consumption by proliferating cells | 24 | [36] | ||
| rate of glucose consumption by quiescent cells | 0.5 | see text | ||
| initial fraction of cells | 0.8 | 0.8 | [20] | |
| critical level of glucose for tumor cell proliferation | 0.55 mM | 0.1 | see text | |
| critical level of glucose for tumor cell survival | 0.055 mM | 0.01 | see text | |
| Heaviside smoothing parameter | – | 1000 (numerical)/ ∞ (analytical) | see text | |
| initial radius of tissue region | 1 cm | 100 (num. + an. full)/ ∞ (an. limit) | see text | |
| Only for the full model: | ||||
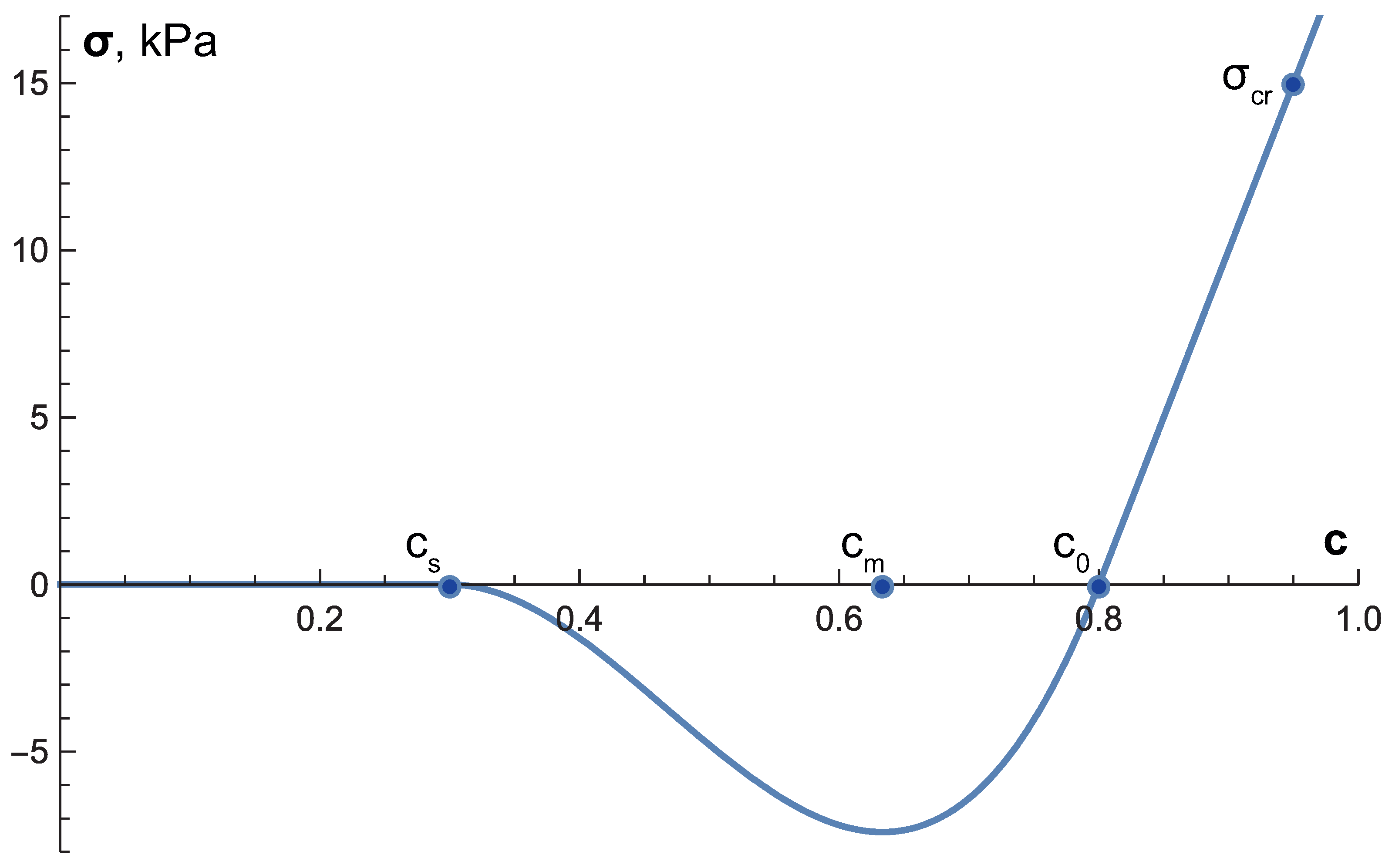
| critical stress for cell proliferation | 15 kPa | 15 | [9] + see text | |
| tissue hydraulic conductivity | 3 & varied | [40] + see text | ||
| k | solid stress function coefficient | 100 kPa | 100 | [9] |
| minimum cell-sensing cell fraction | 0.3 | 0.3 | [20] | |
2.4. Numerical Solving
3. Estimation of Growth Curves in the Limit of Infinite Tissue Hydraulic Conductivity
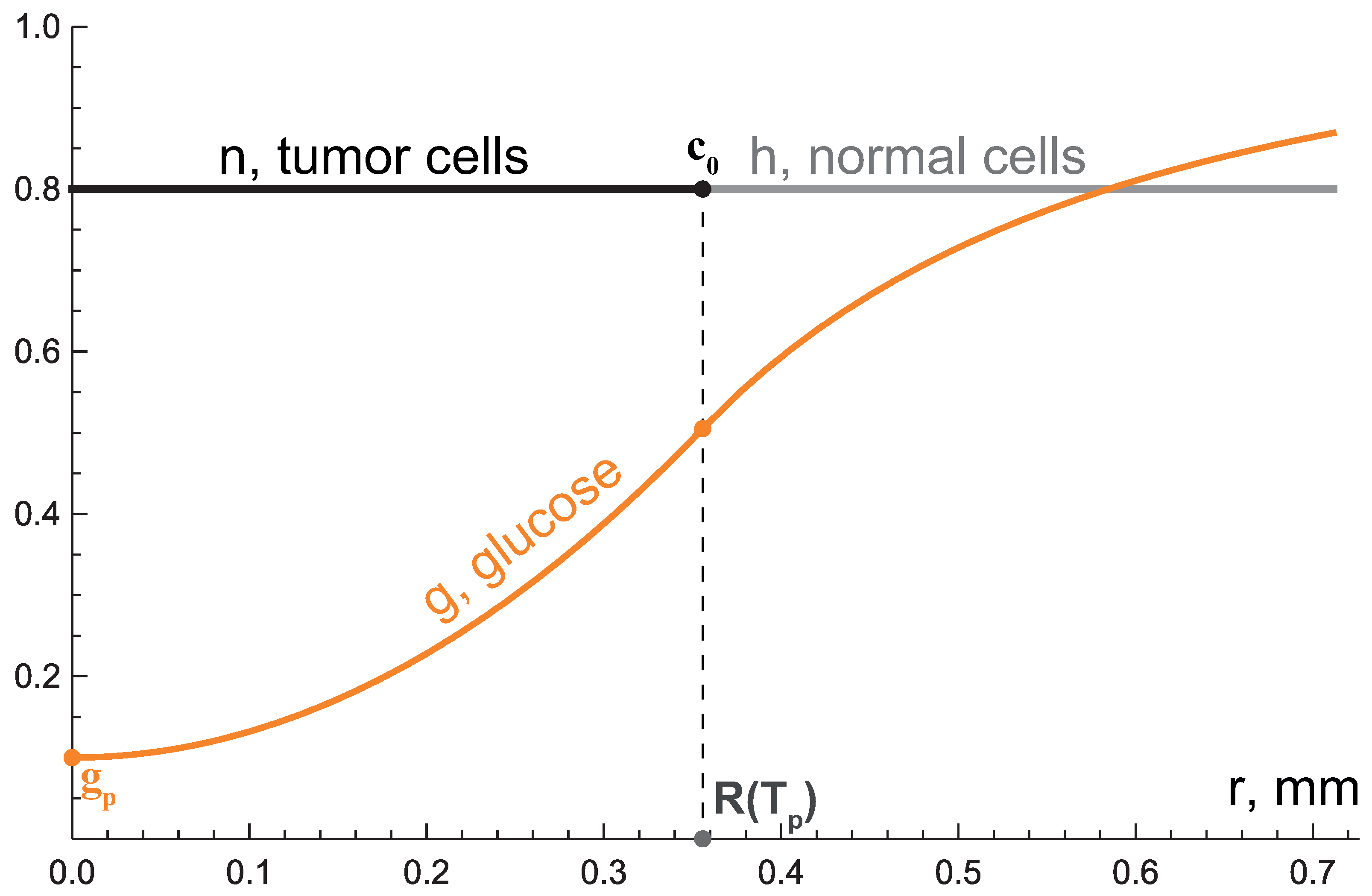
3.1. First Growth Stage: Exponential Phase
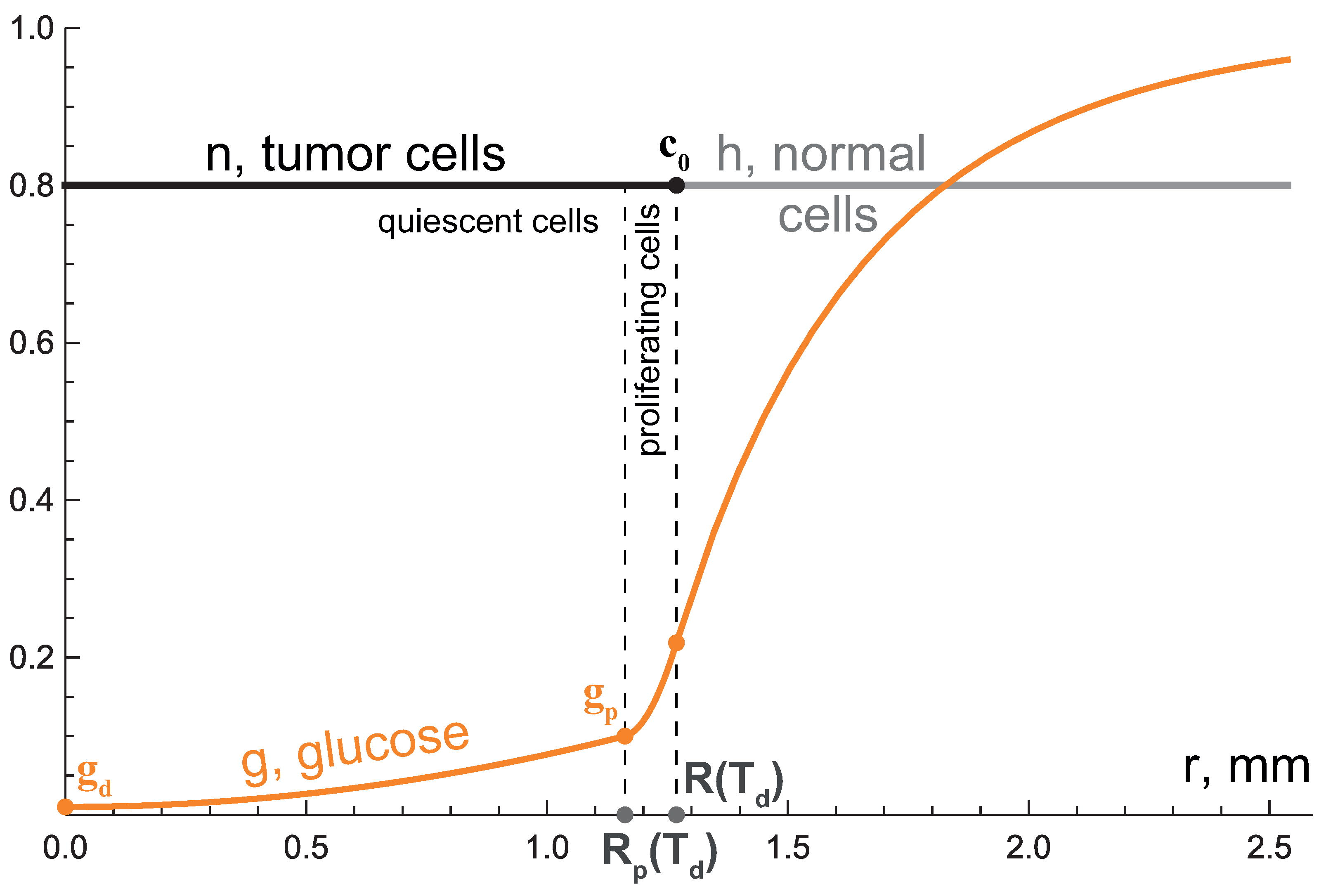
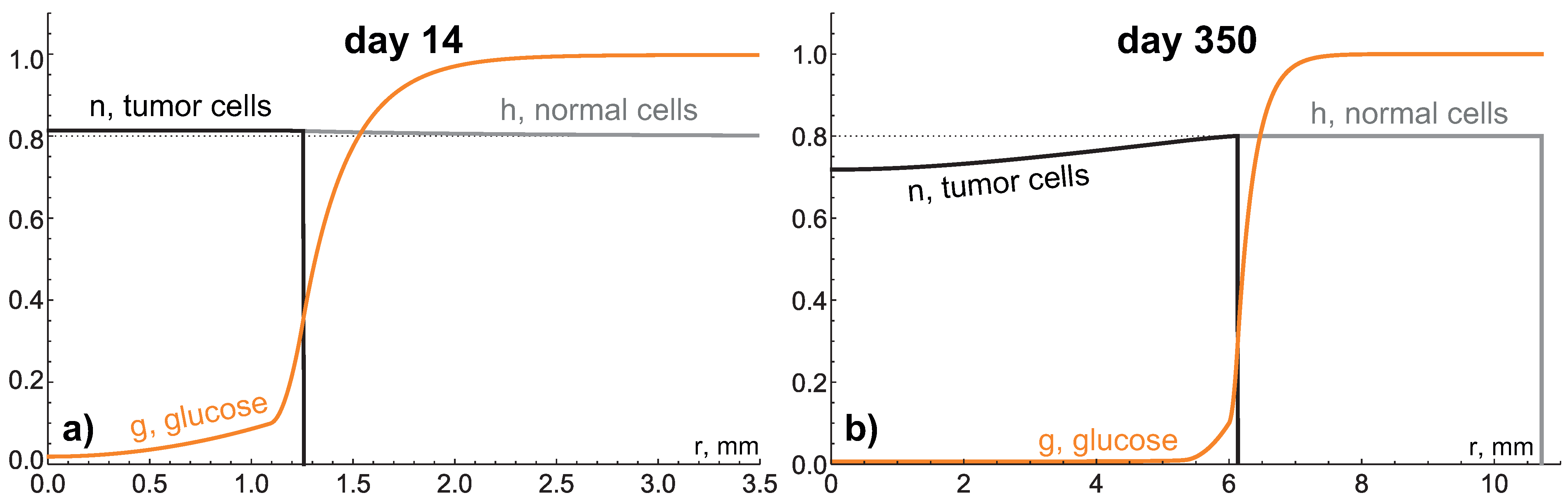
3.2. Second Growth Stage: Two-Layered Tumor
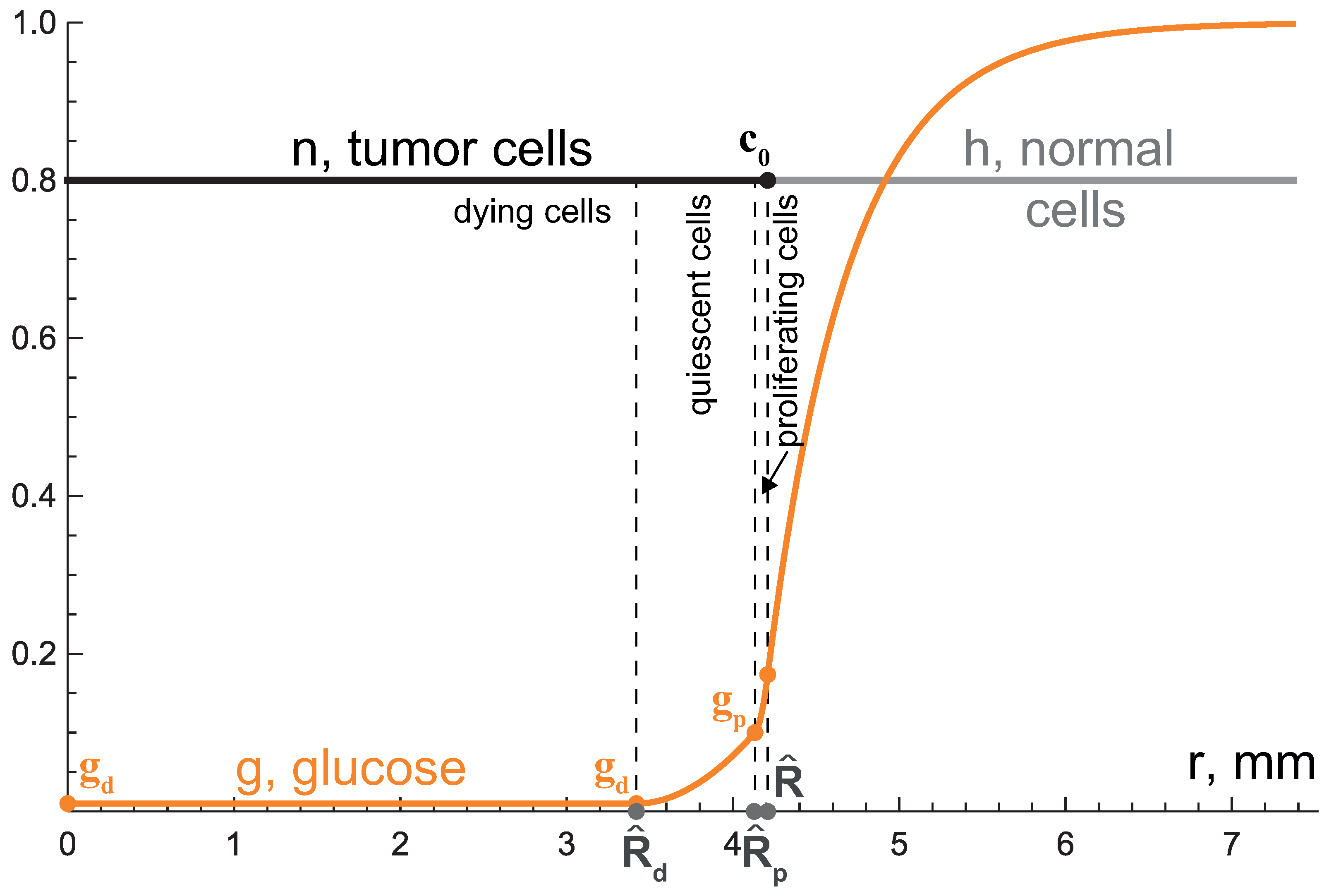
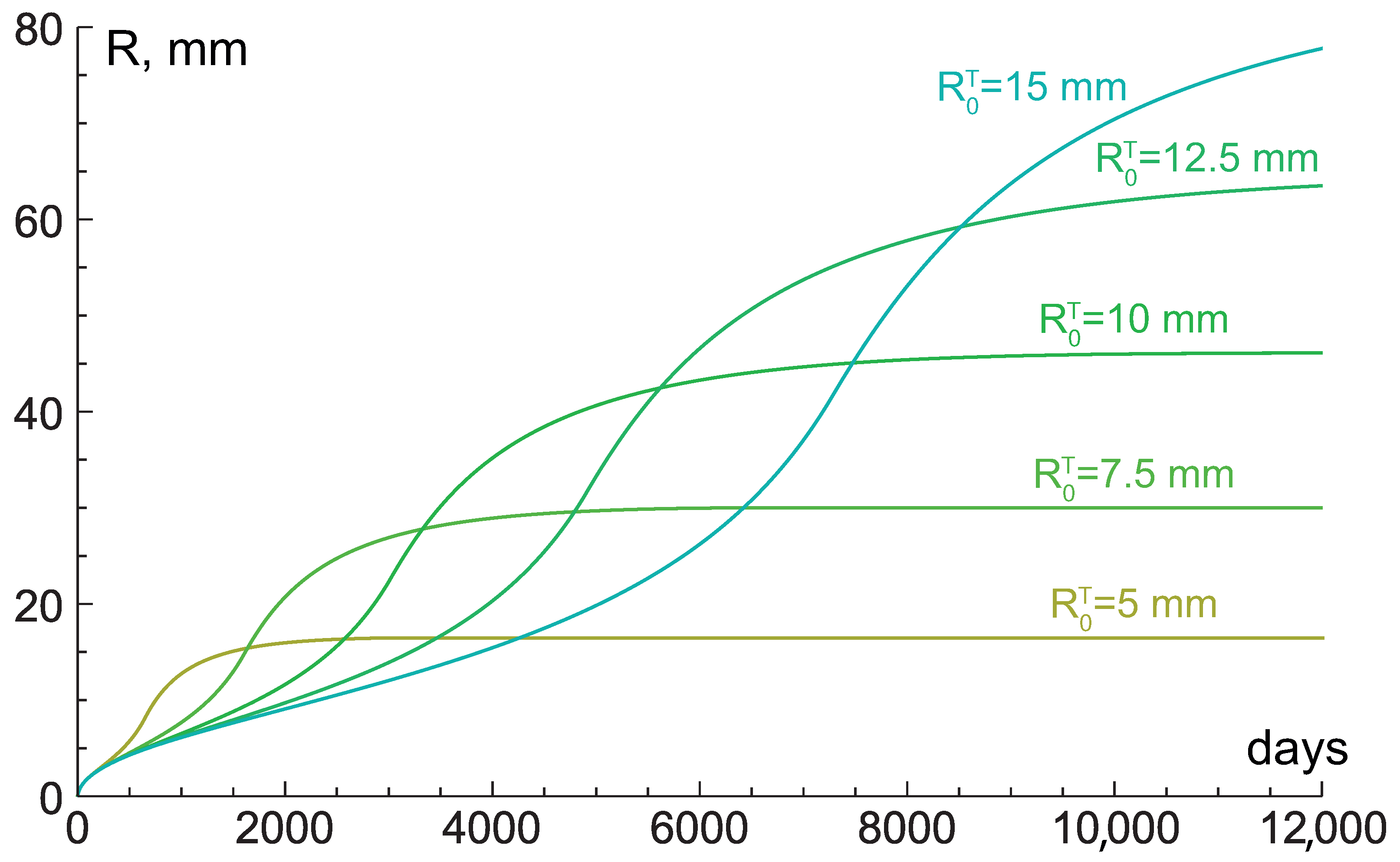
3.3. Third Growth Stage: Tending to Plateau
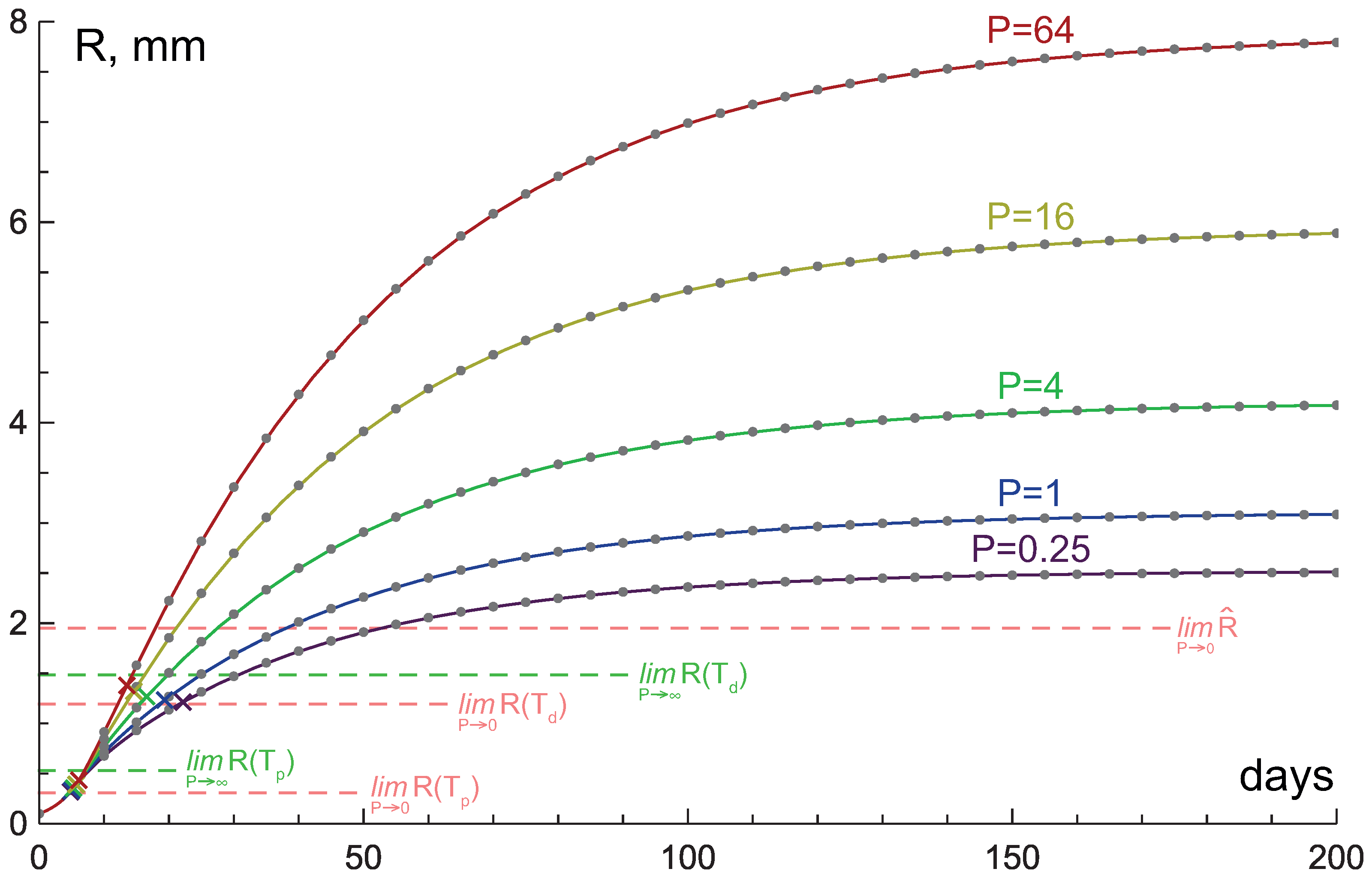
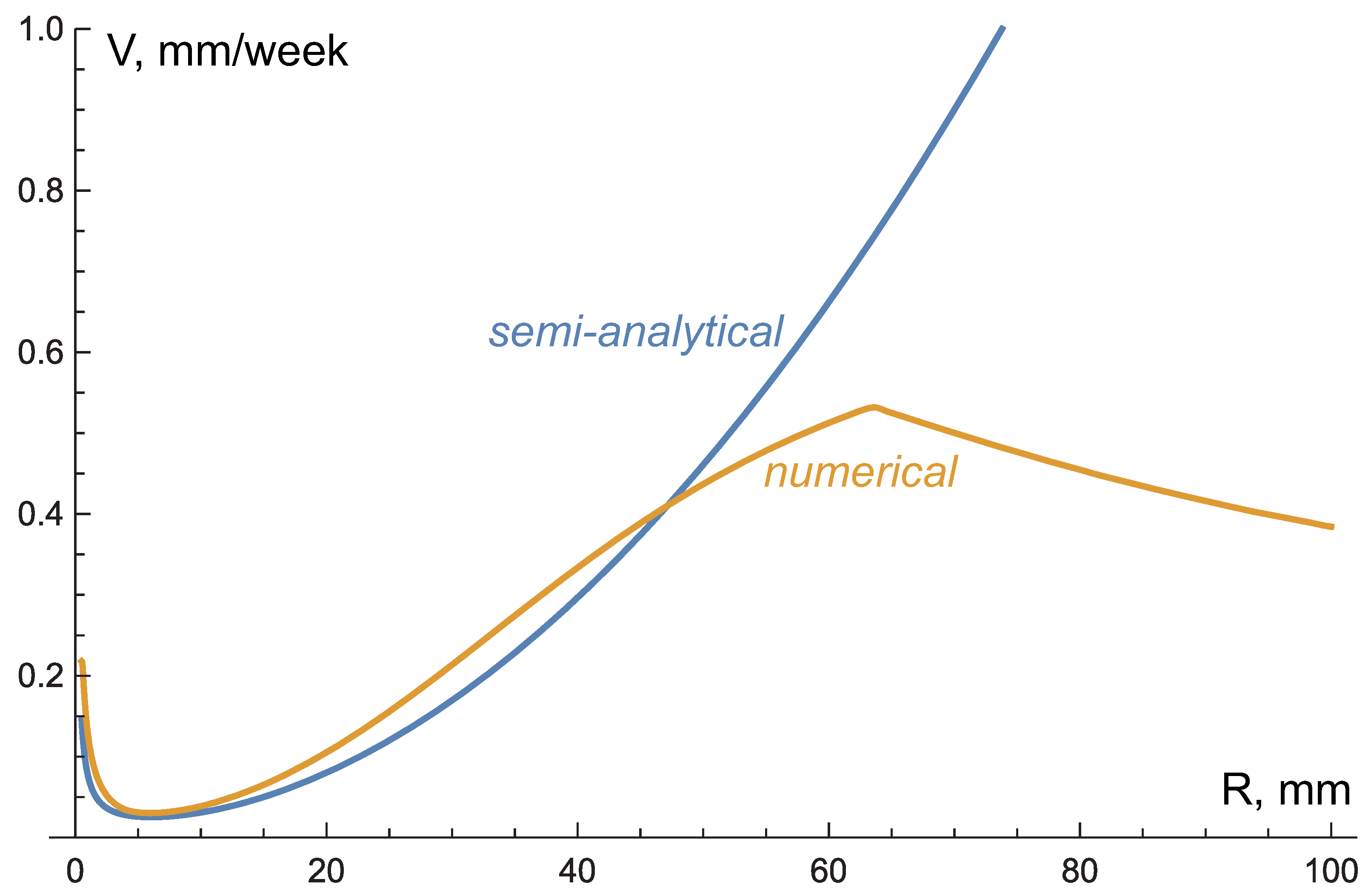
3.4. Comparison with Numerical Simulations
4. Study of Influence of Tissue Hydraulic Conductivity and Nutrient Supply Level on Tumor Growth
4.1. High Hydraulic Conductivity: When the Infinite Hydraulic Conductivity Limit Is Applicable
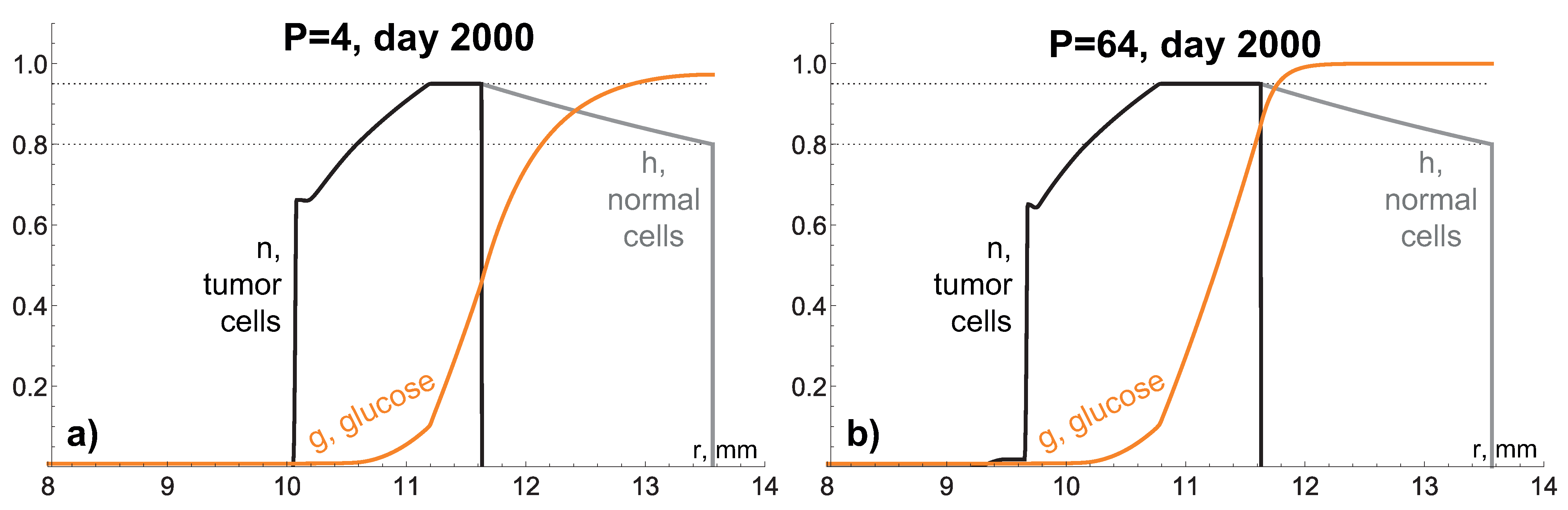
4.2. Intermediate Hydraulic Conductivity: Fluid-Filled Core Forms under High Nutrient Inflow Level
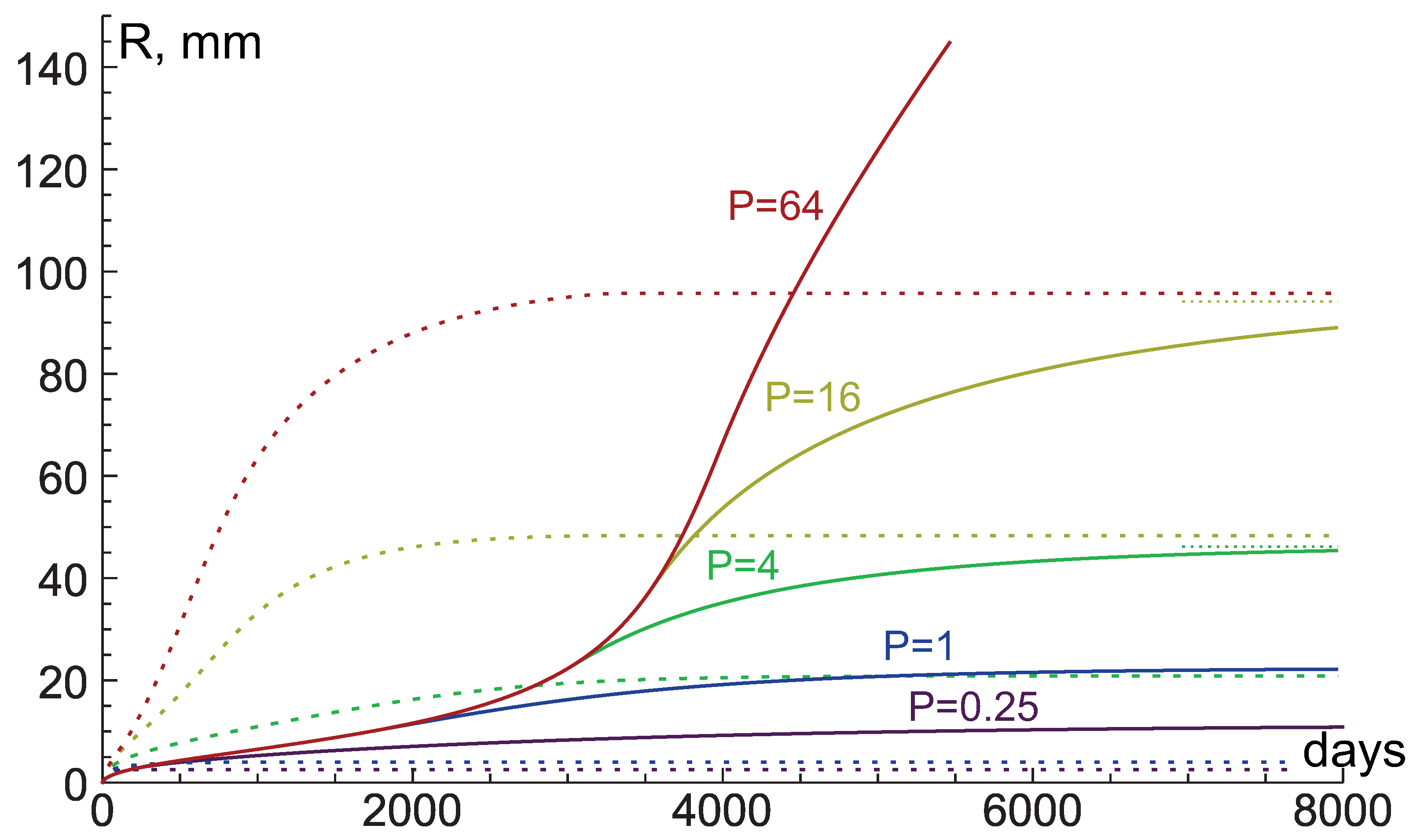
4.3. Low Hydraulic Conductivity: Crucial Condition for Giant Benign Tumors
4.4. Very Low Hydraulic Conductivity: Stress-Induced Growth Restriction and Explosive Acceleration
5. Discussion
5.1. Biological Relevance of the Results
5.2. Prospects of the Model Development
Supplementary Materials
Funding
Conflicts of Interest
Appendix A. Estimations of Glucose Distributions for the Tumor Growth Curves Approximations
References
- Hanahan, D.; Weinberg, R.A. The hallmarks of cancer. Cell 2000, 100, 57–70. [Google Scholar] [CrossRef] [Green Version]
- Sutherland, R.M.; McCredie, J.A.; Inch, W.R. Growth of multicell spheroids in tissue culture as a model of nodular carcinomas. J. Natl. Cancer Inst. 1971, 46, 113–120. [Google Scholar] [PubMed]
- Freyer, J.; Tustanoff, E.; Franko, A.; Sutherland, R. In situ oxygen consumption rates of cells in V-79 multicellular spheroids during growth. J. Cell. Physiol. 1984, 118, 53–61. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, H.; Siems, W.; Müller, M.; Dumdey, R.; Rapoport, S.M. ATP-producing and consuming processes of Ehrlich mouse ascites tumor cells in proliferating and resting phases. Exp. Cell Res. 1991, 194, 122–127. [Google Scholar] [CrossRef]
- Ward, J.P.; King, J. Mathematical modelling of avascular-tumour growth II: Modelling growth saturation. Math. Med. Biol. A J. IMA 1999, 16, 171–211. [Google Scholar] [CrossRef]
- Hahnfeldt, P.; Panigrahy, D.; Folkman, J.; Hlatky, L. Tumor development under angiogenic signaling: A dynamical theory of tumor growth, treatment response, and postvascular dormancy. Cancer Res. 1999, 59, 4770–4775. [Google Scholar] [PubMed]
- Lazebnik, Y. What are the hallmarks of cancer? Nat. Rev. Cancer 2010, 10, 232–233. [Google Scholar] [CrossRef]
- Helmlinger, G.; Netti, P.A.; Lichtenbeld, H.C.; Melder, R.J.; Jain, R.K. Solid stress inhibits the growth of multicellular tumor spheroids. Nat. Biotechnol. 1997, 15, 778–783. [Google Scholar] [CrossRef] [PubMed]
- Mascheroni, P.; Stigliano, C.; Carfagna, M.; Boso, D.P.; Preziosi, L.; Decuzzi, P.; Schrefler, B.A. Predicting the growth of glioblastoma multiforme spheroids using a multiphase porous media model. Biomech. Model. Mechanobiol. 2016, 15, 1215–1228. [Google Scholar] [CrossRef] [PubMed]
- Seano, G.; Nia, H.T.; Emblem, K.E.; Datta, M.; Ren, J.; Krishnan, S.; Kloepper, J.; Pinho, M.C.; Ho, W.W.; Ghosh, M.; et al. Solid stress in brain tumours causes neuronal loss and neurological dysfunction and can be reversed by lithium. Nat. Biomed. Eng. 2019, 3, 230–245. [Google Scholar] [CrossRef]
- Demou, Z.N. Gene expression profiles in 3D tumor analogs indicate compressive strain differentially enhances metastatic potential. Ann. Biomed. Eng. 2010, 38, 3509–3520. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.Y.; Wu, C.H.; Hung, T.W.; Wang, C.J. Endoplasmic reticulum stress-induced resistance to doxorubicin is reversed by mulberry leaf polyphenol extract in hepatocellular carcinoma through inhibition of COX-2. Antioxidants 2020, 9, 26. [Google Scholar] [CrossRef] [Green Version]
- Chauhan, V.P.; Martin, J.D.; Liu, H.; Lacorre, D.A.; Jain, S.R.; Kozin, S.V.; Stylianopoulos, T.; Mousa, A.S.; Han, X.; Adstamongkonkul, P.; et al. Angiotensin inhibition enhances drug delivery and potentiates chemotherapy by decompressing tumour blood vessels. Nat. Commun. 2013, 4, 2516. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mascheroni, P.; Boso, D.; Preziosi, L.; Schrefler, B.A. Evaluating the influence of mechanical stress on anticancer treatments through a multiphase porous media model. J. Theor. Biol. 2017, 421, 179–188. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mpekris, F.; Voutouri, C.; Papageorgis, P.; Stylianopoulos, T. Stress alleviation strategy in cancer treatment: Insights from a mathematical model. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mechanik 2018, 98, 2295–2306. [Google Scholar] [CrossRef]
- Mascheroni, P.; López Alfonso, J.C.; Kalli, M.; Stylianopoulos, T.; Meyer-Hermann, M.; Hatzikirou, H. On the impact of chemo-mechanically induced phenotypic transitions in gliomas. Cancers 2019, 11, 716. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Byrne, H.M.; King, J.R.; McElwain, D.S.; Preziosi, L. A two-phase model of solid tumour growth. Appl. Math. Lett. 2003, 16, 567–573. [Google Scholar] [CrossRef]
- Franks, S.; King, J. Interactions between a uniformly proliferating tumour and its surroundings: Uniform material properties. Math. Med. Biol. 2003, 20, 47–89. [Google Scholar] [CrossRef]
- Jones, A.; Byrne, H.; Gibson, J.; Dold, J. A mathematical model of the stress induced during avascular tumour growth. J. Math. Biol. 2000, 40, 473–499. [Google Scholar] [CrossRef] [PubMed]
- Byrne, H.; Preziosi, L. Modelling solid tumour growth using the theory of mixtures. Math. Med. Biol. J. IMA 2003, 20, 341–366. [Google Scholar] [CrossRef]
- Lewin, T.D.; Maini, P.K.; Moros, E.G.; Enderling, H.; Byrne, H.M. A three phase model to investigate the effects of dead material on the growth of avascular tumours. Math. Model. Nat. Phenom. 2020, 15, 22. [Google Scholar] [CrossRef] [Green Version]
- Voutouri, C.; Mpekris, F.; Papageorgis, P.; Odysseos, A.D.; Stylianopoulos, T. Role of constitutive behavior and tumor-host mechanical interactions in the state of stress and growth of solid tumors. PLoS ONE 2014, 9, e104717. [Google Scholar] [CrossRef] [PubMed]
- Stylianopoulos, T.; Martin, J.D.; Snuderl, M.; Mpekris, F.; Jain, S.R.; Jain, R.K. Coevolution of solid stress and interstitial fluid pressure in tumors during progression: Implications for vascular collapse. Cancer Res. 2013, 73, 3833–3841. [Google Scholar] [CrossRef] [Green Version]
- Preziosi, L.; Vitale, G. A multiphase model of tumor and tissue growth including cell adhesion and plastic reorganization. Math. Model. Methods Appl. Sci. 2011, 21, 1901–1932. [Google Scholar] [CrossRef]
- Mascheroni, P.; Carfagna, M.; Grillo, A.; Boso, D.; Schrefler, B.A. An avascular tumor growth model based on porous media mechanics and evolving natural states. Math. Mech. Solids 2018, 23, 686–712. [Google Scholar] [CrossRef]
- Preziosi, L.; Ambrosi, D.; Verdier, C. An elasto-visco-plastic model of cell aggregates. J. Theor. Biol. 2010, 262, 35–47. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vander Heiden, M.G.; Cantley, L.C.; Thompson, C.B. Understanding the Warburg effect: The metabolic requirements of cell proliferation. Science 2009, 324, 1029–1033. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pinder, G.F.; Gray, W.G. Essentials of Multiphase Flow and Transport in Porous Media; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Levick, J.R. An Introduction to Cardiovascular Physiology; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Holash, J.; Maisonpierre, P.; Compton, D.; Boland, P.; Alexander, C.; Zagzag, D.; Yancopoulos, G.; Wiegand, S. Vessel cooption, regression, and growth in tumors mediated by angiopoietins and VEGF. Science 1999, 284, 1994–1998. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baumgartner, W.; Hinterdorfer, P.; Ness, W.; Raab, A.; Vestweber, D.; Schindler, H.; Drenckhahn, D. Cadherin interaction probed by atomic force microscopy. Proc. Natl. Acad. Sci. USA 2000, 97, 4005–4010. [Google Scholar] [CrossRef] [Green Version]
- Kuznetsov, M.; Kolobov, A. Transient alleviation of tumor hypoxia during first days of antiangiogenic therapy as a result of therapy-induced alterations in nutrient supply and tumor metabolism—Analysis by mathematical modeling. J. Theor. Biol. 2018, 451, 86–100. [Google Scholar] [CrossRef]
- Kuznetsov, M.; Kolobov, A. Investigation of solid tumor progression with account of proliferation/migration dichotomy via Darwinian mathematical model. J. Math. Biol. 2020, 80, 601–626. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, M. Mathematical modeling shows that the response of a solid tumor to antiangiogenic therapy depends on the type of growth. Mathematics 2020, 8, 760. [Google Scholar] [CrossRef]
- Kuznetsov, M.; Kolobov, A. Optimization of Dose Fractionation for Radiotherapy of a Solid Tumor with Account of Oxygen Effect and Proliferative Heterogeneity. Mathematics 2020, 8, 1204. [Google Scholar] [CrossRef]
- Freyer, J.; Sutherland, R. A reduction in the in situ rates of oxygen and glucose consumption of cells in EMT6/Ro spheroids during growth. J. Cell. Physiol. 1985, 124, 516–524. [Google Scholar] [CrossRef] [PubMed]
- Izuishi, K.; Kato, K.; Ogura, T.; Kinoshita, T.; Esumi, H. Remarkable tolerance of tumor cells to nutrient deprivation: Possible new biochemical target for cancer therapy. Cancer Res. 2000, 60, 6201–6207. [Google Scholar] [PubMed]
- Sonveaux, P.; Végran, F.; Schroeder, T.; Wergin, M.C.; Verrax, J.; Rabbani, Z.N.; De Saedeleer, C.J.; Kennedy, K.M.; Diepart, C.; Jordan, B.F.; et al. Targeting lactate-fueled respiration selectively kills hypoxic tumor cells in mice. J. Clin. Investig. 2008, 118, 3930–3942. [Google Scholar] [CrossRef] [Green Version]
- Tuchin, V.; Bashkatov, A.; Genina, E.; Sinichkin, Y.P.; Lakodina, N. In vivo investigation of the immersion-liquid-induced human skin clearing dynamics. Tech. Phys. Lett. 2001, 27, 489–490. [Google Scholar] [CrossRef]
- Netti, P.A.; Berk, D.A.; Swartz, M.A.; Grodzinsky, A.J.; Jain, R.K. Role of extracellular matrix assembly in interstitial transport in solid tumors. Cancer Res. 2000, 60, 2497–2503. [Google Scholar]
- Fu, B.M.; Shen, S. Structural mechanisms of acute VEGF effect on microvessel permeability. Am. J. Physiol. Heart Circ. Physiol. 2003, 284, H2124–H2135. [Google Scholar] [CrossRef] [Green Version]
- Dickson, P.V.; Hamner, J.B.; Sims, T.L.; Fraga, C.H.; Ng, C.Y.; Rajasekeran, S.; Hagedorn, N.L.; McCarville, M.B.; Stewart, C.F.; Davidoff, A.M. Bevacizumab-induced transient remodeling of the vasculature in neuroblastoma xenografts results in improved delivery and efficacy of systemically administered chemotherapy. Clin. Cancer Res. 2007, 13, 3942–3950. [Google Scholar] [CrossRef] [Green Version]
- Pyaskovskaya, O.; Kolesnik, D.; Kolobov, A.; Vovyanko, S.; Solyanik, G. Analysis of growth kinetics and proliferative heterogeneity of Lewis lung carcinoma cells growing as unfed culture. Exp. Oncol. 2008, 30, 269–275, PMID: 19112423. [Google Scholar]
- Stylianopoulos, T.; Martin, J.D.; Chauhan, V.P.; Jain, S.R.; Diop-Frimpong, B.; Bardeesy, N.; Smith, B.L.; Ferrone, C.R.; Hornicek, F.J.; Boucher, Y.; et al. Causes, consequences, and remedies for growth-induced solid stress in murine and human tumors. Proc. Natl. Acad. Sci. USA 2012, 109, 15101–15108. [Google Scholar] [CrossRef] [Green Version]
- Akers, T.K. Physiological Effects of Pressure on Cell Function. In Cell Physiology Source Book; Elsevier: Amsterdam, The Netherlands, 1995; pp. 655–662. [Google Scholar]
- Zhang, X.Y.; Luck, J.; Dewhirst, M.W.; Yuan, F. Interstitial hydraulic conductivity in a fibrosarcoma. Am. J. Physiol. Heart Circ. Physiol. 2000, 279, H2726–H2734. [Google Scholar] [CrossRef] [PubMed]
- Boris, J.P.; Book, D.L. Flux-corrected transport. I. SHASTA, a fluid transport algorithm that works. J. Comput. Phys. 1973, 11, 38–69. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes 3rd Edition: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Likhitmaskul, T.; Asanprakit, W.; Charoenthammaraksa, S.; Lohsiriwat, V.; Supaporn, S.; Vassanasiri, W.; Sattaporn, S. Giant benign phyllodes tumor with lactating changes in pregnancy: A case report. Gland Surg. 2015, 4, 339. [Google Scholar] [PubMed]
- Udapudi, D.G.; Vasudeva, P.; Srikantiah, R.; Virupakshappa, E. Massive benign phyllodes tumor. Breast J. 2005, 11, 521. [Google Scholar] [CrossRef] [PubMed]
- Viva, W.; Juhi, D.; Kristin, A.; Micaela, M.; Marcus, B.; Ibrahim, A.; Dirk, B. Massive uterine fibroid: A diagnostic dilemma: A case report and review of the literature. J. Med. Case Rep. 2021, 15, 1–6. [Google Scholar] [CrossRef]
- Moravek, M.B.; Yin, P.; Ono, M.; Coon V, J.S.; Dyson, M.T.; Navarro, A.; Marsh, E.E.; Chakravarti, D.; Kim, J.J.; Wei, J.J.; et al. Ovarian steroids, stem cells and uterine leiomyoma: Therapeutic implications. Hum. Reprod. Update 2015, 21, 1–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laufer, J.; Augarten, A.; Szeinberg, A.; Engelberg, S. Pathological case of the month. Arch. Pediatr. Adolesc. Med. 1994, 148, 1067–1068. [Google Scholar] [CrossRef] [PubMed]
- Mollitt, D.L.; Golladay, E.S.; Gloster, E.S.; Jimenez, J.F. Cystosarcoma phylloides in the adolescent female. J. Pediatr. Surg. 1987, 22, 907–910. [Google Scholar] [CrossRef]
- Casciari, J.; Sotirchos, S.; Sutherland, R. Mathematical modelling of microenvironment and growth in EMT6/Ro multicellular tumour spheroids. Cell Prolif. 1992, 25, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Kessenbrock, K.; Plaks, V.; Werb, Z. Matrix metalloproteinases: Regulators of the tumor microenvironment. Cell 2010, 141, 52–67. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Räsänen, K.; Vaheri, A. Activation of fibroblasts in cancer stroma. Exp. Cell Res. 2010, 316, 2713–2722. [Google Scholar] [CrossRef] [PubMed]
- Wijeratne, P.A.; Vavourakis, V.; Hipwell, J.H.; Voutouri, C.; Papageorgis, P.; Stylianopoulos, T.; Evans, A.; Hawkes, D.J. Multiscale modelling of solid tumour growth: The effect of collagen micromechanics. Biomech. Model. Mechanobiol. 2016, 15, 1079–1090. [Google Scholar] [CrossRef] [PubMed] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuznetsov, M. Combined Influence of Nutrient Supply Level and Tissue Mechanical Properties on Benign Tumor Growth as Revealed by Mathematical Modeling. Mathematics 2021, 9, 2213. https://doi.org/10.3390/math9182213
Kuznetsov M. Combined Influence of Nutrient Supply Level and Tissue Mechanical Properties on Benign Tumor Growth as Revealed by Mathematical Modeling. Mathematics. 2021; 9(18):2213. https://doi.org/10.3390/math9182213
Chicago/Turabian StyleKuznetsov, Maxim. 2021. "Combined Influence of Nutrient Supply Level and Tissue Mechanical Properties on Benign Tumor Growth as Revealed by Mathematical Modeling" Mathematics 9, no. 18: 2213. https://doi.org/10.3390/math9182213
APA StyleKuznetsov, M. (2021). Combined Influence of Nutrient Supply Level and Tissue Mechanical Properties on Benign Tumor Growth as Revealed by Mathematical Modeling. Mathematics, 9(18), 2213. https://doi.org/10.3390/math9182213






