Efficiency Evaluation of Regional Environmental Management Systems in Russia Using Data Envelopment Analysis
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. DEA Background
3.2. Weights Restrictions
3.3. Non-Radial Model
3.4. Weight Restrictions Adjustment
| Input: Inputs and outputs for all DMUs |
| Output: Efficiency scores |
| 1: procedureAdjustWeightRestrictions |
| 2: Set initial weight restrictions and solve CCR-AR model (4) and (5) |
| 3: if DM does not agree with efficiency scores of some DMUs then |
| 4: do |
| 5: Construct sections of the frontier for these DMUs |
| 6: Identify the reasons for inconsistencies |
| 7: Determine new weights restrictions and solve CCR-AR model |
| 8: while The efficiency scores are not following the DM’s opinion |
| 9: end if |
| 10: end procedure |
4. Empirical Analysis
4.1. Data Source and Variables Selection
4.2. Weights Selection
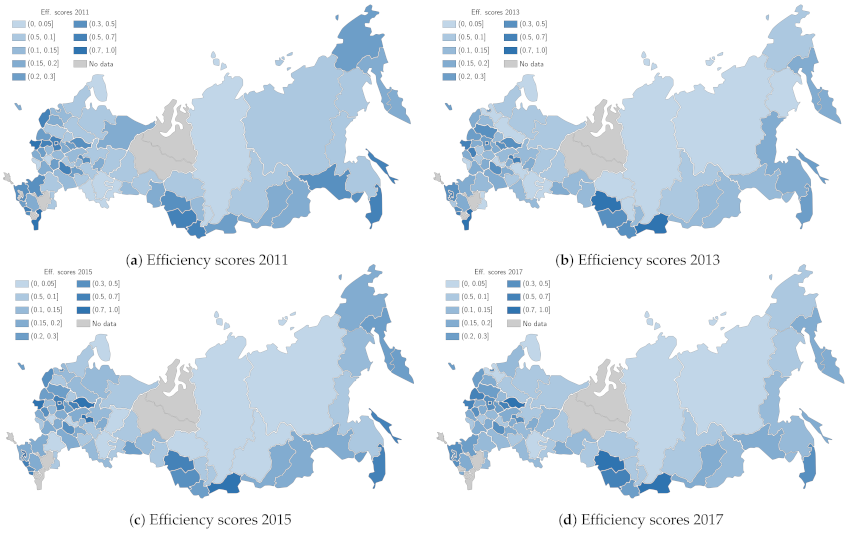
4.3. DEA Evaluation Results
5. Discussion and Conclusions
5.1. Discussion and Future Research Directions
5.2. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schaltegger, S.; Sturm, A. Ökologische Rationalität: Ansatzpunkte zur Ausgestaltung von ökologieorientierten Managementinstrumenten. Die Unternehm. 1990, 44, 273–290. [Google Scholar]
- Bian, Y.; Yang, F. Resource and environment efficiency analysis of provinces in China: A DEA approach based on Shannon’s entropy. Energy Policy 2010, 38, 1909–1917. [Google Scholar] [CrossRef]
- Bian, Y.; He, P.; Xu, H. Estimation of potential energy saving and carbon dioxide emission reduction in China based on an extended non-radial DEA approach. Energy Policy 2013, 63, 962–971. [Google Scholar] [CrossRef]
- Song, M.; An, Q.; Zhang, W.; Wang, Z.; Wu, J. Environmental efficiency evaluation based on data envelopment analysis: A review. Renew. Sustain. Energy Rev. 2012, 16, 4465–4469. [Google Scholar] [CrossRef]
- Lin, B.; Du, K. Energy and CO2 emissions performance in China’s regional economies: Do market-oriented reforms matter? Energy Policy 2015, 78, 113–124. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Wei, Y.M.; Zhang, X. A comparative analysis of China’s regional energy and emission performance: Which is the better way to deal with undesirable outputs? Energy Policy 2012, 46, 574–584. [Google Scholar] [CrossRef]
- Wu, J.; Lv, L.; Sun, J.; Ji, X. A comprehensive analysis of China’s regional energy saving and emission reduction efficiency: From production and treatment perspectives. Energy Policy 2015, 84, 166–176. [Google Scholar] [CrossRef]
- Welch, E.; Barnum, D. Joint environmental and cost efficiency analysis of electricity generation. Ecol. Econ. 2009, 68, 2336–2343. [Google Scholar] [CrossRef]
- Hoang, V.N.; Alauddin, M. Input-Orientated Data Envelopment Analysis Framework for Measuring and Decomposing Economic, Environmental and Ecological Efficiency: An Application to OECD Agriculture. Environ. Resour. Econ. 2012, 51, 431–452. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, C. A performance evaluation of the energy, environmental, and economic efficiency and productivity in China: An application of global data envelopment analysis. Appl. Energy 2015, 147, 617–626. [Google Scholar] [CrossRef]
- Nabavi-Pelesaraei, A.; Abdi, R.; Rafiee, S.; Mobtaker, H.G. Optimization of energy required and greenhouse gas emissions analysis for orange producers using data envelopment analysis approach. J. Clean. Prod. 2014, 65, 311–317. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, J.; Fu, Z. Tourism eco-efficiency of Chinese coastal cities—Analysis based on the DEA-Tobit model. Ocean Coast. Manag. 2017, 148, 164–170. [Google Scholar] [CrossRef]
- Wang, X.; Ding, H.; Liu, L. Eco-efficiency measurement of industrial sectors in China: A hybrid super-efficiency DEA analysis. J. Clean. Prod. 2019, 229, 53–64. [Google Scholar] [CrossRef]
- Moutinho, V.; Fuinhas, J.A.; Marques, A.C.; Santiago, R. Assessing eco-efficiency through the DEA analysis and decoupling index in the Latin America countries. J. Clean. Prod. 2018, 205, 512–524. [Google Scholar] [CrossRef]
- Matsumoto, K.; Chen, Y. Industrial eco-efficiency and its determinants in China: A two-stage approach. Ecol. Indic. 2021, 130, 108072. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, Z.; Xia, P. An extended DEA-based measurement for eco-efficiency from the viewpoint of limited preparation. J. Clean. Prod. 2018, 195, 721–733. [Google Scholar] [CrossRef]
- Ratner, S.; Zaretskaya, M. Evaluating Efficiency of Russian Regional Environmental Management Systems. Qual.-Access Success 2020, 21, 120–125. [Google Scholar]
- Yang, L.; Yang, Y. Evaluation of eco-efficiency in China from 1978 to 2016: Based on a modified ecological footprint model. Sci. Total Environ. 2019, 662, 581–590. [Google Scholar] [CrossRef]
- Yamasaki, J.; Ikaga, T.; Itsubo, N. Eco-Efficiency Assessment of Japanese Municipalities Based on Environmental Impacts and Gross Regional Product. Sustainability 2019, 11, 4045. [Google Scholar] [CrossRef] [Green Version]
- Voinea, C.L.; Hoogenberg, B.J.; Fratostiteanu, C.; Bin Azam Hashmi, H. The Relation between Environmental Management Systems and Environmental and Financial Performance in Emerging Economies. Sustainability 2020, 12, 5309. [Google Scholar] [CrossRef]
- Liu, H.; Yang, R.; Zhou, Z.; Huang, D. Regional Green Eco-Efficiency in China: Considering Energy Saving, Pollution Treatment, and External Environmental Heterogeneity. Sustainability 2020, 12, 7059. [Google Scholar] [CrossRef]
- Li, X.N.; Feng, Y.; Wu, P.Y.; Chiu, Y.H. An Analysis of Environmental Efficiency and Environmental Pollution Treatment Efficiency in China’s Industrial Sector. Sustainability 2021, 13, 2579. [Google Scholar] [CrossRef]
- Ma, J.; Yin, Z.; Guo, Z. Meta-Evaluation for the Evaluation of Environmental Management: Standards and Practices. Sustainability 2021, 13, 2567. [Google Scholar] [CrossRef]
- Ge, X.; Xu, J.; Xie, Y.; Guo, X.; Yang, D. Evaluation and Dynamic Evolution of Eco-Efficiency of Resource-Based Cities—A Case Study of Typical Resource-Based Cities in China. Sustainability 2021, 13, 6802. [Google Scholar] [CrossRef]
- Cuesta, R.A.; Lovell, C.K.; Zofío, J.L. Environmental efficiency measurement with translog distance functions: A parametric approach. Ecol. Econ. 2009, 68, 2232–2242. [Google Scholar] [CrossRef]
- Orea, L.; Wall, A. Measuring Eco-efficiency Using the Stochastic Frontier Analysis Approach. In Advances in Efficiency and Productivity; Aparicio, J., Lovell, C.A.K., Pastor, J.T., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 275–297. [Google Scholar] [CrossRef]
- Orea, L.; Wall, A. A Parametric Approach to Estimating Eco-Efficiency. J. Agric. Econ. 2017, 68, 901–907. [Google Scholar] [CrossRef]
- Moutinho, V.; Madaleno, M. Assessing Eco-Efficiency in Asian and African Countries Using Stochastic Frontier Analysis. Energies 2021, 14, 1168. [Google Scholar] [CrossRef]
- Gumus, S.; Egilmez, G.; Kucukvar, M.; Park, Y.S. Integrating expert weighting and multi-criteria decision making into eco-efficiency analysis: The case of US manufacturing. J. Oper. Res. Soc. 2016, 67, 616–628. [Google Scholar] [CrossRef]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Siksnelyte, I.; Zavadskas, E.K.; Streimikiene, D.; Sharma, D. An Overview of Multi-Criteria Decision-Making Methods in Dealing with Sustainable Energy Development Issues. Energies 2018, 11, 2754. [Google Scholar] [CrossRef] [Green Version]
- Yao, S. Fuzzy-based multi-criteria decision analysis of environmental regulation and green economic efficiency in a post-COVID-19 scenario: The case of China. Environ. Sci. Pollut. Res. 2021, 28, 30675–30701. [Google Scholar] [CrossRef]
- Vlachokostas, C.; Michailidou, A.; Achillas, C. Multi-Criteria Decision Analysis towards promoting Waste-to-Energy Management Strategies: A critical review. Renew. Sustain. Energy Rev. 2021, 138, 110563. [Google Scholar] [CrossRef]
- Zhou, C.; Shi, C.; Wang, S.; Zhang, G. Estimation of eco-efficiency and its influencing factors in Guangdong province based on Super-SBM and panel regression models. Ecol. Indic. 2018, 86, 67–80. [Google Scholar] [CrossRef]
- Martín-Gamboa, M.; Iribarren, D.; García-Gusano, D.; Dufour, J. A review of life-cycle approaches coupled with data envelopment analysis within multi-criteria decision analysis for sustainability assessment of energy systems. J. Clean. Prod. 2017, 150, 164–174. [Google Scholar] [CrossRef]
- Keshavarz, E.; Toloo, M. A hybrid data envelopment analysis and multi-attribute decision making approach to sustainability assessment. Expert Syst. 2020, 37, 1–17. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Yuan, Y.; Goto, M. A literature study for DEA applied to energy and environment. Energy Econ. 2017, 62, 104–124. [Google Scholar] [CrossRef]
- Mardani, A.; Streimikiene, D.; Balezentis, T.; Saman, M.Z.M.; Nor, K.M.; Khoshnava, S.M. Data Envelopment Analysis in Energy and Environmental Economics: An Overview of the State-of-the-Art and Recent Development Trends. Energies 2018, 11, 2002. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; You, J.; Li, H.; Shao, L. Energy Efficiency Evaluation Based on Data Envelopment Analysis: A Literature Review. Energies 2020, 13, 3548. [Google Scholar] [CrossRef]
- Deng, G.; Li, L.; Song, Y. Provincial water use efficiency measurement and factor analysis in China: Based on SBM-DEA model. Ecol. Indic. 2016, 69, 12–18. [Google Scholar] [CrossRef]
- Gómez-Calvet, R.; Conesa, D.; Gómez-Calvet, A.R.; Tortosa-Ausina, E. On the dynamics of eco-efficiency performance in the European Union. Comput. Oper. Res. 2016, 66, 336–350. [Google Scholar] [CrossRef]
- Masternak-Janus, A.; Rybaczewska-Błażejowska, M. Comprehensive Regional Eco-Efficiency Analysis Based on Data Envelopment Analysis: The Case of Polish Regions. J. Ind. Ecol. 2017, 21, 180–190. [Google Scholar] [CrossRef]
- Chen, L.; Jia, G. Environmental efficiency analysis of China’s regional industry: A data envelopment analysis (DEA) based approach. J. Clean. Prod. 2017, 142, 846–853. [Google Scholar] [CrossRef]
- Jebali, E.; Essid, H.; Khraief, N. The analysis of energy efficiency of the Mediterranean countries: A two-stage double bootstrap DEA approach. Energy 2017, 134, 991–1000. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, T. Regional energy-environmental performance and investment strategy for China’s non-ferrous metals industry: A non-radial DEA based analysis. J. Clean. Prod. 2017, 163, 187–201. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Chang, Y.; Zhang, L. Industrial eco-efficiency in China: A provincial quantification using three-stage data envelopment analysis. J. Clean. Prod. 2017, 143, 238–249. [Google Scholar] [CrossRef]
- Zhao, L.; Sun, C.; Liu, F. Interprovincial two-stage water resource utilization efficiency under environmental constraint and spatial spillover effects in China. J. Clean. Prod. 2017, 164, 715–725. [Google Scholar] [CrossRef]
- Huang, J.; Xia, J.; Yu, Y.; Zhang, N. Composite eco-efficiency indicators for China based on data envelopment analysis. Ecol. Indic. 2018, 85, 674–697. [Google Scholar] [CrossRef]
- Rybaczewska-Błażejowska, M.; Masternak-Janus, A. Eco-efficiency assessment of Polish regions: Joint application of life cycle assessment and data envelopment analysis. J. Clean. Prod. 2018, 172, 1180–1192. [Google Scholar] [CrossRef]
- Zhang, A.; Li, A.; Gao, Y. Social Sustainability Assessment across Provinces in China: An Analysis of Combining Intermediate Approach with Data Envelopment Analysis (DEA) Window Analysis. Sustainability 2018, 10, 732. [Google Scholar] [CrossRef] [Green Version]
- Grigoroudis, E.; Petridis, K. Evaluation of National Environmental Efficiency Under Uncertainty Using Data Envelopment Analysis. In Understanding Risks and Uncertainties in Energy and Climate Policy: Multidisciplinary Methods and Tools for a Low Carbon Society; Doukas, H., Flamos, A., Lieu, J., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 161–181. [Google Scholar] [CrossRef] [Green Version]
- Lu, C.C.; Lu, L.C. Evaluating the energy efficiency of European Union countries: The dynamic data envelopment analysis. Energy Environ. 2019, 30, 27–43. [Google Scholar] [CrossRef]
- Piao, S.R.; Li, J.; Ting, C.J. Assessing regional environmental efficiency in China with distinguishing weak and strong disposability of undesirable outputs. J. Clean. Prod. 2019, 227, 748–759. [Google Scholar] [CrossRef]
- Ratner, S.V. Dynamic Problems of Estimation of Ecological-Economic Efficiency of Regions Based on Basic Models of Data Envelopment Analysis. Autom. Remote Control 2019, 80, 2245–2258. [Google Scholar] [CrossRef]
- Shi, X. Environmental Efficiency Evaluation of Chinese Industry Systems by Using Non-Cooperative Two-Stage DEA Model. Math. Probl. Eng. 2019, 2019, 9187541. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Guo, S.; Zhao, H. Provincial energy efficiency of China quantified by three-stage data envelopment analysis. Energy 2019, 166, 96–107. [Google Scholar] [CrossRef]
- Zhou, Y.; Kong, Y.; Sha, J.; Wang, H. The role of industrial structure upgrades in eco-efficiency evolution: Spatial correlation and spillover effects. Sci. Total Environ. 2019, 687, 1327–1336. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, M.; del Valle, I.; Tapia, C. Measuring eco-efficiency in European regions: Evidence from a territorial perspective. J. Clean. Prod. 2020, 276, 123246. [Google Scholar] [CrossRef]
- Hermoso-Orzáez, M.J.; García-Alguacil, M.; Terrados-Cepeda, J.; Brito, P. Measurement of environmental efficiency in the countries of the European Union with the enhanced data envelopment analysis method (DEA) during the period 2005–2012. Environ. Sci. Pollut. Res. 2020, 27, 15691–15715. [Google Scholar] [CrossRef]
- Wu, D.; Wang, Y.; Qian, W. Efficiency evaluation and dynamic evolution of China’s regional green economy: A method based on the Super-PEBM model and DEA window analysis. J. Clean. Prod. 2020, 264, 121630. [Google Scholar] [CrossRef]
- Li, Y.; Zuo, Z.; Xu, D.; Wei, Y. Mining Eco-Efficiency Measurement and Driving Factors Identification Based on Meta-US-SBM in Guangxi Province, China. Int. J. Environ. Res. Public Health 2021, 18, 5397. [Google Scholar] [CrossRef]
- Moutinho, V.; Madaleno, M. A Two-Stage DEA Model to Evaluate the Technical Eco-Efficiency Indicator in the EU Countries. Int. J. Environ. Res. Public Health 2021, 18, 3038. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, J.; Choi, G. A two-stage eco-efficiency evaluation of China’s industrial sectors: A dynamic network data envelopment analysis (DNDEA) approach. Process Saf. Environ. Prot. 2021, 148, 879–892. [Google Scholar] [CrossRef]
- Zhu, C.; Zhu, N.; Shan, W.U.H. Eco-Efficiency of Industrial Investment and Its Influencing Factors in China Based on a New SeUo-SBM-DEA Model and Tobit Regression. Math. Probl. Eng. 2021, 2021, 5329714. [Google Scholar] [CrossRef]
- Zhu, Q.; Chen, J.; Li, F. A comprehensive analysis of China’s regional energy and environment efficiency from supply chain perspective. Int. J. Log. Res. Appl. 2021, 1–16. [Google Scholar] [CrossRef]
- Ratner, S.; Ratner, P. DEA-based dynamic assessment of regional environmental efficiency. Appl. Comput. Sci. 2017, 13, 48–60. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef] [Green Version]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Farrell, M.J. The measurement of productive efficiency. J. R. Stat. Soc. 1957, 120, 253–281. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Yang, G. A survey and analysis of the first 40 years of scholarly literature in DEA: 1978–2016. Socio-Econ. Plan. Sci. 2018, 61, 4–8. [Google Scholar] [CrossRef]
- Cooper, W.W.; Seiford, L.M.; Tone, K. Data Envelopment Analysis. A Comprehensive Text with Models, Applications, References and DEA-Solver Software, 2nd ed.; Springer Science and Business Media: New York, NY, USA, 2007. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.; Athanassopoulos, A.; Dyson, R.; Thanassoulis, E. Weights restrictions and value judgements in Data Envelopment Analysis: Evolution, development and future directions. Ann. Oper. Res. 1997, 73, 13–34. [Google Scholar] [CrossRef]
- Wong, Y.H.B.; Beasley, J.E. Restricting Weight Flexibility in Data Envelopment Analysis. J. Oper. Res. Soc. 1990, 41, 829–835. [Google Scholar] [CrossRef]
- Thompson, R.G.; Singleton, F.D.; Thrall, R.M.; Smith, B.A. Comparative Site Evaluations for Locating a High-Energy Physics Lab in Texas. Interfaces 1986, 16, 35–49. [Google Scholar] [CrossRef]
- Thompson, R.G.; Dharmapala, P.; Rothenberg, L.J.; Thrall, R.M. DEA/AR efficiency and profitability of 14 major oil companies in U.S. exploration and production. Comput. Oper. Res. 1996, 23, 357–373. [Google Scholar] [CrossRef]
- Krivonozhko, V.E.; Utkin, O.B.; Safin, M.M.; Lychev, A.V. On some generalization of the DEA models. J. Oper. Res. Soc. 2009, 60, 1518–1527. [Google Scholar] [CrossRef]
- Krivonozhko, V.E.; Førsund, F.R.; Lychev, A.V. Improving the frontier in DEA models. Dokl. Math. 2016, 94, 715–719. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Anouze, A.L.; Thanassoulis, E. A semi-oriented radial measure for measuring the efficiency of decision making units with negative data, using DEA. Eur. J. Oper. Res. 2010, 200, 297–304. [Google Scholar] [CrossRef]
- Sharp, J.A.; Meng, W.; Liu, W. A modified slacks-based measure model for data envelopment analysis with ‘natural’ negative outputs and inputs. J. Oper. Res. Soc. 2007, 58, 1672–1677. [Google Scholar] [CrossRef]
- Portela, M.C.A.S.; Thanassoulis, E.; Simpson, G. Negative data in DEA: A directional distance approach applied to bank branches. J. Oper. Res. Soc. 2004, 55, 1111–1121. [Google Scholar] [CrossRef] [Green Version]
- Lin, R.; Yang, W.; Huang, H. A modified slacks-based super-efficiency measure in the presence of negative data. Comput. Ind. Eng. 2019, 135, 39–52. [Google Scholar] [CrossRef]
- Andersen, P.; Petersen, N.C. A Procedure for Ranking Efficient Units in Data Envelopment Analysis. Manag. Sci. 1993, 39, 1261–1264. [Google Scholar] [CrossRef]
- Adler, N.; Friedman, L.; Sinuany-Stern, Z. Review of ranking methods in the data envelopment analysis context. Eur. J. Oper. Res. 2002, 140, 249–265. [Google Scholar] [CrossRef]
- Cooper, W.W.; Park, K.S.; Pastor, J.T. RAM: A Range Adjusted Measure of Inefficiency for Use with Additive Models, and Relations to Other Models and Measures in DEA. J. Product. Anal. 1999, 11, 5–42. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W. Programming with Linear Fractional Functionals. Nav. Res. Logist. Q. 1962, 9, 181–186. [Google Scholar] [CrossRef]
- Volodin, A.V.; Krivonozhko, V.E.; Ryzhikh, D.A.; Utkin, O.B. Construction of three-dimensional sections in data envelopment analysis by using parametric optimization algorithms. Comput. Math. Math. Phys. 2004, 44, 589–603. [Google Scholar]
- Afanasiev, A.P.; Krivonozhko, V.E.; Lychev, A.V.; Sukhoroslov, O.V. Multidimensional frontier visualization based on optimization methods using parallel computations. J. Glob. Optim. 2020, 76, 563–574. [Google Scholar] [CrossRef]
- Jin, F.; Garg, H.; Pei, L.; Liu, J.; Chen, H. Multiplicative Consistency Adjustment Model and Data Envelopment Analysis-Driven Decision-Making Process with Probabilistic Hesitant Fuzzy Preference Relations. Int. J. Fuzzy Syst. 2020, 22, 2319–2332. [Google Scholar] [CrossRef]
- Jin, F.; Cao, M.; Liu, J.; Martínez, L.; Chen, H. Consistency and trust relationship-driven social network group decision-making method with probabilistic linguistic information. Appl. Soft Comput. 2021, 103, 107170. [Google Scholar] [CrossRef]
- Rosstat. Regiony Rossii. Sotsial’no-Ekonomicheskie Pokazateli (Russian Regions. Socio-Economic Indicators). Available online: https://rosstat.gov.ru/folder/210/document/13204 (accessed on 10 June 2020).
- Rosstat. Ohrana Okruzhayushchej Sredy v Rossii (Environmental Protection in Russia). Available online: https://rosstat.gov.ru/folder/210/document/13209 (accessed on 10 June 2020).
- Analytical Credit Rating Agency. Komu na Rusi Dyshat’ Horosho (Who Can Breathe Well in Russia). Available online: https://www.acra-ratings.ru/research/2328/ (accessed on 11 August 2020).
- All-Russian Public Organization “Green Patrol”. Nacional’nyj Ekologicheskij Rejting (National Environmental Rating). Available online: https://greenpatrol.ru/ru/stranica-dlya-obshchego-reytinga/ekologicheskiy-reyting-subektov-rf?tid=426 (accessed on 11 August 2020).
- All-Russia People’s Front. Rejting Ekologicheskogo Razvitiya Gorodov Rossii 2017 (Environmental Development Rating of Russian Cities 2017). Available online: https://onf.ru/sites/default/files/projects_docs/21112017.pdf (accessed on 11 August 2020).

| Ref. | DMUs | RTS | DEA Model and Methodology | Application Area |
|---|---|---|---|---|
| [40] | 31 provinces in China | CRS | SBM model and factor analysis | Water use |
| [41] | 27 EU countries | CRS | Two-stage efficiency measurement based on DDF model | Environmental performance |
| [42] | 16 Polish regions | CRS | CCR model and Hellwig’s method and coefficient of determination | Environmental efficiency |
| [43] | 30 regions in China | CRS | SBM model based on undesirable outputs | Environmental efficiency of industry |
| [44] | 24 Mediterranean countries | VRS | SBM model and two-stage double bootstrap | Energy efficiency |
| [45] | 30 regions in China | VRS | SBM model and Tobit regression and truncated regression models | Energy-environmental performance |
| [46] | 30 provinces in China | VRS | Three-stage analysis based on BCC model & SFA | Industrial eco-efficiency |
| [47] | 31 provincial administrative regions in China | CRS | Two-stage US-SBM model & spatial autocorrelation analysis using Moran’s I | Water resource utilization efficiency |
| [48] | 30 Chinese provinces | CRS | Meta-frontier Super-US-SBM model | Composite eco-efficiency indicators |
| [49] | 16 Polish regions | VRS | BCC model | Life cycle assessment |
| [50] | 30 provinces in China | CRS | Intermediate approach and performance indices | Social sustainability |
| [34] | 21 cities in Guangdong province, China | CRS | Super-SBM and panel regression models | Estimation of eco-efficiency |
| [51] | 108 countries | CRS | Slack-based models with undesirable outputs | National environmental efficiency |
| [52] | 28 EU countries | VRS | SBM model and dynamic DEA | Energy efficiency |
| [53] | 30 provinces in China | VRS | Models with strong and weak disposability of undesirable outputs and Malmquist–Luenberger index | Environmental efficiency |
| [54] | 17 regions of Central Federal District, Russia | CRS | CCR model and Malmquist index | Ecological-economic efficiency |
| [55] | 30 regional industry systems in China | CRS | Two-stage CCR model and regression analysis | Environmental efficiency |
| [13] | 30 provinces in China | CRS | SBM model and GML productivity index and panel Tobit model | Air pollution emission efficiency |
| [56] | 30 Chinese provinces | VRS | Three-stage DEA approach based on BCC model and SFA | Energy efficiency |
| [57] | 48 cities in Bohai Rim, China | CRS | Super-US-SBM model and Moran’s I | Eco-efficiency |
| [58] | 282 European regions | VRS | Hyperbolic distance function measure and metafrontier approach | Eco-efficiency |
| [59] | 28 EU countries | CRS | Environmental Efficiency Index | Environmental efficiency |
| [60] | 30 provinces of China | VRS | Super-PEBM model and window analysis | Green economic efficiency |
| [61] | 14 prefecture-level cities in Guangxi Province, China | CRS | Meta-US-SBM model and Tobit Model | Mining industry eco-efficiency |
| [62] | 27 EU Countries | CRS | CCR model and fractional regression model | Eco-efficiency |
| [63] | 30 regions in mainland China | VRS | Dynamic network DEA approach based on the SBM model | Eco-eficiency |
| [64] | 30 provinces in China | CRS | Super-US-SBM model and regression analysis | Eco-efficiency of industrial investment |
| [65] | 30 province-level regions of Chinese mainland | VRS | Two-stage DEA approach based on BCC model | Energy and environment efficiency |
| Variables | Min | Max | Mean | St.Dev. |
|---|---|---|---|---|
| Inputs | ||||
| −0.0 | 2.04 | −0.25 | 0.30 | |
| − | 3.25 | −0.50 | 0.37 | |
| Outputs | ||||
| − | ||||
| − | ||||
| − | ||||
| − | ||||
| 643.24 | 138.11 | |||
| 0.946 | −0.0325 | 0.243 |
| Variable | Upper/Lower Bound of the Weight Restrictions in CCR-AR Model | Weight in SBM Model |
|---|---|---|
| —share of investments in fixed assets aimed at reducing environmental pollution | — | 0.5 |
| —share of current costs in the region’s GRP | — | 0.5 |
| —difference in the intensity of emissions from stationary sources | 0.1/0.3 | 0.182 |
| —difference in the intensity of emissions from road transport | 0.1/0.3 | 0.182 |
| —difference in the intensity of discharge of untreated sewage | 0.1/0.3 | 0.182 |
| —difference in the intensity of fresh water consumption | 0.05/0.1 | 0.09 |
| —difference in the intensity of waste generation | 0.1/0.3 | 0.182 |
| —difference in the share of recycling and reuse of waste | 0.1/0.3 | 0.182 |
| CCR Model | CCR-AR Model | SBM Model | |
|---|---|---|---|
| CCR model | 1 | ||
| CCR-AR model | 0.9852815 | 1 | |
| SBM model | 0.6622165 | 0.6295127 | 1 |
| CCR Model | CCR-AR Model | SBM Model |
|---|---|---|
| Regions with the highest values of the efficiency score | ||
| Bryansk Oblast-11 | Moscow-11 | Stavropol Krai-11 |
| Moscow-11 | Dagestan-11 | Astrakhan Oblast-13 |
| Dagestan-11 | Dagestan-13 | Arkhangelsk Oblast-11 |
| Dagestan-13 | Tuva Republic-15 | Orenburg Oblast-13 |
| Ivanovo Oblast-15 | Bryansk Oblast-11 | North Ossetia-Alania-13 |
| Tuva Republic-15 | Ivanovo Oblast-15 | Dagestan-11 |
| Ivanovo Oblast-17 | Ivanovo Oblast-17 | Tuva Republic-17 |
| Novosibirsk Oblast-17 | Moscow-13 | Moscow Oblast-11 |
| Moscow-13 | Adygea-15 | Kabardino-Balkar Republic-11 |
| North Ossetia-Alania-13 | Tuva Republic-13 | Chuvash Republic-11 |
| Adygea-15 | Moscow-15 | Kemerovo Oblast-15 |
| Kostroma Oblast-15 | Novosibirsk Oblast-17 | Kostroma Oblast-15 |
| Tuva Republic-13 | Moscow-17 | Kemerovo Oblast-17 |
| Moscow-15 | Mari El Republic-15 | Karelia-11 |
| Kabardino-Balkar Republic-11 | Tuva Republic-17 | Ivanovo Oblast-15 |
| Regions with the lowest values of the efficiency score | ||
| Murmansk Oblast-15 | Astrakhan Oblast-13 | Murmansk Oblast-13 |
| Murmansk Oblast-13 | Murmansk Oblast-15 | Kemerovo Oblast-13 |
| Bashkortostan-11 | Vologda Oblast-13 | Krasnoyarsk Krai-13 |
| Vologda Oblast-13 | Sakha (Yakutia) Republic-17 | Tver Oblast-11 |
| Sakha (Yakutia) Republic-17 | Bashkortostan-13 | Sakha (Yakutia) Republic-17 |
| Kemerovo Oblast-13 | Murmansk Oblast-13 | Sakha (Yakutia) Republic-13 |
| Bashkortostan-13 | Sakha (Yakutia) Republic-13 | Krasnoyarsk Krai-15 |
| Krasnoyarsk Krai-17 | Krasnoyarsk Krai-17 | Vologda Oblast-13 |
| Sakha (Yakutia) Republic-13 | Murmansk Oblast-17 | Perm Krai-15 |
| Murmansk Oblast-17 | Kemerovo Oblast-13 | Volgograd Oblast-15 |
| Krasnoyarsk Krai-11 | Krasnoyarsk Krai-11 | Komi Republic-15 |
| Krasnoyarsk Krai-15 | Krasnoyarsk Krai-15 | Khabarovsk Krai-11 |
| Krasnoyarsk Krai-13 | Krasnoyarsk Krai-13 | Komi Republic-13 |
| Volgograd Oblast-15 | Volgograd Oblast-15 | Amur Oblast-13 |
| Lipetsk Oblast-11 | Lipetsk Oblast-11 | Lipetsk Oblast-11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ratner, S.; Lychev, A.; Rozhnov, A.; Lobanov, I. Efficiency Evaluation of Regional Environmental Management Systems in Russia Using Data Envelopment Analysis. Mathematics 2021, 9, 2210. https://doi.org/10.3390/math9182210
Ratner S, Lychev A, Rozhnov A, Lobanov I. Efficiency Evaluation of Regional Environmental Management Systems in Russia Using Data Envelopment Analysis. Mathematics. 2021; 9(18):2210. https://doi.org/10.3390/math9182210
Chicago/Turabian StyleRatner, Svetlana, Andrey Lychev, Aleksei Rozhnov, and Igor Lobanov. 2021. "Efficiency Evaluation of Regional Environmental Management Systems in Russia Using Data Envelopment Analysis" Mathematics 9, no. 18: 2210. https://doi.org/10.3390/math9182210
APA StyleRatner, S., Lychev, A., Rozhnov, A., & Lobanov, I. (2021). Efficiency Evaluation of Regional Environmental Management Systems in Russia Using Data Envelopment Analysis. Mathematics, 9(18), 2210. https://doi.org/10.3390/math9182210








