Analytical and Numerical Connections between Fractional Fickian and Intravoxel Incoherent Motion Models of Diffusion MRI
Abstract
:1. Introduction
2. Definitions and Properties
2.1. Biexponential Model
2.2. Stretched Exponential Model
3. Materials and Methods
3.1. Biexponential Representation of the Stretched Exponential Model Parameters
3.2. Biexponential Estimates of the Stretched Exponential Model Parameters
3.2.1. Error Analysis
3.2.2. Error Analysis in the Presence of Noise
3.2.3. Model Simulations and Cross-Model Error Analysis
3.3. In Vivo MRI Acquisition
4. Results
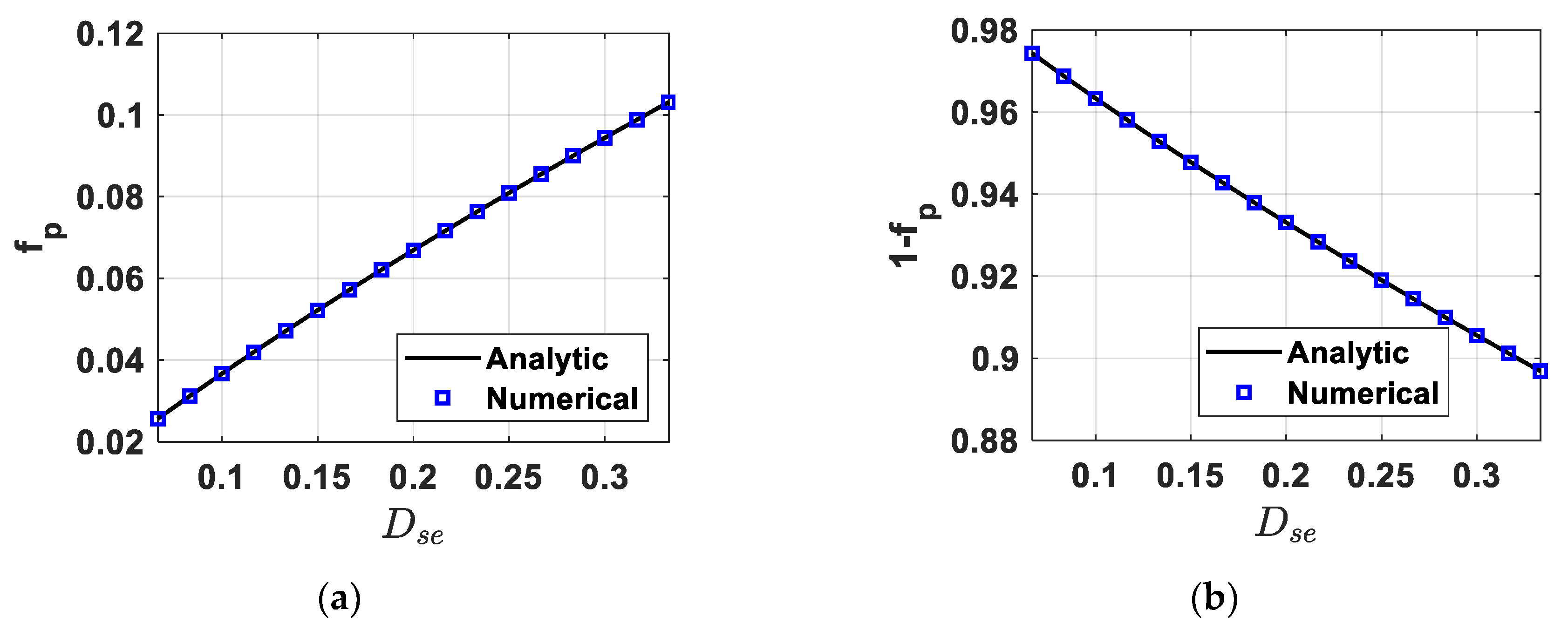
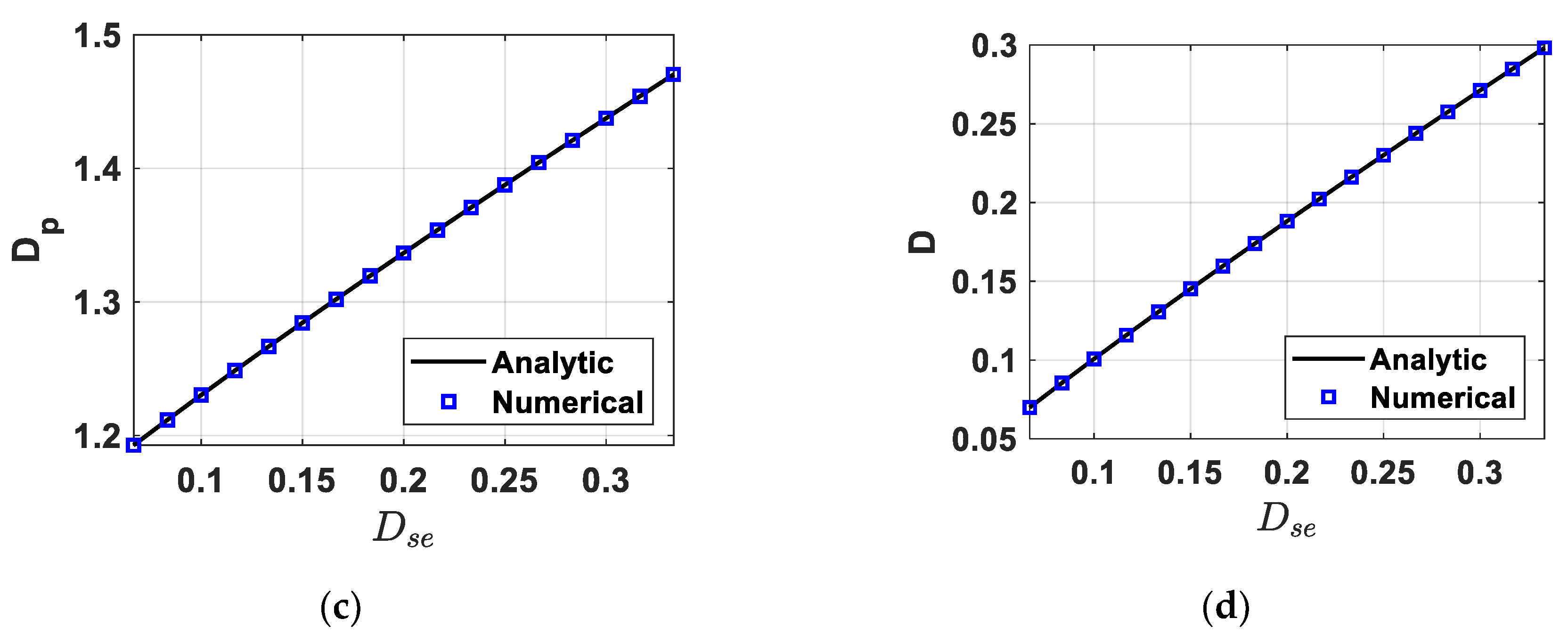
4.1. Fully-Determined Case
4.2. Over-Determined Case
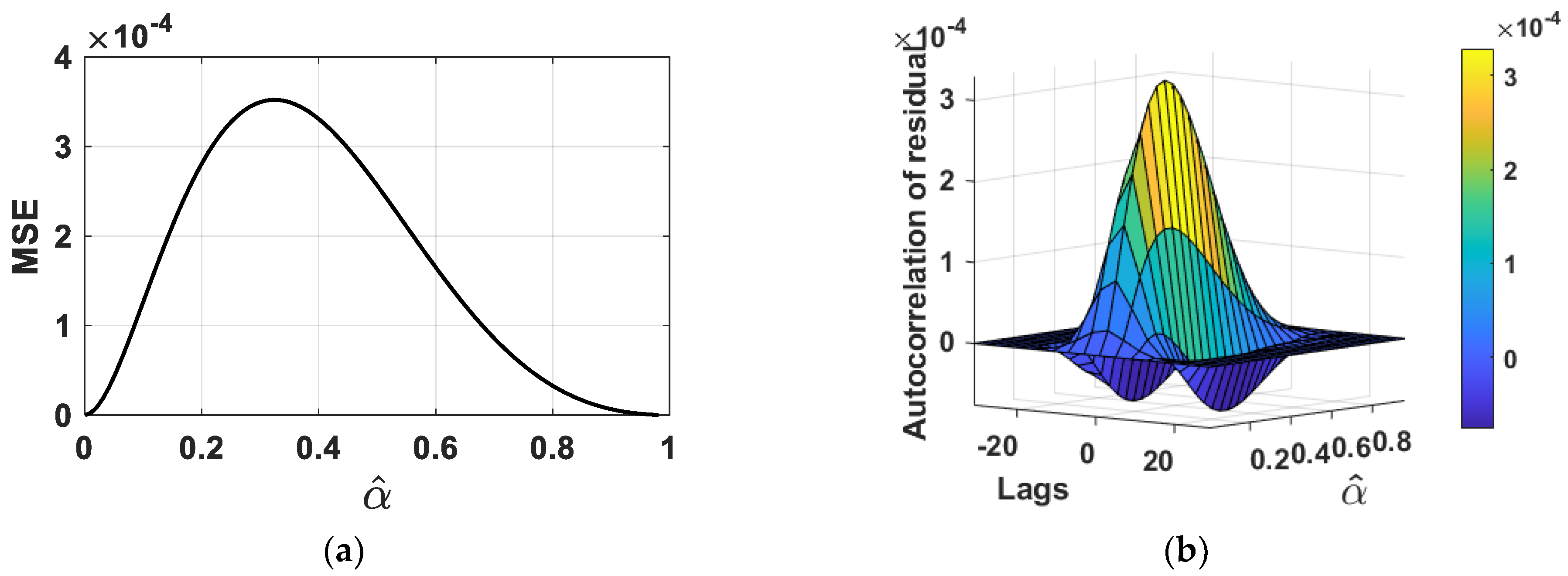
4.3. Analysis of Fit Error
4.4. In Vivo Results
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hendrickse, P.; Degens, H. The role of the microcirculation in muscle function and plasticity. J. Muscle Res. Cell Motil. 2019, 40, 127–140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neviere, R.; Mathieu, D.; Chagnon, J.L.; Lebleu, N.; Millien, J.P.; Wattel, F. Skeletal muscle microvascular blood flow and oxygen transport in patients with severe sepsis. Am. J. Respir. Crit. Care Med. 1996, 153, 191–195. [Google Scholar] [CrossRef]
- Lindner, J.R. Cause or Effect? Microvascular Dysfunction in Insulin-Resistant States. Circ. Cardiovasc. Imaging 2018, 11, e007725. [Google Scholar] [CrossRef] [Green Version]
- Toth, P.; Tarantini, S.; Csiszar, A.; Ungvari, Z. Functional vascular contributions to cognitive impairment and dementia: Mechanisms and consequences of cerebral autoregulatory dysfunction, endothelial impairment, and neurovascular uncoupling in aging. Am. J. Physiol. Heart Circ. Physiol. 2017, 312, H1–H20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bammer, R. Basic principles of diffusion-weighted imaging. Eur. J. Radiol. 2003, 45, 169–184. [Google Scholar] [CrossRef]
- Le Bihan, D.; Breton, E.; Lallemand, D.; Aubin, M.L.; Vignaud, J.; Laval-Jeantet, M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology 1988, 168, 497–505. [Google Scholar] [CrossRef] [PubMed]
- Hall, M. Continuity, the Bloch-Torrey equation, and Diffusion MRI. arXiv 2016, arXiv:1608.02859. [Google Scholar]
- Mazaheri, Y.; Afaq, A.; Rowe, D.B.; Lu, Y.; Shukla-Dave, A.; Grover, J. Diffusion-weighted magnetic resonance imaging of the prostate: Improved robustness with stretched exponential modeling. J. Comput. Assist. Tomogr. 2012, 36, 695–703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, J.; Suo, S.; Liu, G.; Zhang, S.; Zhao, Z.; Xu, J.; Wu, G. Comparison of Monoexponential, Biexponential, Stretched-Exponential, and Kurtosis Models of Diffusion-Weighted Imaging in Differentiation of Renal Solid Masses. Korean J. Radiol. 2019, 20, 791–800. [Google Scholar] [CrossRef]
- Seo, N.; Chung, Y.; Park, Y.; Kim, E.; Hwang, J.; Kim, M.-J. Liver fibrosis: Stretched exponential model outperforms mono-exponential and bi-exponential models of diffusion-weighted MRI. Eur. Radiol. 2018, 28, 1–11. [Google Scholar] [CrossRef]
- Bai, Y.; Lin, Y.; Tian, J.; Shi, D.; Cheng, J.; Haacke, E.M.; Hong, X.; Ma, B.; Zhou, J.; Wang, M. Grading of Gliomas by Using Monoexponential, Biexponential, and Stretched Exponential Diffusion-weighted MR Imaging and Diffusion Kurtosis MR Imaging. Radiology 2015, 278, 496–504. [Google Scholar] [CrossRef]
- Li, C.; Ye, J.; Prince, M.; Peng, Y.; Dou, W.; Shang, S.; Wu, J.; Luo, X. Comparing mono-exponential, bi-exponential, and stretched-exponential diffusion-weighted MR imaging for stratifying non-alcoholic fatty liver disease in a rabbit model. Eur. Radiol. 2020, 30, 6022–6032. [Google Scholar] [CrossRef]
- Dietrich, O.; Biffar, A.; Baur-Melnyk, A.; Reiser, M.F. Technical aspects of MR diffusion imaging of the body. Eur. J. Radiol. 2010, 76, 314–322. [Google Scholar] [CrossRef]
- Stejskal, E.O.; Tanner, J.E. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time—Dependent Field Gradient. J. Chem. Phys. 1965, 42, 288–292. [Google Scholar] [CrossRef] [Green Version]
- Jensen, J.H.; Helpern, J.A. Effect of gradient pulse duration on MRI estimation of the diffusional kurtosis for a two-compartment exchange model. J. Magn. Reson. 2011, 210, 233–237. [Google Scholar] [CrossRef] [Green Version]
- Reiter, D.A.; Adelnia, F.; Cameron, D.; Spencer, R.G.; Ferrucci, L. Parsimonious modeling of skeletal muscle perfusion: Connecting the stretched exponential and fractional Fickian diffusion. Magn. Reson. Med. 2021, 86, 1045–1057. [Google Scholar] [CrossRef] [PubMed]
- Ingo, C.; Sui, Y.; Chen, Y.; Parrish, T.B.; Webb, A.G.; Ronen, I. Parsimonious continuous time random walk models and kurtosis for diffusion in magnetic resonance of biological tissue. Front. Phys. 2015, 3. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bennett, K.M.; Schmainda, K.M.; Bennett, R.T.; Rowe, D.B.; Lu, H.; Hyde, J.S. Characterization of continuously distributed cortical water diffusion rates with a stretched-exponential model. Magn. Reson. Med. 2003, 50, 727–734. [Google Scholar] [CrossRef] [PubMed]
- Berberan-Santos, M.N.; Valeur, B. Luminescence decays with underlying distributions: General properties and analysis with mathematical functions. J. Lumin. 2007, 126, 263–272. [Google Scholar] [CrossRef]
- Johnston, D.C. Stretched exponential relaxation arising from a continuous sum of exponential decays. Phys. Rev. B 2006, 74, 184430. [Google Scholar] [CrossRef] [Green Version]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Fernández Rodríguez, A.; de Santiago Rodrigo, L.; López Guillén, E.; Rodríguez Ascariz, J.M.; Miguel Jiménez, J.M.; Boquete, L. Coding Prony’s method in MATLAB and applying it to biomedical signal filtering. BMC Bioinf. 2018, 19, 451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adelnia, F.; Shardell, M.; Bergeron, C.M.; Fishbein, K.W.; Spencer, R.G.; Ferrucci, L.; Reiter, D.A. Diffusion-weighted MRI with intravoxel incoherent motion modeling for assessment of muscle perfusion in the thigh during post-exercise hyperemia in younger and older adults. NMR Biomed. 2019, 32, e4072. [Google Scholar] [CrossRef]
- Cameron, D.; Bouhrara, M.; Reiter, D.A.; Fishbein, K.W.; Choi, S.; Bergeron, C.M.; Ferrucci, L.; Spencer, R.G. The effect of noise and lipid signals on determination of Gaussian and non-Gaussian diffusion parameters in skeletal muscle. NMR Biomed. 2017, 30, 3718. [Google Scholar] [CrossRef] [Green Version]
- Anjum, M.A.R.; Gonzalez, F.M.; Swain, A.; Leisen, J.; Hosseini, Z.; Singer, A.; Umpierrez, M.; Reiter, D.A. Multi-component T2∗ relaxation modelling in human Achilles tendon: Quantifying chemical shift information in ultra-short echo time imaging. Magn. Reson. Med. 2021, 86, 415–428. [Google Scholar] [CrossRef] [PubMed]
- Anjum, M.A.R. High-Resolution Multidimensional Parametric Estimation for Nuclear Magnetic Resonance Spectroscopy; Victoria University of Wellington: Wellington, New Zealand, 2019. [Google Scholar]
- Ivanov, K.P.; Kalinina, M.K.; Levkovich Yu, I. Blood flow velocity in capillaries of brain and muscles and its physiological significance. Microvasc. Res. 1981, 22, 143–155. [Google Scholar] [CrossRef]
- Reiter, D.A.; Magin, R.L.; Li, W.; Trujillo, J.J.; Pilar Velasco, M.; Spencer, R.G. Anomalous T2 relaxation in normal and degraded cartilage. Magn. Reson. Med. 2016, 76, 953–962. [Google Scholar] [CrossRef] [PubMed] [Green Version]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, J.; Anjum, M.A.R.; Swain, A.; Reiter, D.A. Analytical and Numerical Connections between Fractional Fickian and Intravoxel Incoherent Motion Models of Diffusion MRI. Mathematics 2021, 9, 1963. https://doi.org/10.3390/math9161963
Yao J, Anjum MAR, Swain A, Reiter DA. Analytical and Numerical Connections between Fractional Fickian and Intravoxel Incoherent Motion Models of Diffusion MRI. Mathematics. 2021; 9(16):1963. https://doi.org/10.3390/math9161963
Chicago/Turabian StyleYao, Jingting, Muhammad Ali Raza Anjum, Anshuman Swain, and David A. Reiter. 2021. "Analytical and Numerical Connections between Fractional Fickian and Intravoxel Incoherent Motion Models of Diffusion MRI" Mathematics 9, no. 16: 1963. https://doi.org/10.3390/math9161963
APA StyleYao, J., Anjum, M. A. R., Swain, A., & Reiter, D. A. (2021). Analytical and Numerical Connections between Fractional Fickian and Intravoxel Incoherent Motion Models of Diffusion MRI. Mathematics, 9(16), 1963. https://doi.org/10.3390/math9161963





