Abstract
In this study, we explored elementary preservice teachers’ (PSTs’) competence to make diagnostic inferences about students’ levels of understanding of fractions and their approaches to developing appropriate tiered assessment items. Although recent studies have investigated beginning teachers’ diagnostic competency, teachers’ ability to design and evaluate diagnostic assessment items has remained largely underexplored. Fifty-seven PSTs, who enrolled in a mathematics methods course at a midwestern university in the U.S., participated in developing and attempting to differentiate diagnostic assessment items considering individual students’ varied levels of understanding. An inductive content analysis approach was used in identifying general patterns of PSTs’ approaches and strategies in designing and revising tiered assessment items. Our findings revealed the following: (a) the PSTs were well versed in students’ cognitive difficulties; (b) when modifying the core questions to be more or less difficult, the PSTs predominantly used strategies related to procedural fluency of the questions; and (c) some strategies PSTs used to modify questions did not necessarily yield the intended level of difficulty. Further, we discussed the challenges and opportunities teacher education programs face in teaching PSTs how to effectively design tiered assessment items.
1. Introduction
There is a general consensus that student learning is directly related to the quality of teaching, which largely depends on teachers’ competence in planning, instruction, and assessment [1]. One such competency is teachers’ capacity to gather information on students’ learning progress, make a diagnosis, and respond through an on-going and interactive process [2,3,4]. In particular, teachers’ ability to recognize and understand students’ difficulties, make diagnostic inferences about a wide range of students’ strengths and weaknesses, provide feedback, and design appropriate tasks to promote students’ thinking is critical [5,6,7,8].
Therefore, teachers’ assessment skills are integral to carrying out the kind of adaptive teaching that improves student learning. However, research shows that there has been insufficient development of teachers’ diagnostic competence [9]. Research also shows that teachers often do not design and implement diagnostic assessments and do not spend sufficient time analyzing student work and progress [10]. In the meantime, there has been much work in the field of mathematics education to produce a set of concrete academic standards for what students are expected to learn. However, those standards themselves “do not [explicitly] define the intervention methods or materials necessary to support students who are well below or well above grade-level expectations” [11] (p. 4). This leaves teachers in a position where they need to make diagnostic inferences (as assessment skills) about students’ strengths and weaknesses to support student learning and to develop instruction materials reflecting student needs.
There have been recent studies on teacher education investigating beginning teachers’ diagnostic competency to analyze student thinking, e.g., [12,13]. However, these studies paid relatively little attention to preservice teachers’ ability to design and evaluate diagnostic assessment items beyond their use of predetermined categories, terms, or concepts to analyze individual students’ performances. To address this gap in the literature, we explored elementary preservice teachers’ (PSTs’) capacity to design diagnostic assessments. As an exploratory empirical study, this study aimed to investigate elementary PSTs’ approaches to developing tiered assessment items to make diagnostic inferences about students’ understanding of fractions (cf. [14] about problem posing in fractions). By analyzing the patterns of strategies PSTs use to develop tiered diagnostic assessment items, we intended to provide educators of future mathematics teachers with ideas for improving their PSTs’ diagnostic competence. This study answered the following overarching questions: (a) how do PSTs anticipate student confusion/difficulties in solving fraction problems? (b) what strategies do PSTs use in designing diagnostic assessments to adjust the levels of assessment tasks according to individual student thinking based on their anticipated student confusion/difficulties? and (c) how do PSTs’ strategies differ depending on target concepts or representations used in the tasks?
2. Theoretical Framework
This section reviews the current literature relevant to the present study. We reviewed studies about teaching fractions and examined the ideas of (1) diagnostic competence and (2) problem posing. We also reviewed extant research on teachers’ mathematics assessment item development.
2.1. Teaching Fractions
Lee and Lee [15] stated, “a fraction itself does not tell anything about the actual size of the whole or the actual size of the parts but only represents the relationship between the part and the whole” (p. 7). Regarding the relationship in terms of fractional quantities, research [16,17,18] underscored the importance of constructing mental actions called operations, specifically, partitioning (i.e., dividing a whole into equal parts) and iterating. The denominator of a fraction represents the unit, and the numerator represents how many units fit into the given fraction. In the portioning operation, students try to figure out how to partition the given whole equally in order to find a unit fraction (see [19]). In the iterating operation, students repeat the unit fraction multiple times to produce proper or improper fractions. Confrey [16] combined these two operations into one and called it the splitting operation (cf. other ways to identify the part and the whole in [20]).
Research has documented that PSTs with relatively strong computational skills and procedural knowledge about algorithms and rules could struggle to understand the logic underlying the procedures or the interrelationships among mathematical ideas [21,22,23] and that PSTs have difficulty effectively using pedagogically appropriate representations or models to support students’ learning of fractions [24]. Regarding the modeling of fractions in the classroom, three types of pedagogical models are widely used [25]: (1) area models (e.g., circular or rectangular objects); (2) linear models (e.g., fraction strips, Cuisenaire rods, or number lines); and (3) set models (e.g., bi-level counters or tallies). Cramer and Whitney [26] indicated that the concept of improper fractions builds on to the linear models. Other studies (see [25]) noted that set models draw on students’ prior knowledge of whole number strategies and better reflect real-world uses of fractions. Research [27,28] supports the view that different models have different advantages, and students benefit from doing mathematics with multiple representations of fractions including three fractional models: real-world situations, verbal symbols, and manipulatives.
2.2. Teachers’ Diagnostic Competence
Diagnostic competence refers to the ability to accurately assess the characteristics of individuals, tasks, or programs and relevant preconditions [7]. Through diagnostic assessments, teachers can identify students’ strengths and weaknesses, use those inferences to inform their instruction, provide students with appropriate feedback, e.g., [29], and better support students’ learning. This pedagogical practice echoes the goal of formative assessment in that the ultimate goal is to plan a differentiated instruction that accommodates individual students’ learning needs [30,31]. In the end, differentiation highlights the needs of individual students and aims to maximize the students’ learning capacity [32,33]. Thus, diagnostic competence is necessary for teaching, and a teacher’s expertise in diagnosis positively contributes to interactions with students [34]. Therefore, teachers need to be competent at recognizing what students know and understand and what they do not know and understand [4,30]. In other words, teachers’ diagnostic competence in both cognitive and non-cognitive areas is a prerequisite to their ability to teach specific concepts and skills to their students [7]. For teachers to notice what and how students think, it is important to identify students’ misconceptions and provide opportunities for students to learn from mistakes and progress. Yang and Ricks [8,35] present the “Three-Point Framework” (as cited in [36], p. 126) to describe the process by which Chinese teachers decide instructional goals and design mathematical tasks. More specifically, teachers need to know not only the main mathematical concepts/ideas of their lessons or tasks (key point) but also common errors or misconceptions (difficult point) that students may have in the process of learning the key point. To address the difficult point, teachers should make important instructional decisions including interventions to support students who struggle so that they can overcome the difficulty (critical point) and master the key point. Lee and Choy [36] suggested the three-point framework to characterize teachers’ awareness of their content, student difficulty, and strategies to support students.
Despite its importance, there is insufficient development of diagnostic competence, and, subsequently, many teachers do not design and implement diagnostic assessments to evaluate individual students’ skills and levels of understanding [10,12]. Furthermore, teacher educators argue that many teachers start their teaching careers with less training on assessment issues compared to other discipline-specific areas [37]. Considering that teachers’ diagnostic competence, especially their ability to identify the key, difficult, and critical points, is an essential component of their teaching quality, there is no doubt that it should be included in teacher education programs.
2.3. Teachers’ Problem Posing—Eliciting and Interpreting
Prior research has established that problem solving is considered an important part of mathematics learning, but the same level of attention has not been given to problem posing [38]. Similarly, relatively little attention has been given to PSTs’ problem-posing ability in teacher education programs. In response, teacher educators have suggested including problem posing as a critical element of teacher education programs to allow teachers to become more adept at posing problems for students and assisting them to become better problem posers themselves [39,40,41,42].
In an effort to promote high-quality mathematics teaching, recent research on mathematics teacher education, especially that of novice teachers, has paid attention to these skills: eliciting and interpreting students’ thinking through carefully formulated problems and questions to support developing their competence as future mathematics teachers [43]. As shown in Figure 1, when novice teachers learn to elicit and interpret students’ thinking, they develop a diagnostic competence. It requires them to formulate and pose questions, listen to and interpret students’ thinking, and develop additional prompts and tasks that will determine what individual students know and can do. Thus, the first step toward developing novice teachers’ diagnostic competence is to provide them with opportunities to design questions and tasks meant to elicit students’ thinking. Then, when novice teachers more accurately understand their students’ thinking, they can reformulate questions and tasks to be better suited to the way their students think. By doing this, teachers can recognize where students are in the learning process and identify the misconceptions or errors that underlie the student’s understanding; this ultimately serves the goal of diagnostic assessments—informing teachers’ instructional design and delivery [44].
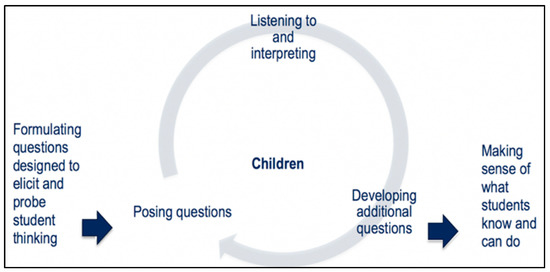
Figure 1.
Decomposed components of eliciting and interpreting student thinking [43,45]. Note. From Eliciting and Interpreting Student Thinking (Image), by TeachingWorks. CC BY-NC 3.0.
2.4. Teachers’ Ability to Develop Mathematics Assessment Items
Some studies have investigated teachers’ or PSTs’ competence in mathematical task design and/or task modification. There are a number of caveats that concern the quality of tasks; one is that teachers need to consider both pedagogical and mathematical aspects when they generate or modify tasks [46]. The mathematical aspect may initially concern procedural fluency (i.e., selecting efficient procedures, National Council of Teachers of Mathematics [47]) and computational fluency and further extends to “deep and diverse” [46] (p. 240) mathematical ideas in tasks. That said, some studies show that teachers or PSTs had unbalanced perspectives. For example, in a study of elementary PSTs’ problem posing behavior, Crespo and Sinclair [41] reported that participants showed a tendency to generate pedagogically valuable problems only, neglecting to consider the mathematical aspects.
Studies have also reported teachers’ or PSTs’ strategies for developing and modifying assessment items. Crespo [40] examined the changes in a group of elementary PSTs’ problem posing strategies over time. Whereas preservice teachers’ initial strategies tended to make problems easy to solve and to pose familiar problems and problems blindly, later problem posing practices significantly differed by employing multiple approaches, more complex cognitive demands, and fewer leading questions.
Vistro-Yu [48] claimed that there are benefits to revising existing problems, for example, through replacement, addition, modification, contextualization, inversion, and reformulation. In an analysis of secondary and middle school teachers’ problem posing practices, Stickles [49] also categorized teachers’ problem reformulation strategies. These include changing contexts, simplifying the original problem, extending the problem by adding assumptions or constraints or by posing a generalized version of the original problem, switching the provided and sought information, combining two or more of these strategies, and simply changing the wording. Stickles’ study [49] reported that both preservice and in-service teachers struggled to generate their own problems, whereas they had more success in reformulating existing problems. These studies showed that teachers and PSTs use varied strategies to generate or reformulate mathematical problems but experience difficulties posing mathematically as well as pedagogically sound problems. This warrants further support and education for teachers. In general, this literature review suggests that teachers’ problem-posing ability is closely related to their diagnostic competence and that there is a need to further investigate teachers’ competence in posing and calibrating assessment items to better support teachers. Thus, our expectation is that the approach in this study will contribute to improving teacher education programs.
3. Methods
3.1. Participants and Context
The participants in this study were 57 undergraduate PSTs enrolled in three sections of a required elementary mathematics methods course in a midwestern university in the United States. Participation in the study was voluntary, and there was no excluded participant. The first two authors of this article were the instructors of these sections. They shared key course activities and assignments. Declining to participate was made available for all students, while students who took part in research did not receive extra course credit, and the study began after students’ course grades had been posted. Participants had successfully completed two mathematics content courses focusing on number theory and geometry prior to this methods course. For most participants, this was their last or second-to-last semester before beginning their one-semester student teaching experience. PSTs were required to have some field experiences throughout the program at local schools for participatory observation and limited levels of instruction under the supervision of cooperating teachers. For this methods course, the PSTs were required to develop an assessment and conduct a one-on-one interview with a student in the field. At the time of data collection, the PSTs had reviewed fraction-related Common Core State Standards [11,50] for various grades and had explored fraction progressions across grades 3–5. Before developing their own assessment items, PSTs examined existing sample assessment items in the standardized assessments that aligned with CCSS [11,50].
3.2. Tasks and Data Collection
The data were collected from a multi-phased course assignment that asked PSTs to develop a diagnostic assessment for a fourth-grade student, conduct a one-on-one assessment interview, and reflect upon the results. As shown in Figure 2, the entire project occurred in five phases throughout a semester. Out of this multi-phased process, the scope of the present study is limited to the data collected in Phases 2 and 3, which, for each PST, contained three sets of tasks with three tiered questions each and anticipated student confusion. The PSTs completed this assignment (see Appendix A) within and outside of class time.
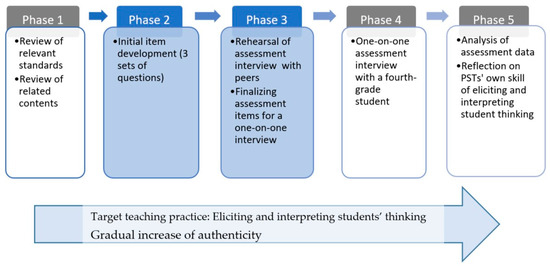
Figure 2.
One-on-one assessment development progression.
This assignment (as the instrument in this study) was intended to develop PSTs’ skills at eliciting and interpreting individual students’ thinking, which is considered to be a high-leverage practice [43] in which teachers must be competent in assessing student thinking or else they might face significant obstacles in their efforts to teach effectively [51]. This study designed this assignment to create the opportunity for the participants to experience the task design as an integral part of assessment practices with varying degrees of authenticity throughout the process, from practicing with peers in a university classroom to conducting an interview with a fourth-grade student in a field setting. In the development of the instrument, we intentionally focused on fractions because they are considered to be high-leverage content in elementary curriculum [45,52]. More specifically, the study required the PSTs to use specific representations (area and linear models) in the first two question sets and left open the representation option for the last question set to see how they utilize various representation modes in posing questions. The task also required the PSTs to present tiered questions—a core, less-challenging, and more-challenging question each—to identify their strategies in eliciting and interpreting different students’ thinking.
In Phase 2, each PST independently developed three sets of assessment items. In written planning documents, PSTs identified related standards and anticipated student confusion/difficulties and solution strategies. In this process, PSTs were allowed to search for references and sources to design their assessment items (e.g., curriculum standards document, sample standardized assessment items). The assignment required the PSTs to incorporate specific representations, content, and skills in each set of questions. Table 1 shows the required components and target standards for each question set.

Table 1.
Required components and target standards for each question set.
The first set of tasks aimed at assessing students’ understanding of fraction concepts using the area model, and the second set used the number line representation. The third set asked students to compare fractions. Each set of tasks also consisted of three tired questions, which are (1) a core question, (2) a less challenging question, and (3) a more challenging question, to calibrate the level of questions according to the individual students. PSTs were not required to provide justifications other than presenting tiered problems. However, some PSTs chose to provide written justifications in the planning document. The PSTs also prepared follow-up prompts to effectively elicit students’ thinking. In Phase 3, the PSTs conducted a rehearsal with peers to try out their plans and finalize the assessment items.
This study utilized two main data sources, which were written or drawn in the planning document: (a) student confusion/difficulties as anticipated by PSTs and (b) three sets of tasks (9 questions) that each PST designed.
3.3. Data Analysis
As an exploratory empirical study, this study aimed to find trends within the data and reflect on their meaning [53]. Instead of formal hypothesis testing, we performed inductive content analysis by using data-driven open coding [54,55]. To do so, all work samples (n = 82) from the PSTs (i.e., three tiered questions each PST developed in each set of tasks) were collected for analysis. We analyzed tasks (n = 57) only when tiered questions aligned with mathematical content and representation. Excluded tasks included those that did not present all three-tiered tasks and those that did not incorporate required components (i.e., relevant standards, required representation, see Table 1). The tasks were analyzed the way PSTs differentiated the questions’ level of difficulty (e.g., from the core to the less challenging question and from the core to the more challenging question). In particular, we analyzed the aspects PSTs maintained or modified in the three sets of questions. Initially, the researchers independently reviewed the three sets of tasks from each PST to identify recurring themes and intentions. Later, the research team jointly compared coding structures, reconciled differences, and refined the independently identified themes. Once we identified the themes for coding, two research assistants jointly coded the data using the coding scheme so that the discussion on coding discrepancies could be resolved immediately. Upon completion of coding, we identified the frequencies of coded themes. In the results section, we used selected examples of posed problems to illustrate the common themes identified.
4. Findings
In reporting results, we described the overall patterns evident across question sets and explained the PST’s differentiation strategies used in each set. Additionally, we reported frequencies to show the distribution of PST strategies. As each PST’s work reveals multiple aspects and strategies, we coded our analysis concerning one piece of a PST’s work into multiple categories, resulting in some categories totaling more than 100%.
4.1. PSTs’ Anticipation of Student Difficulties
Three student difficulty themes emerged across all three questions (see Table 2): difficulties in (a) understanding basic concepts related to fractions (e.g., equal partitioning, recognizing a fraction as a number), (b) knowing and applying rules/algorithms, and (c) understanding equivalent fractions. Notably, Question 2 (about the use of the number line representation) had fewer expected difficulties in the basic concept. In Question 3 (comparing fractions), PSTs largely anticipated students’ confusion with the rules associated with comparing fractions. Other themes did not appear across all three questions but still are worth mentioning. First, PSTs did not anticipate any representation-related issues for Question 3 where the use of representation was not specified. Second, PSTs anticipated some student difficulties in Questions 2 and 3 when improper fractions or mixed numbers were used or the size of fractions increased. Third, no one anticipated such difficulties for Question 1. Fourth, PSTs did not anticipate that directions or question formats would cause difficulties in Questions 1 and 2.

Table 2.
Student difficulties to address in assessment (as reported by PSTs).
4.2. Unaltered Aspect of Assessment
When asked to adjust a core question to be more or less challenging to diagnose individual students’ thinking, some PSTs either made minor changes or chose not to change.
Aspects commonly unaltered in the modifications of the three question sets. Table 3 shows the aspects PSTs retained when proposing questions at adjusted levels of difficulty.

Table 3.
How PSTs maintained assessment items.
A majority of PSTs did not make substantial changes in the categories of directions, type/format of the question, and the use of contextualization when asked to modify the questions. Overall, PSTs preferred to use short-answer questions and decontextualized questions. There were only two cases in which most of the aspects were changed. Figure 3 shows some examples of how PSTs maintained components of questions.
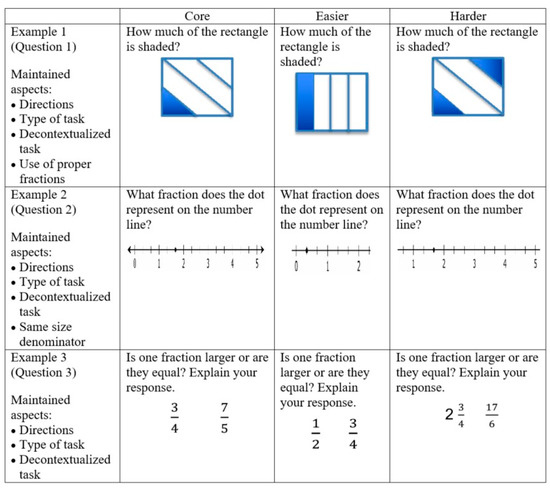
Figure 3.
Maintained aspects of assessment items.
In all examples (Figure 3), directions, types of question (i.e., short-answer questions), and contextualization (i.e., asking context-free questions) remained. This suggests that PSTs may believe that directions, types of questions, and contextualization were not critical for making accurate diagnostic assessment items.
Retained aspects appeared in specific question sets. Although there were common aspects PSTs tended to maintain across all three questions, some maintained aspects were more specific to each question (see Table 4).

Table 4.
Maintained aspects for Questions 1, 2, and 3.
Aspects unaltered in specific questions. In Question 1, a majority of PSTs tended not to change the whole from one whole shape (e.g., one square, one circle, one rectangle), and, in some cases, PSTs used the exact same shapes. More PSTs retained the use of congruent parts, where the size of the unit fraction was obvious, while fewer PSTs retained non-congruent parts across differentiated questions. In Question 2, PSTs maintained the presentation of number lines’ key components of numbers. In particular, most PSTs used number lines that clearly labeled whole numbers across differentiated questions. For Question 3, in which they were not required to use a specific representation, the majority of PSTs left it as a symbol-only question.
4.3. Modification Strategies
This section summarizes modification strategies that led to substantial changes among tiered assessment items. Of those substantial changes, PSTs made a wide range of modifications.
Modification strategies in three question sets. When PSTs attempted to adjust the questions’ level of difficulty, they used several common strategies across all three questions (see Table 5). The main categories in Table 3 and Table 5 are similar, but details (i.e., subcategories) are different. Whereas subcategories in Table 3 report retained aspects, subcategories in Table 5 show modified aspects.

Table 5.
Modification strategies in three question sets.
To make questions less challenging, the PSTs changed fractions into unit fractions or fractions with smaller denominators. To make questions more challenging, PSTs changed the fractions into non-unit fractions or fractions with larger denominators. To modify questions to be more difficult, the PSTs used relatively more open-ended tasks and pressed for student explanations.
Although the “bigger the denominator, the harder the problem” strategy was popular among PSTs when making questions more difficult, it is worthwhile to note that changing the size of denominators did not seem to result in their intended difficulty. Figure 4 shows cases where the adjusted size of denominators did not have much of an impact on the level of difficulty.
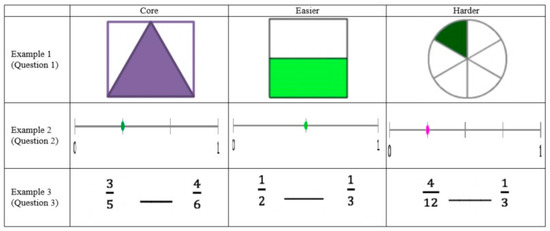
Figure 4.
Examples in which a larger denominator does not increase item difficulty.
In example 1, one PST justified his/her change by providing a written comment that the larger denominator (6) would make the question more challenging than the smaller denominator (2) had. In example 3, the PST used the “bigger the denominator, the harder the problem” strategy as well, but we believe that the core question could have been made more challenging still.
The PSTs used another general modification strategy using unit fractions or non-unit proper fractions for less challenging questions and mixed numbers or improper fractions for more challenging questions. In Question 1, it is notable that only one PST used a mixed number to make a question more challenging, whereas all other PSTs used fractions less than 1 when asked to use the area model of fractions. This may have to do with PSTs’ anticipation of students’ difficulties presented earlier. For Question 1, the PSTs did not anticipate any difficulties due to the types of fractions used (e.g., improper fractions or mixed numbers).
Modification strategies in specific question sets. The PSTs used some question-specific modification strategies, as shown in Table 6. The main categories in Table 4 and Table 6 are similar, but details (i.e., subcategories) are different. Whereas subcategories in Table 4 report retained aspects, subcategories in Table 6 show modified aspects.

Table 6.
Modification strategies in Questions 1, 2, and 3.
In Question 1, PSTs used two major modification strategies using a simpler or more complicated shape as a whole and differentiating the arrangement of parts. As shown in Figure 5, a PST demonstrated these strategies. To make the question easier, the PSTs used a rectangle as a whole and arranged all shaded parts continuously so that the numerator could be easily identified. For the harder question, an atypical shape was used as the whole, and the numerator parts were discrete. One observation to note here is that PSTs defined the entire shape as the whole, whether it was typical or atypical so that shaded part of the figure always represents a value less than 1. In the example in Figure 5, the harder question still represented 2/6 of the whole. It was very rare for PSTs in Question 1 to create a composite figure representing an improper fraction or mixed number.
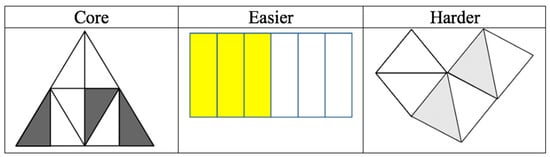
Figure 5.
Examples in which an entire composite figure serves the reference unit so that the figure represents a proper fraction only.
For Question 2, a popular strategy PSTs used was adding or deleting key components of the number line. To make a question harder, some PSTs presented an incomplete or empty number line or a number line that does not show the location of zero (see Figure 6).
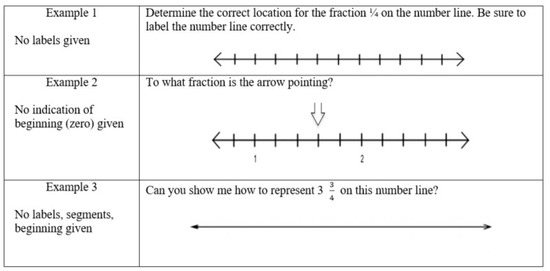
Figure 6.
Strategies that omit various components of the number line in Question 2.
For Question 3, PSTs utilized either like or unlike denominators. In particular, many PSTs used two fractions—one fraction with a specific denominator and another that could be easily simplified to have that same denominator. For their challenging questions, PSTs presented a set of fractions with different denominators. Within this set of fractions, the denominators were co-prime or such that a quick simplification could not make them the same. A word of caution: just like the “bigger the denominator, the harder the problem” strategy, the “unlike denominator makes the problem harder” strategy did not result in the intended outcome, as shown in Table 7.

Table 7.
Cases where unlike denominators were used did not increase the level of difficulty in Question 3.
In these examples, despite PSTs’ intentions, it is unclear whether the questions labelled “harder” are more challenging than the core. In example (a), it is not convincing that comparing two unit fractions is more challenging than the presented core question. In example (b), if students notice that both fractions are one part away from the whole, it could be a much easier question than the presented core question. Examples (c–e) contain one improper fraction and one proper fraction. This means that an easy comparison is possible without further computations.
As reflected in PSTs’ answer keys, some proposed an algorithm to find a common denominator to compare fractions (e.g., to compare a/b and c/d, multiply each fraction by the denominator of the other whether it is absolutely needed for comparison: ((a × d))/((b × d)) ___ ((c × b))/((d × b))). The PST who developed example (b) presented the following explanation for comparing 5/6 and 7/8:
The larger fraction is 7/8. In order for the fractions to be compared, a common denominator has to be found. Looking at the denominators, 48 is a multiple of both 6 and 8. In this case, 5/6 cannot be multiplied by a factor of 6/6, and 7/8 cannot be multiplied by 8/8 because that would still result in opposite denominators. Instead, 5/6 has to be multiplied by 8/8 and 7/8 by 6/6 in order for there to be a common denominator of 48. Once each fraction has been multiplied, 5/6 is now 40/48 and 7/8 is now 42/48. Looking at the numerators, 42 is the larger of the two numbers, making it the larger fraction.
This may be linked with the PSTs’ anticipation of student difficulties. For Question 3, most PSTs were concerned with knowing and using rules associated with comparing fractions.
5. Discussion
This study uncovered the PSTs’ collective thoughts on the design of diagnostic assessments. In this section, we revisit the results from this study and address remaining questions developed around several issues that would initiate further research and have implications for teacher education programs.
5.1. Awareness of Varied Levels of Sophistication
Our results suggest that the PSTs were quite well versed in students’ cognitive difficulties. There were various types of students’ errors, misconceptions, and confusion that PSTs anticipated across three questions. These anticipated difficulties echo a concept Yang and Ricks [8,35] called a difficult point. The variety of difficulty levels in our study suggests that PSTs may understand the common errors or misconceptions fourth-grade students may hold in relation to learning the main mathematical concepts/ideas about fractions. We could call this the key point. Understanding key and difficult points was necessary for PSTs to differentiate between levels of difficulty (i.e., the critical points) and correctly diagnose students’ needs and provide support. This implies that as teacher educators work to support PSTs to develop diagnostic competence, the hard work will lie in fostering PSTs’ knowledge of key and difficult points concerning fractions to effectively differentiate assessment items (i.e., maintaining or modifying) and devise instructional strategies that help their students overcome the critical point of fractions.
Several researchers [9,10,37] raised concerns about PSTs’ diagnostic competence. Our results tell us that, with appropriate training, PSTs (novice teachers) can develop from their preparation programs as good problem posers. However, our results indicate that all PSTs do not necessarily have the same level of understanding of the key point and the difficult point, as shown in the varying sophistication of their responses. In particular, we note that more than one-third of PSTs simply said that not knowing rules or algorithms were the anticipated student difficulties for Questions 1 and 3. Although not knowing rules or algorithms can be one of the difficulties, it does not tell us much about students’ mathematical understanding. Some students may be able to perform the algorithm by memorization without understanding, whereas others may not be able to perform the algorithm even though they have a good understanding of the target concepts. Given this situation, one immediate challenge for mathematics teacher educators is how to help PSTs examine students’ learning trajectories or learning progressions to develop sophisticated identification of the key point, the difficult point, and the critical point.
5.2. Consideration of Mathematical Aspects and Pedagogical Aspects
The strategies these PSTs used to modify the core questions into more and less challenging questions were mostly related to mathematical aspects of the questions. The PSTs did not change the three questions significantly in terms of directions, type/format, or use of contextualization. The PSTs were somewhat persistent in keeping questions short and decontextualized. As a “modify” strategy, they resorted to methods such as “the bigger the denominator, the harder the problem”, “no mark on the number line makes the question harder”, and “unlike fractions make harder”, in Questions 1, 2, and 3, respectively. Liljedahl and colleagues [46] argued that teachers should consider both pedagogical aspects and mathematical aspects when designing or modifying tasks. The strategies the PSTs used in modifying questions showed how the PSTs unevenly addressed those aspects of the questions. More specifically, the PSTs attended more to mathematical aspects (e.g., by changing the size of fractions) of the core questions and less to pedagogical aspects (e.g., changing the directions of questions). This may be different from the tendency Crespo and Sinclair [41] reported about their PSTs’ problem-posing behavior. One conjecture explaining this discrepancy is that the PSTs in our study were asked to both pose and modify questions. The modification process, however, may have led the PSTs to attend more to the mathematical aspects of the questions. Our intent is not to debate pedagogy versus mathematics here. It is only natural to assume beginning mathematics educators have varied levels of mathematical knowledge and pedagogy. We also remain cautious about what exactly the mathematical aspects predicate here, since the mathematics may range from modifying a surface property of mathematical structure, carrying out procedures seamlessly, to engaging in high-level thinking and reasoning about mathematics [56,57]. Although “the bigger the denominator, the harder the problem”, is only a surface property that fails to capture the intrinsic mathematical property of the quotient (see [56] for different reasoning types in mathematics), our results suggest that PSTs still view assessment as consisting of mathematics and cognition of knowledge and skills. As such, teacher educators need to provide PSTs with opportunities to understand assessments as various tools capable of catering to the different ways students understand mathematics. Needless to say, if teachers are expected to be effective mathematics problem posers and modifiers, teacher educators must integrate problem posing and modifying into their instructional activities to support PSTs in developing that diagnostic competence. That said, teacher educators should scaffold PSTs’ learning so that they learn to pose and modify questions, addressing the mathematical aspects including procedures, concepts, and mathematical thinking and reasoning, as well as the dimensions outside of mathematical aspect too.
5.3. Calibration of Intended Difficulty
Some strategies used by PSTs to modify the core questions into harder questions did not necessarily make the core questions harder as intended. It could be that the PSTs were still developing their ability to apply the knowledge of students’ difficult point into their modification of questions. It could also be that the PSTs needed to learn more about how students develop their sense of fractions. Related to this, Crespo [40] found that PSTs initially tend to lower problem difficulty so that it is easy for students to solve. They design problems familiar to students at first. Later, they employ multiple strategies as they engage in problem-posing practices. In posing and modifying questions, the PSTs in our study were required to modify the core questions into both easier and harder questions. Borrowing Crespo’s language [40], we posit that the PSTs in our study may have employed multiple strategies as they were modifying existing questions. The significance of this finding is that our PSTs could use multiple strategies to modify questions, but the strategies they use may not result in their intended level of difficulty. Many mathematics teachers, regardless of experience, find existing mathematics assessment items to use in their classrooms (as assessment resources are increasingly readily available, especially online). Teachers may need to modify these items to meet their classroom contexts. Therefore, as PSTs learn to modify questions, teacher educators should address the misuse of these strategies, which was observed in our study.
5.4. Limitations of the Study
The scope of this study was the participants’ experiences of designing diagnostic assessments in the domain of fractions. Although it was a deliberate choice—as it is considered a high-leverage content area in the elementary curriculum—the topic itself might have been a challenge for some PSTs. It is known as one of the more difficult areas of curriculum for many students and teachers. Asking participants to work on one domain could be a limitation of this study. We might have elicited different results if other mathematical domains were included. In addition, PSTs developed their own core questions and adjusted difficulty levels. As a result, some PSTs’ core questions were much harder or easier than others. Future studies may investigate what kinds of strategies emerge when starting with the same core questions in order to capture the level of sophistication in both task-general and task-specific modification strategies.
6. Conclusions
To summarize, this study found (in response to the first research question: how do PSTs anticipate student confusion/difficulties in solving fraction problems?) that the participants were cognizant of students’ various cognitive difficulties including types of students’ errors, misconceptions, and confusion, but that they had a limited knowledge about the specific nature or condition of student thinking and reasoning leading to misconception and confusion. The study also found (in response to the second research question: what strategies do PSTs use in designing diagnostic assessments to adjust the levels of assessment tasks?) that the participants chose to revise the shapes of a whole and the parts, the labels on the number line, the values of numerators and denominators, the type/directions of the task, the type of fractions, and the task contexts. Lastly, this study found (in response to the third research question: how do PSTs’ strategies differ depending on target concepts or representations used in the tasks?) that the participants attended predominantly to the procedural and arithmetical aspect of the task with numerators and denominators as well as the mathematical aspect of the task to (de)composing the shapes of a whole and the parts and representing fractions on a number line diagram. Further, the study found that the participants were not as much attentive to the task for improving the directions, contexts, and the problem type/format. Most importantly, the participants used multiple strategies to modify questions, though, the strategies they used were not successful in achieving their intended level of difficulty.
Although limited by its exploratory nature, the results of this study can contribute to improving mathematics teacher education in which our design and results could be incorporated into mathematics methods courses. This study can also contribute to the literature as the results indicate PSTs’ diagnostic competence as unknown or inexperienced (see [58]) can be discerned and characterized as consisting of distinctive domains such as using, designing, or evaluating diagnostic assessment items. Further, this study shows PSTs could benefit from hands-on activities of assessment design regarding how the key, difficult, and critical points of a mathematical concept closely relate to each other. This study also shows that teacher educators need to ensure PSTs have the opportunity to use differentiated assessment items with diverse students. PSTs then need the opportunity to analyze their efforts to differentiate assessment items to determine if they succeeded in identifying students’ needs, thereby improving their learning. As such, teacher educators should provide PSTs the opportunity to engage in problem posing activities, such as mathematical assessment projects, and provide them with the opportunity to discuss their understanding of students’ difficulties with peers (see also [59]). Doing this consistently will not only help increase the PSTs’ knowledge of key, difficult, and critical points of fractions and other mathematical concepts in elementary school but will also encourage PSTs to practice differentiating assessments. In the future, the study plans to tie in other phases in the assessment curriculum (see Figure 2) so that we can gain clear insight into PSTs’ learning to develop appropriate assessment practices in teacher education. To confirm and expand the results from this exploratory study in the US context, future research on PSTs’ diagnostic competence in other countries could investigate the cycle involved in modifying assessment items and describe similarities and differences. Such cross-cultural comparison has the potential [60] to add much to the international comparative studies (e.g., [61] about comparing educational systems in Finland and Singapore) about PSTs’ diagnostic competence. PSTs can implement an assessment item on students, re-modify the item, and then implement it again. In using authentic assessment data, we could learn more about how PSTs in different cultures or education systems develop assessment skills, make appropriate instructional decisions, and implement effective strategies.
Author Contributions
Conceptualization, J.-E.L. and W.L.; Data curation, J.-E.L. and B.P.; Formal analysis, B.P. and W.L.; Funding acquisition, J.-E.L. and W.L.; Investigation, J.-E.L., B.P. and W.L.; Methodology, J.-E.L. and W.L.; Project administration, J.-E.L.; Writing—original draft, J.-E.L., B.P. and W.L.; Writing—review—editing, J.-E.L. and W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Yonsei University Research Grant 2020-22-0457.
Institutional Review Board Statement
The study was approved by the Institutional Review Board of Oakland University (Project # 526015-1 approved on 4 November 2013).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Directions for Math Assessment Planning Document
Assessment Items: Develop three sets of fraction-related questions.
- (1)
- Question Set #1
- Target standard: understand a fraction 1/b as the quantity formed by 1 part when a whole is partitioned into b equal parts; understand a fraction a/b as the quantity formed by a pieces of 1/b.
- Required representation to include: Area model
- (2)
- Question Set #2
- Target standard: understand a fraction as a number on the number line; represent fractions on a number line diagram.
- Required representation to include: a number line model
- (3)
- Question Set #3
- Target standard: explain the equivalence of fractions in special cases and compare fractions by reasoning about their size.
- Representation to include: use any representation of your choice.
For each question set, be sure to include the following components:
- (1)
- Present a core question.
- (2)
- Anticipated confusion: list particular aspects of math content that may be potentially confusing or misconstrued by the student.
- (3)
- Follow-up questions: refer to the mathematical goals and possible student confusion. Thinking of various possible scenarios, list follow-up questions/prompts that will either confirm students’ understanding or reveal students’ misconceptions.
- (4)
- Differentiated questions: prepare at least one less challenging question (i.e., easier than the core question) and one advanced question (i.e., harder than the core question) for differentiation.
- (5)
- Answer key: provide the answer key for core questions and follow-up questions along with your explanations (your explanations should be appropriate for the target grade level). A completed key should also show your note regarding correct concept applications and appropriate pedagogies.
You may use this as a template. Make sure to fill in all required components.
Question Set #
| Target Standard: |
| Core question: |
| Anticipated confusion: |
| Follow-up questions: |
Differentiated questions
|
| Answer key: |
References
- Feiman-Nemser, S. From preparation to practice: Designing a continuum to strengthen and sustain teaching. Teach. Coll. Rec. 2001, 103, 1013–1055. [Google Scholar] [CrossRef]
- Cooney, T.J. Teachers’ decision making. In Mathematics, Teachers and Children; Pimm, D., Ed.; Hodder & Stoughton: London, UK, 1988; pp. 273–286. [Google Scholar]
- Krolak-Schwerdt, S.; Glock, S.; Böhmer, M. (Eds.) Teachers’ Professional Development: Assessment, Training, and Learning; Sense Publishers: Rotterdam, The Netherlands, 2014. [Google Scholar]
- van de Pol, J.; Volman, M.; Oort, F.; Beishuizen, J. The effects of scaffolding in the classroom: Support contingency and student independent working time in relation to student achievement, task effort and appreciation of support. Instr. Sci. 2015, 43, 615–641. [Google Scholar] [CrossRef] [Green Version]
- Choy, B.H.; Thomas, M.O.J.; Yoon, C. The FOCUS framework: Characterising productive noticing during lesson planning, delivery and review. In Teacher Noticing: Bridging and Broadening Perspectives, Contexts, and Frameworks; Schack, E.O., Fisher, M.H., Wilhelm, J.A., Eds.; Springer: Cham, Switzerland, 2017; pp. 445–466. [Google Scholar]
- Südkamp, A.; Kaiser, J.; Möller, J. Teachers’ judgments of students’ academic achievement. In Teachers’ Professional Development: Assessment, Training, and Learning; Krolak-Schwerdt, S., Glock, S., Böhmer, M., Eds.; Sense Publishers: Rotterdam, NL, USA, 2014; pp. 5–25. [Google Scholar]
- Vogt, F.; Rogalla, M. Developing adaptive teaching competency through coaching. Teach. Teach. Educ. 2009, 25, 1051–1060. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Ricks, T.E. Chinese lesson study: Developing classroom instruction through collaborations in school-based teaching research group activities. In How Chinese Teach Mathematics and Improve Teaching; Li, Y., Huang, R., Eds.; Routledge: New York, NY, USA, 2013; pp. 51–65. [Google Scholar]
- Prediger, S. How to develop mathematics-for-teaching and for understanding: The case of meanings of the equal sign. J. Math. Teach. Educ. 2010, 13, 73–93. [Google Scholar] [CrossRef]
- Edelenbos, P.; Kubanek-German, A. Teacher assessment: The concept of diagnostic competence. Lang. Test. 2004, 21, 259–283. [Google Scholar] [CrossRef]
- Common Core State Standards Initiatives. Common Core State Standards for Mathematics; National Governors Association Center for Best Practices and the Council of Chief State School Officers: Washington, DC, USA, 2010; Available online: http://www.corestandards.org/wp-content/uploads/Math_Standards1.pdf (accessed on 10 June 2020).
- Phelps-Gregory, C.; Spitzer, S. Developing prospective teachers’ ability to diagnose evidence of student thinking: Replicating a classroom intervention. In Diagnostic Competence of Mathematics Teachers. Mathematics Teacher Education; Leuders, T., Philipp, K., Leuders, J., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 11, pp. 223–240. [Google Scholar]
- Reinhold, S. Revealing and promoting pre-service teachers’ diagnostic strategies in mathematical interviews with first-graders. In Diagnostic Competence of Mathematics Teachers. Mathematics Teacher Education; Leuders, T., Philipp, K., Leuders, J., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 11, pp. 129–148. [Google Scholar]
- Kılıç, Ç. Pre-service primary teachers’ free problem-posing performances in the context of fractions: An example from Turkey. Asia-Pac. Educ. Res. 2013, 22, 677–686. [Google Scholar] [CrossRef]
- Lee, M.Y.; Lee, J. Pre-service teachers’ perceptions of the use of representations and suggestions for students’ incorrect use. Eurasia J. Math. Sci. Technol. Educ. 2019, 15, 1–21. [Google Scholar] [CrossRef]
- Confrey, J. Splitting, similarity, and rate of change: A new approach to multiplication and exponential functions. In The Development of Multiplicative Reasoning in Learning of Mathematics; Harel, G., Confrey, J., Eds.; State University of New York Press: New York, NY, USA, 1994; pp. 291–330. [Google Scholar]
- Lamon, S.J. Rational numbers and proportional reasoning: Toward a theoretical framework for research. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F.K., Jr., Ed.; Information Age Publishing: Charlotte, NC, USA, 2007; Volume 1, pp. 629–667. [Google Scholar]
- Steffe, L.P.; Olive, J. Children’s Fractional Knowledge; Springer: New York, NY, USA, 2010. [Google Scholar]
- Lamon, S.J. The development of unitizing: Its role in children’s partitioning strategies. J. Res. Math. Educ. 1996, 27, 170–193. [Google Scholar] [CrossRef]
- Steffe, L.P. Fractional commensurate, composition, and adding schemes: Learning trajectories of Jason and Laura: Grade 5. J. Math. Behav. 2003, 22, 237–295. [Google Scholar] [CrossRef]
- Lee, M.Y. Pre-service teachers’ flexibility with referent units in solving a fraction division problem. Educ. Stud. Math. 2017, 96, 327–348. [Google Scholar] [CrossRef]
- Olanoff, D.; Lo, J.; Tobias, J. Mathematical content knowledge for teaching elementary mathematics: A focus on fractions. Math. Enthus. 2014, 11, 267–310. [Google Scholar]
- Stoddart, T.; Connell, M.; Stofflett, R.; Peck, D. Reconstructing elementary teacher candidates’ understanding of mathematics and science content. Teach. Teach. Educ. 1993, 9, 229–241. [Google Scholar] [CrossRef]
- Rosli, R.; Han, S.; Capraro, R.; Capraro, M. Exploring preservice teachers’ computational and representational knowledge of content and teaching fractions. Res. Math. Educ. 2013, 17, 221–241. [Google Scholar] [CrossRef] [Green Version]
- van de Walle, J.; Karp, K.S.; Bay-Williams, J.M. Elementary and Middle School Mathematics: Teaching Developmentally, 8th ed.; Pearson: Upper Saddle River, NJ, USA, 2013. [Google Scholar]
- Cramer, K.; Whitney, S. Learning rational number concepts and skills in elementary classrooms. In Teaching and Learning Mathematics: Translating Research to the Elementary Classroom; Lambdin, D.V., Lester, F.K., Eds.; NCTM: Reston, VA, USA, 2010; pp. 15–22. [Google Scholar]
- Chong, Y.O. Teaching proportional reasoning in elementary school mathematics. J. Educ. Res. Math. 2015, 25, 21–58. [Google Scholar]
- Empson, S.B.; Junk, D.; Dominguez, H.; Turner, E. Fractions as the coordination of multiplicatively related quantities: A cross-sectional study of children’s thinking. Educ. Stud. Math. 2006, 63, 1–28. [Google Scholar] [CrossRef]
- Guo, W.; Wei, J. Teacher Feedback and Students’ Self-regulated Learning in Mathematics: A Study of Chinese Secondary Students. Asia-Pac. Educ. Res. 2019, 28, 265–275. [Google Scholar] [CrossRef]
- Black, P.; Wiliam, D. Assessment and Classroom Learning. Assess. Educ. 1998, 5, 7–74. [Google Scholar] [CrossRef]
- Nichols, P.D.; Meyers, J.L.; Burling, K.S. A framework for evaluating and planning assessments intended to improve student achievement. Educ. Meas. Issues Pract. 2009, 28, 14–23. [Google Scholar] [CrossRef]
- Tomlinson, C.A. How to Differentiate Instruction in Mixed-Ability Classrooms, 2nd ed.; Association for Supervision & Curriculum Development: Alexandria, VA, USA, 2001. [Google Scholar]
- Tomlinson, C.A.; Eidson, C.C. Differentiation in Practice: A Resource Guide for Differentiating Curriculum, Grades 5–9; Association for Supervision and Curriculum Development: Alexandria, VA, USA, 2003. [Google Scholar]
- Kaplan, H.A.; Argün, Z. Teachers’ diagnostic competences and levels pertaining to students’ mathematical thinking: The case of three math teachers in Turkey. Educ. Sci. Theory Pract. 2017, 17, 2143–2174. [Google Scholar]
- Yang, Y.; Ricks, T.E. How crucial incidents analysis support Chinese lesson study. Int. J. Lesson Learn. Stud. 2012, 1, 41–48. [Google Scholar] [CrossRef]
- Lee, M.Y.; Choy, B.H. Mathematical teacher noticing: The key to learning from Lesson Study. In Teacher Noticing: Bridging and Broadening Perspectives, Contexts, and Frameworks; Schack, E.O., Fisher, M., Wilhelm, F., Eds.; Springer: New York, NY, USA, 2017; pp. 121–140. [Google Scholar]
- Jang, E.E.; Wagner, M. Diagnostic feedback in language classroom. In Companion to Language Assessment; Kunnan, A., Ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2013; Volume II, pp. 693–711. [Google Scholar]
- Singer, F.M.; Ellerton, N.F.; Cai, J. (Eds.) Mathematical Problem Posing: From Research to Effective Practice; Springer: New York, NY, USA, 2015. [Google Scholar]
- Cai, J.; Chen, T.; Li, X.; Xu, R.; Zhang, S.; Hu, Y.; Zhang, L.; Song, N. Exploring the impact of a problem-posing workshop on elementary school mathematics teachers’ conceptions on problem posing and lesson design. Int. J. Educ. Res. 2020, 102, 101404. [Google Scholar] [CrossRef]
- Crespo, S. Learning to pose mathematical problems: Exploring changes in preservice teachers’ practices. Educ. Stud. Math. 2003, 52, 243–270. [Google Scholar] [CrossRef]
- Crespo, S.; Sinclair, N. What makes a problem mathematically interesting? Inviting prospective teachers to pose better problems. J. Math. Teach. Educ. 2008, 11, 395–415. [Google Scholar] [CrossRef]
- Olson, J.C.; Knott, L. When a problem is more than a teacher’s question. Educ. Stud. Math. 2013, 83, 27–36. [Google Scholar] [CrossRef]
- TeachingWorks (n.d.-a). High-Leverage Practices. Available online: http://www.teachingworks.org/work-of-teaching/high-leverage-practices (accessed on 5 December 2019).
- Ketterlin-Geller, L.R.; Shivraj, P.; Basaraba, D.; Yovanoff, P. Considerations for using mathematical learning progressions to design diagnostic assessments. Meas. Interdiscip. Res. Perspect. 2019, 17, 1–22. [Google Scholar] [CrossRef]
- TeachingWorks (n.d.-b). High-Leverage Content. Available online: http://www.teachingworks.org/work-of-teaching/high-leverage-content (accessed on 5 December 2019).
- Liljedahl, P.; Chernoff, E.; Zazkis, R. Interweaving mathematics and pedagogy in task design: A tale of one task. J. Math. Teach. Educ. 2007, 10, 239–249. [Google Scholar] [CrossRef]
- National Council of Teachers of Mathematics. Procedural Fluency in Mathematics: A position of the National Council of Teachers of Mathematics; NCTM: Reston, VA, USA, 2014. [Google Scholar]
- Vistro-Yu, C. Using innovation techniques to generate ‘new’ problems. In Mathematical Problem Solving: Yearbook 2009; Kaur, B., Yeap, B.H., Kapur, M., Eds.; Association of Mathematics Education and World Scientific: Singapore, 2009; pp. 185–207. [Google Scholar]
- Stickles, P. An Analysis of Secondary and Middle School Teacher’s Mathematical Problem Posing. Unpublished. Ph.D. Dissertation, Indiana University, Bloomington, IN, USA, 2006. [Google Scholar]
- National Governors Association Center for Best Practices & Council of Chief State School Officers. Common Core State Standards; National Governors Association Center for Best Practices & Council of Chief State School Officer: Washington, DC, USA, 2010; Available online: https://ccsso.org/resource-library/ada-compliant-math-standards (accessed on 10 June 2020).
- Ball, D.; Forzani, F. Building a common core for learning to teach: And connecting professional learning to practice. Am. Educ. 2011, 35, 17–21, 38–39. [Google Scholar]
- Lewis, G.; Perry, R. Lesson study to scale up research-based knowledge: A randomized, controlled trial of fractions learning. J. Res. Math. Educ. 2017, 48, 261–299. [Google Scholar] [CrossRef]
- Creswell, J.W. Research Design: Qualitative, Quantitative and Mixed Methods Approaches; Sage: Thousand Oaks, CA, USA, 2017. [Google Scholar]
- DeCuir-Gunby, J.T.; Marshall, P.L.; McCulloch, A.W. Developing and using a codebook for the analysis of interview data: An example from a professional development research project. Field Methods 2011, 23, 136–155. [Google Scholar] [CrossRef]
- Grbich, C. Qualitative Data Analysis: An Introduction, 2nd ed.; Sage: Thousand Oaks, CA, USA, 2013. [Google Scholar]
- Lithner, J. A research framework for creative reasoning. Educ. Stud. Math. 2008, 67, 255–276. [Google Scholar] [CrossRef]
- Stein, M.K.; Grover, B.W.; Henningsen, M. Building student capacity for mathematical thinking and reasoning: An analysis of mathematical tasks used in reform classrooms. Am. Educ. Res. J. 1996, 33, 455–488. [Google Scholar] [CrossRef]
- Shaughnessy, M.; Boerst, T.A. Uncovering the skills that preservice teachers bring to teacher education: The practice of eliciting a student’s thinking. J. Teach. Educ. 2018, 69, 40–55. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.-E.; Son, J.-W. Two teacher educators’ approaches to developing preservice elementary teachers’ mathematics assessment literary: Intentions, outcomes, and new learning. Teach. Learn. Inquiry ISSOTL J. 2015, 3, 47–62. [Google Scholar]
- Stigler, J.W.; Gallimore, R.; Hiebert, J. Using video surveys to compare classrooms and teaching across cultures: Examples and lessons from the TIMSS video studies. Educ. Psychol. 2000, 35, 87–100. [Google Scholar] [CrossRef]
- Lee, D.H.L.; Hong, H.; Niemi, H.A. Contextualized account of holistic education in Finland and Singapore: Implications on Singapore educational context. Asia-Pac. Educ. Res. 2014, 23, 871–884. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).