On the Connection between the GEP Performances and the Time Series Properties
Abstract
:1. Introduction
2. Materials and Methods
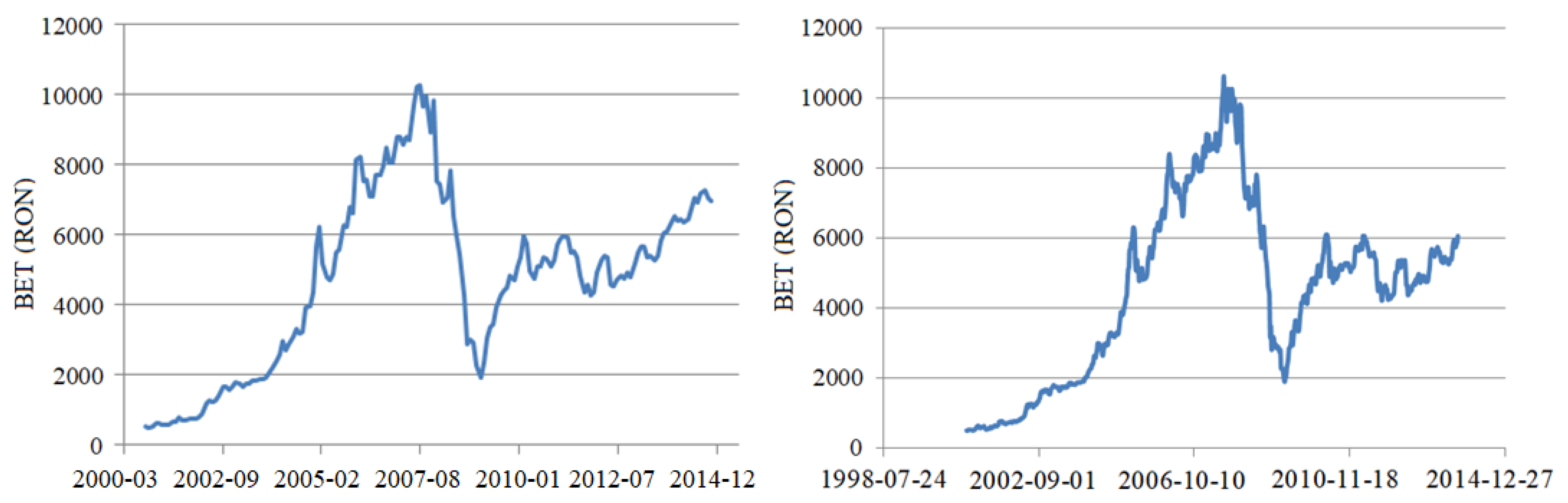
2.1. Studied Data and Statistical Tests
2.2. Methods
- (1)
- Create chromosomes of the initial population;
- (2)
- Express chromosomes and evaluate their fitness;
- If the stopping criterion is satisfied, designate results and stop;
- If stopping criterion is not satisfied, go to the next step;
- (3)
- Select chromosomes and keep the fittest for the next generation;
- (4)
- Perform genetic modifications via genetic operators and gene recombination;
- (5)
- Select next-generation individuals;
- (6)
- Go to (2).
- The window size, w, was considered between 1 and 12. In the following, we report only the overall best result experiments;
- The mutation rate of random constants: 0.01;
- Maximum number of iterations: 1000;
- Functions used in expressions: addition, subtraction, multiplication, division, square root;
- Linking function: addition.
- The fitness function is the mean squared error (MSE):
3. Results and Discussion
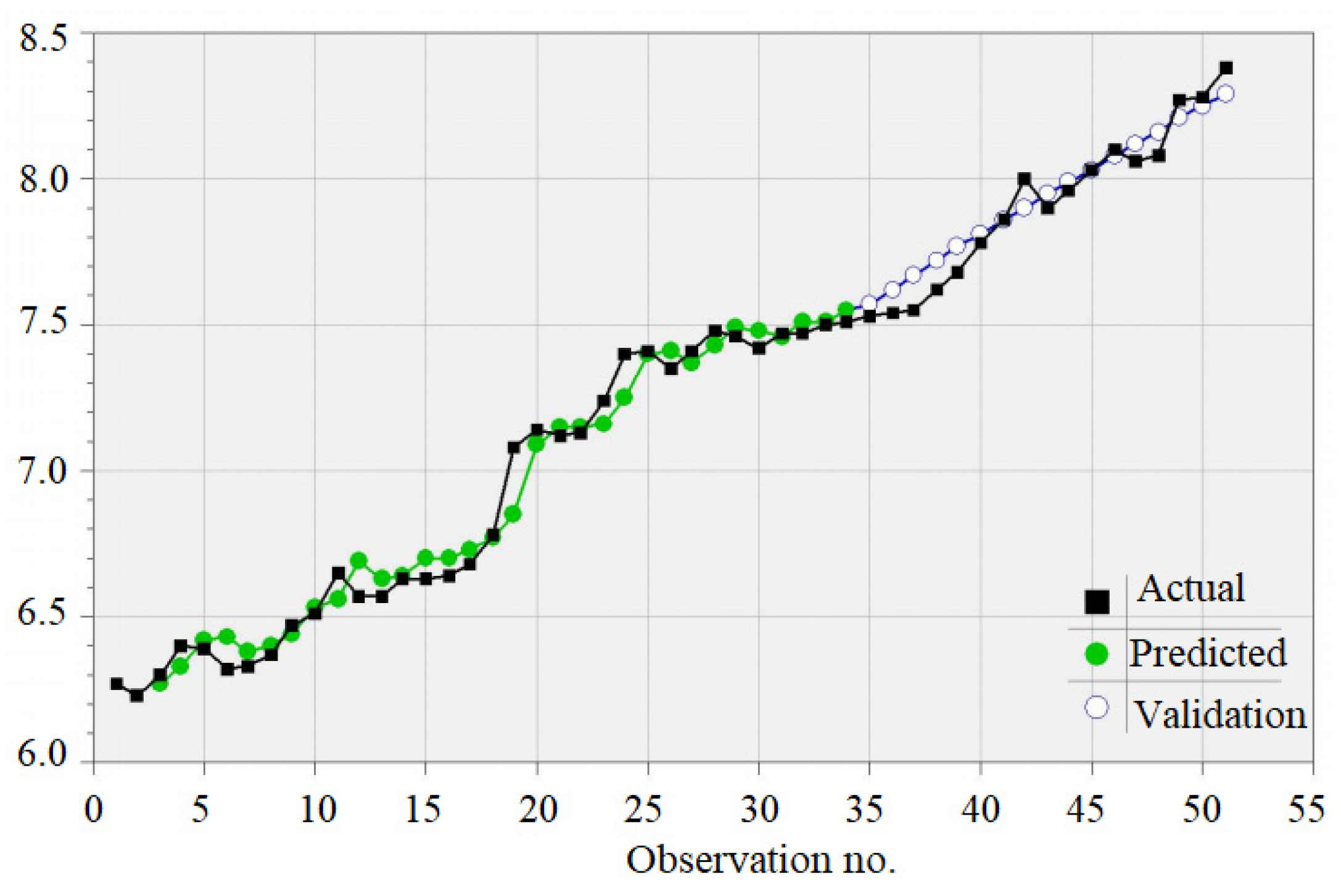
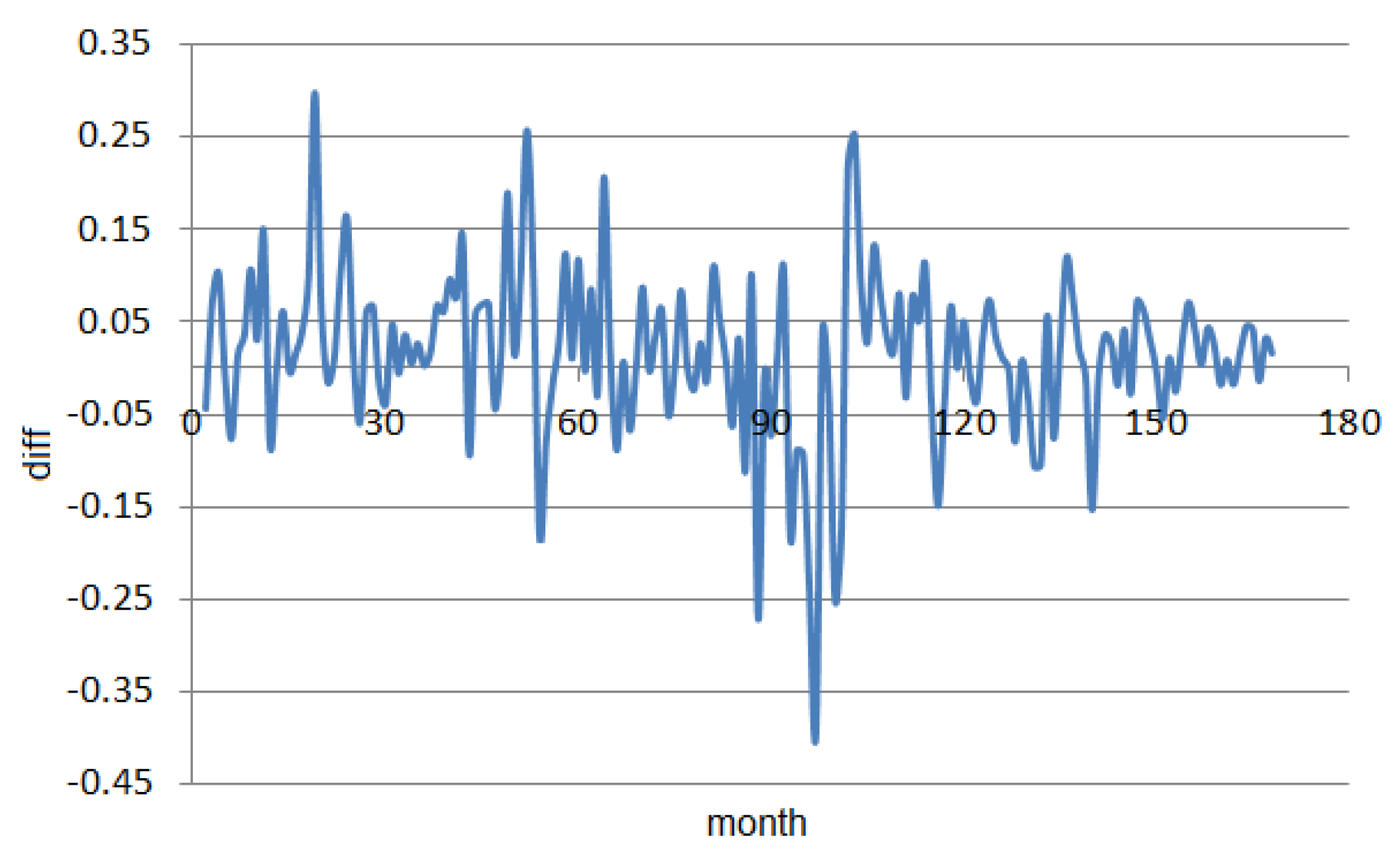
3.1. Results of Statistical Analysis and the GEP Models for the Monthly Series
3.2. Results of Statistical Analysis and the GEP Models for the Monthly Series
3.3. ARIMA Models for Monthly Series
- For S1_m, RMSE = 0.1788, MSE = 0.0320, MAE = 0.0759, MAPE = 1.1035;
- For S2_m, RMSE = 0.09165, MSE = 0.0084, MAE = 0.0638, MAPE = 0.7226;
- For S3_m, RMSE = 0.2200, MSE = 0.0484, MAE = 0.1594, MAPE = 1.8826.
- In terms of MAPE, the models for the detrended series are the worst.
- Taking into account RMSE, MSE, and MAE, the raw series models have similar performances with those for the detrended series for all but S3. Still, the model for S2_md is worse than for S2, since the first one does not satisfy the hypotheses on the residuals.
- In terms of MAPE, the ARIMA models for S2_ms and S4_ms are better than those of S2_m and S4_m. Even if the MAPE for S1_ms is smaller than for S1_m, the residual is not white noise, so the first model cannot be considered better than the corresponding one for the raw data series.
- Comparative results have been obtained for U1_m and U1_ms.
- The other goodness of fit indicators generally have comparative values for the rest of the initial and deseasonalized series.
3.4. ARIMA Models for Weekly Series
4. Conclusions
- (1)
- The normality and homoskedasticity do not have a major influence on the models’ performances;
- (2)
- The trend removal results in better GEP models;
- (3)
- The seasonality elimination does not lead to an improvement of the modeling quality.
- (4)
- The trend removal results in worse ARIMA models;
- (5)
- Generally, GEP performed better than ARIMA on the study series.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sinclair, T.M.; Stekler, H.O.; Kitzinger, L. Directional forecasts of GDP and inflation: A joint evaluation with an application to Federal Reserve predictions. Appl. Econ. 2008, 40, 2289–2297. [Google Scholar] [CrossRef]
- Wagner, N.; Michalewicz, Z.; Khouja, M.; Mcgregor, R.R. Time series forecasting for dynamic environments: The dyfor genetic program model. IEEE Trans. Evol. Comput. 2007, 11, 433–452. [Google Scholar] [CrossRef] [Green Version]
- Box, G.; Jenkins, G. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, FA, USA, 1970. [Google Scholar]
- Li, Z.; Han, J.; Song, Y. On the forecasting of high-frequency financial time series based on ARIMA model improved by deep learning. J. Forecast. 2020, 39, 1081–1097. [Google Scholar] [CrossRef]
- Pahlavani, M.; Roshan, R. The Comparison among ARIMA and hybrid ARIMA-GARCH Models in Forecasting the Exchange Rate of Iran. Int. J. Bus. Dev. Stud. 2015, 7, 31–50. [Google Scholar]
- Hamilton, J. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Kuan, C.-M. Lecture on the Markov switching model. Inst. Econ. Acad. Sin. 2002, 8, 1–30. [Google Scholar]
- Harvey, A.C.; Ruiz, E.; Shephard, N. Multivariate stochastic variance models. Rev. Econ. Stud. 1994, 61, 247–264. [Google Scholar] [CrossRef] [Green Version]
- Gray, S.F. Modeling the conditional distribution of interest rates as a regime switching process. J. Financ. Econ. 1996, 42, 27–62. [Google Scholar] [CrossRef]
- Chatfield, C. Time Series Forecasting; Chapman and Hall Text in Statistical Science: London, UK, 2000. [Google Scholar]
- Lee, C.F.; Chen, G.-M.; Rui, O.M. Stock returns and volatility on China’s stock markets. J. Fin. Res. 2014, 24, 523–543. [Google Scholar] [CrossRef]
- Lo, A.W. The Adaptive Markets Hypothesis: Market Efficiency from an evolutionary perspective. J. Portf. Manag. 2004, 30, 15–29. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Băutu, E. A hybrid approach for modeling financial time series. Int. Arab J. Inf. Technol. 2012, 9, 327–335. [Google Scholar]
- Bărbulescu, A. Do the time series statistical properties influence the goodness of fit of GRNN models? Study on financial series. Appl. Stoch. Model. Bus. 2018, 34, 586–596. [Google Scholar] [CrossRef]
- Simian, D.; Stoica, F.; Bărbulescu, A. Automatic Optimized Support Vector Regression for Financial Data Prediction. Neural Comput. Appl. 2020, 32, 2383–2396. [Google Scholar] [CrossRef]
- Chen, S. Genetic Algorithms and Genetic Programming in Computational Finance; Kluwer Academic Publishers: Amsterdam, The Nederlands, 2002. [Google Scholar]
- Karathanasopoulos, A.; Sermpinis, G.; Laws, J.; Dunis, C. Modelling and trading the Greek stock market with Gene Expression and Genetic Programing algorithms. J. Forecast. 2014, 33, 596–610. [Google Scholar] [CrossRef] [Green Version]
- Peng, X. TSVR: An efficient twin support vector machine for regression. Neural Netw. 2010, 23, 365–372. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Tay, F.E.H. Financial forecasting using support vector machines. Neural Comput. Appl. 2001, 10, 184–192. [Google Scholar] [CrossRef]
- Emad, W.S.; Danil, V.P.; Donald, C.W. Comparative study of stock trend prediction using time delay, recurrent and probabilistic neural networks. IEEE Trans. Neural Netw. 1998, 9, 1456–1470. [Google Scholar]
- Lin, C.T.; Prasad, M.; Saxena, A. An Improved Polynomial Neural Network Classifier Using Real Coded Genetic Algorithm. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 1389–1401. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming: Mathematical Modeling by an Artificial Intelligence, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Huang, C.H.; Yang, C.B.; Chen, H.H. Trading strategy mining with gene expression programming. In Proceedings of the 2013 International Conference on Applied Mathematics and Computational Methods in Engineering, Rhodes Island, Greece, 21–27 September 2013; pp. 37–42. [Google Scholar]
- Chen, H.H.; Yang, C.B.; Peng, Y.H. The trading on the mutual funds by gene expression programming with Sortino ratio. Appl. Soft Comput. 2014, 15, 219–230. [Google Scholar] [CrossRef]
- Lee, C.-H.; Yang, C.-B.; Chen, H.-H. Taiwan stock investment with gene expression programming. Procedia Comput. Sci. 2014, 35, 137–146. [Google Scholar] [CrossRef] [Green Version]
- Sermpinis, G.; Laws, J.; Karathanasopoulos, A.; Dunis, C. Forecasting and trading the EUR/USD exchange rate with Gene Expression and Psi Sigma Neural Networks. Expert Syst. Appl. 2012, 31, 8865–8877. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Dumitriu, C.S. Artificial intelligence models for financial time series. Ovidius Univ. Ann. Econ. Sci. Ser. 2021, in press. [Google Scholar]
- Ariton, V.; Palade, V.; Postolache, F. Combined deep and shallow knowledge in a unified model for diagnosis by abduction. EuroEconomica 2008, 1, 33–42. [Google Scholar]
- Dragomir, F.L. Modeling Resource in E-Commerce. In Proceedings of the 10th International Conference on Knowledge Management: Projects, Systems and Technologies, Bucharest, Romania, 23–24 November 2017; Security and Defence Faculty “Carol I” National Defence University: Bucharest, Romania, 2017; pp. 38–41. [Google Scholar]
- Dragomir, F.L. Models of Digital Markets. In Proceedings of the 10th International Conference on Knowledge Management: Projects, Systems and Technologies, Bucharest, Romania, 23–24 November 2017; Security and Defence Faculty “Carol I” National Defence University: Bucharest, Romania, 2017; pp. 47–51. [Google Scholar]
- Bărbulescu, A.; Dumitriu, C.S. Markov Switching Model for Financial Time Series. Ovidius Univ. Ann. Econ. Sci. Ser. 2021, in press. [Google Scholar]
- Postolache, F.; Bumbaru, S.; Ariton, V. Complex systems virtualization in the current’s economical context. EuroEconomica 2010, 3, 29–50. [Google Scholar]
- Bucharest Stock Exchange. Available online: http://www.bvb.ro (accessed on 10 April 2019).
- Bucharest Exchange Trading. Available online: www.bvb.ro/info/indices/2017/2017.10.10%20-%20BET%20Factsheet.pdf (accessed on 10 April 2019).
- Gel, Y.R.; Gastwirth, J.L. A robust modification of the Jarque-Bera test of normality. Econ. Lett. 2008, 99, 30–32. [Google Scholar] [CrossRef]
- Razali, N.M.; Yap, B.W. Power comparisons of Shapiro–Wilk, Kolmogorov–Smirnov, Lilliefors and Anderson–Darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- Levene, H. Robust Test for Equality of Variances. In Contributions to Probability and Statistics: Essays in Honor of Harold Hotelling; Olkin, I., Ed.; Stanford University Press: Palo Alto, CA, USA, 1960; pp. 278–292. [Google Scholar]
- Gibbons, J.D.; Chakraborti, S. Nonparametric Statistical Inference, 4th ed.; Marcel Dekker: New York, NY, USA, 2003. [Google Scholar]
- Wald, A.; Wolfowitz, J. On a test whether two samples are from the same population. Ann. Math. Stat. 1940, 11, 147–162. [Google Scholar] [CrossRef]
- Brockwell, P.J.; Davis, R.A. Introduction to Time Series and Forecasting; Springer: New York, NY, USA, 2002. [Google Scholar]
- Kendall, M.G. Rank Correlation Methods, 5th ed.; Oxford University Press: London, UK, 1990; pp. 56–80. [Google Scholar]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar]
- Phillips, P.C.B.; Perron, P. Testing for a unit root in time series regression. Biometrika 1988, 75, 335–346. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.B.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root. J. Econ. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change-point problem. Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Hawkins, D.M.; Olwell, D.H. Cumulative Sum Charts and Charting for Quality Improvement; Springer: New York, NY, USA, 1998. [Google Scholar]
- Gedikli, A.; Aksoy, H.; Unal, N.E.; Kehagias, A. Modified dynamic programming approach for offline segmentation of long hydrometeorological time series. Stoch. Environ. Res. Risk Assess. 2010, 24, 547–557. [Google Scholar] [CrossRef]
- Bărbulescu, A. Studies on Time Series. Applications in Environmental Sciences; Springer: New York, NY, USA, 2016. [Google Scholar]
- Diebold, F.X.; Mariano, R.S. Comparing the predictive accuracy. J. Bus. Econ. Stat. 1995, 13, 253–263. [Google Scholar]


| No. | Type of Test | Null and Alternative Hypotheses | Tests Performed |
|---|---|---|---|
| I. | Normality | H0: The series is Gaussian H1: The series is not Gaussian | Robust Jarque-Bera [36], Anderson-Darling, and Shapiro-Wilk tests [37] |
| II. | Homoskedasticity | H0: The series is homoskedastic H1: The series is heteroskedastic | Levene test [38] |
| III. | Randomness | H0: The series comes from a random process H1: The series does not come from a random process | Runs test [39,40] Autocorrelation function [41] |
| IV. | Trend existence | H0: The series does not have a monotonic trend H1: The series has a monotonic trend | Mann-Kendall test [42] |
| V. | Unit root tests | H0: The series has a unit root H1: The series is stationary | Augmented Dickey-Fuller test (ADF) [43], Phillips-Perron test(PP) [44] |
| VI. | Stationarity | H0: The series is stationary (a) in level or (b) around a deterministic trend H1: The series is not stationary (a) in level or (b) around a deterministic trend | KPSS test [45] |
| VII. | Breakpoint | H0: The series has no breakpoint H1: The series has at least a breakpoint | Pettitt test [46], CUSUM [47], mDP [48] |
| Type of Test | Series | ||||||
|---|---|---|---|---|---|---|---|
| S_m | S1_m | S2_m | S3_m | S4_m | U1_m | ||
| I. | Normality | yes | yes | no | no | no | yes |
| II. | Homoskedasticity | yes | no | yes | no | no | yes |
| III. | Randomness | yes | yes | yes | yes | yes | yes |
| IV. | Trend existence | yes | yes | yes | yes | yes | no |
| V. | Unit root | no | no | no | no | no | no |
| VI. | a. Level stationarity | yes | yes | yes | yes | yes | yes |
| b. Trend stationarity | yes | yes | yes | no | yes | yes | |
| Series | Training | Test | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S_m | S1_m | S2_m | S3_m | S4_m | S_m | S1_m | S2_m | S3_m | S4_m | |
| Correlation actual- predicted values | 0.965 | 0.893 | 0.850 | 0.785 | 0.743 | 0.617 | 0.980 | 0.570 | 0.577 | 0.960 |
| RMSE | 0.213 | 0.213 | 0.102 | 0.234 | 0.101 | 0.405 | 0.141 | 0.070 | 0.130 | 0.096 |
| MSE | 0.053 | 0.045 | 0.010 | 0.016 | 0.010 | 0.164 | 0.020 | 0.004 | 0.016 | 0.009 |
| MAE | 0.091 | 0.087 | 0.072 | 0.118 | 0.057 | 0.355 | 0.114 | 0.055 | 0.118 | 0.086 |
| MAPE | 1.205 | 1.323 | 0.830 | 1.529 | 0.690 | 4.129 | 1.421 | 0.608 | 1.529 | 0.979 |
| Removed trend | none | none | none | none | none | none | none | none | none | none |
| Series | Training | Test | ||||||
|---|---|---|---|---|---|---|---|---|
| S_m | S1_m | S2_m | S4_m | S_m | S1_m | S2_m | S4_m | |
| Correlation actual-predicted values | 0.965 | 0.895 | −0.292 | 0.743 | 0.558 | 0.980 | 0.200 | −0.874 |
| RMSE | 0.228 | 0.212 | 0.275 | 0.096 | 0.147 | 0.226 | 0.097 | 0.239 |
| MSE | 0.052 | 0.044 | 0.075 | 0.009 | 0.021 | 0.051 | 0.009 | 0.057 |
| MAE | 0.091 | 0.087 | 0.193 | 0.056 | 0.123 | 0.184 | 0.074 | 0.215 |
| MAPE | 1.203 | 1.320 | 2.239 | 0.669 | 1.419 | 2.274 | 2.811 | 2.451 |
| Indicators | Regressors: Lag 1 and Lag 12 | Regressors: Lag 1 | ||
|---|---|---|---|---|
| Training Test | Training Test | |||
| Correlation actual-predicted values | 0.958 | 0.515 | 0.956 | −0.933 |
| RMSE | 0.101 | 0.136 | 0.104 | 0.183 |
| MSE | 0.010 | 0.018 | 0.010 | 0.033 |
| MAE | 0.073 | 0.114 | 0.074 | 0.151 |
| MAPE | 0.868 | 1.312 | 0.879 | 1.729 |
| Trend Equation | Variance Explained by the Trend | |
|---|---|---|
| S_m | Yt = 7.2878 + 0.0112t | 47.938% |
| S1_m | Yt = 6.1794 + 0.0422t | 97.307% |
| U1_m | Yt = 8.5511 + 0.3236 | 7.392% |
| S2_m | Yt = 8.5607 + 0.0202t | 84.604% |
| S3_m | Yt = 10.2396 − 1.0992 | 92.758% |
| S4_m | Yt = 8.3897 + 0.03742 | 54.772% |
| Indicators/Series | Training | Test | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S_md | S1_md | S2_md | S3_md | S4_md | S_md | S1_md | S2_md | S3_md | S4_md | |
| Correlation actual- predicted values | 0.988 | 0.988 | 0.927 | 0.810 | 0.576 | 0.975 | 0.980 | 0.567 | 0.699 | 0.942 |
| RMSE | 0.130 | 0.070 | 0.071 | 0.124 | 0.084 | 0.485 | 0.062 | 0.073 | 0.150 | 0.034 |
| MSE | 0.017 | 0.005 | 0.005 | 0.015 | 0.007 | 0.236 | 0.003 | 0.005 | 0.022 | 0.001 |
| MAE | 0.078 | 0.054 | 0.058 | 0.097 | 0.053 | 0.426 | 0.050 | 0.056 | 0.115 | 0.025 |
| MAPE | 1.006 | 0.791 | 0.664 | 1.126 | 0.633 | 4.956 | 0.630 | 0.625 | 1.482 | 0.290 |
| Removed trend | linear | linear | linear | exp | exp | linear | linear | linear | exp | exp |
| Indicators/Series | Training | Test | ||||||
|---|---|---|---|---|---|---|---|---|
| S_md | S1_md | S2_ md | S4_md | S_md | S1_md | S2_md | S4_md | |
| Correlation actual-predicted values | 0.989 | 0.991 | 0.928 | 0.989 | 0.448 | 0.839 | 0.444 | 0.448 |
| RMSE | 0.129 | 0.061 | 0.075 | 0.121 | 0.656 | 0.295 | 0.108 | 0.656 |
| MSE | 0.016 | 0.003 | 0.005 | 0.016 | 0.431 | 0.087 | 0.011 | 0.431 |
| MAE | 0.078 | 0.048 | 0.059 | 0.078 | 0.587 | 0.239 | 0.088 | 0.587 |
| MAPE | 1.009 | 0.711 | 0.681 | 1.009 | 6.828 | 3.023 | 0.977 | 6.828 |
| Removed trend | linear | linear | linear | linear | linear | linear | linear | linear |
| Indicators | Regressors: Lag 1 and Lag 12 | Regressors: Lag 1 | ||
|---|---|---|---|---|
| Training | Test | Training | Test | |
| Correlation actual-predicted values | 0.958 | 0.168 | 0.954 | −0.916 |
| RMSE | 0.102 | 0.171 | 0.106 | 0.180 |
| MSE | 0.010 | 0.029 | 0.011 | 0.032 |
| MAE | 0.077 | 0.152 | 0.077 | 0.148 |
| MAPE | 0.902 | 1.754 | 0.904 | 1.694 |
| Removed trend | linear | linear | exp | exp |
| Indicators/Series | Training | Test | ||||||
|---|---|---|---|---|---|---|---|---|
| S_ms | S1_ms | S2_ms | S4_ms | S_ms | S1_ms | S2_ms | S4_ms | |
| Correlation actual-predicted values | 0.065 | 0.911 | 0.855 | 0.743 | 0.617 | 0.961 | 0.442 | 0.960 |
| RMSE | 0.231 | 0.198 | 0.096 | 0.101 | 0.405 | 0.212 | 0.105 | 0.096 |
| MSE | 0.053 | 0.039 | 0.009 | 0.010 | 0.164 | 0.044 | 0.011 | 0.009 |
| MAE | 0.091 | 0.080 | 0.055 | 0.057 | 0.355 | 0.187 | 0.083 | 0.086 |
| MAPE | 1.205 | 1.206 | 0.635 | 0.690 | 4.129 | 2.314 | 0.910 | 0.979 |
| Removed trend | none | none | none | none | none | none | none | none |
| Indicators/Series | Regressors: Lag 1 and Lag 12 | Regressors: Lag 1 | ||
|---|---|---|---|---|
| Training | Test | Training | Test | |
| Correlation actual-predicted values | 0.958 | 0.420 | 0.956 | −0.933 |
| RMSE | 0.102 | 0.112 | 0.104 | 0.184 |
| MSE | 0.010 | 0.031 | 0.011 | 0.034 |
| MAE | 0.152 | 0.097 | 0.075 | 0.151 |
| MAPE | 0.902 | 0.857 | 0.879 | 1.727 |
| Removed trend | none | none | none | none |
| Trend Equation | Variance Explained by the Trend | |
|---|---|---|
| S_w | Yt = 7.2800 + 0.0026t | 47.650% |
| S1_w | Yt = 6.1372 + 0.0100t | 97.412% |
| U1_w | Yt = 8.7731 − 0.0005 t | 5.589% |
| S2_w | Yt = 8.5569 + 0.0047t | 86.379% |
| S3_w | Yt = 11.3341 − 2.1602 | 89.660% |
| S4_w | Yt = 8.4420 + 0.0117 | 49.732% |
| Type of Test | Series | ||||||
|---|---|---|---|---|---|---|---|
| S_w | S1_w | S2_w | S3_w | S4_w | U1_w | ||
| I. | Normality | yes | yes | yes | yes | yes | yes |
| II. | Homoskedasticity | yes | yes | yes | yes | yes | yes |
| III. | Randomness | yes | yes | yes | yes | yes | yes |
| IV. | Trend existence | yes | yes | yes | yes | yes | yes |
| V. | Unit root | no | no | no | no | no | no |
| VI. | a. Level stationarity | yes | yes | yes | yes | yes | yes |
| b. Trend stationarity | yes | yes | yes | yes | yes | yes | |
| Series | Training | Test | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S_w | S1_w | S2_w | S3_w | S4_w | U1_w | S_w | S1_w | S2_w | S3_w | S4_w | U1_w | |
| Correlation actual-predicted values | 0.992 | 0.976 | 0.957 | 0.952 | 0.930 | 0.991 | 0.610 | 0.968 | 0.604 | 0.268 | 0.901 | 0.916 |
| RMSE | 0.111 | 0.102 | 0.053 | 0.101 | 0.052 | 0.048 | 0.226 | 0.080 | 0.055 | 0.216 | 0.042 | 0.063 |
| MSE | 0.012 | 0.010 | 0.003 | 0.010 | 0.003 | 0.002 | 0.051 | 0.006 | 0.003 | 0.047 | 0.002 | 0.004 |
| MAE | 0.034 | 0.032 | 0.030 | 0.055 | 0.027 | 0.032 | 0.197 | 0.066 | 0.045 | 0.149 | 0.031 | 0.055 |
| MAPE | 0.448 | 0.493 | 0.339 | 0.638 | 0.323 | 0.380 | 2.294 | 0.828 | 0.491 | 1.887 | 0.356 | 0.642 |
| Regressors (lag) | 1 & 5 | 1 | 1 & 5 | 1 | 1 & 5 | 1 5 | 1 & 5 | 1 | 1 & 5 | 1 | 1 & 5 | 1 5 |
| Series | Training | Test | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S_wd | S1_wd | S2_wd | S3_wd | S4_wd | U1_wd | S_wd | S1_wd | S2_wd | S3_wd | S4_wd | U1_wd | |
| Correlation actual-predicted values | 0.998 | 0.997 | 0.982 | 0.981 | 0.944 | 0.989 | 0.556 | 0.976 | 0.600 | 0.213 | 0.938 | 0.836 |
| RMSE | 0.060 | 0.033 | 0.034 | 0.065 | 0.046 | 0.050 | 0.487 | 0.058 | 0.059 | 0.204 | 0.045 | 0.187 |
| MSE | 0.004 | 0.001 | 0.001 | 0.004 | 0.002 | 0.002 | 0.237 | 0.003 | 0.003 | 0.041 | 0.002 | 0.035 |
| MAE | 0.032 | 0.025 | 0.025 | 0.043 | 0.026 | 0.032 | 0.439 | 0.049 | 0.046 | 0.142 | 0.037 | 0.152 |
| MAPE | 0.405 | 0.367 | 0.285 | 0.505 | 0.307 | 0.380 | 5.101 | 0.620 | 0.507 | 1.803 | 0.423 | 1.740 |
| Removed trend | lin. | lin. | lin. | exp | exp | lin | lin | lin. | lin. | exp | exp | lin |
| Regressors (lag) | 1 & 5 | 1 5 | 1 & 5 | 1 | 1 | 1 | 1 & 5 | 1 5 | 1 & 5 | 1 | 1 | 1 |
| Series | Model Type | Coefficients | The Goodness of Fit Indicators | |||||
|---|---|---|---|---|---|---|---|---|
| AR1 | Drift | MA1 | RMSE | MSE | MAE | MAPE | ||
| S_m | ARIMA (0,1,1) with drift | - | 0.2449 | 0.0156 | 0.0875 | 0.0076 | 0.0621 | 0.7638 |
| S1_m | ARIMA (0,1,0) with drift | - | 0.0422 | - | 0.0707 | 0.0050 | 0.0531 | 0.7386 |
| S2_m | ARIMA (0,1,0) | - | - | - | 0.0755 | 0.0057 | 0.0551 | 0.6203 |
| S3_m | ARIMA (0,1,0) with drift | - | −0.0949 | - | 0.1508 | 0.0227 | 0.1187 | 1.4401 |
| S4_m | ARIMA (0,1,1) | - | - | 0.2774 | 0.0552 | 0.0030 | 0.0432 | 0.5073 |
| U1_m | ARIMA (1,1,0) | 0.2152 | - | - | 0.0893 | 0.0080 | 0.0630 | 0.7375 |
| A–D | Levene | ACF | PACF | Remark | ||
|---|---|---|---|---|---|---|
| S_m | ARIMA (0,1,1) with drift | 0.000 | 0.012 | 4 | 4 | Yes |
| S1_m | ARIMA (0,1,0) with drift | 0.195 | 0.708 | none | none | No |
| S2_m | ARIMA (0,1,0) | 0.335 | 0.199 | none | none | No |
| S3_m | ARIMA (0,1,0) with drift | 0.942 | 0.179 | none | none | No |
| S4_m | ARIMA (0,1,1) | 0.247 | 0.017 | 6 | 6 | Yes |
| U1_m | ARIMA (1,1,0) | 0.000 | 0.000 | none | none | Yes |
| Series | Model Type | Coefficients | The Goodness of Fit Indicators | |||||
|---|---|---|---|---|---|---|---|---|
| AR Coefficients | Drift | MA1 | RMSE | MSE | MAE | MAPE | ||
| S_md | ARIMA (0,1,1) | - | - | 0.2462 | 0.0875 | 0.0077 | 0.0626 | 111.8606 |
| S1_md | ARIMA (1,0,0) with 0 mean | - | 0.7873 | - | 0.6720 | 0.4516 | 0.0530 | 41.9276 |
| S2_md | ARIMA (1,0,0) with 0 mean | AR1 = 0.6492 | - | - | 0.0693 | 0.0048 | 0.0552 | 197.9489 |
| S3_md | ARIMA (0,1,0) | - | - | - | 0.2260 | 0.0511 | 0.1675 | 65.7451 |
| S4_md | ARIMA (2,0,0) | AR1 = 1.2211 AR2 = −0.3352 | - | - | 0.0540 | 0.0029 | 0.0417 | 103.3804 |
| U1_md | ARIMA (3,0,1) | AR1 = 2.0902 AR2 = −1.2549 AR3 = 0.1561 | - | −0.9868 | 0.0858 | 0.0074 | 0.0610 | 87.0538 |
| Series | Model Type | A–D | Levene | ACF | PACF | Remark |
|---|---|---|---|---|---|---|
| S_md | ARIMA (0,1,1) | 0.000 | 0.001 | 4 | 4 | Yes |
| S1_md | ARIMA (1,0,0) with 0 mean | 0.248 | 0.843 | none | none | No |
| S2_md | ARIMA (1,0,0) with 0 mean | 0.005 | 0.032 | none | none | Yes |
| S3_md | ARIMA (0,1,0) | 0.089 | 0.237 | none | none | No |
| S4_md | ARIMA (2,0,0) | 0.164 | 0.012 | 4 | 4 | Yes |
| U1_md | ARIMA (3,0,1) | 0.005 | 0.000 | none | none | Yes |
| Coefficients | The Goodness of Fit Indicators | |||||||
|---|---|---|---|---|---|---|---|---|
| Series | Model Type | AR1 | Drift | MA1 | RMSE | MSE | MAE | MAPE |
| S_ms | ARIMA (0,1,1) with drift | - | 0.01564 | 0.0156 | 0.0904 | 0.0080 | 0.0635 | 0.7816 |
| S1_ms | ARIMA (0,1,0) with drift | - | 0.0424 | - | 0.0740 | 0.0055 | 0.0540 | 0.0127 |
| S2_ms | ARIMA (0,1,0) with drift | - | 0.0156 | - | 0.0572 | 0.0033 | 0.0422 | 0.4753 |
| S4_ms | ARIMA (0,1,0) with drift | 0.0154 | - | 0.0606 | 0.0037 | 0.0431 | 0.5044 | |
| U1_ms | ARIMA (0,1,0) | - | - | - | 0.0954 | 0.0091 | 0.0654 | 0.7698 |
| Series | Model Type | A–D | Levene | ACF | PACF | Remark |
|---|---|---|---|---|---|---|
| S_ms | ARIMA (0,1,1) with drift | 0.942 | 0.001 | 4 | 4 | Yes |
| S1_ms | ARIMA (0,1,0) with drift | 0.017 | 0.723 | none | none | Yes |
| S2_ms | ARIMA (0,1,0) with drift | 0.061 | 0.833 | none | none | No |
| S4_ms | ARIMA (0,1,0) with drift | 0.001 | 0.017 | none | none | Yes |
| U1_ms | ARIMA (0,1,0) | 0.000 | 0.000 | 1 | 1 | Yes |
| Series | Model Type | Coefficients | The Goodness of Fit Indicators | |||||
|---|---|---|---|---|---|---|---|---|
| AR Coef. | Drift | MA Coef. | RMSE | MSE | MAE | MAPE | ||
| S_w | ARIMA (1,0,5) | AR1 = −0.9765 | - | MA1 = 0.0167 MA2 = −0.8277 MA3 = 0.0373 MA4 = −0.1195 MA5 = −0.0816 | 0.0373 | 0.0014 | 0.0260 | 0.3219 |
| S1_w | ARIMA (0,1,0) with drift | - | 0.0101 | - | 0.0320 | 0.0010 | 0.0242 | 0.3404 |
| S2_w | ARIMA (0,1,0) | - | 0.0041 | - | 0.0342 | 0.0012 | 0.0258 | 0.2910 |
| S3_w | ARIMA (0,1,0) with drift | - | −0.017 | - | 0.0681 | 0.0046 | 0.0471 | 0.0012 |
| S4_w | ARIMA (4,1,1) with drift | AR1 = −0.6230 AR2 = 0.1165 AR3 = 0.0737 AR4 = −0.1307 | 0.0030 | MA1 = 0.5924 | 0.0292 | 0.0009 | 0.0208 | 0.2444 |
| U1_w | ARIMA (3,1,0) with drift | AR1 = 0.0034 AR2 = 0.1779 AR3 = 0.0934 | - | - | 0.0391 | 0.0015 | 0.0267 | 0.3123 |
| Series | Model Type | Coefficients | The Goodness of Fit Indicators | |||||
|---|---|---|---|---|---|---|---|---|
| AR | Drift | MA1 | RMSE | MSE | MAE | MAPE | ||
| S_wd | ARIMA (0,0,1) with 0 mean | - | - | 0.2462 | 0.0875 | 0.0077 | 0.0626 | 111.8606 |
| S1_wd | ARIMA (1,0,0) with 0 mean | - | 0.7873 | - | 0.6720 | 0.4516 | 0.0530 | 41.9276 |
| S2_wd | ARIMA (1,0,0) with 0 mean | AR1 = 0.6492 | - | - | 0.0693 | 0.0048 | 0.0552 | 197.9489 |
| S3_wd | ARIMA (0,1,0) | - | - | - | 0.2260 | 0.0511 | 0.1675 | 65.7451 |
| S4_wd | ARIMA (2,0,0) | AR1 = 1.2211 AR2 = −0.3352 | - | - | 0.0540 | 0.0029 | 0.0417 | 103.3804 |
| U1_wd | ARIMA (3,0,1) | AR1 = 2.0902 AR2 = −1.2549 AR3 = 0.1561 | - | −0.9868 | 0.0858 | 0.0074 | 0.0610 | 87.0538 |
| Series | Model Type | A–D | Levene | ACF | PACF | Remark |
|---|---|---|---|---|---|---|
| S_w | ARIMA (1,0,5) | 0.000 | 0.000 | none | none | Yes |
| S1_w | ARIMA (0,1,0) with drift | 0.004 | 0.130 | 11 | 11 | Yes |
| S2_w | ARIMA (0,1,0) | 0.117 | 0.287 | none | none | No |
| S3_w | ARIMA (0,1,0) with drift | 0.000 | 0.285 | 2 | 3 | Yes |
| S4_w | ARIMA (4,1,1) with drift | 0.000 | 0.000 | none | none | Yes |
| U1_w | ARIMA (3,1,0) with drift | 0.000 | 0.000 | 12 | 12 | Yes |
| Series | Model Type | A–D | Levene | ACF | PACF | Remark |
|---|---|---|---|---|---|---|
| S_w | ARIMA (0,0,1) with 0 mean | 0.000 | 0.000 | 12 | 12 | Yes |
| S1_w | ARIMA (1,0,0) with 0 mean | 0.003 | 0.146 | none | 11 | Yes |
| S2_w | ARIMA (1,0,0) with 0 mean | 0.087 | 0.317 | 10 | 11 | Yes |
| S3_w | ARIMA (0,1,0) | 0.000 | 0.352 | none | none | Yes |
| S4_w | ARIMA (2,0,0) | 0.000 | 0.000 | none | none | Yes |
| U1_w | ARIMA (3,0,1) | 0.000 | 0.000 | 12 | 11 | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bărbulescu, A.; Dumitriu, C.Ș. On the Connection between the GEP Performances and the Time Series Properties. Mathematics 2021, 9, 1853. https://doi.org/10.3390/math9161853
Bărbulescu A, Dumitriu CȘ. On the Connection between the GEP Performances and the Time Series Properties. Mathematics. 2021; 9(16):1853. https://doi.org/10.3390/math9161853
Chicago/Turabian StyleBărbulescu, Alina, and Cristian Ștefan Dumitriu. 2021. "On the Connection between the GEP Performances and the Time Series Properties" Mathematics 9, no. 16: 1853. https://doi.org/10.3390/math9161853
APA StyleBărbulescu, A., & Dumitriu, C. Ș. (2021). On the Connection between the GEP Performances and the Time Series Properties. Mathematics, 9(16), 1853. https://doi.org/10.3390/math9161853







