Abstract
The longest common subsequence (LCS) problem is a prominent –hard optimization problem where, given an arbitrary set of input strings, the aim is to find a longest subsequence, which is common to all input strings. This problem has a variety of applications in bioinformatics, molecular biology and file plagiarism checking, among others. All previous approaches from the literature are dedicated to solving LCS instances sampled from uniform or near-to-uniform probability distributions of letters in the input strings. In this paper, we introduce an approach that is able to effectively deal with more general cases, where the occurrence of letters in the input strings follows a non-uniform distribution such as a multinomial distribution. The proposed approach makes use of a time-restricted beam search, guided by a novel heuristic named Gmpsum. This heuristic combines two complementary scoring functions in the form of a convex combination. Furthermore, apart from the close-to-uniform benchmark sets from the related literature, we introduce three new benchmark sets that differ in terms of their statistical properties. One of these sets concerns a case study in the context of text analysis. We provide a comprehensive empirical evaluation in two distinctive settings: (1) short-time execution with fixed beam size in order to evaluate the guidance abilities of the compared search heuristics; and (2) long-time executions with fixed target duration times in order to obtain high-quality solutions. In both settings, the newly proposed approach performs comparably to state-of-the-art techniques in the context of close-to-uniform instances and outperforms state-of-the-art approaches for non-uniform instances.
1. Introduction
In the field of bioinformatics, strings are commonly used to model sequences such as DNA, RNA, and protein molecules or even time series. Strings represent fundamental data structures in many programming languages. Formally, a string s is a finite sequence of letters over (usually) a finite alphabet . A subsequence of a string s is any sequence obtained by removing arbitrary letters from s. Similarities among several strings can be determined by considering common subsequences, which may serve for deriving relationships and possibly to distill different aspects of the of input strings, such as mutations. More specifically, one such measure of similarity can be defined as follows. Given a set of m input strings , the longest common subsequence (LCS) problem [1] aims at finding a subsequence of maximum length that is common for all strings from the set of input strings S. The length of the LCS for two or more input strings is a widely used measure in computational biology [2], file plagiarism check, data compression [3,4], text editing [5], detecting road intersections from GPS traces [6], file comparison (e.g., in the Unix command ) [7] and revision control systems such as Git. For a fixed m, polynomial algorithms based on dynamic programming (DP) are known [8] in the literature. These dynamic programming approaches run in time, where n denotes the length of the longest input string. Unfortunately, these approaches quickly become impractical when m and n get large. For an arbitrary large number of input strings, the LCS problem is -hard [1]. In practice, heuristic techniques are typically used for larger m and n. Constructive heuristics, such as the Expansion algorithm and the Best-Next heuristic [9,10], appeared first in the literature to tackle the LCS problem. Significantly better solutions are obtained by more advanced metaheuristic approaches. Most of these are based on Beam Search (BS), see for example, [11,12,13,14,15]. These approaches differ in various important aspects, which include the heuristic guidance, the branching scheme and the filtering mechanisms.
Djukanovic et al. (2019), in [16], proposed a generalized BS framework for the LCS problem with the purpose of unifying all previous BS-based approaches from the literature. By respective parametrization, each of the previously introduced BS-based approaches from the literature could be expressed, which also enabled a more direct comparison of all of them. Moreover, a heuristic guidance that approximates the expected length of an LCS on uniform random strings was proposed. This way, a new state-of-the-art BS variant that leads on most of the existing random and quasi-random benchmark instances from the literature was obtained.
Concerning exact approaches for the LCS problem, an integer linear programming model was considered in [17]. It turned out not to be competitive enough as it was not applicable to most of the commonly used benchmark instances from the literature. This was primarily due to the model size—too many binary variables and a huge number of constraints are needed even for small-sized problem instances. Dynamic programming approaches also quickly run out of memory for small-to-middle sized benchmark instances or typically return only weak solutions, if any. Chen et al. (2016) [18] proposed a parallel FAST_LCS search algorithm that mitigated some of the runtime weaknesses. Wang et al. (2011) in [14] proposed another parallel algorithm called QUICK-DP, which is based on the dominant point approach and employs a quick divide-and-conquer technique to compute the dominant points. One more parallel and space efficient algorithm based on a graph model, called the Leveled-DAG, was introduced by Peng and Wang (2017) [19]. Li et al. (2016) in [20] suggested the TOP_MLCS algorithm, which is based on a directed acyclic layered-graph model (called the irredundant common subsequence graph) and parallel topological sorting strategies used to filter out paths representing suboptimal solutions. A more enhanced version of the latter approach that utilizes Branch-and-Bound is proposed by Wang et al. (2021) in [21]. An approximate algorithm based on the topological sorting strategy was developed and applied to COVID-19 data by Li et al. (2020) in [22]. A specific Path Recorder Directed Acyclic Graph (PRDAG) model was designed and used for developing the Path Recorder Algorithm (PRA) by Wei et al. (2020) in [23]. Recently, Djukanovic et al. (2020) in [24] proposed an search that is able to outperform TOP_MLCS and previous exact approaches in terms of memory usage and the number of instances solved to optimality. Nevertheless, the applicability of this exact search approach is still limited to small-sized instances. The same holds for the other exact techniques from the literature. In [24], the search also served as a basis for a hybrid anytime algorithm, which can be stopped at almost any time and can then be expected to yield a reasonable heuristic solution. In this approach, classical search iterations are intertwined with iterations of Anytime column search [25]. This hybrid was able to outperform some other state-of-the-art anytime algorithms from the literature, such as PRO_MLCS [26] and Anytime Pack Search [27], in terms of solution quality. To the best of our knowledge, this hybrid approach is still the leading method for the LCS problem on a wide range of benchmark sets from the literature.
The methods so-far proposed in the literature were primarily tested on independent random and quasi-random strings, where the number or occurrences of letters in each string is similar for each letter. In fact, we are aware of just one benchmark set with different distributions (BB, see Section 4), where the input strings are constructed in such a way so that they exhibit high similarity, but still the letters’ frequencies are similar. In practical applications, this assumption of uniform or close-to-uniform distribution of letters does not need to hold. Some letters may occur substantially more frequently than others. For example, if we are concerned with finding motifs in sentences of any spoken language, each letter has its characteristic frequency [28]. Text in natural languages can be modeled by a multinomial distribution over the letters. The required level of model adaptation can vary depending on the distribution assumptions such as letter dependence of a particular language. Letter frequencies in a language can also differ depending on text types (e.g., poetry, fiction, scientific documents, business documents). For example, it is interesting that the letter ‘E’ is the most frequent letter in both English (12.702%) [28] and German (17.40%) [29], but only the second most common letter in Russian [30]. Moreover, the letter ‘N’ is very frequent in German (9.78%), but not so common in English (6.749%) and Russian (6.8%). Motivated by this consideration, we develop a new BS-based algorithm exhibiting an improved performance for instances with different string distributions.
Unlike the BS proposed by Djukanovic et al. (2019) in [16], our BS variant applies a novel guidance heuristic at its core as a replacement of the so far leading approximate expected length calculation. In addition to an improved performance in the context of non-uniform instances, the novel heuristic is easier to implement than the approximate expected length calculation (which required a Taylor series expansion and an efficiently implemented divide-and-conquer approach) and there are no issues with numerical stability. Our new BS version is time restricted in the sense that its running time approximately fits a desired target time limit. Moreover, it obtains high-quality results without the need for extensive parameters tuning.
The main contributions of this article can be summarized as follows:
- We propose a novel search guidance for a BS which performs competitively on the standard LCS benchmark sets known from the literature and, in some cases, even produces new state-of-the-art results.
- We introduce two new LCS benchmark sets based on multinomial distributions, whose main property is that letters occur with different frequencies. The proposed new BS variant excels in these instances in comparison with previous solution approaches.
- A new time-restricted BS version is described. It automatically adapts the beam width over BS levels with regard to given time restrictions, such that the overall running time of BS approximately fits a desired target time limit. A tuning of the beam width to achieve comparable running times among different algorithms is hereby avoided.
In the following, we introducing some commonly used notation before giving an overview of the remainder of this article.
1.1. Preliminaries
By S, we always refer to the set of m input strings, that is, , . The length of a string s is denoted by , and its i-th letter, , is referred to by . Let n refer to the length of a longest string and to the length of a shortest string in S. A continuous subsequence (substring) of string s that starts with the letter at index i and ends with the letter at index j is denoted by ; if , this refers to the empty string . The number of occurrences of a letter in string s is denoted by . For a subset of the alphabet , the number of appearances of each letter from A in s is denoted by . For an m-dimensional integer vector and the set of strings S, we define the set of suffix-strings , which induces a respective LCS subproblem. For each letter , the position of the first occurrence of a in is denoted by , . Last but not least, if a string s is a subsequence of a given string r, we write .
1.2. Overview
This article is organized as follows: Section 2 provides theoretical aspects concerning the calculation of the probability that a given string is a subsequence of a random string chosen from a multinomial distribution. Section 3 describes the BS framework for solving the LCS problem, as well as the novel heuristic guidance. Moreover, the time-restricted BS variant is also proposed. In Section 4, a comprehensive experimental study and comparison is conducted. Section 5 extends the experiments by considering instances derived from a textual corpus. Finally, Section 6 draws conclusions and outlines interesting future work.
2. Theoretical Aspects of Different String Distributions
Most papers in the literature are dedicated to the development and improvement of methods for finding an LCS of instances on strings that come from a uniform distribution. In our work, we propose new methods for the more general case, where strings are assumed to come from a multinomial distribution of strings. More precisely, for an alphabet , as a sample space for the letter of the strings, a multinomial distribution is determined by specifying a (real) number for each letter such that represents the probability of seeing letter and . Note that the uniform distribution is a special case of the multinomial distribution , with .
Assuming that the selection of each letter in a string is independent, each string can be considered a random vector composed of independent random variables, resulting in its probability distribution being completely determined by a given multinomial distribution. By a random string, in this paper, we refer to a string whose letters are chosen randomly in accordance with the given multinomial distribution.
Let r be a given string. We now aim to determine the probability that a random string s, chosen from the same multinomial distribution as string r, is a subsequence of the string r. We denote this probability by . In the next theorem, we propose a new recurrence relation to calculate this probability.
Theorem 1.
Let r be a given string and s be a random string chosen from the same multinomial distribution. Then,
Proof.
It is clear from the definition of a subsequence that the empty string is a subsequence of every string and that a string cannot be a subsequence of a shorter one. Therefore, the cases and are trivial. In the remaining case (),
follows from the law of total probability. □
The probability in recurrence relation (1) is dependent not only on the length of string r, but also on the letter distribution of this string. Therefore, it is hard to come up with a closed-form expression for the general case of a multinomial distribution . One way to deal with this problem is to consider some special cases of the multinomial distribution, for which closed-form expressions may be obtained.
2.1. Multinomial Distribution—Special Case 1: Uniform Distribution
The most frequently used form of the multinomial distribution considered in the literature is the uniform distribution. Since in this case, every letter has the same occurrence probability, probability in the recurrence relation (1) depends only on the lengths and and can be written more simply as . This case is covered by Mousavi and Tabataba in [12], where the recurrence relation (1) is reduced as follows:
Probabilities can be calculated using dynamic programming as described by Mousavi and Tabataba in [12].
2.2. Multinomial Distribution—Special Case 2: Single Letter Exception
Let one letter have occurrence probability , and each other letter have occurrence probability . For this multinomial distribution, recurrence relation (1) reduces to:
where
Note that, besides lengths and , (3) depends only on whether or not a letter in the string r is equal to .
2.3. Multinomial Distribution—Special Case 3: Two Sets of Letters
We now further generalize the previous case. Let be a partitioning of the alphabet , that is, let be nonempty sets such that and . Let us assume that every letter in has the same occurrence probability and also that every letter in has the same occurrence probability. We define
where is the probability mass assigned to the set . For this multinomial distribution, recurrence relation (1) reduces to
where
This probability therefore depends on whether or not a letter in r belongs to the set or not.
2.4. The Case of Independent Random Strings
Another approach to calculating the probability that a string s is a subsequence of a string r is based on the assumption that both s and r are random strings chosen from the same multinomial distribution and are independent as a random vector. Using this setup, we established a recurrence relation for calculating probability .
Theorem 2.
Let r and s be random independent strings chosen from the same multinomial distribution . Then,
Proof.
The first two cases are trivial, so it remains to show the last case. Using the law of total probability, we obtain
Probability can be calculated with another application of the law of total probability, using the assumption that random strings s and r are mutually independent:
□
Except for the obvious dependency on the multinomial distribution , probability is determined by the lengths of strings s and r, only. Therefore, as in the case of the uniform distribution, we can abbreviate this probability with , where and . This allows us to pre-compute a probability matrix for all relevant values of k and l by means of dynamic programming.
3. Beam Search for Multinomially Distributed LCS Instances
In this section, we propose a new BS variant, which is characterized as follows:
- It makes use of a novel heuristic for search guidance that combines two complementary scoring functions by means of a convex combination.
- Our algorithm is a time-restricted BS variant, which dynamically adapts the beam width depending on the progress over the levels. In that way, the algorithm does not require a time-consuming tuning of the beam size with regard to the instance size.
3.1. Beam Search Framework
Beam search (BS) is a well-known search heuristic that is widely applied to many problems from various research fields, such as scheduling [31], speech recognition [32], machine learning tasks [33], packing problems [34], and so forth. It is a reduced version of breadth-first-search (BFS), where, instead of expanding all not-yet-expanded nodes from the same level, only a specific number of up to nodes that appear most promising are selected and considered for expansions. In this way, BS keeps the search tree polynomial in size. The selection of the up to nodes for further expansion is made according to a problem-specific heuristic guidance function h. The effectivity of the search thus substantially depends on this function. More specifically, BS works as follows. First, an initial beam B is set up with a root node r representing an initial state, in the case of the LCS problem, this is the empty partial solution. At each major iteration, all nodes from beam B are expanded in all possible ways by considering all feasible actions. The obtained child nodes are kept in the set of extensions . Note that, for some problems, efficient filtering techniques can be applied to discard nodes from that are dominated by other nodes, that is, nodes that cannot yield better solutions. It is controlled by an internal parameter . This (possibly filtered) set of extensions is then sorted according to the nodes’ values obtained from the guidance heuristic h, and the top nodes (or less if is smaller) then form the beam B of the next level. The whole process is repeated level-by-level until B becomes empty. In general, to solve a combinatorial optimization problem, information about the longest (or shortest) path from the root node to a feasible goal node is kept to finally return a solution that maximizes or minimizes the problem’s objective function. The pseudocode of such a general BS is given in Algorithm 1.
| Algorithm 1 Beam Search. |
|
3.2. State Graph for the LCS Problem
The state graph for the LCS problem that is used by all BS variants is already well known in the literature, see, for example [16,24]. It is defined as a directed acyclic graph , where a node represents the set of partial solutions, which:
- have the same length ;
- induce the same subproblem denoted by w.r.t. the position vector .
We say that a partial solution s induces a subproblem iff is the smallest prefix of among all prefixes that has s as a subsequence.
An arc exists between two nodes and carries label , iff
- ;
- the partial solution that induces is obtained by appending to the partial solution inducing .
The root node of G refers to the original LCS problem on input string set S and can be said to be induced by the empty partial solution .
For deriving the successor nodes of a node , we first determine the subset of the letter that feasibly extends the partial solutions represented by v. The candidates for letter are therefore all letters that appear at least once in each string in the subproblem given by strings . This set may be reduced by determining and discarding dominated letters. We say that letter dominates letter iff
Dominated letters can be safely omitted since they lead to suboptimal solutions. Let be the set of feasible and non-dominated letters. For each letter , graph G contains a successor node of v, where , (remember that denotes the position of the first appearance of letter a in string from position onward). A node v that has no successor node, that is, when , is called a non-extensible node, or goal node. Among all goal nodes v we are looking for one representing a longest solution string, that is, a goal node with the largest . Note that any path from the root node r to any node in represents the feasible partial solution obtained by collecting and concatenating the labels of the traversed arcs. Thus, it is not necessary to store actual partial solutions s in the nodes. In the graph G, any path from root r to a non-extensible node represents a common, non-extensible subsequence of S. Any longest path from r to a goal node represents an optimal solution to problem instance S. As an example of a full state graph of an instance, see Figure 1.
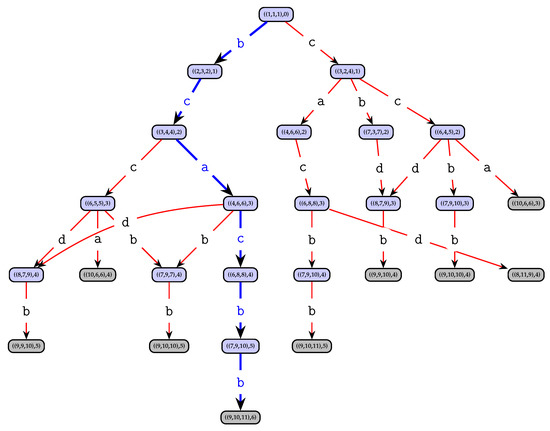
Figure 1.
State graph for the LCS problem instance on strings and alphabet . Light gray nodes are non-extensible goal nodes. The longest path in this state graph is shown in blue, leads from the root to node and corresponds to the solution , having length six.
We still have to explain the filtering of dominated nodes from the set , that is, procedure Filter in Algorithm 1. We adopt the efficient restricted filtering proposed in [13], which is parameterized by a filter size . The idea is to select only the (up to) best nodes from and to check the dominance relation (6) for this subset of nodes in combination with all other nodes in . If the relation is positively evaluated, the dominated node is removed from . Note that parameter settings and represent the two extreme cases of no filtering and full filtering, respectively. A filter size of may be meaningful, as full filtering may be too costly in terms of running time for larger beam widths.
3.3. Novel Heuristic Guidance
We now present a new heuristic for evaluating nodes in the BS in order to rank them and to select the beam of the next level. This heuristic, called the Geometric mean probability sum (Gmpsum), in particular aims at unbalanced instances and is a convex combination of the following two scores.
- The Geometric mean (Gm) score is based on the geometric mean and the geometric standard deviation of the letters’ occurrences across all input strings of the respective subproblem. It is calculated on a per letter basis and aggregated into a single numeric value;
More specifically, for a given node v and a letter , let us define
as the vector indicating for each remaining string of the respective subproblem the number of occurrences of letter . By and , we denote the geometric mean and geometric standard deviation, respectively, which are calculated for by
By , we denote the known upper bound on the length of an LCS for the subproblem represented by node v from [11], which is calculated as
Then, the Gm score is calculated as
Overall, the Gm score is thus a weighted average of the adjusted geometric means ( of the number of letter occurrences, and the weight of each letter is determined by normalizing the minimal number of the letter occurrences across all strings with the sum of the minimal number occurrences across all letters. The motivation behind this calculation is three-fold:
- Letters with higher average numbers of occurrences across the strings will increase the chance of finding a longer common subsequence (composed of these letters).
- Higher deviations around the mean naturally reduce this chance.
- The minimal numbers of occurrences of a letter across all input strings is an upper bound on the length of common subsequences that can be formed by this single letter. Therefore, by normalizing it with the sum of all minimal letter occurrences, an impact of each letter in the overall summation is quantified.
The Gm score is relevant if its underlying sampling geometric mean and standard deviation are based on a sample of sufficient size. In all our experiments, the minimal number of input strings is therefore ten. Working on samples of smaller sizes would likely make the Gm score not that useful.
In addition to the Gm score, we consider the Psum score. For a given node v, we define
Then, the Psum score is calculated by
Unlike the Gm score, which considers mostly general aspects of an underlying probability distribution, Psum better captures more specific relations among input strings. It represents the sum of probabilities that a string of length k will be a common subsequence for all remaining input strings relevant for further extensions. Index k goes from one to , that is, the length of the shortest possible non-empty subsequence up to the length of the longest possible one, which corresponds to the size of the shortest input string residual. The motivation behind using a simple (non-weighted) summation across all potential subsequence lengths is three-fold:
- The exact length of the resulting subsequence is not known in advance. Note that, in the case of the Hp heuristic proposed in [12], the authors heuristically determine an appropriate value of k for each level in the BS.
- The summation across all k provides insight into the overall potential of node v—approximating the integral on the respective continuous function. Note that it is not required for this measure to have an interpretation in absolute terms since throughout the BS it is used strictly to compare different alternative extensions on the same level of the BS tree.
- A more sophisticated approach that assigns different weights to the different k values would impose the challenge of deciding these specific weights. This would bring us back to the difficult task of an expected length prediction, which would be particularly hard when now considering the arbitrary multinomial distribution.
Finally, the total Gmpsum score is calculated by the linear combination
where is a strategy parameter. Based on an empirical study with different benchmark instances and values for parameter , we came up with the following rules of thumb to select .
- Since Gm and Psum have complementary focus, that is, they capture and award (or implicitly penalize) different aspects of the extension potential, their combined usage is indeed meaningful in most cases, that is, .
- Gm tends to be a better indicator when instances are more regular, that is, when each input string better fits the overall string distribution.
- Psum tends to perform better when instances are less regular, that is, when input strings are more dispersed around the overall string distribution.
Regarding the computational costs of the Gmpsum calculation, the Gm score calculation requires time. This can be concluded from (7), where the most expensive part is the iteration through all letters from and finding the minimal number of the letter occurrences across all m input strings ( and have the same time complexity). Note that the number of occurrences of each letter across all possible suffixes of all m input string positions is calculated in advance, before starting the beam search, and is stored in an appropriate three-dimensional array, see [24]. The worst case computational complexity of this step is . This is because the number of occurrences of a given letter across all positions inside the given input string can be determined in a single linear pass. Since this is done only at the start, and the expected number of Gm calls is much higher than , this up front calculation can be neglected in the overall computational complexity The Psum score given by (8) takes time to be calculated due to a definition of . Similar to Gm, the calculation of matrix P is performed in pre-processing—its computational complexity corresponds to the number of entries, that is, , see (5).
Finally, the total computational complexity of Gmpsum can be concluded to be . The total computational complexity of the beam search is therefore a product of the number of calls of Gmpsum and the time complexity of Gmpsum. Note that the number of Gmpsum calls equals the number of nodes created within a BS run. Since the LCS length, that is, the number of BS levels, is unknown, we use here as the upper bound. Overall, the BS guided by Gmpsum runs in time if no filtering is performed. In the case of filtering, at each level of the BS, time is required, which gives total time for executing the filtering within the BS. According to this, the BS guided by Gmpsum and utilizing (restricted) filtering requires time.
3.4. A Time-Restricted BS
In this section, we extend the basic BS from Algorithm 1 to a time-restricted beam search (TRBS). This BS variant is motivated by the desire to compare different algorithms with the same time-limit. The core idea we apply is to dynamically adapt the beam width in dependence of the progress over the levels.
Similarly to the standard BS from Algorithm 1, TRBS is parameterized with the problem instance to solve, the guidance heuristic h, and the filtering parameter . Moreover, what was previously the constant beam width now becomes only the initial value. The goal is to achieve a runtime that comes close to a target time , now additionally specified as an input. At the end of each major iteration, that is, level, if , that is, the time limit is actually enabled, the beam width for the next level is determined as follows.
Let be the time required for the current iteration.
We estimate the remaining number of major iterations (levels) by taking the maximum of lower bounds for the subinstances induced by the nodes in . More specifically,
Thus, for each node and each letter a we consider the minimal number of occurrences of the letter across all string suffixes and select the one that is maximal. In other words, this LCS lower bound is based on considering all common subsequences in which a single letter is repeated as often as possible. In the literature, this procedure is known by the name Long-run [35] and provides a –approximation.
Let be the actual time still remaining in order to finish at time .
Let be the expected remaining time when we would continue with the current beam width and the time spent at each level would stay the same as it was when measured for the current level.
Depending on the discrepancy between the actual and expected remaining time, we possibly increase or decrease the beam width for the next level:
In this adaptive scheme, the thresholds for the discrepancy to increase or decrease the beam width, as well as the factor by which the beam width is modified, were determined empirically. Note that there might be better estimates of the LCS length than ; however, this estimate is inexpensive to obtain, and even if it underestimates or overestimates the LCS length in the early phases, gradually it converges toward the actual LCS length as the algorithm progresses. This allows TRBS to smoothly adapt its expected remaining runtime to the desired one. Note that we only adapt the beam width and do not set it completely anew based on the runtime measured for the current level in order to avoid erratic changes of the beam width in the case of a larger variance of the level’s runtimes. Based on preliminary experiments, we conclude that the proposed approach in general works well in achieving the desired time limit, while not changing dramatically up and down in the course of a whole run. However, of course, how close we get to the time limit being met depends on the actual length of the LCS. For small solution strings, the approach has fewer opportunities to adjust and then tends to overestimate the remaining time, thus utilizing less time than desired.
4. Experimental Results
In this section we evaluate our algorithms and compare them with the state-of-the-art algorithms from the literature. The proposed algorithms are implemented in C# and executed on machines with Intel i9-9900KF CPUs with @ 3.6 GHz and 64 Gb of RAM under Microsoft Windows 10 Pro OS. Each experiment was performed in single-threaded mode. We conducted two types of experiments:
- short-runs: these are limited-time scenarios—that is, BS configurations with are used—executed in order to evaluate the quality of the guidance of each of the heuristics towards promising regions of the search space.
- long-runs: these are fixed-duration scenarios (900 s) in which we compare the time-restricted BS guided by the Gmpsum heuristic with the state-of-the-art results from the literature. The purpose of these experiments is the identification of new state-of-the-art solutions, if any.
4.1. Benchmark Sets
All relevant benchmark sets from the literature were considered in our experiments:
- Benchmark sets Rat, Virus and Random, each one consisting of 20 single instances, are well known from the related literature [36]. The first two sets are biologically motivated, originating from the NCBI database. In the case of the third set, instances were randomly generated. The input strings in these sets are 600 characters long. Moreover, they contain instances based on alphabets of size four and 20.
- Benchmark set ES, introduced in [37], consists of randomly distributed input strings whose length varies from 1000 to 5000, while alphabet sizes range from two to 100. This set consists of 12 groups of instances.
- Benchmark set BB, introduced in [38], is different to the others because the input strings of each instance are generated such that there is a high similarity between them. For this purpose, first, a randomly generated base string was generated. Second, all input strings were generated based on the base string by probabilistically introducing small mutations such as delete/update operations of each letter. This set consists of eight groups (each one containing 10 single instances).
- Benchmark set Bacteria, introduced in [39], is a real-world benchmark set used in the context of the constrained longest common subsequence problem. We made use of these instances by simply ignoring all pattern strings (constraints). This set consists of 35 single instances.
- Finally, we introduce two new sets of instances:
- –
- The input strings of the instances of benchmark set Poly were generated such that the number of occurrences of each letter in each input string were determined by a multinomial distribution with known probabilities , such that ; see [40] for how to sample such distributions. More specifically, we used the multinominal distribution with and for generating the input strings. The number of the occurrences of different letters was very much unbalanced in the obtained input strings. This set consists of 10 instances for each combination of the input string length and the number of input strings , which makes a total of 60 problem instances.
- –
- Benchmark set Abstract, which will be introduced in Section 5, is a real-world benchmark set whose input strings are characterized by close-to-polynomial distributions of the different letters. The input strings originate from abstracts of scientific papers written in English.
4.2. Considered Algorithms
All considered algorithms make use of the state-of-the-art BS component. In order to test the quality of the newly proposed Gmpsum heuristic for the evaluation of the partial solutions at each step of BS, we compared it to the other heuristic functions that were proposed for this purpose in the literature: Ex [16], Pow [13], and Hp [12]. The four resulting BS variants are labeled BS-Gmpsum, BS-Ex, BS-Pow, and BS-Hp, respectively. These four BS variants were applied with the same parameter settings ( and ) in the short-run scenario in order to ensure that all of them used the same amount of resources.
In the long-run scenario, we tested the proposed time-restricted BS (TRBS) guided by the novel Gmpsum heuristic, which is henceforth labeled as TRBS-Gmpsum. Our algorithm was compared to the current state-of-the-art approach from the literature: + ACS [24]. These two algorithms were compared in the following way:
- Concerning + ACS, the results for benchmark sets Random, Virus, Rat, Es and Bb were taken from the original paper [24]. They were obtained with a computation time limit of 900 s per run. For the new benchmark sets—that is, Poly and Bacteria—we applied the original implementation of + ACS with a time limit of 900 s on the above-mentioned machine.
- TRBS-Gmpsum was applied with a computation time limit of 600 s per run to all instances of benchmark sets Random, Virus, Rat, Es and Bb. Note that we reduced the computation time limit used in [24] by 50% because the CPU of our computer was faster than the one used in [24]. In contrast, the time limit for the new instances was set to 900 s. Regarding restricted-filtering, the same setting () as for the short-run experiments was used.
4.3. Tuning of Parameter
As already mentioned in the previous section, the values of parameters (beam width) and (for filtering dominated nodes) were adopted from [16] (for the short-run executions) and from [24] (for the long-run executions). Regarding the strategy parameter that controls the impact of both scores in the Gmpsum score, we performed short-run evaluations across a discrete set of possible values: . The conclusion was that the best performing values were for Bb, for Virus and Bacteria, for Random, Rat and Poly, and for ES. The same settings for were used in the context of the long-run experiments.The settings of the parameters of our algorithms BS-Gmpsum and TRBS-Gmpsum are displayed in Table 1 and Table 2.

Table 1.
Values of parameters and for all benchmark sets.

Table 2.
The settings of parameter per each benchmark set.
4.4. Summary of the Results
Before studying the results for each benchmark set in detail, we present a summary of the results in order to provide the reader with a broad picture of the comparison. More specifically, the results of the short-run scenarios are summarized in Table 3, while those for the long-run scenarios are given in Table 4. Table 3 displays the results in such a way that each line corresponds to a single benchmark set. The meanings of the columns are as follows: the first column contains the name of the benchmark set, while the second column provides the number of instances—respectively, instance groups—in the set. Then there are four blocks of columns, one for each considered BS variant. The first column of each block shows the obtained average solution quality () over all instances of the benchmark set. The second column indicates the number of instances—respectively, instance groups—for which the respective BS variant achieves the best result (#b.). Finally, the third column provides the average running time () in seconds over all instances of the considered benchmark set.

Table 3.
Short-run results summary.

Table 4.
Long-run results summary.
The following conclusions can be drawn:
- Concerning the fully random benchmark sets Random and Es, in which input strings were generated uniformly at random and are independent, it was already well-known previously that the heuristic guidance Ex performs strongly. Nevertheless, it can be seen that BS-Gmpsum performs nearly as well as BS-Ex, and clearly better than the remaining two BS variants.
- In the case of the quasi-random instances of benchmark sets Virus and Rat, BS-Gmpsum starts to show its strength by delivering the best solution qualities in 31 out of 40 cases. The second best variant is BS-Ex, which still performs very well, and is able to achieve the best solution qualities in 24 out of 40 cases.
- For the special Bb benchmark set, in which input strings were generated in order to be similar to each other, Gmpsum was revealed to perform comparably to the best variant BS-Pow.
- Concerning the real-world benchmark set Bacteria, BS-Gmpsum is able to deliver the best results for 18 out of 35 groups, which is slightly inferior to the BS-Hp variant with 22 best-performances, and superior to variants BS-Ex (12 cases) and BS-Pow (15 cases). Concerning the average solution quality obtained for this benchmark set, BS-Gmpsum is able to deliver the best among all considered approaches.
- Concerning the multinominal non-uniformly distributed benchmark set Poly, BS-Gmpsum clearly outperforms all other considered BS variants. In fact, BS-Gmpsum is able to find the best solutions for all six instance groups. Moreover, it beats the other approaches in terms of the average solution quality.
- Overall, BS-Gmpsum finds the best solutions in 80 (out of 121) instances or instance groups, respectively. The second best variant is BS-Ex, which is able to achieve the best performance in 62 cases. In contrast, BS-Hp and BS-Pow are clearly inferior to the other two approaches. We conclude that BS-Gmpsum performs well in the context of different letter distributions in the input strings, and it is worth trying this variant first when nothing is known about the distribution in the considered instance set.
- Overall, the running times of all four BS variants are comparable. The fastest one is BS-Hp, while BS-Gmpsum requires somewhat more time compared to the others since it makes use of a heuristic function that combines two functions.
Table 4 provides a summary of the long-run scenarios, that is, it compares the current state-of-the-art algorithm + ACS with TRBS-Gmpsum. As the benchmark instances are the same as in the short-run scenarios, the first two table columns are the same as in Table 4. Then there are two blocks of columns, presenting the results of A* + ACS and TRBS-Gmpsum in terms of the average solution quality over all instances of the respective benchmark set (), and the number of instances (or instance groups) for which the respective algorithm archived the best result (#b.).
The following can be concluded based on the results obtained for the long-run scenarios:
- Concerning Random and Es, + ACS is—as expected—slightly better than TRBS-Gmpsum in terms of the number of best results achieved. However, when comparing the average performance, there is hardly any difference between the two approaches: 109.9 vs. 109.7 for the Random benchmark set, and 243.82 vs. 243.73 for the Es benchmark set.
- In the context of benchmark sets Rat and Virus, TRBS-Gmpsum improves over the state-of-the-art results by a narrow margin. This holds both for the number of best results achieved and for the average algorithm performance.
- Concerning benchmark set Bb, TRBS-Gmpsum significantly outperforms + ACS. In six out of eight groups it delivers the best average solution quality, while + ACS does so only for three cases.
- The same holds for the real-world benchmark set Bacteria, that is, TRBS-Gmpsum achieves the best results for 33 out of 35 instances, in contrast to only 10 instances in the case of A* + ACS. Moreover, the average solution quality obtained is much better for TRBS-Gmpsum, namely 862.63 vs. 829.26.
- Finally, the performances of both approaches for benchmark set Poly are very much comparable.
- Overall, we can conclude that TRBS-Gmpsum is able to deliver the best results in 101 out of 121 cases, while + ACS does so only in 77 cases. This is because TRBS-Gmpsum provides a consistent solution quality across instances characterized by various kinds of letter distributions. It can therefore be stated that TRBS-Gmpsum is a new state-of-the-art algorithm for the LCS problem.
In summary, for the 32 random instances—respectively, instance groups—from the literature (sets Random and Es) + ACS performs quite strongly due to the presumed randomness of the instances. However, the new TRBS-Gmpsum approach is not far behind. A weak point of + ACS becomes obvious when instances are not generated uniformly at random. In the 40 cases with quasi-random input strings (sets Rat and Virus), TRBS-Gmpsum performs the best in 37 cases, while + ACS does so in 31 cases. When input strings are similar to each other—see the eight instance groups of set Bb— + ACS performs weakly compared to TRBS-Gmpsum. This tendency is reinforced in the context of the instances of set Poly (six instance groups) for which TRBS-Gmpsum clearly outperforms + ACS in all cases. The same holds for the real-world benchmark set Bacteria. The overall conclusion yields that TRBS-Gmpsum works very well on a wide range of different instances. Moreover, concerning the instances from the previous literature (80 instances/groups), our TRBS-Gmpsum approach is able to obtain new state-of-the-art results in 13 cases. This will be shown in the next section.
4.5. New State-of-the-Art Results for Instances from the Literature
Due to space restrictions, we provide the complete set of results for each problem instance in the Supplementary Materials of the repository whose the link is given in the Data Availability Statement at the end of the paper.
The tables reporting the new state-of-the-art results are organized as follows. The first column contains the name of the corresponding benchmark set, while the following two columns identify, respectively, the instance (in the case of Rat and Virus) and the instance group (in the case of Bb and Es). Afterwards, there are two columns that provide the best result known from the literature. The first of these columns provides the result, and the second column indicates the algorithm (together with the reference) that was the first one to achieve this result. Next, the tables provide the results of Bs-Ex, Bs-Pow, Bs-Hp and Bs-Gmpsum in the case of the short-run scenario, the results of A* + ACS and TRBS-Gmpsum, respectively, in the case of the long-run scenario. Note that computation times are only given for the short-run scenario, because time served as a limit in the long-run scenario.
Concerning the short-run scenario (Table 5), BS-Gmpsum was able to produce new best results in 17 cases. This even includes four cases of the benchmark set Es, which was generated uniformly at random. The four cases of sets Virus and Rat are remarkable, in which the currently best-known solution was improved by two letters (see, for example, the case of set Rat and the instance , and ). Concerning the more important long-run scenario (Table 6), the best-known results so far were improved in 14 cases. Especially remarkable is the case of set Bb, for which an impressive improvement of around 24 letters was achieved.

Table 5.
New best results for the instances from the literature in the short-run scenario.

Table 6.
New best results for the instances from the literature in the long-run scenario.
4.6. Results for Benchmark Sets Poly and Bacteria
The tables reporting the results for benchmark set Poly are structured in the same way as those described above in the context of the other benchmark sets. The difference is that instance groups are identified by means of (first column), m (second column), and n (third column). The best results per instance group—that is, per table row—are displayed in bold font.
The results of the short-run scenario for benchmark set Poly are given in Table 7. According to the obtained results, a clear winner is BS-Gmpsum, which obtains the best average solution quality for all six instance groups. This indicates that Gmpsum is clearly better as a search guidance than the other three heuristic functions for this benchmark set. As previously mentioned, this is due to the strongly non-uniform nature of the instances, that is, the intentionally generated imbalance of the number of occurrences of different letters in the input strings. Nevertheless, the absolute differences between the results of BS-Gmpsum and BS-Ex are not so high. The results of the long-run executions for benchmark set Poly are provided in Table 8. It can be observed that TRBS-Gmpsum and the state-of-the-art technique A* + ACS perform comparably.

Table 7.
Short-run results for benchmark set Poly.

Table 8.
Long-run results for benchmark set Poly.
Remember that, as in the case of Poly, the instances of benchmark set Bacteria have been used for the first time in a study concerning the LCS problem. They were initially proposed in a study concerning the constrained LCS problem [39]. The results are again presented in the same way as described before. This set consists of 35 instances. Therefore, each line in Table 9 (short-run scenario) and Table 10 (long-run scenario) deals with one single instance, which is identified by (always equal to 4), m (varying between 2 and 383), (the length of the shortest input string) and (the length of the longest input string). The best results are indicated in bold font. The results obtained for the short-run scenario allow us to observe that BS-Hp performs very well for this benchmark set. In fact, it obtains the best solution in 22 out of 35 cases. However, BS-Gmpsum is not far behind with 18 best solutions. Moreover, BS-Gmpsum obtains a slightly better average solution quality than Bs-Hp. Concerning the long-run scenario, as already observed before, TRBS-Gmpsum clearly outperforms A* + ACS. In fact, the differences are remarkable in some cases, such as, for example, instance number 32 (fourth but last line in Table 10) for which TRBS-Gmpsum obtains a solution of value 1241, while A* + ACS finds—in the same computation time—a solution of value 1204.

Table 9.
Short-run results for benchmark set Bacteria.

Table 10.
Long-run results for benchmark set Bacteria.
4.7. Statistical Significance of the So-Far Reported Results
In this section, we study the results of the short-run and long-run executions from a statistical point of view. In order to do so, Friedman’s test was performed simultaneously considering all four algorithms in the case of the short-run scenario, and the two considered algorithms in the case of the long-run scenario. All these tests and the resulting plots were generated using R’s scmamp package [41].
Given that, in all cases, the test rejected the hypothesis that the algorithms perform equally, pairwise comparisons were performed using the Nemenyi post-hoc test [42]. The corresponding critical difference (CD) plots considering all benchmark sets together are shown in Figure 2 and Figure 3a. Each algorithm is positioned in the segment according to its average ranking with regard to the average solution quality over all (121) the considered instance groups. The critical difference was computed with a significance level of 0.05. The performances of those algorithms whose difference is below the CD are regarded as performing statistically in an equivalent way—that is, no difference of statistical significance can be detected. This is indicated in the figures by bold horizontal bars joining the respective algorithm markers.
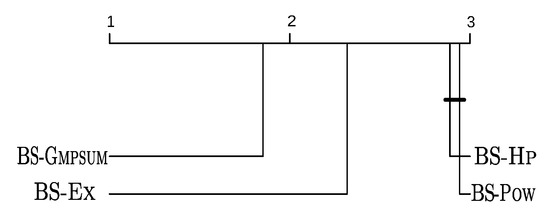
Figure 2.
Critical difference (CD) plot over all considered benchmark sets (short-run executions).

Figure 3.
Critical difference (CD) plots concerning the long-run scenario.
Concerning short-run executions, BS-Gmpsum is clearly the overall best-performing algorithm, with statistical significance. BS-Ex is in the second position. Moreover, the difference between BS-Hp and BS-Pow is not statistically significant. Concerning the long-run scenario, the best average rank is obtained by TRBS-Gmpsum. In the case of benchmark set Bacteria, the difference between TRBS-Gmpsum and + ACS is significant, see Figure 3b. For the other benchmark sets, the two approaches perform statistically equivalently.
5. Textual Corpus Case Study
In the previous section, we showed that the proposed method is highly competitive with state-of-the art methods and generally outperforms them on instances sampled from non-uniform distributions. In order to further investigate the behavior of the proposed method in real-world instances with non-uniform distribution, we performed a case study on a corpus of textual instances originating from abstracts of scientific papers written in English. This set will henceforth be called Abstract. It is known that letters in the English language are polynomially distributed [28]. The most frequent letter is e, with a relative frequency of 12.702%. The next most common letter is t (9.056%), followed by a (8.167%), and o (7.507%), and so forth.
In order to make a meaningful choice of texts we followed [43], where the authors measured the similarity between scientific papers, mainly from the field of artificial intelligence, by making use of various algorithms and metrics. By using tf-idf statistics with cosine similarity, their algorithm identified similar papers from a large paper collection. After that, the similarity between the papers proposed by their algorithm was manually checked and tagged by an expert as either similar (positive) or dissimilar (negative). The results of this research can be found at https://cwi.ugent.be/respapersim (accessed on 14 March 2021).
Keeping in mind that the LCS problem is also a measure of text similarity, we decided to check whether the abstracts of similar papers have longer common subsequences than abstracts of dissimilar papers. Therefore, the purpose of this case study is twofold: (1) to execute the LCS state-of-the art methods along with the method proposed in this paper and to compare their performances on this specific instance set; and (2) to check whether the abstracts of similar papers have a higher LCS than those of dissimilar papers.
Based on these considerations, we formed two groups of twelve papers each, named POS and NEG. Group POS contains twelve papers which were identified as similar, while group NEG contains papers which are not similar to each other. We extracted abstracts from each paper and pre-processed them in order to remove all letters except for those letters from the English alphabet. In addition, each uppercase letter was replaced with its lowercase pair.
For each of the two groups, we created a set of test instances as follows. For each we generated different instances containing k input strings (considering all possible combinations). This resulted in the following set of instances for both POS and NEG:
- One instance containing all 12 abstracts as input strings.
- Twelve instances containing 11 out of 12 abstracts as input strings.
- Sixty-six instances containing 10 out of 12 abstracts as input strings.
Repeating our experimental setup presented in the previous section, we performed both short- and long-runs for the described instances. The obtained results for the short-run scenarios are shown in Table 11. The table is organized into five blocks of columns. The first block provides general information about the instances: NEG vs. POS, number of input strings (column with heading m), and the total number of instances (column #). The remaining four blocks contain the results of BS-Ex, BS-Pow, BS-Hp and BS-Gmpsum, respectively. For each considered group of instances and each method, the following information about the obtained results is shown:

Table 11.
Short-run results for the textual corpus instances (Abstract).
- : solution quality of the obtained LCS for the considered group of instances;
- #b.: number of cases in which the method reached the best result for the considered group of instances;
- : average execution time in seconds for the considered group of instances.
The results from Table 11 clearly indicate that the best results for instances based on group NEG are obtained by BS-Gmpsum. More precisely, BS-Gmpsum works best for the instance with 12 input strings, for eight out of 12 instances with 11 input strings and for 50 out of 66 instances with 10 input strings. In contrast, the second-best approach (BS-Ex) reached the best result for 29 out of 66 instances with 10 input strings and seven out of 12 instances with 11 input strings. The remaining two methods were less successful for this group of instances. For the instances derived from group POS, BS-Gmpsum also achieved very good results. More specifically, BS-Gmpsum obtained the best results in almost all instances with 11 input strings. For instances with 10 input strings, BS-Ex obtained the best results in 42 out of 66 cases, with BS-Gmpsum performing comparably (best result in 39 out of 66 cases). For the instance with 12 strings, the best solution was found by the BS-Ex. Similarly to the instances from the NEG group, BS-Hp and BS-Pow are clearly less successful.
A summary of these results is provided in the last three rows of Table 11. Note that, in total, this table deals with 158 problem instances: 79 regarding group NEG, and another 79 regarding group POS. The summarized results show that the new Gmpsum guidance is, overall, more successful than its competitors. More precisely, BS-Gmpsum achieved the best results in 59 out of 79 cases concerning NEG, and in 50 out of 79 cases concerning POS. Moreover, it can be observed that the average LCS length regarding the POS instances is greater than that regarding the NEG instances, across all m values.
Table 12 contains information about the long-run executions. The results obtained by + ACS and TRBS-Gmpsum are shown. The table is organized in a similar way to Table 11, with the exception that it does not contain information about execution times, since computation time served as the stopping criterion. As can be seen from the overall results at the bottom of Table, TRBS-Gmpsum obtains more best results than + ACS for both groups of instances (NEG and POS). More precisely, it obtained the best result for the instances with 12 input strings, both in the case of POS and NEG, while A* + ACS achieved the best result only in the case of the POS instance with 12 input strings. Concerning the results for the instances with 11 input strings, it can be noticed that—in the case of the NEG instances—TRBS-Gmpsum delivers 11 out of 12 best results, while the + ACS method does so only in two out of twelve cases. Regarding the POS instances with 11 input strings, the difference becomes smaller. More specifically, TRBS-Gmpsum achieves nine out of 12 best results, while + ACS achieved six out of 12 best results. A corresponding comparison can be made for the instances with 10 input strings. For the instances concerning group NEG, TRBS-Gmpsum delivers the best results for 60 out of 66 instances, while + ACS can find the best results only in 31 cases. Finally, in the case of the POS instances, the best results were achieved in 45 out of 66 cases by TRBS-Gmpsum, and in 41 out of 66 cases by + ACS. The long-run results also indicate that abstracts of similar papers are characterized by generally longer LCS measures.

Table 12.
Long-run results for the textual corpus instances (Abstract).
6. Conclusions and Future Work
In this paper, we considered the prominent longest common subsequence problem with an arbitrary set of input strings. We proposed a novel search guidance, named Gmpsum, for tree search algorithms. This new guidance function was defined as a convex combination of two complementary heuristics: (1) the first one is suited for instances in which the distribution of letters is close to uniform-at-random; and (2) the second is convenient for all cases in which letters are non-uniformly distributed. The combined score produced by these two heuristics provides a guidance function which navigates the search towards promising regions of the search space, on a wide range of instances with different distributions. We ran short-run experiments in which beam search makes use of a comparable number of iterations under different guidance heuristics. The conclusion was that the novel guidance heuristic performs statistically equivalently to the best-so-far heuristic from the literature on close-to-random instances. Moreover, it was shown that it significantly outperforms the known search guidance functions on instances with a non-uniform letter frequency per input string. This capability of the proposed heuristic to deal with a non-uniform scenario was validated on two newly introduced benchmark sets: (1) Poly, whose input strings are generated from a multinomial distribution; and (2) Abstract, which are real-world instances whose input strings follow a multinomial distribution and originate from abstracts of scientific papers written in English. In a second part of the experimentation, we performed long-run executions. For this purpose we combined the Gmpsum guidance function with a time-restricted BS that dynamically adapts its beam width during execution such that the overall running time is very close to the desired time limit. This algorithm was able to significantly outperform the best approach from the literature ( + ACS). More specifically, the best-known results from the literature were at least matched for 63 out of the 80 considered instance groups. Moreover, regarding the two new benchmark sets (Poly and Bacteria), the time-restricted BS guided by Gmpsum was able to deliver solutions that were equally as good as, and in most cases better than, those of + ACS, in 38 out of 41 instance groups.
In future work we plan to adapt Gmpsum to other LCS-related problems such as the constrained longest common subsequence problem [44], the repetition-free longest common subsequence problem [45], the LCS problem with a substring exclusion constraint [46], and the longest common palindromic subsequence problem [47]. It would also be interesting to incorporate this new guidance function into the leading hybrid approach + ACS to possibly further boost the obtained solution quality.
Author Contributions
B.N. was responsible for conceptualization, methodology, and writing. A.K. was responsible for software implementation, writing and methodology. M.D. was responsible for conceptualization, witting and visualization. M.G. was responsible for resources and writing. C.B. was responsible for writing, editing and supervision. G.R. was responsible for concept polishing, supervision, and funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
The research was fully funded by the Austrian Science Fund (FWF) under project No. W1260-N35.
Data Availability Statement
The reported results can be found at https://github.com/milanagrbic/LCSonNuD (accessed on 22 April 2021).
Acknowledgments
This research was partially supported by the Ministry for Scientific and Technological Development, Higher Education and Information Society, Government of Republic of Srpska, B&H under the Project “Development of artificial intelligence methods for solving computer biology problems”, project No. 19.032/-961-24/19. Marko Djukanovic was funded by the Doctoral Program Vienna Graduate School on Computational Optimization (VGSCO), Austrian Science Foundation, project No. W1260-N35. Christian Blum was funded by project CI-SUSTAIN of the Spanish Ministry of Science and Innovation (PID2019-104156GB-I00).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LCS | Longest Common Subsequence |
| BS | Beam Search |
| ACS | Anytime column search |
| APS | Anytime pack search |
| A* + ACS | The hybrid of A* and ACS |
| TRBS | Time restricted BS |
| GM | Geometric mean score |
| PSUM | Probability sum score |
| GMPSUM | Geometric mean probability sum score |
| TRBS-GMPSUM | TRBS guided by GMPSUM |
| BS-GMPSUM | BS guided by GMPSUM |
References
- Maier, D. The Complexity of Some Problems on Subsequences and Supersequences. J. ACM 1978, 25, 322–336. [Google Scholar] [CrossRef]
- Minkiewicz, P.; Darewicz, M.; Iwaniak, A.; Sokołowska, J.; Starowicz, P.; Bucholska, J.; Hrynkiewicz, M. Common Amino Acid Subsequences in a Universal Proteome—Relevance for Food Science. Int. J. Mol. Sci. 2015, 16, 20748–20773. [Google Scholar] [CrossRef]
- Storer, J. Data Compression: Methods and Theory; Computer Science Press: Rockville, MD, USA, 1988. [Google Scholar]
- Beal, R.; Afrin, T.; Farheen, A.; Adjeroh, D. A new algorithm for “the LCS problem” with application in compressing genome resequencing data. BMC Genom. 2016, 17, 544. [Google Scholar] [CrossRef][Green Version]
- Kruskal, J.B. An overview of sequence comparison: Time warps, string edits, and macromolecules. SIAM Rev. 1983, 25, 201–237. [Google Scholar] [CrossRef]
- Xie, X.; Liao, W.; Aghajan, H.; Veelaert, P.; Philips, W. Detecting Road Intersections from GPS Traces Using Longest Common Subsequence Algorithm. ISPRS Int. J. Geo-Inf. 2017, 6, 1. [Google Scholar] [CrossRef]
- Bergroth, L.; Hakonen, H.; Raita, T. A survey of longest common subsequence algorithms. In Proceedings of the SPIRE 2000—The 7th International Symposium on String Processing and Information Retrieval, Coruna, Spain, 27–29 September 2000; pp. 39–48. [Google Scholar]
- Gusfield, D. Algorithms on Strings, Trees, and Sequences; Computer Science and Computational Biology; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Fraser, C.B. Subsequences and Supersequences of Strings. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 1995. [Google Scholar]
- Huang, K.; Yang, C.; Tseng, K. Fast Algorithms for Finding the Common Subsequences of Multiple Sequences. In Proceedings of the ICS 2004—The 9th International Computer Symposium, Funchal, Portugal, 13–16 January 2004. [Google Scholar]
- Blum, C.; Blesa, M.J.; López-Ibáñez, M. Beam search for the longest common subsequence problem. Comput. Oper. Res. 2009, 36, 3178–3186. [Google Scholar] [CrossRef]
- Mousavi, S.R.; Tabataba, F. An improved algorithm for the longest common subsequence problem. Comput. Oper. Res. 2012, 39, 512–520. [Google Scholar] [CrossRef]
- Tabataba, F.S.; Mousavi, S.R. A hyper-heuristic for the longest common subsequence problem. Comput. Biol. Chem. 2012, 36, 42–54. [Google Scholar] [CrossRef]
- Wang, Q.; Korkin, D.; Shang, Y. A fast multiple longest common subsequence (MLCS) algorithm. IEEE Trans. Knowl. Data Eng. 2011, 23, 321–334. [Google Scholar] [CrossRef]
- Djukanovic, M.; Raidl, G.R.; Blum, C. Anytime algorithms for the longest common palindromic subsequence problem. Comput. Oper. Res. 2020, 114, 104827. [Google Scholar] [CrossRef]
- Djukanovic, M.; Raidl, G.; Blum, C. A Beam Search for the Longest Common Subsequence Problem Guided by a Novel Approximate Expected Length Calculation. In Proceedings of the LOD 2019—The 5th International Conference on Machine Learning, Optimization, and Data Science, Siena, Italy, 10–13 September 2019. [Google Scholar]
- Blum, C.; Festa, P. Longest Common Subsequence Problems. In Metaheuristics for String Problems in Bioinformatics; Wiley: Hoboken, NJ, USA, 2016; Chapter 3; pp. 45–60. [Google Scholar]
- Chan, H.T.; Yang, C.B.; Peng, Y.H. The Generalized Definitions of the Two-Dimensional Largest Common Substructure Problems. In Proceedings of the 33rd Workshop on Combinatorial Mathematics and Computation Theory, Taipei, Taiwan, 13–14 May 2016; pp. 1–12. [Google Scholar]
- Peng, Z.; Wang, Y. A Novel Efficient Graph Model for the Multiple Longest Common Subsequences (MLCS) Problem. Front. Genet. 2017, 8, 104. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, Y.; Zhang, Z.; Wang, Y.; Ma, D.; Huang, J. A novel fast and memory efficient parallel MLCS algorithm for long and large-scale sequences alignments. In Proceedings of the IEEE 32nd International Conference on Data Engineering, Helsinki, Finland, 16–20 May 2016; pp. 1170–1181. [Google Scholar]
- Wang, C.; Wang, Y.; Cheung, Y. A branch and bound irredundant graph algorithm for large-scale MLCS problems. Pattern Recognit. 2021, 119, 108059. [Google Scholar] [CrossRef]
- Li, Y.; Liu, B.; Wang, Z.; Cui, J.; Yao, K.; Lv, P.; Shen, Y.; Xu, Y.; Guan, Y.; Ma, X. COVID-19 Evolves in Human Hosts. arXiv 2020, arXiv:2003.05580. [Google Scholar] [CrossRef]
- Wei, S.; Wang, Y.; Yang, Y.; Liu, S. A path recorder algorithm for Multiple Longest Common Subsequences (MLCS) problems. Bioinformatics 2020, 36, 3035–3042. [Google Scholar] [CrossRef]
- Djukanovic, M.; Raidl, G.R.; Blum, C. Finding Longest Common Subsequences: New anytime A* search results. Appl. Soft Comput. 2020, 95, 106499. [Google Scholar] [CrossRef]
- Vadlamudi, S.G.; Gaurav, P.; Aine, S.; Chakrabarti, P.P. Anytime column search. In Proceedings of the AI’12—The 25th Australasian Joint Conference on Artificial Intelligence, Sydney, Australia, 4–7 December 2012; pp. 254–265. [Google Scholar]
- Yang, J.; Xu, Y.; Sun, G.; Shang, Y. A New Progressive Algorithm for a Multiple Longest Common Subsequences Problem and Its Efficient Parallelization. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 862–870. [Google Scholar] [CrossRef]
- Vadlamudi, S.G.; Aine, S.; Chakrabarti, P.P. Anytime pack search. Nat. Comput. 2016, 15, 395–414. [Google Scholar] [CrossRef]
- Lewand, R.E. Cryptological Mathematics; American Mathematical Soc.: Providence, RI, USA, 2000; Volume 16. [Google Scholar]
- Beutelspacher, A. Kryptologie; Springer: Berlin, Germany, 1996; Volume 7. [Google Scholar]
- Bakaev, M. Impact of familiarity on information complexity in human-computer interfaces. In Proceedings of the MATEC Web of Conferences, EDP Sciences, Munich, Germany, 6–8 June 2016; Volume 75, p. 08003. [Google Scholar]
- Ow, P.S.; Morton, T.E. Filtered beam search in scheduling. Int. J. Prod. Res. 1988, 26, 35–62. [Google Scholar] [CrossRef]
- Ney, H.; Haeb-Umbach, R.; Tran, B.H.; Oerder, M. Improvements in beam search for 10000-word continuous speech recognition. In Proceedings of the ICASSP-92: 1992 IEEE International Conference on Acoustics, Speech, and Signal Processing, San Francisco, CA, USA, 23–26 March 1992; Volume 1, pp. 9–12. [Google Scholar]
- Kumar, A.; Vembu, S.; Menon, A.K.; Elkan, C. Beam search algorithms for multilabel learning. Mach. Learn. 2013, 92, 65–89. [Google Scholar] [CrossRef]
- Araya, I.; Riff, M.C. A beam search approach to the container loading problem. Comput. Oper. Res. 2014, 43, 100–107. [Google Scholar] [CrossRef]
- Jiang, T.; Li, M. On the approximation of shortest common supersequences and longest common subsequences. SIAM J. Comput. 1995, 24, 1122–1139. [Google Scholar] [CrossRef]
- Shyu, S.J.; Tsai, C.Y. Finding the longest common subsequence for multiple biological sequences by ant colony optimization. Comput. Oper. Res. 2009, 36, 73–91. [Google Scholar] [CrossRef]
- Easton, T.; Singireddy, A. A large neighborhood search heuristic for the longest common subsequence problem. J. Heuristics 2008, 14, 271–283. [Google Scholar] [CrossRef]
- Blum, C.; Blesa, M.J. Probabilistic beam search for the longest common subsequence problem. In Proceedings of the International Workshop on Engineering Stochastic Local Search Algorithms, Brussels, Belgium, 6–8 September 2007; pp. 150–161. [Google Scholar]
- Djukanovic, M.; Kartelj, A.; Matic, D.; Grbic, M.; Blum, C.; Raidl, G. Solving the Generalized Constrained Longest Common Subsequence Problem with Many Pattern Strings; Technical Report AC-TR-21-008. 2021. Available online: https://www.ac.tuwien.ac.at/files/tr/ac-tr-21-008.pdf (accessed on 25 June 2021).
- Kesten, H.; Morse, N. A property of the multinomial distribution. Ann. Math. Stat. 1959, 30, 120–127. [Google Scholar] [CrossRef]
- Calvo, B.; Santafé Rodrigo, G. scmamp: Statistical Comparison of Multiple Algorithms in Multiple Problems. 2016. Available online: https://journal.r-project.org/archive/2016/RJ-2016-017/RJ-2016-017.pdf (accessed on 25 June 2021).
- Pohlert, T. The pairwise multiple comparison of mean ranks package (PMCMR). R Package 2014, 27, 9. [Google Scholar]
- Magara, M.B.; Ojo, S.O.; Zuva, T. A comparative analysis of text similarity measures and algorithms in research paper recommender systems. In Proceedings of the 2018 Conference on Information Communications Technology and Society (ICTAS), Durban, South Africa, 8–9 March 2018; pp. 1–5. [Google Scholar]
- Gotthilf, Z.; Hermelin, D.; Lewenstein, M. Constrained LCS: Hardness and Approximation. In Proceedings of the CPM 2008—The 19th Annual Symposium on Combinatorial Pattern Matching, Pisa, Italy, 18–20 June 2008; Volume 5029, pp. 255–262. [Google Scholar]
- Adi, S.S.; Braga, M.D.; Fernandes, C.G.; Ferreira, C.E.; Martinez, F.V.; Sagot, M.F.; Stefanes, M.A.; Tjandraatmadja, C.; Wakabayashi, Y. Repetition-free longest common subsequence. Discret. Appl. Math. 2010, 158, 1315–1324. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, X. A Simple Algorithm for Solving for the Generalized Longest Common Subsequence (LCS) Problem with a Substring Exclusion Constraint. Algorithms 2013, 6, 485–493. [Google Scholar] [CrossRef]
- Chowdhury, S.R.; Hasan, M.M.; Iqbal, S.; Rahman, M.S. Computing a Longest Common Palindromic Subsequence. Fundam. Informaticae 2014, 129, 329–340. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).