Abstract
In this article, the tampered failure rate model is used in partially accelerated life testing. A non-decreasing time function, often called a time transformation function", is proposed to tamper the failure rate under design conditions. Different types of the proposed function, which have sufficient conditions in order to be accelerating functions, are investigated. A baseline failure rate of the exponential distribution is considered. Some point estimation methods, as well as approximate confidence intervals, for the parameters involved are discussed based on generalized progressively hybrid censored data. The determination of the optimal stress change time is discussed under two different criteria of optimality. A real dataset is employed to explain the theoretical outcomes discussed in this article. Finally, a Monte Carlo simulation study is carried out to examine the performance of the estimation methods and the optimality criteria.
1. Introduction
In the modern era, the products of manufacturing have attained a high quality and have become reliable. Thus, it is very hard to acquire sufficient failure information for products under normal functioning conditions. Moreover, testing their lifetimes under these conditions takes a long time and is very expensive. To overcome these problems, accelerated life tests (ALTs) or partially ALTs (PALTs) are applied to obtain sufficient information about the products’ failure data quickly and in a short time. In ALTs, products are tested under higher-than-regular levels of stress to obtain early failure times. In PALTs, products are tested under both regular and accelerated conditions. The stress factors may be pressure, vibration, temperature, cycling rate, voltage, or any other factor that immediately affects the lifetime of the products. The information obtained from the accelerated or partially accelerated tests is used to predict the failure behavior of the products under normal conditions. Various techniques can be used to implement stress in ALTs. Common techniques are the progressive-stress, step-stress, and constant-stress techniques. For a good survey on ALTs, see [1,2,3,4,5,6].
In a PALT experiment, a random sample of units is put through a life test at a normal stress level, and then the stress is raised after a pre-fixed time or a pre-fixed number of failed units. The experiment continues under accelerated conditions until the units fail or the experiment’s time is finished. For more details, see [4] and [7,8,9,10,11,12,13].
Three major models relate the distribution under accelerated stress to that under normal stress. The models are (i) the tampered random variable (TRV) model suggested in [14], (ii) the cumulative exposure (CE) model given by [15], and (iii) the tampered failure rate (TFR) model suggested in [16].
Several authors used the TFR model in ALTs; Wang and Fei [17] studied the conditions under which the coincidence of the TRV, TFR, and CE models occurred. They also generalized the TFR model from the step-stress ALT setting to the progressive-stress ALT setting (see also [10,18,19,20,21]).
In our paper, we focus on the TFR model. As in Bhattacharyya and Soejoeti [16], the stress is raised after a change time point by multiplying the initial failure rate function (FRF) by an unknown factor (which may depend on ). If is the total FRF in the PALT, then their proposed TFR model is defined by
Censoring schemes have a major role in lifetime and reliability studies. In many practical experiments that depend on the lifetimes of items, the experiment may be finished before all of the items have failed due to the experimental time considered and the associated cost. In such situations, only a part of the failure information of the items is recorded, and the data obtained are called censored data.
Type-I and type-II censoring schemes are two of the most common censoring schemes implemented in life tests. Epstein [22] suggested a mixture of type-I and type-II censoring schemes called the hybrid censoring scheme. In many situations, it is planned in advance to remove items before failure at various steps of the experiment, but the above models of censoring schemes do not have the flexibility to allow for items to be removed from the experiment at various steps other than the experiment’s end point. To solve this problem, Cohen [23] introduced a type-II progressive censoring scheme as a generalization for the above models of censoring schemes.
The type-II progressive censoring scheme can be implemented as follows: Assume that a random sample of n items is subjected to a life test experiment and that the number of observed failures is predetermined before beginning the experiment with a pre-assigned progressive censoring scheme (). At the first failure time , operating items are selected at random and excluded from the experiment. At the next failure time , operating items are selected at random and excluded from the experiment. The procedure is continued in the same manner until the last failure time occurs, at which all of the remaining operating items are excluded from the experiment. Then, the experiment is stopped at .
A major drawback of the type-II progressive censoring scheme is that if the items are of a high quality and are reliable, the experimental time may be quite long. Kundu and Joarder [24] attempted to address this drawback in a modified scheme known as a type-I progressive hybrid censoring scheme, in which and (), as well as the experimental time , were assigned before beginning the experiment. In this situation, the experiment was finished at time min. Except at the end time point, this scheme is the same as the type-II progressive censoring scheme.
One limitation of the type-I progressive hybrid censoring scheme is that the practical sample size is random and can be extremely small. Hence, statistical inference techniques can either be invalid or may be less successful. A new generalization of progressive censoring, which is called the generalized type-I progressive hybrid censoring scheme, was suggested by Cho et al. [25] to avoid defects that appeared in the type-I progressive hybrid censoring scheme. This censoring scheme ensures the satisfaction of at least a constant number of observed items to provide the efficiency required for statistical analysis, and it also controls the total time of the experiment to stay close to the optimum time if the number of observed failures is very small up to time . In this situation, the experiment is finished at the time , and all of the remaining operating items are excluded from the experiment.
Several authors have discussed statistical inference based on the generalized type-I progressive hybrid censoring scheme. For example, Cho et al. [25,26] developed the exact likelihood inference technique for an exponential distribution and an entropy estimation technique for a Weibull distribution. Koley and Kundu [27] and Wang et al. [28] discussed the maximum likelihood and Bayes estimation techniques for exponential and Weibull competing risk models. Zhang and Shi [29] discussed the statistical prediction problem of unobserved failure times based on the simple step-stress ALT with the generalized exponential competing risk model.
What is new in the current article is the implementation of PALTs when the failure rate is accelerated under design conditions through a non-decreasing time function, which is often called a “time transformation function". Three different types of time functions are considered. The sufficient condition under which the time function can be an accelerating function is discussed in detail with each type. Based on generalized progressively hybrid censored data, some point and interval estimations for the parameters involved are discussed. The problem of determining the optimal stress change time is studied through two different criteria of optimality.
The remaining sections of the article are laid out as follows: In Section 2, the model is described with generalized type-I progressive hybrid censoring. Some estimation methods are discussed in Section 3. The optimal stress change time is verified in Section 4 based on two optimality criteria. An application to a real dataset is introduced in Section 5. Simulation studies are presented in Section 6, followed by concluding remarks in Section 7.
2. Model Description and Generalized Type-I Progressive Hybrid Censoring
DeGroot and Goel [14] considered a PALT in which a test unit is first run at normal conditions and, if it does not fail for a specified time , then it is run at accelerated conditions until failure occurs.
According to the TFR model (1), we assume that the n units to be tested are initially under normal conditions up to a fixed time , and if they do not fail by this time, they are placed under accelerated conditions until failure occurs or the experimental time goes to its end—whichever is realized first. The acceleration occurs by multiplying the FRF of the units under normal conditions by a factor .
What is new here is the choice of to be a non-negative increasing function of time t, , (), that is continuous and differentiable. Therefore, Model (1) becomes
According to Model (2), the accelerated conditions increase over time, causing failures to occur more quickly than those previously considered when is considered constant. This also saves time and cost in the experiments.
In lifetime testing experiments and reliability studies, the exponential distribution (ED) is one of the most commonly discussed distributions due to its simplicity and easy mathematical manipulations, as it produces a simple, elegant, and closed-form solution to many problems. We assume that the random variable T follows the ED with scale parameter . Then, the probability density function (PDF), cumulative distribution function (CDF), and FRF of T are given, respectively, by
In the following, based on the FRF (3), the function defined in the CDF (4) will be deduced for three different cases of , where is a positive parameter.
- Case A: If , then , , is deduced as followswhereThe sufficient condition for the function to be an accelerating function is (see Mann et al. [30])
- Case B: If , then, as shown in Case A, , , can be written in the formwhereThe sufficient condition for the function to be an accelerating function is
- Case C: If , then, as shown in Case A, , , can be written in the formwhereThe sufficient condition for the function to be an accelerating function is
Hence, based on the FRF (3), the CDF (4) of the total lifetime T in the PALT for Cases A, B, and C can be rewritten in the form
where
The corresponding PDF is given by
where
Remark 1.
It can be noticed that for the three Cases A, B, and C, at , and hence, the FRF under accelerated conditions tends to the FRF under normal conditions, similarly to what happens in Model (1).
Based on Equation (3), the total FRF in Model (2) is plotted in Figure 1 for three cases of , where it can be noticed that the FRF increases over time after the change time , and further increases also happen by increasing the value of parameter .
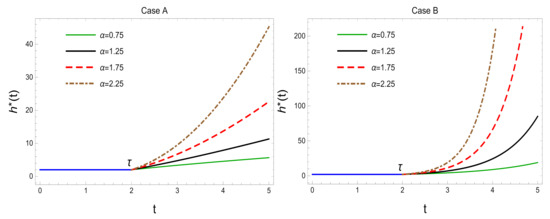
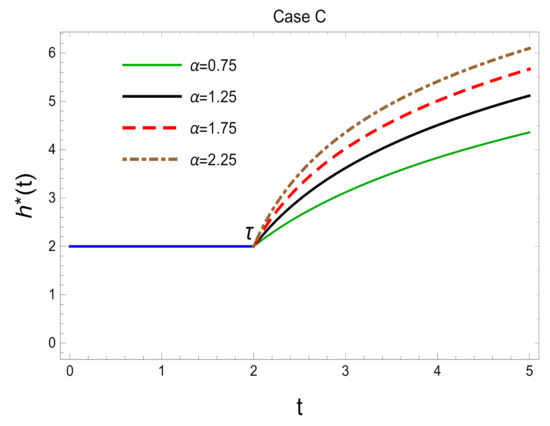
Figure 1.
FRFs in Model (2) considering the three cases of and with .
2.1. Generalized Type-I Progressive Hybrid Censoring
In a PALT, the generalized type-I progressive hybrid censoring can be described as follows:
- Suppose that a set n of randomly chosen units is subjected to a lifetime testing experiment.
- The units are initially tested at normal stress conditions up to a fixed time . If they do not fail by this time, then they are tested under accelerated conditions.
- Suppose that the experimental time and the integers and () are assigned before beginning the experiment, such that , .
- At the first failure time , operating units are selected at random and excluded from the experiment. At the next failure time , operating units are selected at random and excluded from the experiment, and this technique continues. Finally, the experiment is finished at the time , and all of the remaining operating units are excluded from the experiment. The values of the final censoring number are given in Table 1.
 Table 1. Values of , , , and for Cases 1–5.
Table 1. Values of , , , and for Cases 1–5. - Let r() be the number of units that fail under normal (accelerated) stress conditions before (after) time , and let D be the number of units that fail before time . Then, the experimental end time is given byOne of the next six cases may be noticed with the following observations:
- Case 1: If the experimental time is reached before the k-th failure time occurs and failures occur up to time , , then we will not eliminate any operating units from the experiment directly following the -th, ..., -th failure times and will eliminate all of the remaining operating units from the experiment at the k-th failure time, thereby stopping the experiment at , where ; see Figure 2. In this case, we permit the experiment to continue after experimental time is reached to ensure that at least the k-th failure time occurs. In this case, and the following observations will be noticed:
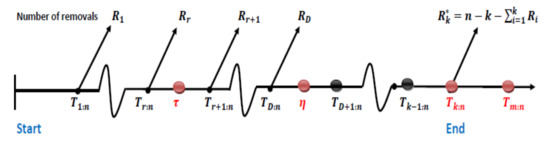 Figure 2. Case 1. The process of generating order statistics from the PALT under generalized type-I progressive hybrid censoring when .
Figure 2. Case 1. The process of generating order statistics from the PALT under generalized type-I progressive hybrid censoring when . - Case 2: If the k-th failure time occurs between times and , , and failures occur up to time , then all of the remaining operating units = are eliminated from the experiment, thereby stopping the experiment at ; see Figure 3. In this case, and the following observations will be noticed:
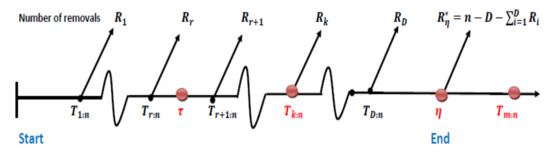 Figure 3. Case 2. The process of generating order statistics from PALT under generalized type-I progressive hybrid censoring when .
Figure 3. Case 2. The process of generating order statistics from PALT under generalized type-I progressive hybrid censoring when . - Case 3: If the k-th failure time occurs before time , , and failures occur up to time , then all of the remaining operating units = are eliminated from the experiment, thereby stopping the experiment at ; see Figure 4. In this case, and the following observations will be noticed:
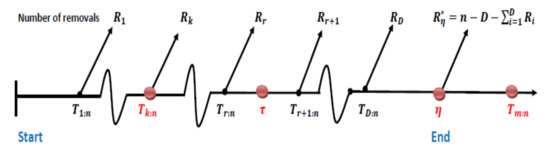 Figure 4. Case 3. The process of generating order statistics from PALT under generalized type-I progressive hybrid censoring when .
Figure 4. Case 3. The process of generating order statistics from PALT under generalized type-I progressive hybrid censoring when . - Case 4: If the k-th failure time occurs after time and the m-th failure time occurs before time , , then all of the remaining operating units =n−m− are eliminated from the experiment, thereby stopping the experiment at ; see Figure 5. In this case, and the following observations will be noticed:
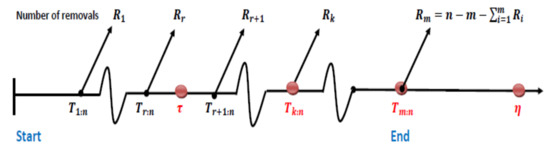 Figure 5. Case 4. The process of generating order statistics from PALT under generalized type-I progressive hybrid censoring when .
Figure 5. Case 4. The process of generating order statistics from PALT under generalized type-I progressive hybrid censoring when . - Case 5: If the k-th failure time occurs before time and the m-th failure time occurs between times and , , then all of the remaining operating units =n−m− are eliminated from the experiment, thereby stopping the experiment at ; see Figure 6. In this case, and the following observations will be noticed:
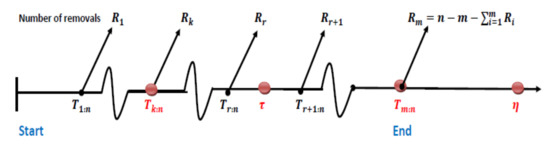 Figure 6. Case 5. The process of generating order statistics from PALT under generalized type-I progressive hybrid censoring when .
Figure 6. Case 5. The process of generating order statistics from PALT under generalized type-I progressive hybrid censoring when . - Case 6: If the m-th failure time occurs before time , , then all of the remaining operating units =n−m− are eliminated from the experiment, thereby stopping the experiment at ; see Figure 7. In this case, , , and the following observations will be noticed:
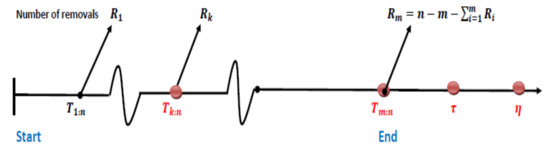 Figure 7. Case 6. The process of generating order statistics from PALT under generalized type-I progressive hybrid censoring when .
Figure 7. Case 6. The process of generating order statistics from PALT under generalized type-I progressive hybrid censoring when .
3. Estimation Methods
This section deals with procedures of obtaining maximum likelihood estimates (MLEs) and percentile estimates (PEs) of the underlying parameters and based on data collected from the PALT under generalized type-I progressive hybrid censoring.
3.1. Maximum Likelihood Estimation
The likelihood function based on generalized type-I progressively hybrid censored data from the PALT presented in Cases 1–6, which were given in the previous section, is given by
- For Cases 1–5:where , and the values of the experimental end time , , , and the final censored number for Cases 1–5 are presented in Table 1. It can be noticed that, with respect to Case 1, some values of , may be changed during the test rather than being fixed before beginning the experiment.
- For Case 6:where .
Generally, maximizing the natural logarithm of the likelihood function to determine the MLEs of the underlying parameters is easier than maximizing the likelihood function. Using the CDF (14) and PDF (16), the natural logarithm of the likelihood function takes the form:
- For Cases 1–5, the MLEs of and can be calculated by equating to zero the first partial derivatives of (20) with respect to and . Then, the likelihood equations take the formswhereFrom (22), the MLE of can be obtained as a function of as follows:By substituting in (23) and solving the likelihood equation with respect to by using any numerical iteration method, the MLE of can be obtained.
- For Case 6, no failures were detected under accelerated stress conditions, so the MLE of does not exist, but the MLE of can be calculated by equating to zero the first partial derivative of (21) with respect to . Then, the MLE of is given by
Remark 2.
It can be noticed that:
- In Cases 1,2, and 4, if , no failures were detected under normal stress conditions; then, the MLE of β does not exist.
- In Case 3, if , no failures were detected under accelerated stress conditions; then, the MLE of α does not exist.
Based on the common asymptotic normality theory of MLEs, we can consider that and can be approximated by a standard normal distribution, i.e.,
where and are the variances of and , which can be obtained from the inverse of the local Fisher information matrix (FIM), i.e.,
where
where the caret denotes that the derivative is evaluated at . The second partial derivatives of the natural logarithm of the likelihood function with respect to and can be obtained without difficulty.
Suppose that and . Then, for , a normal approximation confidence interval (NACI) for can be defined as
where is the MLE of and is the upper percentile of the distribution.
Sometimes, the lower bound of the NACI may have a negative value for the positive parameter. So, Meeker and Escobar [31] suggested using a log transformation confidence interval (LTCI) for this parameter. Based on the normal approximation of a log-transformed MLE, , , can be approximated to a standard normal distribution, i.e.,
where .
Therefore, a LTCI for can be defined as
3.2. Percentile Estimation
A percentile method for estimating unknown parameters was proposed by Kao [32]. It is simply natural to estimate the unknown parameter by adjusting a straight line to the theoretical points obtained by the CDF and the percentile points of the sample if data were collected from a closed-form CDF. The empirical CDF applied in this process can be described as
where is defined as in Table 1 and
Based on generalized type-I progressive hybrid censoring under the PALT, the PEs of the parameters and can be obtained as follows:
- For Cases 1–5: It is possible to obtain the PEs and of and by minimizing the next quantity with respect to and .
- Case A:
- Case B:
- Case C:
whereMinimizing the quantity can be done by solving and with respect to and . - For Case 6, the PE of does not exist, but the PE of can be obtained by minimizing the next quantity with respect to :where is given by (33).
4. Common Optimality Criteria
The current section aims to study the problem of determining the optimal time, , of the increase in the stress level under generalized type-I progressively hybrid censored data supposing the ED as a lifetime model. The criteria of A-optimality and D-optimality, which allow the optimal value of to be determined, are considered; see, for example, [33,34,35].
- A-optimality criterionThis criterion is concerned with the maximization of the trace of the FIM, which provides an overall information measure based on the marginal information about the parameters. It is preferred when the estimates are, at most, moderately correlated. Therefore, the optimal value of can be obtained by maximizing the trace of the FIM (29) of MLEs and , i.e.,
- D-optimality criterionThis criterion is concerned with maximizing the determinant of the FIM, which provides an overall measure of variability by taking into account the correlation between the estimates. It is preferred that it is applied when the estimates are highly correlated. It is also pertinent for the construction of the joint confidence region for the parameters. Therefore, the optimal value of can be obtained by maximizing (minimizing) the determinant of the FIM (inverse of the FIM) ((29) and (28)) of the MLEs and , i.e.,
The maximization of the [] can be achieved by solving the equation with respect to . The solution cannot be obtained in a closed form. So, an iterative method is needed in order to obtain a numerical solution.
5. Real Dataset
In this section, we consider a real dataset in order to explain the procedures of inference presented in the last sections. The real dataset was collected from an ALT experiment by Zhu [36] as follows: A sample of light bulbs was subjected to a life test at a stress level of 2.25 V, and then the sample subjected to accelerated conditions with a stress level 2.44 V at the time point of hours. The stress level of 2.25 V is considered to correspond to the normal stress conditions. The failure times of light bulbs were noticed, light bulbs were removed from the experiment, and then the experiment was finished. The dataset is shown in Table 2. One logical question now is that of whether or not the CDF (14), with the ED as a lifetime distribution under normal stress conditions, fits the real dataset that appears in Table 2. For this reason, the Kolmogorov–Smirnov (K-S) test statistic and its corresponding p-value were used. Table 3 shows the results, in which it can be noticed that all of the p-values are greater than 0.05, so the ED fits the given real dataset well. This is shown also by drawing the empirical CDFs of the given real dataset together with the CDFs (14) in Cases A, B, and C; see Figure 8.

Table 2.
The failure times of 64 light bulbs from a PALT experiment with .

Table 3.
MLEs of the parameters , the K-S statistic, and the p-value.
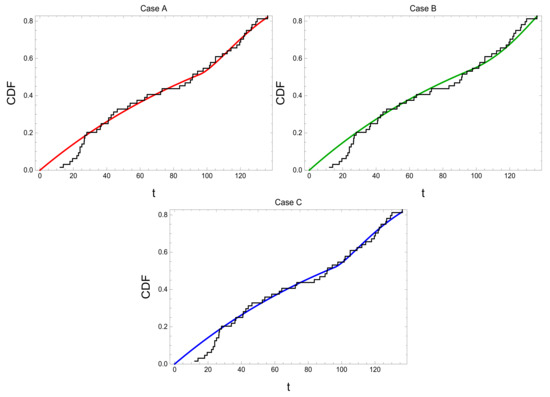
Figure 8.
Empirical CDF of the given real dataset together with the CDF (14) for Cases A, B, and C.
We consider and three values of 116 (Scheme I), 125 (Scheme II), and 140 (Scheme III) in order to apply the generalized type-I progressive hybrid censoring to the real dataset; see Table 4. The MLEs, PEs, NACIs, and LTCIs of the parameters and were calculated, and the optimal values of under two optimality criteria— and —of increasing stress level were calculated, as presented in Table 5.

Table 4.
The samples under generalized type-I progressive hybrid censoring considering .

Table 5.
MLEs, PEs, NACIs, and LTCIs of the parameters and and the optimal values, and , for Cases A, B, and C.
6. Simulation Study
As it is theoretically difficult to assess the efficiency of estimation methods, a Monte Carlo simulation was used to overcome this difficulty. In the current section, through a Monte Carlo simulation, we conduct a numerical study in order to assess the efficiency and performance of the estimation methods and optimality criteria considered in the last sections. The following steps were used:
- Assign values of the sample size n, stress change time , and parameters , and assign values of , and .
- Generate n observations from the Uniform(0,1) distribution.
- Apply the generalized type-I progressive hybrid censoring to the random sample obtained in Step 3, as shown in Section 2.1.
- Find the value of r, which is the number of observations with values , as follows:
- Compute the MLEs, PEs, NACIs, and LTCIs of , as shown in Section 3.
- Compute the optimal values, and , of the stress change time, as shown in Section 4.
- Replicate Steps 2–7 (= 5000) times.
- Calculate the mean of the estimates, mean squared error (MSE), and relative absolute bias (RAB) of over samples as follows:where is an estimate of .
- Using Step 9, calculate the mean of the estimates of the parameters with their MSEs and RABs.
- Calculate the average of the RABs (ARAB) and MSEs (AMSE) as follows:
- Evaluate the 95% NACIs and LTCIs of the parameters , and then evaluate their average interval lengths (AILs) and coverage probabilities (COVPs). In addition, also evaluate the average of the AILs (AAIL) as follows:
The next three CSs are used in the generation of the samples:
- CS1:
- CS2:
- CS3:
The results of the calculations are recorded in Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11, taking into account the following population parameter values: (for Case A), (for Case B), (for Case C), and . The following values were taken into account through the simulation analysis: , of the sample size, of the sample size, , and .

Table 6.
PEs and MLEs of and with their MSEs, RABs, AMSEs, and ARABs based on 5000 simulations. The population parameter values are and for Case A.

Table 7.
AILs and COVPs (in %) of the 95% CIs of and based on 5000 simulations. The population parameter values are and for Case A.

Table 8.
PEs and MLEs of and with their MSEs, RABs, AMSEs, and ARABs based on 5000 simulations. The population parameter values are and for Case B.

Table 9.
AILs and COVPs (in %) of the 95% CIs of and based on 5000 simulations. The population parameter values are and for Case B.

Table 10.
PEs and MLEs of and with their MSEs, RABs, AMSEs, and ARABs based on 5000 simulations. The population parameter values are and for Case C.

Table 11.
AILs and COVPs (in %) of the 95% CIs of and based on 5000 simulations. The population parameter values are and for Case C.
6.1. Simulation Results
Based on the results of the calculations recorded in Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11, the following points can be observed:
- The MLEs are better than the PEs through the ARABs and AMSEs.
- The NACIs are better than the LTCIs through the AAILs.
- The optimal values and are close one to each other each time for Cases A and B. However, for Case C, the optimal value is less than and approaches the proposed value .
- For fixed values of m and , by increasing n, the RABs, MSEs, MRABs, MMSEs, AIL, and AAIL decrease.
- For fixed values of n and , by increasing m, the RABs, MSEs, MRABs, MMSEs, AIL, and AAIL decrease.
- For fixed values of n and m, by increasing , the RABs, MSEs, MRABs, MMSEs, AIL, and AAIL decrease.
- By increasing , or , the COVPs are close to 95% for Cases A and B. However, for Case C, the COVPs are higher than 95% because greater values of the MSEs of the estimates than those for Cases A and B were obtained, which led to wider CIs
- For fixed values of n and , by increasing m, the optimal values and increase.
- For fixed m and , by increasing n, the optimal values and decrease.
- For fixed n and m, by increasing , the optimal values and increase.
Except in rare situations, which might be consequent to fluctuations in the data, the above findings are accurate. Based on the above observations, we recommend using the accelerating function for the power series (Case A) or exponential (Case B) functions.
7. Concluding Remarks
We applied PALTs to units whose lifetimes under normal stress conditions are exponentially distributed and proposed the use of the TFR model when the failure rate under normal stress conditions is tampered by a non-decreasing function of time, which is sometimes called a “time transformation function”. Three different types of the proposed function were considered. The sufficient conditions for the proposed functions to be accelerating functions were discussed. Based on generalized type-I progressively hybrid censored data, we discussed the MLEs and PEs, as well as the approximate CIs, of the included parameters. The determination of the optimal stress change time was discussed for two different criteria of optimality. A real dataset was used to explain the procedures of inference presented in the paper. In the end, a Monte Carlo simulation study was carried out to examine the performance of the estimation methods and the optimality criteria. From the numerical results, we suggest the use of the ML method and the NACI to estimate the parameters included in the situations of acceleration and censoring used. In addition, the results are completed with a recommendation for the use of the power series or exponential functions as accelerating functions.
Author Contributions
Conceptualization, A.H.A.-H.; Data curation, A.F.H.; Formal analysis, A.F.H.; Funding acquisition, A.F.H.; Investigation, A.H.A.-H.; Methodology, A.H.A.-H.; Project administration, A.F.H.; Resources, A.H.A.-H.; Software, A.F.H.; Supervision, A.H.A.-H. and A.F.H.; Validation, A.H.A.-H. and A.F.H.; Visualization, A.H.A.-H. and A.F.H.; Writing—original draft, A.F.H.; Writing—review & editing, A.H.A.-H.. All authors have read and agreed to the published version of the manuscript.
Funding
Academy of Scientific Research and Technology (ASRT), Egypt, under the initiatives of the Science Up Faculty of Science (Grant No. 6589).
Data Availability Statement
The data are used to support the findings of this study are included within the paper.
Acknowledgments
The authors are grateful to the Associate Editor and the anonymous referees for providing some useful comments on an earlier version of this paper. This paper was financially supported by the Academy of Scientific Research and Technology (ASRT), Egypt, under the initiatives of the Science Up Faculty of Science (Grant No. 6589).
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Nelson, W. Accelerated Testing: Statistical Models, Test Plans and Data Analysis; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Bagdonavičius, V.; Nikulin, M. Accelerated Life Models: Modeling and Statistical Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 2002. [Google Scholar]
- AL-Hussaini, E.K.; Abdel-Hamid, A.H. Accelerated life tests under finite mixture models. J. Stat. Comput. Simul. 2006, 76, 673–690. [Google Scholar] [CrossRef]
- Abdel-Hamid, A.H.; AL-Hussaini, E.K. Estimation in step-stress accelerated life tests for the exponentiated exponential distribution with type-I censoring. Comput. Stat. Data Anal. 2009, 53, 1328–1338. [Google Scholar] [CrossRef]
- AL-Hussaini, E.K.; Abdel-Hamid, A.H.; Hashem, A.F. One-sample Bayesian prediction intervals based on progressively type-II censored data from the half-logistic distribution under progressive-stress model. Metrika 2015, 78, 771–783. [Google Scholar] [CrossRef]
- Nadarajah, S.; Abdel-Hamid, A.H.; Hashem, A.F. Inference for a geometric-Poisson-Rayleigh distribution under progressive-stress model based on type-I progressive hybrid censoring with binomial removals. Qual. Reliab. Eng. Int. 2018, 34, 649–680. [Google Scholar] [CrossRef]
- Bai, D.S.; Chung, S.W. Optimal design of partially accelerated life tests for the exponential distribution under type-I censoring. IEEE Trans. Reliab. 1992, 41, 400–406. [Google Scholar] [CrossRef]
- Gouno, E.; Sen, A.; Balakrishnan, N. Optimal step-stress test under progressive type-I censoring. IEEE Trans. Reliab. 2004, 53, 388–393. [Google Scholar] [CrossRef]
- Abdel-Hamid, A.H.; AL-Hussaini, E.K. Step partially accelerated life tests under finite mixture models. J. Stat. Comput. Simul. 2008, 78, 911–924. [Google Scholar] [CrossRef]
- Abdel-Hamid, A.H.; AL-Hussaini, E.K. Inference and optimal design based on step—Partially accelerated life tests for the generalized Pareto distribution under progressive type-I censoring. Commun. Stat. Simul. Comput. 2014, 44, 1750–1769. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Kundu, D.; Ng, H.K.T.; Kannan, N. Point and interval estimation for a simple step-stress model with type-II censoring. J. Qual. Technol. 2007, 39, 35–47. [Google Scholar] [CrossRef]
- Ismail, A.A. Inference in the generalized exponential distribution under partially accelerated tests with progressive Type-II censoring. Theor. Appl. Fract. Mech. 2012, 59, 49–56. [Google Scholar] [CrossRef]
- Samanta, D.; Kundu, D. Order restricted inference of a multiple step-stress model. Comput. Stat. Data Anal. 2018, 117, 62–75. [Google Scholar] [CrossRef]
- DeGroot, M.H.; Goel, P.K. Bayesian estimation and optimal design in partially accelerated life testing. Naval Res. Logist. Q. 1979, 26, 223–235. [Google Scholar] [CrossRef]
- Nelson, W. Accelerated life testing step-stress models and data analysis. IEEE Trans. Reliab. 1980, R-29, 103–108. [Google Scholar] [CrossRef]
- Bhattacharyya, G.K.; Soejoeti, Z. A tampered failure rate model for step-stress accelerated life test. Commun. Statist. Theory Methods 1989, 18, 1627–1643. [Google Scholar] [CrossRef]
- Wang, R.; Fei, H. Statistical inference of Weibull distribution for tampered failure rate model in progressive stress accelerated life testing. J. Syst. Sci. Complex. 2004, 17, 237–243. [Google Scholar]
- Ali Mousa, M.A.M. Empirical bayes estimators for the burr type XII accelerated life testing model based on type-2 censored data. J. Stat. Comput. Simul. 1995, 52, 95–103. [Google Scholar] [CrossRef]
- Tang, Y.; Guan, Q.; Xu, P.; Xu, H. Optimum design for type-I step-stress accelerated life tests of twoparameter Weibull distributions. Commun. Stat. Theory Methods 2012, 41, 3863–3877. [Google Scholar] [CrossRef]
- Xu, H.; Fei, H. Models comparison for step-stress accelerated life testing. Commun. Stat. Theory Methods 2012, 41, 3878–3887. [Google Scholar] [CrossRef]
- Zhang, C.; Shi, Y.; Wu, M. Statistical inference for competing risks model in step-stress partially accelerated life tests with progressively Type-I hybrid censored Weibull life data. J. Comput. Appl. Math. 2016, 297, 65–74. [Google Scholar] [CrossRef]
- Epstein, B. Truncated life-tests in the exponential case. Ann. Math. Stat. 1954, 25, 555–564. [Google Scholar] [CrossRef]
- Cohen, A.C. Progressively censored samples in life testing. Technometrics 1963, 5, 327–329. [Google Scholar] [CrossRef]
- Kundu, D.; Joarder, A. Analysis of type-II progressively hybrid censored data. Comput. Stat. Data Anal. 2006, 50, 2509–2528. [Google Scholar] [CrossRef]
- Cho, Y.; Sun, H.; Lee, K. Exact likelihood inference for an exponential parameter under generalized progressive hybrid censoring scheme. Stat. Methods 2015, 23, 18–34. [Google Scholar] [CrossRef]
- Cho, Y.; Sun, H.; Lee, K. Estimating the entropy of a Weibull distribution under generalized progressive hybrid censoring. Entropy 2015, 17, 102–122. [Google Scholar] [CrossRef] [Green Version]
- Koley, A.; Kundu, D. On generalized progressive hybrid censoring in presence of competing risks. Metrika 2017, 80, 401–426. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Tripathi, Y.M.; Lodhi, C. Inference for Weibull competing risks model with partially observed failure causes under generalized progressive hybrid censoring. J. Comput. Appl. Math. 2020, 368. [Google Scholar] [CrossRef]
- Zhang, C.; Shi, Y. Statistical prediction of failure times under generalized progressive hybrid censoring in a simple step-stress accelerated competing risks model. J. Syst. Eng. Electr. 2017, 28, 282–291. [Google Scholar]
- Mann, N.R.; Schafar, R.E.; Singpurwalla, N.D. Methods for Statistical Analysis of Reliability and Life Data; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Meeker, W.Q.; Escobar, L.A. Statistical Method for Reliability Data; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Kao, J.H.K. A graphical estimation of mixed Weibull parameters in life testing electron tube. Technometrics 1959, 1, 389–407. [Google Scholar] [CrossRef]
- Ng, H.K.T.; Chan, P.S.; Balakrishnan, N. Optimal progressive censoring plans for the Weibull distribution. Technometrics 2004, 46, 470–481. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Han, D. Optimal step-stress testing for progressively type-I censored data from exponential distribution. J. Stat. Plan. Inference 2009, 139, 1782–1798. [Google Scholar] [CrossRef]
- Wu, S.J.; Lin, Y.P.; Chen, S.T. Optimal step-stress test under type I progressive group-censoring with random removals. J. Stat. Plan. Inference 2008, 138, 817–826. [Google Scholar] [CrossRef]
- Zhu, Y. Optimal Design and Equivalency of Accelerated Life Testing Plans. Ph.D. Thesis, The State University of New Jersey, New Brunswick, NJ, USA, 2010. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).