Stochastic Analysis of the Time Continuum †
Abstract
1. Introduction
2. Materials and Methods
2.1. The Intuitionistic Mathematics
2.2. The Time Operator
3. Results
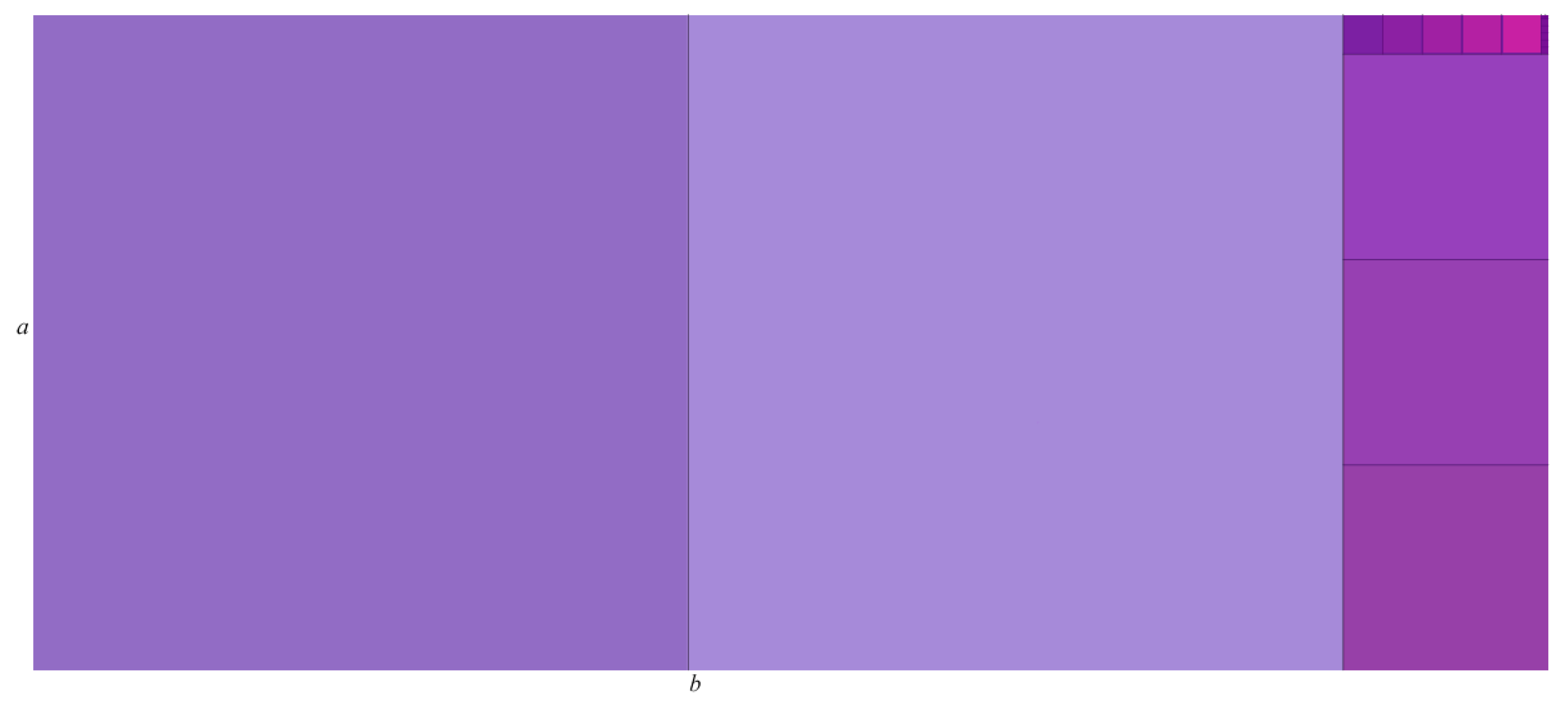
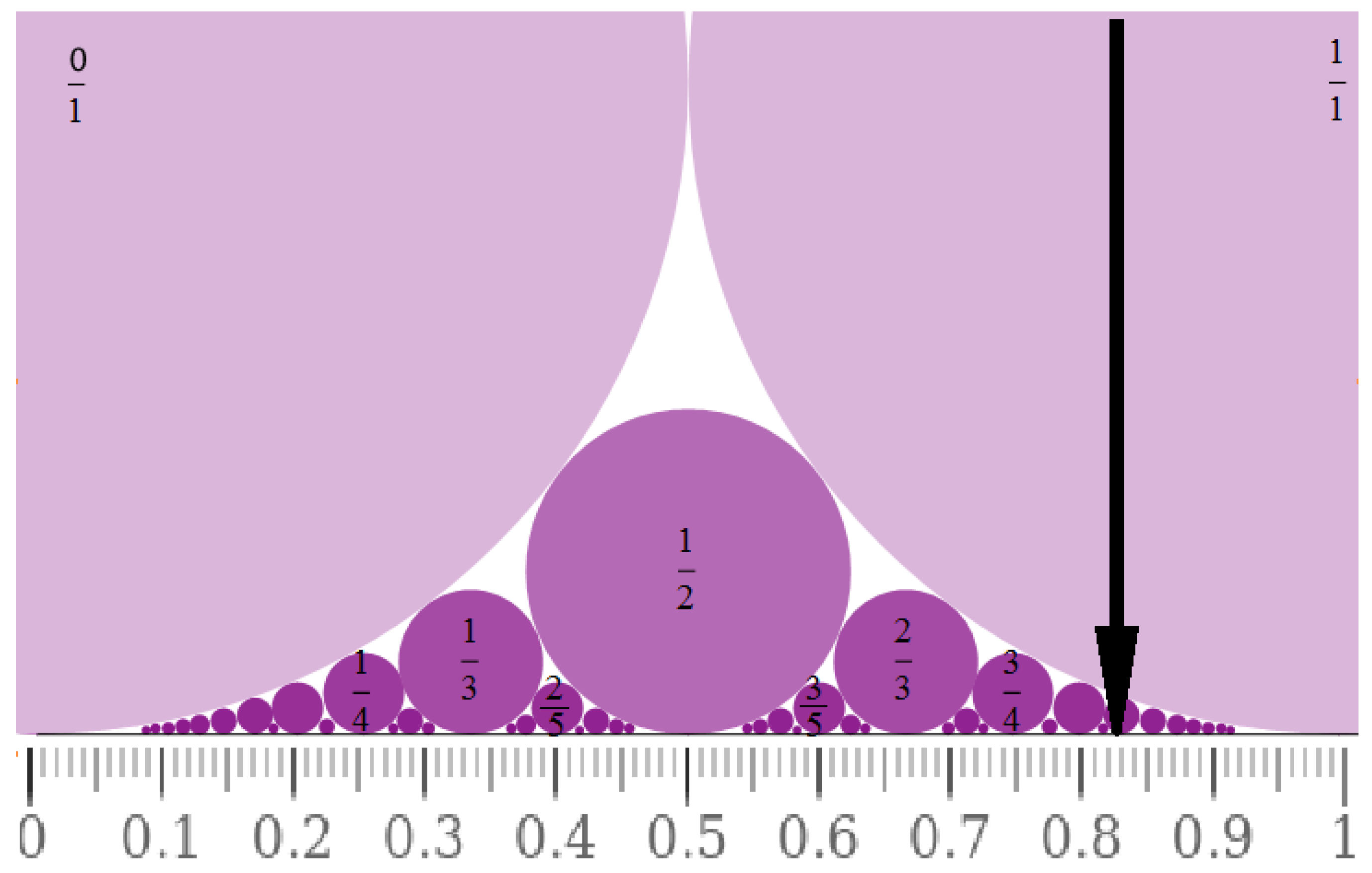
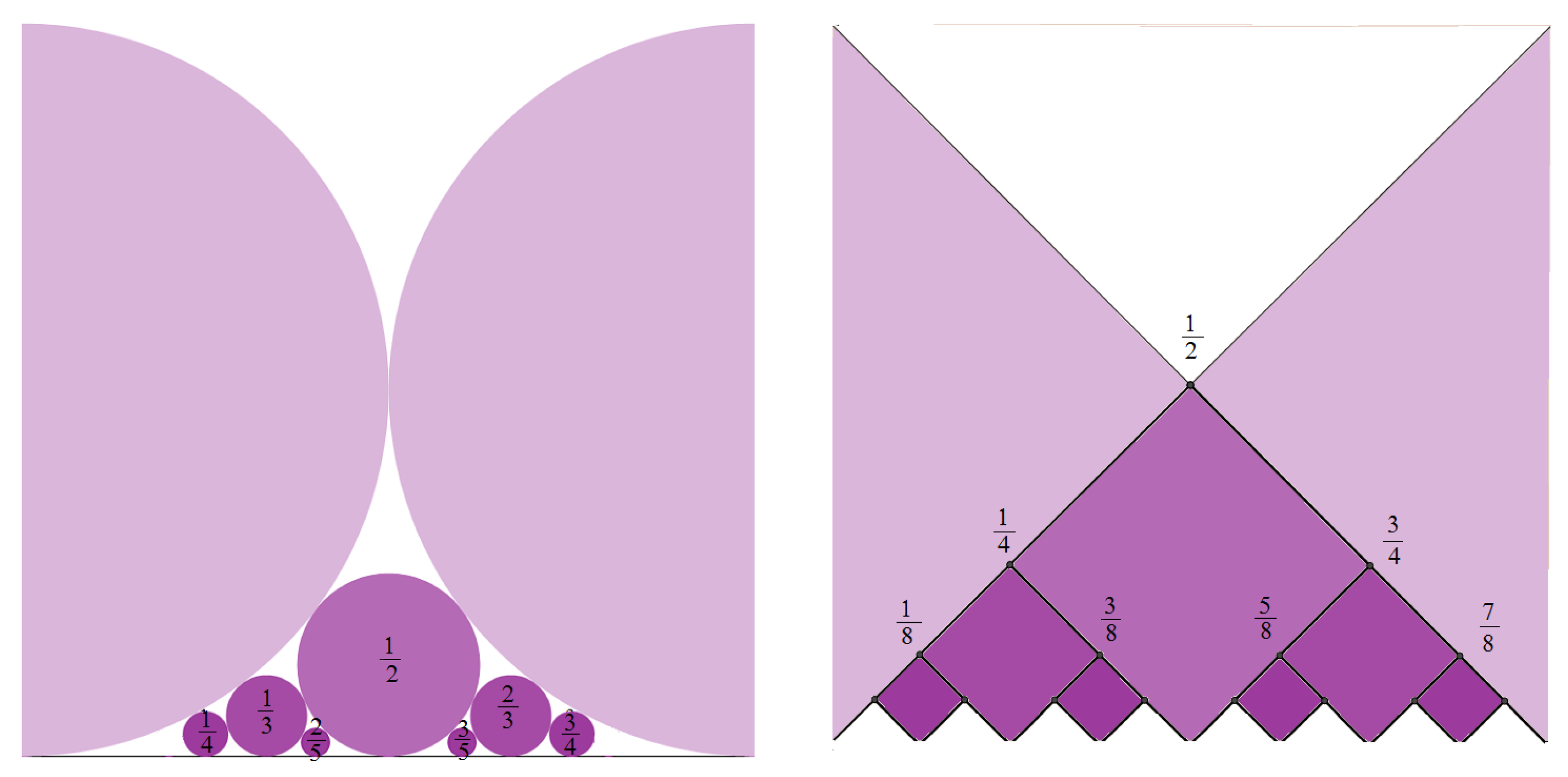
3.1. The Continuum of Reals
3.1.1. Real Numbers
3.1.2. The Continuum Structure
3.2. Wavelets and Multiresolution Hierarchy
3.2.1. The Signal Space
3.2.2. Signal Ensembles
4. Discussion
4.1. Self-Organization of the Time Continuum
4.1.1. Local and Global Complexity
Go to the top of Highgate Hill on a clear summer morning at five o’clock, and look at Westminster Abbey. You will receive an impression of a building enriched with multitudinous vertical lines. Try to distinguish one of these lines all the way down from the one next to it: You cannot. Try to count them: You cannot. Try to make out the beginning or end of any of them: You cannot. Look at it generally, and it is all symmetry and arrangement. Look at it in its parts, and it is all inextricable confusion.
4.1.2. Dynamical Identity
4.2. The Measurement Problem
4.2.1. Quantum Measurement
4.2.2. The Euclidean Paradigm
4.2.3. Psychophysical Parallelism
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chaitin, G.J. Randomness in arithmetic and the decline and fall of reductionism in pure mathematics. Chaos Soliton. Fract. 1995, 5, 143–159. [Google Scholar] [CrossRef]
- Sambrook, T.; Whiten, A. On the nature of complexity in cognitive and behavioural science. Theor. Psychol. 1997, 7, 191–213. [Google Scholar] [CrossRef]
- Grassberger, P. Toward a quantitative theory of self-generated complexity. Int. J. Theor. Phys. 1986, 25, 907–938. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Young, K. Computation at the onset of chaos. In Complexity, Entropy, and the Physics of Information; Zurek, W., Ed.; Addison-Wesley: Boston, MA, USA, 1990; pp. 223–269. [Google Scholar]
- Simon, H.A. The architecture of complexity. In Proceedings of the American Philosophical Society; Springer: Boston, MA, USA, 1962; pp. 467–482. [Google Scholar]
- Tasić, V. Mathematics and the Roots of Postmodern Thought; Oxford University Press Inc.: New York, NY, USA, 2001. [Google Scholar]
- Shalizi, C.R.; Shalizi, K.L.; Haslinger, R. Quantifying self-organization with optimal predictors. Phys. Rev. Lett. 2004, 93, 1–4. [Google Scholar] [CrossRef]
- Antoniou, I.; Misra, B.; Suchanecki, Z. Time Operator: Innovation and Complexity; John Wiley & Sons: New York, NY, USA, 2003. [Google Scholar]
- Milovanović, M.; Vukmirović, S. The time operator of reals. In Proceedings of the 4th Conference on Complexity, Future Information Systems and Risk COMPLEXIS 2019, Heraklion, Greece, 2–4 May 2019; pp. 75–84. [Google Scholar]
- Brouwer, L.E.J. Over de grondslagen der wiskunde, Maas & van uchtelen Amsterdam-Leipzig, 1907. In Mathematics and the Roots of Postmodern Thought; Tasić, V., Ed.; Oxford University Press: New York, NY, USA, 2001; p. 46. [Google Scholar]
- Brouwer, L.E.J. Mathematik, Wissenschaft and Sprache. Monatshefte der Mathematik und Physik 1929, 36, 153–164. [Google Scholar] [CrossRef]
- Brouwer, L.E.J. Intuitionistische Betrachtungen über den Formalismus. KNAW Proc. 1928, 31, 374–379. [Google Scholar]
- Bell, J.L. A Primer of Infinitesimal Analysis; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Meyerson, E. Identité et Réalité; F. Alcan: Paris, France, 1908. [Google Scholar]
- D‘Alambert, J. Dimension. s.s. (Physique & Géometrie). In Encyclopédie, ou Dictionnaire Raisonné des Sciences, des Arts et des MéTiers, Par Une Société de Gens de Lettres, Tome QuatrièMe; Didert, D., d‘Alambert, J., Eds.; Briasson: Paris, France, 1754; pp. 1009–1010. [Google Scholar]
- Lagrange, J.L. Théorie des Fonctions Analytiques; Imprimerie de la Republique: Paris, France, 1796. [Google Scholar]
- Prigogine, I. Time and Complexity in the Physical Science; W. H. Freeman & Co.: New York, NY, USA, 1980. [Google Scholar]
- Toulmin, S. The Return to Cosmology: Postmodern Science and the Theology of Nature; University of California Press: Berkeley, CA, USA, 1985. [Google Scholar]
- Koopman, B.O. Hamiltonian systems and transformations in Hilbert space. Proc. Natl. Acad. Sci. USA 1931, 17, 315. [Google Scholar] [CrossRef] [PubMed]
- Misra, B.; Prigogine, I.; Courbage, M. From deterministic dynamics to probabilistic descriptions. Physica A 1979, 98, 1–26. [Google Scholar] [CrossRef]
- Misra, B.; Prigogine, I. Irreveribility and nonlocality. Lect. Math. Phys. 1983, 7, 421–429. [Google Scholar] [CrossRef]
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Ford, L.R. Fractions. Am. Math. Mon. 1938, 45, 586–601. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing: The Sparse Way; Elsevier Inc.: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Farey, J.S. On a curious property of vulgar fractions. Philos. Mag. 1816, 47, 385–386. [Google Scholar] [CrossRef][Green Version]
- Minkowski, H. Zur Geometrie der Zahlen. In Verhandlungen des III Internationalen Mathematiker-Kongresses; heiDOK.: Heidelberg, Germany, 1904; pp. 164–173. [Google Scholar]
- Warmus, M. Calculus of approximations. Bull. Acad. Pol. Sci. 1965, 4, 253–259. [Google Scholar]
- Florack, L. Image Structure; Springer: Dordecht, The Netherlands, 1997. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Antoniou, I.E.; Gustafson, K.E. The time operator of wavelets. Chaos Solitons Fract. 2000, 11, 443–452. [Google Scholar] [CrossRef]
- Antoniou, I.; Gustafson, K. Wavelets and stochastic processes. Math. Comput. Simul. 1999, 49, 81–104. [Google Scholar] [CrossRef]
- Gustafson, K. Wavelets and expectations: A different path to wavelet. In Harmonic, Wavelets and p-adic Analysis; Egorov, Y.V., Mumford, D., Meyer, Y., Chuong, N.M., Khrennikov, A.Y., Eds.; World Scientific Publishing Co.: London, UK, 2007; pp. 5–22. [Google Scholar]
- Lucretius. On the Nature of Things; Oxford at the Clarendon Press: Oxford, UK, 1948. [Google Scholar]
- Koenderink, J.J. Scale in perspective. In Gaussian Scale-Space Theory; Sporring, J., Nielsen, M., Florack, L., Johansen, P., Eds.; Springer: Dordecht, The Netherlands, 1997; pp. xv–xx. [Google Scholar]
- Crouse, M.C.; Nowak, R.D.; Baraniuk, R.G. Wavelet-based statistical signal processing using hidden Markov model. IEEE Trans. Sign. Proc. 1998, 46, 886–902. [Google Scholar] [CrossRef]
- Milovanović, M.; Rajkovć, M. Quantifying self-organization with optimal wavelets. Europhys. Lett. 2013, 102, 40004. [Google Scholar] [CrossRef]
- Rabiner, L. A tutorial on hidden Markov model and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–285. [Google Scholar] [CrossRef]
- Ruskin, J. Modern Painters; Smith, Elder & Co.: London, UK, 1844. [Google Scholar]
- Greenwood, D.D. Mapping; The University of Chicago Press: Chicago, IL, USA, 1964. [Google Scholar]
- Milovanović, M.; Medić-Simić, G. Aesthetical criterion in art and science. Neural Comput. Appl. 2021, 3, 2137–2156. [Google Scholar] [CrossRef]
- Bachelard, G. La Poétique de l‘Espace; Les Presses Universitaires de France: Paris, France, 1961. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman & Co.: New York, NY, USA, 1983. [Google Scholar]
- Antoniou, I.; Sadovnichii, V.A.; Shkarin, S.A. New extended spectral decomposition of the Rényi map. Phys. Lett. A 1999, 258, 237–243. [Google Scholar] [CrossRef]
- Morrison, P.; Morrison, P. Powers of Ten: A Book about the Relative Size of Things in the Universe and the Effect of Adding Another Zero; Scientific American Library: New York, NY, USA, 1982. [Google Scholar]
- Lochs, G. Vergleich der Genauigkeit von Dezimalbruch und Kettenbruch. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 1964, 27, 142–144. [Google Scholar] [CrossRef]
- Mayer, D.; Roepstorff, G. On the relaxation time of Gauss’s continued fraction map, I. The Hilbert space approach (Koopmanism). J. Stat. Phys. 1987, 47, 149–171. [Google Scholar] [CrossRef]
- Mayer, D.; Roepstorff, G. On the relaxation time of Gauss’ continued-fraction map, II. The Banach space approach (Transfer operator method). J. Stat. Phys. 1988, 50, 331–344. [Google Scholar] [CrossRef]
- Antoniou, I.; Shkarin, S.A. Analicity of smooth eigenfunctions and spectral analysis of the Gauss map. J. Stat. Phys. 2003, 111, 355–369. [Google Scholar] [CrossRef]
- Milovanović, M. Dynamical identity of the Brouwer continuum. In Proceedings of the 5th Conference on Information Theory and Complex Systems, TINKOS 2017, Belgrade, Serbia, 9–10 November 2017. [Google Scholar]
- Von Franz, M.-L. Number and Time: Reflections Leading toward a Unification of Depth Psychology and Physics; Northwestern University Press: Evanston, IL, USA, 1974. [Google Scholar]
- Glivenko, V. Sur quelque point de logique de M. Brouwer. Acad. R. Belgique Bull. 1929, 15, 183–188. [Google Scholar]
- Brouwer, L.E.J. Bewijs dat jedere volle functie gelijkmatig continu is. KNAW Verslagen 1924, 33, 189–193. [Google Scholar]
- Heidelberger, M. The mind-body problem in the origin of logical empiricism: Herbert Feigl and psychophysical parallelism. In Logical Empiricism: Historical and Contemporary Perspectives; Parrini, P., Salmon, W.C., Salmon, M.H., Eds.; Pittsburgh University Press: Pittsburgh, PA, USA, 2003; pp. 233–262. [Google Scholar]
- Fechner, G.T. Elemente der Psychophysik; Erster Theil, Breitkopf und Härtel: Leipzig, Germany, 1860. [Google Scholar]
- Sheynin, O. Fechner as a statistician. Brit. J. Math. Stat. Psychol. 2004, 57, 53–72. [Google Scholar] [CrossRef] [PubMed]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milovanović, M.; Vukmirović, S.; Saulig, N. Stochastic Analysis of the Time Continuum. Mathematics 2021, 9, 1452. https://doi.org/10.3390/math9121452
Milovanović M, Vukmirović S, Saulig N. Stochastic Analysis of the Time Continuum. Mathematics. 2021; 9(12):1452. https://doi.org/10.3390/math9121452
Chicago/Turabian StyleMilovanović, Miloš, Srđan Vukmirović, and Nicoletta Saulig. 2021. "Stochastic Analysis of the Time Continuum" Mathematics 9, no. 12: 1452. https://doi.org/10.3390/math9121452
APA StyleMilovanović, M., Vukmirović, S., & Saulig, N. (2021). Stochastic Analysis of the Time Continuum. Mathematics, 9(12), 1452. https://doi.org/10.3390/math9121452






