Sparse HJ Biplot: A New Methodology via Elastic Net
Abstract
1. Introduction
2. Materials and Methods
2.1. Biplot and HJ-Biplot
- : is the data matrix
- : is the matrix of data whose columns contain the eigenvectors of
- : is the matrix of data whose columns contain the eigenvectors of
- : is the diagonal matrix containing the eigenvalues of
- and must be orthonormal, that is, and to guarantee the uniqueness of the factorisation.
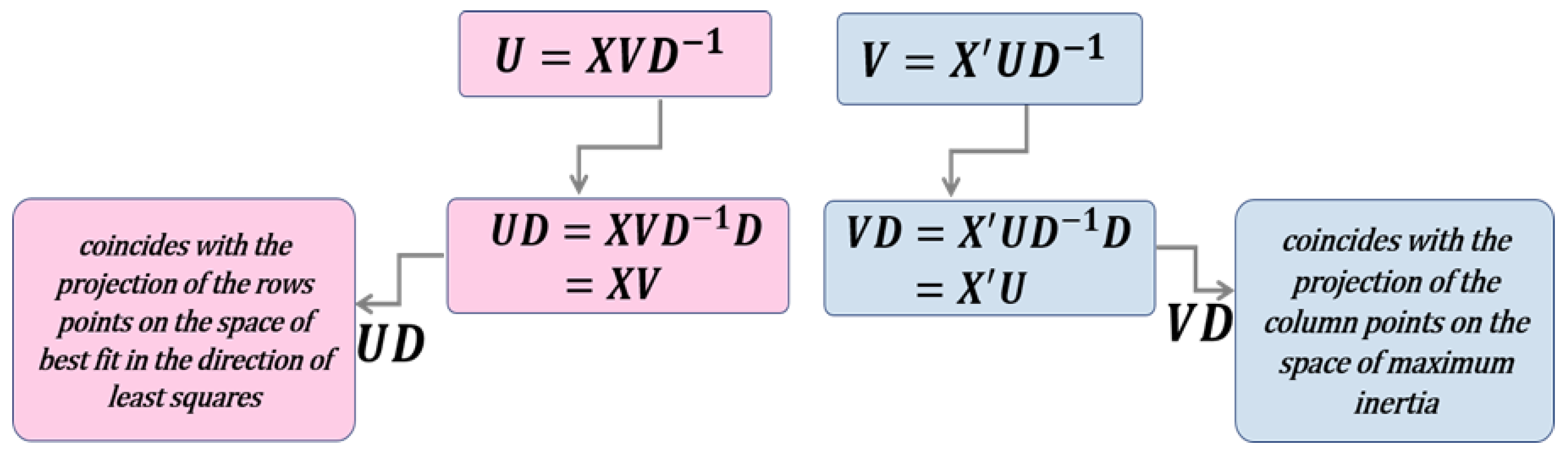
- The proximity between the points that represent the row markers is interpreted as the similarity between them. Consequently, nearby points allow the identification of clusters of individuals with similar profiles.
- The standard deviation of a variable can be estimated by the module of the vector which represents it.
- Correlations between variables can be captured from the angles between vectors. If two variables are correlated, they will have an acute angle; if the angle they form is obtuse the variables will present a negative correlation; and, if the angle is a right angle it indicates that the variables are not correlated.
- The points orthogonally projected onto a variable approximates the position of the sample values in that variable.
2.2. Disjoint HJ Biplot
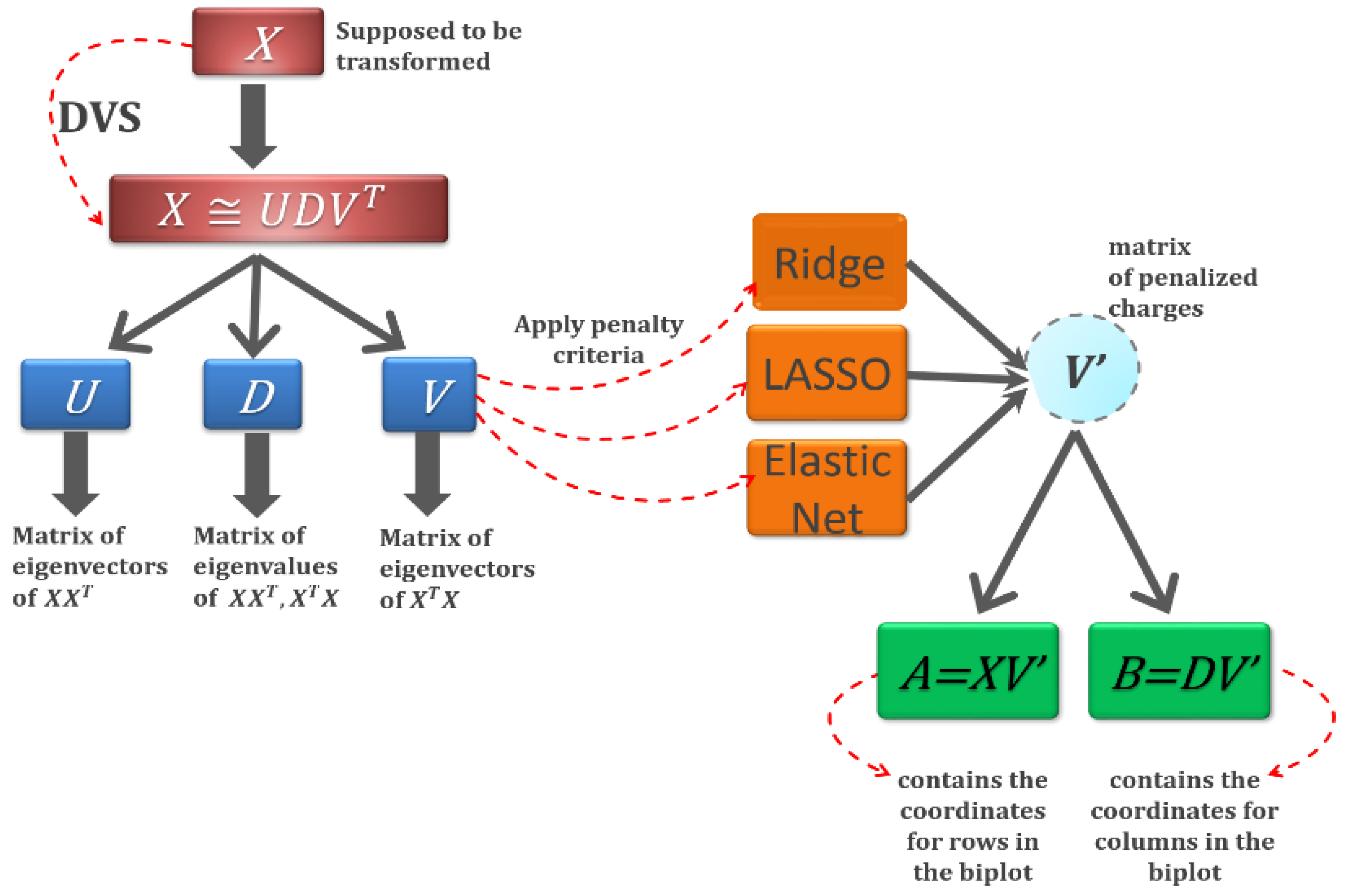
2.3. Sparse HJ Biplot
| Algorithm 1 Sparse HJ biplot algorithm using elastic net regularisation. |
| 1. Consider a data matrix. |
| 2. A tolerance value is set (1 × 10−5). |
| 3. The data is transformed (centred or standardised). |
| 4. Decomposition of the original data matrix is performed via SVD. |
| 5. A is taken as the loadings of the first k components V[, 1:k]. |
|
6. is calculated by:
|
|
7. A is updated via SVD of : |
|
8. The difference between A and B is updated: |
| 9. Steps 4, 5 and 6 are repeated until tolerance. |
| 10. The columns are normalized using |
| 11. We then calculate the row markers and column markers. |
| 12. The elastic net HJ biplot obtained by the previous steps is plotted. |
2.4. Software
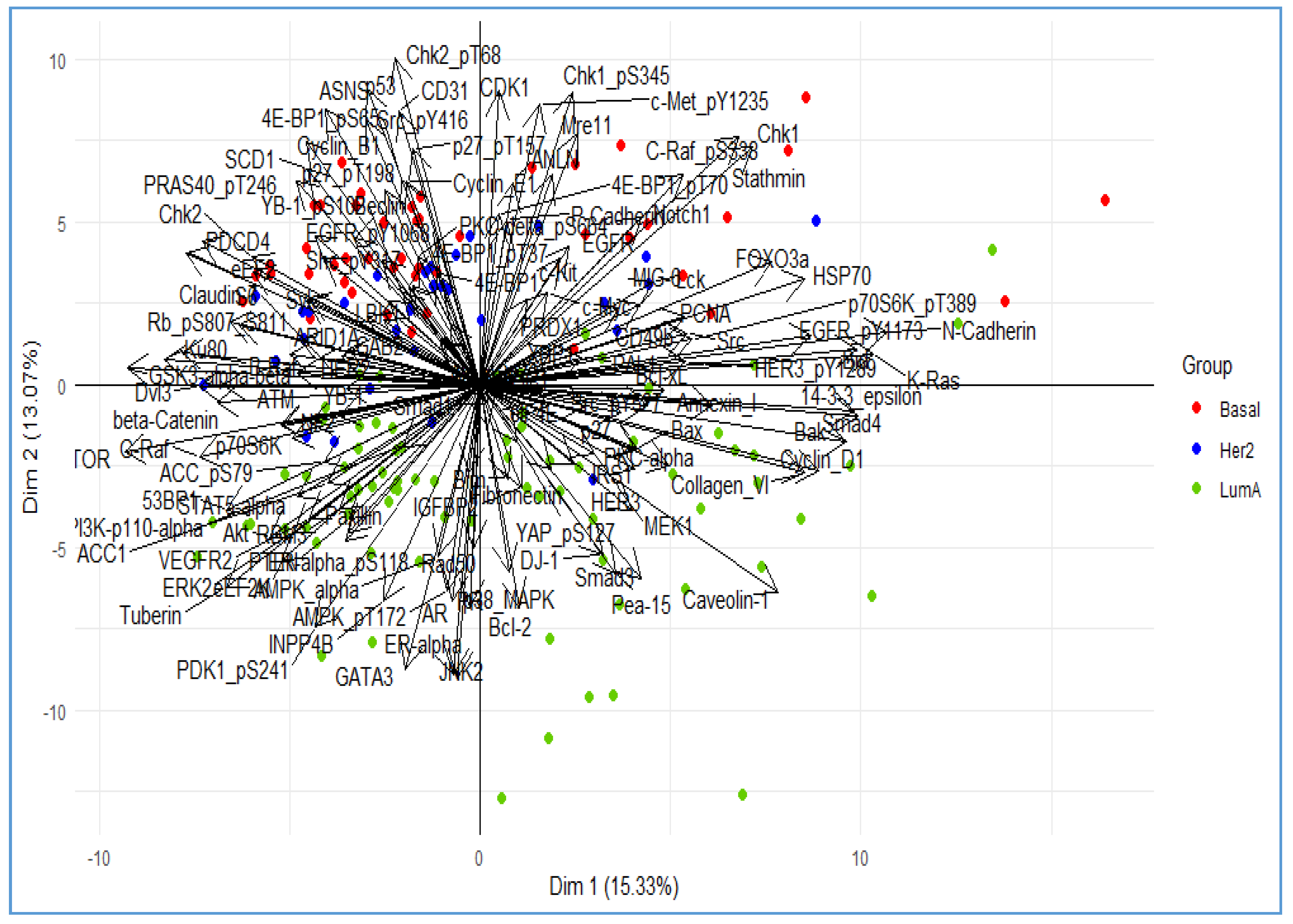
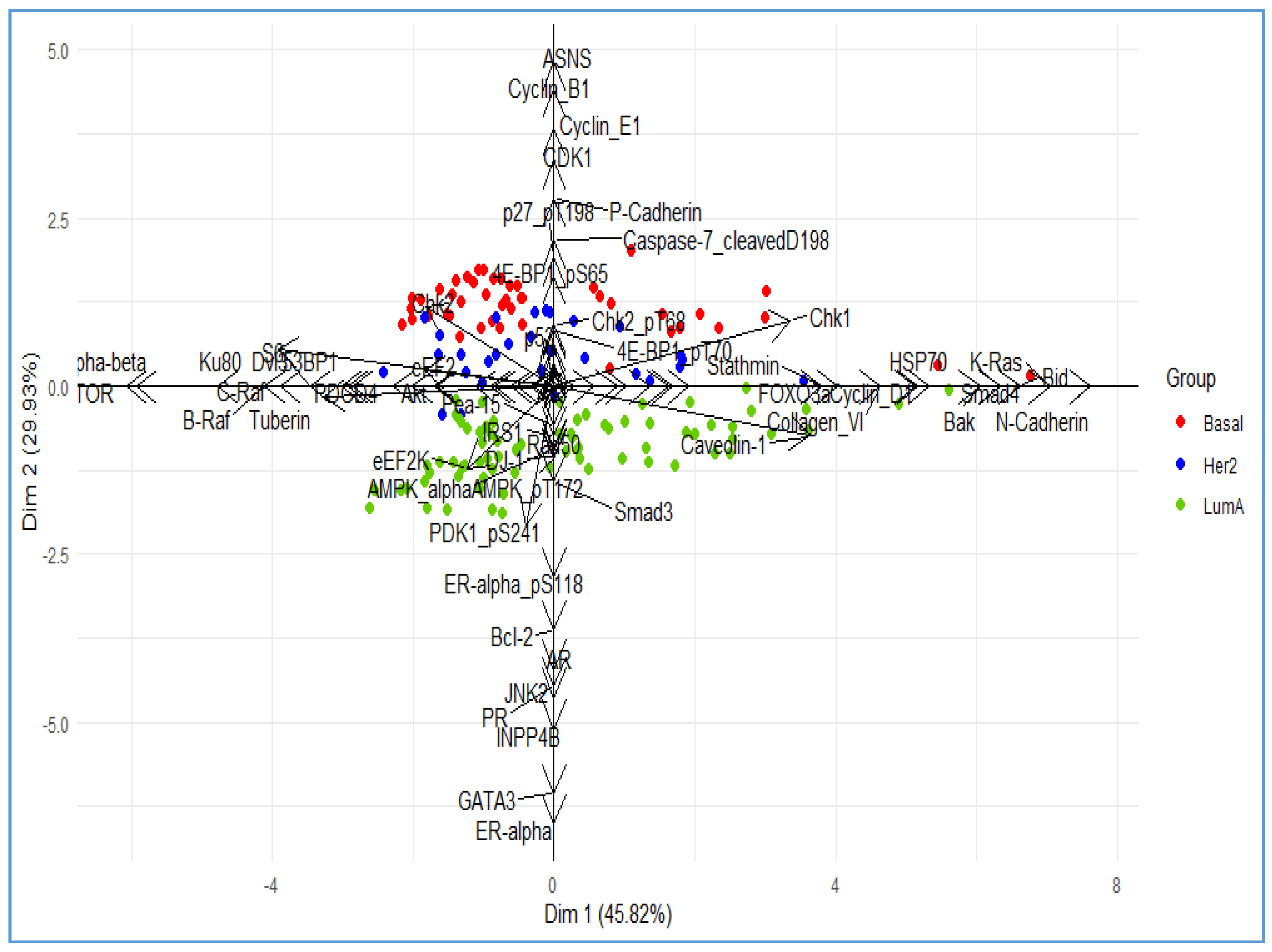
3. Illustrative Example
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pearson, K.F.R.S. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a Complex of Statistical Variables into Principal Components. J. Educ. Psychol. 1933, 24, 417. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal Component Analysis; Wiley Online Library: Hoboken, NJ, USA, 2002. [Google Scholar]
- Eckart, C.; Young, G. The approximation of one matrix by another of lower rank. Psychometrika 1936, 1, 211–218. [Google Scholar] [CrossRef]
- Hausman, R.E. Constrained Multivariate Analysis. In Optimisation in Statistics; Zanakis, S.H., Rustagi, J.S., Eds.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1982; pp. 137–151. [Google Scholar]
- Vines, S.K. Simple principal components. J. R. Stat. Soc. Ser. C Appl. Stat. 2000, 49, 441–451. [Google Scholar] [CrossRef]
- McCabe, G.P. Principal Variables. Technometrics 1984, 26, 137–144. [Google Scholar] [CrossRef]
- Cadima, J.; Jolliffe, I.T. Department of Mathematical Sciences Loading and correlations in the interpretation of principle compenents. J. Appl. Stat. 1995, 22, 203–214. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Rotation of principal components: Choice of normalization constraints. J. Appl. Stat. 1995, 22, 29–35. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Uddin, M. The Simplified Component Technique: An Alternative to Rotated Principal Components. J. Comput. Graph. Stat. 2000, 9, 689–710. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Trendafilov, N.; Uddin, M. A Modified Principal Component Technique Based on the LASSO. J. Comput. Graph. Stat. 2003, 12, 531–547. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T.; Tibshirani, R. Sparse Principal Component Analysis. J. Comput. Graph. Stat. 2006, 15, 265–286. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least Angle Regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Moghaddam, B.; Weiss, Y.; Avidan, S. Spectral Bounds for Sparse PCA: Exact and Greedy Algorithms. Adv. Neural Inf. Process. Syst. 2006, 18, 915. [Google Scholar]
- D’Aspremont, A.; El Ghaoui, L.; Jordan, M.; Lanckriet, G.R.G. A Direct Formulation for Sparse PCA Using Semidefinite Programming. SIAM Rev. 2007, 49, 434–448. [Google Scholar] [CrossRef]
- Shen, H.; Huang, J.Z. Sparse principal component analysis via regularized low rank matrix approximation. J. Multivar. Anal. 2008, 99, 1015–1034. [Google Scholar] [CrossRef]
- Witten, D.M.; Tibshirani, R.; Hastie, T. A penalized matrix decomposition, with applications to sparse principal components and canonical correlation analysis. Biostatistics 2009, 10, 515–534. [Google Scholar] [CrossRef]
- Farcomeni, A. An exact approach to sparse principal component analysis. Comput. Stat. 2009, 24, 583–604. [Google Scholar] [CrossRef]
- Qi, X.; Luo, R.; Zhao, H. Sparse principal component analysis by choice of norm. J. Multivar. Anal. 2013, 114, 127–160. [Google Scholar] [CrossRef]
- Vichi, M.; Saporta, G. Clustering and disjoint principal component analysis. Comput. Stat. Data Anal. 2009, 53, 3194–3208. [Google Scholar] [CrossRef]
- Mahoney, M.W.; Drineas, P. CUR matrix decompositions for improved data analysis. Proc. Natl. Acad. Sci. USA 2009, 106, 697–702. [Google Scholar] [CrossRef]
- Trendafilov, N.T. From simple structure to sparse components: A review. Comput. Stat. 2014, 29, 431–454. [Google Scholar] [CrossRef]
- Zhang, Z.; Xuelong, L.; Yang, J.; Li, X.; Zhang, D. A Survey of Sparse Representation: Algorithms and Applications. IEEE Access 2015, 3, 490–530. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Gabriel, K.R. The Biplot Graphic Display of Matrices with Application to Principal Component Analysis. Biometrika 1971, 58, 453–467. [Google Scholar] [CrossRef]
- Galindo-Villardón, P. Una Alternativa de Representacion Simultanea: HJ-Biplot. Qüestiió Quad. D’Estad. I Investig. Oper. 1986, 10, 13–23. [Google Scholar]
- Nieto-Librero, A.B.; Sierra, C.; Vicente-Galindo, M.; Ruíz-Barzola, O.; Galindo-Villardón, M.P. Clustering Disjoint HJ-Biplot: A new tool for identifying pollution patterns in geochemical studies. Chemosphere 2017, 176, 389–396. [Google Scholar] [CrossRef] [PubMed]
- Cancer Genome Atlas Network. Comprehensive Molecular Portraits of Human Breast Tumours. Nature 2012, 490, 61. [Google Scholar] [CrossRef] [PubMed]
- Rohart, F.; Gautier, B.; Singh, A.; Cao, K.-A.L. mixOmics: An R package for ‘omics feature selection and multiple data integration. PLoS Comput. Biol. 2017, 13, e1005752. [Google Scholar] [CrossRef]
- Galindo-Villardón, P.; Cuadras, C.M. Una Extensión del Método Biplot y su relación con otras técnicas. Publ. Bioestad. Biomatemática 1986, 17, 13–23. [Google Scholar]
- Greenacre, M.J. Correspondence analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 613–619. [Google Scholar] [CrossRef]
- Cubilla-Montilla, M.; Nieto-Librero, A.-B.; Galindo-Villardón, M.P.; Galindo, M.P.V.; Garcia-Sanchez, I.-M. Are cultural values sufficient to improve stakeholder engagement human and labour rights issues? Corp. Soc. Responsib. Environ. Manag. 2019, 26, 938–955. [Google Scholar] [CrossRef]
- Cubilla-Montilla, M.I.; Galindo-Villardón, P.; Nieto-Librero, A.B.; Galindo, M.P.V.; García-Sánchez, I.M. What companies do not disclose about their environmental policy and what institutional pressures may do to respect. Corp. Soc. Responsib. Environ. Manag. 2020, 27, 1181–1197. [Google Scholar] [CrossRef]
- Murillo-Avalos, C.L.; Cubilla-Montilla, M.; Sánchez, M.; Ángel, C.; Vicente-Galindo, P. What environmental social responsibility practices do large companies manage for sustainable development? Corp. Soc. Responsib. Environ. Manag. 2021, 28, 153–168. [Google Scholar] [CrossRef]
- Nieto-Librero, A.B.; Galindo-Villardón, P.; Freitas, A. Package biplotbootGUI: Bootstrap on Classical Biplots and Clustering Disjoint Biplot. Available online: https://CRAN.R-project.org/package=biplotbootGUI (accessed on 4 April 2021).
- Erichson, N.B.; Zheng, P.; Manohar, K.; Brunton, S.L.; Kutz, J.N.; Aravkin, A.Y. Sparse Principal Component Analysis via Variable Projection. SIAM J. Appl. Math. 2020, 80, 977–1002. [Google Scholar] [CrossRef]
- Cubilla-Montilla, M.; Torres-Cubilla, C.A.; Galindo-Villardón, P.; Nieto-Librero, A.B. Package SparseBiplots. Available online: https://CRAN.R-project.org/package=SparseBiplots (accessed on 4 April 2021).
- Wickham, H. Ggplot2. Wiley Interdiscip. Rev. Comput. Stat. 2011, 3, 180–185. [Google Scholar] [CrossRef]
- Gligorijević, V.; Malod-Dognin, N.; Pržulj, N. Integrative methods for analyzing big data in precision medicine. Proteomics 2016, 16, 741–758. [Google Scholar] [CrossRef]
- McCue, M.E.; McCoy, A.M. The Scope of Big Data in One Medicine: Unprecedented Opportunities and Challenges. Front. Veter Sci. 2017, 4, 194. [Google Scholar] [CrossRef]
- Montilla, M.I.C. Contribuciones al Análisis Biplot Basadas en Soluciones Factoriales Disjuntas Y en Soluciones Sparse. Ph.D. Thesis, Universidad de Salamanca, Salamanca, Spain, 2019. [Google Scholar]
- González García, N. Análisis Sparse de Tensores Multidimensionales. Ph.D. Thesis, Universidad de Salamanca, Salamanca, Spain, 2019. [Google Scholar]
- Hernández-Sánchez, J.C.; Vicente-Villardón, J.L. Logistic biplot for nominal data. Adv. Data Anal. Classif. 2016, 11, 307–326. [Google Scholar] [CrossRef][Green Version]
- Lavit, C.; Escoufier, Y.; Sabatier, R.; Traissac, P. The Act (Statis Method). Comput. Stat. Data Anal. 1994, 18, 97–119. [Google Scholar] [CrossRef]
- Jaffrenou, P.-A. Sur l’analyse Des Familles Finies de Variables Vectorielles: Bases Algébriques et Application à La Description Statistique. Ph.D. Thesis, Thèse de Troisième Cycle, Université de Lyon, Lyon, France, 1978. [Google Scholar]
- Tucker, L.R. Some mathematical notes on three-mode factor analysis. Psychometrika 1966, 31, 279–311. [Google Scholar] [CrossRef] [PubMed]
- Kroonenberg, P.M.; De Leeuw, J. Principal component analysis of three-mode data by means of alternating least squares algorithms. Psychometrika 1980, 45, 69–97. [Google Scholar] [CrossRef]
- Harshman, R.A. Foundations of the PARAFAC Procedure: Models and Conditions for an “Explanatory” Multi-Modal Factor Analysis. Work. Pap. Phon. 1970, 16, 1–84. [Google Scholar]

| Proteins | HJ Biplot | Disjoint Biplot | Elastic Net HJ Biplot | ||||||
|---|---|---|---|---|---|---|---|---|---|
| D1 | D2 | D3 | D1 | D2 | D3 | D1 | D2 | D3 | |
| 14-3-3_epsilon | 9.835 | −0.791 | 0.698 | 1 | 0 | 0 | 6.330 | 0 | 0 |
| 4E-BP1 | −1.127 | 3.408 | −0.752 | 0 | 0 | 1 | 0 | 0 | 0 |
| 4E-BP1_pS65 | −2.074 | 6.317 | −2.116 | 0 | 0 | 1 | 0 | 1.633 | 0 |
| 4E-BP1_pT37 | −1.862 | 2.997 | −5.079 | 0 | 0 | 1 | 0 | 0 | 0 |
| 4E-BP1_pT70 | 0.486 | 5.227 | −1.753 | 0 | 0 | 1 | 0 | 0.832 | 0 |
| 53BP1 | −6.654 | −3.875 | 1.235 | 0 | 0 | 1 | −3.015 | 0 | 0 |
| A-Raf_pS299 | −4.47 | 2.681 | −1.221 | 0 | 1 | 0 | 0 | 0 | 0 |
| ACC1 | −4.007 | −3.042 | −0.894 | 0 | 0 | 1 | 0 | 0 | 0 |
| ACC_pS79 | −4.094 | −2.386 | −2.147 | 0 | 0 | 1 | 0 | 0 | 0 |
| AMPK_alpha | −1.103 | −5.287 | 1.69 | 1 | 0 | 0 | 0 | −0.917 | 0 |
| AMPK_pT172 | −0.86 | −6.362 | 1.486 | 1 | 0 | 0 | 0 | −1.075 | 0 |
| ANLN | 0.877 | 6.213 | 5.348 | 1 | 0 | 0 | 0 | 0 | 2.111 |
| AR | −0.729 | −6.68 | 4.084 | 1 | 0 | 0 | 0 | −4.209 | 0 |
| ARID1A | −3.643 | 0.852 | 1.409 | 1 | 0 | 0 | 0 | 0 | 0 |
| ASNS | −4.067 | 8.449 | −1.908 | 0 | 0 | 1 | 0 | 4.819 | 0 |
| ATM | −5.234 | −1.222 | −0.396 | 0 | 1 | 0 | −1.118 | 0 | 0 |
| Akt | −5.513 | −4.694 | −0.288 | 0 | 0 | 1 | −1.664 | 0 | 0 |
| Akt_pS473 | −1.049 | 1.326 | −7.186 | 0 | 0 | 1 | 0 | 0 | 0 |
| Akt_pT308 | −1.782 | 3.054 | −5.25 | 0 | 0 | 1 | 0 | 0 | 0 |
| Annexin_I | 6.102 | −0.652 | −4.703 | 1 | 0 | 0 | 1.919 | 0 | 0 |
| B-Raf | −7.829 | 0.995 | 2.763 | 1 | 0 | 0 | −4.104 | 0 | 0 |
| Bak | 9.633 | −1.78 | −1.534 | 1 | 0 | 0 | 6.042 | 0 | 0 |
| Bax | 4.12 | −1.972 | −2.539 | 1 | 0 | 0 | 0 | 0 | 0 |
| Bcl-2 | 1.021 | −6.875 | 4.678 | 1 | 0 | 0 | 0 | −3.623 | 0 |
| Bcl-xL | 4.824 | −0.207 | 1.384 | 1 | 0 | 0 | 0.189 | 0 | 0 |
| Beclin | −3.283 | 4.485 | 6.71 | 1 | 0 | 0 | 0 | 0 | 2.459 |
| Bid | 9.885 | 1.076 | 1.13 | 1 | 0 | 0 | 6.612 | 0 | 0 |
| Bim | 0.715 | −2.899 | 3.656 | 1 | 0 | 0 | 0 | 0 | 0 |
| C-Raf | −7.355 | −2.215 | −0.384 | 1 | 0 | 0 | −3.880 | 0 | 0 |
| C-Raf_pS338 | 5.312 | 6.464 | 3.593 | 1 | 0 | 0 | 1.686 | 0 | 2.060 |
| CD31 | −2.116 | 8.398 | 7.088 | 1 | 0 | 0 | 0 | 0 | 4.871 |
| CD49b | 3.632 | 2.32 | 3.552 | 0 | 0 | 1 | 0 | 0 | 0 |
| CDK1 | 0.488 | 9.008 | −0.729 | 1 | 0 | 0 | 0 | 3.351 | 0.892 |
| Caspase-7_cleavedD198 | 1.906 | 6.466 | −1.048 | 1 | 0 | 0 | 0 | 2.174 | 0 |
| Caveolin-1 | 7.827 | −6.415 | −1.311 | 1 | 0 | 0 | 3.643 | −0.742 | −0.702 |
| Chk1 | 6.792 | 7.605 | 1.289 | 1 | 0 | 0 | 3.358 | 0.985 | 0.563 |
| Chk1_pS345 | 2.418 | 8.966 | 5.551 | 1 | 0 | 0 | 0 | 0 | 4.071 |
| Chk2 | −6 | 3.914 | −2.176 | 1 | 0 | 0 | −1.815 | 1.190 | 0 |
| Chk2_pT68 | −2.247 | 10.009 | 4.991 | 1 | 0 | 0 | 0 | 0.914 | 4.810 |
| Claudin-7 | −4.187 | 0.804 | 4.021 | 1 | 0 | 0 | 0 | 0 | 0 |
| Collagen_VI | 8.506 | −2.722 | −0.097 | 1 | 0 | 0 | 4.628 | 0 | 0 |
| Cyclin_B1 | −4.571 | 7.465 | −2.745 | 1 | 0 | 0 | 0 | 4.414 | 0 |
| Cyclin_D1 | 8.872 | −2.678 | 2.491 | 1 | 0 | 0 | 5.170 | 0 | 0 |
| Cyclin_E1 | −1.927 | 6.257 | −3.637 | 1 | 0 | 0 | 0 | 3.837 | 0 |
| DJ-1 | 3.216 | −5.246 | 2.356 | 1 | 0 | 0 | 0 | −1.053 | 0 |
| Dvl3 | −7.369 | −0.063 | −0.467 | 1 | 0 | 0 | −3.462 | 0 | 0 |
| E-Cadherin | −4.731 | 1.337 | 3.855 | 1 | 0 | 0 | −0.142 | 0 | 0 |
| EGFR | 2.315 | 4.231 | −2.325 | 0 | 0 | 1 | 0 | 0.244 | 0 |
| EGFR_pY1068 | −0.772 | 1.862 | −2.4 | 0 | 0 | 1 | 0 | 0 | 0 |
| EGFR_pY1173 | 8.702 | 1.484 | 1.23 | 0 | 1 | 0 | 5.321 | 0 | 0 |
| ER-alpha | −0.686 | −8.918 | 5.329 | 0 | 1 | 0 | 0 | −6.509 | 0 |
| ER-alpha_pS118 | −3.542 | −4.816 | 6.177 | 1 | 0 | 0 | 0 | −2.834 | 0 |
| ERK2 | −4.911 | −4.53 | −1.404 | 0 | 1 | 0 | −0.903 | 0 | 0 |
| FOXO3a | 7.666 | 3.783 | 1.127 | 1 | 0 | 0 | 4.027 | 0 | 0 |
| Fibronectin | 1.852 | −2.596 | −0.897 | 1 | 0 | 0 | 0 | 0 | 0 |
| GAB2 | −3.465 | 1.083 | −0.098 | 1 | 0 | 0 | 0 | 0 | 0 |
| GATA3 | −1.972 | −8.738 | 5.216 | 0 | 1 | 0 | 0 | −6.058 | 0 |
| GSK3-alpha-beta | −9.243 | 0.501 | −0.787 | 1 | 0 | 0 | −5.924 | 0 | 0 |
| GSK3-alpha-beta_pS21_S9 | −6.718 | −0.029 | −4.263 | 0 | 0 | 1 | −2.273 | 0 | 0 |
| HER2 | −3.51 | −0.115 | 0.883 | 0 | 0 | 1 | 0 | 0 | 0 |
| HER2_pY1248 | −0.973 | 1.28 | −0.442 | 0 | 0 | 1 | 0 | 0 | 0 |
| HER3 | 3.995 | −3.859 | 0.899 | 0 | 1 | 0 | 0 | 0 | 0 |
| HER3_pY1289 | 5.381 | 0.692 | −1.768 | 0 | 0 | 1 | 1.365 | 0 | 0 |
| HSP70 | 8.525 | 3.238 | 0.181 | 0 | 1 | 0 | 5.127 | 0 | 0 |
| IGFBP2 | 1.102 | −3.158 | 1.768 | 1 | 0 | 0 | 0 | 0 | 0 |
| INPP4B | −2.524 | −6.657 | 6.597 | 1 | 0 | 0 | 0 | −5.098 | 0 |
| IRS1 | 4.045 | −2.6 | 5.377 | 1 | 0 | 0 | 0 | −0.741 | 0 |
| JNK2 | −0.584 | −9.036 | 1.984 | 1 | 0 | 0 | 0 | −4.625 | −0.041 |
| JNK_pT183_pT185 | 2.476 | −2.463 | −0.011 | 1 | 0 | 0 | 0 | 0 | 0 |
| K-Ras | 10.304 | 0.949 | 0.456 | 1 | 0 | 0 | 7.040 | 0 | 0 |
| Ku80 | −8.303 | 0.743 | 0.447 | 1 | 0 | 0 | −4.768 | 0 | 0 |
| LBK1 | −2.52 | 1.968 | 7.864 | 1 | 0 | 0 | 0 | 0 | 1.173 |
| Lck | 4.528 | 3.158 | −3.052 | 0 | 1 | 0 | 0.055 | 0 | 0 |
| MAPK_pT202_Y204 | −0.304 | −2.731 | −3.607 | 1 | 0 | 0 | 0 | 0 | 0 |
| MEK1 | 2.993 | −2.122 | −2.706 | 1 | 0 | 0 | 0 | 0 | 0 |
| MEK1_pS217_S221 | −5.209 | −1.263 | −2.992 | 0 | 0 | 1 | −0.514 | 0 | 0 |
| MIG-6 | 4.206 | 2.429 | 1.513 | 0 | 1 | 0 | 0 | 0 | 0 |
| Mre11 | 2.55 | 7.729 | 7.37 | 1 | 0 | 0 | 0 | 0 | 4.444 |
| N-Cadherin | 10.669 | 1.608 | 0.799 | 1 | 0 | 0 | 7.616 | 0 | 0 |
| NF-kB-p65_pS536 | −4.992 | 0.915 | −2.066 | 0 | 0 | 1 | −0.330 | 0 | 0 |
| NF2 | −4.468 | −1.197 | 1.559 | 0 | 0 | 1 | −0.284 | 0 | 0 |
| Notch1 | 4.22 | 5.154 | 0.049 | 0 | 1 | 0 | 0 | 0.221 | 0 |
| P-Cadherin | 0.692 | 5.044 | −4.532 | 1 | 0 | 0 | 0 | 2.793 | 0 |
| PAI-1 | 2.668 | 0.836 | −1.01 | 1 | 0 | 0 | 0 | 0 | 0 |
| PCNA | 5.345 | 2.069 | −2.278 | 1 | 0 | 0 | 0.893 | 0 | 0 |
| PDCD4 | −7.3 | 4.39 | 2.29 | 1 | 0 | 0 | −2.851 | 0 | 0.807 |
| PDK1_pS241 | −4.328 | −7.468 | 1.103 | 0 | 0 | 1 | −0.406 | −2.068 | 0 |
| PI3K-p110-alpha | −2.045 | −1.893 | −0.058 | 0 | 1 | 0 | 0 | 0 | 0 |
| PKC-alpha | 4.107 | −2.008 | −2.34 | 1 | 0 | 0 | 0 | 0 | 0 |
| PKC-alpha_pS657 | 2.787 | −0.643 | −0.587 | 1 | 0 | 0 | 0 | 0 | 0 |
| PKC-delta_pS664 | −1.622 | 3.93 | 6.058 | 1 | 0 | 0 | 0 | 0 | 1.686 |
| PR | −0.264 | −6.858 | 5.072 | 0 | 0 | 1 | 0 | −4.465 | 0 |
| PRAS40_pT246 | −4.816 | 6.243 | −2.556 | 0 | 1 | 0 | 0 | 0.549 | 0 |
| PRDX1 | 1.244 | 2.609 | −0.483 | 1 | 0 | 0 | 0 | 0 | 0 |
| PTEN | −3.443 | −4.129 | 0.798 | 1 | 0 | 0 | 0 | 0 | 0 |
| Paxillin | −3.448 | −4.577 | −2.127 | 1 | 0 | 0 | 0 | 0 | 0 |
| Pea-15 | 3.573 | −5.791 | 0.144 | 1 | 0 | 0 | 0 | −0.581 | 0 |
| RBM3 | −3.695 | −3.794 | 0.379 | 1 | 0 | 0 | 0 | 0 | 0 |
| Rad50 | −0.172 | −5.001 | 2.657 | 0 | 1 | 0 | 0 | −0.962 | 0 |
| Rb_pS807_S811 | −6.574 | 1.905 | −2.987 | 1 | 0 | 0 | −2.009 | 0 | 0 |
| S6 | −7.718 | 4.048 | −0.745 | 1 | 0 | 0 | −3.914 | 0.543 | 0 |
| S6_pS235_S236 | −2.383 | 2.566 | −6.953 | 1 | 0 | 0 | 0 | 0.644 | 0 |
| S6_pS240_S244 | −2.97 | 2.075 | −7.177 | 1 | 0 | 0 | 0 | 0.350 | 0 |
| SCD1 | −4.54 | 6.624 | 4.302 | 1 | 0 | 0 | 0 | 0 | 2.683 |
| STAT3_pY705 | 4.967 | −2.48 | −2.268 | 1 | 0 | 0 | 0.564 | 0 | 0 |
| STAT5-alpha | −4.779 | −3.47 | −2.199 | 0 | 0 | 1 | −0.608 | 0 | 0 |
| Shc_pY317 | −4.083 | 3.86 | 2.936 | 0 | 1 | 0 | 0 | 0 | 0.740 |
| Smad1 | 0.205 | −0.579 | 2.104 | 1 | 0 | 0 | 0 | 0 | 0 |
| Smad3 | 4.219 | −5.98 | 2.297 | 1 | 0 | 0 | 0 | −1.414 | 0 |
| Smad4 | 9.908 | −0.979 | −1.163 | 1 | 0 | 0 | 6.333 | 0 | 0 |
| Src | 5.433 | 1.57 | −0.883 | 1 | 0 | 0 | 1.023 | 0 | 0 |
| Src_pY416 | −2.997 | 8.115 | 2 | 1 | 0 | 0 | 0 | 0.303 | 2.653 |
| Src_pY527 | 4.385 | −0.67 | −5.883 | 1 | 0 | 0 | 0.282 | 0 | 0 |
| Stathmin | 7.149 | 7.29 | 4.099 | 1 | 0 | 0 | 3.795 | 0 | 1.895 |
| Syk | −4.569 | 2.55 | −4.518 | 0 | 0 | 1 | −0.140 | 0.699 | 0 |
| Transglutaminase | −2.552 | 3.844 | −0.091 | 0 | 1 | 0 | 0 | 0 | 0 |
| Tuberin | −6.672 | −6.243 | −0.289 | 1 | 0 | 0 | −3.259 | −0.161 | 0 |
| VEGFR2 | −4.498 | −4.125 | 2.757 | 0 | 1 | 0 | −0.236 | −0.168 | 0 |
| XBP1 | 1.892 | 1.07 | 4.482 | 1 | 0 | 0 | 0 | 0 | 0 |
| XRCC1 | 1.111 | −0.622 | 2.963 | 0 | 0 | 1 | 0 | 0 | 0 |
| YAP_pS127 | 0.955 | −1.745 | −1.806 | 0 | 1 | 0 | 0 | 0 | 0 |
| YB-1 | −3.686 | −0.954 | 1.81 | 0 | 1 | 0 | 0 | 0 | 0 |
| YB-1_pS102 | −2.047 | 2.807 | −6.06 | 1 | 0 | 0 | 0 | 0 | 0 |
| alpha-Catenin | −4.342 | 4.573 | 7.605 | 1 | 0 | 0 | 0 | 0 | 3.159 |
| beta-Catenin | −6.877 | −0.545 | 0.895 | 1 | 0 | 0 | −2.921 | 0 | 0 |
| c-Kit | 2.082 | 3.856 | −2.432 | 1 | 0 | 0 | 0 | 0.042 | 0 |
| c-Met_pY1235 | 1.579 | 8.612 | 6.828 | 1 | 0 | 0 | 0 | 0 | 4.546 |
| c-Myc | 1.778 | 2.82 | 2.362 | 1 | 0 | 0 | 0 | 0 | 0 |
| eEF2 | −5.963 | 3.474 | −1.39 | 1 | 0 | 0 | −1.832 | 0.245 | 0 |
| eEF2K | −5.193 | −5.415 | 2.727 | 0 | 1 | 0 | −1.232 | −1.218 | 0 |
| eIF4E | 1.789 | −0.64 | −1.43 | 1 | 0 | 0 | 0 | 0 | 0 |
| mTOR | −9.332 | −2.094 | 2.38 | 1 | 0 | 0 | −6.073 | 0 | 0 |
| mTOR_pS2448 | −4.804 | 0.348 | −1.92 | 1 | 0 | 0 | 0 | 0 | 0 |
| p27 | 3.678 | −0.86 | 2.963 | 1 | 0 | 0 | 0 | 0 | 0 |
| p27_pT157 | −1.764 | 7.218 | 4.386 | 1 | 0 | 0 | 0 | 0 | 2.536 |
| p27_pT198 | −2.494 | 5.968 | −1.246 | 1 | 0 | 0 | 0 | 1.908 | 0 |
| p38_MAPK | 0.767 | −5.788 | −0.57 | 1 | 0 | 0 | 0 | 0 | −0.006 |
| p38_pT180_Y182 | 0.215 | −1.303 | −3.117 | 1 | 0 | 0 | 0 | 0 | 0 |
| p53 | −2.966 | 9.064 | 4.314 | 1 | 0 | 0 | 0 | 0.846 | 3.663 |
| p70S6K | −4.922 | −1.661 | 1.338 | 1 | 0 | 0 | −0.838 | 0 | 0 |
| p70S6K_pT389 | 5.575 | 1.371 | −1.5 | 1 | 0 | 0 | 1.619 | 0 | 0 |
| p90RSK_pT359_S363 | −6.319 | 1.839 | −1.653 | 1 | 0 | 0 | −1.687 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cubilla-Montilla, M.; Nieto-Librero, A.B.; Galindo-Villardón, M.P.; Torres-Cubilla, C.A. Sparse HJ Biplot: A New Methodology via Elastic Net. Mathematics 2021, 9, 1298. https://doi.org/10.3390/math9111298
Cubilla-Montilla M, Nieto-Librero AB, Galindo-Villardón MP, Torres-Cubilla CA. Sparse HJ Biplot: A New Methodology via Elastic Net. Mathematics. 2021; 9(11):1298. https://doi.org/10.3390/math9111298
Chicago/Turabian StyleCubilla-Montilla, Mitzi, Ana Belén Nieto-Librero, M. Purificación Galindo-Villardón, and Carlos A. Torres-Cubilla. 2021. "Sparse HJ Biplot: A New Methodology via Elastic Net" Mathematics 9, no. 11: 1298. https://doi.org/10.3390/math9111298
APA StyleCubilla-Montilla, M., Nieto-Librero, A. B., Galindo-Villardón, M. P., & Torres-Cubilla, C. A. (2021). Sparse HJ Biplot: A New Methodology via Elastic Net. Mathematics, 9(11), 1298. https://doi.org/10.3390/math9111298








