A Triangular Plate Bending Element Based on Discrete Kirchhoff Theory with Simple Explicit Expression
Abstract
1. Introduction
2. Displacement Function of the SDKT Element
2.1. Transverse Displacement Function of the Element
2.2. The Kirchhoff Hypothesis
2.3. Displacement Function of the Element
3. Stiffness Matrix of the SDKT Element
4. Comparison with the DKT Element
4.1. The Brief Formulation of DKT Element
- (a)
- At the corner nodes i,
- (b)
- At the mid-side nodes k,where xi = (xi, yi) are the coordinates of the nodes i; lk represents the length of the element side ij; s and n indicate the tangent and normal direction of the element side ij, respectively; and i = 1, 2, 3 and j = 2, 3, 1 when k = 4, 5, 6.
4.2. Some Comments on SDKT Element
5. Numerical Examples
5.1. Patch Test
5.2. Square Plate under Uniform Load
5.3. Square Plate under Point Load
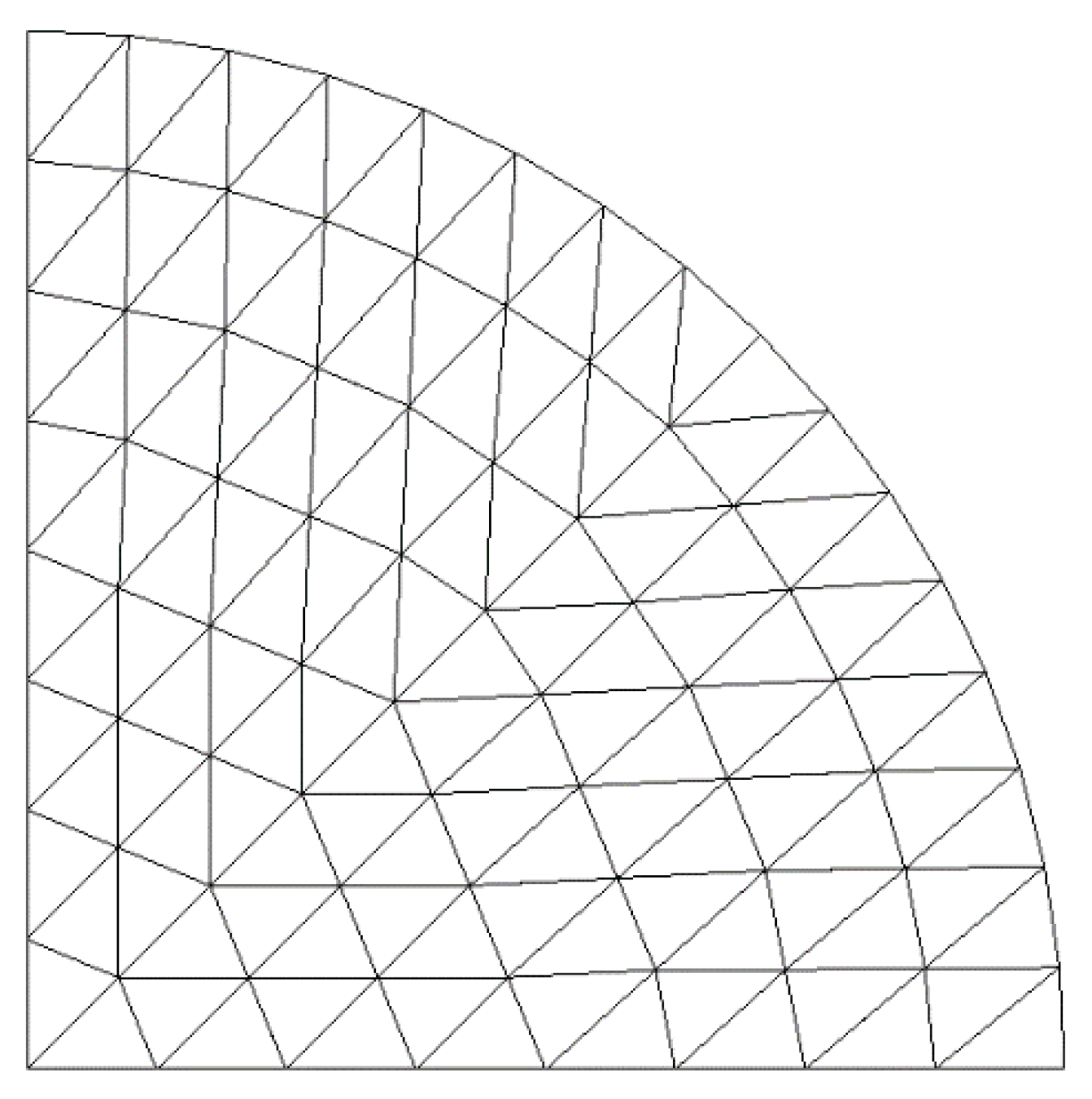
5.4. Circular Plate under Uniform Load
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Iura, M.; Atluri, S.N. Advances in finite rotations in structural mechanics. CMES Comp. Model. Eng. 2003, 4, 213–216. [Google Scholar]
- Gal, E.; Levy, R. Geometrically nonlinear analysis of shell structures using a flat triangular shell finite element. Arch. Comput. Methods Eng. 2006, 13, 331–388. [Google Scholar] [CrossRef]
- Clough, R.W.; Tocher, J.L. Finite element stiffness matrices for analysis of plate bending. In Proceedings of the Conference on Matrix Methods in Structural Mechanics, Dayton, OH, USA, 26–28 October 1965; pp. 515–545. [Google Scholar]
- Bazeley, G.P.; Cheung, Y.K.; Irons, B.M. Triangular elements in plate bending conforming and non-conforming solutions. In Proceedings of the Conference on Matrix Methods in Structural Mechanics, Dayton, OH, USA, 26–28 October 1965; pp. 547–576. [Google Scholar]
- Razzaque, A. Program for triangular bending elements with derivative smoothing. Int. J. Numer. Methods Eng. 1973, 6, 333–343. [Google Scholar] [CrossRef]
- Cheung, Y.K.; Chen, W.J. Refined nine-parameter triangular thin plate bending element by using refined direct stiffness method. Int. J. Numer. Methods Eng. 1995, 38, 283–298. [Google Scholar] [CrossRef]
- Stricklin, J.A.; Haisler, W.E.; Tisdale, P.R.; Gunderson, R. A rapidly converging triangular plate element. AIAA J. 1969, 7, 180–181. [Google Scholar] [CrossRef]
- Batoz, J.L.; Bathe, K.J.; Ho, L.W. A study of three-node triangular plate bending elements. Int. J. Numer. Methods Eng. 1980, 15, 1771–1812. [Google Scholar] [CrossRef]
- Batoz, J.L. An explicit formulation for an efficient triangular plate-bending element. Int. J. Numer. Methods Eng. 1982, 18, 1077–1089. [Google Scholar] [CrossRef]
- Felippa, C.A.; Bergan, P.G. A triangular bending element based on an energy-orthogonal free formulation. Comput. Methods Appl. Mech. Eng. 1987, 61, 129–160. [Google Scholar] [CrossRef]
- Allman, D.J. Triangular finite element bending with constant and linearly varying bending elements. In Proceedings of the Symposium on High Speed Computing of Elastic Structures, Liege, Belgium, 23–28 August 1971; pp. 105–110. [Google Scholar]
- Xu, Z. A simple and efficient triangular finite element for plate bending. Acta Mechnica Sin. 1986, 2, 185–192. [Google Scholar]
- Maunder, E.A.W.; Almeida, J.P.M. A triangular hybrid equilibrium plate element of general degree. Int. J. Numer. Methods Eng. 2005, 63, 315–350. [Google Scholar] [CrossRef]
- Choo, Y.S.; Choi, N.; Lee, B.C. A new hybrid-Trefftz triangular and quadrilateral plate elements. Appl. Math. Model. 2010, 34, 14–23. [Google Scholar] [CrossRef]
- Long, Z.F. Generalized conforming triangular elements for plate bending. Commun. Numer. Methods Eng. 1993, 9, 53–63. [Google Scholar]
- Kasparek, E.M. An efficient triangular plate element with C1-continuity. Int. J. Numer. Methods Eng. 2008, 73, 1010–1026. [Google Scholar] [CrossRef]
- Chen, W.J.; Cheung, Y.K. Refined 9-Dof triangular Mindlin plate elements. Int. J. Numer. Methods Eng. 2001, 51, 1259–1281. [Google Scholar]
- Hughes, T.; Taylor, R.; Kanoknukulchai, W. A simple and efficient finite element for plate bending. Int. J. Numer. Methods Eng. 1977, 11, 1529–1543. [Google Scholar] [CrossRef]
- Reissner, E. The effect of transverse shear deformation on the bending of elastic plates. J. Appl. Mech. 1945, 12, 69–77. [Google Scholar] [CrossRef]
- Mindlin, R.D. Influence of rotatory inertia and shear on flexural motions of isotropic elastic plates. J. Appl. Mech. 1951, 18, 31–38. [Google Scholar] [CrossRef]
- Senjanovi´c, I.; Vladimir, N.; Hadži´c, N. Modified Mindlin plate theory and shear locking-free finite element formulation. Mech. Res. Commun. 2014, 55, 95–104. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Too, J.M. Reduced integration technique in general analysis of plates and shells. Int. J. Numer. Methods Eng. 1971, 3, 275–290. [Google Scholar] [CrossRef]
- Pugh, E.D.; Hinton, E.; Zienkiewicz, O.C. A study of triangular plate bending element with reduced integration. Int. J. Numer. Methods Eng. 1978, 12, 1059–1078. [Google Scholar] [CrossRef]
- Malkus, D.S.; Hughes, T.J.R. Mixed finite element methods-reduced and selective integration techniques: A unification of concepts. Comput. Method. Appl. Mech. Eng. 1978, 15, 63–81. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Cohen, M.; Haroun, M. Reduced and selective integration techniques in finite element analysis of plates. Nucl. Eng. Des. 1978, 46, 203–222. [Google Scholar] [CrossRef]
- Bathe, K.J.; Dvorkin, E.N. A four-node plate bending element based on Mindlin/Reissner plate theory and a mixed interpolation. Int. J. Numer. Methods Eng. 1985, 21, 367–383. [Google Scholar] [CrossRef]
- Nguyen, X.H.; Rabczuk, T.; Stephane, B.; Debongnie, J.F. A smoothed finite element method for plate analysis. Comput. Method. Appl. Mech. Eng. 2008, 197, 1184–1203. [Google Scholar] [CrossRef]
- Lee, S.W.; Pian, T.H.H. Improvement of plate and shell finite elements by mixed formulation. AIAA J. 1978, 16, 29–34. [Google Scholar] [CrossRef]
- Katili, I. A new discrete Kirchhoff-Mindlin element based on Mindlin-Reissner plate theory and assumed shear strain fields—Part I: An extended DKT element for thick-plate bending analysis. Int. J. Numer. Methods Eng. 1993, 36, 1859–1883. [Google Scholar] [CrossRef]
- Brasile, S. An isostatic assumed stress triangular element for the Reissner–Mindlin plate-bending problem. Int. J. Numer. Methods Eng. 2008, 74, 971–995. [Google Scholar] [CrossRef]
- Batoz, J.L.; Katili, I. On a simple triangular Reissner/Mindlin plate element based on incompatible modes and discrete constraints. Int. J. Numer. Methods Eng. 1992, 35, 1603–1632. [Google Scholar] [CrossRef]
- Batoz, J.L.; Lardeur, P. A discrete shear triangular nine d.o.f. element for the analysis of thick to very thin plates. Int. J. Numer. Methods Eng. 1989, 29, 533–560. [Google Scholar] [CrossRef]




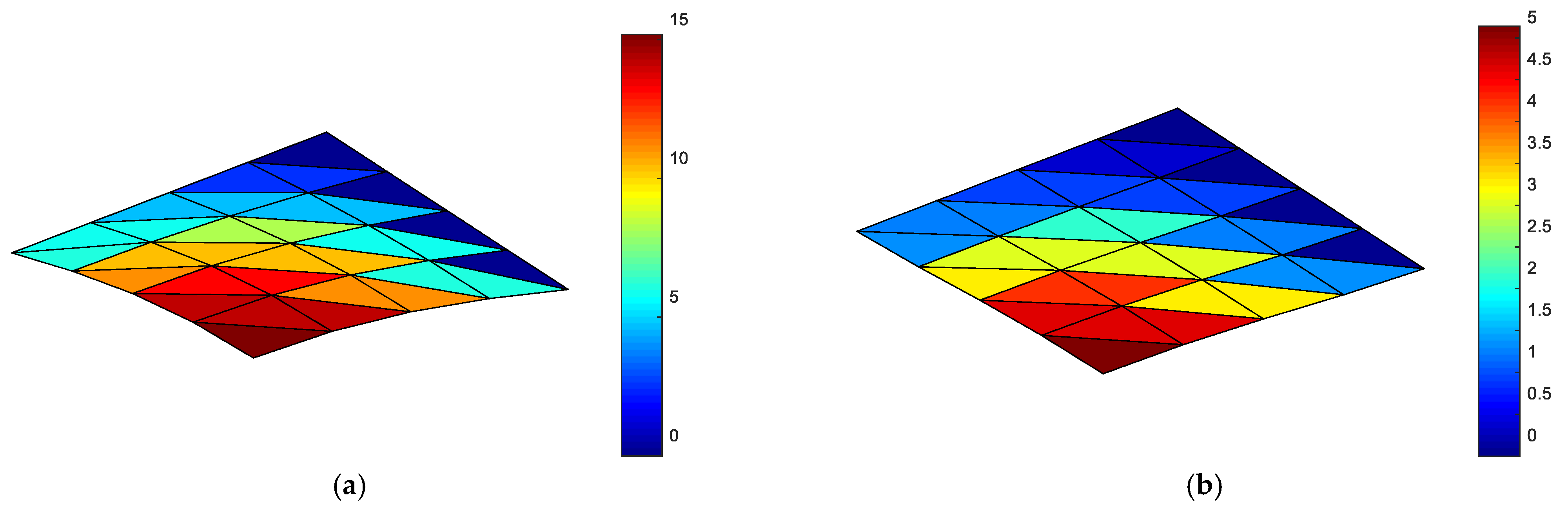




| Element | Displacement at Node 5 | Moment in the Element | ||||
|---|---|---|---|---|---|---|
| BCIZ | 1.049 | 1.95 | −1.63 | No constant moment state | ||
| DKT | 1.090 | 1.90 | −1.70 | −2.381 | −2.381 | −0.641 |
| SDKT | 1.090 | 1.90 | −1.70 | −2.381 | −2.381 | −0.641 |
| Exact | 1.090 | 1.90 | −1.70 | −2.381 | −2.381 | −0.641 |
| Mesh | Element (Error) | ||
|---|---|---|---|
| BCIZ | DKT | SDKT | |
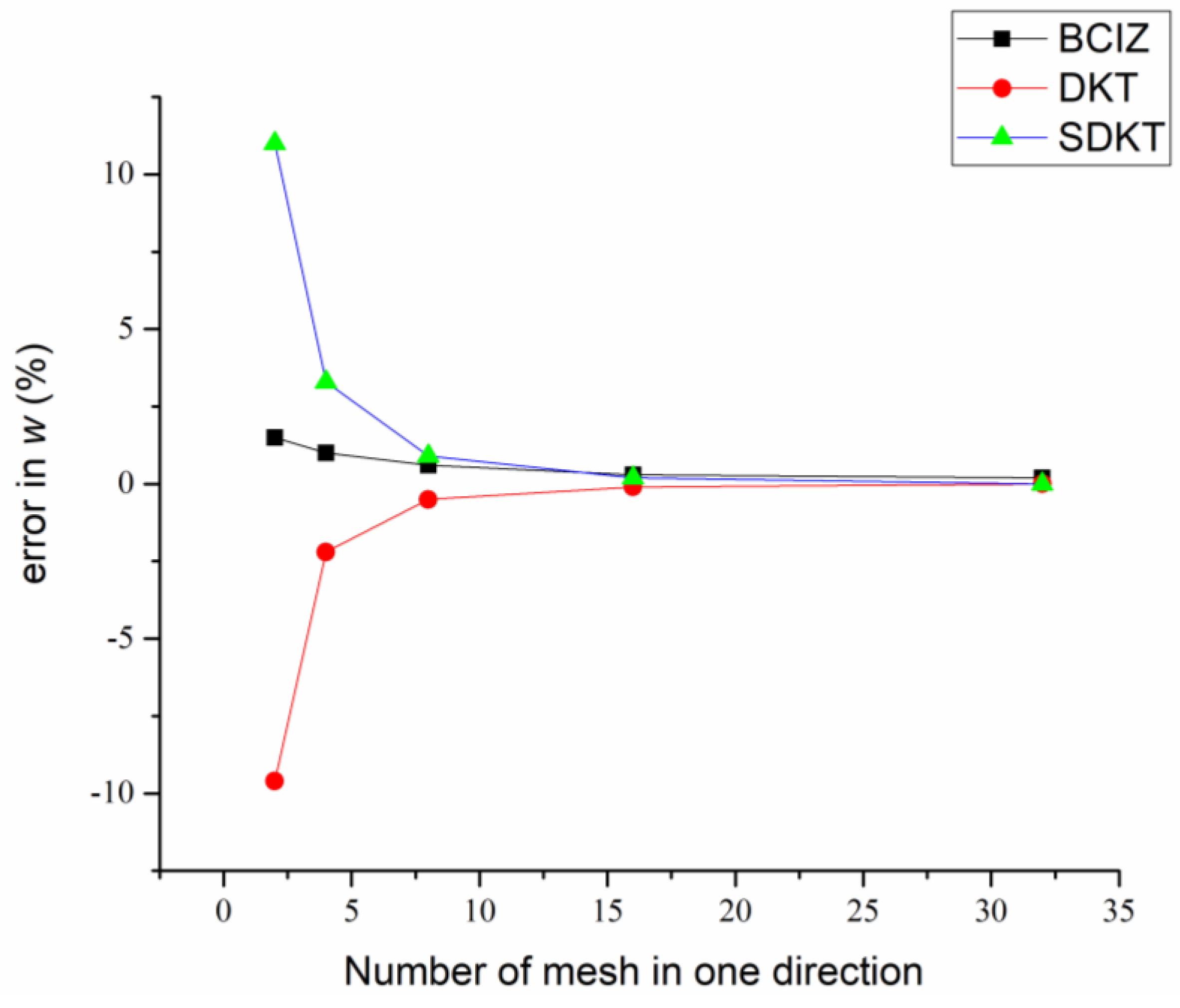
| 2 × 2 | 0.4123 (1.5%) | 0.3673 (−9.6%) | 0.4509 (11.0%) |
| 4 × 4 | 0.4104 (1.0%) | 0.3972 (−2.2%) | 0.4197 (3.3%) |
| 8 × 8 | 0.4087 (0.6%) | 0.4040 (−0.5%) | 0.4097 (0.9%) |
| 16 × 16 | 0.4076 (0.3%) | 0.4057 (−0.1%) | 0.4071 (0.2%) |
| 32 × 32 | 0.4069 (0.2%) | 0.4061 (0.0%) | 0.4064 (0.0%) |
| Exact | 0.4062 | ||
| Mesh | Element (Error) | ||
|---|---|---|---|
| BCIZ | DKT | SDKT | |
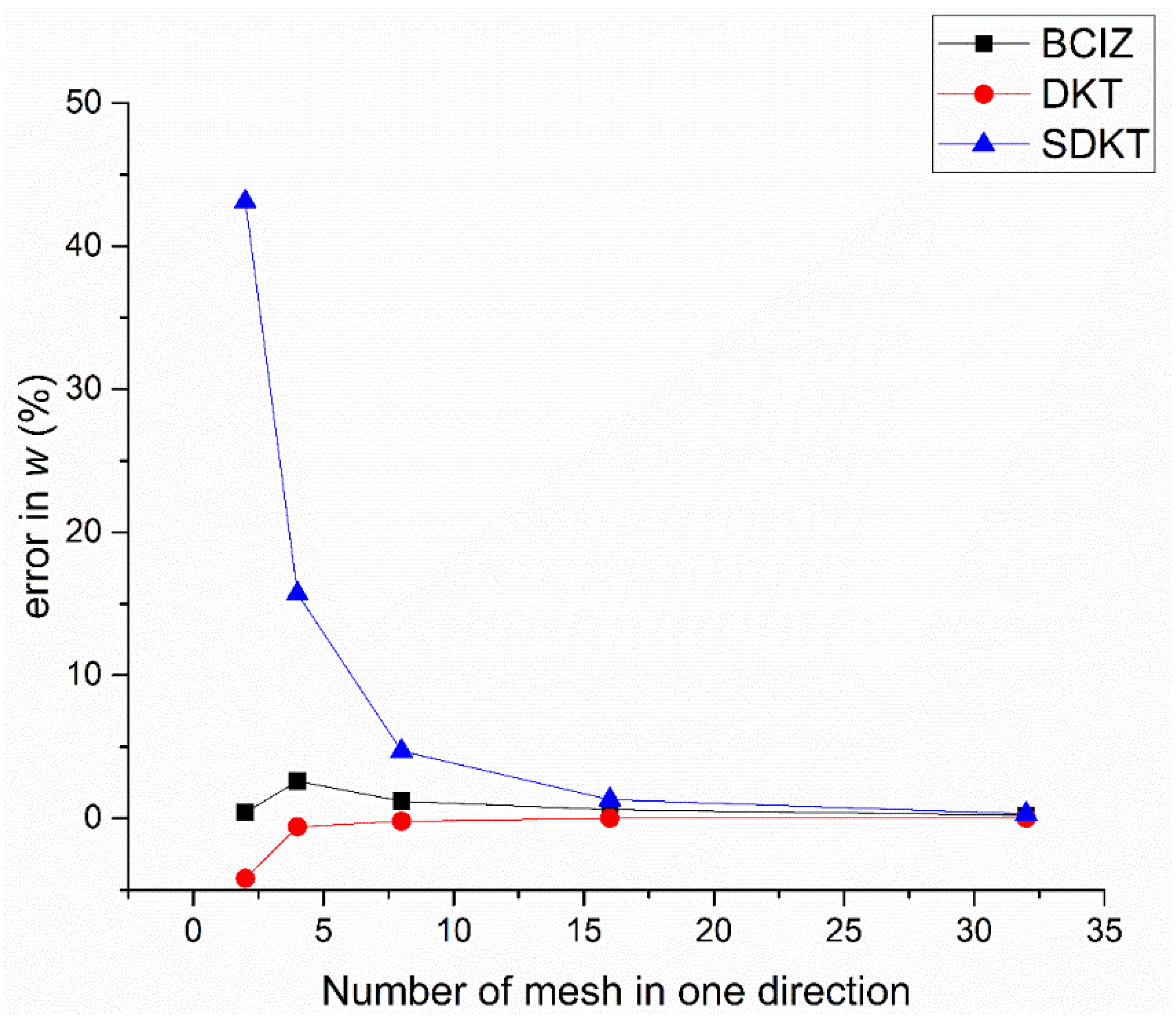
| 2 × 2 | 0.1270 (0.4%) | 0.1212 (−4.2%) | 0.1810 (43.1%) |
| 4 × 4 | 0.1298 (2.6%) | 0.1257 (−0.6%) | 0.1463 (15.7%) |
| 8 × 8 | 0.1280 (1.2%) | 0.1263 (−0.2%) | 0.1324 (4.7%) |
| 16 × 16 | 0.1272 (0.6%) | 0.1265 (0.0%) | 0.1281 (1.3%) |
| 32 × 32 | 0.1268 (0.2%) | 0.1265 (0.0%) | 0.1269 (0.3%) |
| Exact | 0.1265 | ||
| Mesh | Element (Error) | ||
|---|---|---|---|
| BCIZ | DKT | SDKT | |
| 2 × 2 | 1.3715 (18.2%) | 1.2820 (10.5%) | 1.5929 (37.3%) |
| 4 × 4 | 1.2418 (7.1%) | 1.1993 (3.4%) | 1.3010 (12.2%) |
| 8 × 8 | 1.1927 (2.8%) | 1.1719 (1.0%) | 1.2031 (3.7%) |
| 16 × 16 | 1.1734 (1.2%) | 1.1635 (0.3%) | 1.1728 (1.1%) |
| 32 × 32 | 1.1657 (0.5%) | 1.1611 (0.1%) | 1.1637 (0.3%) |
| Exact | 1.160 | ||
| Mesh | Element (Error) | ||
|---|---|---|---|
| BCIZ | DKT | SDKT | |
| 2 × 2 | 0.6531 (16.4%) | 0.6342 (13.0%) | 0.9275 (65.3%) |
| 4 × 4 | 0.6118 (9.0%) | 0.5905 (5.2%) | 0.6939 (23.6%) |
| 8 × 8 | 0.5829 (3.9%) | 0.5706 (1.7%) | 0.6038 (7.6%) |
| 16 × 16 | 0.5703 (1.6%) | 0.5640 (0.5%) | 0.5740 (2.3%) |
| 32 × 32 | 0.5650 (0.7%) | 0.5620 (0.1%) | 0.5649 (0.7%) |
| Exact | 0.5612 | ||
| Number of Nodes | Element (Error) | ||
|---|---|---|---|
| BCIZ | DKT | SDKT | |
| 25 | 0.01619 (3.6%) | 0.01613 (3.2%) | 0.01933 (23.7%) |
| 81 | 0.01581 (1.2%) | 0.01576 (0.8%) | 0.01655 (5.9%) |
| 289 | 0.01570 (0.4%) | 0.01566 (0.2%) | 0.01586 (1.5%) |
| 1089 | 0.01566 (0.2%) | 0.01563 (0.0%) | 0.01568 (0.3%) |
| Exact | 0.01563 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, L.; Cheng, Z. A Triangular Plate Bending Element Based on Discrete Kirchhoff Theory with Simple Explicit Expression. Mathematics 2021, 9, 1181. https://doi.org/10.3390/math9111181
Tian L, Cheng Z. A Triangular Plate Bending Element Based on Discrete Kirchhoff Theory with Simple Explicit Expression. Mathematics. 2021; 9(11):1181. https://doi.org/10.3390/math9111181
Chicago/Turabian StyleTian, Longgang, and Ziling Cheng. 2021. "A Triangular Plate Bending Element Based on Discrete Kirchhoff Theory with Simple Explicit Expression" Mathematics 9, no. 11: 1181. https://doi.org/10.3390/math9111181
APA StyleTian, L., & Cheng, Z. (2021). A Triangular Plate Bending Element Based on Discrete Kirchhoff Theory with Simple Explicit Expression. Mathematics, 9(11), 1181. https://doi.org/10.3390/math9111181






