A Mathematical Approach to Law and Deal Modelling: Legislation and Agreements

Abstract

Social norms are a set of rules to be followed by the people of a community in order to have a better coexistence, to which the behaviors, tasks, and activities of the human being must be adjusted. The set or system of norms, rules, or duties regulates the actions of individuals among themselves. This work presents a new and original approach to the situations of agreement as well as to the constructions of regulations. This is done by giving a mathematical formalization to the set of all possible agreements or regulations, so that, then, the proximity between them is defined by means of a premetric. Thanks to this mathematical structure that tries to capture the problematic of agreements and modifications of regulations, some currently issues related to game theory or law are now reduced to mathematical optimization problems.

1. Motivation

The objective of legal systems around the world is to regulate people’s coexistence [1]. This objective gives a central role to the definition and measurement of the legal framework in everyday interactions, as well as to the way in which these norms regulate the behavior of a population. In this sense, over the last decades, a good deal of theoretical and empirical work has been devoted to the task of explaining the compositition of agreements and consensus in a lot of related areas, such as climate change [2,3], goverments coalitions [4,5], cooperation and coordination on social dilemmas [6], among others. Likewise, the evolution of large-scale cooperation in humans has been the focal point of several disciplines in the last few decades [7,8,9]. It is argued that genetic relatedness can explain the emergence of cooperation [10]. However, humans cooperate on vast scales, more substantially than their genetic relatedness allows. Some of the explanations for this phenomenon include punishment, direct and indirect reciprocity, group competition, etc. (see, for instance, [11,12,13]). Furthermore, the socio-economic spectrum in which we live is replete with binding agreements and/or treaties between two or more countries, companies, political parties, etc.

In the international environment, in recent yeare there has been a proliferation of free trade agreements, such as the European Union, the Trans-Pacific Partnership Treaty, or the Transatlantic Trade and Investment Partnership, and even environmental treaties and protocols, such as the Kyoto Protocol. However, what makes some countries sign these treaties and others not? Also, what makes countries comply with the agreements or not? Undoubtedly, the regulation distance within the agreed agreements and what each participant is willing to accept or renounce makes the difference between signing and not signing. Most of the proposals for solving these differences are based on fragmenting the regulations that are imposed in the agreements to satisfy the greatest number of participants. This type of fragmentation of the legal framework is noted by [14] to promote the multiplication of international commitments. However, the difference in the starting point of the participants in the treaties may or may not make the agreement a success.

This situation of non-compliance does not only occur in international environments. Within a country’s borders, undesirable situations can arise with respect to compliance with national regulations, even in public health situations. One of the great battles of modern jurists and politicians is how we should implement the enforcement of laws. Given an ultimate goal, should we implement all the laws or rules in order to achieve it simultaneously? Alternatively, does a gradual sequencing in the introduction of the different rules cause the number of non-compliances to decrease? Take, for example, the recent COVID-19 global pandemic case. All countries, even regions, have adopted different measures in both form and timing. All measures have been designed to contain the spread of the virus and/or to control space in hospitals to care for the sick. The way that these measures have been implemented has varied widely, and it has been found that, even in this pandemic situation, the adopted measures have been breached by many residents [15]. Perhaps a gradual implementation of the different measures could have resulted in less non-compliance, thus achieving greater effectiveness of the measures adopted.

In this work, we show that the orderly introduction of the rules to be complied with conditions the cost, and we find the one that minimises the cost. The higher or lower cost depends on the proximity between rules, which is defined in the paper (mainly through the probability and ‘severity’ of breaking a rule), and that also allows us to evaluate what kind of agreements or treaties can be signed by the participants, while taking this proximity between the different rules or laws into account.

Consequently, social scientists, practitioners, and legal researchers have been concerned with developing the legal framework of people. Although much work has been done to develop the regulatory character of the legal system [16], we see that little has been done in terms of developing methods to measure the status of people’s legal system. Therefore, we see a need to measure and quantify this legal environment and the distance between existing laws and agreements. The aim of this paper is, using a new information theory approach to compare and evaluate different legal measures, to derive some focal measures of the effect of the legal framework on individuals and populations. In addition, in this paper we contribute to the literature by analyzing how the proximity between diferent positions and norms in agreements affects the evolution of consensus or adoption of the agreement.

The goal of the present work is to introduce a tool in order to measure the proximity or ‘distance’ between games, regulations, or deals. One of the main aims of this study is to know how to change the rules of a game to achieve a more efficient equilibrium. There may be different manners or paths in order to change the law from an initial regulation to a final one. Here, we construct a tool that indicates which is the path when changing the law, that is, a tool that shows us how we have to make changes in the law in order to arrive to a better regulation or deal, but always minimizing the social resistence to the changes. The second goal of the paper is to achieve the most preferred deal in no-agreement situations. Again, for that purpose, a distance function between deals is required.

Likewise, throughout the paper, we use the concepts of agreement, treaty, or rule interchangeably. Although, from a legal point of view, they may be different, we are interested in the relationship between the participants to them. From a legal point of view, an agreement is, in law, a decision taken jointly by two or more persons, or by a board, assembly, or court. It is also the name given to a pact, treaty, convention, or resolution taken within an institution (any type of organization or company, public or private, national or international). Therefore, it is the manifestation of a convergence of wills (decision by consensus) with the purpose of producing legal effects. The main legal effect of the agreement is that it is binding on the parties that enter into it (Pacta sunt servanda), giving rise to obligations and rights for them to the extent provided for by the applicable law. The legal validity of an agreement requires that the consent of the grantors is valid and its object is certain and determined, not out of commerce, or impossible. As to the form of its conclusion, oral or written, the legislations usually require certain formalities that depend on the nature of the obligations agreed upon (see [17] for an extensive review on deals and rules).

The introduced technique allows us to achieve the closest agreement-point in case of blocking situation.

As far as we know, the presented method is a new mathematical approach to the problem posed. However, there are other approaches in the literature that studied problems around the relationship between law, game theory, and agreements, but using different techniques. For instance, related to game theory and law, we can find works, such as [18,19]. In the field of coalitions and agreements, there are studies, such as [20,21], which are related with this topic.

The rest of the paper is organized, as follows. Section 2 introduces the mathematical tools and notation needed. Section 3 provides a mathematical structure to the problematic of the agreements and regulations, so that, then, Section 4 presents some applications through the introduced new approach. A final section of conclusions ends the paper.

2. Preliminaries: Mathematical Tools

In the present section, we include some mathematical concepts that shall be needed throughout the paper. These are mainly related to order the structures and metric spaces.

From now on, X will stand for a nonempty set.

Definition 1.

A binary relation $\mathcal{R}$ on X is a subset of the cartesian product $X\times X$. Given two elements $x,y\in X$, $x\mathcal{R}y$ denotes that the $(x,y)\in \mathcal{R}$.

Being associated to a binary relation $\mathcal{R}$ on a set X, its negation (respectively, its transpose) is the binary relation ${\mathcal{R}}^c$ (respectively, ${\mathcal{R}}^t$) on X defined by $(x,y)\in {\mathcal{R}}^c\iff (x,y)\notin \mathcal{R}$ for every $x,y\in X$ (respectively, given by $(x,y)\in {\mathcal{R}}^t\iff (y,x)\in \mathcal{R},$ for every $x,y\in X)$.

A binary relation $\mathcal{R}$ that is defined on a set X is said to be:

(i) 

reflexive if $x\mathcal{R}x$ holds for every $x\in X$,

(ii) 

irreflexive if $\neg \left(x\mathcal{R}x\right)$ holds for every $x\in X$,

(iii) 

symmetric if $\mathcal{R}$ and ${\mathcal{R}}^t$ coincide,

(iv) 

antisymmetric if $\mathcal{R}\cap {\mathcal{R}}^t\subseteq \Delta =\{(x,x):x\in X\}$,

(v) 

asymmetric if $\mathcal{R}\cap {\mathcal{R}}^t=⌀$,

(vi) 

total if $\mathcal{R}\cup {\mathcal{R}}^t=X\times X$,

(vii) 

transitive if $x\mathcal{R}y\wedge y\mathcal{R}z\Rightarrow x\mathcal{R}z$ for every $x,y,z\in X$.

When working with particular cases of orderings, the notation is usually different. We include it here for sake of completeness, and we will use it throughout the present manuscript.

Definition 2.

A preorder ≾ on X is a binary relation which is reflexive and transitive. An antisymmetric preorder is said to be an order. A total preorder ≾ on a set X is a preorder such that if $x,y\in X$ then $(x\precsim y)\vee (y\precsim x)$ holds. In the case of preorders, it is well known that the corresponding indifference is transitive, i.e., it is an equivalence relation. Given a preorder ≾ on X, we shall denote, by $x\bowtie y$, when x and y are not comparable, i.e., when $\neg (x\precsim y)$ as well as $\neg (y\precsim x)$.

Definition 3.

Let ≺ denote an asymmetric binary relation on $(X,\tau )$. Given $a\in X$ the sets $L_{\prec }\left(a\right)=\{t\in X:t\prec a\}$ and $U_{\prec }\left(a\right)=\{t\in X:a\prec t\}$ are called, respectively, the strict lower and upper contours of a relative to ≺. We say that ≺ is τ-continuous (or just continuous) if for each $a\in X$ the sets $L_{\prec }\left(a\right)$ and $U_{\prec }\left(a\right)$ are τ-open.

We will denote the order topology that is generated by ≺ as ${\tau }_{\prec }$, and it is defined by means of the subbasis that is provided by the lower and upper contour sets.

Let ≾ denote a reflexive binary relation on $(X,\tau )$. Given $a\in X$ the sets $L_{\precsim }\left(a\right)=\{t\in X:t\precsim a\}$ and $U_{\precsim }\left(a\right)=\{t\in X:a\precsim t\}$ are called, respectively, the weak lower and upper contours of a relative to ≾. We say that ≾ is τ-lower semicontinuous ( $\tau$-upper semicontinuous) if for each $a\in X$ the sets $L_{\precsim }\left(a\right)$ (resp. $U_{\precsim }\left(a\right)$) are τ-closed.

The concept of $\tau$-(semi)continuity is a key notion when dealing with continuous representations of, not only in the well-known case of total preorders (see [22,23,24]), but also preorders; thus, it is a very common and usually necessary concept in the field of order structures.

Now, we include some definitions that are related to metrics and their generalizations.

Definition 4.

A metric on a set X is a function $d:X\times X\to [0,+\infty )$ (also called distance) satisfiying the following three properties:

(M1)

$d(x,x)=0\mathrm{for}\mathrm{all}x\in X.$

(M2)

$d(x,y)=0\Rightarrow x=y.$

(M3)

$d(x,y)=d(y,x).$

(M4)

$d(x,z)\le d(x,y)+d(y,z).$

There are several generalizations of metrics (see [25,26,27]) relaxing the aforementioned axioms. In our context, we shall use the following notions.

Definition 5.

A nonnegative real-valued function d on $X\times X$ is a quasi-semi distance if, for all $x,y,z\in X:$

(M1)

$d(x,x)=0.$

(M4)

$d(x,z)\le d(x,y)+d(y,z).$

A premetric on a set X is a nonnegative real-valued function d on $X\times X$, such that:

(M1)

$d(x,x)=0forallx\in X.$

Given a function $d:X\times X\to {\mathbb{R}}^{+}$, we will define $d^{-1}(x,y)=d(y,x)$ and $d^s(x,y)=max\{d(x,y),d(y,x)\}$. Notice that, if d is a quasi-semi distance, $d^{-1}$ is a quasi-semi distance and $d^s$ is a distance.

The following proposition is well-known and it warrants that any premetric defines a topology on the set. [25,26,27]

Proposition 1.

Let d be a premetric on X. Subsequently, d induces a topology on X by means of the following open balls, for any $r>0$ and any $x\in X$:

$$B_r\left(x\right)=\{y\in X:d(x,y)<r\}.$$

Finally, we include one statistical distance that quantifies the proximity between two probability distributions. There are several distances defined between probability distributions; in the present paper, we shall work with a f-divergence function that is known as Kullback Leibler divergence [28,29,30].

Definition 6.

Let p and q be two probability functions on the same event space $\mathcal{F}$. The Kullback Leibler divergence (also called relative entropy) from q to p (or the relative entropy from q to p) is defined by

$${\displaystyle D\left(p\right|\left|q\right)=\sum _{x\in \mathcal{F}}p\left(x\right)·log\left(\frac{p\left(x\right)}{q\left(x\right)}\right)=E_{p}log\left(\frac{p\left(X\right)}{q\left(X\right)}\right).}$$

The relative entropy is defined whenever condition

$$q\left(x\right)=0\Rightarrow p\left(x\right)=0,x\in X\left(1\right)$$

is satisfied.

The entropy of p is defined by

$${\displaystyle H\left(p\right)=-\sum _{x\in \mathcal{F}}p\left(x\right)·log\left(p\left(x\right)\right).}$$

3. Comparing Regulations and Societies

Through the present paper, we introduce a tool that allows for quantifying negotiations. It gives us a manner to objectify agreements from a theoretical point of view, which could help for impartiality, in particular when there is an ‘oracle’ or ‘institution’ that want to achieve an agreement between the agents. This new technique allows us to find the most preferred deal in disagreement situations. Furthermore, if we want to incorporate a regulation by adding rules at different times, this method gives us the best manner or order in which the rules must be added, so that they clash as little as possible with the custom of society (as it is shown in Example 1). Thus, we may construct the best (or ‘less aggressive’) path from a deal to a new one. This may also be interesting in order to keep the consensus.

For these purposes, we need to formalize some of the ideas by attributing them a mathematical definition. As far as we know, there is no previous knowledge on the subject, so this is the first mathematical approach to the problem posed.

First, let $\Omega$ be a set of rules ${\left\{R_i\right\}}_{i\in I}$ called Law, which is used when defining a regulation or legal framework G, which is, in fact, a subset of $\Omega$. Second, let ${\left\{A_n\right\}}_{n=1}^N$ be a finite family of agents or players; these players will be the signers of the possible deal or the society that lives under the regulation G. The set of rules G, which is, the regulation, will be the sample space ${\Omega }_G$ of a probability space, where the events space is the $\sigma$-algebra $\mathcal{F}=\mathcal{P}\left(G\right)$, which is the set of subsets of rules of the regulation that could be broken.

If we change a rule, two interesting questions arise:

$\left(Q1\right)$

What is the probability that the rule will be broken by an agent A? Or, what is the probability that the rule will be broken by n players?

$\left(Q2\right)$

What is the minimum punishment that must be imposed in order to avoid breaking the rule? Or, in other words, how much should be compensated in order to guaranty that the rule will be cumplied?

The answer to question 2 would give us the individual cost or severity of enforcing the rule and, with the answer to question 1, we will be able to measure the proximity between the regulation of the deal or game with the habits of the current society of players.

We assume that we have this information at our disposal. From an applied point of view, it may be estimated, or it may be deduced from historical data. In any case, from a theoretical point of view, we will need this information (or the corresponding estimation, frequencies, or approximation).

Furthemore, the answer to both questions may be related. We may think that, if a rule is broken usually by plenty of players, then the individual cost or severity must be small (for example, if we are thinking on forbidden smoke somewhere), whereas, if a rule is rarely broken (a murder, major tax fraud), then the individual cost is bigger. Hence, this individual cost or severity may be defined by means of the probability of being broken.

Now, we formalize the main concepts.

Definition 7.

Let Ω be a set of rules ${\left\{R_i\right\}}_{i\in I}$, called Law and $A={\left\{A_n\right\}}_{n=1}^N$ a finite set of players. A subset $G={\left\{R_k\right\}}_{k\in K\subseteq I}\subseteq \Omega$ is said to be a regulation or legal framework under the Law. For a given regulation G, G itself is a sample space ${\Omega }_G$, where the corresponding events space is defined by the set of subsets ${\mathcal{F}}_G=\mathcal{P}\left(G\right)$. An event $x\in {\mathcal{F}}_G$ is a set of rules that may be broken (each of one). Thus, for each $n\in \{1,2,\dots ,N\}$, let $P_n:{\mathcal{F}}_G\to [0,1]$ be the probability of player $A_n$ breaking a subset of rules $x\in {\mathcal{F}}_G$ (i.e., breaking each of the rules that are involved in x). By means of these probabilities, we define the mean function $P:{\mathcal{F}}_G\to [0,1]$ of the expected ratio of offenders by $P\left(x\right)=\frac{1}{N}{\displaystyle \sum _{n=1}^N}{P}_n\left(x\right)$. Thus, the expected number of offenders for a subset of rules in a regulation (that is, for an event) $x\in {\mathcal{F}}_G$ is $N·P\left(x\right)$. Let $g:{\mathcal{F}}_G\to \mathbb{R}$ be the (individual) punishment associated to an event $x\in {\mathcal{F}}_G$ (i.e., associated to breaking each of the rules involved in x).

A legal game (or l-game, for short) ${\Psi }_G$ is now a probabilistic space $({\Omega }_G,{\mathcal{F}}_G,P)$ associated to a legal framework G (defined under the Law Ω) and a society or family of agents A. The idiosyncrasies of this society A are reflected in the probability functions P. Thus, the same regulation that is applied on another society B implies a different probability function $P^{\prime }$. If it is also endowed with a punishment function g, then we say that it is a punished l-game.

From now, Γ denotes the set of all possible l-games that may be defined with a given Law Ω on a society A. Thus, $\Gamma =\{(G,{\mathcal{F}}_G,P_G):G\subseteq \Omega \}$, and we shall call it by Game of games. Therefore, when referring to Γ, the Law and society are assumed to be fixed. We shall say that a rule $R_i\in \Omega$ is titere if $P\left(x\right)=0$, for any $x\in {\mathcal{F}}_G$, such that $R_i\in x$.

Subsequently, the expected severity of a punished l-game (per capita) is defined by

$${\displaystyle Eg\left({\Psi }_G\right)=\sum _{x\in {\mathcal{F}}_G}P\left(x\right)·g\left(x\right).}$$

Thus, the expected severity of the l-game is the sum of the products of the expected ratio of offenders and the individual cost or severety.

The entropy [28,29,30] of a (not necessarily punished) l-game is

$${\displaystyle H\left({\Psi }_G\right)=-\sum _{x\in {\mathcal{F}}_G}P\left(x\right)·log\left(P\left(x\right)\right).}$$

Thus, the entropy may also be interpreted as the expected severity per capita when $g\left(x\right)=log\left(\frac{1}{P\left(x\right)}\right)$, for any $x\in {\mathcal{F}}_G$.

By continuity, it is assumed that $0·log\left(0\right)=0$ and $0·log\left(\frac{1}{0}\right)=0$.

Remark 1.

(1) 

Notice that, for a given regulation $G\subseteq \Omega$, ${\displaystyle \sum _{x\in {\mathcal{F}}_G}}{P}_n\left(x\right)=1$ for each $n\in \{1,2,\dots ,N\}$ and, hence, ${\displaystyle \sum _{x\in {\mathcal{F}}_G}}P\left(x\right)=1$. Therefore, function P is, in fact, a probability function. In the case where the signers are countries or a few players, P may be defined by means of the individual’s probability functions $P_n$ ($n=1,\cdots ,N$). On the other hand, for the case of regulations that are applied on societies (i.e., with thousands of persons involved), funtion P might be directly estimated or defined by means of frequency data, without requiring the definitions of the individual’s probability functions $P_n$ ($n=1,\dots ,N$). It is interesting that, for the first case aforementioned, this function P may be defined with weights, such that the weigth of some players may be bigger than others regarding to the their importance in the game (for example, if we want to weigth a family of countries in a deal by means of their GDP, population, contamination, …)

(2) 

The (individual) punishment $g\left(x\right)$ (for any $x\in {\mathcal{F}}_G$) may be assumed to be in $[0,1]$, although it can be defined on the set of positive real numbers. It is assumed that $g(\varnothing )=0$, which is, there is no punishment when there are no offenders.

Notice that, if the individual punishment that is associated to breaking a family of rules is defined by means of the probability function P as $log\left(\frac{1}{P\left(x\right)}\right)$ (such that, the punishment also changes, depending on the number of offenders), then the expected severity per capita is defined by the entropy:

$${\displaystyle Eg\left({\Psi }_G\right)=\sum _{x\in {\mathcal{F}}_G}P\left(x\right)·log\left(\frac{1}{P\left(x\right)}\right).}$$

From now on, we will forget the player’s probability functions $P_n$ (for each $n=1,\dots ,N$), and we will work just with the (weighted) mean P.

Notice that a legal game consists on a set of rules applied on a society, the idiosyncrasy of that society is reflected in the probability function P. Thus, the l-game arising from a regulation G in a society A may change just by changing the society, i.e., the consecuences of a regulation may differ from one society to another. In this line, we introduce the idea of distance between societies in the spirit of Kullback Leibler divergence. [28,29,30] It will give us the behavior difference between two societies that live under the same regulation. What it works in a society, may fail in another.

Definition 8.

Let ${\Psi }_G$ and ${\Phi }_G$ be two legal games with the same regulation but with different societies A and B, which are characterized by a different probability function, p and q, respectively. The KL-social divergence from A to B under G (denoted by $D_G\left(A\right|\left|B\right)$) is the Kullback Leibler divergence from q to p, which is,

$${\displaystyle D_G\left(A\right|\left|B\right)=D\left(p\right|\left|q\right)=\sum _{x\in {\mathcal{F}}_G}p\left(x\right)·log\left(\frac{p\left(x\right)}{q\left(x\right)}\right)=E_{p}log\left(\frac{p\left(X\right)}{q\left(X\right)}\right).}$$

Remark 2.

(1) 

This mathemathical concept of social divergence may be useful when trying to import/export a regulation from one country or region to another. A successful regulation may fail when it is applied in another society. Thus, it may be interesting to measure the proximity between those societies regarding the regulation. Hence, before trying to apply that new regulation, it may be important to minimize the distance between societies (as regards to the corresponding regulation) by means of an adequate punishment function, awareness campaigns, incentives, education, …

(2) 

The idea of KL-social divergence has been defined by means of Kullback Leiber divergence; this explains the initials KL. However, as explained in Preliminaries, there are several divergences or distances that measure how different two probability distributions are from each other. Depending on that selection, we may define one social divergence or another. However, all of these distances should satisfy some coherence conditions in order to faithfully reproduce the problem in our mathematical model.

In the following lines, we present a distance function that allows us to measure the difference between l-games, in particular, between regulations that are applied on the same society. Before that, we collect a few conditions that should be satisfied by such a distance. By means of these conditions, we want to translate the main properties of a negotiation or legislation to our mathematical model.

Definition 9.

Let Ω be a Law and A a society. Let G be a regulation in Ω (thus, $G\subseteq \Omega$) and R a rule in $\Omega \backslash G$. The l-games arising from G and $G\cup \left\{R\right\}$ are denoted by Ψ and ${\Psi }^{\prime }$, respectively. Let d be a distance function on the set of l-games Γ. Subsequently, the following coherence conditions are defined:

($C1$)

The bigger the severity of rule R, the bigger the distance from Ψ to ${\Psi }^{\prime }$.

($C2$)

The more likely it is that the rule R will be breached, the greater the distance from Ψ to ${\Psi }^{\prime }$.

Definition 10.

Let ${\Psi }_1$ and ${\Psi }_2$ be two punished l-games that are defined under a Law Ω associated to two regulations $G_1$ and $G_2$, respectively, with the corresponding probability functions $p_1$ and $p_2$ and the punishment functions $g_1$ and $g_2$, respectively. Subsequently, the premetric from ${\Psi }_2$ to ${\Psi }_1$ is defined by

$${\displaystyle D({\Psi }_1\left|\right|{\Psi }_2)=\sum _{x\in \mathcal{F}\left(G_1\right)}{p}_1\left(x\right)·|g_1\left(x\right)-g_2\left(x\right)|,}$$

where $g_2\left(x\right)$ is 0 whenever $x\notin {\mathcal{F}}_{G_2}$.

Remark 3.

(1) 

First, notice that the premetric function d satisfies the coherence conditions that are introduced in Definition 9.

(2) 

With definition above, notice that $D({\Psi }_1\left|\right|\{\varnothing \})=E_{p}g\left({\Psi }_1\right)$, whereas $D\left(\{\varnothing \}\right|\left|{\Psi }_1\right)=0$, for any l-game ${\Psi }_1$. $D\left({\Psi }_1\right|\left|{\Psi }_2\right)$ may be read as the ‘social resistance’ to pass from ${\Psi }_2$ to ${\Psi }_1$. Thus, the value $D({\Psi }_1\left|\right|\{\varnothing \})=E_{p}g\left({\Psi }_1\right)$ may be interpreted as the ‘severity’, ‘cost’, or ‘social resistence’ of the regulation $G_1$ when it is implemented from scratch. On the other hand, $D\left(\{\varnothing \}\right|\left|{\Psi }_1\right)=0$ means that removing rules does not imply a ‘severity’, ‘cost’, or ‘social resistence’. The distance function can be symmetrized in order to impose an strictly positive value to $D\left(\{\varnothing \}\right|\left|{\Psi }_1\right)$, as suggested in the next point.

(3) 

This premetric fails to be symmetric; however, it can be easily symmetrized, as follows:

$$D^{+}({\Psi }_1,{\Psi }_2)=D({\Psi }_1\left|\right|{\Psi }_2)+D({\Psi }_2\left|\right|{\Psi }_1).$$

Or, by means of the maximum:

$$D^s({\Psi }_1,{\Psi }_2)=max\left\{D\right({\Psi }_1\left|\right|{\Psi }_2),D({\Psi }_2\left|\right|{\Psi }_1\left)\right\}.$$

(4) 

However, D as well as $D^{+}$ and $D^s$ may fail to satisfy the triangle inequality.

Theorem 1.

The distance function D is a premetric on Γ and, hence, it defines a topology ${\tau }_D$ on the set.

The distance functions $D^{+}$ and $D^s$ are symmetric premetrics on Γ and, hence, each of them defines a topology (${\tau }_{D^{+}}$ and ${\tau }_{D^s}$, respectively) on the set.

Proof. 

It is straighforward to check that D is in fact a premetric and, therefore, $D^{+}$ and $D^s$ are symmetric premetrics on $\Gamma$. Hence, by Proposition 1, they define a topology on $\Gamma$ by means of the corresponding open balls. □

Notice that, through the definitions that are included until this point, now our set of all possible regulations in a society under a Law (assuming that each regulation is endowed with the corresponding probability function related to the society) is a complete and weighted and directed graph of $2^{|\Omega |}=\left|\mathcal{P}(\Omega )\right|$ nodes, where each node is a l-game and each edge $({\Psi }_1,{\Psi }_2)$ is weighted by the value that is determined by the function $D({\Psi }_2,{\Psi }_1)$. If D is symmetric, then the graph can be considered to be undirected. Here, notice that not just any arbitrary combination of rules can make (legal) sense; thus, from an applied point of view, the number of possible regulations that arise from the Law $\Omega$ may be smaller that $2^{|\Omega |}$.

If necessary, we may use the path-distance that arose from the weighted graph. It is known that, if the graph is connected and undirected, then this path-distance is, in fact, a distance and, hence, it satisfies the triangle inequality. In the case of a directed and complete graph, then the path-distance fails to be symmetric and, hence, it is a quasi-metric. [31]

Theorem 2.

Let D be a quasi-premetric on Γ. Hence, Γ is a complete and directional graph where the weigth of each edge $(v,u)$ corresponds to $D(u,v)$ (which may differ from $D(v,u)$ if D fails to be symmetric). Subsequently, path-distance $D_p$ is a (quasi) metric on Γ where $D_p(u,v)$ is defined as the shortest distance between them where distance is measured along the edges of the graph. In particular, $D_p$ satisfies the triangle inequality.

Remark 4.

Again, if the individual punishment associated to breaking a family of rules is defined by means of the probability (such that the punishment also changes depending on the number of offenders), then the distance from ${\Psi }_2$ to ${\Psi }_1$ maybe defined by means of the joint entropy. [28,29,30] That could also be useful when comparing societies that are not under exactly the same regulation.

Definition 11.

Let Ω be a Law of a finite set of possible rules and $A={\left\{A_n\right\}}_1^N$ a finite set of players. Let $G_1$ and $G_2$ be two regulations under the Law, and $p_1$ and $p_2$ the corresponding probabilities (respectively) that arise when they are applied in a society A. We denote, by ${\Psi }_1$ and ${\Psi }_2$, the l-games $(G_1,{\mathcal{F}}_1,p_1)$ and $(G_2,{\mathcal{F}}_2,p_2)$, respectively. We shall say that ${\Psi }_2$ is a l-subgame of ${\Psi }_1$ (and denote it by ${\Psi }_2{⊑}_{sub}{\Psi }_1$) if $G_1\subseteq G_2$ and any titere of $G_2$ is also a titere in $G_1$.

We denote, by $sub({\Psi }_1,{\Psi }_2)$, the set of l-subgames of ${\Psi }_1$ and ${\Psi }_2$ (it may be empty).

Remark 5.

(1) 

With definition above, notice that, if we add a rule to a game, then we achieve a new subgame of the first one, i.e., when adding rules, we define subgames.

(2) 

When the Law Ω and society A are fixed, we extend the notation $D\left({\Psi }_1\right|\left|{\Psi }_2\right)$ between games to the set of regulations $\mathcal{P}(\Omega )$ by $D(G_1\left|\right|G_2)=D({\Psi }_1\left|\right|{\Psi }_2)$, where ${\Psi }_1$ and ${\Psi }_2$ are the corresponding l-games that arise from $G_1$ and $G_2$ (respectively) when they are applied in the society A.

Proposition 2.

The relation ${⊑}_{sub}$ of being a l-subgame is a preorder relation on Γ.

Proof. 

It is clear that ${⊑}_{sub}$ is reflexive. Let us see that it is transitive. Suppose that ${\Psi }_3{⊑}_{sub}{\Psi }_2{⊑}_{sub}{\Psi }_1$, then $G_1\subseteq G_2\subseteq G_3$ and, in particular, $G_1\subseteq G_3$. On the other hand, any titere of $G_3$ is also a titere in $G_2$, as well as any titere of $G_2$ is also a titere in $G_1$, thus, any titere of $G_3$ is also a titere in $G_1$.

Therefore, we conclude that ${\Psi }_3{⊑}_{sub}{\Psi }_1$, which is, ${⊑}_{sub}$ is transitive and, hence, it is a preorder. □

Example 1.

Let ${\left\{A_i\right\}}_{i=1,2,3}$ be a set of three players, which are the herdsmans of the classical communal example. Each herdsman has a single cow, which need 90$ for feed. The communal can feed two cows, but, if the three of them try to feed there, then it is not enough and each herdsman has an additional cost of 50$.

Initially there is no rule, so that all of the players decide to bring their cow to the communal. Hence, the equlibrium state is $(-50,-50,-50)$. In order to improve this situation, the following rules are studied:

$R_1:$ A tax (33$) to any user.

$R_2:$ A raffle (one cannot use it).

$R_3:$ A compensation (66$ for any one who reject to use it).

Therefore, the Law is $\Omega =\{R_1,R_2,R_3\}$. Any combination of the aforementioned rules is also possible; hence, we have $2^3=8$ possible regulations, as denoted by $G_i\subseteq \Omega$. Under each regulation, a new equilibrium state may arise.

We may assume that the punishment for breaching $R_1$ (i.e., for using the communal without paying the tax) is $g\left(R_1\right)=$100$, the punishment for breaching $R_2$ is also $g\left(R_2\right)=$100$, and for $R_3$ is $g\left(R_3\right)=$166$.

The theoretical punishment for breaching a law that is not included in the regulation is 0 (this assumption is needed for the construction of the distance).

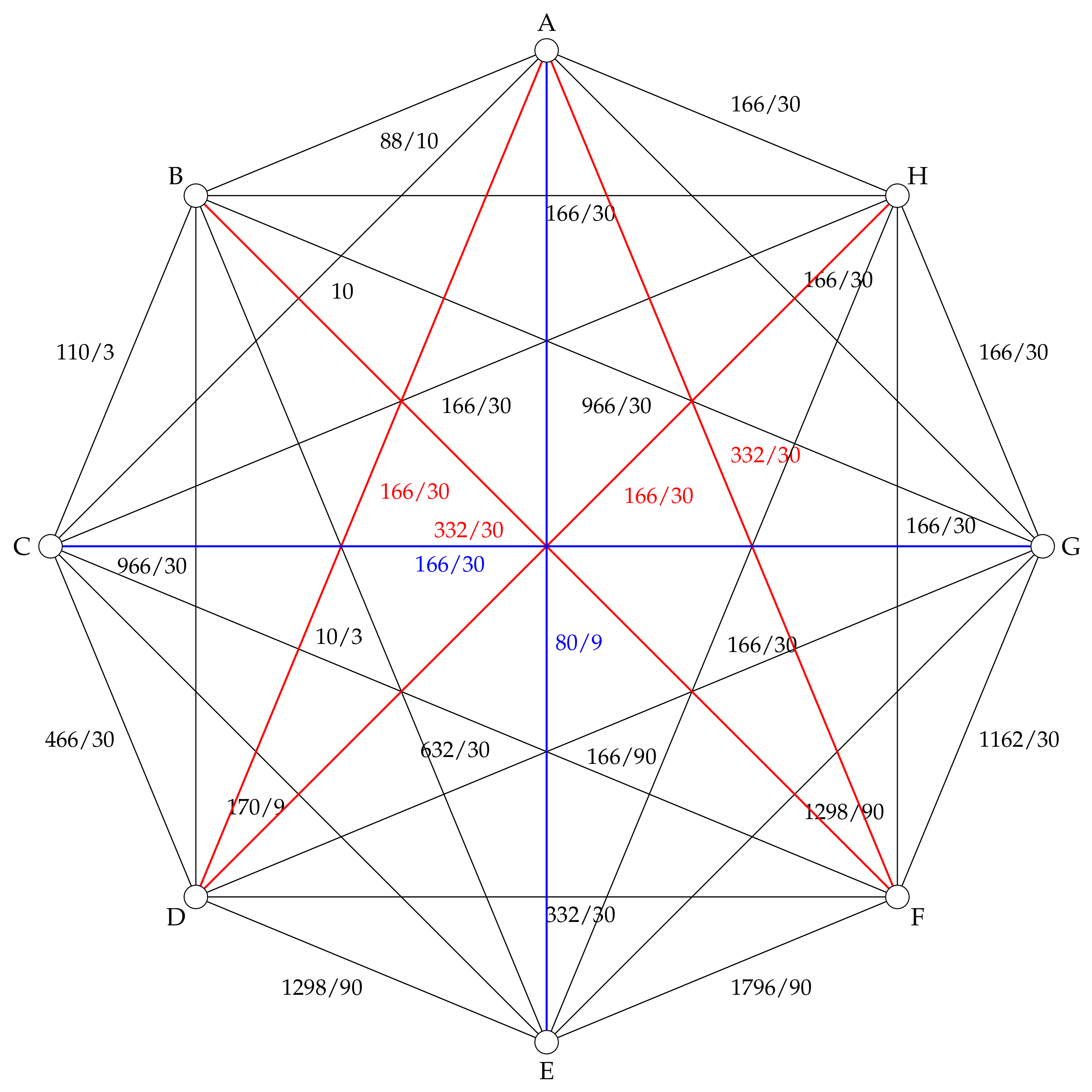
Now, we estimate the probability of breaching each law. We may do that for each player or just as an average or mean. Here, we did for each player, assuming that one of them is very lawful, the second one not so much, and the third one is a cheat. With the probabilities that are assumed for each player, the corresponding mean (without weights, since we assume that all of the players are equally important (one cow for each herdsman)) is reflected in

Table 1. Probability of breaching each rule (or set of rules) under each regulation.

Unfulfilled Rules /Regulation	A	B	C	D	E	F	G	H
$A=\{\varnothing \}$	1	x	x	x	x	x	x	x
$B=\left\{tax\right\}$	22/30	8/30	x	x	x	x	x	x
$C=\left\{raffle\right\}$	9/10	x	1/10	x	x	x	x	x
$D=\{comp.\}$	29/30	x	x	1/30	x	x	x	x
$E=\{tax,raffle\}$	82/90	5/90	0	x	3/90	x	x	x
$F=\{tax,comp.\}$	28/30	0	x	0	x	2/30	x	x
$G=\{raffle,comp.\}$	87/90	x	0	2/90	x	x	1/90	x
$H=\{tax,raffle,comp.\}$	29/30	0	0	0	0	0	0	1/30

:

In Table 1, notice that the probability that is assigned to ∅ is the probability of breaching no rule. On the other hand, in some context the probability of breaching a single rule (or a subset of rules) is 0, since it implies breaching another one. For instance, under regulation F, if a player breaks the compensation rule, it means that (s)he is using the communal as well as (s)he is not paying the tax (here, we assume that it is bureaucratically impossible to ask for compensation as well as pay the tax); thus, (s)he is not breaching the $compeansation$ or the $tax$, but it is breaking the set of rules $\{tax,compensation\}$. In any case, although the probability of breaching the single rule is 0, the corresponding punishment exists (at least theoretically, and it will be used when defining distances).

With these data, the distances between regulations (as defined in Definition 10) have been illustrated in the graph shown in Figure 1.

4. Applications: Law Modifications and No-Agreement Situations

Thanks to the mathematical approach to those questions that are related to regulations and deals, the corresponding decisions may now be chosen by answering optimization problems over graphs. In the present section, some of these questions and solutions are given.

4.1. First Application: The Shortest Path, the Legal Gradiant

In the present section, we show how to change the rules of a game in order to achieve a more efficient equilibrium. There may be different manners or paths to change the law from a initial regulation to a final one, but some of them may be better than others when we want to minimize the social resistence to the changes.

The set of all possible deals is a complete and weighted and directed graph of $2^{|\Omega |}=\left|\mathcal{P}(\Omega )\right|$ nodes, where each node is a deal (i.e. a subset of $\Omega$) and each edge $(G_1,G_2)$ is weighted by the value that is determined by the function $D(G_2,G_1)$, as was shown in the section before. If D is symmetric, then the graph can be considered to be undirected.

Therefore, our political problem of legislating while minimizing social resistance is just the well-known problem of finding the shortest path between two vertices in a graph, such that the sum of the weights is minimized. [31]

Example 2.

From Figure 1 of Example 1, we may observe that, if we want to arrive to regulation H by adding rules one-by-one from A, then any possible path is longer (i.e., worst, since the conflict with respect to the previous situation is bigger) than the (shortest) path $(A,D,G,H)$, whose length is ${12}^{\prime }91$, whereas the length of the second shortest path $(A,C,E,H)$ is ${34}^{\prime }422$ (and the third one would be $(A,B,G,H)$, with length ${46}^{\prime }5$). Thus, with the assumed data (mainly, the probabilities and the punishment), the compensation must be the first rule to be introduced.

4.2. Second Application: Searching Agreement and Consensus

When making agreements between N players, each player has a preference on the possible agreements that may be agreed. The presented distance may be a tool in order to achieve a deal, arriving to an ‘intermediate’ deal between the preferences of the players.

Returning to the previous case that is illustrated in Example 2, we present the following simple case:

Example 3.

From Figure 1 of Example 1, we may observe that, for example, if in the region where the communal lies there are two main political parties, such that one of them wants to introduce the regulation H for the communal, whereas the other prefers to continue with no regulation, then, the deal D as well as G could be the midpoint between these two regulations.

Suppose that, in a negotiation, there are N players that do not approach positions and, such that each player n has a family of most preferred deals ${\left\{G_{n_k}^{*}\right\}}_{k=1,\dots ,m_n}$ (arguing on the set of all possible regulations on $\Omega$).

In this blocking situation, we may wonder which is the minimum distance $r\in$, such that ${\displaystyle \bigcap _{n=1}^N}\left({\displaystyle \bigcup _{k=1}^{m_n}}{B}_r\left(G_{n_k}^{*}\right)\right)\ne \varnothing$, as well as it satisfies an optimal condition with respect to the player’s preferences, in case they exist. We are currently just searching that deal that is as close as possible to all of the most preferred options. Once we know where that meeting point is, then we can apply the study that is presented in Section 4.1 in order to make the path from the initial deal to that closest deal.

Now, we assume that each player $A_n$ has a preference ${\precsim }_n$ (for each $n=1,2,\dots ,N$) on the set of all possible games $\{G:G\subseteq \Omega \}=\mathcal{P}(\Omega )$. We assume that each preference ${\precsim }_n$ is a preorder. The goal of the present section is to achieve an optimal deal for disagreement situations. For that purpose, the following concept is defined.

Definition 12.

Let Ω be a finite set of possible rules and $A={\left\{A_n\right\}}_1^N$ a finite set of players with their corresponding preferences ${\precsim }_n$ on $\mathcal{P}(\Omega )$ (for each $n=1,2,\dots ,N$). A deal $G^o\subseteq \Omega$ is said to be a Pareto optimal deal if for any other deal G, $G^o{\prec }_{m}G$ implies $G{\prec }_n{G}^o$, with $n,m\in \{1,\dots ,N\}$.

Now, we introduce some interesting concepts for the study of negotiation problems.

Definition 13.

We shall say that a signer of a deal G is ar -signer (with respect to a metric D), with $r\ge 0$, if she agrees to sign any other deal $G^{\prime }$, such that the distance from G to $G^{\prime }$ is smaller than r, that is, $D(G^{\prime },G)<r$. The value of r is said to be the deal threshold of the signer.

A Game of games Γ is said to be a r -step Game of games if $D({\Psi }_1,{\Psi }_2)\ge r$, for any ${\Psi }_1,{\Psi }_2\in \Gamma$.

Given a $r_1$-step Game of games, a $r_2$-signer is said to be stubborn whenever $r_2<r_1$. Additionally, it is said to be a boycotter if $r_2=0$.

Thus, an sttuborn player is not going to sign any other deal, except his/her most preferred options. A boycotter is a player that sign nothing.

Example 4.

In the case that is illustrated in Example 2, the length of each step in the path $(A,D,G,H)$ is, at most, $166/30$; thus, any player with a deal-threshold bigger than this value would accept the deal.

On the other hand, there is no path from A to H, such that the length of each step is smaller than that value. Thus, consensus would be possible over time whenever all the players are r-signers, with $r\ge 166/30$, for each step carried out at the time.

The following concept introduces the idea of compatibility between the agent’s preference and the distance, in the sense that the closer a l-game is to the maximal elements (with respect to the preference relation), the more preferred it is.

Definition 14.

Let Ω be a finite set of possible rules and $A={\left\{A_n\right\}}_1^N$ a finite set of players with their corresponding preferences ${\precsim }_n$ on $\mathcal{P}(\Omega )$ (for each $n=1,2,\dots ,N$). For each $n=1,\dots ,N$, we denote, by $M_n=\{G_{n_1}^{*},\dots ,G_{n_{m_n}}^{*}\}$, the maximal elements of $\mathcal{P}(\Omega )$ with respect to ${\precsim }_n$. Let D be a distance function on $\mathcal{P}(\Omega )$. We say that the preferences and the measure D are compatible if, for any maximal chain C in $(\mathcal{P}(\Omega ),{\precsim }_n)$ and any $G_1,G_2\in C$, the following condition holds true:

$$G_1{\precsim }_n{G}_2\Rightarrow D(G_2,G_n^C)\le D(G_1,G_n^C),$$

where $G_n^C$ is the maximal element of C with respect to ${\precsim }_n$.

Remark 6.

Notice that, given a preference ${\precsim }_n$ and a compatible distance D, it may hold that $min{\left\{D(G_{n_k}^{*},y)\right\}}_{k=1,\dots ,m_n}<min{\left\{D(G_{n_k}^{*},x)\right\}}_{k=1,\dots ,m_n}$ as well as $y{\prec }_{n}x$, for some $x,y\in \mathcal{P}(\Omega )$.

In order to achieve that Pareto optimal deal, we will use a compatible distance on the set of games, which is, a distance, such that the player’s preferences are lower semicontinuous. Anyway, even in the case of no preferences, we may apply this method just arguing on distances, since we may assume that the player’s preferences are empty and, hence, lower semicontinuous.

First, for each player’s preference, we construct the corresponding compatible linear extension.

Definition 15.

Let Ω be a finite set of possible rules and $A={\left\{A_n\right\}}_1^N$ a finite set of players with their corresponding preferences ${\precsim }_n$ on $\mathcal{P}(\Omega )$ (for each $n=1,2,\dots ,N$). Assume that these preferences are compatible with respect to a distance D.

The distance linear order ${⪯}_n^D$ for a player $A_n$ is defined, as follows (for any $n=1,\dots ,N$):

$$x{\le }_n^{D}y\iff min{\left\{D(G_{n_k}^{*},y)\right\}}_{k=1,\dots ,m_n}\le min{\left\{D(G_{n_k}^{*},x)\right\}}_{k=1,\dots ,m_n}.$$

The proof of the following proposition is straightforward.

Proposition 3.

The distance linear order is a total preorder.

Theorem 3.

Let Ω be a finite set of possible rules and $A={\left\{A_n\right\}}_1^N$ a finite set of players with their corresponding preferences ${\precsim }_n$ on $\mathcal{P}(\Omega )$ (for each $n=1,2,\dots ,N$). Let D be a distance on $\mathcal{P}(\Omega )$. Let $M_n=\{G_{n_1}^{*},\dots ,G_{n_{m_n}}^{*}\}$ be the maximal elements of $\mathcal{P}(\Omega )$ with respect to ${\precsim }_n$.

If ${\precsim }_n$ is ${\tau }_U$-lower semicontinuous with respect to the topology that is defined as

$${\displaystyle {\tau }_U={\{U_r=\bigcup _{k=1}^{k=m_n}{B}_r\left(G_{n_k}^{*}\right)\}}_{r\ge 0}\cup \{\varnothing \}}$$

then

1. 

The distance linear order ${<}_n^D$ is a linear extension of ${\prec }_n$.

2. 

The preference ${\precsim }_n$ and the distance D are compatible.

Proof 

(1)

Let $x,y\in X=\mathcal{P}(\Omega )$ such that $x{\prec }_{n}y$. Since ${\precsim }_n$ is ${\tau }_U$-lower semicontinuous, $y\in U=X\backslash L_{{\precsim }_n}\left(x\right)\in {\tau }_U$, whereas $x\notin U$. Thus, there exists a radius $r>0$ such that ${\displaystyle y\in U_r=\bigcup _{k=1}^{k=m_n}{B}_r\left(G_{n_k}^{*}\right)\subseteq U}$ as well as $x\notin U_r$. Therefore, $min{\left\{D(G_{n_k}^{*},y)\right\}}_{k=1,\dots ,m_n}<r\le min{\left\{D(G_{n_k}^{*},x)\right\}}_{k=1,\dots ,m_n}$ and thus, $x{<}_n^{D}y.$

(2)

Let $x,y\in X=\mathcal{P}(\Omega )$ be, such that $x{\prec }_{n}y$ and $G^{*}\in M_n$ the maximal element of a maximal chain C containing x and y. By reduction to the absurd, suppose that there is $r>0$ such that $x\in B_r\left(G^{*}\right)$ as well as $y\notin B_r\left(G^{*}\right)$. Subsequently, ${\displaystyle x\in \bigcup _{k=1}^{k=m_n}{B}_r\left({\overline{G}}_{n_k}^{*}\right)=U}$, whereas ${\displaystyle y\notin \bigcup _{k=1}^{k=m_n}{B}_r\left(G_{n_k}^{*}\right)=U}$. Thus, $F=X\backslash U$ is closed and $y\in X\backslash U$. Because the preorder ${\precsim }_n$ is ${\tau }_U$-lower semicontinuous, $L_{{\precsim }_n}\left(y\right)$ is contained in F and, hence, $x\in L_{{\precsim }_n}\left(y\right)\subseteq F$. Therefore, ${\displaystyle x\notin \bigcup _{k=1}^{k=m_n}{B}_r\left({\overline{G}}_{n_k}^{*}\right)=U}$ and, hence, in particular $x\notin B_r\left(G^{*}\right)$ arrived to the desired contradiction.

□

Theorem 4.

Let Ω be a finite set of possible rules and $A={\left\{A_n\right\}}_1^N$ a finite set of players with their corresponding preferences ${\precsim }_n$ on $\mathcal{P}(\Omega )$ (for each $n=1,2,\dots ,N$). Assume that these preferences are ${\tau }_U$-lower semicontinuous. Let ${\le }_n$ be the distance linear extension of ${\precsim }_n$, for each $n=1,\dots ,N$.

Subsequently, the maximal elements of $⊑={\displaystyle \bigcap _{n=1}^N}{\le }_n$ are all the Pareto optimal deals.

Proof. 

Let M be a maximal element of ${\displaystyle \bigcap _{n=1}^N}{\le }_n$. Suppose that there is another element $x\in X=\mathcal{P}\left(\mathcal{R}\right)$, such that $M{\prec }_{n}x$ for some $n\in \{1,\dots ,N\}$. Because ${<}_n$ extends ${\prec }_n$, then it holds true that $M{<}_{n}x$. On the other hand, M is a maximal element of ${\displaystyle \bigcap _{n=1}^N}{\le }_n$; therefore, there is at least one index $k\in \{1,\dots ,N\}$, such that $x{\prec }_{k}M$ (otherwise, $M⊏x$ and, hence, M is not maximal, arriving to a contradiction). Thus, M is a Pareto optimal deal. □

Finally, according to Theorem 4, in a disagreement situation where the preferences are ${\tau }_U$-lower semicontinuous, we may find the set of all Pareto optimal deals. Subsequently, by means of the distance, we may choose that Pareto optimal deal, which is also the closest from the most preferred deals, according to each player’s preference. This motivates the following definition.

Definition 16.

Let Ω be a finite set of possible rules and $A={\left\{A_n\right\}}_1^N$ a finite set of players with their corresponding preferences ${\precsim }_n$ on $\mathcal{P}(\Omega )$ (for each $n=1,2,\dots ,N$). Assume that these preferences are compatible with respect to a distance D. Let ${\le }_n$ be the distance linear extension of ${\precsim }_n$, for each $n=1,\dots ,N$.

A maximal element $G^{*}$ of ${\displaystyle \bigcap _{n=1}^N}{\le }_n$ is the Closest Pareto optimal deal if

$$max{\left\{D(G_{n_k}^{*},G^{*})\right\}}_{k=1,\dots ,m_n}\le max{\left\{D(G_{n_k}^{*},G)\right\}}_{k=1,\dots ,m_n},$$

for any other maximal element G of ${\displaystyle \bigcap _{n=1}^N}{\le }_n$.

Remark 7.

In the study above, we have treated all players equally and symmetrically, regardless of their flexibility in reaching agreements. However, it can be approached asymmetrically, building balls of larger or smaller radius, depending on the flexibility of each player. This and other questions are left as a future work.

5. Conclusions

The main goal of this work is to present a new and original breaking mathematical approach for agreement situations as well as regulation modifications. The present paper presents the mathematical formalization of several concepts in the field of regulations, negotiations, and agreements in the context of a society or a family of agents, as well as a mathematical structure that tries to capture the nature of some of these phenomena. As a consequence, several problems that are related to agreements, negotiations, regulations, etc. may be studied and just solved as mathematical optimization problems.

This work is a new approach. It has given a mathematical model for negotiations and regulation constructions, as well as for a comparison of societies. However, this model may increase its complexity for other types of problems. Nevertheless, a limitation of the work could be the absence of data that would have to be solved with different data estimates.