The Connection between the PQ Penny Flip Game and the Dihedral Groups
Abstract
1. Introduction
1.1. Related Work
1.2. Contribution
1.3. Organization
2. Background
2.1. The Penny Flip Game
- A strategy is a function that associates an admissible action to every round that the player makes a move. It is convenient to represent strategies as finite sequences of moves from the player’s repertoire;
- A strategy for Picard is a winning strategy if for every strategy of Q, Picard wins the game with probability ;
- Symmetrically, a strategy for Q is a winning strategy if for every strategy of Picard, Q wins the game with probability ;
- A strategy for Picard or Q is dominated if there exists another strategy that has greater probability to win for every strategy of the other player. A strategy that dominates all other strategies is called dominant.
2.2. Dihedral Groups
- ,
- , when , and
- , when .
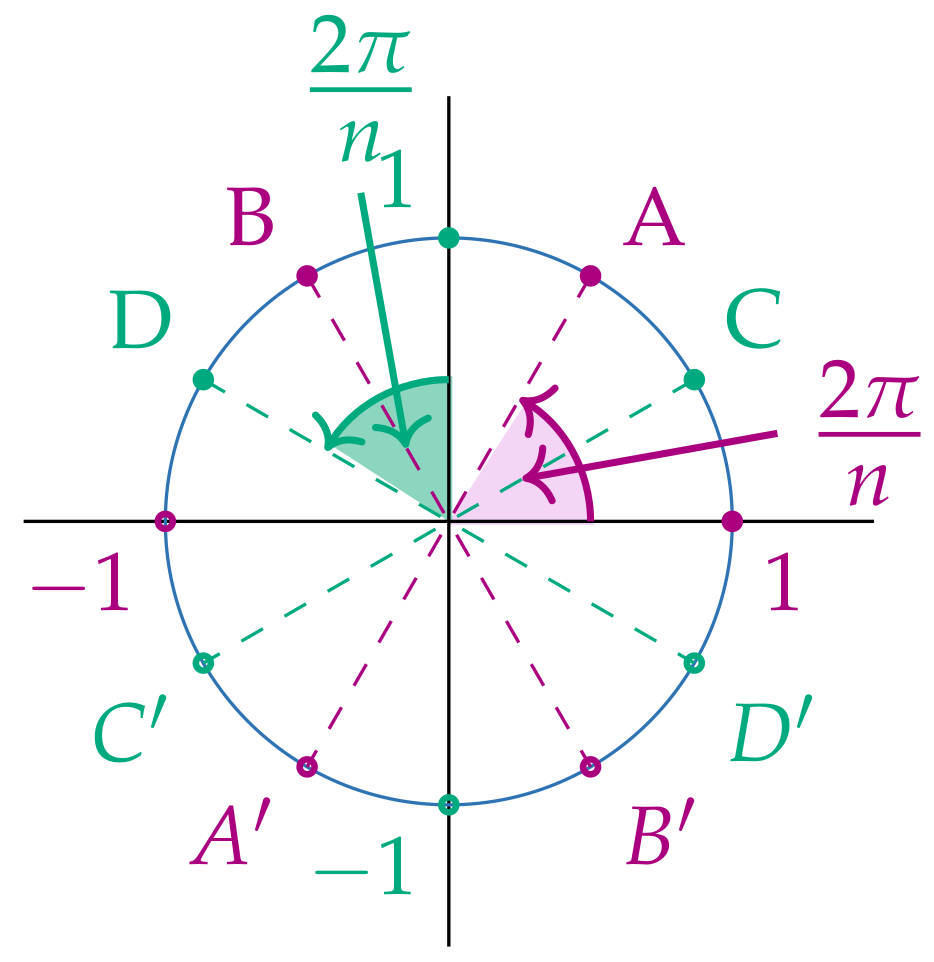
- There are also n reflection symmetries.
- –
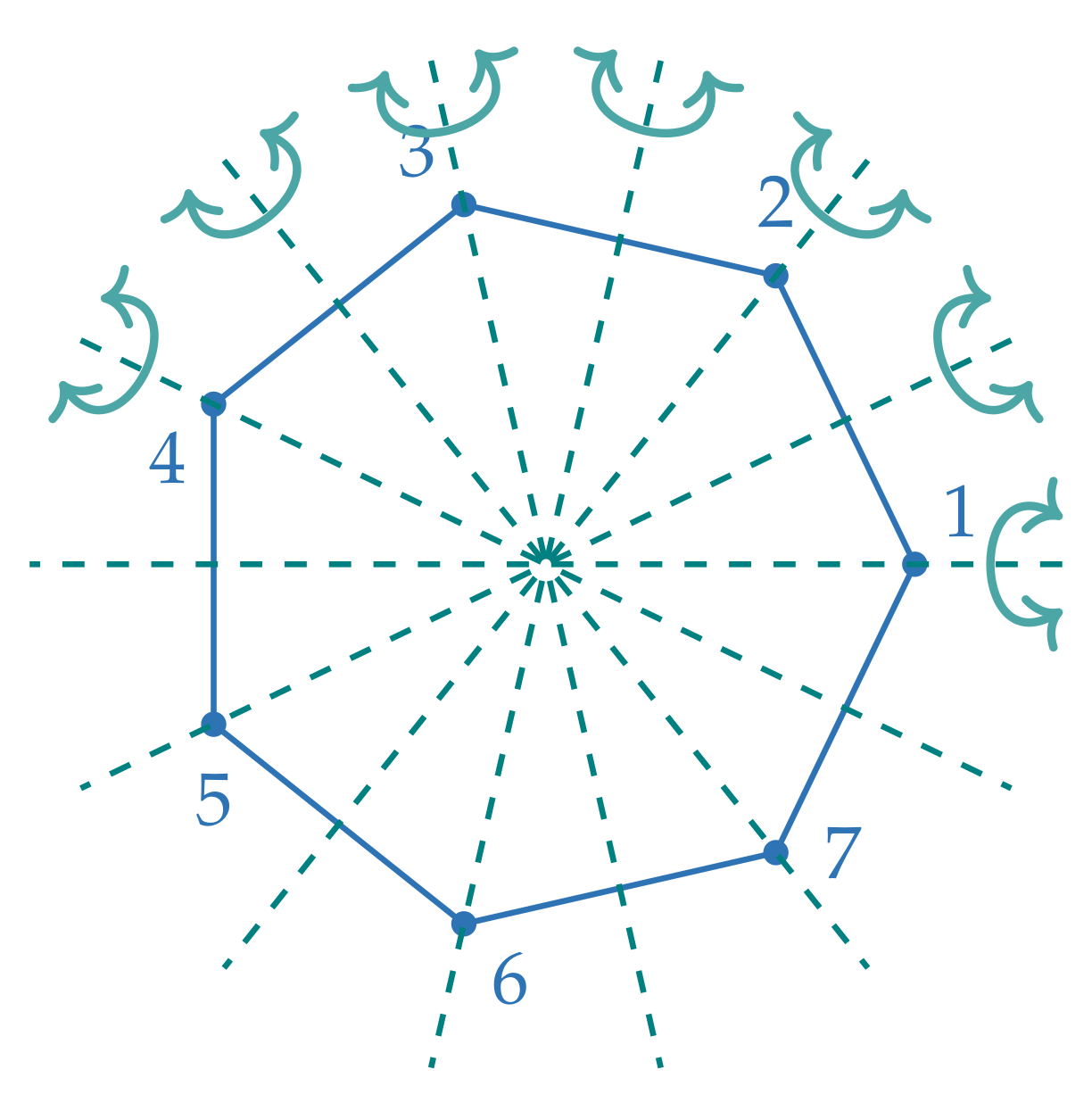
- If n is odd these are the reflections in the lines defined by a vertex and the center of the regular n-gon. As an example, see Figure 3 depicting the reflection symmetries of the regular heptagon.
- –
- If n is even, these are reflections in the lines through opposite vertices and reflections in the lines passing through midpoints of opposite faces. An example that will play an important role in this study is given in Figure 4, showing the reflection symmetries of the regular octagon.
3. The Connection between PQG and D8
3.1. Matrix Representations of Rotations and Reflections
3.2. Orbits and Stabilizers
- (A1)
- for every .
- (A2)
- , for all and all .
- 1.
- Given , the G-orbit of x, denoted by , is the set .
- 2.
- Given , the G-orbit of S, denoted by , is the union of the orbits , for each
- 3.
- Given , the stabilizer of x, denoted by , is the set .
- 4.
- Given , the fixed set of g, denoted by , is the set .
- 5.
- Given , the fixed set of X, denoted by , is the intersection of the fixed sets , for each .
4. Analyzing Q’s Strategy in Terms of Groups
- 1.
- and have the same orbit:
- 2.
- The orbit of B is:
- The stabilizers of and in are
- The stabilizers of and are
- 1.
- The fixed set of F in is the set
- 2.
- The fixed set of in is the set
| Algorithm 1: Q’s Winning Strategy. |
|
5. Enlarging the Operational Space of the Game
- Picard, who embodies the classical player, can flip the coin. If he is deprived of this ability, then the resulting game becomes trivial and meaningless. He should not be able to do more than that, as this would endow them with quantum capabilities. Formally, this is expressed by specifying:
- Q, who stands for the quantum player, must exhibit quantumness. Thus, at least one of their actions must lie outside the classical realm. In more technical terms, their repertoire must contain at least one operator from other than I and F.
- 1.
- Given a strategy σ, designates the equivalence class that contains σ. Any member of is a representative of .
- 2.
- To every class the state path is associated as follows: if is any representative of , is defined to be , where
5.1. Inside
- Let us first establish that if Q leaves the coin at state , or sends it to state , then he will not be able to win with probability . To see this more clearly, let us recall that, by Theorem 2, . If leaves the coin at state , i.e., , then , which is impossible because represents an element of . The same reasoning shows that if Q’s first move sends the coin to state , then he will not be able to win with probability .
- In the original , Q won by sending the coin to state . In , this can be achieved with 4 different ways: , and . State is fixed by I and F according to (23), which means that no matter what Picard plays, the coin will remain in this state. Finally, Q can send the coin back to the state with 4 different ways: , and . This means that Q has 16 different winning strategies, which, in view of Definition 9, are equivalent. Thus, they constitute one equivalence class of winning strategies. Strategy is a representative of this class, but any other strategy would also do. For this class the corresponding state path is .
- Algorithm 1 enables us to discover one more winning strategy for Q. Q has another option, which is to drive the coin to state . This can also be achieved with 4 different ways: , or . Picard cannot change this state either because is fixed by I and F, according to (23). During the final round Q has the opportunity to send the coin back to the state with 4 different ways: , or . Hence, Q has 16 more winning strategies, which are equivalent. They make the second equivalence class of winning strategies and any one of them, e.g., can be its representative. For this class, the corresponding state path is .
- Picard, unfortunately for him, has no winning strategy.
- 1.
- Q has exactly two classes of winning and dominant strategies, each containing 16 equivalent strategies:where
- is one of or ,
- is one of or ,
- is one of or , and
- is one of or .
- 2.
- The winning state paths corresponding to and are
- 3.
- Picard has no winning strategy.
5.2. The Smaller Dihedral Groups and
- , and do not contain the reflection F. This can be verified by comparing Formula (9) with formula (14) for , and 7 and . This is based on the assumption that Picard, the classical player, must be able to flip the coin, as emphasized in (24).
- does contain the reflection F. However, the orbit is . This means that Q can only flip the coin from heads to tails or vice versa. If , then the degenerates to the classical coin tossing game. Q is no longer a quantum entity and, as explained in Example 1, no longer possesses a winning strategy. From this perspective, it becomes meaningless to play the in .
5.3. The Dihedral Groups ,
- 1.
- if n is a multiple of 4, then the action of on the computational basis B is
- 2.
- if n is even but not a multiple of 4, then the action of on the computational basis B is
- 1.
- If n is a multiple of 8, then:
- 1.
- In every other case:
- 1.
- Q has exactly two classes of winning and dominant strategies, each containing 16 equivalent strategies:where
- is one of or ,
- is one of or ,
- is one of or , and
- is one of or .
- 2.
- The winning state paths corresponding to and are
- 3.
- Picard has no winning strategy.
5.4. The Entire
- 1.
- Q has exactly two classes of winning and dominant strategies, each containing infinite equivalent strategies:where
- is one of or ,
- is one of or ,
- is one of or ,
- is one of or , and
- are possibly different real parameters.
- 2.
- The winning state paths corresponding to and are
- 3.
- Picard has no winning strategy.
6. Extending the Game
- at the start of the game the coin is in a predefined basis state, which is called the initial state and designate by ,
- Picard and Q alternate turns acting on the coin following a specified order, and
- when the game ends, the coin is measured in the computational basis; if it is found in state Picard wins, whereas if it is found in then Q wins.
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| The PQ penny flip game | |
| The dihedral group of order | |
| The unitary group of dimension 2 |
Appendix A. Proofs of the Main Results
Appendix A.1. Proofs for Section 3
Appendix A.2. Proofs for Section 4
- the action of a dihedral group on any state of the quantum coin can be determined by simply multiplying the matrices representing the elements of the group with the ket corresponding to the state; and
- a ket of the form , with , represents the same state as the ket .
- 1.
- and have the same orbit:
- 1.
- The orbit of B is:
- By systematically multiplying the standard matrix representation of the rotations and reflections of , given by Formulas (13) and (14), with one gets and . Of course, and represent the same state. This also applies to the pairs and , and , and . Thus, . In a symmetrical fashion, computing verifies that (A2) holds.
- Simply taking the union of the orbits and gives the desired result.
- The stabilizers of and in are
- The stabilizers of and are
- 1.
- The fixed set of F in is the set
- 2.
- The fixed set of in is the set
- (A3) implies that in the coin can be in one the states contained in . By successively multiplying F with these states, it can be found that: , , , and . These results show that the action of F on the states and does not change the state of the coin. Hence, and (A6) holds.
- The identity I fixes every state in the orbit, so the intersection of with is just , which verifies (A7).
Appendix A.3. Proofs for Section 5
- 1.
- Q has exactly two classes of winning and dominant strategieseach containing 16 equivalent strategies.
- 2.
- The winning state paths corresponding to and are
- 3.
- Picard has no winning strategy.
- There are 4 cases to consider, depending on the state of the coin after Q’s first move .
- (i)
- If Q leaves the coin at state , i.e., , then (A8) implies that , which is absurd. To arrive at this contradiction, the fact that , as a group element, has a unique inverse was used. This result shows that the first move of every winning strategy for Q must drive the coin to a state other than .
- (ii)
- If Q sends the coin to state , i.e., , then (A8) implies that , which is also absurd for the same reason as in the previous case. Hence, the first move of every winning strategy for Q cannot send the coin to state .
- (iii)
- If Q sends the coin to state , which can can be achieved through 4 different ways: , and , then, no matter what Picard plays, the coin will remain in this state because is fixed by I and F, according to (A7). Finally, Q can send the coin back to the state with 4 different ways: and . This means that Q has 16 different winning strategies, which, in view of Definition 9, are equivalent. Thus, they constitute one equivalence class of 16 winning strategies, which is designated by . Any one of them, e.g., can be taken as a representative of this class, so it accurate to write .
- (iv)
- In an analogous way, Q can send the coin to state using 4 different moves: or . Picard is unable to change this state because is also fixed by I and F, according to (A7). This enables Q to send the coin back to with 4 different ways: or . Once again Q has 16 different winning strategies, which, in view of Definition 9, are equivalent. They make the second equivalence class of 16 winning strategies, which is denoted by . Any one of them, for instance , can be taken as a representative of this class, so it is also accurate to write .
This concludes the proof of (A10). - Based on the above analysis of cases and , it is straightforward to verify (A11).
- By Definition 1, Picard has no winning strategy because if Q employs one of their winning strategies, Picard has probability to win the game.
- Picard’s set of moves is , according to assumption (24). As a classical player, Picard must certainly be able to flip the coin, or else the game will be meaningless. On the other hand, he should not be able to employ a true quantum move.
- Q’s actions should contain at least one unitary operator other than the classical I and F operators, in order to exhibit quantumness.
- The dihedral group does not contain the reflection F. One can verify this by comparing Formula (9) with Formula (14) for and . This shows that does not satisfy assumption (24) and, hence, is an inappropriate stage for the .
- contains the reflection F. However, the orbit is . This means that Q can only flip the coin from heads to tails or vice versa. If , then the degenerates to the classical coin tossing game. Q is unable to employ a truly quantum strategy, something that contradicts the second assumption at the beginning of Section 5 and goes against the spirit of the . Moreover, in Q no longer possesses a winning strategy. For these reasons, it is meaningless to play the in .
- The dihedral groups and do not contain the reflection F either. Once again the Formulas (9) and (14) for and 7 and can be used to verify this fact. These groups do not satisfy assumption (24) and are also inadmissible for the .
- 1.
- if , then , and
- 2.
- if , then .
- By Definition 8, if , then there exists an element such that . Every member of has the form for some . These combined with Definition 7, imply that , that is too. Hence, .At the same time, Definition 7 asserts that . Every member of has the form for some . Therefore, , that is too, that is, . This establishes that .
- The proof is completely symmetrical.
- no ket (or its opposite) from the sequence (A35) appears in the sequence (A37), that is , , where ; and
- no ket (or its opposite) from the sequence (A37) appears in the sequence (A35), i.e., , , where .
- The first case gives the system , which is clearly impossible because there is no such that .
- The next case involves the system . Using (A17), this system can be transformed to the equivalent , which, in turn, implies that . The fact that , means that and . Hence, and . Adding the last two equations gives that , which is also impossible because .
- The remaining cases can be dealt with in an entirely analogous manner.
- 1.
- if n is a multiple of 4, then the action of on the computational basis B is
- 2.
- if n is even but not a multiple of 4, then the action of on the computational basis B is
- 1.
- If n is a multiple of 8, then:
- 2.
- In every other case:
- If n is a multiple of 8, then , then (A18) and (A19) become:According to (A24) the range of k is . By setting and in (A24) it follows that and belong to , i.e., the states and belong to the orbit of B. Proposition A3 asserts that F fixes these kets. What remains is to prove that F fixes no other state in the orbit of B. If F also fixes some ket other than and , then there exists a k, but , such thatThe fact that , implies that . Therefore, either or . The former equation leads to and the latter to , which correspond to kets and , respectively. No other values for k arise and, thus, F fixes no other state.
- If n is not a multiple of 8, there are two cases to consider.
- n is a multiple of 4, but not a multiple of 8. This implies that , where m is a positive odd integer. Therefore, (A18) and (A19) become:According to (A24), the range of k is . If there exists a k such that , then k must be equal to , which is absurd. Similarly, the existence of a k such that is impossible because then k must be equal to . The previous calculations establish that and do not belong to the orbit of B. Moreover, F fixes no ket in the orbit of B. If F did fix some ket, then there would be a k, , such thatThe fact that , implies that . Therefore, either or . The former equation leads to and the latter to , which are both impossible. Hence, F fixes no state from the orbit of B.
- n is even, but not a multiple of 4, then it can be proved in an analogous manner that in this case too F fixes no state from the orbit of B.
- 1.
- Q has exactly two classes of winning and dominant strategieseach containing 16 equivalent strategies.
- 2.
- The winning state paths corresponding to and are
- 3.
- Picard has no winning strategy.
- The two classes of winning strategies of Q, , and , which were establish by Theorem A3, are also present in every dihedral group .If in some dihedral group larger than there exists a third class that contains the strategy , then the action of must drive the coin into some state other than or . However, (A9) asserts that , which, in view of (A43), implies that , a contradiction. Hence, there are just two classes of winning strategies and . It remains to prove that and do not contain new winning strategies. Let be such a “new winning” strategy, other than those established in . If is a rotation other than and that sends the coin to state , then, according to (13), there exist and such that . Therefore,The fact that , implies that . Hence, either or . The former equation leads to and the latter to . This means that or , which contradicts the assumption that is different from and . Similar contradictions arise by assuming that is a reflection different from H or or that drives the coin to state . Thus, other than those already existing in , there are no more winning strategies for Q in the larger dihedral groups .
- Based on the above analysis it is straightforward to see that (A50) holds.
- By Definition 1, Picard has no winning strategy.
- 1.
- Q has exactly two classes of winning and dominant strategies, each containing infinite equivalent strategies:where
- is one of or ,
- is one of or ,
- is one of or ,
- is one of or , and
- are possibly different real parameters.
- 2.
- The winning state paths corresponding to and are
- 3.
- Picard has no winning strategy.
- The two classes of winning strategies of Q, and , which were established by Theorem A3, are present in . However, they now contain infinitely many equivalent strategies. To see why this is so, consider a winning strategy in . To this strategy corresponds the collection of infinitely many strategies , where . Every strategy in this collection is equivalent to because the action of every operator on a ket is the same as the action of on . This holds for every strategy in . Hence, in the two classes and contain infinitely many equivalent strategies.Assuming that there exists a third class , let be a strategy in this class. Then the action of must drive the coin into some state other than or . However, (A9) asserts that , which, in view of (A51), implies that , a contradiction. Consequently, there are just two classes of winning strategies and . It remains to prove that and do not contain new winning strategies, i.e., strategies that are not of the form stated in (A53). To arrive at a contradiction, suppose that is a “new winning” strategy. If , then its columns form an orthonormal basis for because it is a unitary operator. This means that they satisfy the following relations:If sends the coin to state , assuming that is not of the form or , thenTogether (A58) and (A57) imply thatIn view of (A59), (A57) becomesAll complex numbers of the form , where , are solutions of the Equation (A60). By choosing and setting , becomes . Hence, is in fact , which means that is of the form or , in stark contrast to the initial assumption. Similar contradictions arise by assuming that drives the coin to state . Thus, the resulting conclusion is that other than the strategies described by (A53), there are no more winning strategies for Q.
- Based on the above analysis it is straightforward to see that (A54) holds.
- By Definition 1, Picard has no winning strategy because if Q employs one of their winning strategies, Picard has probability to win the game.
Appendix A.4. Proofs for Section 6
- , in which case if Q employs the strategy , the state of the coin prior to measurement will either be , if the initial state of the coin is , or , if the initial state of the coin is . This is because , so the coin will stay in one of these states no matter which strategy Picard uses. When the coin is measured, Picard will have exactly probability to win irrespective of which is their target state. Thus, Picard does not possess a winning strategy because, by Definition 1, a winning strategy means that he wins the game with probability .
- , where again, if the same strategy is used by Q, it will prevent Picard from surely winning the game. The coin will be in one of its basis states (which one depends on the initial state and Picard’s first move) when Q acts on it for the first time. His action will drive the coin to state (if the coin was at state ) or (if the coin was at state ). This will be the state of the coin prior to measurement no matter which strategy Picard uses because . When the coin is measured, Picard will have exactly probability to win irrespective of their target state. Hence, Picard does not have a winning strategy because, by Definition 1, a winning strategy means that he wins the game with probability .
- , in which case Q has a winning strategy. If the initial state is the same as Q’s target state, then Q’s winning strategy is ; if it is different, then Q’s winning strategy is . In this case Picard has precisely probability to win, so Picard certainly does not possess a winning strategy.
- , where once more the strategy can be used by Q to prevent Picard from surely winning the game. The coin will be in one of its basis states (which one depends on the initial state and Picard’s first move) when Q acts on it for the first time. His action will drive the coin to state (if the coin was at state ) or (if the coin was at state ). This will be the state of the coin prior to measurement because . When the coin is measured, Picard will have exactly probability to win irrespective of which is their target state. Therefore, Picard does not have a winning strategy because, by Definition 1, a winning strategy means that he wins the game with probability .
- , where n is even and both Picard and Q make moves. Assuming to the contrary that there exists a winning strategy for Q, Definition 1, implies that for every strategy of Picard, Q wins the game with probability . Since this holds for every strategy of Picard, it must also hold for the strategies and . The former implies that after Q’s last action the coin must be at the basis state , whereas the latter implies that after Q’s last action the coin must be at the opposite basis state, which is absurd. Thus, Q does not possess a winning strategy.
- , where n is odd, Q makes moves and Picard make moves. Let be a winning strategy for Q. By Definition 1, if Q employs , he will win the game with probability no matter which strategy Picard chooses. If Picard uses , then after Q’s last action the coin must be at the basis state . On the other hand, if Picard uses , then after Q’s last action the coin must be at the opposite basis state. This contradiction proves that Q does not possess a winning strategy.
- , where n is even and both Picard and Q make moves. Assuming to the contrary that there exists a winning strategy for Q, then Definition 1 implies that for every strategy of Picard, Q wins the game with probability . Since this holds for every strategy of Picard, it must also hold for the strategies and . The former implies thatwhere . Since the composition of unitary operators produces a unitary operator, C is unitary. On the other hand, the latter implies thatIf , then , whereas if , then . By combining this last result with (A61) and (A62), it follows thatwhich is impossible because C is unitary. Thus, Q does not possess a winning strategy.
- , where n is odd, Q makes moves and Picard makes moves. Let be a winning strategy for Q. By Definition 1, if Q employs , he will win the game with probability . If Picard uses , then after Q’s last action the coin must be at the basis state . On the other hand, if Picard uses , then after Q’s last action the coin must be at the opposite basis state. This contradiction proves that Q does not possess a winning strategy.
References
- Maschler, M. Game Theory; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Dixit, A. Games of Strategy; W.W. Norton & Company: New York, NY, USA, 2015. [Google Scholar]
- Myerson, R. Game Theory; Harvard University Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Meyer, D.A. Quantum strategies. Phys. Rev. Lett. 1999, 82, 1052. [Google Scholar] [CrossRef]
- Eisert, J.; Wilkens, M.; Lewenstein, M. Quantum games and quantum strategies. Phys. Rev. Lett. 1999, 83, 3077. [Google Scholar] [CrossRef]
- Wang, X.B.; Kwek, L.; Oh, C. Quantum roulette: An extended quantum strategy. Phys. Lett. A 2000, 278, 44–46. [Google Scholar] [CrossRef]
- Ren, H.F.; Wang, Q.L. Quantum game of two discriminable coins. Int. J. Theor. Phys. 2008, 47, 1828–1835. [Google Scholar] [CrossRef]
- Salimi, S.; Soltanzadeh, M. Investigation of quantum roulette. Int. J. Quantum Inf. 2009, 7, 615–626. [Google Scholar] [CrossRef]
- Anand, N.; Benjamin, C. Do quantum strategies always win? Quantum Inform. Process. 2015, 14, 4027–4038. [Google Scholar] [CrossRef]
- Zhang, P.; Zhou, X.Q.; Wang, Y.L.; Liu, B.H.; Shadbolt, P.; Zhang, Y.S.; Gao, H.; Li, F.L.; O’Brien, J.L. Quantum gambling based on Nash-equilibrium. NPJ Quantum Inform. 2017, 3. [Google Scholar] [CrossRef]
- Andronikos, T.; Sirokofskich, A.; Kastampolidou, K.; Varvouzou, M.; Giannakis, K.; Singh, A. Finite Automata Capturing Winning Sequences for All Possible Variants of the PQ Penny Flip Game. Mathematics 2018, 6, 20. [Google Scholar] [CrossRef]
- Giannakis, K.; Theocharopoulou, G.; Papalitsas, C.; Fanarioti, S.; Andronikos, T. Quantum Conditional Strategies and Automata for Prisoners’ Dilemmata under the EWL Scheme. Appl. Sci. 2019, 9, 2635. [Google Scholar] [CrossRef]
- Rycerz, K.; Frackiewicz, P. A quantum approach to twice-repeated 2 × 2 game. Quantum Inf. Process. 2020, 19. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Aharon, N.; Silman, J. Quantum dice rolling: A multi-outcome generalization of quantum coin flipping. New J. Phys. 2010, 12, 033027. [Google Scholar] [CrossRef]
- Meyer, D.A.; Blumer, H. Parrondo games as lattice gas automata. J. Stat. Phys. 2002, 107, 225–239. [Google Scholar] [CrossRef]
- Giannakis, K.; Papalitsas, C.; Kastampolidou, K.; Singh, A.; Andronikos, T. Dominant Strategies of Quantum Games on Quantum Periodic Automata. Computation 2015, 3, 586–599. [Google Scholar] [CrossRef]
- Andronikos, T. Conditions that Enable a Player to Surely Win in Sequential Quantum Games. Preprints 2021, 2021040298. [Google Scholar] [CrossRef]
- Kastampolidou, K.; Nikiforos, M.N.; Andronikos, T. A Brief Survey of the Prisoners’ Dilemma Game and Its Potential Use in Biology. In Advances in Experimental Medicine and Biology; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 315–322. [Google Scholar]
- Theocharopoulou, G.; Giannakis, K.; Papalitsas, C.; Fanarioti, S.; Andronikos, T. Elements of Game Theory in a Bio-inspired Model of Computation. In Proceedings of the 2019 10th International Conference on Information, Intelligence, Systems and Applications (IISA), Patras, Greece, 15–17 July 2019. [Google Scholar]
- Kastampolidou, K.; Andronikos, T. A Survey of Evolutionary Games in Biology. In Advances in Experimental Medicine and Biology; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 253–261. [Google Scholar]
- Artin, M. Algebra; Pearson Prentice Hall: Hoboken, NJ, USA, 2011. [Google Scholar]
- Dummit, D.; Foote, R. Abstract Algebra; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Lovett, S. Abstract Algebra: Structures and Applications; Taylor & Francis: Abingdon, UK, 2015. [Google Scholar]
- Meier, J. Groups, Graphs and Trees; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Meyer, C.D. Matrix Analysis and Applied Linear Algebra; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Anton, H.; Rorres, C. Elementary Linear Algebra: Applications Version, 11th ed.; Wiley Global Education: Hoboken, NJ, USA, 2013. [Google Scholar]
- Hodge, J.K. Abstract Algebra; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013. [Google Scholar]
- Machì, A. Groups; Springer: Milan, Italy, 2012. [Google Scholar]
- Hall, B. Quantum Theory for Mathematicians; Graduate Texts in Mathematics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Beecher, J. Algebra and Trigonometry; Pearson: London, UK, 2016. [Google Scholar]








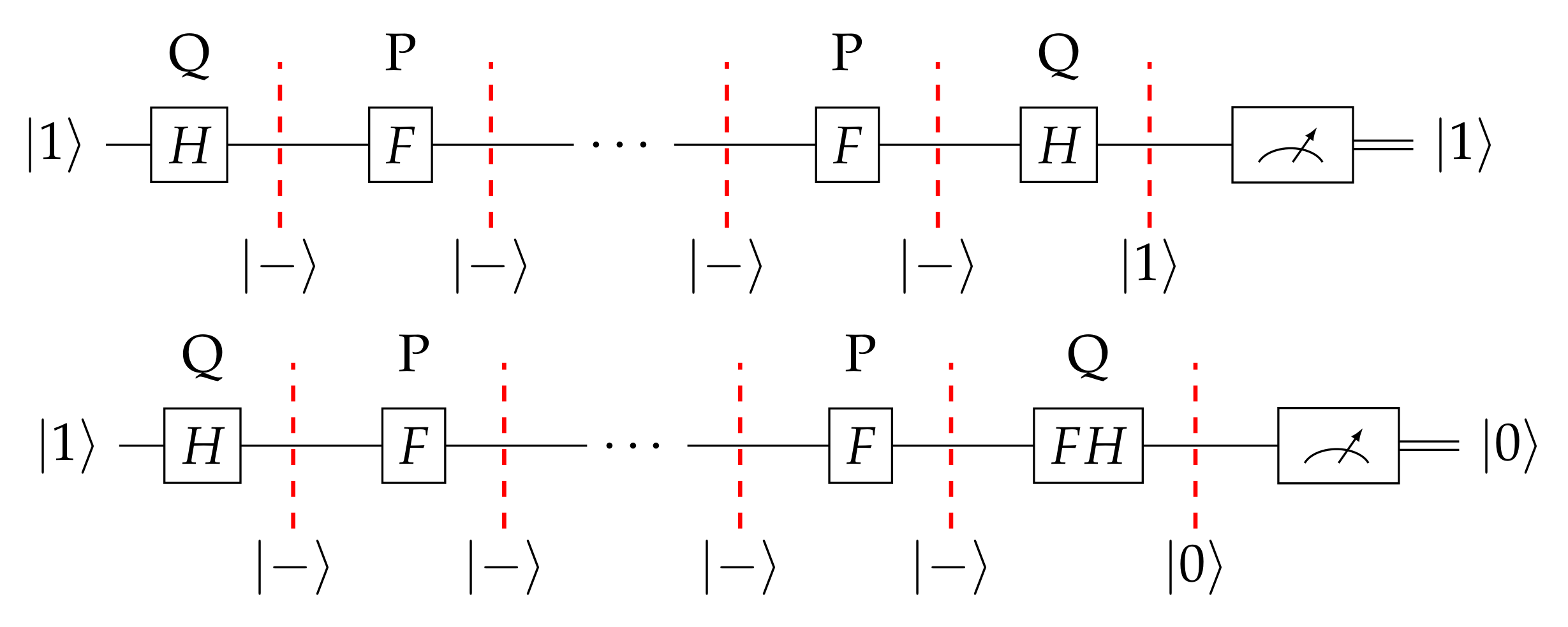
| The Evolution of the | ||||
|---|---|---|---|---|
| Initial State | Round 1 | Round 2 | Round 3 | |
| Ambient Group | Is PQG Playable | WS for Picard | WS for Q |
|---|---|---|---|
| No () | — | — | |
| Yes (classical coin tossing) | No | No | |
| No () | — | — | |
| No () | — | — | |
| No () | — | — |
| The Ambient Group is | ||||
|---|---|---|---|---|
| Initial State | Round 1 | Round 2 | Round 3 | |
| The Ambient Group is() | ||||
| Initial State | Round 1 | Round 2 | Round 3 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andronikos, T.; Sirokofskich, A. The Connection between the PQ Penny Flip Game and the Dihedral Groups. Mathematics 2021, 9, 1115. https://doi.org/10.3390/math9101115
Andronikos T, Sirokofskich A. The Connection between the PQ Penny Flip Game and the Dihedral Groups. Mathematics. 2021; 9(10):1115. https://doi.org/10.3390/math9101115
Chicago/Turabian StyleAndronikos, Theodore, and Alla Sirokofskich. 2021. "The Connection between the PQ Penny Flip Game and the Dihedral Groups" Mathematics 9, no. 10: 1115. https://doi.org/10.3390/math9101115
APA StyleAndronikos, T., & Sirokofskich, A. (2021). The Connection between the PQ Penny Flip Game and the Dihedral Groups. Mathematics, 9(10), 1115. https://doi.org/10.3390/math9101115






