Abstract
For primary school students, the difficulty in solving mathematical problems is highly related to language capacity. A correct solution can only be achieved after being able to deal with different abstract concepts through several stages: comprehension, processing, symbolic representation and relation of the concepts with the right mathematical operations. A model linking the solution of the mathematical problems (PS) with the mental representation (MR) of the problem statement, while taking into account the level of the students (which has influence in the linguistic abilities), is presented in this study. Different statistical tools such as the Analysis of Covariance (ANCOVA), ROC curves and logistic regression models have been applied. The relation between both variables has been proved, showing that the influence of MR in PS is similar in the different age groups, with linking models varying just in the constant term depending on the grade level. In addition, a cutoff in the mental representation test is provided in order to predict the student’s ability in problem resolution.
1. Introduction
International programs for evaluating mathematical literacy are based on a common conceptual and methodological framework. They provide indicators that help in the development of educational policies. The relative position of each country according to the average score obtained in these tests is one of the most significant indexes for public opinion. In the last fifty years, the ranking position in these tests has become a factor that encourages governments to adopt educational policies similar to the countries that appear at the top of it [1,2]. In addition, European Union members have expressed their political commitment to reduce the number of low achievers in this area.
Several organizations such as NAEP (National Assessment of Educational Progress), PISA (Program for International Students Assessment) or TIMSS (Trends in International Mathematics and Sciences Study) report that school performance in general, and problem solving skills in particular, are poor and unsatisfactory in most of the countries. Furthermore, the mechanisms of evaluation at regional, city or school level reveal the same conclusions.
Regarding the evaluation of mathematical learning, the studies designed by these international organizations are mainly focused on different aspects. The principal goal of TIMSS is to evaluate “what they know”, while the purpose of PISA is to determine “what they can do with their knowledge”. The TIMSS report is based on the curriculum designed by each country or educational system. They collect data to evaluate the curriculum achievements of the students and how the teachers accomplish the objectives [3]. By contrast, The PISA report does not focus directly on any particular aspect of the curriculum but instead tries to check whether a 15-year-old student is able to apply the mathematical knowledge in real situations.
The National Council of Teachers of Mathematics (NCTM) has established that problem solving should be the core of school mathematics instruction [4]. This concern is also in the Cockcroft report [5], which is a vision of the educational system in England and Wales commissioned by the British Ministry of Education in the early 1980s. This report notes that learning mathematics requires a lot of work and practice. It establishes that students have to spend time on discussion and comprehension before being ready to address the simplest problems. Even at that time, the Cockcroft report is concerned about the reduction of the time assigned to teach mathematics at schools due to the introduction of new fields in the curriculum. In the conclusions and recommendations, the report establishes that, at any level, the teaching of mathematics must include:
- Theoretical teacher explanation.
- Discussion among the teacher and the students.
- Appropriate practical work.
- Consolidation and practice of basic skills and routines.
- Troubleshooting, including the application of mathematics to real-life situations.
In the first years of school, students are still learning and acquiring vocabulary, which causes a difficulty understanding the semantic structure of the mathematical problems statements. It is clear that a lower language comprehension reduces the ability to correctly solve mathematical problems. At that development stage, children are able to solve real world problems [6], but academic language is acquired slowly, long after the children develop the domain of practical everyday language [7].
A problem can be defined as a situation that presents difficulties for which there are no obvious solutions. More specifically, in [8], a problem is defined as a quantitative situation (or not) that needs a solution where the individuals involved in its resolution do not know the specific way to achieve it. For the authors of [9], the real meaning of problem resolution is applying the knowledge previously acquired.
Arithmetic problems are defined as those where the data are represented by quantities and relationships between them. In these problems, the questions refer to one or more quantities or the numerical connection among them. These problems are the first to appear in the mathematics curriculum at schools, and they are essential throughout their entire school life; therefore, primary school teachers are concerned about the good understanding of them.
The degree of difficulty of the problem statement varies according to several factors, for example, the type of language (academic or colloquial), the presence of irrelevant data, the scale of the quantities, the need to carry out more than one operation for reaching the solution, the comprehension of the vocabulary, etc.
However, it also depends on the orientation of the statement. For instance, consider the three following problems:
- P1.
- In a vase there are three red flowers and five yellow flowers. How many flowers are there in the vase?
- P2.
- Mary has taken three flowers from a vase, and Peter five. How many flowers have they taken?
- P3.
- Peter took three wilted flowers from a bouquet of Mary. Now the bouquet has five flowers; how many flowers did the bouquet have at the beginning?
Although the solution is a identical simple sum in the three problems, students resolve P2 and P3 correctly one or two years later than P1.
1.1. Classification of Additive Problems
Additive problems are those for which the solution is attained by addition and/or subtraction operations. In this paper, the analysis will focus on problems that require just one operation to reach the correct solution. Additive problems are characterized by their syntactic, logical and semantic structure. Concerning this structure, the problems can be essentially classified in three types, namely change, combination and comparison [10,11,12,13,14,15,16]. However, some authors, such as [17], distinguish a fourth category called equality. Then, we deal with various types of problems. In the mathematical tests the students passed, the following four types of problems were considered:
- Change. These problems are characterized by an action that produces a change (increase or decrease) in an initial amount. If the problem is based on the sum operation, , it leads to three different types of problems depending on which variable is the unknown: a, b or c. In a similar way, when a subtraction operation is involved, , there are three other different types of problems also depending on which variable is the unknown.
- Combination. In these problems, there are two amounts that can be considered isolated or being a part of a whole without any action between them. We distinguish two types of problems: when the question is about the set (the union or total) and when the question is about a subset.
- Comparison. These are problems where there is a comparative action between two different quantities. The problem could be either to compute the difference between them or to find an unknown quantity related to the other. When using the words “more” or “less” in the statement of the problem, two different problems (one with “more” and the other with “less”), asking either for the difference, the comparison or the reference quantity appear. This means six different problems for this case.
- Equality. This category involves elements from change and comparison problems. The statement of the problems includes an implicit action based on the comparison of two different quantities. As in previous cases, six different problems are obtained.
The interpretation of the problems requires a series of linguistic skills that implies the comprehension and assimilation of a set of concepts, their symbolic representation and the application of general rules translated into mathematical language. A low level of problem resolution is related with the inability of the students to understand and represent the mathematical concepts and to select the appropriate mathematical operations. The translation from natural to mathematical language is not straightforward: comprehension and knowledge of the relationships between the two languages are needed. The stage of formal operations is regarded as the highest level of human reasoning [18,19,20]. More recent studies such those in [21] confirm that the use of formal thought is low in general.
The relationship between levels of thinking and performance on mathematical problem solving is explored by the authors of [22]. They conducted an experiment mixing two glasses of water at different temperatures, and the students had to predict the final temperature of the water. In order to respond correctly to this question, it the use of certain mathematical strategies is necessary, and they found that the ability to use them increases with age.
Two important factors contribute to the correct resolution of the problems. In first place is the ability to understand the statement of the problem; that is, the students must be able to construct a mental representation of the relevant elements in it [23,24,25]. This mental representation is essential in planning the steps to reach the correct solution and to execute the appropriate mathematical operations. The second important skill needed to solve problems successfully is the influence of mental representation [25,26,27]. Reading comprehension, and therefore semantic-linguistic abilities, are especially helpful in dealing with problem resolution [13,23,28,29]. The problems of linguistic comprehension appear, for example, when the students have difficulties connecting the problem statement described as “less than” and its solution when this last one is attained by a sum operation.
Taking this fact into account, in this work, we propose a test of additive problems using expressions close to practical everyday language in order to facilitate the understanding of the problems. With the collected data the main goals are the following:
- To study the influence of mental representation in the resolution of additive problems for children from 6 to 12 years old.
- To find a model relating language skills and academic course with problem resolution (one-operation problems with either addition or subtraction).
- To quantify the influence of mental representation of problems separately from the cognitive level of the students according to their grade.
- To provide a cutoff in the mental representation test score as a tool for teachers to predict the ability of the students in solving additive problems correctly.
2. Materials and Methods
In this work, the relation between mental representation and problem solving in 6–12-year-old children (which corresponds to the first to sixth courses) will be studied, as well as the evolution of this relationship with age.
A population of 178 students from a Spanish public school with medium-low socio-economic level was tested. It is well known that the reading level, along with the knowledge acquired in previous courses and mental-representation capacity, have a great influence in problem resolution. Since the subjects were collected from different levels, it would be sensible to consider these blocks in the model when studying the relationship between Problem-Solving (PS )and Mental Representation (MR) variables. The sample includes students from first to sixth grade (6 to 12 years old), and thus, three groups of students were considered. The first group, , includes the youngest students (6 to 8 years old) who are learning to read and acquiring abilities of mental representation and understanding the operations of addition and subtraction. It has a size of 74. The group contains 40 students from third and fourth grade (8 to 10 years old), who are able to read and perform operations without difficulties. In fact, they also understand problems with multiplication and division operations. comprises students from fifth and sixth grade (10 to 12 years old), totaling 64. In this group, the students should have the skills to transcript the statement of the problems to mathematical language.
In order to measure the abilities of the students in solving additive problems, a test composed of twenty different types of problems was produced, following the additive problem classification in Section 1.1 and the type of problems described in [30]. The students were asked complete the test in 50 min sessions, and the grading was focused in:
- Identifying non-redundant data.
- Identifying the question.
- Operating and expressing the solution correctly.
The test score ranged from 0 to 10, and two variables were produced: PS, which measures the correct resolution of the problem, and MR, which represents the ability of understanding the statement of the problem. It evaluates the correct writing of the problem statement and the choice of the right mathematical operation, even if the final solution is incorrect. Figure 1 and Table 1 show a summary of these variables. It can be seen that PS shows many outliers, mainly in group , and that the groups in MR could follow a linear trend, which indicates that they are not linearly independent and this is one of the requirements of ANCOVA.
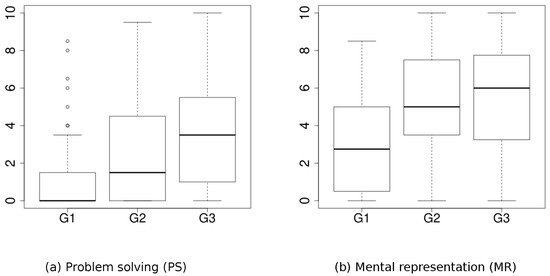
Figure 1.
Problem Solving and Mental Representation box plots.

Table 1.
Summary of Problem-Solving (PS) variables.
2.1. Mathematical Background
To achieve the objectives of this study, the mathematical background to determine a model linking problem solving and mental representation according to the age of the students is presented in Section 2.2. In Section 2.3, a practical tool for teachers to predict the problem-solving skills of a student from their score in the mental representation test is provided.
2.2. Influence of Mental-Representation Level in Problem-Solving
Analysis of covariance (ANCOVA) allows the analysis of the effects of nominal variables (factors) and quantitative variables (covariables) on a quantitative dependent variable (response variable). It is a combination of linear regression and classical analysis of variance that detects the portion of variability of the model explained by the factors [31,32]. In the analysis carried out in this paper, the dependent variable, Y, is the ability of the students to solve problems correctly; the covariable, X, is the score in mental representation of the problems; and the factor, G, defines the groups of students.
From now on, a linear relationship between the covariates and the response variable will be assumed (a variable transformation could be made in other case). In order to determine the relationship between the variables, three models are considered:
- M1:
- Simple linear regression model. Using all the data but not taking into account the existence of groups:
- M2:
- Multiple linear regression model including a categorical variable. A multiple linear regression model adding fictitious variables () accounting for the effects of the different groups. This is the right model when the relationship between X and Y is identical for all the groups, but for a scalar difference from the mean response:where k is the number of groups and takes the value 1 when Y belongs to group i and 0 otherwise. This is equivalent to the independence between covariate X and treatment G.
- M3:
- Simple linear regression models in each group. This is the appropriate model when the relationship between X and Y is different in each group beyond the intercept term, that is, when the coefficients are different:
The most suitable model for the data is decided through the following steps:
- Step 1 (Compare M1 to M3): The first test compares the variance explained by models M1 (without groups) and M3 (the most complex model that takes the groups into account) in order to determine whether the groups are significant or not in the relationship between the two quantitative variables. The null and alternative hypotheses of the test are, respectively:
- :
- The groups are non significant; that is, the gain of variability explained when considering different linear regressions in the groups is small.
- :
- It is necessary to take the groups into account.
The F-statistic to conduct this test, , is described in (4). - Step 2 (Select model) If the test in Step 1 is not significative, model M1 should be selected, and finishing the groups is not needed. Otherwise we conclude that the existence of the groups is important for the variability, and since there are two models that take into account the groups (M2 and M3), they should be compared in order to decide which one is the most convenient (Step 3).
- Step 3 (Compare M2 versus M3): In the case of rejecting the null hypothesis in Step 1, it should be checked whether the M2 model is enough for fitting the data or if the individual linear models in M3 are necessary. The test hypotheses are in this case as follows:
- :
- The relation between the quantitative variables Y and X is the same in every group; that is, the coefficient of X in the model, b, does not depend on the groups. M2 is the right model.
- :
- There is interaction between the groups and the regressor X; that is, the coefficient of X in the regression line varies with the groups. Thus, model M3 is the best one.
That is, the coefficient of X in the regression line varies with the groups. Thus, model M3 is the best one.The F-statistic to conduct this test, , is described in (4). - Step 4 (Select model): If the test in Step 3 is significant, then model M3 should be chosen; otherwise, model M2 should be chosen.
The F-statistics for the tests are
where is the sum of squares of the residuals of model i (that is, the non-explain variability) and is the degrees of freedom of these residuals. follows an F-distribution with and degrees of freedom.
In addition, the data should verify the following requirements:
- Both the dependent and the explanatory variables should be continuous.
- The grouping factor is composed of two or more categories of independent groups.
- The observations must be independent, for example, selecting different people.
- There should not be significant atypical values; this could have a negative effect on the validity of the results.
- For each category of the independent variable, the residuals should follow a normal distribution. This hypothesis may be violated in a certain way while the tests still provide valid results. In order to check normality, Shapiro–Wilk or Kolmogorov–Smirnov tests and P–P or Q–Q charts can be made.
- Homoscedasticity (similar variances of the dependent variable for the different groups) is assumed. This requirement can be checked, for instance, by the Levene test. Even when the hypothesis is violated, the above tests are still reliable provided that the groups sizes do not differ very much (none of the groups is twice the size of any other one).
- The relationship between X and Y should be linear. This assumption can be tested by a simple linear regression analysis between the covariate X and the response Y.
2.3. Predicting Problem-Solving Ability
When the aim is predicting whether or not the student will pass the Problem-Solving test (PS) from the corresponding mark in the Mental-Representation test (MR), such a problem falls into the field of classification problems. In these studies, the objective is dividing the students into groups, depending on the score on a univariate continuum. In this case, there will be two groups: the students who are expected to pass the PS test and the ones who will probably not.
The final aim is to construct a score function such that members of the two classes have distinctly different sets of scores, thereby enabling the classes to be clearly distinguished. It will be assumed that the scores have been designed in such a way that members of class P (Positive, passing the PS test) tend to have large scores and members of class N (Negative, failing the PS test) tend to have small scores. The class assignment or classification is then made by comparing this score with a threshold: if the score is above the cutoff, the students are assigned to one class, and when the score is below the threshold to the other. Objects with scores that are precisely equal to the threshold (not a common occurrence for continuous data) can be assigned arbitrarily.
In the situation studied here, the MR test, X ranging from 0 to 10 is used, and a logistic regression model plays the role of the function S. The logistic regression model has a discrete response variable and a continuous independent variable. The binary response variable, Y, takes the value 1 if the student passes the PS test and 0 in the other case. The prediction of a student passing or not passing the PS test from the value obtained in the MR test X will be made in terms of probability, , using a logistic function
After estimating model (5), in order to distinguish whether a student is classified in any of the groups, a probability cutoff is needed. Once this threshold has been fixed and the predictions made, every datum can be classified as Positive/Negative and Real/Prediction as in Table 2, where A and D are the number of the students of each type correctly classified, and B, C count the wrong predictions.

Table 2.
Summary of training data classification.
Thus, the true positive rate given by the model, Sensitivity, is and the true negative rate, Specificity, is .
The Receiver Operating Characteristic (ROC) curve (see Figure 2) is a graphical representation of Sensitivity against (1-Specificity) [33,34] for every possible cutoff value.
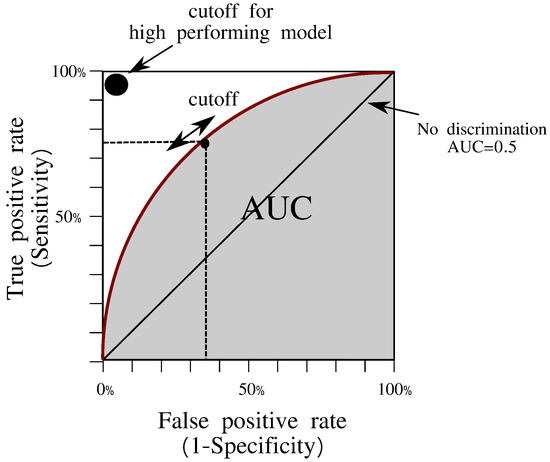
Figure 2.
ROC curves and area under curve (AUC).
The standard criterion for evaluating the performance of the logistic classification model is measuring the area under the curve (AUC), in grey in Figure 2, which indicates the level of separation of the two groups of data. The AUC may vary from , which means a random classification model represented by a diagonal ROC curve in the unit square, to AUC = 1, which corresponds to a perfect classification model. An AUC index between and is considered a poor discrimination, between and is acceptable and greater than that is excellent [35]. The optimal classification threshold is often chosen to be the Youden index, which is defined as the maximum difference between the true positive rate and the false positive rate, that is, between Sensitivity and (1-Specificity). It can be interpreted as the maximum difference between populations N and P, and graphically speaking, it corresponds to the maximum vertical distance between the ROC curve and the diagonal.
3. Results
3.1. Models Relating PS with MR
A study trying to model the students problem-solving capability with the results obtained in the Mental Representation test was performed. First of all it was necessary to screen the data at disposal, since from the preliminary results, it seems that the information in Group 1 was somehow unclear. Moreover, Figure 3 shows the scatterplot of PS vs. MR by groups, including the (tentative) regression line for each group. The heterogeneity in is very high, showing many outliers as noted above. This group comprises the period in which more differences of level among students are noticed, for various reasons including maturity, origin and educational background, producing many outliers, great variability and thus low representability of the measures of central tendency. The asymmetry (see Figure 1) and the presence of many zero values are clear indications of lack of normality as well. Therefore, from now on, group will be discarded, and the study will be performed for and , totaling 104 observations.
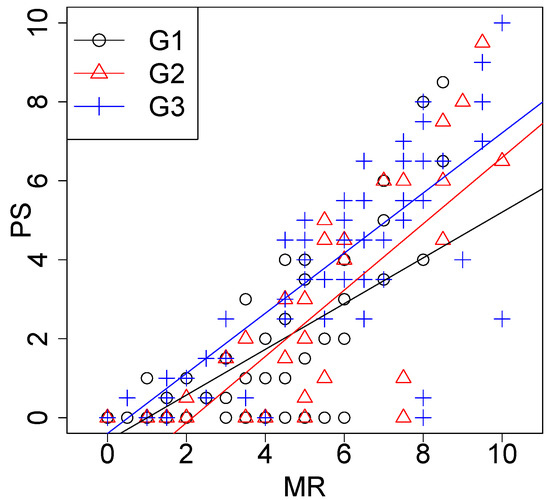
Figure 3.
Problem Solving (PS) versus Mental Representation (MR).
Considering only the data in these two groups, let us note the following:
- The dependent variable and covariate are continuous.
- The independent variable, MR, has two independent categories. The observations are independent since the groups are disjoint.
- There are no atypical values in the and groups.
- The residuals of linear models are approximately normal for groups and .
- The Levene test for checking homocedasticity returns a p-value of 0.419, and thus the homogeneity of variances cannot be rejected.
- The assumption about the linear relationship between PS and MR is corroborated by a simple linear regression analysis.
Following the reasoning in Section 2.1, the following models for data in groups and were obtained.
- M1:
- Simple linear regression model.with degrees of freedom, residual sum of squares, and determination coefficient .
- M2:
- Multiple linear regression model including a categorical variable.with degrees of freedom, and . As explained in (2), is a dummy variable taking values 1 for group and 0 for ; thus, the resulting model has the same slope for both groups, 0.789, a but different intercept term (−1.545 and −0.55, respectively). Therefore, the mean response for samples in is points lower than for .
- M3:
- Simple linear regression model by group.A linear regression model in each one of the groups is computed.
- :
- Model 3 in group:
with 38 degrees of freedom, and .- :
- Model 3 in group:
with 62 degrees of freedom, and , totaling degrees of freedom and .
Now, let us choose the most suitable model following the procedure described in Section 2.1.
Step 1 (Compare M1 versus M3): Computing the test in (4)
and comparing with a Snedecor-F distribution with 2 and 100 degrees of freedom, the p-value of the test is . Consequently, the null hypothesis can be rejected, and we can conclude that the groups are important and should appear in the model describing the data. Now, the question is to decide how they influence the response variable (Step 3).
Step 3 (Compare M2 versus M3): The statistic test (4)
produces a p-value of and shows that there is no significative gain in using model 3; thus, model 2 in (7) is finally selected.
The ANOVA for checking independence between covariate and factor G is not significative (), which agrees with the results obtained. Table 3 shows the mean, standard deviation and number of students in each of the groups for the explanatory variable.

Table 3.
Descriptive statistics of the variable mental representation for groups 2 and 3.
3.2. Classification Models for the Groups
From the Mental Representation test marks, logistic regression models for every group were computed (LR Models in Table 4). In Figure 4, the LR models and the MR variable histograms for the students that have passed the PS test (top) and for those who do not (bottom) are shown. In a variable with two separated classes, the histograms would not be overlapped and an MR value in between them would determine a cutoff. However, as this is not the case, the ROC technique is used to choose a cutoff by maximizing the number of students correctly classified. The coordinates of the ROC functions are the percentage of students correctly classified by the logistic models for different cutoffs (Figure 5).

Table 4.
Logistic regression models.
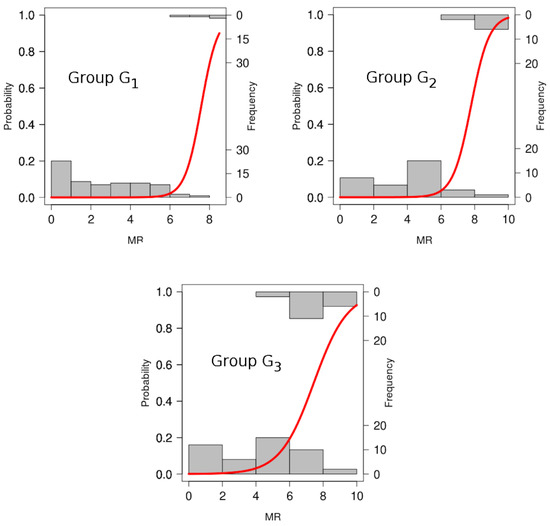
Figure 4.
Logistic Regression Models.
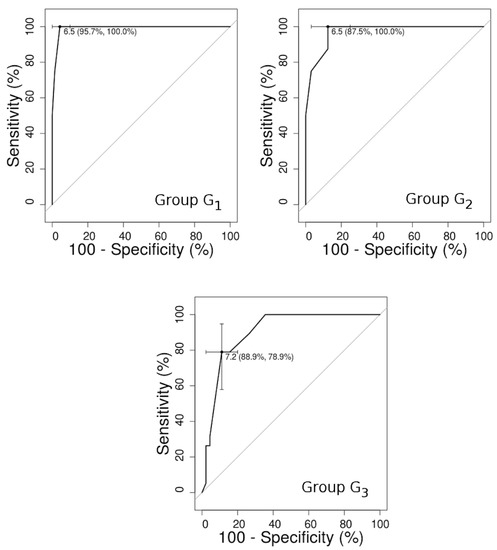
Figure 5.
ROC graphs.
The first coordinate is, for each threshold, the percentage of students passing the PS test who are correctly classified according to the model (true positive rate, sensitivity), and the second one is the percentage of the students not passing the PS test who are wrongly classified (false positive rate, 1-specificity). The optimum maximizing these quantities is shown in Figure 5 and in Table 4.
Groups and have a cutoff of ; i.e., it is supposed that a student obtaining 6.5 or a greater score in the MR test will probably pass the PS test. Nevertheless, the percentage of students passing the PS test in groups and is low. In group , the MR cutoff is , higher than in previous cases. The area under the ROC curve (AUC) is a widely used measure that gives the probability of classifying data correctly. All the models present an AUC over which denotes a good discrimination (Table 4).
All the computations were made with R version 3.2.3 and the ROC curves using pROC package [36].
4. Discussion
The relationship between reading comprehension and capacity for solving mathematical problems has long been considered and studied, mainly from the educational and organizational point of view. In the present work, some models relating both variables in primary school students were discussed from a statistical point of view for children in the last four levels. The study of the particular case of the smallest students, the origin of their heterogeneity and the design of specific tests that can measure the potential influence of new variables opens a new line of research. This is a work in progress.
In the case of restraints on the observations that can be taken, or an observational cost (time, money) and a limiting budget that prevents obtaining information from the whole population under study, a convenient choice of the “most informative” experimental units could be performed before taking samples, employing Optimal Design of Experiments techniques (see, for instance, [37]). For instance, when the population is composed of a great number of schools, teachers in the respective schools are not available for this task, and there is a reduced number of persons in charge of making the study, it might be unfeasible to get results from every place. The same could be applied to different classrooms in the same school, or even different students within the same class, when the tests cannot be performed at the same time for every student and there is a limited time to carry out the study. In such situations, a previous filter of the experimental units (schools/classrooms/students) should be made in order to choose the ones that are expected to provide more information. There are different optimality criteria, and the choice of a specific one depends on the objectives of the practitioners, but it is well known that usually, for a linear regression model such as the one shown in this work, the most informative points are those in the extremes of the observational interval. Therefore, in a study similar to the one performed here, in the case that it is not possible to get information for every experimental unit of the population, it would be advisable to choose those that are expected to produce the highest and smallest marks in the tests. Since usually the ‘best’ (and ‘worst’) institutes/classrooms/students get good (and bad) marks in most disciplines, the level of the experimental units can be estimated from the scores obtained in other courses and from this estimation select the extreme cases for the study.
5. Conclusions
A model relating the ability for problem solving (PS) and mental representation (MR) of primary school students has been studied. From an initial cohort with ages ranging from 6 to 12 years, three groups were initially considered, but after some preliminary tests, the group containing the youngest ones was discarded due to huge differences in the problem-solving scores of children of that age, differences that could be explained by another set of variables such as maturity and preliminary education.
The study of the remaining two groups has shown a significant relationship between the two variables in both groups. The main characteristic of the final model is that the division of groups influences just the mean value, but it has no interaction with the explanatory variable MR, and therefore, the coefficient of this variable is the same for the regression lines in both groups. As expected, the oldest students (group 3) have better scores in problem solving, approximately 1 point higher than group 2 on average. These results are interesting since they prove the influence of mental representation in the ability for problem solving, showing that age has a logically increasing influence on the average level of problem-solving, but not in the type of relationship between the two variables.
In addition, regarding the problems of teachers and institutions struggling with the usual failure of students in problem solving tasks, a tool for predicting the probability of success in this subject is given. A binary classification logistic regression model combined with ROC curve techniques returns a cutoff of the MR variable predicting a high probability of success in PS. The analysis reveals that passing the MR test does not guarantee passing the PS test. Specifically, students successfully passing the PS test usually obtain in the MR test a score higher than for groups 1 and 2, and even greater, , for group 3. The results show that the number of students who pass the PS test is higher in group 3 than in the other two, which is expected because of a higher evolution of language, and according to the classification tool provided, these students obtain on average a higher MR score. All this information can be used to detect the group of students who could have problems in reaching the objectives of learning in problem solving and, on that basis, to design a specific program and methodology to prevent this.
Author Contributions
Conceptualization, M.M.R.-H. and J.M.R.-D.; methodology, M.M.R.-H., R.E.P. and J.M.R.-D.; software, M.M.R.-H., R.E.P. and J.M.R.-D.; validation, M.M.R.-H., R.E.P. and J.M.R.-D.; formal analysis, M.M.R.-H., R.E.P. and J.M.R.-D.; investigation, M.M.R.-H., R.E.P. and J.M.R.-D.; resources, M.M.R.-H., R.E.P. and J.M.R.-D.; data curation, M.M.R.-H., R.E.P. and J.M.R.-D.; writing—original draft preparation, M.M.R.-H., R.E.P. and J.M.R.-D.; writing—review and editing, R.E.P. and J.M.R.-D.; visualization, R.E.P.; supervision, M.M.R.-H., R.E.P. and J.M.R.-D.; project administration, J.M.R.-D.; funding acquisition, J.M.R.-D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Spanish Ministry of Economy and Competiveness and Fondos FEDER and Junta de Castilla y León (Projects ‘MTM2013-47879-C2-2-P’, ‘MTM2016-80539-C2-2-R’, ‘SA130U14’, ‘SA080P17’, ‘SA105P20’).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Steiner-Khamsi, G. The Politics of League Tables. JSSE J. Soc. Sci. Educ. 2003, 2, 1–6. [Google Scholar]
- Takayama, K. The politics of international league tables: PISA in Japan’s achievement crisis debate. Comp. Educ. 2008, 44, 387–407. [Google Scholar] [CrossRef]
- Mullis, I.V.S.; Martin, M. TIMSS 2015 Assessment Frameworks; TIMSS & PIRLS International Study Center, Boston College: Chestnut Hill, MA, USA, 2013. [Google Scholar]
- NCTM. Principles to Actions: Ensuring Mathematical Success for All; National Council of Teachers of Mathematics: Reston, VA, USA, 2014. [Google Scholar]
- Cockcroft, W.H. Mathematics Counts: Report of the Committee of Inquiry into the Teaching of Mathematics in Schools Under the Chairmanship of W.h. Cockcroft; Technical Report; Her Majesty’s Stationery Office (H.M.S.O.): London, UK, 1982. [Google Scholar]
- Carpenter, T.P.; Ansell, E.; Franke, M.L.; Fennema, E.; Weisbeck, L. Models of Problem Solving: A Study of Kindergarten Children’s Problem-Solving Processes. J. Res. Math. Educ. 1993, 24, 428–441. [Google Scholar] [CrossRef]
- Cummins, J. Language, Power, and Pedagogy: Bilingual Children in the Crossfire; Multilingual Matters Ltd.: Clevedon, UK, 2000. [Google Scholar]
- Krulik, S.; Rudnick, J.A. Problem Solving: A Handbook for Teachers; Allyn & Bacon: Newton, MA, USA, 1987. [Google Scholar]
- Leif, J.D.; Leif, R.; Dezaly, R. Didáctica del Cálculo, de las Lecciones de Cosas y de las Ciencias Aplicadas; Kapelusz: Buenos Aires, Argentina, 1961. [Google Scholar]
- Kintsch, W.; Kozminsky, E.; Streby, W.; McKoon, G.; Keenan, J. Comprehension and recall of text as a function of content variables. J. Verbal Learn. Verbal Behav. 1975, 14, 196–214. [Google Scholar] [CrossRef]
- Nesher, P.; Teubal, E. Verbal cues as an interfering factor in verbal problem solving. Educ. Stud. Math. 1975, 6, 41–51. [Google Scholar] [CrossRef]
- Nesher, P.; Katriel, T. A semantic analysis of addition and subtraction word problems in arithmetic. Educ. Stud. Math. 1977, 8, 251–269. [Google Scholar] [CrossRef]
- De Corte, E.; Verschaffel, L. Children’s solution processes in elementary arithmetic problems: Analysis and improvement. J. Educ. Psychol. 1981, 73, 765–779. [Google Scholar] [CrossRef]
- Nesher, P.; Greeno, J.G.; Riley, M.S. The development of semantic categories for addition and subtraction. Educ. Stud. Math. 1982, 13, 373–394. [Google Scholar] [CrossRef]
- Riley, M.S.; Greeno, J.G. Developmental Analysis of Understanding Language About Quantities and of Solving Problems. Cogn. Instr. 1988, 5, 49–101. [Google Scholar] [CrossRef]
- Vergnaud, G. A Classification of Cognitive Tasks and Operations of Thought involved in Addition and Subtraction Problems. In Addition and Subtraction. A Cognitive Perspective; Carpenter, T., Moser, J., Romberg, T., Eds.; Routledge: Hillsdale, NJ, USA, 2020; pp. 39–59. [Google Scholar]
- Carpenter, T.P.; Moser, J.M. The acquisition of addition and subtraction concepts in grades one through three. J. Res. Math. Educ. 1984, 15, 179–202. [Google Scholar] [CrossRef]
- Andrich, D.; Styles, I. Psychometric evidence of intellectual growth spurts in early adolescence. J. Early Adolesc. 1994, 14, 328–344. [Google Scholar] [CrossRef]
- Inhelder, B.; Piaget, J. De la logique de L’enfant à la Logique de L’adolescent; Presses Universitaires de France: Paris, France, 1955. [Google Scholar]
- Sternberg, R.J. Wisdom: Its Nature, Origins, and Development; Cambridge University Press: New York, NY, USA, 1990. [Google Scholar]
- Casal, J.; Funes, J.; Homs, O.; Trilla, J. Exit i Fracas a Catalunya; Fundació Jaume Bofill: Barcelona, Spain, 1995. [Google Scholar]
- Dixon, J.A.; Moore, C.F. The developmental role of intuitive principles in choosing mathematical strategies. Dev. Psychol. 1996, 32, 241–253. [Google Scholar] [CrossRef][Green Version]
- De Corte, E.; Verschaffel, L.; De Win, L. Influence of rewording verbal problems on children’s problem representations and solutions. J. Educ. Psychol. 1985, 77, 460–470. [Google Scholar] [CrossRef]
- Hegarty, M.; Mayer, R.E.; Monk, C.A. Comprehension of arithmetic word problems: A comparison of successful and unsuccessful problem solvers. J. Educ. Psychol. 1995, 87, 18–32. [Google Scholar] [CrossRef]
- Pape, S.J. Compare word problems: Consistency hypothesis revisited. Contemp. Educ. Psychol. 2003, 28, 396–421. [Google Scholar] [CrossRef]
- Van der Schoot, M.; Arkema, A.H.B.; Horsley, T.M.; van Lieshout, E.C. The consistency effect depends on markedness in less successful but not successful problem solvers: An eye movement study in primary school children. Contemp. Educ. Psychol. 2009, 34, 58–66. [Google Scholar] [CrossRef]
- Boonen, A.J.; van der Schoot, M.; van Wesel, F.; de Vries, M.H.; Jolles, J. What underlies successful word problem solving? A path analysis in sixth grade students. Contemp. Educ. Psychol. 2013, 38, 271–279. [Google Scholar] [CrossRef]
- Verschaffel, L.; De Corte, E.; Pauwels, A. Solving compare problems: An eye movement test of Lewis and Mayer’s consistency hypothesis. J. Educ. Psychol. 1992, 84, 85–94. [Google Scholar] [CrossRef]
- Marzocchi, G.M.; Lucangeli, D.; De Meo, T.; Fini, F.; Cornoldi, C. The disturbing effect of irrelevant information on arithmetic problem solving in inattentive children. Dev. Neuropsychol. 2002, 21, 73–92. [Google Scholar] [CrossRef]
- Rodríguez-Hernández, M.; Domínguez-Fernández, J. Dificultades del lenguaje que influyen en la resolución de problemas. Ense Nanza Teach. Rev. Interuniv. DidÁctica 2016, 34, 17–42. [Google Scholar] [CrossRef]
- Draper, N.; Smith, H. Applied Regression Analysis; Wiley Series in Probability and Mathematical Statistics; Wiley: Hoboken, NJ, USA, 1966. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recogn. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Krzanowski, W.J.; Hand, D.J. ROC Curves for Continuous Data; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Hosmer, D.W.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley and Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Atkinson, A.; Donev, A.; Tobias, R. Optimum Experimental Designs, with SAS; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).