Abstract
The protection induced by vaccines against infectious diseases such as malaria, dengue or hepatitis relies on a the creation of immune memory by T cells, key components of the human immune system. The induction of a strong T cell response leading to long lasting memory can be improved by using prime-boost (PB) vaccines, which consist in successive inoculations of appropriate vectors carrying target antigens that can be recognized by specific T cell clones. A problem faced by PB vaccines is the fact that T cell response is often biased towards a few clones that can identify only a small set of antigens, out of the many that could be displayed by the pathogen. This phenomenon, known as immunodominance, can significantly compromise the effectiveness of vaccination. In this work we will use mathematical modeling to better understand the role of T cell population dynamics in the onset of immunodominance in PB vaccines. In particular, we will use mathematical analysis and simulations to compare single-dose vaccines with PB ones, both for homologous (where the same antigen is used in every shot) and heterologous protocols (in which different antigens are used at each step).
1. Introduction
The protection induced by vaccines against certain pathogens requires the generation of effective cell-mediated immunity [1,2,3]. In particular, a great research effort is currently focused on the development of vaccines aimed at eliciting strong response in T cells (a key component of our immune system). A number of studies have shown that the efficiency of T cell-based vaccines can be greatly improved by using prime-boost (PB) regimes [1,4]. The rationale of PB vaccines is to use an initial inoculation (prime) to activate specific clones of T cells. Successive inoculations (boost) force the proliferation of these clones and increase the number of long-lasting memory T cells that can recognize the target antigens [5]. PB vaccines have been successfully tested against pathogens such as malaria [4,6], leishmaniasis [7], dengue [8], AIDS [9], tuberculosis [10], hepatitis [11,12] or influenza [13], and also as a therapeutic approach to the treatment of tumors [14,15,16]. Some of the vaccines against COVID-19 currently being tested require of two inoculations, a strategy typical of PB protocolos.
The immune action of T cells relies on the recognition of specific molecules (antigens) present on the surface of pathogens. This recognition is mediated by a membrane receptor, the T cell receptor (TCR), that binds short peptide sequences (known as epitopes) in the antigens. The distribution of TCRs is clonal, meaning that each T cell only carries one type of TCR in its membrane. On the other hand, the affinity of the TCR for an antigen is determined by the three-dimensional structure of the receptor and the antigen epitopes. Therefore, the ability of individual T cells to recognize a particular epitope will be determined by the structure of its TCR.
In normal conditions, T cells circulate in the blood and the lymphatic systems in an inactive or naïve state. The number of circulating naïve T cells remains relatively constant and is controlled by molecular signals generically known as interleukins. In the case of an infection, specialized innate immune cells (known as antigen presenting cells or APCs) react to the presence of pathogens by migrating to nearby lymph nodes and displaying pathogen antigens on their surfaces. In the lymph nodes, naïve T cells whose TCRs recognize some of the epitopes displayed by APCs differentiate into effector T cells. These newly activated effector T cells proliferate (a process termed clonal expansion) and migrate to the site of the infection. Once there, they kill infected host cells that display pathogen antigens on their surface. After controlling the infection, effector T cells undergo apoptosis and disappear from the organism, returning the T cell population to its pre-infection levels. A few cells survive as memory T cells and revert to an inactive state. In case of future encounters with the same pathogen, memory T cells rapidly reactivate, providing a fast immune response. The goal of T cell-based vaccines is precisely to create a robust T cell memory against specific epitopes of the target pathogen.
In previous works we have introduced population mechanics, a mathematical framework to model the dynamics of T cell populations [17,18]. We have also shown that this approach could be used to improve the efficiency of PB vaccines [19]. Population mechanics relies on the observation that T cell populations show inertia and elasticity [17], features that can be easily modeled in terms of simple second order differential equations. From this viewpoint, T cell population dynamics would emerge from the balance between different stimuli, which to keep to the mechanical analogy being used in this work, will henceforth be denoted as forces. Intrinsic, elastic forces would bring these populations to extinction in the absence of appropriate growth signals. These signals would act as external cues that foster T cell proliferation. The biological origin of such external forces would be, for instance, the interaction with antigens during infections, or with interleukins during normal T cell homeostasis [20,21,22,23].
The antigens, and hence the epitopes, present in a single infectious agent can be very heterogeneous. For this reason, many different T cell clones usually exhibit some degree of affinity for the antigens of a pathogen. However, it has been observed that, even if many clones of T cells are activated in the course of an immune response, the population of effector T cells is usually dominated by just a few clones [24,25]. This process, known as immunodominance, is acknowledged as a major issue in the development of effective T cell-based vaccines [26,27,28]. The reasons for this are that it may bias the vaccine-induced formation of T cell memory: Non-dominant epitopes may be excluded by dominant ones. If a vaccine targets non-dominant epitopes of a particular pathogen, then its efficiency can be compromised.
In this work, we will use population mechanics to analyze the effect of immunodominance on the formation of T cell memory by PB vaccines. The plan of this article is as follows. We will first model immunodominance in T cell responses during acute infections. We will then extend this model to understand the effects of immunodominance in single-dose and PB vaccines.
2. Results
2.1. The Effect of Immunodominance in Acute Infections
The mechanisms underlying immunodominance are not fully understood as yet [29]. However, empirical evidence suggests that the dominance of a clone might be determined by its capability to compete for antigenic stimulation with other clones [27,30]. In turn, the competitive ability of a clone would depend on two factors: the affinity of the TCR for its cognate epitope [31,32,33,34] and the abundance of the clone in the pool of naïve T cells [35,36]. In this section we will use population mechanics to model the relative contribution of these factors to the appearance of immunodominance in acute infections.
The models used in this work are an extension of those presented in Reference [19]. The logic of these models can be summarized as follows. The population of T cells is initially composed of a naïve and a memory subsets. The dynamics of naïve T cells is not explicitly considered in the model. As for memory T cells (denoted by M), they are assumed to be at homeostatic equilibrium before the infection owing to its interaction with a homeostatic interleukin H (see Reference [18] for further details on this point). The infection by a pathogen P triggers the activation of n clones of naïve T cells and the appearance of two new populations: (effector T cells) and (memory T cells). The pathogen is assumed to grow at rate and is eliminated by effector T cells at rate . The condition , for a given threshold , determines the end of the infection. Under these assumptions, the dynamics of T cell populations is driven by antigenic and homeostatic forces as described by this system of differential equations:
The abundance of clone i in the naïve pool is given by the initial value of effector and memory cells of that clone: and . For the sake of simplicity, we will assume that . The initial values of the total memory population ( and ) and the homeostatic interleukin (H) correspond to their values at equilibrium (see Reference [18] for further details):
The homeostatic interleukin is produced at a rate and consumed by memory T cells at rate . The terms and are the intensities of the antigenic force perceived by effector and memory T cells of clone i respectively. The parameter allows to quantify the effect of TCR affinity on the proliferation of effector and memory T cells: clones with greater values of this parameter proliferate faster than clones with lower values. Finally, the terms and correspond to the homeostatic force acting on memory T cells of clone i and on the pool of memory T cells existing before the infection.
Equation (1) can produce negative values for some variables, which is meaningless in the context of cell populations. For this reason, that model must be understood as describing a hybrid dynamical system whose variables are constrained to take on non-negative values only [37,38]. Such variables are characterized by switching between a collection of discrete states, with transitions among states being governed by differential equations (Figure 1).
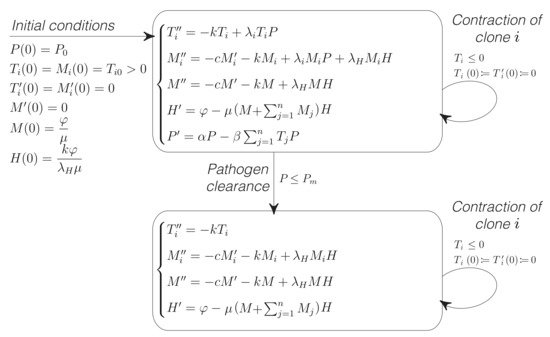
Figure 1.
Hybrid dynamical system described by Equation (1). Equation (1) may lead to negative values for the populations of effector T cells (). To avoid this, the condition determines a discrete change in Equation (1). The variable is set to zero, which is equivalent to remove the variable from the model. In biological terms, this implies that clone i has completed clonal contraction. The condition means that the pathogen has been effectively neutralized. This is modeled by another discrete transition, in this case to remove the variable P from the model. We assume that memory T cell populations do not undergo clonal contraction and that the concentration of the homeostatic interleukin remains always greater than zero. In order to satisfy these biological constrains, the set of parameters must be chosen such that conditions , and hold for .
According to empirical evidence, clones with higher affinities for their cognate antigens are dominant [31,32,33,34], whereas less affine clones exhibit a curtailed expansion [39,40,41]. The hybrid dynamical system described by Equation (1) reproduces these empirical observations (see Figure 2A–C). Also in agreement with experimental evidence, the model predicts that clones with lower affinities can become immunodominant if they are more abundant in the pool of naïve T cells [35,36] (Figure 2D).
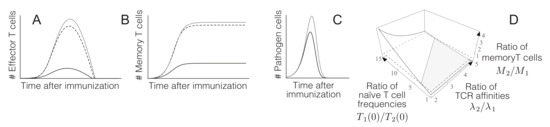
Figure 2.
Immunodominance in acute T cell immune responses. (A) The light grey curve represents clonal expansion and contraction of a given clone in the absence of immunodominance. If the same clone is activated in the presence of a dominant clone (dashed line) it displays a curtailed expansion (solid black line). (B) The presence of a dominant clone (dashed line) markedly reduces the number of memory T cells of the original clone (solid black line). (C) The dominant clone leads to a more rapid elimination of the pathogen (black line) as compared to the less dominant clone alone (light grey line). (D) Ratio between the number of memory T cells of two clones of affinities and respectively. Values above 1 (respectively below 1) indicate dominance of clone 1 (resp. of clone 2). More affine clones dominate when the number of naïve cells are similar (grey area in the figure), whereas less affine clones become dominant if they are present at higher frequency in the pool of naïve T cells. Parameters used in A and B: , , , , , , , , , , and (all in suitable units).
We remark that immunodominance is not explicitly postulated in the equations of the model, but turns out to be an emergent property of their solutions. Specifically, higher epitope affinity or higher precursor frequencies suffice to account for the dominance of some particular clones over others.
2.2. Immunodominance in Single Immunization Vaccines
Although some vaccines contain replication-competent vectors, most currently available vaccines make use of inactivated or attenuated pathogens, or even of selected pathogen antigens [29]. Therefore, in contrast with acute infections, agents triggering an innate immune response in such vaccines do not proliferate, a fact that can be modeled by assuming that the antigen disappears at a constant rate in Equation (1).
Under this assumption, numerical simulations of Equation (1) for two T cell clones reveal a linear relationship between the ratios of memory formation and the ratio of TCR affinities (see Figure 3A). The meaning of such relation can be explained as follows. Let be the affinity of a T cell clone for a vaccine antigen, and the number of memory T cells of this clone that will appear as a consequence of the vaccination. Then the number () of memory T cells of another clone with affinity can be fitted to the line of equation for some as shown in Figure 3A. The particular value of depends on the choice of the model parameters, that is, each combination of parameters determines the slope of the line that defines the memory ratio as a function of the affinity ratio.
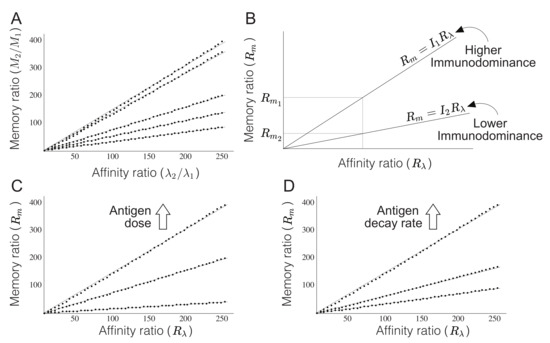
Figure 3.
Immunodominance index. (A) Each dot represents a numerical simulation of the model of immunodominance in single-dose vaccines. In this model, we assume that two clones of affinities and are simultaneously activated in response to the vaccine. For each set of parameter values, the ratio between the number of memory T cells formed of these clones is linearly related with the ratio of their affinities (correlation coefficient in all cases). Different combinations of parameters can be fitted to different lines passing through the origin. (B) The slope of these lines can be used to define an immunodominance index . For a fixed value of , a higher slope implies greater differences in memory formation between concurrent clones. Therefore, higher values of correspond to greater differences in memory formation between dominant and non-dominant clones. (C) Immunodominance index for different vaccine doses (parameter in the equations) and (D) different rates of antigen decay (parameter in the model). These results suggest that higher antigen doses and higher rates of antigen decay intensify the effects of immunodominance.
The constant can be used to define an immunodominance index (Figure 3B). Greater values of this constant represent situations in which a given ratio of affinities gives rise to greater differences in memory formation between two clones (i.e., higher values of ). Therefore, higher values of imply that clones with affinity are subdominant (Figure 3B).
Vaccine strategies must reduce immunodominance in order to generate broad responses to pathogen antigens [1]. In terms of our model, buffering the effects of immunodominance translates into reducing the immunodominance index defined above. In particular, our model allows to simulate alternative vaccination scenarios and to analyze their impact on this index. For instance, parameters (antigen dose) and (rate of vaccine decay in the organism) can be modulated in the design of a vaccine. Our model could be use to choose appropriate values for these parameters in order to reduce the impact of immunodominance on the target epitopes. In this respect, our model suggests that lower doses of antigen or vaccines with higher residence time in the organism might reduce the impact of immunodominance in single-inoculation vaccines (see Figure 3C,D).
2.3. Immunodominance in Prime-Boost Vaccines
We will next analyze how PB strategies can be used to modulate the value of the immunodominance index. To this end we will begin by defining homologous and heterologous PB vaccines. Homologous PB vaccines consist in successive inoculations of the same antigen. In contrast, in heterologous vaccines the prime and boost agents are different. In order to model these two types of PB vaccines we will proceed as follows.
We will begin by assuming that the goal of the vaccine is to create a robust T cell memory against a particular epitope. For the sake of simplicity we will assume that only a particular T cell clone recognizes such epitope and we will label as and the effector and memory T cells of this clone. In the case of homologous PB vaccines, we will denote by A the vaccine antigen and we will consider a second clone of T cells with affinity for a different epitope in A. To model heterologous vaccines we will consider two antigens and as prime and boost agents respectively. Both antigens contain the target epitope. As with homologous vaccines, clone 1 is affine for this epitope. In this case two new clones will compete with clone 1 for access to antigenic stimulation. Clone 2 is assumed to recognize an alternative epitope in the prime agent () and clone 3 in the boost agent (). In all cases we will assume that the target clone is subdominant. The models corresponding to homologous and heterologous PB vaccines are shown in Appendix A and Appendix B respectively.
Under such assumptions, we will simulate different vaccination scenarios to test if they lead to differences regarding the immunodominance status of the target clone. To that end, we will vary the relative doses of prime and boost inoculations and the timing of boost with respect to prime. These variables are key in the design of PB vaccine protocols since they critically determine the amount of memory T cells against the target epitopes (see Reference [19]). In order to evaluate the efficiency of homologous and heterologous PB vaccine protocols we will compare their ability to create memory T cells as compared to single-dose immunizations.
Figure 4 shows the value of the immunodominance index measured for homologous and heterologous PB vaccines as compared to inoculating all the antigens in just one dose. According to our model, homologous PB vaccines can be used to increase or decrease the immunodominance index of subdominant clones, depending on the total dose of antigen and its distribution between prime and boost. In contrast, all the protocols of heterologous PB vaccines sharply reduce the value of this index, relative to single inoculations of the prime antigen alone or to combinations of prime and boost antigens. This result implies that both homologous and heterologous PB vaccines can help to increase the number of memory T cells of particular target clones, even if these are subdominant with respect other clones that respond to other antigens present in prime and boost (see Figure 5A).
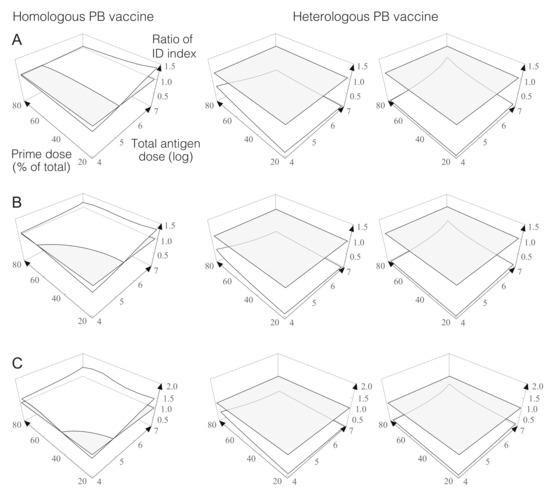
Figure 4.
Effect of homologous and heterologous prime-boost (PB) vaccines on the immunodominance index. Each figure represents the ratio between the immunodominance index measured for PB vaccines and for single-dose vaccines. Values above 1 represent situations in which the immunodominance index is greater in the PB strategy as compared to administering all the antigen in one single dose. Conversely, values below 1 indicate a reduction in the immunodominance index as a consequence of distributing the antigen in two doses. In the case of heterologous vaccines comparison is made with single-dose vaccines containing only the first antigen (left), or a combination of antigens present both in prime and boost agents (right). (A–C) correspond to three different time intervals between prime and boost. Threshold value of 1 is shown in gray for reference. The values of the parameters used these simulations are (in suitable units): , , , , , , , , , .
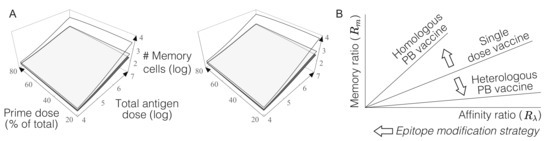
Figure 5.
Effect of homologous and heterologous PB vaccines on the formation of memory T cells of non-dominant clones. (A) The results presented here correspond to a particular choice of clone affinities for PB vaccine scenarios introduced in Figure 4. In particular, we have set (left), and (right). All the protocols of heterologous PB vaccines (white) give raise to more memory T cells of subdominant clone 1 than single-dose vaccines (gray) or homologous PB vaccines (dark-gray). (B) According to the models of population mechanics, PB vaccine strategies can be used to change the relations of immunodominance that emerge from single-dose vaccines. In particular, the immunodominance index of a particular clone can be increased by using appropriate antigen doses in PB homologous vaccines. In contrast, heterologous PB protocols tend to reduce the value of this index, thus broadening T cell immune response triggered by vaccine antigens. These results suggest that T cell population dynamics can be explicitly used to design PB vaccine protocols to modulate immunodominance. These protocols can be combined with other techniques, such as artificial epitope modification, to further reduce immunodominance effects on specific target clones.
3. Discussion
One of the goals of cellular immunity-based vaccines is to generate a robust response by selected T cell clones. The design of this type of vaccines relies to a great extent on empirical, trial-and-error approaches [42,43]. The right doses of appropriate agents are usually selected after experimentally comparing the performance of a set of alternatives. In the case of PB vaccines, the quantity of potential protocols to be tested can be very high, owing to the possibility of combining a number of vectors carrying different doses of target antigens, both as prime or boost agents.
This heuristic approach has lead to increasingly effective vaccines against many pathogens in the last decades. However, it is often difficult to understand the underlying mechanisms that account for the comparative advantages of a particular protocol over another. For instance, it has been empirically observed that priming and boosting with the same antigen induces immune responses dominated by a few clone types [2,44]. In contrast, heterologous PB regimes give rise to broader T cell responses [45,46]. It has also been suggested that avoiding repetitive use of the same vectors reduces immunodominant responses to vector-specific antigens in cancer vaccines [26]. In general, empirical evidence suggests that homologous PB yield better results for antibody-induced vaccines, while heterologous PB strategies induce stronger antigen-specific T cells [1,47]. However, the origin of these differences remains largely unknown [15].
In this work we resort to mathematical modeling to analyze the role of T cell dynamics in the performance of PB vaccines. Specifically, we assume that antigenic stimulation acts as a force that fosters cell proliferation, which allows to formulate simple models of T cell clonal expansion and contraction during acute infection and vaccination. Their success to capture a number of well-known features of T cell immune response suggests that our models can be used to simulate the performance of PB regimes in terms of antigen-specific memory formation. We remark that the models presented in this work focus on the dynamics of T cell populations, and do not take into account other aspects of the immune response, such as induction of cytokine secretion by T cells or by other immune cells [48,49]. On the other hand, they are not intended to explain the mechanisms underlying the formation of memory T cells, or the onset of clonal contraction, but to provide insight about the effect of different vaccination strategies on the enhancement of particular types of T cells clones. In particular, our analysis suggests that observed differences in immunodominance between homologous and heterologous PB vaccines might arise from their different impact on T cell population dynamics. The analysis presented here thus hints at possible strategies to design PB vaccines yielding biased distributions of effector and memory T cell clones towards desired target antigens (Figure 5B).
Finally, we want to stress that we do not intend to make quantitative predictions about the dynamics of T cells elicited by vaccines. This goal would be unrealistic considering the difficulties to obtain accurate data about these dynamics in the organism. Humans have tens of millions of T cell clones that may differ only slightly in the particular spatial structure of their TCRs. Monitoring the clones that proliferate in response to a specific antigen is beyond the reach of currently available experimental tools. Taking this into account, parameterizing the model by using empirical data may well be impossible. In our opinion, this does not imply that the model cannot prove useful. We believe that population mechanics provides a valuable abstraction of the immune response, in the sense that it captures key qualitative features of T cell dynamics (see References [17,18,19]). In this regard, the choice of parameters is only constrained by the condition that they must qualitatively reproduce the observed behavior of T cell populations during acute infections. This condition does not impose a hard restriction on the regions of the space of parameters that can be used in our simulations. No further claim is made in this paper about the biological significance of those parameters.
The numerical simulations shown here are aimed at providing a proof-of-concept argument to show that the conclusions derived are not only compatible with state-of-the art knowledge in the field, but might also suggest particular strategies to improve upon current vaccination protocols. We believe that a better understanding of the dynamic aspects of T cell response could prove useful in controlling the effects of immunodominance. They are key factors to be reckoned with when assessing the performance of vaccines. This in turn calls for the use of mathematical models to simulate different vaccination strategies prior to the experimental trial. Population mechanics, as described in this work, provides a method to achieve that goal. This modeling framework has a distinct modular character, and thus allows to deal with large numbers of different T cell populations. We therefore expect this tool to be particularly useful in theoretical aspects of the design of vaccine strategies.
Author Contributions
Conceptualization, C.F.A. and C.F.-A.; investigation, C.F.A., M.A.H., F.B., F.J.A. and C.F.-A.; analysis, C.F.A., M.A.H., F.B., F.J.A. and C.F.-A.; writing—original draft preparation, C.F.A. and M.A.H.; writing—review and editing, C.F.A., M.A.H., F.B., F.J.A. and C.F.-A.; funding acquisition, M.A.H. and F.B. All authors have read and agreed to the published version of the manuscript.
Funding
C.F.A. and M.A.H. have been partially supported by MINECO Grant MTM2017-85020-P; C.F.A. and F.B. are grateful to the Roechling Foundation for its support. C.F.-A. is grateful to the Fundação para a Ciência e a Tecnologia of Portugal (FCT).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Model of Homologous PB Vaccines
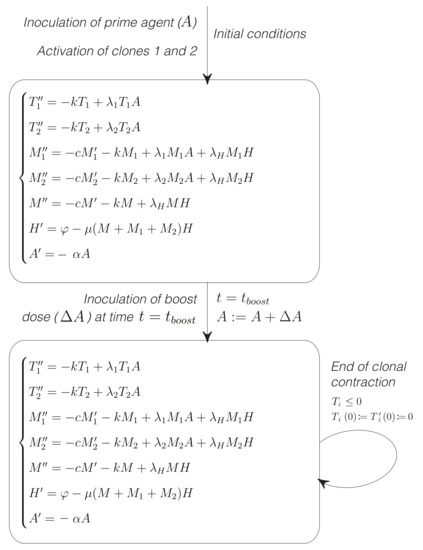
Figure A1.
Hybrid automata diagram of the model of homologous PB vaccines. Simulations start with the inoculation of antigen A. Clone 1 recognizes the target epitope with affinity , while clone 2 binds to an alternative epitope with affinity . Therefore, the target clone is subdominant. A second inoculation of the same agent (boost inoculation) takes place at time . This gives rise to a discrete change in the model, consisting in an instantaneous change of antigen A (, with the dose of the boost inoculation). Different values for the prime and boost doses of A and different boost timings give rise to alternative vaccination protocols. The condition () determines the end of the clonal contraction of clone i.
Appendix B. Model of Heterologous PB Vaccines
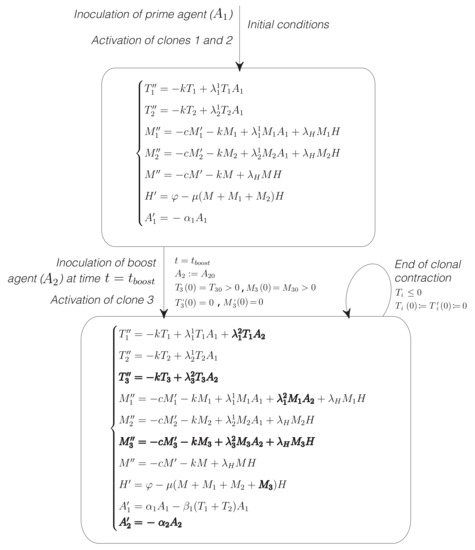
Figure A2.
Hybrid automata diagram of the model of heterologous PB vaccines. In this case we assume that prime consists in the inoculation of an antigen , whereas the boost vector contains a different antigen . Both antigens contain the target epitope, which is recognized by clone 1 with affinity . A second clone recognizes a different epitope of with affinity and a third clone binds an epitope on with affinity . The target clone is therefore subdominant with respect to clones 2 and 3. Simulations start with the activation of clones 1 and 2 in response to the presence of antigen . At time the second antigen () is inoculated. This triggers a discrete change in the equations of the model. The activation of clone 3 introduces three new equations describing the dynamics of effector and memory T cells of clone 3 ( and ) and of the second antigen . The equation of effector and memory T cells of clone 1 also change owing to the appearance of a new antigenic force . Finally, the presence of a new clone of memory T cells () also modifies the dynamics of the homeostatic interleukin H. These changes are marked in bold face in the figure.
References
- Iglesias, M.C.; Appay, V.; Moris, A. Immunologic Memory: T Cells in Humans. In Vaccinology; Morrow, W.J.W., Sheikh, N.A., Schmidt, C.S., Davies, D.H., Eds.; Wiley-Blackwell: West Sussex, UK, 2012; pp. 61–78. [Google Scholar] [CrossRef]
- Murali-Krishna, K.; Altman, J.D.; Suresh, M.; Sourdive, D.J.D.; Zajac, A.J.; Miller, J.D.; Slansky, J.; Ahmed, R. Counting Antigen-Specific CD8 T Cells: A Reevaluation of Bystander Activation during Viral Infection. Immunity 1998, 8, 177–187. [Google Scholar] [CrossRef]
- Robinson, H.L.; Amara, R.R. T cell vaccines for microbial infections. Nat. Med. 2005, 11, S25–S32. [Google Scholar] [CrossRef]
- Reyes-Sandoval, A.; Harty, J.T.; Todryk, S.M. Viral vector vaccines make memory T cells against malaria. Immunology 2007, 121, 158–165. [Google Scholar] [CrossRef]
- Ramshaw, I.A.; Ramsay, A.J. The prime-boost strategy: Exciting prospects for improved vaccination. Immunol. Today 2000, 21, 163–165. [Google Scholar] [CrossRef]
- Rodrigues, M.M.; Cordey, A.S.; Arreaza, G.; Corradin, G.; Romero, P.; Maryanski, J.L.; Nussenzweig, R.S.; Zavala, F. CD8+ cytolytic T cell clones derived against the Plasmodium yoelii circumsporozoite protein protect against malaria. Int. Immunol. 1991, 3, 579–585. [Google Scholar] [CrossRef]
- Jain, K.; Jain, N.K. Vaccines for visceral leishmaniasis: A review. J. Immunol. Methods 2015, 422, 1–12. [Google Scholar] [CrossRef]
- Vannice, K.S.; Roehrig, J.T.; Hombach, J. Next generation dengue vaccines: A review of the preclinical development pipeline. Vaccine 2015, 33, 7091–7099. [Google Scholar] [CrossRef]
- Shete, A.; Thakar, M.; Mehendale, S.; Paranjape, R. Is prime boost strategy a promising approach in HIV vaccine development? J. Aids Clin. Res. 2014, 5. [Google Scholar] [CrossRef]
- Lazarevic, V.; Flynn, J. CD8+ T Cells in Tuberculosis. Am. J. Respir. Crit. Care Med. 2002, 166, 1116–1121. [Google Scholar] [CrossRef]
- Schmidtke, P.; Habermehl, P.; Knuf, M.; Meyer, C.U.; Sänger, R.; Zepp, F. Cell mediated and antibody immune response to inactivated hepatitis A vaccine. Vaccine 2005, 23, 5127–5132. [Google Scholar] [CrossRef]
- Barnes, E.; Folgori, A.; Capone, S.; Swadling, L.; Aston, S.; Kurioka, A.; Meyer, J.; Huddart, R.; Smith, K.; Townsend, R.; et al. Novel Adenovirus-Based Vaccines Induce Broad and Sustained T Cell Responses to HCV in Man. Sci. Transl. Med. 2012, 4, 115ra1. [Google Scholar] [CrossRef] [PubMed]
- Thomas, P.G.; Keating, R.; Hulse-Post, D.J.; Doherty, P.C. Cell-mediated protection in influenza infection. Emerg. Infect. Dis. 2006, 12, 48–54. [Google Scholar] [CrossRef] [PubMed]
- Speiser, D.E.; Lienard, D.; Rufer, N.; Rubio-Godoy, V.; Rimoldi, D.; Lejeune, F.; Krieg, A.M.; Cerottini, J.C.; Romero, P. Rapid and strong human CD8+ T cell responses to vaccination with peptide, IFA, and CpG oligodeoxynucleotide 7909. J. Clin. Investig. 2005, 115, 739–746. [Google Scholar] [CrossRef] [PubMed]
- Lu, S. Heterologous prime-boost vaccination. Curr. Opin. Immunol. 2009, 21, 346–351. [Google Scholar] [CrossRef] [PubMed]
- Le, D.T.; Wang-Gillam, A.; Picozzi, V.; Greten, T.F.; Crocenzi, T.; Springett, G.; Morse, M.; Zeh, H.; Cohen, D.; Fine, R.L.; et al. Safety and Survival With GVAX Pancreas Prime and Listeria Monocytogenes–Expressing Mesothelin (CRS-207) Boost Vaccines for Metastatic Pancreatic Cancer. J. Clin. Oncol. 2015, 33, 1325–1333. [Google Scholar] [CrossRef]
- Arias, C.F.; Herrero, M.A.; Cuesta, J.A.; Acosta, F.J.; Fernandez-Arias, C. The growth threshold conjecture: A theoretical framework for understanding T-cell tolerance. R. Soc. Open Sci. 2015, 2, 150016. [Google Scholar] [CrossRef]
- Arias, C.F.; Herrero, M.A.; Acosta, F.J.; Fernandez-Arias, C. Population mechanics: A mathematical framework to study T cell homeostasis. Sci. Rep. 2017, 7, 9511. [Google Scholar] [CrossRef]
- Fernandez-Arias, C.; Arias, C.F.; Zhang, M.; Herrero, M.A.; Acosta, F.J.; Tsuji, M. Modeling the effect of boost timing in murine irradiated sporozoite prime-boost vaccines. PLOS ONE 2018, 13, e0190940. [Google Scholar] [CrossRef]
- Marrack, P.; Bender, J.; Hildeman, D.; Jordan, M.; Mitchell, T.; Murakami, M.; Sakamoto, A.; Schaefer, B.C.; Swanson, B.; Kappler, J. Homeostasis of αβ TCR+ T cells. Nat. Immunol. 2000, 1, 107–111. [Google Scholar] [CrossRef]
- Fry, T.J.; Connick, E.; Falloon, J.; Lederman, M.M.; Liewehr, D.J.; Spritzler, J.; Steinberg, S.M.; Wood, L.V.; Yarchoan, R.; Zuckerman, J.; et al. A potential role for interleukin-7 in T-cell homeostasis. Blood 2001, 97, 2983–2990. [Google Scholar] [CrossRef]
- Boyman, O.; Purton, J.F.; Surh, C.D.; Sprent, J. Cytokines and T-cell homeostasis. Curr. Opin. Immunol. 2007, 19, 320–326. [Google Scholar] [CrossRef] [PubMed]
- Ku, C.C.; Murakami, M.; Sakamoto, A.; Kappler, J.; Marrack, P. Control of Homeostasis of CD8+ Memory T Cells by Opposing Cytokines. Science 2000, 288, 675–678. [Google Scholar] [CrossRef] [PubMed]
- Bennink, J.R.; Yewdell, J.W. Murine cytotoxic T lymphocyte recognition of individual influenza virus proteins. High frequency of nonresponder MHC class I alleles. J. Exp. Med. 1988, 168, 1935–1939. [Google Scholar] [CrossRef] [PubMed]
- Bennink, J.R.; Yewdell, J.W.; Smith, G.L.; Moss, B. Anti-influenza virus cytotoxic T lymphocytes recognize the three viral polymerases and a nonstructural protein: Responsiveness to individual viral antigens is major histocompatibility complex controlled. J. Virol. 1987, 61, 1098–1102. [Google Scholar] [CrossRef]
- Chen, W.; McCluskey, J. Immunodominance and Immunodomination: Critical Factors in Developing Effective CD8+ T-Cell-Based Cancer Vaccines; Academic Press: Cambridge, MA, USA, 2006; Volume 95, pp. 203–247. [Google Scholar] [CrossRef]
- Liu, J.; Ewald, B.A.; Lynch, D.M.; Nanda, A.; Sumida, S.M.; Barouch, D.H. Modulation of DNA Vaccine-Elicited CD8+ T-Lymphocyte Epitope Immunodominance Hierarchies. J. Virol. 2006, 80, 11991–11997. [Google Scholar] [CrossRef]
- Rodriguez, F.; Harkins, S.; Slifka, M.K.; Whitton, J.L. Immunodominance in Virus-Induced CD8+ T-Cell Responses Is Dramatically Modified by DNA Immunization and Is Regulated by Gamma Interferon. J. Virol. 2002, 76, 4251–4259. [Google Scholar] [CrossRef]
- Sette, A.; Fikes, J. Epitope-based vaccines: An update on epitope identification, vaccine design and delivery. Curr. Opin. Immunol. 2003, 15, 461–470. [Google Scholar] [CrossRef]
- Kedl, R.M.; Kappler, J.W.; Marrack, P. Epitope dominance, competition and T cell affinity maturation. Curr. Opin. Immunol. 2003, 15, 120–127. [Google Scholar] [CrossRef]
- Stewart-Jones, G.B.E.; McMichael, A.J.; Bell, J.I.; Stuart, D.I.; Jones, E.Y. A structural basis for immunodominant human T cell receptor recognition. Nat. Immunol. 2003, 4, 657–663. [Google Scholar] [CrossRef]
- Dzutsev, A.H.; Belyakov, I.M.; Isakov, D.V.; Margulies, D.H.; Berzofsky, J.A. Avidity of CD8 T cells sharpens immunodominance. Int. Immunol. 2007, 19, 497–507. [Google Scholar] [CrossRef]
- Price, D.A.; Brenchley, J.M.; Ruff, L.E.; Betts, M.R.; Hill, B.J.; Roederer, M.; Koup, R.A.; Migueles, S.A.; Gostick, E.; Wooldridge, L.; et al. Avidity for antigen shapes clonal dominance in CD8+ T cell populations specific for persistent DNA viruses. J. Exp. Med. 2005, 202, 1349–1361. [Google Scholar] [CrossRef] [PubMed]
- Trautmann, L.; Rimbert, M.; Echasserieau, K.; Saulquin, X.; Neveu, B.; Dechanet, J.; Cerundolo, V.; Bonneville, M. Selection of T Cell Clones Expressing High-Affinity Public TCRs within Human Cytomegalovirus-Specific CD8 T Cell Responses. J. Immunol. 2005, 175, 6123–6132. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, J.; Neumann-Haefelin, C.; Altay, T.; Gostick, E.; Price, D.A.; Lohmann, V.; Blum, H.E.; Thimme, R. Immunodominance of HLA-A2-Restricted Hepatitis C Virus-Specific CD8+ T Cell Responses Is Linked to Naive-Precursor Frequency. J. Virol. 2011, 85, 5232–5236. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Tatum, A.M.; Watson, A.M.; Schell, T.D. Direct Presentation Regulates the Magnitude of the CD8+ T Cell Response to Cell-Associated Antigen through Prolonged T Cell Proliferation. J. Immunol. 2010, 185, 2763–2772. [Google Scholar] [CrossRef] [PubMed]
- Johansson, K.H.; Lygeros, J.; Zhang, J.; Sastry, S. Hybrid automata: A formal paradigm for heterogeneous modeling. In Proceedings of the CACSD, IEEE International Symposium on Computer-Aided Control System Design (Cat. No. 00TH8537), Anchorage, AK, USA, 25–27 September 2000; pp. 123–128. [Google Scholar] [CrossRef]
- Van Der Schaft, A.J.; Schumacher, J.M. An Introduction to Hybrid Dynamical Systems; Springer: London, UK, 2000; Volume 251. [Google Scholar] [CrossRef]
- Turner, S.J.; La Gruta, N.L.; Kedzierska, K.; Thomas, P.G.; Doherty, P.C. Functional implications of T cell receptor diversity. Curr. Opin. Immunol. 2009, 21, 286–290. [Google Scholar] [CrossRef] [PubMed]
- Weidt, G.; Utermöhlen, O.; Heukeshoven, J.; Lehmann-Grube, F.; Deppert, W. Relationship Among Immunodominance of Single CD8+ T Cell Epitopes, Virus Load, and Kinetics of Primary Antiviral CTL Response. J. Immunol. 1998, 160, 2923–2931. [Google Scholar] [PubMed]
- Appay, V.; Douek, D.C.; Price, D.A. CD8+ T cell efficacy in vaccination and disease. Nat. Med. 2008, 14, 623–628. [Google Scholar] [CrossRef]
- D’Argenio, D.A.; Wilson, C.B. A Decade of Vaccines: Integrating Immunology and Vaccinology for Rational Vaccine Design. Immunity 2010, 33, 437–440. [Google Scholar] [CrossRef]
- Schubert, C. Boosting our best shot. Nat. Med. 2009, 15, 984–988. [Google Scholar] [CrossRef]
- Palmowski, M.J.; Choi, E.M.L.; Hermans, I.F.; Gilbert, S.C.; Chen, J.L.; Gileadi, U.; Salio, M.; Pel, A.V.; Man, S.; Bonin, E.; et al. Competition Between CTL Narrows the Immune Response Induced by Prime-Boost Vaccination Protocols. J. Immunol. 2002, 168, 4391–4398. [Google Scholar] [CrossRef]
- Kardani, K.; Bolhassani, A.; Shahbazi, S. Prime-boost vaccine strategy against viral infections: Mechanisms and benefits. Vaccine 2016, 34, 413–423. [Google Scholar] [CrossRef] [PubMed]
- Narayan, S.; Choyce, A.; Fernando, G.; Leggatt, G. Secondary immunisation with high-dose heterologous peptide leads to CD8 T cell populations with reduced functional avidity. Eur. J. Immunol. 2007, 37, 406–415. [Google Scholar] [CrossRef] [PubMed]
- Woodland, D.L. Jump-starting the immune system: Prime-boosting comes of age. Trends Immunol. 2004, 25, 98–104. [Google Scholar] [CrossRef]
- Woodberry, T.; Gardner, J.; Elliott, S.L.; Leyrer, S.; Purdie, D.M.; Chaplin, P.; Suhrbier, A. Prime Boost Vaccination Strategies: CD8 T Cell Numbers, Protection, and Th1 Bias. J. Immunol. 2003, 170, 2599–2604. [Google Scholar] [CrossRef] [PubMed]
- Athale, S.; Banchereau, R.; Thompson-Snipes, L.; Wang, Y.; Palucka, K.; Pascual, V.; Banchereau, J. Influenza vaccines differentially regulate the interferon response in human dendritic cell subsets. Sci. Transl. Med. 2017, 9. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).