Intelligent Agents in Co-Evolving Knowledge Networks
Abstract
1. Introduction
- (CF1) The structure of the network;
- (CF2) The evolutionary dynamics of the network;
- (CF3) The presence of agents creating knowledge (innovative agents);
- (CF4) The initial knowledge of the agents;
- (CF5) The presence of agents with false beliefs (negative knowledge level);
- (CF6) The presence of unreliable communication channels (negative weights);
- (CF7) The selection rule () of agents for communication and knowledge acquisition;
- (CF8) The filtering rule () of agents for excluding other agents for knowledge acquisition;
- (CF9) The order of implementation of the selection rule (CF7) and the filtering rule (CF8) by the agents of the network;
- (CF10) The attacks at nodes or links;
- (CF11) The position of experts (highly knowledgeable agents) within the network.
2. The Model
- Non-lineardue to the term(Assumption 2);
- Non-homogeneousdue to the different, non-stationary weights(Definition 1).
- If the in-neighbor agentis selected, the corresponding weightmay change due to the relevance feedback learning.
- If the in-neighbor agentis not selected, the corresponding weightis subjected to decay with time.
3. Estimating the Dynamics of Network Co-Evolution
- The average knowledge of the agents and the “knowledge inequality” (standard deviation of knowledge of the agents);
- The average selection entropy of the agents;
- The out-degree centralization of the network.
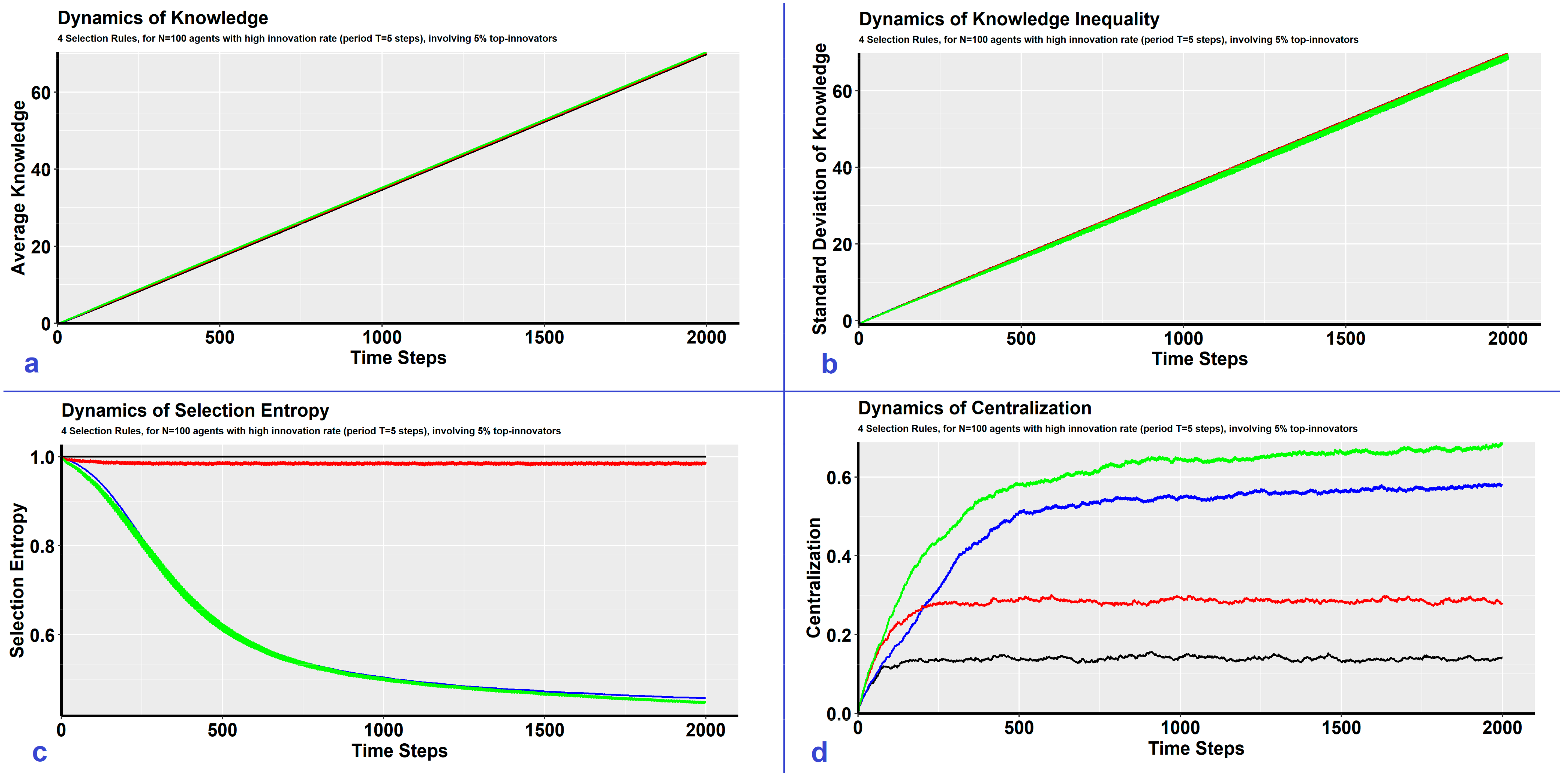
4. The Impact of Intelligence—Selection Rule
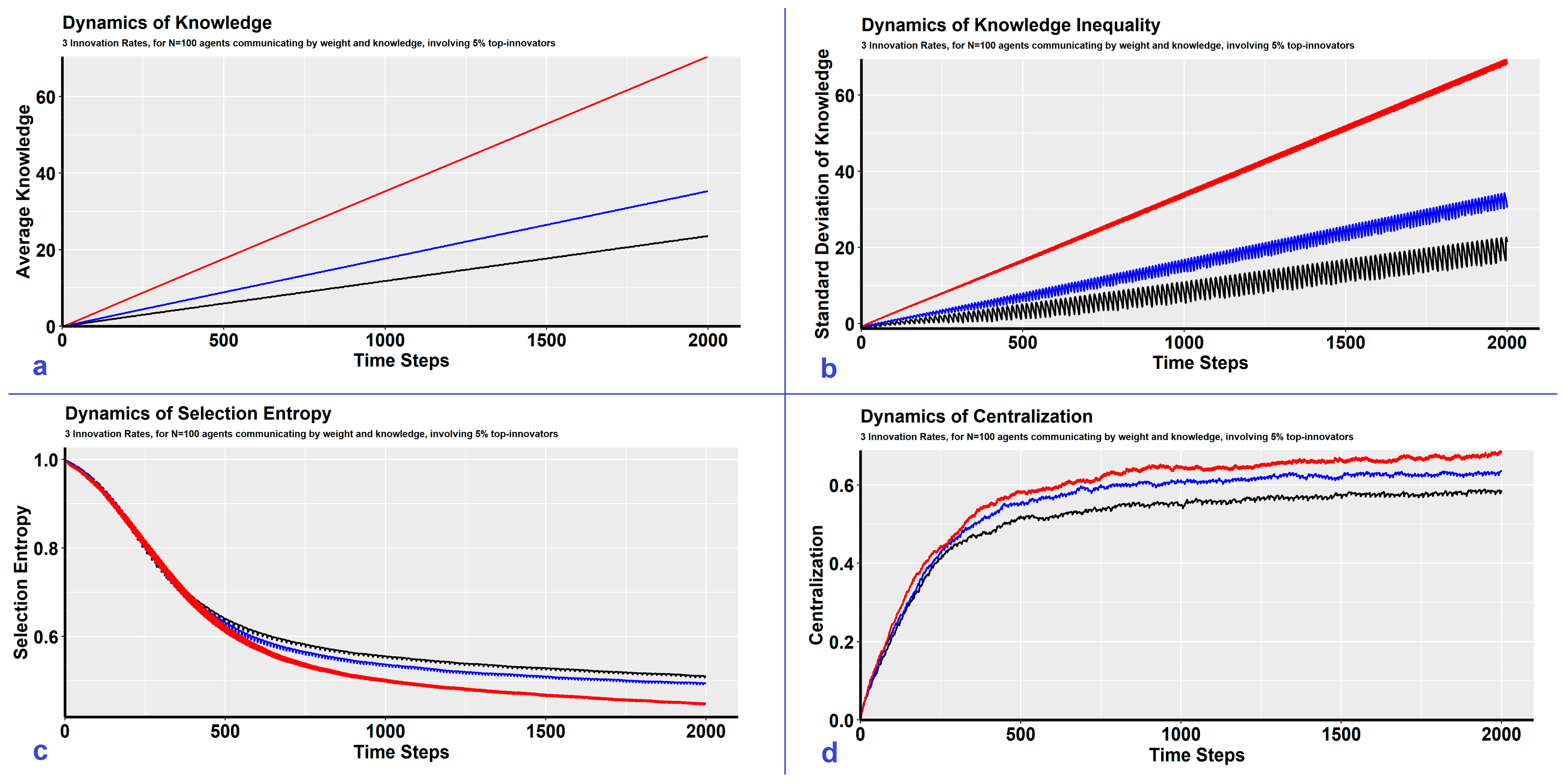
5. The Impact of the Innovation Rate
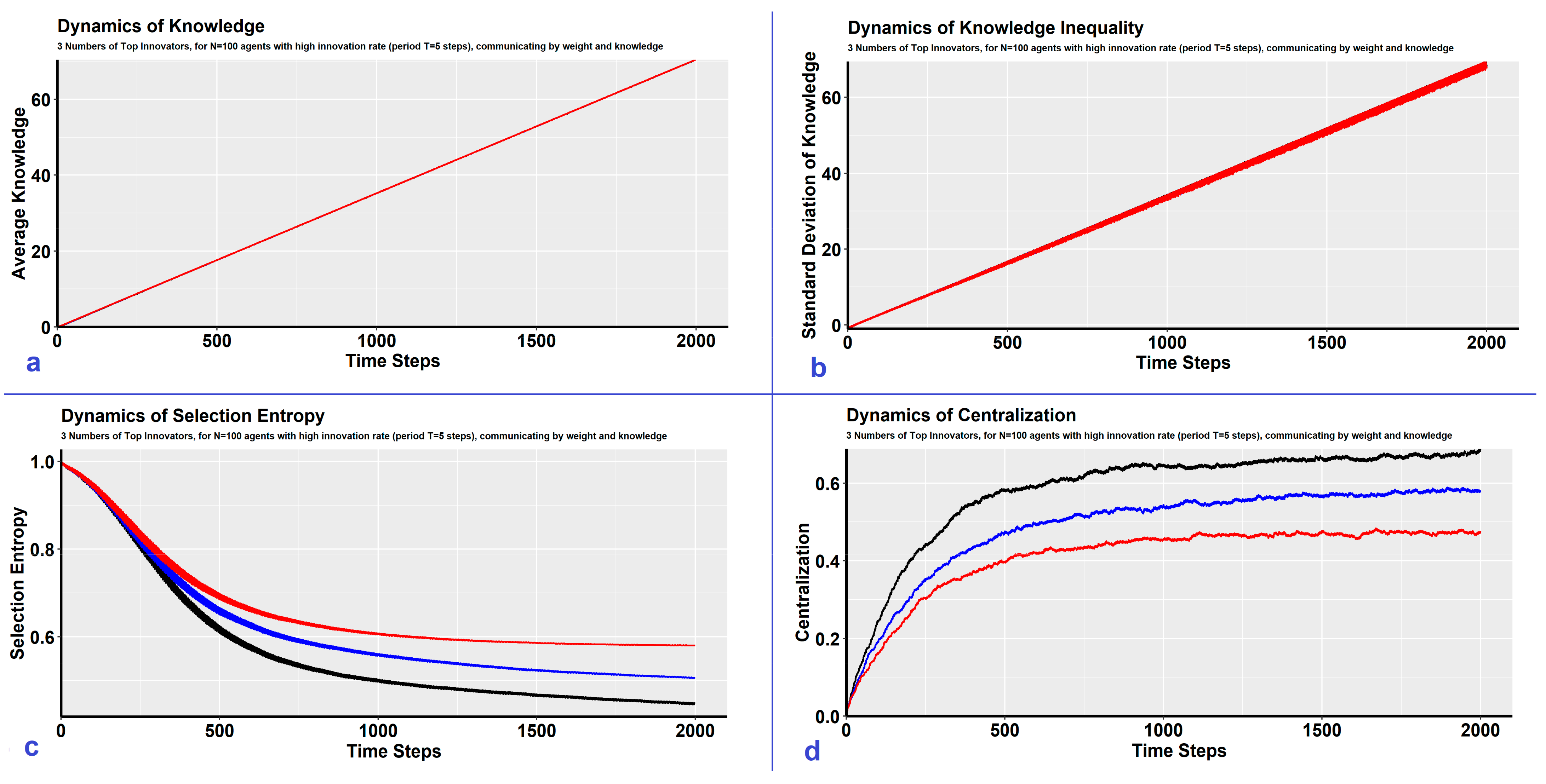
6. The Impact of the Number of Top Innovators
7. The Impact of Network Size
8. Discussion
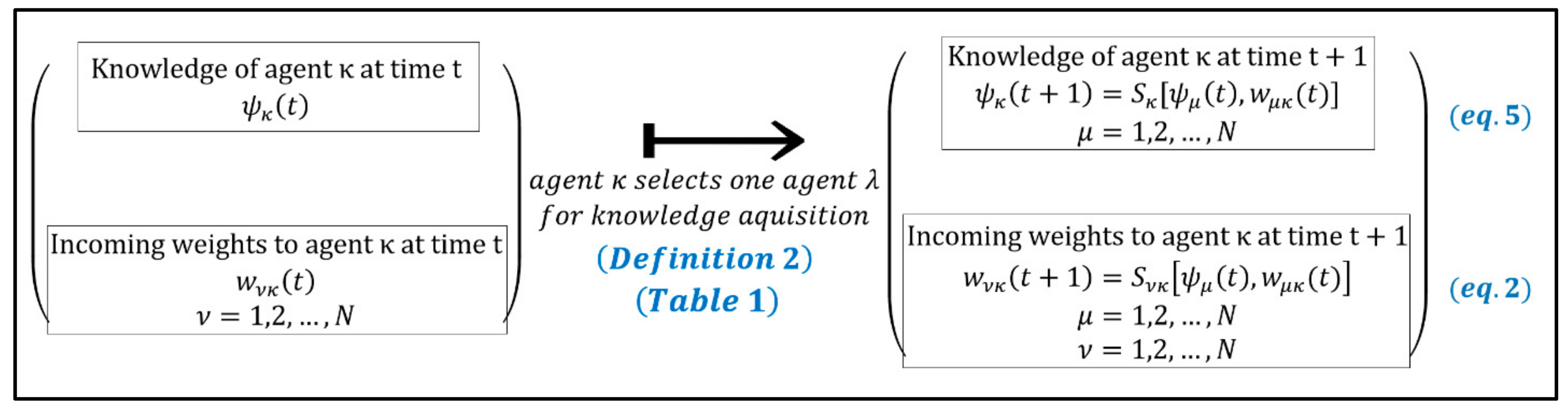
- The agents (human beings or intelligent machines) are able to make mindful decisions for knowledge acquisition. The decisions of intelligent rational agents are realized under bounded rationality [25,26]. If the bound of rationality, concerning the selections of other agents for knowledge acquisition is lower, then the agent is considered as more intelligent (Definition 2, Table 1).
- We formulated the co-evolution of the link weights and the knowledge levels at the local microscopic level of “agent-to-agent” interaction. The model describes the “structural plasticity” of the network as a “learning mechanism”, where weight updates depend on the previous values of both weights and knowledge levels. As a result, the co-evolution is intrinsic/endogenous (Definition 4, Remark 3).
9. Conclusions
10. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kirman, A. The economy as an evolving network. J. Evol. Econ. 1997, 7, 339–353. [Google Scholar] [CrossRef]
- Antoniou, I.; Reeve, M.; Stenning, V. The Information Society as a Complex System. J. Univers. Comput. Sci. 2000, 6, 272–288. [Google Scholar] [CrossRef]
- Schweitzer, F.; Fagiolo, G.; Sornette, D.; Vega-Redondo, F.; Vespignani, A.; White, D.R. Economic Networks: The New Challenges. Science 2009, 325, 422–425. [Google Scholar] [CrossRef] [PubMed]
- Castells, M. The Rise of the Network Society (The Information Age: Economy, Society, and Culture), 2nd ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2000; Volume 1. [Google Scholar]
- Hansen, M.T. Knowledge Networks: Explaining Effective Knowledge Sharing in Multiunit Companies. Organ. Sci. 2002, 13, 232–248. [Google Scholar] [CrossRef]
- Wang, S.; Noe, R.A. Knowledge sharing: A review and directions for future research. Hum. Resour. Manag. Rev. 2010, 20, 115–131. [Google Scholar] [CrossRef]
- Phelps, C.C.; Heidl, R.; Wadhwa, A. Knowledge, Networks, and Knowledge Networks. J. Manag. 2012, 38, 1115–1166. [Google Scholar] [CrossRef]
- Ioannidis, E.; Varsakelis, N.; Antoniou, I.; Evangelos, I.; Nikos, V.; Ioannis, A. False Beliefs in Unreliable Knowledge Networks. Phys. A Stat. Mech. Its Appl. 2017, 470, 275–295. [Google Scholar] [CrossRef]
- Ioannidis, E.; Varsakelis, N.; Antoniou, I. Communication Policies in Knowledge Networks. Phys. A Stat. Mech. Its Appl. 2018, 492, 360–374. [Google Scholar] [CrossRef]
- Ioannidis, E.; Varsakelis, N.; Antoniou, I. Experts in Knowledge Networks: Central Positioning and Intelligent Selections. Phys. A Stat. Mech. Its Appl. 2018, 509, 890–905. [Google Scholar] [CrossRef]
- Ioannidis, E. Modeling Knowledge Networks. Ph.D. Thesis, Aristotle University of Thessaloniki, Thessaloniki, Greece, 2018. Available online: https://ikee.lib.auth.gr/record/297396/files/GRI-2018-21354.pdf (accessed on 20 November 2020).
- Cowan, R.; Jonard, N. The dynamics of collective invention. J. Econ. Behav. Organ. 2003, 52, 513–532. [Google Scholar] [CrossRef]
- Cowan, R.; Jonard, N. Network structure and the diffusion of knowledge. J. Econ. Dyn. Control 2004, 28, 1557–1575. [Google Scholar] [CrossRef]
- Kim, H.; Park, Y. Structural effects of R&D collaboration network on knowledge diffusion performance. Expert Syst. Appl. 2009, 36, 8986–8992. [Google Scholar] [CrossRef]
- Tang, F.; Xi, Y.; Ma, J. Estimating the effect of organizational structure on knowledge transfer: A neural network approach. Expert Syst. Appl. 2006, 30, 796–800. [Google Scholar] [CrossRef]
- Tang, F.; Mu, J.; MacLachlan, D.L. Disseminative capacity, organizational structure and knowledge transfer. Expert Syst. Appl. 2010, 37, 1586–1593. [Google Scholar] [CrossRef]
- Lin, M.; Li, N. Scale-free network provides an optimal pattern for knowledge transfer. Phys. A Stat. Mech. Its Appl. 2010, 389, 473–480. [Google Scholar] [CrossRef]
- Xuan, Z.; Xia, H.; Du, Y. Adjustment of knowledge-connection structure affects the performance of knowledge transfer. Expert Syst. Appl. 2011, 38, 14935–14944. [Google Scholar] [CrossRef]
- Xia, H.; Du, Y.; Xuan, Z. Structural Evolution in Knowledge Transfer Network: An Agent-Based Model. In Artificial Intelligence: Foundations, Theory, and Algorithms; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2013; Volume 424, pp. 31–38. [Google Scholar]
- Luo, S.; Du, Y.; Liu, P.; Xuan, Z.; Wang, Y. A study on coevolutionary dynamics of knowledge diffusion and social network structure. Expert Syst. Appl. 2015, 42, 3619–3633. [Google Scholar] [CrossRef]
- Jian-Guo, L.; Zhou, Q.; Guo, Q.; Yang, Z.-H.; Xie, F.; Han, J.-T. Knowledge diffusion of dynamical network in terms of interaction frequency. Sci. Rep. 2017, 7, 10755. [Google Scholar] [CrossRef]
- Liu, J.-G.; Yang, G.-Y.; Hu, Z.-L. A Knowledge Generation Model via the Hypernetwork. PLoS ONE 2014, 9, e89746. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Yang, G.-Y.; Hu, Z.-L.; Liu, J.-G. Knowledge diffusion in the collaboration hypernetwork. Phys. A Stat. Mech. Appl. 2015, 419, 429–436. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, W.; Zhao, L. A study of knowledge supernetworks and network robustness in different business incubators. Phys. A Stat. Mech. Appl. 2016, 447, 545–560. [Google Scholar] [CrossRef]
- Simon, H.A. A Behavioral Model of Rational Choice. Q. J. Econ. 1955, 69. [Google Scholar] [CrossRef]
- Simon, H.A. Rational Decision Making in Business Organizations. Am. Econ. Rev. 1979, 69, 493–513. Available online: http://www.jstor.org/stable/1808698 (accessed on 20 November 2020).
- Wang, J.-P.; Guo, Q.; Yang, G.-Y.; Liu, J.-G. Improved knowledge diffusion model based on the collaboration hypernetwork. Phys. A Stat. Mech. Appl. 2015, 428, 250–256. [Google Scholar] [CrossRef]
- Lin, M.; Wei, J. The impact of innovation intermediary on knowledge transfer. Phys. A Stat. Mech. Appl. 2018, 502, 21–28. [Google Scholar] [CrossRef]
- Ioannidis, E.; Varsakelis, N.; Antoniou, I. Promoters versus Adversaries of Change: Agent-Based Modeling of Organizational Conflict in Co-Evolving Networks. Mathematics 2020, 8, 2235. [Google Scholar] [CrossRef]
- Wi, H.; Oh, S.; Mun, J.; Jung, M. A team formation model based on knowledge and collaboration. Expert Syst. Appl. 2009, 36, 9121–9134. [Google Scholar] [CrossRef]
- Gladstones, W.H.; Regan, M.A.; Lee, R.B. Division of Attention: The Single-Channel Hypothesis Revisited. Q. J. Exp. Psychol. Sect. A 1989, 41, 1–17. [Google Scholar] [CrossRef]
- Pashler, H. Dual-task interference in simple tasks: Data and theory. Psychol. Bull. 1994, 116, 220–244. [Google Scholar] [CrossRef]
- Indermühle, R.; Troche, S.; Rammsayer, T. Personality and the psychological refractory period: No evidence for an extraversion- or intelligence-related effect. Can. J. Behav. Sci. Rev. Can. des Sci. du Comport. 2011, 43, 214–221. [Google Scholar] [CrossRef]
- Cowan, R.; Jonard, N.; Özman, M. Knowledge dynamics in a network industry. Technol. Forecast. Soc. Chang. 2004, 71, 469–484. [Google Scholar] [CrossRef]
- Knuth, D.E. Two Notes on Notation. Am. Math. Mon. 1992, 99, 403–422. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, H.; Wu, W. Knowledge service decision making in business incubators based on the supernetwork model. Phys. A Stat. Mech. Appl. 2017, 479, 249–264. [Google Scholar] [CrossRef]
- Ioannidis, E.; Varsakelis, N.; Antoniou, I. Change agents and internal communications in organizational networks. Phys. A Stat. Mech. Appl. 2019, 528, 121385. [Google Scholar] [CrossRef]
- Havlin, S.; Ben-Avraham, D. Diffusion in disordered media. Adv. Phys. 1987, 36, 695–798. [Google Scholar] [CrossRef]
- Skarpalezos, L.; Kittas, A.; Argyrakis, P.; Cohen, R.; Havlin, S. Anomalous biased diffusion in networks. Phys. Rev. E 2013, 88, 012817–012823. [Google Scholar] [CrossRef]
- Wang, H.; Chen, C.; Qu, B.; Li, D.; Havlin, S. Epidemic mitigation via awareness propagation in communication networks: The role of time scales. New J. Phys. 2017, 19, 073039. [Google Scholar] [CrossRef]
- Zhuang, E.; Chen, G.; Feng, G. A network model of knowledge accumulation through diffusion and upgrade. Phys. A Stat. Mech. Appl. 2011, 390, 2582–2592. [Google Scholar] [CrossRef]
- Graupe, D. Principles of Artificial Neural Networks, 3rd ed.; World Scientific: Singapore, 2013. [Google Scholar]
- Fan, K.; Pedrycz, W. Opinion evolution influenced by informed agents. Phys. A Stat. Mech. Appl. 2016, 462, 431–441. [Google Scholar] [CrossRef]
- Zhu, H.-M.; Zhang, S.-T.; Jin, Z. The effects of online social networks on tacit knowledge transmission. Phys. A Stat. Mech. Appl. 2016, 441, 192–198. [Google Scholar] [CrossRef]
- Gladwell, M. The Tipping Point: How Little Things Can Make a Big Difference; Hachette Book Group: New York, NY, USA, 2002. [Google Scholar]
- Dunbar, R. How Many Friends Does One Person Need? Dunbar’s Number and Other Evolutionary Quirks; Harvard University Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Tur, E.M.; Azagra-Caro, J.M. The coevolution of endogenous knowledge networks and knowledge creation. J. Econ. Behav. Organ. 2018, 145, 424–434. [Google Scholar] [CrossRef]
- Morone, P.; Taylor, R. Knowledge diffusion dynamics and network properties of face-to-face interactions. J. Evol. Econ. 2004, 14, 327–351. [Google Scholar] [CrossRef]
- Cremonini, M. Introducing serendipity in a social network model of knowledge diffusion. Chaos Solitons Fractals 2016, 90, 64–71. [Google Scholar] [CrossRef]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef]
- Angelidis, G.; Ioannidis, E.; Makris, G.; Antoniou, I.; Varsakelis, N. Competitive Conditions in Global Value Chain Networks: An Assessment Using Entropy and Network Analysis. Entropy 2020, 22, 1068. [Google Scholar] [CrossRef]
- Thurner, S.; Klimek, P.; Hanel, R. Introduction to the Theory of Complex Systems; Oxford University Press (OUP): Oxford, UK, 2018. [Google Scholar]
- Zimmermann, M.G.; Eguíluz, V.M.; Miguel, M.S. Coevolution of dynamical states and interactions in dynamic networks. Phys. Rev. E 2004, 69, 065102. [Google Scholar] [CrossRef]
- Vazquez, F.; Eguíluz, V.M.; Miguel, M.S. Generic Absorbing Transition in Coevolution Dynamics. Phys. Rev. Lett. 2008, 100, 108702. [Google Scholar] [CrossRef]
- Biely, C.; Hanel, R.; Thurner, S. Socio-economical dynamics as a solvable spin system on co-evolving networks. Eur. Phys. J. B 2008, 67, 285–289. [Google Scholar] [CrossRef][Green Version]
- Diakonova, M.; Eguíluz, V.M.; Miguel, M.S. Noise in coevolving networks. Phys. Rev. E 2015, 92, 032803. [Google Scholar] [CrossRef]
- Min, B.; Miguel, M.S. Fragmentation transitions in a coevolving nonlinear voter model. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef]
- Raducha, T.; Min, B.; Miguel, M.S. Coevolving nonlinear voter model with triadic closure. EPL Europhys. Lett. 2018, 124, 1–6. [Google Scholar] [CrossRef]
- Kurzweil, R. The Age of Spiritual Machines: When Computers Exceed Human Intelligence; Viking Press: New York, NY, USA, 1999. [Google Scholar]
- Pan, R.K.; Petersen, A.M.; Pammolli, F.; Fortunato, S. The memory of science: Inflation, myopia, and the knowledge network. J. Inf. 2018, 12, 656–678. [Google Scholar] [CrossRef]
- Cairncross, F. The Death of Distance: How the Communications Revolution Is Changing our Lives; Harvard University Press: Cambridge, MA, USA, 2001. [Google Scholar]
| Selection Rule | Selection Probability | Bound of Rationality |
|---|---|---|
| Random | All incoming links have equal selection probability. There is no rationality, as communication is random. The agent has no intelligence. | |
| Knowledge | More knowledgeable in-neighbors have higher selection probability Rationality is limited to the awareness of the knowledge of the in-neighbors. The agent has knowledge-based intelligence. | |
| Weight | Higher incoming weights have higher selection probability. Rationality is limited to the awareness of the incoming weights. The agent has weight-based intelligence. | |
| Knowledge-Weight | Higher product of have higher selection probability Rationality is limited to the awareness of the incoming weights and the knowledge of the in-neighbors. The agent has both knowledge and weight-based intelligence. The agent has finer discrimination capability, lower bound of rationality and higher intelligence (Definition 2), compared to the other cases. |
| Knowledge | All agents have Equal Initial knowledge level, with value |
| Links | Off-diagonal weights are initially equal, with value Fully connected network structure with evolving weights |
| Diagonal weights are constant in time (Remark 2) The value of most diagonal weights is . We assume a small number (5%, 10%, 15%) of randomly distributed “top innovators” (highly innovative agents) with |
| Parameter | Values |
|---|---|
| Selection Rule (CF7) for knowledge acquisition (Definition 2, Table 1) | Random |
| Knowledge | |
| Weight | |
| Knowledge and Weight | |
| Innovation Rate (CF3) (period for innovation production, Assumption 3) | Low steps |
| Medium steps | |
| High steps | |
| Number of Top Innovators (CF3) (highly innovative agents, Table 2) | Few |
| Some | |
| Many | |
| Network Size | Small agents |
| Medium agents | |
| High agents |
| Parameter (Table 3) | |||||
|---|---|---|---|---|---|
| Increase of Intelligence (CF7) | Increase of Innovation Rate (CF3) | Decrease of Number of Top Innovators (CF3) | Decrease of Network Size | ||
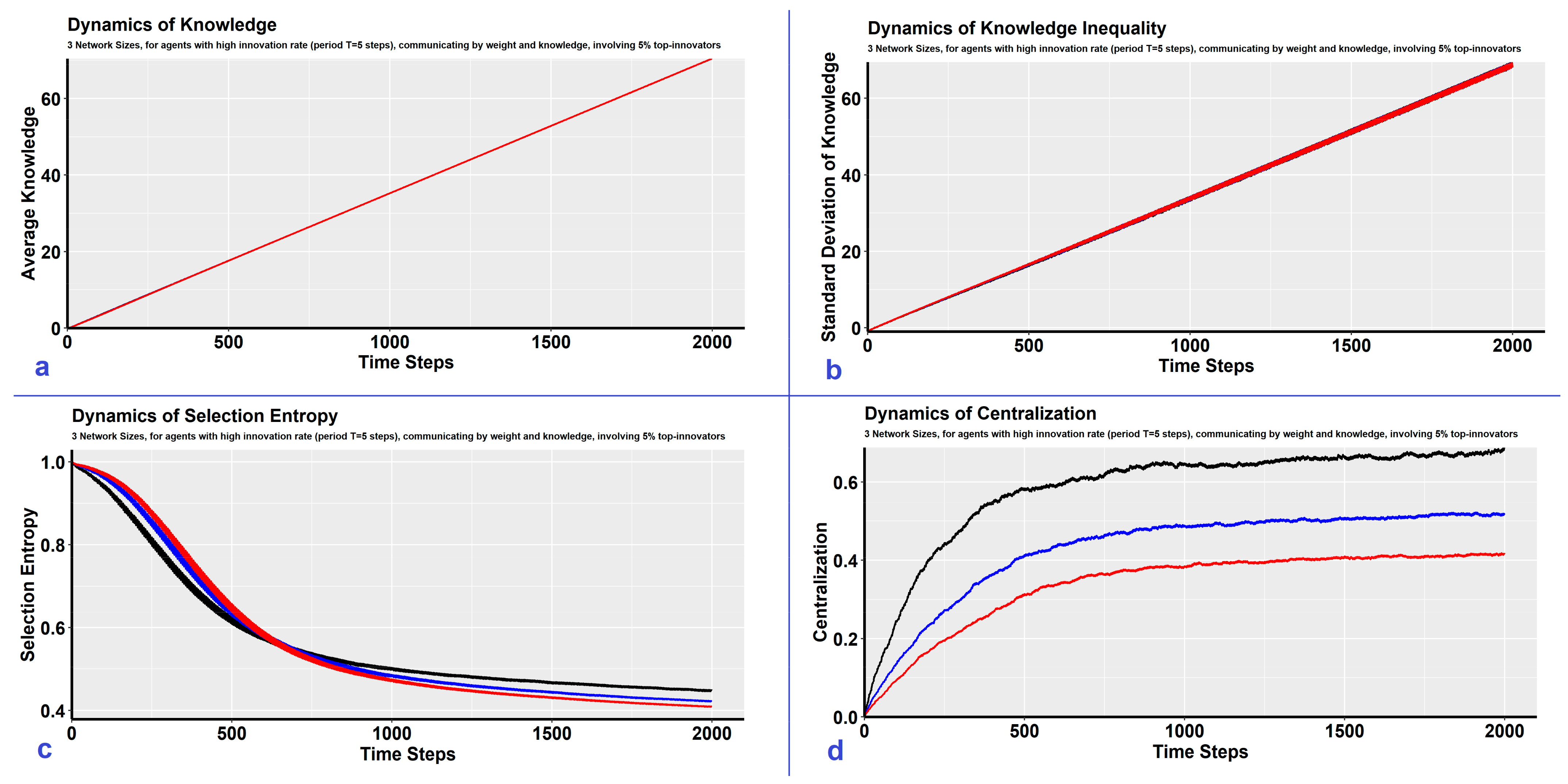
| Impact Assessment | Average Knowledge | negligible impact (Figure 2a) | increase (Figure 3a) | negligible impact (Figure 4a) | negligible impact (Figure 5a) |
| Knowledge Inequality | negligible impact (Figure 2b) | increase (Figure 3b) | negligible impact (Figure 4b) | negligible impact (Figure 5b) | |
| Selection Entropy | decrease (Figure 2c) | decrease (Figure 3c) | decrease (Figure 4c) | negligible impact (Figure 5c) | |
| Network Centralization | increase (Figure 2d) | increase (Figure 3d) | increase (Figure 4d) | increase (Figure 5d) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ioannidis, E.; Varsakelis, N.; Antoniou, I. Intelligent Agents in Co-Evolving Knowledge Networks. Mathematics 2021, 9, 103. https://doi.org/10.3390/math9010103
Ioannidis E, Varsakelis N, Antoniou I. Intelligent Agents in Co-Evolving Knowledge Networks. Mathematics. 2021; 9(1):103. https://doi.org/10.3390/math9010103
Chicago/Turabian StyleIoannidis, Evangelos, Nikos Varsakelis, and Ioannis Antoniou. 2021. "Intelligent Agents in Co-Evolving Knowledge Networks" Mathematics 9, no. 1: 103. https://doi.org/10.3390/math9010103
APA StyleIoannidis, E., Varsakelis, N., & Antoniou, I. (2021). Intelligent Agents in Co-Evolving Knowledge Networks. Mathematics, 9(1), 103. https://doi.org/10.3390/math9010103







