In the literature, ad-hoc verifications are traditionally used; meaning, verifications that employ more than one distinct formalism.
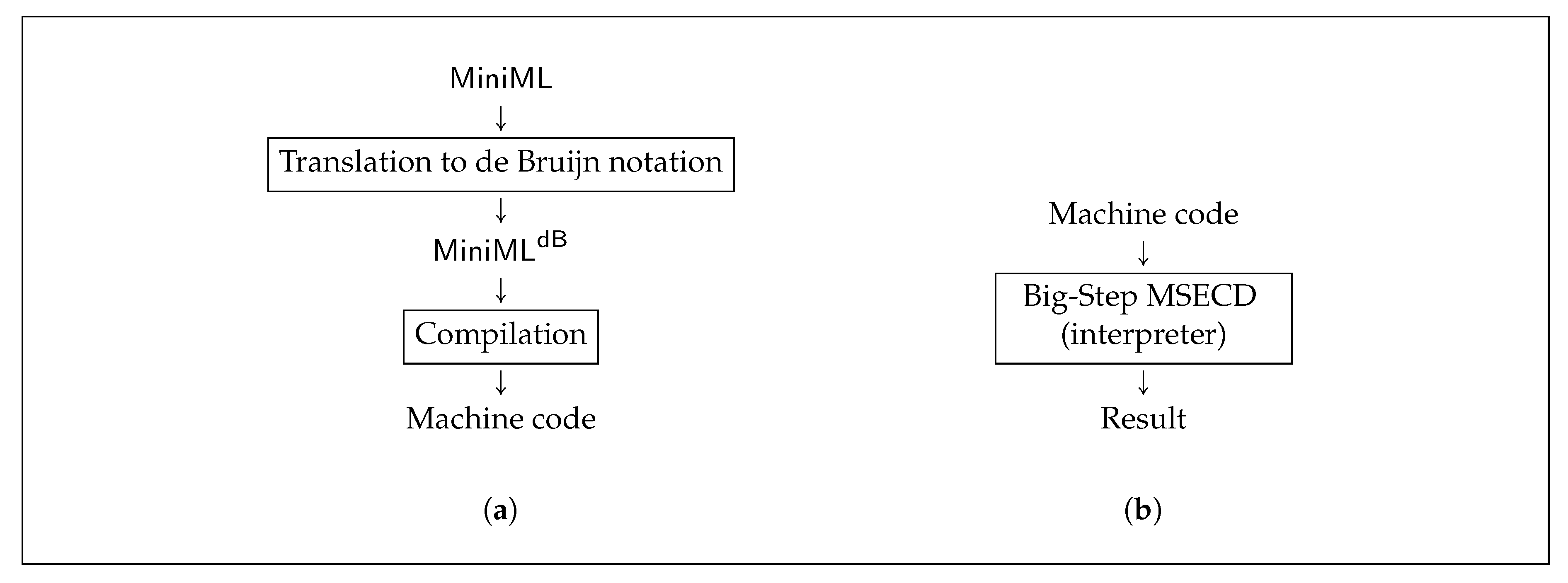
The main idea of this work is to extend natural semantics so that it becomes a simple, easy, and intuitive unifying framework for verifying total correctness of compilers in Coq (with the ability that you can get a verified compiler that can be used in real life).
1.1. Related Work
Since CompCert C [
1,
2,
3,
4,
5] project’s inception led by Leroy, there has been great progress in the literature dedicated to compiler verification using proof assistants, Coq in particular. In this work, we address specifically functional programming languages verification. In principle, verification of functional programming languages to abstract machines.
An unusual technique exposed by Hardin et al. [
16] to carry out the verification of a functional language to an abstract machine is to use small-step semantics, both in the source language and in the abstract machine, together with a decompilation function and a measure to establish correctness. The idea of this technique is to perform a bottom-up simulation in which every machine transition corresponds to zero or one source level reductions. The machine states are mapped back to source level expressions using a decompilation function. More precisely, if from a machine state
s a state
is reached via a machine transition
, and
e is the source language expression corresponding to the state
s via decompilation, then there exists an expression
corresponding to
via decompilation, such that
or
e reduces to
via source language small-step semantics
. When a machine performs a transition from a state to another and the decompilation of both states corresponds to the same expression in the source language, the machine performs a
silent transition. To guarantee that there are not infinitely many silent machine transitions, a measure defined on the machine states is used. i.e., if
and the decompilation of
s and
corresponds to the same expression
e, then
s measure is greater than that of
.
Gregoire and Leroy [
9] and Gregoire [
17] use this technique to verify a compiler from a strong reduction lambda calculus to an abstract machine in Coq; more precisely, to verify the correctness of a compiler from the Calculus of Inductive Constructions (CIC) to a variant of the ZAM machine [
18] (adapted to support weak symbolic reduction), obtaining a compiler-based verified implementation to evaluate Coq terms. In addition, they show that this compiler-based implementation is more efficient than the original Coq interpreter as expected. More recently, Kunze et al. [
19] employ a very similar technique to verify the correctness of a compiler from a call-by-value lambda calculus to an abstract machine in Coq.
However, Leroy [
8,
14] and Leroy and Grall [
15] point out that a correctness proof using this technique is difficult, and also that the definition of a decompilation is complicated, hard to reason about, and hard to extend (especially for optimizing compilation phases). In consequence, they propose a solution based on big-step semantics. In fact, they state that proving semantic preservation for compilers both for terminating and diverging programs using big-step semantics is the original motivation of their work.
The Leroy [
14] and Leroy and Grall [
15] technique consists of using (coinductive) big-step semantics in the source language but small-step semantics in the machine. In this way, for the termination case, if a source language expression
e evaluates to
v via big-step semantics
, then reducing the machine code
c via transitive closure of small-step semantics
, takes the machine to a state with
at the top of the stack, where
c corresponds to
e compilation and
is the machine value corresponding to
v. For the non-termination case, if
e diverges using coinductive big-step semantics, then
c also diverges in the machine. Leroy and Grall mention that their technique provides a simpler way to prove semantics preservation, in particular for the non-termination case.
Currently, it is well known [
14,
15,
20,
21] that big-step semantics are easier and more convenient for compiler correctness proofs, and also for efficient interpreters [
21]. Thus, we have on one hand that Leroy and Grall main motivation is to use big-step semantics for compiler correctness proofs, and on the other that big-step semantics has proved to be easier and more convenient for compiler correctness proofs. Our aim is to take big-step semantics to its deepest consequences exploiting it where it has proved to be useful. This is why we propose (coinductive) natural semantics as framework for compiler verification.
(Coinductive) natural semantics as framework for compiler verification in Coq as proposed in this paper is a technique very similar in spirit to that of Leroy and Grall, but going further since not only (coinductive) big-step semantics is used in the source language but also in the target machine (let us recall that Leroy and Grall employ small-step semantics in the machine). Furthermore, to the best of the author’s knowledge, it is the first time that coinductive natural semantics is proposed and used to define computations that do not terminate in an abstract machine. In this way, we obtain a fully-based (coinductive) natural semantics technique for a functional language to an abstract machine compiler correctness verification in Coq.
Establishing correctness is even easier, intuitive and simple since natural semantics are also used in the machine. If a source language expression e is evaluated to a value v via source language natural semantics , then c is evaluated to a final machine state with at the top of the stack via machine natural semantics ; where c is the compilation of e via natural semantics , and is the compilation of v via natural semantics , and s is any machine stack. If e diverges via coinductive natural semantics , then c also diverges via machine coinductive natural semantics . We can note here, how only (coinductive) natural semantics is sufficient to establish correctness; we do not need to use any other distinct formalism.
A potential use of this framework is to take it as basis to verify a conventional compiler to abstract machine implementation of (the core of) a realistic functional language such as OCaml. The official INRIA OCaml implementation comes with two compilers [
22], the first one generates code of the ZAM machine, and the second one generates C-- code. We speculate that this framework can also be used as basis to verify the compiler that generates C-- since Dargaye [
23] already uses big-step semantics (although not as unifying framework and only tackling terminating computations) to verify a compiler from Mini-ML to Cminor (an early intermediate language of the CompCert C compiler). The idea of generating Cminor (or some other Compcert C intermediate language) code instead of C-- is immediate since, in this way, we can connect the compiler’s back-end to CompCert C and obtain as final result verified assembly code. This use takes more relevance if we take into account that Coq itself is an OCaml program (even though some portions of Coq are verified in Coq [
24,
25,
26], the extracted verified OCaml code will eventually run on an OCaml implementation).
Another line of work is dedicated to systematically derive an abstract machine from a lambda calculus [
27,
28,
29,
30,
31,
32,
33]. The general idea in these works is from a lambda calculus to carry out a series of transformations until the desired abstract machine is obtained. One of the most exploited transformations in some of these works is refocusing [
34], although a great variety of transformations are used. The compilation correctness is a direct consequence of the correctness of the transformations. Some of them, in addition, address Coq formalization [
29,
30,
31,
32,
33]. The closest works to ours are those which starting from a natural semantics of a lambda calculus derive an abstract machine [
27,
30]. Specifically, the most similar work in nature to ours is [
30]. In [
30], the STG machine is derived from natural semantics of a lazy lambda calculus and the derivation is formalized in Coq. However, in [
30] only the case for terminating computations is tackled.
In all these works, the emphasis is on the corresponding machine derivation. In contrast, in a functional language implementation the target abstract machine is usually designed by hand and only then (if any) proved correct w.r.t source lambda calculus semantics (see, for example, [
18]). Hence, (coinductive) natural semantics as framework as presented in this paper is best suited to verify functional languages implementations (which targets abstract machines), since it assumes that the target machine (and intermediate languages) are given (not to be derived).
Moreover, if for some reason (for example, semantic justification of the target abstract machine) it is considered relevant to systematically derive the target abstract machine from the source calculus, we conjecture that the corresponding derivation can also be carried out in our (coinductive) natural semantics framework. This is because each transformation which leads to the derived machine could be seen as an (intermediate) translation and be defined in natural semantics. Also, the input and output language of each transformation could be seen as an (intermediate) language and its corresponding semantics be defined in natural semantics. Certainly, the derived abstract machine would be a big-step machine.
Other works tackle the verification of a small functional language in Coq, but to the authors’ knowledge none of them use (coinductive) natural semantics as unifying framework; instead, they use ad-hoc verifications. For instance, Chlipala [
35] offers a compiler from a small impure functional language to an idealized assembly language. He starts from de Bruijn notation and employs natural semantics for the source and target languages, but not to specify the compilation, his effort only cover terminating computations. Benton and Hur [
36] deal with the compilation of a small typed functional language to the SECD machine, but they use denotational semantics for the source language and small-step semantics for the target machine. In addition, Benton and Hur employ a biorthogonality step-indexed logical relation to establish correctness. As mentioned before, Dargaye [
23] develops a compiler from Mini-ML to C minor, but it is not designed to be a standalone general-purpose Mini-ML implementation. Instead, it was conceived to work only on the code generated by the Coq extraction mechanism. The Coq extraction mechanism generates code of a real-life functional language, by default OCaml, but it is also able to generate Scheme and Haskell code. This is why in Dargaye’s work, it only makes sense to cover terminating computations since the Coq’s calculus, the Calculus of Inductive Constructions, is strongly normalizing [
37], meaning in Coq all computations must terminate. For this reason, all extracted code from Coq should be terminating, while in Coq this property is ensured by Coq’s type checker [
26]; the code generation translation performed by the Coq extraction mechanism is not verified, although some efforts are conducted in this direction [
6,
24,
25,
38,
39,
40].
The CertiCoq project [
6,
40,
41] aims to provide a verified extraction pipeline from the core language of Coq, Gallina, to machine language. Therefore, in CertiCoq it also only makes sense to cover terminating computations. This fact is explicitly stated in [
6]: ‘… we can restrict our reasoning to terminating programs since Coq is strongly normalizing. This way we avoid backward simulations (forward simulations proofs are much simpler) and avoid proving preservation of divergence’. Similarly, Savary Bélanger [
40] indicates: ‘In CertiCoq, we are only concerned with terminating programs: Gallina is strongly normalizing, and our proof of correctness ensures that programs do not acquire non-terminating behaviors along the way’.
Instead of producing machine code directly, CertiCoq generates C light (a CompCert C intermediate language) code. Hence, it uses CompCert C as verified compiler back-end to produce machine language. This way, CertiCoq compiler performs a series of phases from Galllina to Cligth. In CertiCoq, (intermediate) languages semantics and proofs of correctness are based on big-step semantics (for terminating computations). However, big-step semantics is refined with other notions such as step-indexed logical relations and context-based semantics [
40,
42] to account for additional properties, for instance, compositionality. In addition, the idea of adapting this technique to be useful for general-purpose programming languages is barely mentioned in [
40]. Albeit, for this purpose, Savary Bélanger [
40] suggests to employ small-step semantics. For their part, Paraskevopoulou and Appel [
42], in order to prove closure conversion correctness, they already extend this technique to cover non-termination computations under certain conditions. Closure conversion is a phase performed by CertiCoq.
Our (coinductive) natural semantics framework is best suited to verify usual functional language to abstract machine implementations since it accounts for both terminating and non-terminating computations (total correctness). In addition, it can express terminating and non-terminating computations in an abstract machine. In contrast, by design [
6] CertiCoq only covers terminating evaluations on one hand, and on the other it targets C light which is why no abstract machine is used. This situation reflects the fact that our (coinductive) natural semantics framework and CertiCoq pursuit different goals. Although our (coinductive) natural semantics framework is a framework to conduct total correctness compiler verification in Coq, CertiCoq is a verified compiler (from Coq’s core calculus to Clight). Hence, it is not an explicit CertiCoq main objective to offer an infrastructure to perform compiler verification [
6], even although, the infrastructure and techniques developed to verify the CertiCoq compiler could be adapted to be used to verify other compilers as well.
Step-indexed logical relations as shown by Ahmed [
43] serve to establish contextual equivalence between programs. We remark that step-indexed logical relations provide a way to deal with two compiler problems in particular; specifically, compositionality and secure compilation.
In [
44], Ahmed and Blume show how to use step-indexed logical relations together with small-step semantics to deal with a notion of secure compilation. Ahmed and Blume demonstrate their method, applying it to a typed closure conversion transformation. Patrignani et al. [
45] offer a recent survey of the formal approaches and techniques used in secure compilation. Certainly, this survey includes in particular works that employ step-indexed logical relations. Abate et al. [
46] study generalizations of trace-based compiler correctness criteria including some which accounts for secure compilation.
In order to account for compositionality, Perconti and Ahmed [
47] propose the use of a language in which all languages involved in a compilation pipeline can be embedded. Then, using a step-indexed logical relation and small-step semantics compositional compiler correctness is established in terms of the combined language. For their part, Neis et al. [
48] introduce parametric inter-language simulations (PILS) as a technique particularly suited to compositional compiler verification for higher-order imperative languages. In particular, they demonstrate their technique with Pilsner, a verified compositional compiler from a ML-like language to an assembly-like language. Patterson and Ahmed [
49] provide a framework for expressing different notions of compiler correctness, especially those which consider compiler compositionality.
Dreyer et al. [
50], in order to avoid tedious, error-prone and obscuring step-indexed arithmetic, instead of using explicit indices, they propose to ‘hide’ indices, internalizing them into a logic. The idea is to replace indices with a modal operator, this way obtaining a modal logic which they name LSLR. In particular, this idea is reused in IRIS. IRIS [
7,
51,
52,
53] is a concurrent separation logic framework implemented and verified in Coq. In this regard, Krebbers et al. [
53] comment: ‘We also show that the step-indexed “later” modality of Iris is an
essential source of complexity, in that removing it leads to a logical inconsistency’. Recently, Linn Georges et al. [
54] formalize a capability machine in IRIS. As Linn Georges et al. [
54] point out, capability machines are promising targets for secure compilers. Hence, the idea to extend IRIS to be used as secure compiler framework is imminent; in particular, to verify secure compilers from high-level concurrent languages to capability machines. However, to the authors’ knowledge, IRIS has never been used in this manner. A very similar goal is pursued by Cuellar et al. [
55] and Cuellar [
56] but extending CompCert C. To this end, they introduce the Concurrent Permission Machine (CPM). Certainly, C (with concurrency) is the source language in these works.
In retrospective, on one hand step-indexed logical relations have proved to be useful, in particular in secure compilation, compiler compositionality and concurrency; on the other hand, natural semantics has proved to be easier and more convenient than other formalisms (for instance, small-step semantics) for compiler correctness proofs. Hence, we speculate that both natural semantics and step-indexed logical relations can be combined in a single formalism that has the best properties of each one of them. In other words, we envisage the ambitious goal of reaching a single formalism that features secure compilation, compositional compilation, concurrency and be simple, easy and intuitive as possible.
Currently, our (coinductive) natural semantics framework does not account for secure compilation, compositionality nor concurrency. However, we conjecture that step-indexed logical relations can be adopted in it to address some or even all these features. The price paid for this effort would be to deal with the known complexity of step-indexed logical relations (although it could be ameliorated, for instance, by internalizing the indices in a natural semantics modal logic). At present, our (coinductive) natural semantics framework is simple, easy and intuitive.
The following are related semantics: coinductive big-step operational semantics [
14,
15], trace-based coinductive operational semantics [
57], pretty-big-step semantics [
20] and flag-based big-step semantics [
21].
The only one of these works that presents the verification of the correctness of a compiler is Leroy’s (an ad-hoc verification). This means that (coinductive) natural semantics is not used in any of them as a unifying framework for the verification of compiler correctness. Specifically, it is not used in the definition of the semantics of the machine (nor in that of its interpreter), it is not used to define the translations, and it is not used (both in the source language and in the target language) to establish, nor to prove the correctness of the translations. What it does, in each of them, is to present a natural semantics with coinduction of a high-level language (which would usually correspond to the source language in a compiler) and it is this aspect that we review next.
Leroy [
14] first expresses finite computations with natural semantics ‘evaluation’ and infinite computations ‘divergence’ with coinductive natural semantics, separately; this solution is clear and clean. After, he offers an alternative solution in which one finite and infinite computations are expressed in a single coinductive natural semantics ‘coevaluation’; however, this semantics does not behave well in the sense that on one hand, there are infinite computations that it is not able to express, and on the other, there are infinite computations that are evaluated to any value
v. Nakata and Uustalu [
57] remark that this behavior appears accidental and undesired.
Nakata and Uustalu [
57] define a coinductive natural semantics of the While language that expresses finite and infinite computations; the careful and ad-hoc design of semantics follows, and within it that of small-step semantics. Additionally, Nakata and Uustalu define an interpreter using the trace monad and they show that it is correct regarding such semantics. Nakata and Uustalu’s work [
57] is the only one of the related works presented here in which an interpreter is presented.
Charguéraud [
20] introduces pretty-big-step semantics, a semantics based on ‘coevaluation’ of Leroy. Unfortunately, pretty-big-step semantics inherits the not well behavior of ‘coevaluation’. In turn, Bach Poulsen and Mosses [
21] define flag-based big-step semantics based on pretty-big-step semantics. Unfortunately, flag-based big-step semantics, through pretty-big-step semantics, also inherits the not well behavior of ‘coevaluation’.
In this work, we present (coinductive) natural semantics as a framework for the verification of total correctness of compilers in Coq. Once we have a simple, easy, clear, and intuitive solution for this task, we can seek to improve it in the future. In particular, we use a natural parameter in the interpreters to bound the recursion. Recently, Leroy [
58] has defined an interpreter of While using the partiality monad in Coq; we plan to adopt the partiality monad in our Mini-ML compiler and in the framework in general to avoid the use of this parameter.
On the other hand, we can seek to reach a single coinductive natural semantics ‘
’ able to express terminating computations, as well as non-terminating computations. Charguéraud [
20] mentions that in principle, this semantics can be used directly to prove total correctness of the translations; however, he points out that the conclusion in the correctness theoremis usually of the form
, and that the current support of coinduction in Coq only allows using coinductive predicates in the conclusion. In particular, it does not allow using the existential quantifier ‘∃’ or the connective ‘∧’ when a proof is done by coinduction. Bach Poulsen and Mosses [
21] run a similar criticism to the current coinduction support in Coq. Fortunately, our (coinductive) natural semantics is ideal here since, when using (inductive) natural semantics ‘⇒’ to express finite computations and coinductive natural semantics ‘
’ to express infinite computations (separately), the proof of the termination case where the conclusion requires an ∃ and an ∧ can be done by induction, whereas, in this way, in the case of non-termination, in the conclusion neither the ∃ nor the ∧ is required, only the coinductive predicate
is used, so it can be proved by coinduction (with the current support of Coq).
Even then, it would be possible to aim at having a single semantics in order to have a more concise definition. If so, the framework could automate the translation from it to the two separated semantics (⇒ and ); also, the framework could establish and prove the equivalence between the first one and the union of the last two semantics. Having arrived at these two semantics, the current results of the framework can be used.
The central problem is that (to the authors’ knowledge) to date, there is not a single coinductive natural semantics in the literature that expresses finite and infinite computations, and that it does behave well. The first author, based on Leroy’s ‘coevaluation’, has succeeded in defining a single coinductive natural semantics (of the pure lambda calculus extended with constants) that expresses terminating and non-terminating computations, and that it does behave well in Coq. Also, he has proved the equivalence of this semantics with the union of the two semantics (⇒ and
) that express, respectively, finite and infinite computations separately. Apparently, this result is sound [
59] and we plan to present it in future works.
To continue, it would be possible to deal with the problem of decreasing the number of rules necessary in a coinductive natural semantics definition. This is the main goal of pretty-big-step semantics and flag-based big-step semantics. To this end and going further, we envisage that the results in this work and those of pretty-big-step semantics and flag-based big-step semantics (future work and perhaps other works as well) can be integrated in a coinductive natural semantics framework having all the desired properties of each of them. In other words, it is our intention that the resulting coinductive natural semantics framework synthesizes all the major advances in natural semantics.
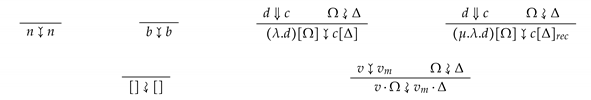
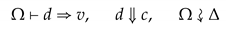
 vm and for all stack s,
vm and for all stack s,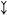 vm, since c is the result of d compilation, c is a single machine instruction hence follows simply by definition.
vm, since c is the result of d compilation, c is a single machine instruction hence follows simply by definition.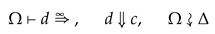
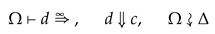


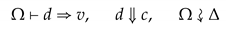
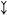 vm and for all stack s,
vm and for all stack s,Δ. We claim that there exists , the proof of n
n follows by definition. Using the hypothesis, by ⇓ definition necessarily . We are now in a position to prove the main goal which follows by ⇒ definition of IConst.
Δ. We claim that there exists , the proof of b
b follows by definition. Using the hypothesis, by ⇓ definition necessarily . We are now in a position to prove the main goal which follows by ⇒ definition of IConstb.
Δ, v
vm then which is proved by straightforward induction on . (Also, it can by proved by induction on Ω.)
Δ. Using the hypothesis, by ⇓ definition necessarily , . We claim that there exists , the proof of
c1[Δ] follows by definition, and Ω
Δ. We are now in a position to prove the main goal which follows by ⇒ definition of IClos.
Δ. Using the hypothesis, by ⇓ definition necessarily , . We claim that there exists , the proof of
c1[Δ]rec follows by definition, and Ω
Δ. We are now in a position to prove the main goal which follows by ⇒ definition of .
Δ.
We claim that there exists , the proof offollows by definition. Using the hypothesis, by ⇓ definition necessarily , , . We are now in position to prove the main goal .
Δ. Using the hypothesis, by ⇓ definition necessarily , , , . We are now in position to prove the main goal .
vm).
Δ. Using the hypothesis, by ⇓ definition necessarily , , , . We are now in position to prove the main goal .
vm).
Δ. Using the hypothesis, by ⇓ definition necessarily , , . We are now in position to prove the main goal
vm1).
vm).
Δ. Using the hypothesis, by ⇓ definition necessarily , , .
We are now in position to prove the main goal .Δ1, by induction hypothesis
(such thatc[Δ1]).
vm2).
vm).
Δ. Using the hypothesis, by ⇓ definition necessarily , , .
We are now in position to prove the main goal .Δ1, by induction hypothesis
(such thatc[Δ1]rec).
vm2).
vm).
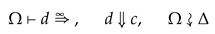
Δ. Using the hypothesis,
>by ⇓ definition necessarily , , .We must prove .Δ. Using the hypothesis, by ⇓ definition necessarily , , . We must prove .
Δ. Using the hypothesis, by ⇓ definition necessarily , , . We must prove .
Δ. Using the hypothesis, by ⇓ definition necessarily , , . We must prove .
vm1).
Δ. Using the hypothesis, by ⇓ definition necessarily , , , . We must prove .
Δ. Using the hypothesis, by ⇓ definition necessarily , , , . We must prove .
Δ. Using the hypothesis, by ⇓ definition necessarily , , , . We must prove .
Δ. Using the hypothesis, by ⇓ definition necessarily , , .
We must prove .Δ. Using the hypothesis, by ⇓ definition necessarily , , .
We must prove .vm).
Δ. Using the hypothesis, by ⇓ definition necessarily , , .
We must prove .vm).
Δ. Using the hypothesis, by ⇓ definition necessarily , , . We must prove .
Δ1, , by Theorem A2 on
(such thatc′[Δ1].
vm2).
Δ. Using the hypothesis, by ⇓ definition necessarily , , . We must prove .
Δ1, , by Theorem A2 on
(such thatc′[Δ1]rec.
vm2).
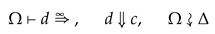
 Δ. We must prove .
Δ. We must prove .