Abstract
Security objectives are the triad of confidentiality, integrity, and authentication, which may be extended with availability, utility, and control. In order to achieve these goals, cryptobiometrics is essential. It is desirable that a number of characteristics are further met, such as cancellation, irrevocability, unlinkability, irreversibility, variability, reliability, and biometric bit-length. To this end, we designed a cryptobiometrics system featuring the above-mentioned characteristics, in order to generate cryptographic keys and the rest of the elements of cryptographic schemes—both symmetric and asymmetric—from a biometric pattern or template, no matter the origin (i.e., face, fingerprint, voice, gait, behaviour, and so on). This system uses perfect substitution and transposition encryption, showing that there exist two systems with these features, not just one (i.e., the Vernam substitution cipher). We offer a practical application using voice biometrics by means of the Welch periodogram, in which we achieved the remarkable result of an equal error rate of (0.0631, 0.9361). Furthermore, by means of a constructed template, we were able to generate the prime value which specifies the elliptic curve describing all other data of the cryptographic scheme, including the private and public key, as well as the symmetric AES key shared between the templates of two users.
MSC:
94A60; 14G50
1. Introduction. The Objectives of Security, Cryptography, and Biometrics
The purpose of security has been framed within the communication model of Claude E. Shannon [1] and is usually specified by three elements, the so-called CIA triad (confidentiality, integrity, and authentication).
Confidentiality exists when no agent external to the sender and receiver involved in the communication process knows (either partially or totally) the transmitted message. Integrity involves the unaltered preservation (partial or total) of the message. Authentication refers to the fact that the message sent is associated solely and differentiated to its sender and to no one else—with the sender not being able to deny being the source. This latter aspect leads us to sometimes consider a fourth element, non-repudiation, even though many do not consider it as detached from the third.
However, it has been increasingly thought that this model should be made more ample by extending it to six characteristics through adding availability (as the communication process may be suspended, hindered, or stopped), utility (it is useless to have a message which attains the other characteristics if it is no longer useful), and control (referring to who has the capacity to control and possess the information, even though they may not be able to know it). This extended model was proposed by Donn B. Parker [2,3,4].
In this article, we focus on the classical CIA triad, leaving the rest of the characteristics aside.
Cryptography is an applied science whose objective is communications security. Through its use, one can obtain confidentiality, integrity, and partial authentication. We discuss the reasons for this partiality (or non-completeness), with respect to authentication, below.
Security within information and telecommunication systems is based on “something-I-know” (e.g., a PIN, a password, and so on), “something-I-have” (e.g., a card, a USB token, and so on), or ”something-I-am” (i.e., a biometric datum). The difficulties and problems that exist in the two first cases (theft, copy, ease of deduction of the key if it is short; excessive length of the key leading to keeping it as something-I-have; it not being an authenticator of the user; and so on) are intended to be solved by cryptobiometrics in the third case, “something-I-am.” Cryptobiometrics permits the authentication and linking or generation of long keys (as required) securely, based on the biological data of a real subject that uses the system, thereby eliminating the need to memorize, save, or uncover keys, as these are generated (and therefore “hidden”) using patterns of the subject’s biology and behavior.
As biometrics refers to patterns linked to individual features, peculiarities, and physical structures (i.e., biology) or their behavior (behavioral psycho-sociology), it is very difficult to copy, distribute, and share them, making them more difficult to deny and more truly authenticable, and preventing forgetting of the biometric pattern (as it is inherent to the subject). Furthermore, they cannot be lost (as a token can be). Considering the above (and in general), it is more difficult to attack any of these characteristics than when using “something-I-have” or “something-I-know.”
2. Cryptobiometrics and Ways of Obtaining Keys
The combination of cryptography and biometrics into cryptobiometrics has been proposed to solve the partial authentication issue in sole cryptography. On the other hand, cryptobiometrics also attempts, as the conjunction of biometrics and Cryptographic, to obtain non-traceability (i.e., irreversibility plus unlinkability), cancellability, and irrevocability together with the previous purely cryptographic characteristics of confidentiality and integrity, which are all desirable aspects for the security of any robust system. All of these are addressed and solved in our system.
In spite of its wide development in recent years [5,6,7,8,9,10,11,12,13], cryptobiometrics still has problems which have not been fully solved, along with other purely biometric problems. We consider these, in more detail, in the following:
- Variability: Biometric data varies, whereas cryptography calls for exact and invariable data, as only one change in one bit of the key invalidates its identification and utility.
- Irreversibility: Cryptobiometric keys are not pure biometric data, which usually remain permanent and immutable in each human being, and are never to be obtained in a direct manner, which would oblige the need to revoke them (thus not permitting their later use) in the case of being compromised. Instead, they are generated as the result of some type of secure and irreversible mathematical transformation using that pure data.
- Cancellability: Biometric data are inexhaustible as, from them, many different keys can be generated as required. Thus, from a given biometric feature (iris, fingerprint, face, odor, gait, and so on), one is able to extract as many keys (of different lengths) as desired, according to the different applications.
- Irrevocability: In spite of the possibility of canceling cryptobiometric keys, our genuine biometric data can still be used, as they cannot be revoked.
- Unlinkability: Even if an attacker knows many keys, be it proceeding from the same or from a different pattern, they cannot obtain the original biometric datum.
- Reliability: Biometrics seeks an acceptable reliability average value, depending on the application and situation, between false rejection rate and false acceptance rate, while looking for the most possible reduced values. However, we always speak of the maximum probability of acceptance, rejection, or identification.
- Biometric bit-length: At present, symmetric cryptographic keys of order 10–10 and asymmetric keys of order 10–10 are required. However, not all biometric features (e.g., the iris is better than the fingerprint, and the latter better than typing patterns) enable us to extract such a number of bits, due to extraction difficulties, environmental variability, errors, and so on; or, they may (for reasons intrinsic to the very biometric feature) be highly variable in different samples and circumstances. It is, therefore, necessary to find better mathematical techniques which are capable of extracting a sufficient number of representative bits.
The purely cryptobiometric characteristics which are the object of our system are irreversibility, cancellability, irrevocability, and unlinkability (leaving the rest aside), being clearly biometric, and therefore, linked to each biometric modality.
Cryptobiometrics provides diverse scenarios, from simple and more imperfect (represented by a total decoupling between biometrics and cryptography) up to the most cohesive: key-release, key-binding, and key-generation.
- Key-release: The key is totally detached with respect to the biometric pattern. It is not really regarded as a cryptobiometrics system; the comparison between the identified or verified external biometric capture and the pattern saved releases a cryptographic key that has no relation whatsoever to the biometric datum. It is of no interest and is cited here only as a proposal previous to the two following methods.
- Key-binding: Departing from a key that has no relation with the biometric datum, a complete monolithic cohesion is realized a posteriori between the biometric pattern and the key.The development of this model started with Soutar, Roberge, Stojanov, Gilroy, and Kumar [14,15]. The procedure, originating from the ideas patented by Tomko, Soutar, and Schmidt [16,17] and by Tomko and Stoianov [18], involves the use of correlation functions in the phase of processing, followed by carrying out binding with the key, generating (ad hoc) a lookup table from the key’s bits and a series of points in the pattern image.Juels and Wattemberg [19] introduced the so-called “fuzzy commitment,” where the key corresponds to a codeword generated after a process of correction of errors, and it later applies the binding with the value obtained from the biometric datum. The differential of bits with a new entry is corrected using error-correcting codes. In this model, the scheme of Hao, Anderson, and Daugman [5] was applied to the iris; some important improvements were added, such as the concatenation of diverse error-correcting codes (Hadamard and Reed–Solomon). Apart from that, using the iris, similar fuzzy commitment schemes have been made in other modalities (e.g., fingerprint, face, and so on) [20,21,22].Goh and Ngo [23], in turn, applied quantification transformations (projections) in facial biometry to generate random information streams.Juels and Sudan [24] developed the “fuzzy vault” over the model “fuzzy commitment,” the practical application of which has been shown by Clancy, Kiyavash, and Lin [25]. It generates a polynomial from the key, with no relation with the biometric data, where the characteristics of the subject are placed in particular points of the polynomial, followed by the insertion of masking data. This scheme has been later applied in numerous biometric categories: fingerprint, iris, palms of hands, face, and so on [26,27,28,29], improving its design [30].On the other hand, Dodis, Ostrovsky, Reyzin, and Smith [31] theoretically developed the so-called “fuzzy extractor/secure sketch,” with which they were able to extract quasi-random information from a biometric input, which was shown to be tolerant to variations and errors.Linnartz and Tuyls [32] proposed the “shielding functions” model in a theoretical manner, where the key and the biometric data were operated upon by these functions, thereby generating support data (or “helper data”) that could be later used to generate the key again, in the case of authenticated input data.On the other hand, Van der Veen, Kevenaar, Schrijen, Akkermans, and Zuo [33] followed the “fuzzy commitment” model together with “helper data,” already introduced theoretically by Tuyls and Goseling [34] and later by Verbitskiy and Denteneer [35].Other techniques have combined aspects of the “fuzzy vault” and “helper data” [36,37].“Password hardening,” proposed by Monrose, Reiter, Li, and Wetzel, adds biometric information to a previous password [38,39,40,41]; the Teoh, Ngo, and Goh BioHashing scheme [23,42,43,44,45] also falls within the key-binding classification.More recently, the work of Iida and Kiya has focused on error-correcting codes and fuzzy commitment schemes for JPEG image [46]. The different methodology of Malarvizhi, Selvarani, and Raj uses fuzzy logic and adaptive genetic algorithms [47]. It is also worth mentioning the proposal of Liew, Shaw, Li and Yang, who made use of Bernoulli mapping and chaotic encryption [48]; and the use of face and fingerprint biometrics along with watermarking and hyper-chaotic maps by Abdul, Nafea, and Ghouzali [49].Another approach is that of Priya, Kathigaikumar, and Mangai, who used random bits mixed in an AES cipher [50]. Asymmetric encryption and irrevocability were used by Barman, Samanta, and Chattopadhyay [51]. The fuzzy extractor with McEliece encryption, which is resistant to quantum attacks, was proposed by Kuznetsov, Kiyan, Uvarova, Serhiienko, and Smirnov [52]. In the work of Chang, Garg, Hasan, and Mishra, a cancelable multi-biometric authentication fuzzy extractor has been proposed, where a novel bit-wise encryption scheme irreversibly transforms a biometric template to a protected one using a secret key generated from another biometric template [53].We also note the works of Damasevicius, Maskeliunas, Kazanavicius, and Wozniak, who used data from electroencephalography and Bose–Chaudhuri–Hocquenghem error-correcting codes [54]. Olanrewaju, Oyebiyi, Misra, Maskeliunas, and Damasevicius [55] used the same type of correction codes with Principal Component Analysis and fast Chebyshev transform hashing for ear biometrics. Some other works have discarded the use of error-correcting codes, such as that of Chai, Goi, Tay, and Jin, where an alignment-free and cancelable iris key binding scheme was constructed through the use of a non-invertible transform [56]. Finally, another work used another type of biometrics which is not very common: key binding with finger vein [57].
- Key-generation: The key is extracted from the biometric pattern.The first proposal in this area was the patent of Bodo [58], where the cryptographic key was obtained fully from the biometric data, even though it posed cancellability and security problems related to the theft of data specific to the subject.An improvement was proposed by Davida, Frankel, Matt, and Peralta [59,60], which generated the key from the hash function over the biometric data after the correction of errors.Other approaches and proposals have been designed using the quantification and intervals of biometric features, such as those of Vielhauer, Steinmetz, and Mayerhofer [61] or Feng and Wah [62].Drahanský, in turn, obtained the key from quantification and the use of graphs [63].Other authors have utilized the combined use of quantification and “fuzzy extractors/secure sketches” as key generators [64,65,66].More recently, the proposal of Aness and Chen used discriminative binary feature learning and quantization [67], and Yuliana, Wirawan, and Suwadi [68] combined pre-processing with multi-level quantization. Furthermore, Chen, Wo, Xie, Wu, and Han improved quantization techniques against leakage and similarity-based attacks [69].With regards to cancellability, a crucial aspect of the works of Ratha, Connell, Zuo, and Bolle [70,71], and later, of Savvides, Kumar, and Khosla [72], introduced biometric cancellability, proposing systems that protect the original biometric data. Along with the above, the closest in time was the study of Trivedi, Thounaojam, and Pal [73], or those who used symmetric cryptography, such as Barman, Samanta, and Chattopadhyay [74]. A secured feature matrix from the template and AES cipher was used by Gaddam and Lal [75]. We also note the novel approach using random slopes of Kaur and Khanna [76], and the technique for achieving cancellability through geometric triangulation and steganography of Neethu and Akbar [77]. The work of Punithavathi and Subbiah [78] introduced partial DCT-based cancellability for IoT applications. In key-binding, cancellability and revocability are naturally simpler; however, in key-generation, the situation is not as easy or simple.
3. Voice Biometry
3.1. Introduction
Voice data comprises one of the existing biometric identification, recognition, and authentication features. We know that human beings can recognize familiar voices and identify multitudes of people only by voice, even though we tend to express ourselves differently and may not even say the same words in the same way at different times [79].
The voice is produced by the excitation of the vocal tract, which is between the lips and the glottis, leading to the vibration of air particles. The resultant sound waves are able to be picked up and vibrate the primary auditory structure of the receiver, which finally converts these vibrating movements back into auditory signals in the brain. Different types of sounds are the acoustic results of sound waves, and as such, we can analyze them by using signal processing technologies [80,81,82].
3.1.1. Speech Recognition
Voice recognition has two main phases. In the first phase—enrollment—samples are taken of the voice of the speaker; their main and differentiating characteristics are extracted, thereby constituting the template which is then stored in the system. In the subsequent phase—recognition (verification or identification)—a speech sample is taken, which is then compared with the data stored in the system.
When we speak of voice recognition, we must distinguish between two aspects: On the one hand, verification (or authentication), through which a person claims to be a specific person, the truth or falsehood of which is verified by the system, through comparing one sample with their template or pattern (which had been previously generated in her enrollment process) stored in the system. The other is identification, through which it is intended to compare a voice sample with a wide (as much as necessary) set of templates of diverse users, in order to determine who the user is (whenever they are in the system).
In voice biometrics, a distinction can also made between text-dependent or text-independent techniques, depending on whether or not the samples are from the same phrase or common text.
Our implemented system involves verification and is text-independent [83,84,85].
3.1.2. Voice Recognition Techniques
There are two main classes (or types) of speech recognition techniques:
- (1)
- Template Matching: A maximum accuracy or maximum likelihood is sought between the samples previously stored as a voice template and the new voice sample input. This is called the speaker-dependent model.
- (2)
- Feature Analysis: This is also called the speaker-independent model, as it searches for characteristics within human discourse, and from them, it searches for similarities among the input speakers compared to the stored data in the system.
Our system follows the Template Matching method [86].
3.2. Methodology
3.2.1. Spectral Analysis of Frequencies
Speech can be modeled as the response of a time-invariant linear system (i.e., the voice system) to a train of near-periodic pulses (for voiced sounds) or broadband noise (for unvoiced sounds).
The articulation of the entire vocal tract can be modeled as a slowly time-varying filter system, thereby giving the range of speech frequencies. Thus, speech is a non-stationary signal. Its characteristics usually remain very constant over short intervals, between 30 and 40 ms. Although the frequency of the human sound signal reaches a range of about 15 kHz, or even higher, it can be filtered up to 3 kHz while still being perfectly intelligible.
With a suitable window L we can, thus, collect the invariance of the signal properties, and through the DFT (discrete Fourier transform), we can display the properties in the frequency domain of the signal in the interval. The time-dependent Fourier transform provides a very useful description of the properties of the signal over time, as the spectrogram in Figure 1 shows [87].
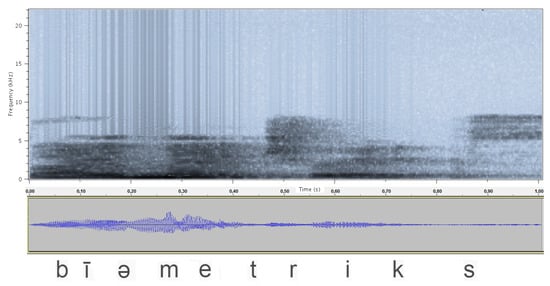
Figure 1.
Bottom: Waveform of the sounds of the word “biometrics,” where you can see the consistency in time of each sound that makes it up. Top: Spectrogram of the time-dependent Fourier transform of the waveform.
3.2.2. Periodogram of the Signal
In general, noise-like signals, as with the sound expressions of the human voice, are much better modeled when they are considered to be random signals, due to the difficulty of applying deterministic modeling to them. An especially relevant estimator in speech recognition is the power spectrum, or power density spectrum, of the signal under the DFT, from which we can obtain the periodogram, based on direct Fourier transformation of finite-length segments of the signal [88,89].
If we are looking for an estimator of the power density spectrum of a signal, we can apply a low-pass anti-aliasing filter to obtain sampling without aliasing (Figure 2). In this way, is a discrete-time stationary random signal where we have a very adequate proportional approximation, given by

Figure 2.
Scheme of steps for processing a signal from its original form to its value discretized by the discrete Fourier transform (DFT).
With this, we define the periodogram as:
where is the discrete initial signal, is the discretization of the window which selects a certain finite quantity, and where L is the number of samples of the finite-length segment, with U being a normalizing factor with value
3.2.3. Welch Method
Improved expression of the periodogram data (Figure 3) can be done through periodogram averaging (Figure 4).
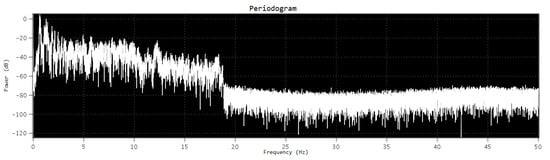
Figure 3.
Periodogram of the previous signal (with sample rate 100).
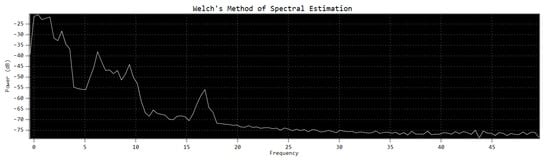
Figure 4.
Welch estimate from the previous periodogram (with FFT size = 256 and U = 0.3958).
A sequence is divided into segments of length L samples, with a window of length L, forming
For , the segments are contiguous; if , the segments overlap.
This system achieves a straightforward method of trading off between spectral resolution and reduction of the variance of the spectral estimate.
On the other hand, the periodogram, as an estimator, is asymptotically unbiased. The variance of the periodogram estimate does not decrease to zero as the length of the segment increases, and so, it is not a good estimator. However, dividing the signal under study into small segments and averaging their respective periodograms achieves a well-behaved estimator [90,91].
The phases of the Welch method are as follows:
- Dividing the signal (overlapping segments).
- Windowing and FFT.
- Averaging.
- Dividing the signal (overlapping segments). We divide the signal into overlapping segments. We consider overlapped samples herein.
- Windowing and FFT. We use an efficient algorithm for computing the DFT, known as fast Fourier transform (FFT); a Hamming window with an FFT size of and normalization constant , obtained from the window ; and the size of the FFT.As the window is not rectangular, it is technically referred not to as a periodogram, but instead, a modified periodogram.
- Averaging. The average and normalized values are calculated from the vectorized values of the overlapped fragments of the windowed and FFT-processed signal.
4. Proposed Model
Of the three types of relationship between biometrics and cryptography—key-release, key-binding, and key-generation—our system is of the third type, key-generation, in which the key is extracted from the biometric pattern. In this way, our model is a key-generation system which is both fully cryptographic and biometric in all of its parts and elements. It does not use functions other than cryptographic ones in any of its parts, as we consider this to be the best way to achieve security objectives.
In reference to the seven characteristics mentioned above which a cryptobiometric system must meet, our system complies with all of them: Irreversibility, cancellability, irrevocability, and unlinkability are characteristics of the system itself.
The other properties—variability, reliability, and biometric bit-length—depend on the biometric system considered. In our case, we experimentally apply our model to voice biometrics and explore how these three characteristics are also achieved.
An additional aspect that we want to highlight, which we will see later in the security analysis, is that the system meets the requirements of being perfectly secret, making it impossible to cryptanalyze.
In this way, considering all of the above, our system meets the highest demands and qualities of a cryptobiometric system.
In the following, we broadly indicate how our system can be implemented in both symmetric and asymmetric encryption modes, showing examples of the main protocols as well as the Diffie–Hellman key-exchange.
4.1. Schemes of Ciphers
Our model can be implemented in both symmetric, such as DES (deprecated) or AES, and asymmetric ciphers such as RSA, Elgamal, Paillier, or elliptic curve, and for Diffie–Hellman key-exchange, thereby completing the basic cryptographic suite. These are the examples that we present below, in order to exemplify the methodology.
Note, however, that RSA and the other schemes listed here are more extensive in their functionality than the encryption–decryption function itself (although that was originally their main use), and therefore, they can be used both for public-key encryption, hybrid encryption, digital signatures, and key-exchange, among other capabilities. However, we wanted to show the broad range of application of our system, which is capable of being implemented in various scenarios such as those mentioned here [92].
The different elements of a cryptosystem are usually merely random. In our case, we generate them cryptobiometrically, linking them to the subject; although they do have the property of being cancellable, when necessary.
RSA Cipher
The RSA algorithm, proposed by Ron Rivest, Adi Shamir, and Leonard Adleman [93], bases its strength on the computerized difficulty of factorizing compound numbers of large primes (integer factorization problem).
Each user, A and B, carries out the following process:
Starting with two high prime numbers, p and q, which are secret, their product is made public . The Euler value, , is also secret. The secret key, , and the public key, , preserve the modular relation .
With the value of the message to be ciphered defined as X, the encryption (E) and decryption (D) processes can be expressed as:
Encryption: ,
Decryption: .
The elements that A (with B similar) generate in this cryptosystem are ; the rest are obtained from these. Their respective binary lengths are of order .
Elgamal Cipher
Taher Elgamal [94] proposed a public-key ciphering scheme based on the discrete exponentiation problem or the discrete logarithm over the multiplicative group of a finite field . Let G be a cyclic group of order n and f be its generator (i.e., ). Then, the exponential function of base f is defined as , where x belongs to . Its inverse operation is the discrete logarithm, with the latter over an element t in the base f of G, and the integer x in the interval as , such that . With this, the discrete logarithm problem can be described as “given a prime number p, a generator f of , and an element t of , find an integer x within the interval such as .”
The Elgamal cipher takes elements of G as clear messages or plain text. Let A be the user who wants to send a message X to a user B. By selecting a finite group G and a generator f of it, none of them are secret (i.e., available or public); A selects a random number a (private key) and calculates its public key in G, . User B would similarly do with their private key b to obtain .
Encryption: A generates a random number s and calculates . A takes from user B and sends to B the pair .
Decryption: B calculates in G from the first coordinate received by raising it to his own private key b. With this, gets the quotient with the second coordinate received and the recently calculated one, thereby obtaining the value X.
The elements that users A and B generate in this cryptosystem are , the rest being obtained from these values, all with binary lengths of order .
Elliptic Curve Cipher
Victor S. Miller [95] and Neal Koblitz [96] were the initiators of this type of cryptography.
An elliptic curve over , , is defined as the set of points that satisfy , adding a point for infinity, , with u and v being elements of satisfying . These can be defined in a very similar way in the reals and in .
The discrete logarithm over an elliptic curve, as we have seen with Elgamal’s method, is defined as the difficulty to “find an integer x that belongs to the Galois field as ,” P and B being points of the curve E.
The cipher over an elliptic curve E first makes public a finite field , an elliptic curve E, and a base point J in E. Each user, , selects a secret number as a private key and makes public the point that is to be their public key, .
Encryption: User A wants to send the message to B. She takes a random integer k and calculates the point within E. User A takes the public key of user B, , and calculates and . Finally, A sends the pair of points to B.
Decryption: User B, in order to recover the original message, multiplies the first of the points times its private key b, obtaining . With a simple subtraction, he gets the message point in the following manner: .
The elements that users A and B generate in this cryptosystem are , the rest being obtained from these values, all with binary lengths of order .
Paillier Cipher
The Paillier cipher system, proposed by Pascal Paillier [97], bases its security on the factorization intractability of high numbers, as well as on the quadratic residuosity problem.
The first step in this scheme is the selection of two secret large prime numbers p and q. Their product, , is made public (as in the RSA system). The Euler value is kept secret. The primes p and q have to be of similar length; this condition is attained by ensuring that .
On the other hand, we define a parameter , the so-called Carmichael function, a parameter g within , and a value , where .
Thus, the private key is the pair and the public key the pair .
If the value of the message to be ciphered is defined as X, in the interval , the encryption (E) and decryption (D) processes can be expressed as:
Encryption: Select a random value a in the interval . The result is calculated as .
Decryption: The deciphered value is .
The elements that A (with B similar) generates in this cryptosystem are ; the rest are obtained from these values. Their respective binary lengths are of order .
Diffie–Hellman Key-Exchange
Whitfield Diffie and Martin Hellman [98] developed, utilizing some concepts of Ralph Merkle [99], a protocol to interchange a common secret key with no possibility of being known by another agent in the process of communication or exchange.
The two actors sending and receiving (A and B) the protocol publicly select a finite multiplicative field G of order n (generally ) and a generate element f within G. User A produces a random number a by calculating , which is sent to B. Actor B also produces a random number b by calculating , which is sent to A. User A calculates , while B calculates , this being the shared and secret element, .
It is true that with high values for the order of G and random values a and b, due to the inherent difficulty of the discrete logarithm problem, the exchange is secure. However, there exists a problem of man-in-the-middle attack. This can be solved through authentication of the actors; for example, using the station-to-station (STS) protocol of B. O’Higgins, W. Diffie, L. Strawczynski, and R. do Hoog [100], using asymmetric cryptography such as that in the elliptic curve Diffie–Hellman (ECDH) method [101], or through other protocols, depending on the requirements involved [102].
Both the original DH and its variant DH-STS, among others, add the use of prior asymmetric cryptography to send both and , or the concatenation signed by the private keys of actors. This situation calls for the prior use of asymmetric cryptographic keys, and therefore, for previous authentication, thereby generating a vicious circle in our problem. To solve this situation, during these sendings, the asymmetric cryptography of the cryptobiometrics key just seen has to be used.
The elements that users A and B generate in this cryptosystem are , the rest being obtained from these values, all with binary lengths of order .
AES Cipher
AES (Advanced Encryption Standard) has been, from 2002, the cipher symmetric standard (FIPS PUB 197) for the Rijndael cipher of Joan Daemen and Vincent Rijmen, which has been selected by the government of the U.S.A. [103] and is the successor of the DES cipher [104].
AES is a substitution and permutation network with a block size of 128 bits, the key being able to have 128, 192, or 256 bits. It works in the Galois Fields and uses logic operations among text message elements, with sub-keys resulting from the original key, shiftings, mixing of columns in element matrices, or substitutions based on a specific data table (the S-Box).
As it is a system between parties that share the same key, we must first establish asymmetric keys (with a key generated cryptobiometrically, as indicated in this article), in order to build and generate the common symmetric key K for AES in a secure and authenticated manner.
In this case, the only element that users A and B generate in this cryptosystem is , of binary length of order .
4.2. Protocols
We distinguish two scenarios.
Asymmetric ciphers
In the case of asymmetric schemes, our purpose is to obtain some of their respective elements. The main elements that determine them are as follows:
For RSA, of binary lengths on the order of ; for Elgamal, of order ; for elliptic curve, of order ; for Paillier, of order ; for Diffie–Hellman key-exchange, of order .
In the protocol, by generalization, any of the above elements will be called e and its length will be .
The protocol for user A (similarly for user B) is:
- User A generates their own template , which we can consider to be a binary vector of any length, .
- A also generates a random value , a binary vector .
- The binary values and are adjusted to the right, where options can be given. Then, the following is calculated:being the outputs of the hash functions and of binary length h.
- Over-randomization:
- (a)
- User A generates a random number of length (normally, the output of a hash function is lower in length than the order of our elements, for security reasons).
- (b)
- A generates a set of h different values from the set .
- (c)
- Calculate the perfect substitution transposition cipher of length .
- Depending on the element e that we are considering, we can have the following cases:
- (a)
- generates a prime number: Here, user A carries out prime, where is a procedure to generate a prime number—applying the usual methods of generation through primality tests—from : using its value (if it is already prime), the next closest prime, or a strong prime.
- (b)
- generates an element of G, generally , , , : In this case, we do not have to make any changes in e; in any case, calculate its modular value in G.
- (c)
- generates a point of an elliptic curve: Here, user A carries out , with being a procedure to generate , the x coordinate of a point J located on the elliptic curve, such that .
Symmetric ciphers
Our objective for symmetric ciphers is to obtain the key K from the biometric data of both users A and B. The sequence of steps for this protocol is:
- User A generates their own template , which we can consider to be a binary vector of any length, .
- User B generates their own template , again a binary vector of any length, .
- A also generates a random value , a binary vector .
- B also generates a random value , a binary vector .
- The binary values and are adjusted to the right, where options can be given. Then, the following is calculated:those being the outputs of the hash functions and of binary length h.
- The binary values and are adjusted to the right, where options can be given. Then, the following is calculatedbeing the outputs of the hash functions and of binary length h.
- Over-randomization:
- (a)
- User A generates a random value with the length of the symmetric key t; generally, (normally, the output of a hash function is higher in length than the order of our element K).
- (b)
- User B generates a random value with the length of the symmetric key t; generally (normally, the output of a hash function is higher in length than the order of our element K).
- (c)
- A generates a set of t different values from the set .
- (d)
- B generates a set of t different values from the set .
- (e)
- User A applies the perfect substitution transposition cipher of length t.
- (f)
- User B applies the perfect substitution transposition cipher of length t.
- User A sends B the vector , using the asymmetric cryptography of a cryptobiometrically generated key.
- User B sends A the vector , using the asymmetric cryptography of a cryptobiometrically generated key.
- Both users apply .
4.3. Main Elements of the Protocols
The Biometric Pattern (Template)
No matter the biometric technique used—physical feature or behavior, monomodal or multimodal—the different algorithms generate a numeric representation of the data. On the other hand, we always consider templates with a vector structure or which are susceptible of a vectorized form.
Regardless of the origin of the data, which may vary according to the biometric type and the algorithm and technique used, our original data will be the biometric pattern or template T, in the case of monomodal biometrics.
In the case of multimodal biometrics, biometric fusion is a wide field which has reached great maturity, although it requires specific analyses relating to the various cases in which it is implemented, focused on what, when, and how to fuse. Both the sources of fusion (multi-sensor, multi-algorithm, multi-instance, multi-sample, and multi-modal) and the level of fusion (sensor, feature, score, rank, and decision) must be considered. All of this leads us to consider the quality of the data, soft biometric attributes, contextual information to improve accuracy, and ancillary information, among other aspects [105]. As biometric fusion is not the object of this study, in relation to our system, we only need the template as input. In this way, we can indicate that (in the same way as in the case of single biometric modality), a fusion template is required to carry out the procedure indicated here for key-generation, without considering the way it is achieved: either through concatenation of patterns of the diverse biometrics, or perhaps more appropriately, by an interleaving among them or some other similar technique—for example, using Bloom filters [106,107,108], multiple Bayesian models [109], or convolutional neural networks [110].
We have to say that, in the different scenarios of creating the template T, the results will differ, although will be very similar to each other. However, in any case, our system always offers cryptographic data from a template of the same subject.
We can also consider the typical use of error-correcting codes () for verification and identification procedures, which we can consider as a set of bits attached to the template: . Without loss of generality and for simplicity, we denote the entire set by the template .
Hash Functions and Randomization
Let H be a hash function , with , which is a mapping such that the inverse process is not easy to achieve, is resistant to pre-image and second pre-image attacks, and is also collision resistant.
To improve security, we use two different types of hash functions, and , such that and , with .
These functions have to be diverse in their construction, possibly with different characteristics in their strengths and weaknesses, as well as differing in their susceptibilities to attacks.
The method of using and consists of by means of the concatenation hash functions and outputs of the template with circular shifts to the left by i bits (), with the random value of length —the output of which is finally hashed by .
The output in asymmetric cryptography is denoted by , and that of symmetric cryptography by and , all of them belonging to .
Our proposal:
We use two types of hash functions: SHA-2 (H1) and SHA-3 (H2), with their 512-bit output variants in both cases.
The set of hash functions SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224, and SHA-512/256 comprises the suite SHA-2 (FIPS PUB 180-2; FIPS PUB 180-3; FIPS PUB 180-4) [111].
The SHA-2 family, which is very similar in structure to SHA-1 (FIPS PUB 180-1), modifying the constants, shifts, number of rounds, set of registers, and length of elements, among others, has a very similar method for executing each round or iteration. This led to the proposal of the family SHA-3 which is different to SHA-2, which depended on SHA-1 (which, in turn, depends on SHA-0; FIPS PUB 180), which is very similar, except for the lack of a circular shift; all of these build on MD-5, designed by Ronald Rivest [112].
We know of collision and (first and second) pre-image attacks against SHA-0 and SHA-1; as such, they are not considered secure and their use is not recommended [92,113,114]. With regard to SHA-2, we cannot speak of practical attacks, although the weaknesses of SHA-0/-1, SHA-2 being so related to them, motivated the desire for a different way to carry out hash functions. This was the reason for the construction of SHA-3.
Even though SHA-0, SHA-1, and SHA-2 were creations of the NSA (National Security Agency), SHA-3—a functional subset of the Keccak hash function—was designed by Guido Bertoni, Joan Daemen, Michael Peeters, and Gilles Van Assche. Its construction does not follow the Merkle–Damgård scheme (as SHA-0-1-2 did), but instead, the sponge scheme, which makes it very diverse in its possible attacks and weaknesses, something that was assessed in the competition that led to its selection, carried out by the NIST (National Institute of Standards and Technology) between 2007 and 2012, in which Keccak was finally selected (with 224-/256-/384-/512-bit output options, of which we use the 512-bit variant in our scheme) as the winning candidate [115,116].
Attacks on hash functions, be it pre-image or collision, usually act on versions of a reduced number of rounds. Thus, the best attacks on SHA-2 are: collision of 31 rounds over the total of 64 to SHA-256 with complexity [117]; collision of 28/64 to SHA-512/256 with practical complexity [118]; collision of 27/80 to SHA-512 with practical complexity [118]; pre-image of 45/64 to SHA-256 with complexity [119]; and pre-image of 50/80 to SHA-512 with complexity [119]. In reference to SHA-3, there exists a pre-image attack of eight rounds (over the total 24), requiring a time of and space (memory) of [120]. Therefore, even quantum attacks seem to not be very effective against these systems [121].
In view of these results, using both types of hash functions (i.e., SHA-2 and SHA-3) was considered. First, because they are very different from each other (as we have already indicated), their strengths may lie in different aspects. On the other hand, in our system, the hash function SHA-3 is performed last (although only once), which must therefore be resistant against any pre-image or collision attack, and so, is the first to be resolved; this appeared to be as appropriate as it seems to be the most robust of the existing hash functions.
On the other hand, the random variables are generated by pseudo-random generators (PRG). We consider, for the random value used in the hash structure, a bit length of (i.e., not too high, although still seeking high cancellability and suitable to fit in the binary processors [122]).
Over-Randomization with Perfect Ciphers
(a) Perfect Secret Ciphers
(a.1) The Substitution Perfect Secret Cipher: Vernam Cipher
The Vernam cipher (or one-time-pad) is a cipher which is impossible to cryptanalyze; therefore, it is a perfect cipher. It was invented by Frank Miller [123,124] and reinvented by Gilbert Sandford Vernam [125].
This cipher is based on polyalphabetic encryption but taking the key to the maximum possible difficulty, such that the key (random) is as long as the message. The application of the function on each bit implies that, if the message can be expressed binarily as the sequence and the key as , the ciphertext is , where . At the same time, .
This exclusive (or ) is totally balanced, with it not being possible, given , to know the entries and , should there exist one possible and one impossible pair with the same probability.
If the key is really random (in reality, it will always be pseudo-random) and of the same size as the text of the original message, kept secret, and never reused (neither totally nor partially, before or later), we can obtain an encryption that cannot be broken or cryptanalyzed [126].
It is said that the ciphering is perfect when the knowledge of the ciphertext does not provide information of the original message: ; that is, that the probability a posteriori that the original text is x if the ciphered text is y is identical to the probability a priori that the original text is x.
The deficiencies in the system are only that: the use of a key must be as truly random as possible; the key must be kept secure, at least until deciphering the message or while it is determined that a given ciphertext corresponds to a given original message; and in the sending of the key (key distribution) to the user who deciphers the ciphertext.
(a.2) The Transposition Perfect Secret Cipher: Random Cipher
For random transposition ciphering, let us suppose, after binary codification with a set of n bits, we obtain, as output, only the number of 0 values and the number of 1 values, where .
A random transposition does not provide information, it only gives the number of and . Thus, ; that is, that the probability a posteriori that the original text is x if the ciphertext is y is identical to the probability a priori that the original text is x. The cipher does not give any information at all when taking a random transposition (not reusing the random value totally nor partially), as there exist many possible combinations of the zeros and the ones to generate myriad possible messages, as would occur with the perfect secret substitution cipher.
This is why there is not only one perfect cipher (i.e., Vernam’s), but also another perfect one for transposition; it can be described, in a general manner, as a list of how many times each symbol of the destination alphabet appears: symbol appears times, symbol appears times,…, and symbol appears times.
(b) Over Randomization
We make a distinction between asymmetric and symmetric cryptography.
(b.1) Asymmetric Cryptography
The user generates a random binary number of length . Departing from the templates of length h, we proceed to accommodate its bits in h other places of of length .
At present, security requirements force the length of the elements that we are considering in our asymmetric cryptographic schemes, of order , to be greater in binary length than the usual lengths of the outputs of the hash functions, h. In our proposal, if bits and , in general, bits.
A possible way to achieve this is to annex a set of random bits, up to the required length . However, we follow a more complex randomization process, which we call over-randomization, using Vernam’s perfect secret cipher, a substitution cipher, and a cipher that is its counterpart (i.e., its dual function)—a transposition cipher that is also perfect. The full function is of length .
First, the user generates a set of h different values from the set .
The bits of are placed in those of (beginning with the bit more to the right of ) in h places given by , obtaining a perfect transposition cipher. However, they are not located merely in the obtained random places, but rather than placing them, they are ciphered by the Vernam system with the previous bit (): and .
These locations of must be kept safe, as for the rest of random variables, in order to justify the authentication dependence of the template with the keys and elements generated in the cryptobiometrics process.
(b.2) Symmetric Cryptography
In this case, each actor A and B has generated their random values and , and with their respective biometric templates and , have applied the hash function structure to obtain and .
Now, over-randomization is applied, each actor respectively generating a random value / of binary length of the symmetric key K, such that . At present, the output of a hash function of length h is generally higher in length than the binary length of a symmetric key. In our proposal, if bits, then bits in general.
Next, each user generates a set / of t different values from the set . Then, A applies the function and B applies , both of length t.
User A does the following (and B similarly):
The bits of are placed in those of (beginning with the bit more to the right of ) in the t places given by , thereby obtaining a perfect transposition cipher. However, they are not located merely in the obtained random places, but instead, they are ciphered by the Vernam system with the previous bit (): and .
As we stated previously, in the asymmetric case, the locations of and must be kept safe, as for the rest of random variables, in order to justify the authentication dependence of the templates with the key generated in the cryptobiometrics process.
Generation of a point in the elliptic curve
The procedure to obtain a point of the elliptic curve , , is as follows:
From the values u, v, and , calculate .
By the Tonelli–Shanks theorem [127], if the Legendre symbol and , then .
Looking for one prime number after another successively from the original p that meets these equalities, we obtain the value of the prime that defines and the point .
Strong Primes
The prime numbers selected for ciphering must have a series of characteristics that make them difficult to figure out, even if their product be known. There are a series of requirements, condensed into the fact of their being strong primes. A strong prime p has to meet the following conditions:
(a) (with a high prime and A any integer);
(b) (with a high prime and B any integer);
(c) (with a high prime and C any integer).
However, these conditions are not necessary when large primes are used; for instance, 1024-bit primes, which are presently recommended for security requirements [92], give a value with around 2014 bits for the product . On one hand, to find strong primes is considered too costly—not obtaining better security because of the huge size of the selected primes, even when these primes do not meet these strength conditions. On the other hand, even when several attacks against the factorization problem are blocked using strong primes, there is one concrete attack, which uses Hendrik W. Lenstra Jr.’s elliptic curves [128], which can precisely seek not-very-large factorizations, such as those given with low values of A, B, and C.
Another requirement sought for is a low value of .
A more rigid requisite is to seek so-called safe primes, where and .
4.4. Security Analysis
The proposed model, a cryptobiometrics system, takes a biometric template as input and consists of two sub-systems, the first being the hash structure, and the second, which we call over-randomization, being composed of two perfectly secret systems.
The Holy Grail of security is Shannon’s concept of perfect secrecy. This means that the ciphertext reveals no information at all about the plaintext. Part of our system, the second sub-system, has this degree of security. However, in general, this property cannot always be achieved and what is sought is to be semantically secure. The first sub-system of our model achieves this level. Semantically secure is the computational complexity analog of perfect secrecy, which implies that any information revealed cannot be feasibly extracted. A semantically secure cryptosystem is one where only negligible information about the plaintext can be feasibly extracted from the ciphertext; that is, any probabilistic polynomial-time algorithm () which is given the ciphertext C of a certain message M, taken from any distribution of messages and the message’s length, cannot determine any partial information of the message with probability non-negligibly higher than all other s that only have access to the message length and not the ciphertext [129].
Our security analysis is only limited to the cryptobiometrics components considered here. That is why the security of the schemes of ciphers should be subject to a separate analysis outside our system, considering the usual aspects of each cipher, as well as CPA (chosen-plaintext attacks) and CCA (chosen-ciphertext attacks).
For simplicity and better understanding, we have offered examples of the cryptographic schemes RSA, Elgamal, elliptic curve, Paillier, and AES, together with the Diffie–Hellman scheme, which are not semantically secure. However, there are schemes that are, such as the Cramer–Shoup asymmetric cryptosystem [130] or authenticated symmetric encryptions. However, these aspects are not the object of our cryptobiometrics proposal.
Our cryptobiometrics system begins with the template of the user (or users) and generates from it the main parameters of the encryption schemes and protocols. The entire cryptographic scheme is built using these elements, although with a biometric basis, which also allows the following main properties:
- Irreversibility: Given an output of our system, an eventual attacker cannot reconstruct (similar with or ), the genuine biometric data.As we examine below, this aspect is achieved by the security properties of the first sub-system of hash functions and the subsequent sub-system of over-randomization with perfect encryption.
- Cancellability: From an input , , or , we can generate as many outputs as we want.This property is achieved, in the scenario of asymmetric ciphers, through all those initial moments in which the parameters of the cryptographic scheme must be generated, on which all the encrypted communications subsequently take place, by the random values , , and . The binary length of is n, and is the binary length of . On the other hand, with , we have the h-element variations of elements (with repetition not allowed), , as possible options. Thus, the number of possible options is given by .In the scenario of symmetric ciphers, cancellability is achieved by the random values , , and (similarly , , and ). The binary length of is n, and t is the binary length of .On the other hand, with we have, as possible options, the h-element variations of t elements with repetition not allowed . Thus, the number of possible options for the user A is given by .
- Irrevocability: The elements obtained for the schemes of ciphers can be changed, when necessary, and the biometric data of the initial template, , , or , can be used together with new random values, masking the template, which can be used permanently and irrevocably.
- Unlinkability: For a single biometric sample , , or , we should be able to generate different outputs in a way such that it is not feasible to determine whether those outputs belong to a single subject or not.The proof of this is that, although the template is the same, as it originates from biological and/or behavioral aspects of a subject, the random variables of the system, as well as the properties of the hash functions (one-way or pre-image resistance, resistance to second pre-image, and collision resistance), and the perfect secret property of the over-randomization sub-system, by which the probability a posteriori that the original text is x if the ciphered text is y, is identical to the probability a priori that the original text is x.
Analysis of the hash structure
Let us examine the security of the first sub-system of our model: the hash structure.
If we consider a hash function to be ideal, in the sense that it hashes from to uniformly at random and behaves as a random oracle (i.e., returns a random element each time it is invoked; except if queried twice on the same input, upon which it returns the same output both times). This function H is suitably secure if it fulfills the following three properties:
- Pre-image resistance: this property means that H is a one-way function, and so, for a randomly chosen , it is hard to find, given , an such that .
- Second pre-image resistance: given , it is hard to find such that .
- Collision resistance: it is hard to find a pair , , such that .
Taking into account our hash structure, which we can express, in a general way, as
where is an i-bit circular shift to the left and indicates concatenation, let us analyze its security:
For random , , or , the implementation on the respective template, , , or , offers a random input value in each of the blocks , or , with i from 0 to .
In addition, any change in an input bit of a hash function leads to an entirely unpredictable output with no correlation between both outputs.
On the other hand, if and are pre-image resistant, the concatenation of values of the output of is still pre-image resistant with respect to each . However, if what we know is the final output of , as it is pre-image resistant, we cannot calculate any value of the original set which is a pre-image of that value.
If and are second pre-image resistant, even if we were given a target value in and in each of the concatenation, we cannot obtain other values that would give the same value in the output of the set of concatenations and the subsequent hash function.
Finally, if and are collision resistant, we cannot obtain any pair of values that have the same image for , and for the structure itself, where the concatenation of images is applied to the function, we cannot obtain any pair of different values that give the same output.
With all these qualities, our hash function structure is pre-image, second pre-image, and collision resistant.
On the other hand, although it may happen that an attacker can know the value of the template, the random value is not known, which is a value that should never be repeated. With both of the above, the values will be calculated, whose outputs are not known, being the inputs to the different hash functions , and with them neither the outputs. These outputs, concatenated, constitute the input, which is unknown, to the hash function . In this way, it is clear that our construction of hash functions is secure.
With respect to the hash functions considered, as we have shown before, theoretically, the output value of 512 bits converts to the probabilities of first and second pre-image on one hand, and to of collision on the other hand. Thus, the best attacks for SHA-2 are collision of 27/80 with practical complexity, and pre-image of 50/80 with complexity ; that for SHA-3 is pre-image of 8/24, with very elevated (space and time) complexity conditions.
Analysis of the over-randomization structure
Let us examine the security of the second sub-system of our model: the over-randomization structure.
The strongest security assurance is perfect secrecy. Perfect secrecy was defined by Claude E. Shannon: an encryption scheme with generation, encryption, and decryption, , with message space M, ciphertext space C, and key space K has perfect secrecy if, for every probability distribution on M, every message , and every ciphertext for which , .
This concept of perfect secrecy is also called unconditional security. The basic idea is that intercepting any ciphertext should not give any information about the associated plaintext, nor any information about future encrypted messages; even assuming unbounded computational power.
Shannon’s theorem says: Let be an encryption scheme such that . Then, the system has perfect secrecy if and only if the following conditions hold:
- -
- The probability distribution on K is uniform.
- -
- For every and every , there exists a unique such that .
Theorem 1.
The Vernam substitution cipher of our over-randomization model is perfectly secret.
Proof.
Following Shannon’s theorem, it is clear that or Vernam encryption used in our over-randomization model is a cipher with . The key generation chooses keys from according to a uniform distribution. Further, , and , so .
Alternatively, it is easy to prove that and , , and , . □
Theorem 2.
The transposition cipher of our over-randomization model is perfectly secret.
Proof.
In the same way that the previous encryption scheme is perfect, let us now prove the same for its dual system, now not in substitution, but in transposition.
In the asymmetric case, we have:
The key space K, which for our case is , is random with uniform probability equal to , taking values from the set . In addition, its cardinality is . Additionally, , that we can consider as the set M, comes from the output of the hash functions, with cardinality . From the random variable of length , h values will be taken, resulting in a cardinality of . Therefore, .
The resulting set (with only those h bits changed) is the result (without considering the operation of the perfect substitution encryption scheme) of a new relocation of the bits of , according to the random order given by . Thus, for every and every , there exists a unique such that because, if there was another value such that , there would be a different ordering of the bits of m, which would mean that some of the bits of the possible values c and , both belonging to the set C, were different, and so, . Thus, for every and every , there exists a unique such that .
In the symmetric case, we have:
The key space K which, for user A (similar to user B) is , is random with uniform probability equal to taking values from the set , where . In addition, its cardinality . Additionally, , that we can consider as the set M (with only those t bits changed), comes from the output of the hash functions, such that, although its cardinality is , only t values will be taken (as selected by ), and so, its cardinality is . From the random variable of length , all t values will be taken, resulting in its cardinality being . Therefore, .
The resulting set of length t, is the result (without considering the operation of the perfect substitution encryption scheme) of a new relocation of the t bits of , according to the random order given by . Thus, for every and every , there exists a unique such that as, if there was another value such that , there would be a different ordering of the bits of m, which this would mean that some of the bits of the possible values c and , both belonging to the set C, were different, and so, . Thus, for every and every , there exists a unique such that . □
If the substitution system as well as the transposition system are perfectly secret, we must analyze if its sequential union (i.e., how we apply them) is also perfectly secret.
Theorem 3.
The sequential union of two perfectly secret systems is perfectly secret.
Proof.
From the partial results of perfect secrecy of both sub-systems, and . Furthermore, , so , and thus, we have .
On the other hand, as we have already obtained, the probability distribution on is uniform. Moreover, for every and every , there exists a unique such that , and for every and every , there exists a unique such that . As and , for every and every , there exists a unique such that .
This completes the proof of Shannon’s theorem for the two perfectly encrypted systems chained together. □
From the results above, we can affirm that our cryptobiometrics system is semantically secure, as this is the lowest level of security of all its constituent parts.
5. Experiments
The voice database was Mozilla’s “Common Voice” [131].
A total of 25 different experiments were carried out, trying to discriminate one person (with 50 text-independent voice fragments per person) against other people (200 different and text-independent fragments), with training-test percentages of 80–20% of the total samples.
The speech fragments taken for processing had a time length of T = 4000 ms.
The people in the database were men and women who were diverse in age, almost all of them speaking in the Spanish language (from Spain and Spanish America), while a few of them spoke in the English language.
We show, in Figure 5, the experimental results in terms of the ROC (receiver operating characteristic) curve, which graphically offers the ratio between sensitivity (true positive rate; on the vertical axis) and specificity (1-specifity), or false positive rate (on the horizontal axis), for our binary classifier system, as the discrimination threshold was varied. The value of the area under the curve (AUC) was and the point of equal error rate (EER)—the point where the false positive rate and the false negative rate are equal—was .
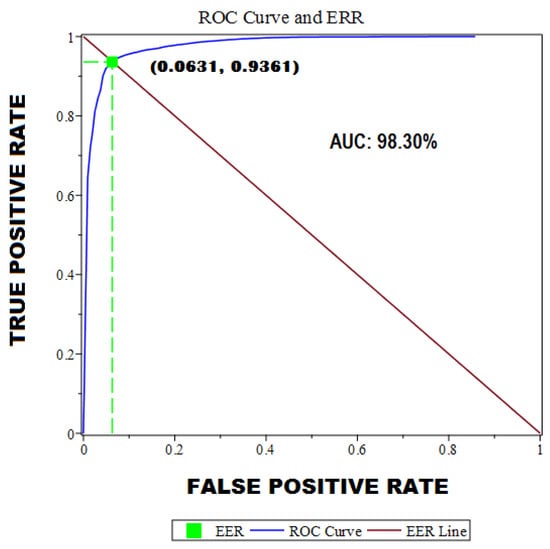
Figure 5.
ROC curve, EER point, and area under the ROC curve (AUC) of the experiments carried out.
The experiments provided, for each case from , a vector of elements, after carrying out the Welch estimation. Thus, for each person p, with the different values of their text-independent voice samples, we obtained a mean vector and its variance . From these, we could construct a certain threshold for each person p. These were the data stored for use in the voice recognition system during the matching process against a text-independent verification.
Thus, at the moment in which a person had to recognize themself in the verification process, they provided their voice signal, thereby generating their input vector after applying estimation signal processing through the Welch periodogram.
At this time, the vectors and of this person were applied to each of the values of the vector , accounting for the percentage of values within the expected range: , for every value .
It was this percentage that affirmatively or negatively resolved the verification of the subject.
Generation of Fundamental Elements of Cryptographic Schemes
As an example, let us consider asymmetric encryption with elliptic curve, and symmetric encryption with AES.
Elliptic Curve
Consider, as an example template , the mean and variance vectors of the person of the preceding biometric data: and .
After formatting it as a string value with five digits in each value and concatenating it with the identifiers “MEAN” and “VARIANCE,” we obtained the following sequence (not complete):
In binary, had 61,673 bits.
Let us start by looking for a prime number. For the random value , let us suppose it has length 32 bits (which permits an order of cancellations and possible options in the SHA function composition, if we do not modify the length of , which we can also always do):
Applying the various concatenated hash functions of type SHA-2-512 (H1), and finally, the function SHA-3-512 (H2),
the final data is BBBF 5EA0 8623 E288 E41E AC25 9E1E 624A A634 251F E4D7 557C 15D0 A261 5375 8683 5109 F6EC 5DB4 FE18 C77A 1149 B797 264E 36C3 7A7F 97DE E159 FBE1 218E 0556 27DC (hexadecimal), with 512 bits (in incomplete binary expression): .
Carrying out the over-randomization, we considered that, if we sought a prime number with 1024 bits, we had to create a random template of 1024 bits. In our case, we used
and we also generated a random set of 512 positions (out of the 1024 possible):
Applying the function we obtained a final value of after applying and :
which, in decimal, is the value .
From , the prime number can be calculated, which is either the same number (if prime), the next prime that follows, or a strong prime. Calculating the following prime (as, in our case, the number was not so), we obtained (decimal).
If, otherwise, we sought a strong prime from it, we could have used as input, to satisfy the exposed requirements,
- (a)
- (with a high prime and A any integer);
- (b)
- (with a high prime and B any integer);
- (c)
- (with a high prime and C any integer).
With that, we would have the following strong prime , with , , and .
The rest of the elements of the elliptic curve over , , were obtained as elements of : with p, the values u and v can be calculated randomly, modulo the prime p, such that they always fulfilled ; for example, and , in decimal form.
However, to facilitate finding a base point of the elliptic curve, we applied the procedure described above. With this, the obtained prime value was (decimal) and the base point J in E had coordinate (decimal).
As detailed above, in the encryption process of the elliptic curve cipher, user A chooses a secret key a, which could be a random value or a cryptobiometric value, generated as we have done here for the case of p. Considering this last option and taking the same template and a new random value , we obtained E038 4430 2D22 878E E06C C402 CF3D 6792 3817 2372 CA5D 7548 6F72 4E15 8E5F 35D3 B4F2 BFEB 189C 9C87 8F8B 874E AEFE E1A2 C484 B737 26D1 E87F 930F B18B 488C 05C8 (hexadecimal). Generating new values (binary) and (decimal), we obtained, as a result, the value (binary). With , an element of was generated:
Furthermore, A make its key public and generate a random session value k modulo .
Similarly as we have done with elliptic curve encryption, we can compute any other prime q, and with the obtained values of p and q, the application to each of the considered asymmetric encryption schemes is immediate.
AES
In the AES symmetric cipher, assuming that actor A has (assuming, for A, the same value as before was obtained) and actor B has , carrying out the corresponding operations, we obtained:
Operating for user B, we obtained the value
Thus, by exchanging the user keys under a secure asymmetric encryption protocol, they obtained :
in decimal, , from which we could determine the appropriate length for the key, depending on the degree of security, for example, the first 256 bits.
As we have seen, it is clear that the biometric data are not the same at different times and in different conditions, although they may adequately identify each subject and are close between different samples, as was the case for the data of the means and variances of each subject used in our system. Furthermore, the results of false rejection rate and false acceptance rate obtained showed adequate reliability, always depending on the biometric system used. As for the bit-length, which also varied between biometric modalities, the results achieved with the digital signal processing and the power density spectrum analysis with the Welch periodogram allowed us, together with the use of the random variables used in our system, to reach the appropriate lengths for the symmetric and asymmetric encryption schemes.
In this way, we met the requirements of variability, reliability, and biometric bit-length.
6. Conclusions
Cryptography can be used to obtain confidentiality and integrity, but can only achieve partial authentication. We believe that only the combination of cryptography and biometrics (into cryptobiometrics) can achieve total and complete authentication.
A suitable cryptobiometric system must meet a number of main requirements: Our proposal achieved, on one hand, the requirements of irreversibility, cancellability, irrevocability, and unlinkability. On the other hand, the characteristics of variability, reliability, and biometric bit-length, depending on the chosen biometry, were also achieved, as demonstrated by our experimental results.
In this paper, we designed a cryptobiometrics system to generate cryptographic keys (i.e., key-generation type), as well as the rest of the necessary elements in the different and diverse cryptographic schemes. Thus, we indicated the related procedures in both symmetric (e.g., AES) and asymmetric ciphers (e.g., RSA, Elgamal, elliptic curve, Paillier), together with the Diffie–Hellman exchange protocol. In this way, we demonstrated the versatility and breadth of use of our design in any cryptographic and/or biometric framework. Through this system, the basic elements of the different cryptographic schemes which are later used in various confidential communications can be calculated. Each of these basic elements is inevitably linked to the biometric data of the subject, in the case of asymmetric cryptography. For the symmetric case, a common key K will be generated between both actors A and B, through gathering biometric aspects of both actors.
On the other hand, our system integrates substitution and transposition ciphers, the unity of which achieves diffusion and confusion, both desirable elements of a good cipher, as considered by Shannon [126]. Our proposal not only integrates these ciphers, but uses both methods in their most secure way: perfect encryption. We showed that our over-randomization algorithm is perfectly secret. Considering a priori that the Vernam substitution cipher, which is used in our over-randomization system, is perfectly secret, we gave proof that there is another (dual) form of perfectly secret substitution in transposition. We also demonstrated that its sequentiality is perfectly secret. With this feature, there is no possibility of being cryptanalysed; at least in our second sub-system. The first part of the system, with a hash structure, is semantically secure. This makes our system at least semantically secure.
We detailed a practical application of our system using voice biometrics. The verification and text-independent modality were followed, using a template matching method. A total of 25 different experiments, with 50 text-independent voice fragments per person assessed against other people (200 different and text-independent fragments), were carried out. Signal processing methods were used to obtain the data of the Welch periodogram, with very adequate results; that is, an equal error rate (EER) of and area under the curve (AUC) of .
With the voice biometrics generated for one of the users under study, by means of the mean values and variance , we constructed a template . From this, we were able to generate a prime value (as well as a strong prime) totally linked to the biometric data itself (i.e., cryptobiometric data) which specifies the elliptic curve with which all other data of the equation of the curve can be calculated, and furthermore, by the same method, using the template, the private and public key. We also calculated the value of a symmetric key between two users of our voice biometrics study for AES encryption.
We cannot forget the limitations of the system, which we wish to mention at this time. The system depends on the original biometric data, requiring that the biometric sample be of sufficient length. If this were not the case, the strength of the system would reside only in the random value . However, the biggest limitation of the system is that, as is inherent to the use of a perfect cipher, its key is as long as the message to be encrypted, which makes it enormously large. Thus, the lengths of and , which respectively refer to the perfect substitution and transposition encryption steps, imply high binary lengths to be stored and managed. Thus, in the case considered as an example, with a prime value p of 1024 bits, the length of is 512 bits (as the output of the hash function SHA-3-512), the length of is 1024 (same as that of the prime value p searched), and the number of bits of the set of 512 values of is 4353 bits, which comes to an average of 8.5 bits for each value of . Despite this limitation, bear in mind that it is not intended to encrypt a message, with consequent high length, but only to obtain cryptobiometric keys or the main elements of the cipher suite, which are always shorter. In addition, and finally, a limitation that must always be considered in any real and implemented cryptographic system, is the possibility of side-channel attacks.
We believe that this proposal, despite the mentioned limitations, unites the cryptographic aspects of confidentiality and integrity with the biometric physical and behavioral elements of the parties involved in the communication, thereby achieving authenticity, and in this way, adequately accomplishes the security objectives mentioned at the beginning of this work.
Author Contributions
Conceptualization, V.J.-V.; funding acquisition, C.S.-Á.; methodology, V.J.-V.; investigation, V.J.-V.; supervision, V.J.-V. and C.S.-Á.; validation, V.J.-V. and C.S.-Á.; writing—original draft preparation, V.J.-V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was developed within the project Co-Mov, co-funded by Comunidad de Madrid (Spain), the European Social Fund, and the European Regional Development Fund, with grant number Y2018/EMT-4818.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Parker, D.B. Toward a New Framework for Information Security. In The Computer Security Handbook; Bosworth, S., Kabay, M.E., Eds.; John Wiley & Sons: New York, NY, USA, 2002; pp. 27–48. [Google Scholar]
- Parker, D.B. Fighting Computer Crime; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Jara Vera, V.; SánchezÁvila, C. La Criptobiometría y la Redefinición de los Conceptos de Persona e Identidad como Claves para la Seguridad. Proc. DESEi+d 2013, 583–590. [Google Scholar]
- Hao, F.; Anderson, R.; Daugman, J. Combining Crypto with Biometrics Effectively. IEEE Trans. Comput. 2006, 55, 1081–1088. [Google Scholar]
- Kanade, S.; Petrovska-Delacrétaz, D.; Dorizzi, B. Enhancing Information Security and Privacy by Combining Biometrics with Cryptography. Synth. Lect. Inf. Secur. Privacy Trust 2012, 3, 1–140. [Google Scholar] [CrossRef][Green Version]
- Rathgeb, C.; Uhl, A. A Survey on Biometric Cryptosystems and Cancelable Biometrics. EURASIP J. Inf. Secur. 2011, 3, 1–25. [Google Scholar] [CrossRef]
- Campisi, P. Security and Privacy in Biometrics; Springer: London, UK, 2013. [Google Scholar]
- Ngo, D.C.L.; Teoh, A.B.J.; Hu, J. Biometric Security; Cambridge Scholars Publishing: New Castle upon Tyne, UK, 2015. [Google Scholar]
- Rane, S.; Wang, Y.; Draper, S.C.; Ishwar, P. Secure Biometrics: Concepts, Authentication Architectures, and Challenges. IEEE Signal Process. Mag. 2013, 30, 51–64. [Google Scholar] [CrossRef]
- Bhanu, B.; Kumar, A. Deep Learning for Biometrics; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Marcel, S.; Nixon, M.S.; Fierrez, J.; Evans, N. Handbook of Biometric Anti-Spoofing: Presentation Attack Detection; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Gomez-Barrero, M.; Galbally, J. Reversing the Irreversible: A Survey on Inverse Biometrics. Comput. Secur. 2020, 90, 101700. [Google Scholar] [CrossRef]
- Soutar, C.; Roberge, D.; Stojanov, S.A.; Gilroy, R.; Vijaya Kumar, B.V.K. Biometric Encryption Using Image Processing. Proc. SPIE Opt. Secur. Counterfeit Deterrence Tech. 1998, 3314, 178–188. [Google Scholar]
- Soutar, C.; Roberge, D.; Stojanov, S.A.; Gilroy, R.; Vijaya Kumar, B.V.K. Biometric Encryption-Enrollment and Verification Procedures. Proc. SPIE Opt. Secur. Counterfeit Deterrence Tech. 1998, 3386, 24–35. [Google Scholar]
- Tomko, G.J.; Soutar, C.; Schmidt, G.J. Fingerprint Controlled Public Key Cryptographic System. U.S. Patent 5541994, 30 July 1996. [Google Scholar]
- Tomko, G.J.; Soutar, C.; Schmidt, G.J. Biometric Controlled Key Generation. U.S. Patent 5680460, 21 October 1997. [Google Scholar]
- Tomko, G.J.; Stoianov, A. Method and Apparatus for Securely Handling a Personal Identification Number or Cryptographic Key Using Biometric Techniques. U.S. Patent 5712912, 27 January 1998. [Google Scholar]
- Juels, A.; Wattenberg, M. A Fuzzy Commitment Scheme. In Proceedings of the 6th ACM Conference on Computer and Communications Security, Kent Ridge Digital Labs, Singapore, 2–4 November 1999; pp. 28–36. [Google Scholar]
- Teoh, A.B.J.; Kim, J. Secure Biometric Template Protection in Fuzzy Commitment Scheme. IEICE Electron. Express 2007, 4, 724–730. [Google Scholar] [CrossRef]
- Tong, V.; Sibert, H.; Lecoeur, J.; Girault, M. Biometric Fuzzy Extractors Made Practical: A Proposal Based on Fingercodes. In Advances in Biometrics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 604–613. [Google Scholar]
- Ao, M.; Li, S. Near Infrared Face Based Biometric Key Binding. In Advances in Biometrics; Springer: Berlin/Heidelberg, Germany, 2009; pp. 376–385. [Google Scholar]
- Goh, A.; Ngo, D.C.L. Computation of Cryptographic Keys from Face Biometrics. In Communications and Multimedia Security. Advanced Techniques for Network and Data Protection; Springer: Berlin/Heidelberg, Germany, 2003; pp. 1–13. [Google Scholar]
- Juels, A.; Sudan, M. A Fuzzy Vault Scheme. Des. Codes Cryptogr. 2006, 38, 237–257. [Google Scholar] [CrossRef]
- Clancy, T.; Kiyavash, N.; Lin, D. Secure Smartcardbased Fingerprint Authentication. In Proceedings of the 2003 ACM SIGMM Workshop on Biometrics Methods and Applications, Berkley, CA, USA, 2–8 November 2003; pp. 45–52. [Google Scholar]
- Lee, Y.; Bae, K.; Lee, S.; Park, K.; Kim, J. Biometric Key Binding: Fuzzy Vault Based on Iris Images. In Proceedings of the International Conference on Biometrics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 800–808. [Google Scholar]
- Wu, X.; Wang, K.; Zhang, D. A Cryptosystem Based on Palmprint Feature. In Proceedings of the 19th Pattern Recognition, Tampa, FL, USA, 8–11 December 2008; pp. 1–4. [Google Scholar]
- Wu, Y.; Qiu, B. Transforming a Pattern Identifier into Biometric Key Generators. In Proceedings of the IEEE International Conference on Multimedia and Expo, Suntec City, Singapore, 19–23 July 2010; pp. 78–82. [Google Scholar]
- Uludag, U.; Jain, A.K. Fuzzy Fingerprint Vault. In Proceedings of the Biometrics: Challenges Arising from Theory to Practice, Cambridge, UK, 22–27 August 2004; pp. 13–16. [Google Scholar]
- Moon, D.; Choi, W.Y.; Moon, K.; Chung, Y. Fuzzy Fingerprint Vault Using Multiple Polynomials. In Proceedings of the IEEE 13th International Symposium on Consumer Electronics, Kyoto, Japan, 9–11 June 2009; pp. 290–293. [Google Scholar]
- Dodis, Y.; Ostrovsky, R.; Reyzin, L.; Smith, A. Fuzzy Extractors: How to Generate Strong Keys from Biometrics and Other Noisy Data. In Proceedings of the Eurocrypt, Advances in Cryptology; Springer; Berlin/Heidelberg, Germany, 2004; pp. 523–540. [Google Scholar]
- Linnartz, J.; Tuyls, P. New Shielding Functions to Enhance Privacy and Prevent Misuse of Biometric Templates. In Proceedings of the 4th Audio- and Video-Based Biometric Person Authentication, Guildford, UK, 9–11 June 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 393–402. [Google Scholar]
- Veen, M.; Kevenaar, T.; Schrijen, G.; Akkermans, T.; Zuo, F. Face Biometrics with Renewable Templates. In Proceedings of the 8th Security, Steganography, and Watermarking of Multimedia Contents (SSWMC), San Jose, CA, USA, 16–19 January 2006; pp. 205–216. [Google Scholar]
- Tuyls, P.; Goseling, J. Capacity and Examples of Template-Protecting Biometric Authentication Systems. In Proceedings of the Biometric Authentication; Springer: Berlin/Heidelberg, Germany, 2004; pp. 158–170. [Google Scholar]
- Tuyls, P.; Verbitskiy, E.; Goseling, J.; Denteneer, D. Privacy Protecting Biometric Authentication Systems: An Overview. In Proceedings of the 12th European Signal Processing Conference (EUSIPCO), Vienna, Austria, 6–10 September 2015. [Google Scholar]
- Jain, A.; Nandakumar, K.; Nagar, A. Biometric Template Security. EURASIP J. Adv. Signal Process. 2008, 2008, 1–7. [Google Scholar] [CrossRef]
- Huang, Y.; Malka, L.; Evans, D.; Katz, J. Efficient Privacy-Preserving Biometric Identification. In Proceedings of the 18th Network and Distributed System Security Conference (NDSSC), San Diego, CA, USA, 6–9 February 2011; pp. 1–14. [Google Scholar]
- Monrose, F.; Reiter, M.; Li, Q.; Wetzel, S. Cryptographic Key Generation from Voice. In Proceedings of the 2001 IEEE Symposium on Security and Privacy, Oakland, CA, USA, 12–16 May 2001; pp. 1–12. [Google Scholar]
- Monrose, F.; Reiter, M.; Li, Q.; Wetzel, S. Using Voice to Generate Cryptographic Keys. In Odyssey; 2001; pp. 237–242. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.11.1062&rep=rep1&type=pdf (accessed on 8 September 2020).
- Monrose, F.; Reiter, M.; Wetzel, S. Password Hardening Based on Keystroke Dynamics. Int. J. Inf. Secur. 2002, 1, 69–83. [Google Scholar] [CrossRef][Green Version]
- Monrose, F.; Reiter, M.; Li, Q.; Lopresti, D.; Shih, C. Toward Speech-Generated Cryptographic Keys on Resource-Constrained Devices. In Proceedings of the 11th USENIX Security Symposium, San Francisco, CA, USA, 5–9 August 2002; pp. 283–296. [Google Scholar]
- Teoh, A.B.J.; Ngo, D.C.L.; Goh, A. Biohashing: Two Factor Authentication Featuring Fingerprint Data and Tokenised Random Number. Pattern Recognit. 2004, 37, 2245–2255. [Google Scholar]
- Teoh, A.B.J.; Goh, A.; Ngo, D.C.L. Random Multispace Quantization as an Analytic Mechanism for Biohashing of Biometric and Random Identity Inputs. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1892–1901. [Google Scholar] [CrossRef]
- Teoh, A.B.J.; Ngo, D.C.L.; Goh, A. Personalised Cryptographic Key Generation Based on Facehashing. Comput. Secur. 2004, 23, 606–614. [Google Scholar] [CrossRef]
- Ngo, D.C.L.; Teoh, A.B.J.; Goh, A. Biometric Hash: High-Confidence Face Recognition. IEEE Trans. Circuits Syst. Video Technol. 2006, 16, 771–775. [Google Scholar] [CrossRef]
- Iida, K.; Kiya, H. Secure and Robust Identification Based on Fuzzy Commitment Scheme for JPEG Image. In Proceedings of the IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB), Nara, Japan, 1–3 June 2016; pp. 1–5. [Google Scholar]
- Malarvizhi, N.; Selvarani, P.; Raj, P. Adaptive Fuzzy Genetic Algorithm for Multi Biometric Authentication. Comput. Sci. Multimed. Tools Appl. 2019, 79, 9131–9144. [Google Scholar] [CrossRef]
- Liew, C.Z.; Shaw, R.; Li, L.; Yang, Y. Survey on Biometric Data Security and Chaotic Encryption Strategy with Bernoulli Mapping. In Proceedings of the International Conference on Medical Biometrics, Shenzhen, China, 30 May–1 June 2014; pp. 174–180. [Google Scholar]
- Abdul, W.; Nafea, O.; Ghouzali, S. Combining Watermarking and Hyper-Chaotic Map to Enhance the Security of Stored Biometric Templates. Comput. J. 2020, 63, 479–493. [Google Scholar] [CrossRef]
- Priya, S.S.S.; Kathigaikumar, P.; Mangai, N.M.S. Mixed Random 128 Bit Key Using Fingerprint Features and Binding Key for AES Algorithm. In Proceedings of the International Conference on Contemporary Computing and Informatics (IC3I), Mysore, India, 27–29 November 2014; pp. 1226–1230. [Google Scholar]
- Barman, S.; Samanta, D.; Chattopadhyay, S. Revocable Key Generation from Irrevocable Biometric Data for Symmetric Cryptography. In Proceedings of the 2015 Third International Conference on Computer, Communication, Control and Information Technology (C3IT), Hooghly, India, 7–8 February 2015; pp. 1–4. [Google Scholar]
- Kuznetsov, A.; Kiyan, A.; Uvarova, A.; Serhiienko, R.; Smirnov, V. New Code Based Fuzzy Extractor for Biometric Cryptography. In Proceedings of the International Scientific-Practical Conference Problems of Infocommunications. Science and Technology (PIC S&T), Kharkiv, Ukraine, 9–12 October 2018; pp. 119–124. [Google Scholar]
- Chang, D.; Garg, S.; Hasan, M.; Mishra, S. Cancelable Multi-Biometric Approach Using Fuzzy Extractor and Novel Bit-Wise Encryption. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3152–3167. [Google Scholar] [CrossRef]
- Damasevicius, R.; Maskeliunas, R.; Kazanavicius, E.; Wozniak, M. Combining Cryptography with EEG Biometrics. Comput. Intell. Neurosci. 2018, 2018, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Olanrewaju, L.; Oyebiyi, O.; Misra, S.; Maskeliunas, R.; Damasevicius, R. Secure Ear Biometrics Using Circular Kernel Principal Component Analysis, Chebyshev Transform Hashing and Bose-Chaudhuri-Hocquenghem Error-Correcting Codes. Signal Image Video Process. 2020, 14, 847–855. [Google Scholar] [CrossRef]
- Chai, T.Y.; Goi, B.M.; Tay, Y.H.; Jin, Z. A New Design for Alignment-Free Chaffed Cancelable Iris Key Binding Scheme. Symmetry 2019, 11, 164. [Google Scholar] [CrossRef]
- Mohsin, A.H.; Zaidan, A.A.; Zaidan, B.B.; Albahri, O.S.; Ariffin, S.A.B.; Alemran, A.; Enaizan, O.; Shareef, A.H.; Jasim, A.N.; Jalood, N.S.; et al. Finger Vein Biometrics: Taxonomy Analysis, Open Challenges, Future Directions, and Recommended Solution for Decentralised Network Architectures. IEEE Access 2020, 8, 9821–9845. [Google Scholar] [CrossRef]
- Bodo, A. Method for Producing a Digital Signature with Aid of a Biometric Feature. German Patent 4243908 A1, 30 June 1994. [Google Scholar]
- Davida, G.I.; Frankel, Y.; Matt, B.J. On Enabling Secure Applications through Off-Line Biometric Identification. In Proceedings of the IEEE Symposium on Security and Privacy, Oakland, CA, USA, 3–6 May 1998; pp. 148–157. [Google Scholar]
- Davida, G.I.; Frankel, Y.; Matt, B.J.; Peralta, R. On the Relation of Error Correction and Cryptography to an Offline Biometric Based Identification Scheme. In Proceedings of the International Workshop on Coding and Cryptography (WCC), Paris, France, 11–14 January 1999; pp. 129–138. [Google Scholar]
- Vielhauer, C.; Steinmetz, R.; Mayerhofer, A. Biometric Hash Based on Statistical Features of Online Signatures. In Proceedings of the 16th International Conference on Pattern Recognition (ICPR), Quebec City, QC, Canada, 11–15 August 2002. [Google Scholar]
- Feng, H.; Wah, C.C. Private Key Generation from On-Line Hand-written Signatures. Inf. Manag. Comput. Secur. 2002, 10, 159–164. [Google Scholar] [CrossRef]
- Drahanský, M. Biometric Security Systems Fingerprint Recognition Technology. Ph.D. Thesis, Dept. Information Technology, Brno University of Technology, Brno, Czech Republic, 2005. [Google Scholar]
- Li, Q.; Guo, M.; Chang, E.C. Fuzzy Extractors for Asymmetric Biometric Representations. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Anchorage, Alaska, 23–28 June 2008; pp. 1–6. [Google Scholar]
- Li, Q.; Chang, E.C. Robust, Short and Sensitive Authentication Tags Using Secure Sketch. In Proceedings of the 8th Workshop on Multimedia and Security, Geneva, Switzerland, 26–27 September 2006; pp. 56–61. [Google Scholar]
- Sutcu, Y.; Li, Q.; Memon, N. Protecting Biometric Templates with Sketch: Theory and Practice. IEEE Trans. Inf. Forensics Secur. 2007, 2, 503–512. [Google Scholar] [CrossRef]
- Anees, A.; Chen, Y.P.P. Discriminative Binary Feature Learning and Quantization in Biometric Key Generation. Pattern Recognit. 2018, 77, 289–305. [Google Scholar] [CrossRef]
- Yuliana, M.; Wirawan, S. A Simple Secret Key Generation by Using a Combination of Pre-Processing Method with a Multilevel Quantization. Entropy 2019, 21, 192. [Google Scholar] [CrossRef]
- Chen, Y.; Wo, Y.; Xie, R.; Wu, C.; Han, G. Deep Secure Quantization: On Secure Biometric Hashing against Similarity-Based Attacks. Signal Process. 2019, 154, 314–323. [Google Scholar] [CrossRef]
- Ratha, N.K.; Connell, J.H.; Bolle, R.M. Enhancing Security and Privacy in Biometrics-Based Authentication Systems. IBM Syst. J. 2001, 40, 614–634. [Google Scholar] [CrossRef]
- Zuo, J.; Ratha, N.K.; Connell, J.H. Cancelable Iris Biometric. In Proceedings of the 19th International Conference on Pattern Recognition (ICPR), Tampa, FL, USA, 8–11 December 2008; pp. 1–4. [Google Scholar]
- Savvides, M.; Kumar, B.V.; Khosla, P. Cancelable Biometric Filters for Face Recognition. In Proceedings of the 17th International Conference on Pattern Recognition (ICPR), Cambridge, UK, 26 August 2004; pp. 922–925. [Google Scholar]
- Trivedi, A.K.; Thounaojam, D.M.; Pal, S. Non-Invertible Cancellable Fingerprint Template for Fingerprint Biometric. Comput. Secur. 2020, 90, 101690. [Google Scholar] [CrossRef]
- Barman, S.; Samanta, D.; Chattopadhyay, S. Approach to Cryptographic Key Generation from Fingerprint Biometrics. Int. J. Biometr. 2015, 7, 226–248. [Google Scholar] [CrossRef]
- Gaddam, S.V.K.; Lal, M. Efficient Cancellable Biometric Key Generation Scheme for Cryptography. Int. J. Netw. Secur. 2010, 11, 57–65. [Google Scholar]
- Kaur, H.; Khanna, P. Random Slope Method for Generation of Cancelable Biometric Features. Pattern Recognit. Lett. 2019, 126, 31–40. [Google Scholar] [CrossRef]
- Neethu, C.; Ali Akbar, N. Revocable Session Key Generation Using Combined Fingerprint Template. In Proceedings of the International Conference on Control, Power, Communication and Computing Technologies (ICCPCCT), Kannur, India, 23–24 March 2018; pp. 584–588. [Google Scholar]
- Punithavathi, P.; Subbiah, G. Partial DCT-Based Cancelable Biometric Authentication with Security and Privacy Preservation for IoT Applications. Multimed. Tools Appl. 2019, 78, 1–28. [Google Scholar] [CrossRef]
- González-Rodríguez, J.; Torre-Toledano, D.; Ortega-García, J. Voice Biometrics. In Handbook of Biometrics; Jain, A.K., Flynn, P., Ross, A.A., Eds.; Springer: Boston, MA, USA, 2008; pp. 151–170. [Google Scholar]
- Quatieri, T.F. Discrete-Time Speech Signal Processing: Principles and Practice; Pearson Education: Lexington, MA, USA, 2008. [Google Scholar]
- Varile, G.B.; Cole, R.; Cole, R.A.; Zampolli, A.; Mariani, J.; Uszkoreit, H.; Zaenen, A. Survey of the State of the Art in Human Language Technology; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Beigi, H. Fundamentals of Speaker Recognition; Springer: New York, NY, USA, 2011. [Google Scholar]
- Saquib, Z.; Salam, N.; Nair, R.P.; Pandey, N.; Joshi, A. A Survey on Automatic Speaker Recognition Systems. Commun. Comput. Inf. Sci. 2010, 123, 134–145. [Google Scholar]
- Tirumala, S.S.; Shahamiri, S.R.; Garhwal, A.S.; Wang, R. Speaker Identification Features Extraction Methods: A Systematic Review. Expert Syst. Appl. 2017, 90, 250–271. [Google Scholar] [CrossRef]
- Meng, Z.; Altaf, M.U.B.; Juang, B.H.F. Active Voice Authentication. Digit. Signal Process. 2020, 101, 1–39. [Google Scholar] [CrossRef]
- Singh, A.P.; Nath, R.; Kumar, S. A Survey: Speech Recognition Approaches and Techniques. In Proceedings of the 5th IEEE Uttar Pradesh Section International Conference on Electrical, Electronics and Computer Engineering (UPCON), Gorakhpur, India, 2–4 November 2018; pp. 1–4. [Google Scholar]
- Stoica, P.; Moses, R. Spectral Analysis of Signals; Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Marple, S.L. Digital Spectral Analysis with Applications; Prentice Hall: Englewood Cliffs, NJ, USA, 1987. [Google Scholar]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing; Prentice Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Welch, P.D. The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging over Short, Modified Periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Stoica, P.; Moses, R. Introduction to Spectral Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 1989; pp. 52–54. [Google Scholar]
- European Union Agency for Network and Information Security (ENISA). Algorithms, Key Size and Parameters Report; ENISA: Heraklion, Greece, 2014. [Google Scholar]
- Rivest, R.; Shamir, A.; Adleman, L. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Elgamal, T. A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms. IEEE Trans. Inf. Theory 1985, 31, 469–472. [Google Scholar] [CrossRef]
- Miller, V.S. Use of Elliptic Curves in Cryptography. In Proceedings of the Crypto, Advances in Cryptology; Springer; Berlin/Heidelberg, Germany, 1985; pp. 417–426. [Google Scholar]
- Koblitz, N. A Course in Number Theory and Cryptography; Springer: New York, NY, USA, 1987. [Google Scholar]
- Paillier, P. Public-Key Cryptosystems Based on Composite Degree Residuosity Classes. In Proceedings of the EUROCRYPT, Advances in Cryptology; Springer; Berlin/Heidelberg, Germany, 1999; pp. 223–238. [Google Scholar]
- Diffie, W.; Hellman, M. New Directions in Cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef]
- Merkle, R.C. Secure Communications over Insecure Channels. Commun. ACM 1978, 21, 294–299. [Google Scholar] [CrossRef]
- O’Higgins, B.; Diffie, W.; Strawczynski, L.; Hoog, R. Encryption and ISDN—A Natural Fit. In Proceedings of the International Switching Symposium (ISS), Phoenix, AZ, USA, 15–21 March 1987; pp. 863–869. [Google Scholar]
- Certicom Research. Standards for Efficient Cryptography, SEC 1: Elliptic Curve Cryptography; Certicom: Waterloo, ON, Canada, 2009; pp. 56–60. [Google Scholar]
- Canetti, R.; Krawczyk, H. Analysis of Key-Exchange Protocols and their Use for Building Secure Channels. Proc. Eurocrypt Adv. Cryptol. 2001, 2045, 453–474. [Google Scholar]
- National Institute of Standards and Technology (NIST). Advanced Encryption Standard (AES). FIPS 197; NIST: Gaithersburg, MD, USA, 2001. [Google Scholar]
- National Institute of Standards and Technology (NIST). Data Encryption Standard (DES). FIPS 46; NIST: Gaithersburg, MD, USA, 1977. [Google Scholar]
- Singh, M.; Singh, R.; Ross, A. A Comprehensive Overview of Biometric Fusion. Inf. Fusion 2019, 52, 187–205. [Google Scholar] [CrossRef]
- Bloom, B.H. Space/Time Trade-offs in Hash Coding with Allowable Errors. Commun. ACM 1970, 13, 422–426. [Google Scholar] [CrossRef]
- Gómez-Barrero, M.; Rathgeb, C.; Li, G.; Ramachandra, R.; Galbally, J.; Bush, C. Multi-Biometric Template Protection Based on Bloom Filters. Inf. Fusion 2018, 42, 37–50. [Google Scholar] [CrossRef]
- Rathgeb, C.; Busch, C. Cancelable Multi-Biometrics: Mixing Iris-Code Based on Adaptative Bloom Filters. Comput. Secur. 2014, 42, 1–12. [Google Scholar] [CrossRef]
- Ding, Y.; Rattani, A.; Ross, A. Bayesian Belief Models for Integrating Match Scores with Liveness and Quality Measures in a Fingerprint Verification System. In Proceedings of the 2016 International Conference on Biometrics (ICB), Halmstad, Sweden, 13–16 June 2016; Volume 4, pp. 1–8. [Google Scholar]
- Liu, Y.; Yan, J.; Ouyang, W. Quality Aware Network for Set to Set Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4694–4703. [Google Scholar]
- National Institute of Standards and Technology (NIST). Secure Hash Standard (SHS); FIPS 180-4; NIST: Gaithersburg, MD, USA, 2015. [Google Scholar]
- Rivest, R. The MD5 Message-Digest Algorithm; RFC. 1321; Massachusetts Institute of Technology, Laboratory for Computer Science: Cambridge, MA, USA, 1992. [Google Scholar]
- National Institute of Standards and Technology (NIST). Recommendation for Applications Using Approved Hash Algorithms.; SP 800-107; NIST: Gaithersburg, MD, USA, 2012. [Google Scholar]
- National Institute of Standards and Technology (NIST). Research Results on SHA-1 Collisions. CSRC; NIST: Gaithersburg, MD, USA, 2017. [Google Scholar]
- National Institute of Standards and Technology (NIST). NIST Selects Winner of Secure Hash Algorithm (SHA-3) Competition; NIST: Gaithersburg, MD, USA, 2012. [Google Scholar]
- National Institute of Standards and Technology (NIST). SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions; FIPS 202; NIST: Gaithersburg, MD, USA, 2015. [Google Scholar]
- Mendel, F.; Nad, T.; Schläffer, M. Improving Local Collisions: New Attacks on Reduced SHA-256. Proc. Eurocrypt Adv. Cryptol. 2013, 7881, 262–278. [Google Scholar]
- Dobraunig, C.; Eichlseder, M.; Mendel, F. Analysis of SHA-512/224 and SHA-512/256. Proc. Asiacrypt Adv. Cryptol. 2015, 9453, 612–630. [Google Scholar]
- Khovratovich, D.; Rechberger, C.; Savelieva, A. Bicliques for Preimages: Attacks on Skein-512 and the SHA-2 Family. In Proceedings of the 19th International Workshop on Fast Software Encryption, Washington, DC, USA, 19–21 March 2012; pp. 244–263. [Google Scholar]
- Morawiecki, P.; Pieprzyk, J.; Srebrny, M. Rotational Cryptanalysis of Round-Reduced Keccak. In Proceedings of the 21st International Workshop on Fast Software Encryption, London, UK, 3–5 March 2014; pp. 241–262. [Google Scholar]
- Amy, M.; Di Matteo, O.; Gheorghiu, V.; Mosca, M.; Parent, A.; Schanck, J. Estimating the Cost of Generic Quantum Pre-image Attacks on SHA-2 and SHA-3. Sel. Areas Cryptogr. 2017, 10532, 317–337. [Google Scholar]
- ECRYPT II; eBACS. ECRYPT Benchmarking of Cryptographic Systems. Available online: http://bench.cr.yp.to (accessed on 28 May 2020).
- Miller, F. Telegraphic Code to Insure Privacy and Secrecy in the Transmission of Telegrams; C.M. Cornwell: New York, NY, USA, 1882. [Google Scholar]
- Bellovin, S.M. Frank Miller: Inventor of the One-Time Pad. Cryptologia 2011, 35, 203–222. [Google Scholar] [CrossRef]
- Vernam, G.S. Secret Signaling System. U.S. Patent 1310719 A, 22 July 1919. [Google Scholar]
- Shannon, C.E. Communication Theory of Secrecy Systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Crandall, R.; Pomerance, C.B. Prime Numbers: A Computational Perspective; Springer Science & Business Media: New York, NY, USA, 2005. [Google Scholar]
- Lenstra, H. Factoring Integers with Elliptic Curves. Ann. Math. 1987, 126, 649–673. [Google Scholar] [CrossRef]
- Bellare, M.; Rogaway, P. Introduction to Modern Cryptography; Mihir Bellare and Phillip Rogaway: San Diego, CA, USA, 1997–2005. [Google Scholar]
- Cramer, R.; Shoup, V. A Practical Public Key Cryptosystem Provably Secure against Adaptive Chosen Ciphertext Attack. In Advances in Cryptology; Springer: Berlin/Heidelberg, Germany, 1998; pp. 13–25. [Google Scholar]
- Mozilla.org. Common Voice. Available online: https://voice.mozilla.org (accessed on 23 July 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).