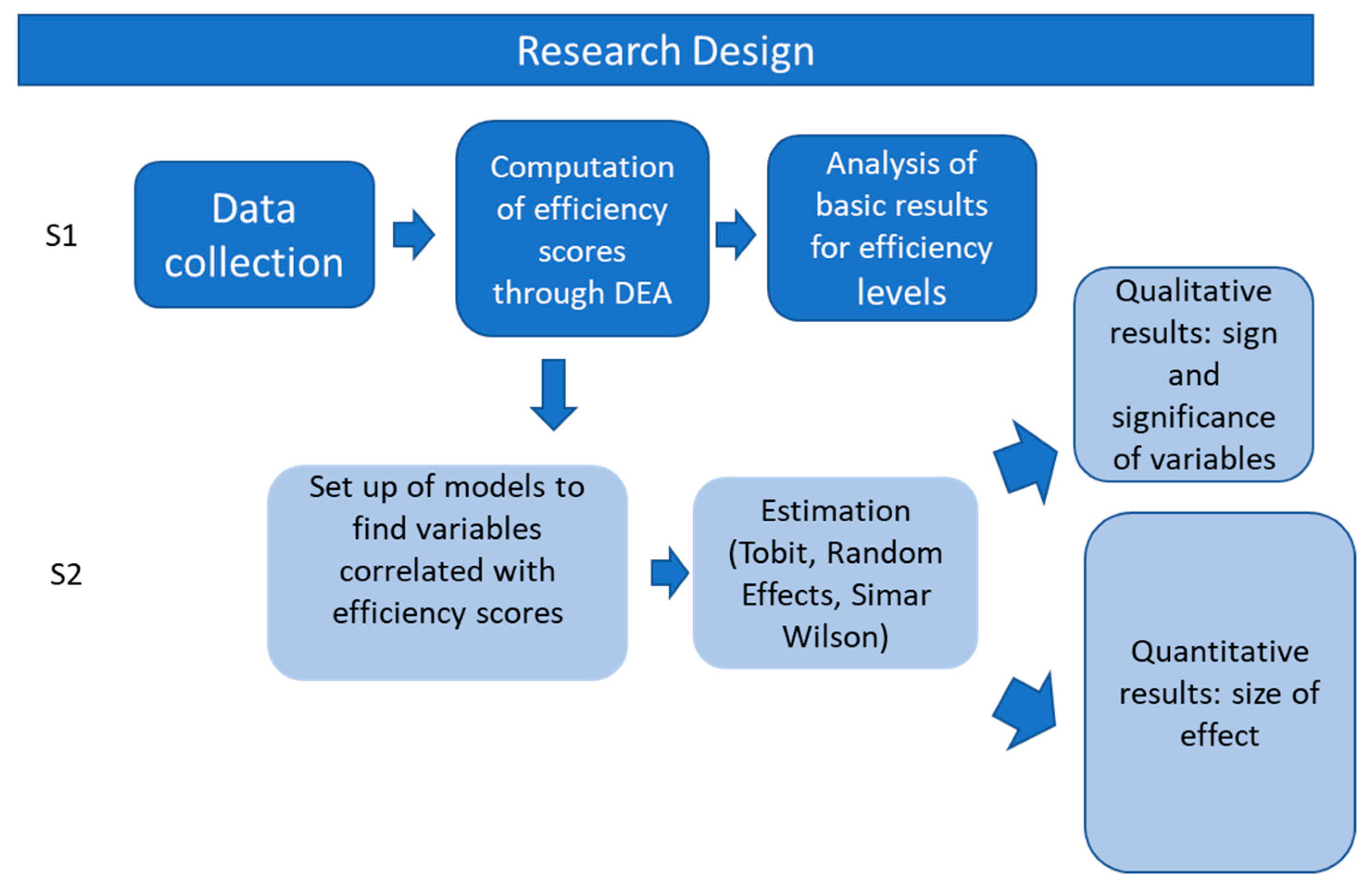
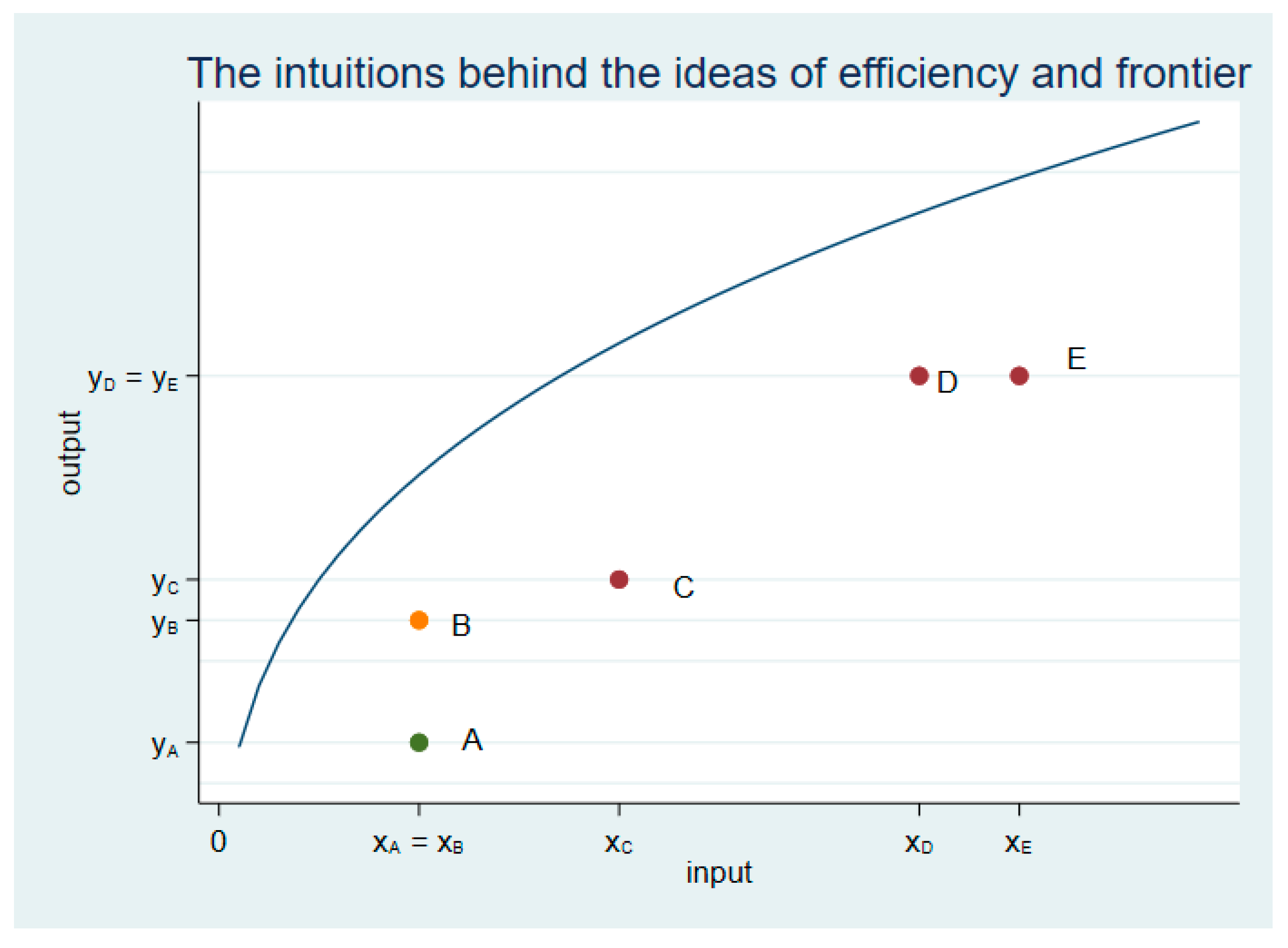
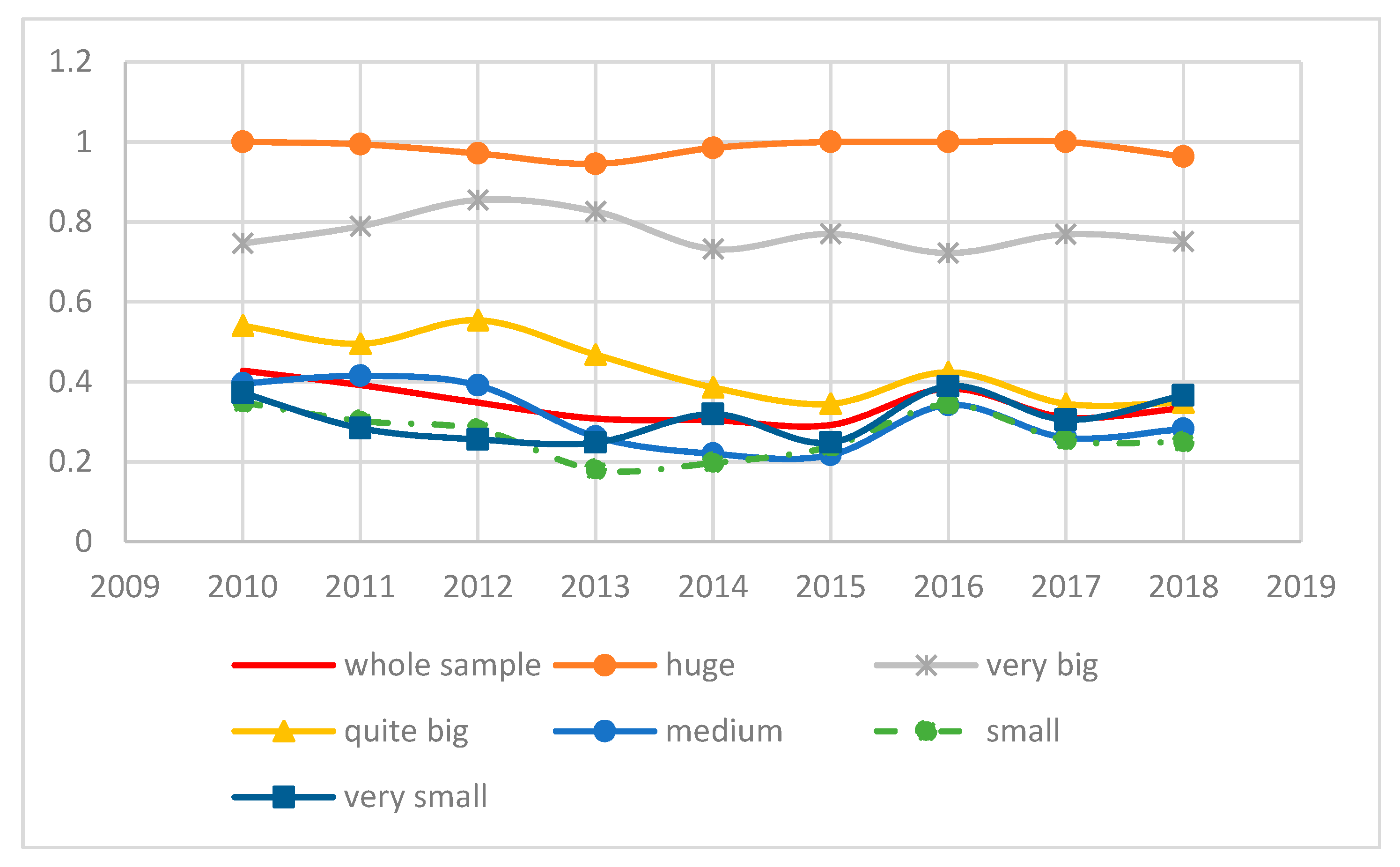5.2.1. Tobit Estimation
Typically, a Tobit model distinguishes between the latent or unobservable dependent variable and the observable dependent variable, where the observed variable is a censored version of the unobserved.
Equation (6) represents a random-effects Tobit specification for the second stage of our analysis:
wre
θit* is the latent or unobservable efficiency,
θit is the observable efficiency,
xit is a matrix of covariates,
β is a vector of coefficients,
ui is the time invariant component of the error term,
εit is the time-varying component of the error term,
i indexes firms and
t time.
In the estimation of Equation (6) we have included several indicators as covariates in order to capture different dimensions of firms, such as main activity, size, margins, financial management and personnel costs. We have also included time dummies to capture the impact of the business cycle and country dummies to allow for idiosyncratic aspects related to the markets where firms operate. The data are structured in a panel over the period 2010–2018 in order to exploit both the cross section and time variations.
Table 4 shows a first set of results obtained from the estimation by maximum likelihood of the model described by Equation (6). In order to avoid multicollinearity among the regressors, we have not included all covariates simultaneously; instead, we have added them sequentially, conforming different specifications of the baseline Equation (6). In other words, Equation (6) describes Models 1–4, the differences among them being the variables considered in
xit in each case.
To correct for heteroskedasticity, estimations have been performed with the observed information matrix (OIM) corrected standard errors. In this particular case, the variance-covariance matrix of the estimators is the matrix of second derivatives of the likelihood function. This correction for heteroskedasticity is robust to the violation of normality if distribution is symmetrical.
The last lines of
Table 4 include the results from a Lagrange multiplier Breusch–Pagan likelihood ratio test of whether the variance of the time invariant component of the error term is equal to zero. This test is can be regarded as an indirect text of the appropriateness of the random effect model. The null hypothesis of equality to 0 of the variance of the
ui component of the error term is rejected at the 99% significance level for the four models, hence supporting the utilization of the random-effects model.
Dummies for countries capture different aspects: on the one hand, cultural and institutional aspects and managerial practices ([
38]). On the other, regulatory and microeconomic and macroeconomics conditions of the particular markets where the firms operate. Regulatory aspects and institutional and macroeconomic conditions in the host country have been shown to impact the performance of multinational firms ([
56,
57]).
Dummies for the United Kingdom (UK), Italy and Sweden are positive and highly significant in all specifications, implying that the institutional framework in these countries, the size of their markets and/or their macroeconomic and institutional conditions affect the efficiency of firms positively. The dummy for Germany is also positive and significant in two specifications (models 2 and 4), although in one of them at a smaller significance level (90% in model 4).
Instead, the dummies for Spain and France display positive and negative signs and are not significant.
UK pharmaceutical firms feature a swift decision-making process which facilitates a successful and fast adjustment to changing market conditions ([
58]). Moreover, the level of distortions in the UK economy is low and factor markets are relatively flexible. In addition, the dynamic biotechnological landscape of the country has allowed the surge of alliances and collaborations. These facts may explain the positive sign of the UK dummy.
German firms typically work in less-flexible environments than their British counterparts; their access to bank funding, though, is comparatively easy. Since sound finance is one important determinant of firms’ success, as will be detailed below, the availability of funding seems quite relevant for the performance of companies in the sector and help explain the positive sign of the dummy.
The Italian industry is populated by highly skilled, agile firms, with a large component of exports and close ties to US companies. These companies encompass an important hub for foreign investment in the industry, which in turn enhances the productivity of local firms through technology diffusion and learning by watching.
Swedish pharmaceutical and biotechnological firms benefit from a market with limited regulation where bureaucracy is kept at a minimum, government support and a highly skilled workforce. These aspects would explain the successful performance of the Swedish pharmaceutical industry.
The positive signs of the country dummies, therefore, are in accordance with particular features of their institutional frameworks and/or industries.
These features, however, are not present in the French and Spanish cases. The French pharmaceutical market has historically been very protected by an outdated industrial policy. Spanish companies have been damaged by a rigid labor market and a low level of interaction between universities, research centers and firms.
We have also captured the main activity of the firms by means of dummies variables. The dummy manufacturers is equal to 1 for those firms whose main activity corresponds to NACE codes 2110 and 2120, and 0 otherwise. Conversely, the dummy biotech is 1 for firms included under the 7211 NACE code and 0 otherwise.
The dummy manufacturers are positively and significantly correlated with efficiency (columns 1 and 3), while biotech displays a negative and significant correlation in one model (column 2) and is not significant in the other (column 4). Overall, these findings are in accordance with those reported in
Section 4 above, which suggest consistently higher levels of efficiency for firms engaged in the production and commercialization of pharmaceutical articles.
Dummies for size have been assigned according to the thresholds detailed in
Section 4 above. Again, the results for the estimations agree with the trends reported in the previous Section. Firms characterized by large sizes, as conveyed by their levels of turnover, are more efficient than their counterparts, since the dummies huge and very big are positively and significantly correlated with efficiency (Models 1 and 4). The dummy that is quite big is positive but not significant.
The positive correlation between size and efficiency, however, holds only for the first two categories we defined, i.e., for sales larger than 426.92 million euros or the 95 percentile in the distribution. For companies with real turnover between 38.86 and 426.92 million euros results are inconclusive.
Those companies whose level of sales is less or equal than 38.86 million and more than 2.10 million euros register smaller efficiency figures ceteris paribus, since the dummies medium and small are negative and significant (column 2). Finally, we do not find a significant correlation between the dummy capturing the very small level of sales and efficiency (column 2). This is not surprising since firms with sales lower than the 25% percentile register poor levels of efficiency in some years but are capable of surpassing the figure attained by medium and small others.
The results for the dummy variables reflecting size and activity are thus consistent with those reported in the previous section. They are also in accord with [
35], who disclose a negative correlation between size and efficiency for a sample of Indian pharmaceutical firms.
Let us turn to the discussion of the variables capturing other aspects of firms in the industry.
As portrayed by column 1 of
Table 4, the profit margin is positively and significantly correlated, at the 99% significance level, with efficiency. This means that more efficient firms operate with higher margins. This result makes sense because the industry we are scrutinizing provides goods and services characterized by high added value which can be reflected in large margins. In fact, Reference [
59] argues that deviations from trend in profit margins are highly correlated with expenditure in R&D for pharmaceutical companies, thus confirming the links between efficiency, margins and R&D.
Interestingly, this finding suggests that successful firm strategies in this sector are featured by both high margins and high intensity of resource utilizations, at the same time. It is common to see that companies tend to choose to focus either on the achievement of high profits per unit or in the optimization of the installed capacity. This dichotomy, however, is not present in the companies in the pharmaceutical industry, according to our results.
The literature has documented that cash flow influences R&D expenditure in the case of the industry we are considering ([
60]). Reference [
61] provide some additional evidence since they find that, for the Spanish firms, the proportion of expenditure in R&D financed with internal resources is 75% for pharmaceuticals and 40% for the rest of the industries. Again, we are confronted with another differential feature of this industry. Whereas it is commonly accepted that firms should heavily rely on external funding and increase their profitability through financial leverage, the empirical evidence for this industry suggests that successful companies enjoy comparatively low ratios of indebtedness. This prudent financial structure is consistent with the high risk and long maturing period associated with the R&D activity.
To test this idea in our sample, we have included in the analysis some variables which capture particular elements of financial management. Column 2 shows that cashflow (as a percentage of sales) is indeed positively and significantly correlated with efficiency. The level of significance is very high, 99%.
Column 3, in turn, displays the estimation results when the variable collection period is included as a regressor in the baseline specification. The point estimate is negative and significant at the 99% level. Higher collection periods increase the amount of working capital necessary to run the daily activity of the firm, while shorter spans imply a sounder financial management. Our findings, therefore, are consistent with the literature, and stress the importance of exhibiting solid, well-financed balance sheets in order to register high levels of productivity. In more detail, Reference [
35] argue that the low efficiency scores achieved by some firms in their sample is associated to their inability to access financial resources.
Column 4 includes a variable capturing the cost of labor, average cost per employee, as a percentage of sales. It is highly significant and negatively correlated with efficiency.
In terms of the validations of Models 1–4, and as stated above, the literature has shown that the Tobit model provides consistent estimates ([
52,
53,
54,
62]).
Moreover, it has been argued that the severity of the problem implied by the presence of heteroskedasticity in Tobit models is a function of the degree of censoring. In our case, censoring is limited, and affects only to 6–7% of the data.
Since the estimations have been performed with OIM corrected standard errors, they are robust to the presence of heteroskedasticity. These standard errors are also robust to the violation of normality if the distribution is symmetric.
Finally, and as detailed below, results from Tobit are quite similar to those obtained by random-effects models. All these considerations lend countenance to the models described in this subsection.