Second-Order Unconditionally Stable Direct Methods for Allen–Cahn and Conservative Allen–Cahn Equations on Surfaces
Abstract
1. Introduction
2. Numerical Method
3. Numerical Experiments
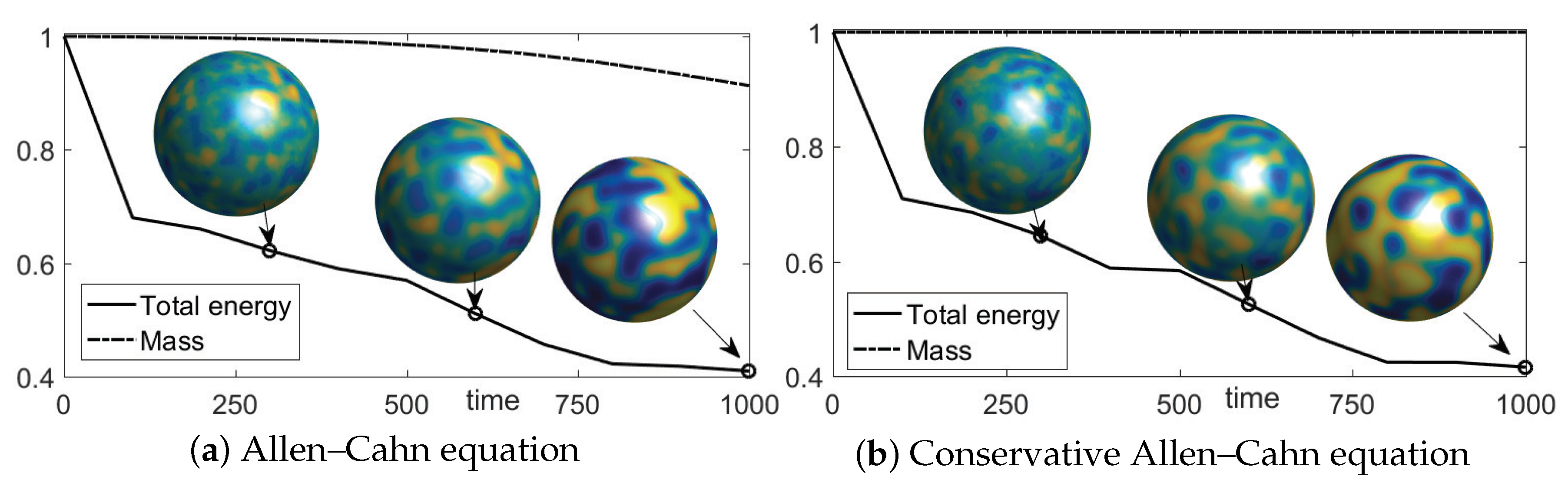
3.1. Spinodal Decomposition on Surfaces
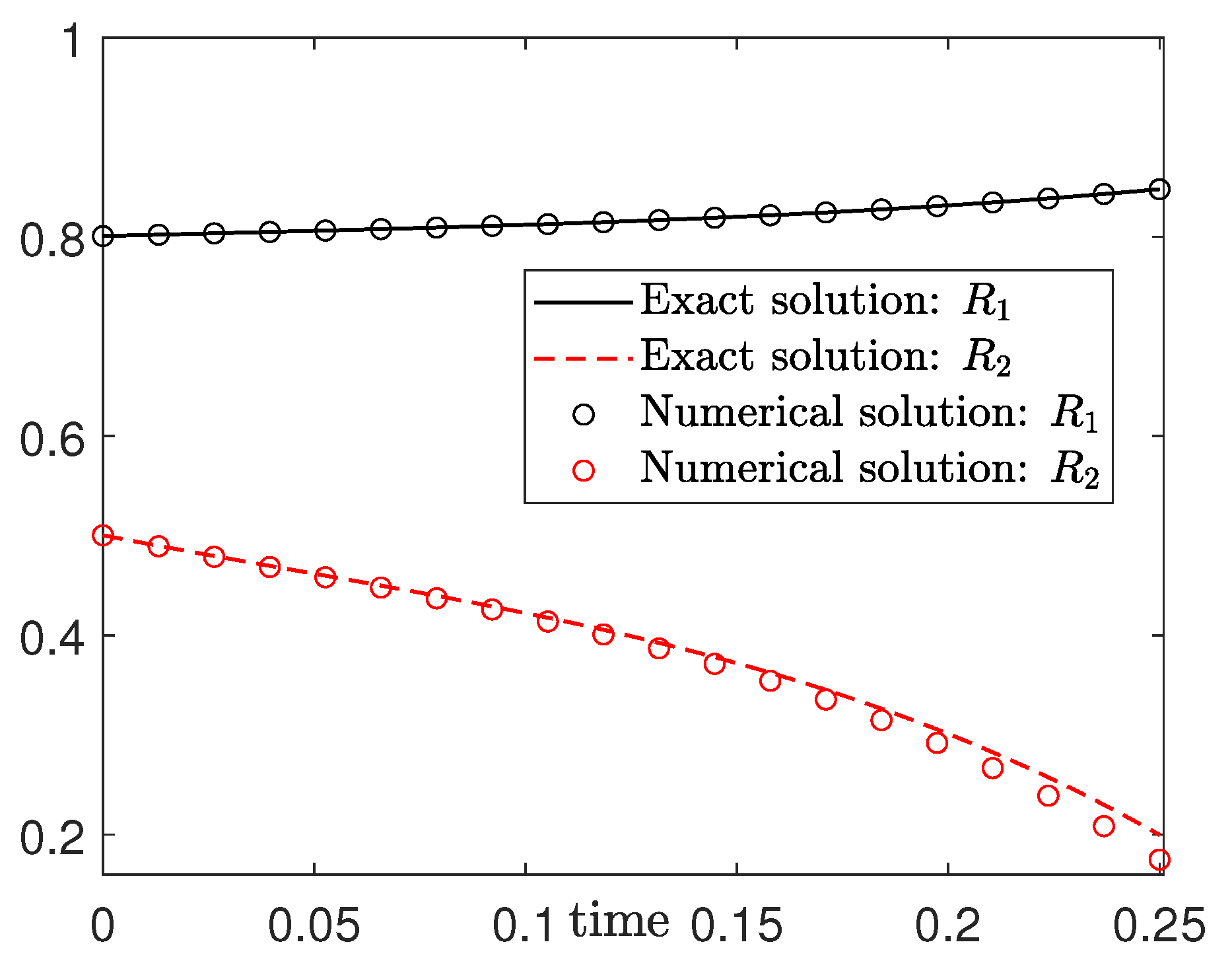
3.2. Convergence Test
3.3. Unconditional Stability
3.4. Mean Curvature Flow
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Allen, S.M.; Cahn, J.W. A microscopic theory for antiphase volume motion and its application to antiphase domain coarsening. Acta. Metall. 1979, 27, 1085–1095. [Google Scholar] [CrossRef]
- Ilmanen, T. Convergence of the Allen-Cahn equation to Brakke’s motion by mean curvature. J. Differ. Geom. 1993, 38, 417–461. [Google Scholar] [CrossRef]
- Bene, M.; Mikula, K. Simulation of anisotropic motion by mean curvaturecomparison of phase-field and sharp-interface approaches. Acta Math. Univ. Comenian. 1998, 67, 17–42. [Google Scholar]
- Li, Y.; Kim, J. Multiphase image segmentation with a phase-field model. Comput. Math. Appl. 2011, 62, 737–745. [Google Scholar] [CrossRef]
- Li, Y.; Kim, J. An unconditionally stable numerical method for bimodal image segmentation. Appl. Math. Comput. 2012, 219, 3083–3090. [Google Scholar] [CrossRef]
- Li, Y.; Kim, J. An unconditionally stable hybrid method for images egmentation. Appl. Numer. Math. 2014, 82, 32–43. [Google Scholar] [CrossRef]
- Li, Y.; Jeong, D.; Choi, J.-L.; Lee, S.; Kim, J. Fast local image inpainting based on the Allen-Cahn model. Digit. Dignal. Process. 2015, 37, 65–74. [Google Scholar] [CrossRef]
- Kobayashi, R.; Warren, J.A.; Carter, W.C. A continuum model of grain boundaries. Phys. D 2000, 140, 141–150. [Google Scholar] [CrossRef]
- Krill Iii, C.E.; Chen, L.-Q. Computer simulation of 3-D grain growth using a phase-field model. Acta Mater. 2002, 50, 3057–3073. [Google Scholar] [CrossRef]
- Li, Y.; Lee, H.G.; Kim, J. A fast, robust, and accurate operator splitting method for phase-field simulations of crystal growth. J. Cryst. Growth 2011, 321, 176–182. [Google Scholar] [CrossRef]
- Li, Y.; Kim, J. Phase-field simulations of crystal growth with adaptive mesh refinement. Int. J. Heat Mass Transfer 2012, 55, 7926–7932. [Google Scholar] [CrossRef]
- Li, Y.; Lee, D.; Lee, C.; Lee, J.; Lee, S.; Kim, J.; Ahn, S.; Kim, J. Surface embedding narrow volume reconstruction from unorganized points. Comput. Vis. Image Underst. 2014, 121, 100–107. [Google Scholar] [CrossRef]
- Li, Y.; Kim, J. Fast and efficient narrow volume reconstruction from scattered data. Pattern. Recogn. 2015, 48, 4057–4069. [Google Scholar] [CrossRef]
- Li, Y.; Guo, S. Triply periodic minimal surface using a modified Allen-Cahn equation. Appl. Math. Comput. 2017, 295, 84–94. [Google Scholar] [CrossRef]
- Yang, X.; Feng, J.J.; Liu, C.; Shen, J. Numerical simulations of jet pinching-off and drop formation using an energetic variational phase-field method. J. Comput. Phys. 2006, 218, 417–428. [Google Scholar] [CrossRef]
- Gu, S.; Zhou, X. Convex splitting method for the calculation of transition states of energy functional. J. Comput. Phys. 2018, 353, 417–434. [Google Scholar] [CrossRef]
- Shen, J.; Yang, X. Numerical approximations of Allen-Cahn and Cahn-Hilliard equations. Discret. Contin. Dyn. Syst. 2010, 28, 1669–1691. [Google Scholar] [CrossRef]
- Li, Y.; Lee, H.G.; Jeong, D.; Kim, J. An unconditionally stable hybrid numerical method for solving the Allen-Cahn equation. Comput. Math. Appl. 2010, 60, 1591–1606. [Google Scholar] [CrossRef]
- Jeong, D.; Lee, S.; Lee, D.; Shin, J.; Kim, J. Comparison study of numerical methods for solving the Allen-Cahn equation. Comput. Mater. Sci. 2016, 111, 131–136. [Google Scholar] [CrossRef]
- Guilln-Gonzlez, F.; Tierra, G. Second order schemes and time-step adaptivity for Allen-Cahn and Cahn-Hilliard models. Comput. Math. Appl. 2014, 68, 821–846. [Google Scholar] [CrossRef]
- Long, J.; Luo, C.; Yu, Q.; Li, Y. An unconditional stable compact fourth-order finite difference scheme for three dimensional Allen-Cahn equation. Comput. Math. Appl. 2019, 77, 1042–1054. [Google Scholar] [CrossRef]
- Joshi, V.; Jaiman, R.K. A positivity preserving and conservative variational scheme for phase-field modeling of two-phase flows. J. Comput. Phys. 2018, 360, 137–166. [Google Scholar] [CrossRef]
- Jeong, D.; Kim, J.S. Conservative Allen-Cahn-Navier-Stokes system for incompressible two-phase fluid flows. Comput. Fluids 2017, 156, 239–246. [Google Scholar] [CrossRef]
- Lehrenfeld, C.; Olshanskii, M.A.; Xu, X. A stabilized trace finite element method for partial differential equations on evolving surfaces. SIAM J. Numer. Anal. 2018, 56, 1643–1672. [Google Scholar] [CrossRef]
- Niu, J.; Xu, M.; Yao, G. An efficient reproducing kernel method for solving the Allen-Cahn equation. Appl. Math. Lett. 2019, 89, 78–84. [Google Scholar] [CrossRef]
- Zhai, S.; Weng, Z.; Feng, X. Fast explicit operator splitting method and time-step adaptivity for fractional non-local Allen-Cahn model. Appl. Math. Model. 2016, 40, 1315–1324. [Google Scholar] [CrossRef]
- Shi, D.; Liu, Q. An efficient nonconforming finite element two-grid method for Allen-Cahn equation. Appl. Math. Lett. 2019, 98, 374–380. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, X.; Gong, Y.; Wang, Q. A novel linear second order unconditionally energy stable scheme for a hydrodynamic Q-tensor model of liquid crystals. Comput. Methods Appl. Mech. Eng. 2017, 318, 803–825. [Google Scholar] [CrossRef]
- Gong, Y.; Zhao, J. Energy-stable Runge-Kutta schemes for gradient flow models using the energy quadratization approach. Appl. Math. Lett. 2019, 94, 224–231. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, G.-D. Convergence analysis for the invariant energy quadratization (IEQ) schemes for solving the Cahn-Hilliard and Allen-Cahn equations with general nonlinear potential. J. Sci. Comput. 2020, 82, 55. [Google Scholar] [CrossRef]
- Kim, J.; Jeong, D.; Yang, S.-D.; Choi, Y. A finite difference method for a conservative Allen-Cahn equation on non-flat surfaces. J. Comput. Phys. 2017, 334, 170–181. [Google Scholar] [CrossRef]
- Mohammadi, V.; Mirzaei, D.; Dehghan, M. Numerical simulation and error estimation of the time-dependent Allen-Cahn equation on surfaces with radial basis functions. J. Sci. Comput. 2019, 79, 493–516. [Google Scholar] [CrossRef]
- Li, Y.; Kim, J.; Wang, N. An unconditionally energy-stable second-order time-accurate scheme for the Cahn–Hilliard equation on surfaces. Commun. Nonlinear Sci. Numer. Simul. 2017, 53, 213–227. [Google Scholar] [CrossRef]
- Cahn, J.W. On spinodal decomposition. Acta Metall. 1961, 9, 795–801. [Google Scholar] [CrossRef]
- Li, Y.; Jeong, D.; Shin, J.; Kim, J.S. A conservative numerical method for the Cahn–Hilliard equation with Dirichlet boundary conditions in complex domains. Comput. Math. Appl. 2013, 65, 102–115. [Google Scholar] [CrossRef]



| Allen–Cahn: -error | |||||||
| Allen–Cahn: Rate | |||||||
| Conservative Allen–Cahn: -error | |||||||
| Conservative Allen–Cahn: Rate |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, B.; Li, Y.; Li, Z. Second-Order Unconditionally Stable Direct Methods for Allen–Cahn and Conservative Allen–Cahn Equations on Surfaces. Mathematics 2020, 8, 1486. https://doi.org/10.3390/math8091486
Xia B, Li Y, Li Z. Second-Order Unconditionally Stable Direct Methods for Allen–Cahn and Conservative Allen–Cahn Equations on Surfaces. Mathematics. 2020; 8(9):1486. https://doi.org/10.3390/math8091486
Chicago/Turabian StyleXia, Binhu, Yibao Li, and Zhong Li. 2020. "Second-Order Unconditionally Stable Direct Methods for Allen–Cahn and Conservative Allen–Cahn Equations on Surfaces" Mathematics 8, no. 9: 1486. https://doi.org/10.3390/math8091486
APA StyleXia, B., Li, Y., & Li, Z. (2020). Second-Order Unconditionally Stable Direct Methods for Allen–Cahn and Conservative Allen–Cahn Equations on Surfaces. Mathematics, 8(9), 1486. https://doi.org/10.3390/math8091486





