Dynamics of a SIR Epidemic Model of Childhood Diseases with a Saturated Incidence Rate: Continuous Model and Its Nonstandard Finite Difference Discretization
Abstract
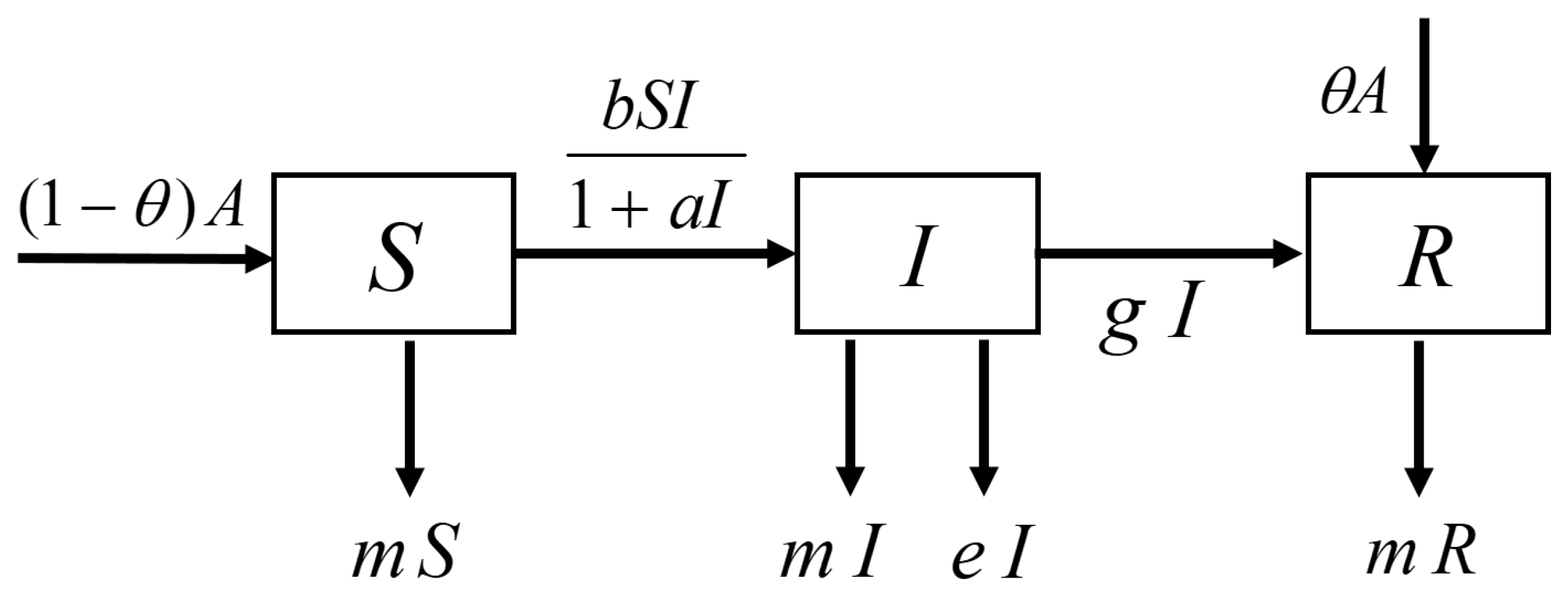
1. Introduction
- (i)
- The first order derivative in the continuous model is approximated by the generalized forward differencewhere and is the denominator function such that with h as the time-step size.
- (ii)
- The nonlinear terms are approximated non-locally.
2. Dynamics of the Continuous Epidemic Model of Childhood Diseases
2.1. Basic Properties of the Continuous Model
2.2. Local Stability Analysis of the Continuous Model
- 1.
- The DFE point is L.A.S.if and is unstable if .
- 2.
- The EE point is L.A.S. if .
2.3. Global Stability Analysis of the Continuous Model
3. Dynamics of the Discrete NSFD Epidemic Model of Childhood Diseases
3.1. Construction of the Discrete NSFD Model
3.2. Local Stability Analysis of the Discrete NSFD Model
- Since , we have
- It is clear that .
- From the definition of and s, we haveBy verifying that is equivalent to , we directly get
3.3. Global Stability Analysis of the Discrete NSFD Model
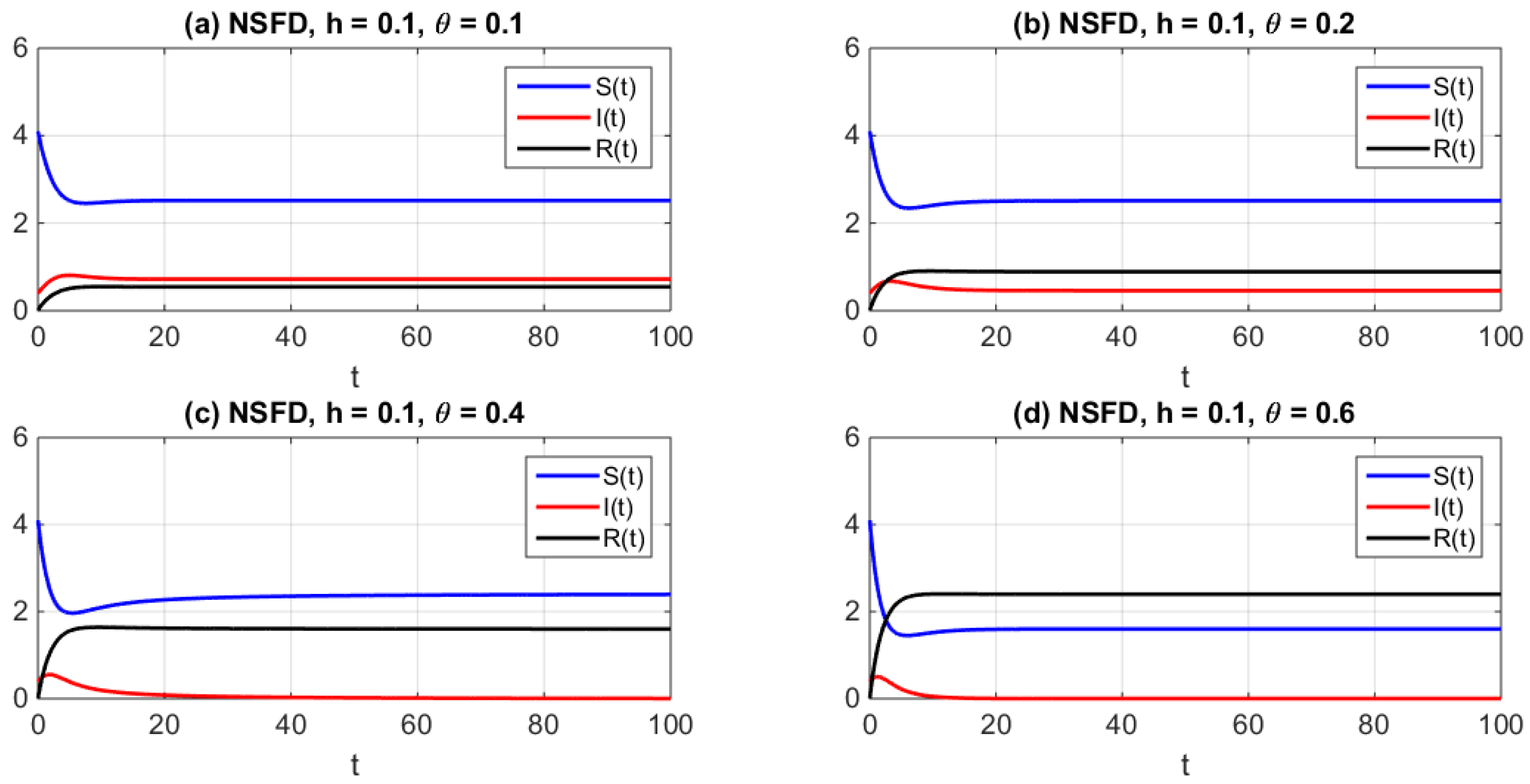
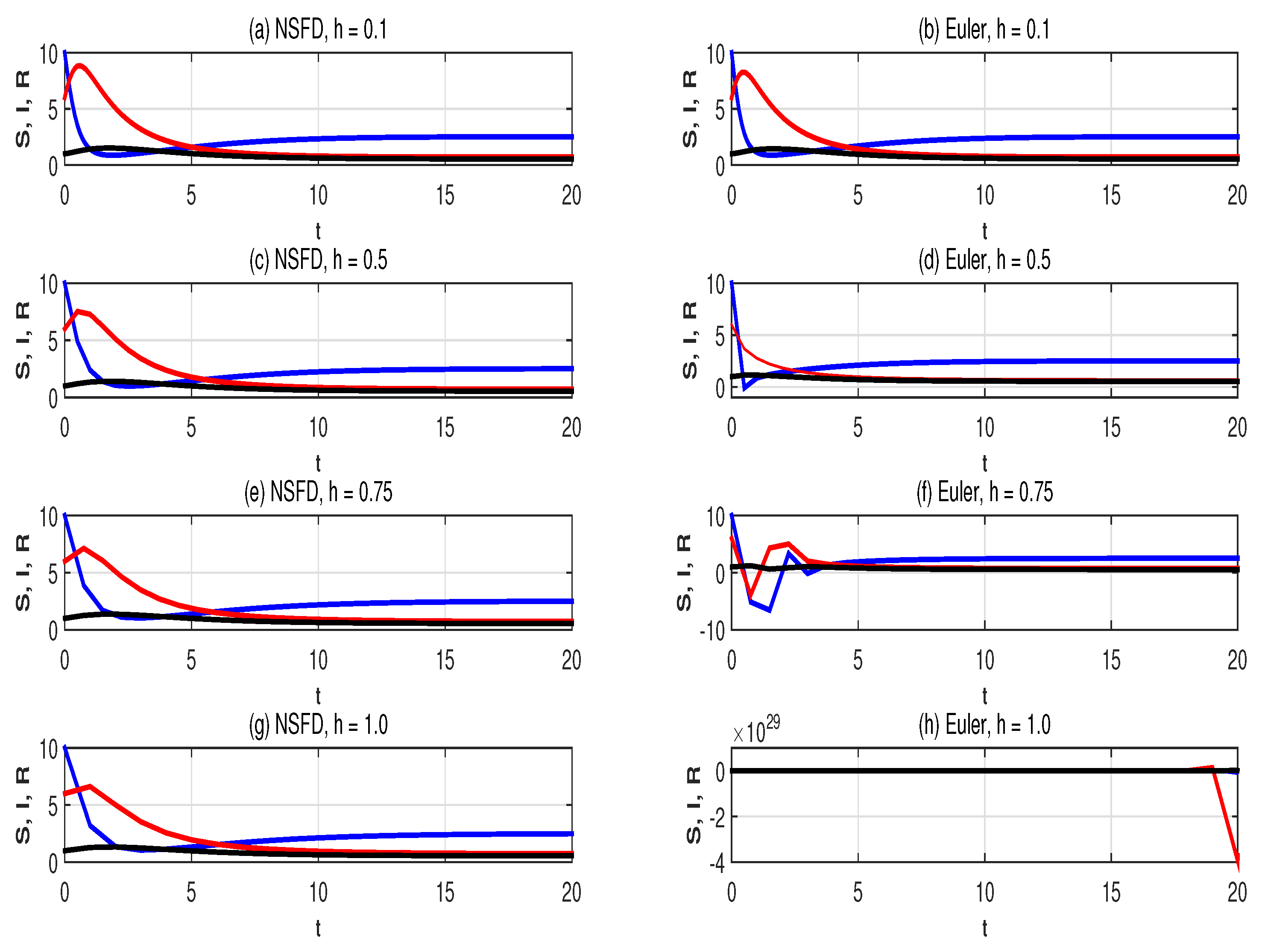
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Makinde, O.D. Adomian decomposition approach to a SIR epidemic model with constant vaccination strategy. Appl. Math. Comput. 2007, 184, 842–848. [Google Scholar] [CrossRef]
- Xu, R.; Ma, Z.; Wang, Z. Global stability of a delayed SIRS epidemic model with saturation incidence and temporary immunity. Comput. Math. Appl. 2010, 59, 3211–3221. [Google Scholar] [CrossRef][Green Version]
- Jana, S.; Nandi, S.K.; Kar, T.K. Complex Dynamics of an SIR Epidemic Model with Saturated Incidence Rate and Treatment. Acta Biotheor. 2016, 64, 65–84. [Google Scholar] [CrossRef] [PubMed]
- Lashari, A.A. Optimal Control of an SIR Epidemic Model with a Saturated Treatment. Appl. Math. Inf. Sci. 2016, 10, 185–191. [Google Scholar] [CrossRef]
- Ghosh, J.K.; Ghosh, U.; Biswas, M.H.A.; Sarkar, S. Qualitative Analysis and Optimal Control Strategy of an SIR Model with Saturated Incidence and Treatment. Differ. Equ. Dyn. Syst. 2019. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Regulation and Stability of Host-Parasite Population Interactions: I. Regulatory Processes. J. Anim. Ecol. 1978, 47, 219–247. [Google Scholar] [CrossRef]
- Yildirim, A.; Cherruault, Y. Analytical approximate solution of a SIR epidemic model with constant vaccination strategy by homotopy perturbation method. Differ. Equ. Dyn. Syst. 2009, 38, 1566–1575. [Google Scholar]
- Mickens, R. Non Standard Finite Difference Models of Differential Equations; World Scientific: Singapore, 1994. [Google Scholar]
- Darti, I.; Suryanto, A. Stability preserving non-standard finite difference scheme for a harvesting Leslie- Gower predator-prey model. J. Differ. Equ. Appl. 2015, 21, 528–534. [Google Scholar] [CrossRef]
- Darti, I.; Suryanto, A. Dynamics preserving nonstandard finite difference method for the modified Leslie–Gower predator-prey model with Holling–type II functional response. Far East J. Math. Sci. 2016, 99, 719–733. [Google Scholar]
- Rao, P.R.S.; Ratnam, K.V.; Murthy, M.S.R. Stability preserving non standard finite difference schemes for certain biological models. Int. J. Dyn. Control 2018, 6, 1496–1504. [Google Scholar]
- Shabbir, M.S.; Din, M.S.; Khan, M.A.; Ahmad, K. A dynamically consistent nonstandard finite difference scheme for a predator–prey model. Adv. Differ. Equ. 2019, 2019, 381. [Google Scholar] [CrossRef]
- Mickens, R.E. A SIR-model with square-root dynamics: An NSFD scheme. J. Differ. Equ. Appl. 2010, 16, 209–216. [Google Scholar] [CrossRef]
- Garba, S.; Gumel, A.; Lubuma, J.S. Dynamically-consistent non-standard finite difference method for an epidemic model. Math. Comput. Model. 2011, 53, 131–150. [Google Scholar] [CrossRef]
- Cui, Q.; Yang, X.; Zhang, Q. An NSFD scheme for a class of SIR epidemic models with vaccination and treatment. J. Differ. Equ. Appl. 2014, 20, 416–422. [Google Scholar] [CrossRef]
- Cui, Q.; Zhang, Q. Global stability of a discrete SIR epidemic model with vaccination and treatment. J. Differ. Equ. Appl. 2015, 21, 111–117. [Google Scholar] [CrossRef]
- Hattaf, K.; Lashari, A.A.; El Boukari, B.; Yousfi, N. Effect of discretization on dynamical behaviour in an epidemiological model. Differ. Equ. Dyn. Syst. 2015, 23, 403–413. [Google Scholar] [CrossRef]
- Fitriah, Z.; Suryanto, A. Nonstandard finite difference scheme for SIRS epidemic model with disease-related death. AIP Conf. Proc. 2016, 1723, 030009. [Google Scholar]
- Darti, I.; Suryanto, A.; Hartono, M. Global stability of a discrete SIR epidemic model with saturated incidence rate and death induced by the disease. Commun. Math. Biol. Neurosci. 2020, 2020, 33. [Google Scholar]
- Cui, Q.; Xu, J.; Zhang, Q.; Wang, K. An NSFD scheme for SIR epidemic models of childhood diseases with constant vaccination strategy. Adv. Differ. Equ. 2014, 2014, 172. [Google Scholar] [CrossRef][Green Version]
- Mickens, R.E. Calculation of denominator functions for nonstandard finite difference schemes for differential equations satisfying a positivity condition. Numer. Methods Partial Differ. Equ. 2007, 23, 672–691. [Google Scholar] [CrossRef]
- Brauer, F.; Castillo-Chavez, C. Mathematical Model in Population Biology and Epidemiology, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Elaydi, S. An Introduction to Difference Equations, 3rd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Enatsu, Y.; Nakata, Y.; Muroya, Y.; Izzo, G.; Vecchio, A. Global dynamics of difference equations for SIR epidemic models with a class of nonlinear incidence rates. J. Differ. Equ. Appl. 2012, 18, 1163–1181. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darti, I.; Suryanto, A. Dynamics of a SIR Epidemic Model of Childhood Diseases with a Saturated Incidence Rate: Continuous Model and Its Nonstandard Finite Difference Discretization. Mathematics 2020, 8, 1459. https://doi.org/10.3390/math8091459
Darti I, Suryanto A. Dynamics of a SIR Epidemic Model of Childhood Diseases with a Saturated Incidence Rate: Continuous Model and Its Nonstandard Finite Difference Discretization. Mathematics. 2020; 8(9):1459. https://doi.org/10.3390/math8091459
Chicago/Turabian StyleDarti, Isnani, and Agus Suryanto. 2020. "Dynamics of a SIR Epidemic Model of Childhood Diseases with a Saturated Incidence Rate: Continuous Model and Its Nonstandard Finite Difference Discretization" Mathematics 8, no. 9: 1459. https://doi.org/10.3390/math8091459
APA StyleDarti, I., & Suryanto, A. (2020). Dynamics of a SIR Epidemic Model of Childhood Diseases with a Saturated Incidence Rate: Continuous Model and Its Nonstandard Finite Difference Discretization. Mathematics, 8(9), 1459. https://doi.org/10.3390/math8091459




