Software Reliability Model with Dependent Failures and SPRT
Abstract
:1. Introduction
2. Wald’s SPRT
3. New SRGM
4. Experiments
4.1. Criteria
4.2. Datasets
5. Results
5.1. Results of Parameter Estimation and Goodness-of-Fit
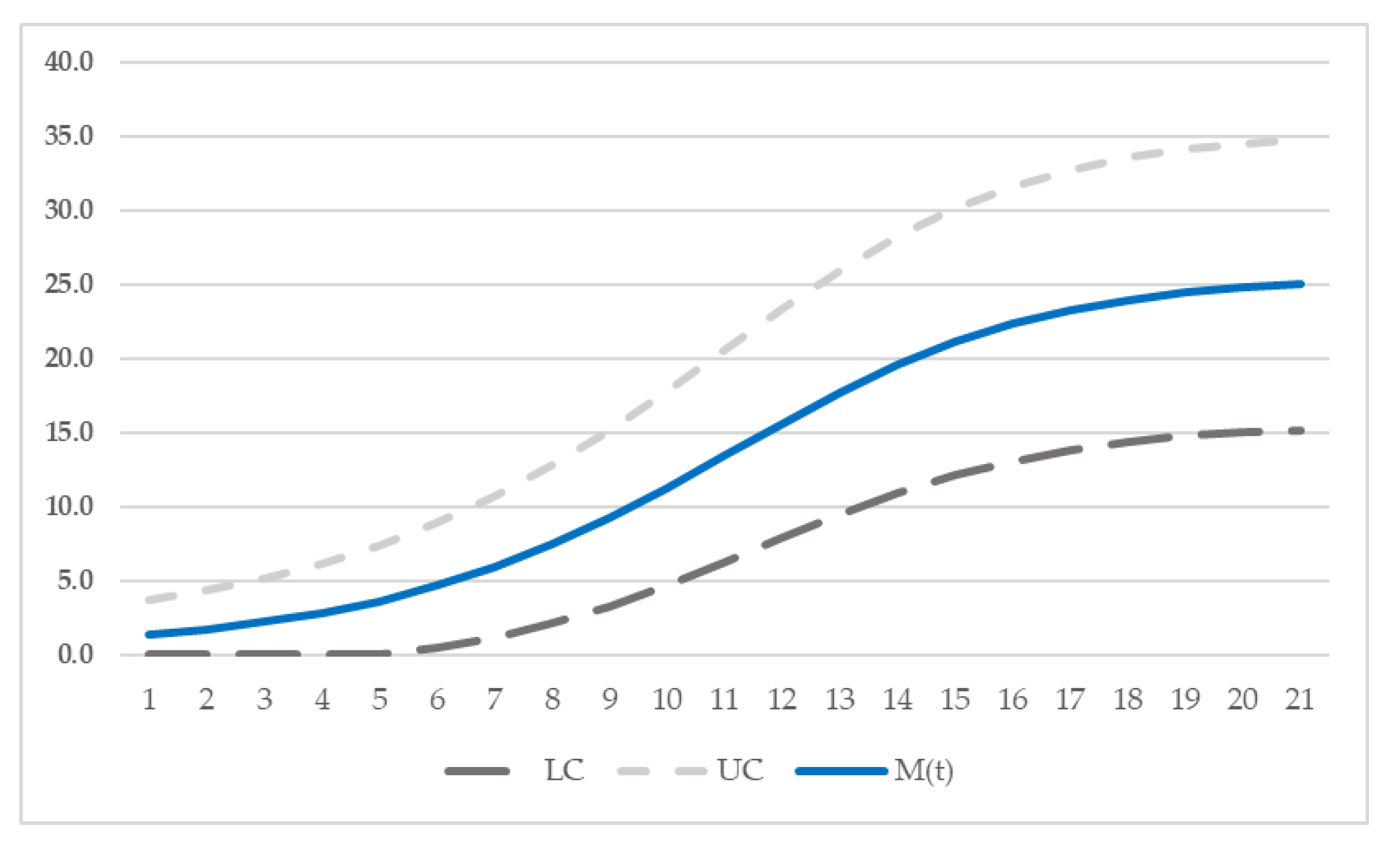
5.2. Confidence Interval
5.3. Results of the SPRT for Datasets
6. Conclusions and Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Goel, A.L.; Okumoto, K. Time dependent error detection rate model for software reliability and other performance measures. IEEE Trans. Reliab. 1979, 28, 206–211. [Google Scholar] [CrossRef]
- Ohba, M.; Yamada, S. S-Shaped Software Reliability Growth Models. In Proceedings of the 4th International Conference on Reliability and Maintainability, Lannion, France, 21–25 May 1984; pp. 430–436. [Google Scholar]
- Yamada, S.; Ohba, M.; Osaki, S. S-shaped software reliability growth models and their applications. IEEE Trans. Reliab. 1984, 33, 289–292. [Google Scholar] [CrossRef]
- Pham, H.; Zhang, X. An NHPP software reliability models and its comparison. Int. J. Reliab. Qual. Saf. Eng. 1997, 4, 269–282. [Google Scholar] [CrossRef]
- Pham, H.; Zhang, X. NHPP Software Reliability and Cost Models with Testing Coverage. Eur. J. Oper. Res. 2003, 145, 443–454. [Google Scholar] [CrossRef]
- Teng, X.; Pham, H. A new methodology for predicting software reliability in the random field environments. IEEE Trans. Reliab. 2006, 55, 458–468. [Google Scholar] [CrossRef]
- Pham, H. Loglog Fault-Detection Rate and Testing Coverage Software Reliability Models Subject to Random Environments. Vietnam J. Comput. Sci. 2014, 1, 39–45. [Google Scholar] [CrossRef] [Green Version]
- Inoue, S.; Ikeda, J.; Yamda, S. Bivariate change-point modeling for software reliability assessment with uncertainty of testing-environment factor. Ann. Oper. Res. 2016, 244, 209–220. [Google Scholar] [CrossRef]
- Chang, I.H.; Pham, H.; Lee, S.W.; Song, K.Y. A testing-coverage software reliability model with the uncertainty of operation environments. Int. J. Syst. Sci. Oper. Logist. 2014, 1, 220–227. [Google Scholar]
- Song, K.Y.; Chang, I.H.; Pham, H. A three-parameter fault-detection software reliability model with the uncertainty of operating environments. J. Syst. Sci. Syst. Eng. 2017, 26, 121–132. [Google Scholar] [CrossRef]
- Song, K.Y.; Chang, I.H.; Pham, H. An NHPP Software Reliability Model with S-Shaped Growth Curve Subject to Random Operating Environments and Optimal Release Time. Appl. Sci. 2017, 7, 1304. [Google Scholar] [CrossRef] [Green Version]
- Song, K.Y.; Chang, I.H.; Pham, H. A software reliability model with a Weibull fault detection rate function subject to operating environments. Appl. Sci. 2017, 7, 983. [Google Scholar] [CrossRef] [Green Version]
- Song, K.Y.; Chang, I.H.; Pham, H. A Testing Coverage Model Based on NHPP Software Reliability Considering the Software Operating Environment and the Sensitivity Analysis. Mathematics 2019, 7, 450. [Google Scholar] [CrossRef] [Green Version]
- Pham, H. On estimating the number of deaths related to Covid-19. Mathematics 2020, 8, 655. [Google Scholar] [CrossRef]
- Chatterjee, S.; Maji, B.; Pham, H. A fuzzy rule-based generation algorithm in interval type-2 fuzzy logic system for fault prediction in the early phase of software development. J. Exp. Theor. Artif. Intell. 2019, 31, 369–391. [Google Scholar] [CrossRef]
- Pham, T.; Pham, H. A generalized software reliability model with stochastic fault-detection rate. Ann. Oper. Res. 2019, 277, 83–93. [Google Scholar] [CrossRef]
- Chatterjee, S.; Shukla, A.; Pham, H. Modeling and analysis of software fault detectability and removability with time variant fault exposure ratio, fault removal efficiency, and change point. Proc. Inst. Mech. Eng. O J. Risk. Reliab. 2019, 233, 246–256. [Google Scholar] [CrossRef]
- Pham, H. A Logistic Fault-Dependent Detection Software Reliability Model. J. UCS 2018, 24, 1717–1730. [Google Scholar]
- Pavlov, N.; Iliev, A.; Rahnev, A.; Kyurkchiev, N. Some Software Reliability Models: Approximation and Modeling Aspects; LAP LAMBERT Academic Publishing: Saarbrucken, Germany, 2018. [Google Scholar]
- Li, Q.; Pham, H. A generalized software reliability growth model with consideration of the uncertainty of operating environments. IEEE Access 2019, 7, 84253–84267. [Google Scholar] [CrossRef]
- Zhu, M.; Pham, H. A software reliability model incorporating martingale process with gamma-distributed environmental factors. Ann. Oper. Res. 2018, 1–22. [Google Scholar] [CrossRef]
- Sharma, M.; Pham, H.; Singh, V.B. Modeling and analysis of leftover issues and release time planning in multi-release open source software using entropy based measure. Comput. Syst. Sci. Eng. 2019, 34, 33–46. [Google Scholar]
- Zhu, M.; Pham, H. A two-phase software reliability modeling involving with software fault dependency and imperfect fault removal. Comput. Lang. Syst. Struct. 2018, 53, 27–42. [Google Scholar] [CrossRef]
- Singh, V.B.; Sharma, M.; Pham, H. Entropy based software reliability analysis of multi-version open source software. IEEE Trans. Softw. Eng. 2017, 44, 1207–1223. [Google Scholar] [CrossRef]
- Caiuta, R.; Pozo, A.; Vergilio, S.R. Meta-learning based selection of software reliability models. Autom. Softw. Eng. 2017, 24, 575–602. [Google Scholar] [CrossRef]
- Tamura, Y.; Yamda, S. Software Reliability Model Selection Based on Deep Learning with Application to the Optimal Release Problem. J. Ind. Eng. Manag. Sci. 2019, 2019, 43–58. [Google Scholar] [CrossRef] [Green Version]
- Tamura, Y.; Matsumoto, M.; Yamada, S. Software reliability model selection based on deep learning. In Proceedings of the 2016 International Conference on Industrial Engineering, Management Science and Application (ICIMSA), Jeju, South Korea, 23–26 May 2016; IEEE: New York, NY, USA, 2019; pp. 1–5. [Google Scholar]
- Wang, J.; Zhang, C. Software reliability prediction using a deep learning model based on the RNN encoder-decoder. Reliab. Eng. Syst. Saf. 2018, 170, 73–82. [Google Scholar] [CrossRef]
- Lee, D.H.; Chang, I.H.; Pham, H.; Song, K.Y. A software reliability model considering the syntax error in uncertainty environment, optimal release time, and sensitivity analysis. Appl. Sci. 2018, 8, 1483. [Google Scholar] [CrossRef] [Green Version]
- Minamino, Y.; Inoue, S.; Yamada, S. Change-Point–Based Software Reliability Modeling and Its Application for Software Development Management. In Recent Advancements in Software Reliability Assurance; CRC Press: Boca Raton, FL, USA, 2019; pp. 59–92. [Google Scholar]
- Rani, P.; Mahapatra, G.S. A Single Change Point Hazard Rate Software Reliability Model with Imperfect Debugging. In Proceedings of the 2019 IEEE International Systems Conference (SysCon), Orlando, FL, USA, 8–11 April 2019; IEEE: New York, NY, USA, 2019; pp. 1–7. [Google Scholar]
- Zeephongsekul, P.; Jayasinghe, C.L.; Fiondella, L.; Nagaraju, V. Maximum-Likelihood Estimation of Parameters of NHPP Software Reliability Models Using Expectation Conditional Maximization Algorithm. IEEE Trans. Reliab. 2016, 65, 1571–1583. [Google Scholar] [CrossRef]
- Candini, F.; Gioletta, A. A Bayesian Monte Carlo-based algorithm for the estimation of small failure probabilities of systems affected by uncertainties. Reliab. Eng. Syst. Saf. 2016, 153, 15–27. [Google Scholar] [CrossRef]
- Wald, A. Sequential Analysis; John Wiley and Sons: New York, NY, USA, 1947. [Google Scholar]
- Stieber, H.A. Statistical Quality Control: How to detect unreliable software components. In Proceedings of the Eighth International Symposium on Software Reliability Engineering, Albuquerque, NM, USA, 2–5 November 1997; IEEE: New York City, NY, USA, 1997; pp. 8–12. [Google Scholar]
- Prasad, R.S.K.; Rao, K.P.G.; Mohan, G.K. Software Reliability using SPRT: Inflection S-shaped Model. Int. J. Appl. Innov. Eng. Manag. 2013, 2, 349–355. [Google Scholar]
- Gutta, S.; Ravi, S.P. Detection of Reliable Pareto Software Using SPRT. Int. J. Comput. Sci. Issues 2014, 11, 130. [Google Scholar]
- Kotha, S.K.; Prasad, R.S. Pareto Type II Software Reliability Growth Model–An Order Statistics Approach. Int. J. Comput. Sci. Trends Technol. 2014, 2, 49–54. [Google Scholar]
- Smitha, C.H.; Prasad, R.S.; Kumar, R.K. Burr Type III Process Model with SPRT for Software Reliability. Int. J. Innov. Res. Adv. Eng. ISSN 2014, 6, 2349–2763. [Google Scholar]
- Chowdary, C.S.; Prasad, D.R.S.; Sobhana, K. Burr Type III Software Reliability Growth Model. IOSR J. Comput. Eng. 2015, 17, 49–54. [Google Scholar]
- Pham, H.; Nordmann, L.; Zhang, X. A general imperfect software debugging model with S-shaped fault detection rate. IEEE Trans. Reliab. 1999, 48, 169–175. [Google Scholar] [CrossRef]
- Pham, H. System Software Reliability; Springer: London, UK, 2006. [Google Scholar]
- Pham, H. A new software reliability model with Vtub-shaped fault-detection rate and the uncertainty of operating environments. Optimization 2014, 63, 1481–1490. [Google Scholar] [CrossRef]
- Li, Q.; Pham, H. NHPP software reliability model considering the uncertainty of operating environments with imperfect debugging and testing coverage. Appl. Math. Model. 2017, 51, 68–85. [Google Scholar] [CrossRef]
- Akaike, H. A new look at statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–719. [Google Scholar] [CrossRef]
- Pillai, K.; Nair, V.S. A model for software development effort and cost estimation. IEEE Trans. Softw. Eng. 1997, 23, 485–497. [Google Scholar] [CrossRef]
- Zhang, X.; Jeske, D.R.; Pham, H. Calibrating software reliability models when the test environment does not match the user environment. Appl. Stoch. Models. Bus. Ind. 2002, 18, 87–99. [Google Scholar] [CrossRef]
- Stringfellow, C.; Andrews, A.A. An empirical method for selecting software reliability growth models. Empir. Softw. Eng. 2002, 7, 319–343. [Google Scholar] [CrossRef]



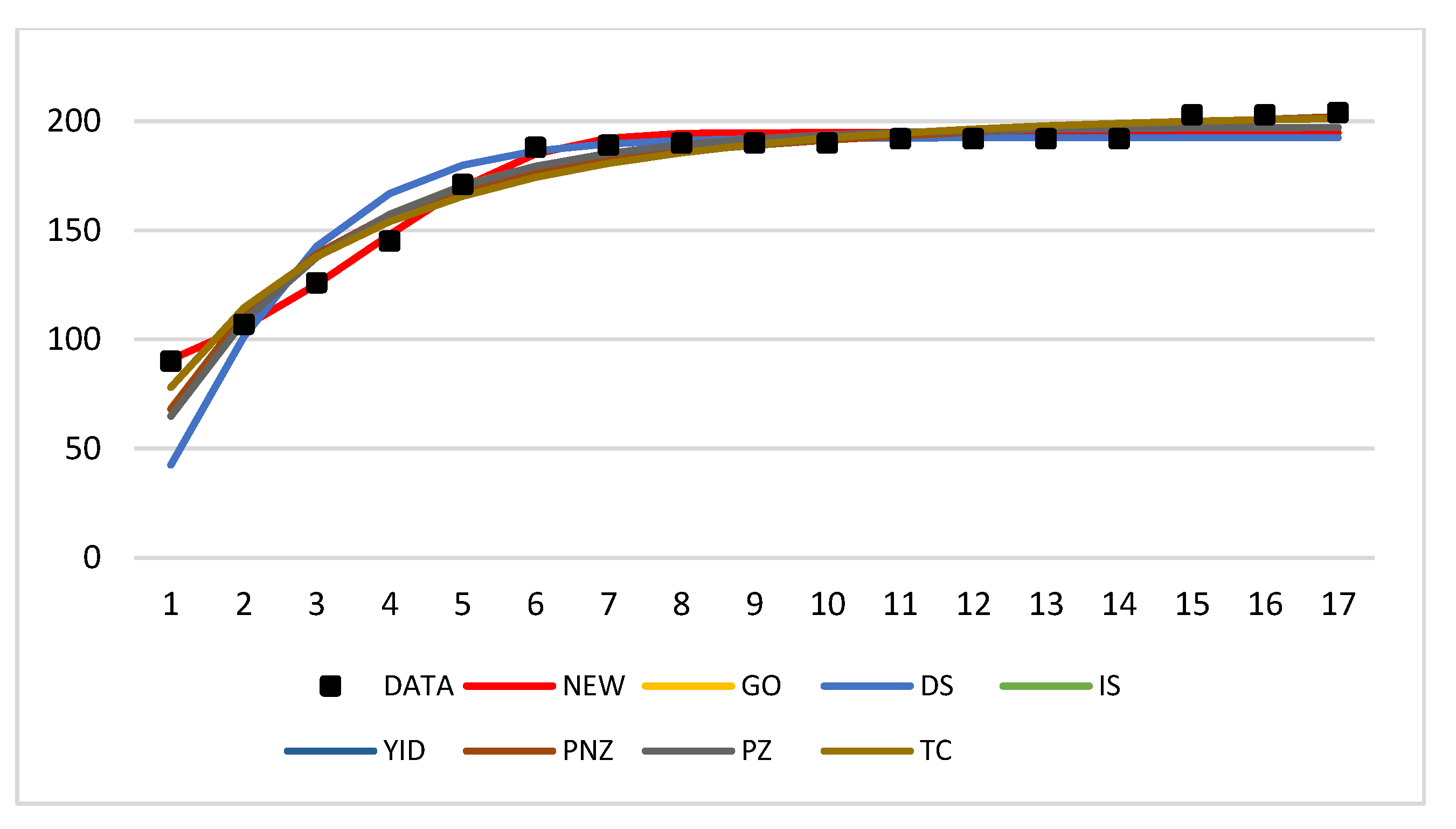
| No. | Model | |
|---|---|---|
| 1 | Goel Okumoto (GO) [1] | |
| 2 | Delayed S-shaped (DS) [3] | |
| 3 | Inflection S-shaped (IS) [2] | |
| 4 | Yamada Imperfect Debugging (YID) [3] | |
| 5 | Pham–Nordmann–Zhang (PNZ) [41] | |
| 6 | Pham–Zhang (PZ) [4] | |
| 7 | Testing Coverage (TC) [9] | |
| 8 | New model |
| Dataset 1 | Dataset 2 | ||||
|---|---|---|---|---|---|
| Time | Failure | Cum. Failure | Time | Failure | Cum. Failure |
| 1 | 1 | 1 | 1 | 90 | 90 |
| 2 | 0 | 1 | 2 | 17 | 107 |
| 3 | 1 | 2 | 3 | 19 | 126 |
| 4 | 1 | 3 | 4 | 19 | 145 |
| 5 | 2 | 5 | 5 | 26 | 171 |
| 6 | 0 | 5 | 6 | 17 | 188 |
| 7 | 0 | 5 | 7 | 1 | 189 |
| 8 | 3 | 8 | 8 | 1 | 190 |
| 9 | 1 | 9 | 9 | 0 | 190 |
| 10 | 2 | 11 | 10 | 0 | 190 |
| 11 | 2 | 13 | 11 | 2 | 192 |
| 12 | 2 | 15 | 12 | 0 | 192 |
| 13 | 4 | 19 | 13 | 0 | 192 |
| 14 | 0 | 19 | 14 | 0 | 192 |
| 15 | 3 | 22 | 15 | 11 | 203 |
| 16 | 0 | 22 | 16 | 0 | 203 |
| 17 | 1 | 23 | 17 | 1 | 204 |
| 18 | 1 | 24 | |||
| 19 | 0 | 24 | |||
| 20 | 0 | 24 | |||
| 21 | 2 | 26 | □ | □ | □ |
| Model | Dataset 1 | Dataset 2 |
|---|---|---|
| GO | ||
| DS | ||
| IS | ||
| YID | ||
| PNZ | ||
| PZ | ||
| TC | ||
| New |
| Model | MSE | PRR | PP | SAE | AIC | Variation | RMSPE | |
|---|---|---|---|---|---|---|---|---|
| GO | 3.8516 | 1.3319 | 4.8508 | 0.9546 | 33.9339 | 65.3611 | 1.8323 | 1.9091 |
| DS | 1.4938 | 12.0680 | 0.9676 | 0.9824 | 19.9967 | 63.9399 | 1.1908 | 1.1913 |
| IS | 0.6744 | 2.8509 | 0.6561 | 0.9925 | 12.9465 | 64.1779 | 0.7727 | 0.7788 |
| YID | 2.3842 | 5.7663 | 0.8579 | 0.9734 | 23.4627 | 67.1715 | 1.4649 | 1.4649 |
| PNZ | 0.7141 | 2.8584 | 0.9698 | 0.9925 | 12.9502 | 66.1785 | 0.7728 | 0.7788 |
| PZ | 0.7621 | 3.2272 | 0.7029 | 0.9924 | 13.1848 | 68.276 | 0.7722 | 0.78 |
| TC | 1.0939 | 102.1599 | 1.7468 | 0.9891 | 16.0532 | 70.5594 | 0.9198 | 0.9348 |
| New | 0.5503 | 0.4518 | 0.8020 | 0.9942 | 11.7685 | 66.8464 | 0.6839 | 0.6839 |
| Model | MSE | PRR | PP | SAE | AIC | Variation | RMSPE | |
|---|---|---|---|---|---|---|---|---|
| GO | 80.6779 | 0.1705 | 0.1013 | 0.9388 | 104.4025 | 184.3314 | 0.6839 | 0.6839 |
| DS | 232.6282 | 1.2915 | 0.3330 | 0.8234 | 142.5442 | 331.8567 | 8.6734 | 8.6955 |
| IS | 86.4395 | 0.1706 | 0.1013 | 0.9388 | 104.3703 | 186.3337 | 14.6423 | 14.7605 |
| YID | 78.8367 | 0.1276 | 0.0866 | 0.9442 | 100.6173 | 157.8252 | 8.6711 | 8.6953 |
| PNZ | 84.9077 | 0.1281 | 0.0867 | 0.9442 | 100.6045 | 159.8744 | 8.2915 | 8.3047 |
| PZ | 100.9894 | 0.1719 | 0.1017 | 0.9387 | 104.3539 | 190.3321 | 8.2915 | 8.3049 |
| TC | 72.2812 | 0.0521 | 0.0479 | 0.9561 | 103.1593 | 158.9319 | 8.6767 | 8.7014 |
| New | 26.8104 | 0.0096 | 0.0092 | 0.9824 | 63.9541 | Nan | 4.6673 | 4.6673 |
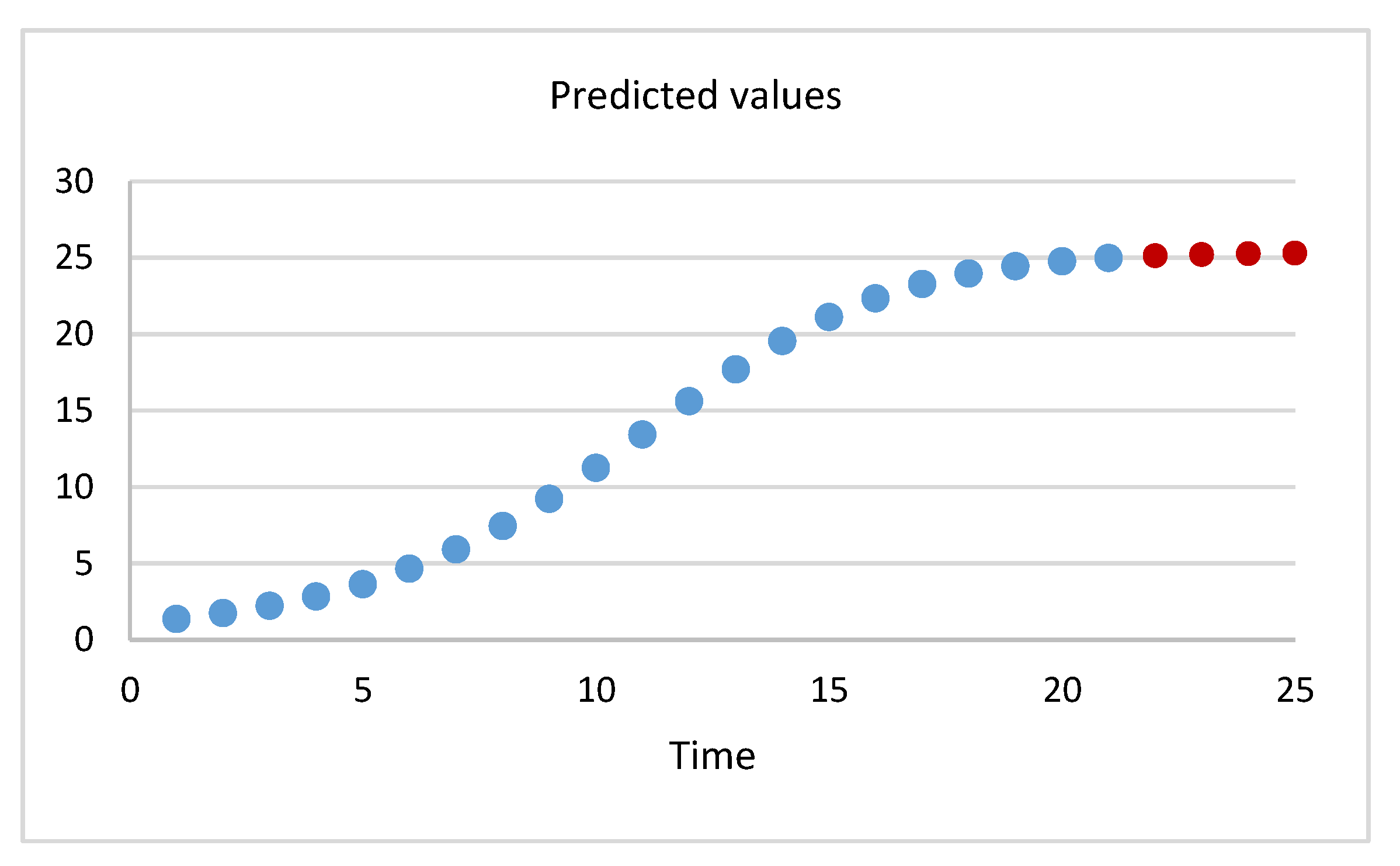
| Time | Time | Time | Time | ||||
|---|---|---|---|---|---|---|---|
| 1 | 1.35543 | 8 | 7.423002 | 15 | 21.09665 | 22 | 25.1102 |
| 2 | 1.727669 | 9 | 9.219 | 16 | 22.33409 | 23 | 25.19946 |
| 3 | 2.209491 | 10 | 11.24305 | 17 | 23.27083 | 24 | 25.2552 |
| 4 | 2.831189 | 11 | 13.411 | 18 | 23.95131 | 25 | 25.28936 |
| 5 | 3.628004 | 12 | 15.60229 | 19 | 24.42872 | ||
| 6 | 4.637697 | 13 | 17.68339 | 20 | 24.75394 | ||
| 7 | 5.895141 | 14 | 19.53903 | 21 | 24.96993 |
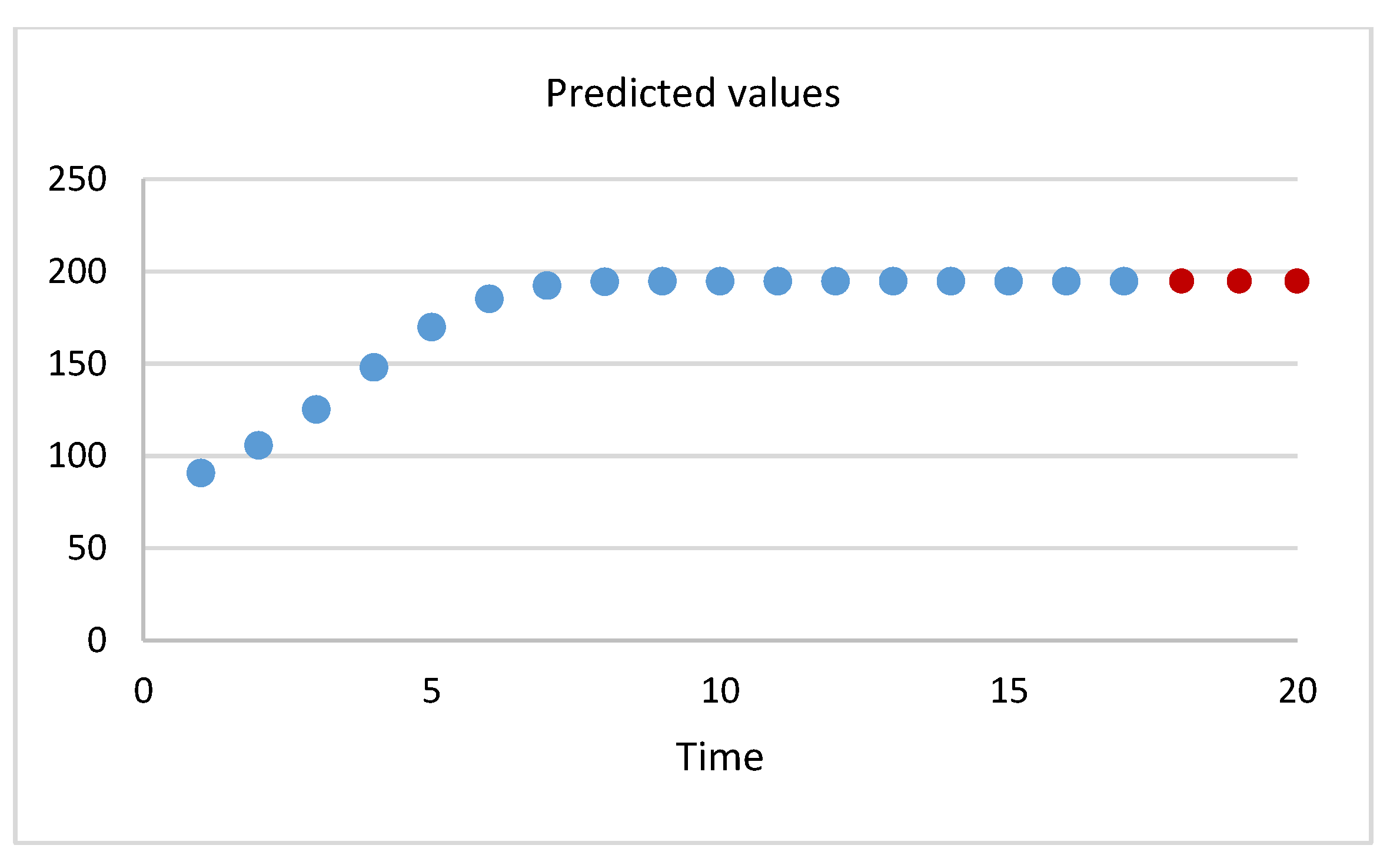
| Time | Time | Time | Time | ||||
|---|---|---|---|---|---|---|---|
| 1 | 90.76292 | 6 | 185.0622 | 11 | 194.766 | 16 | 194.766 |
| 2 | 105.7008 | 7 | 192.2739 | 12 | 194.766 | 17 | 194.766 |
| 3 | 125.2 | 8 | 194.3851 | 13 | 194.766 | 18 | 194.766 |
| 4 | 147.9813 | 9 | 194.7363 | 14 | 194.766 | 19 | 194.766 |
| 5 | 169.7534 | 10 | 194.765 | 15 | 194.766 | 20 | 194.766 |
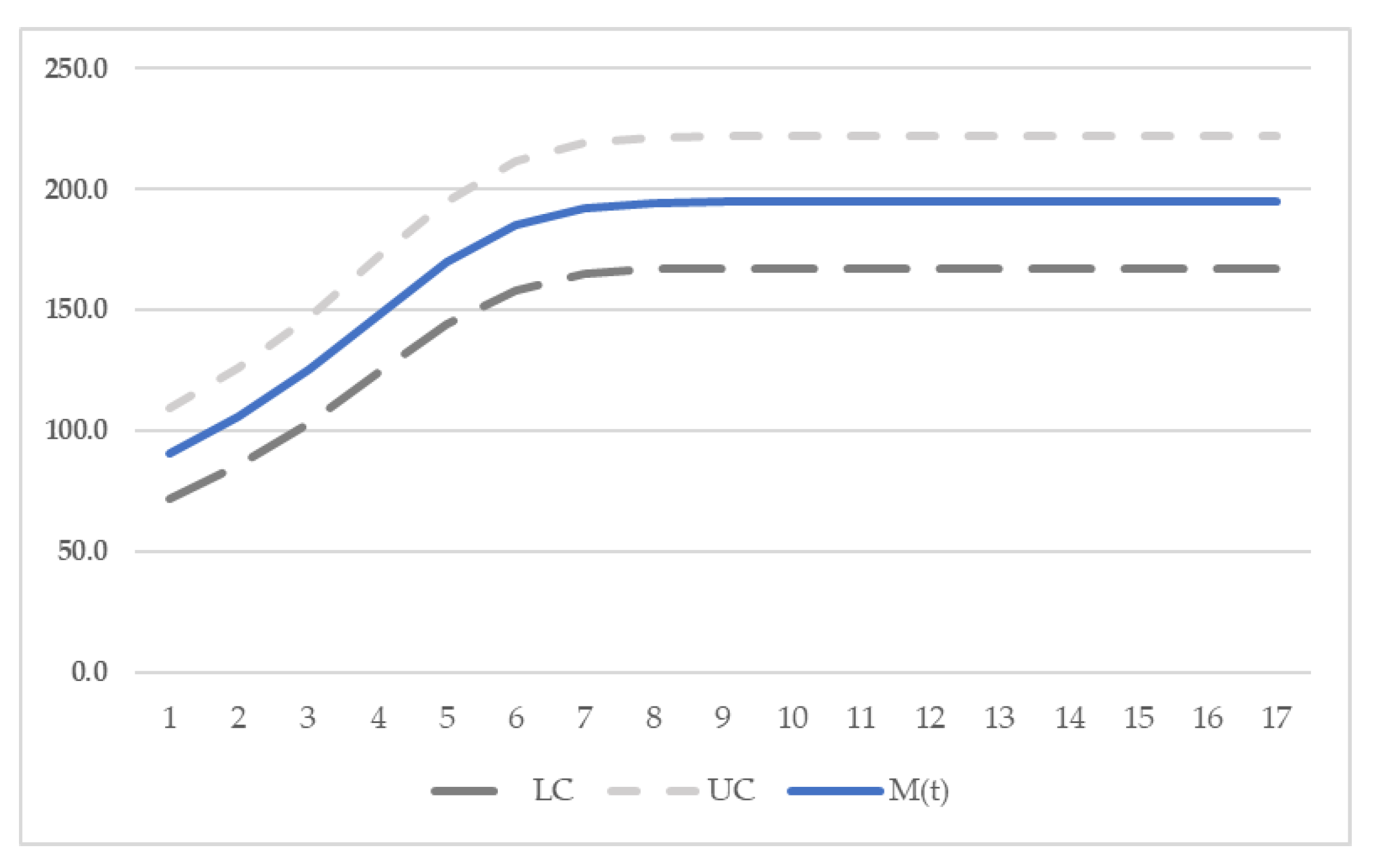
| Dataset 1 | Dataset 2 | ||||
|---|---|---|---|---|---|
| Time | LC | UC | Time | LC | UC |
| 1 | 0.0 | 3.637278 | 1 | 72.09043 | 109.4354 |
| 2 | 0.0 | 4.303861 | 2 | 85.55025 | 125.8514 |
| 3 | 0.0 | 5.122851 | 3 | 103.2694 | 147.1306 |
| 4 | 0.0 | 6.129052 | 4 | 124.1388 | 171.8238 |
| 5 | 0.0 | 7.361210 | 5 | 144.2171 | 195.2896 |
| 6 | 0.416853 | 8.858541 | 6 | 158.3993 | 211.7251 |
| 7 | 1.136366 | 10.65392 | 7 | 165.0965 | 219.4513 |
| 8 | 2.083043 | 12.76296 | 8 | 167.0589 | 221.7113 |
| 9 | 3.267999 | 15.17000 | 9 | 167.3854 | 222.0871 |
| 10 | 4.671164 | 17.81494 | 10 | 167.4121 | 222.1180 |
| 1 | 6.233412 | 20.58859 | 11 | 167.4130 | 222.1190 |
| 2 | 7.860481 | 23.34409 | 12 | 167.4130 | 222.1190 |
| 3 | 9.441424 | 25.92536 | 13 | 167.4130 | 222.1190 |
| 14 | 10.87541 | 28.20265 | 14 | 167.4130 | 222.1190 |
| 15 | 12.09433 | 30.09898 | 15 | 167.4130 | 222.1190 |
| 16 | 13.0715 | 31.59667 | 16 | 167.4130 | 222.1190 |
| 17 | 13.81599 | 32.72567 | 17 | 167.4130 | 222.1190 |
| 18 | 14.35923 | 33.54339 | |||
| 19 | 14.74152 | 34.11592 | |||
| 20 | 15.00246 | 34.50541 | |||
| 21 | 15.176 | 34.76385 | |||
| Case | |||
|---|---|---|---|
| Case 1 (for parameter ) | 0.9 | 0.1 | 0.1 |
| Case 2 (for parameter ) | 0.03 | 0.1 | 0.1 |
| Dataset 1 | Dataset 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| T | N(t) | Acceptance Region | Rejection Region | Result | T | N(t) | Acceptance Region | Rejection Region | Result |
| 1 | 1 | −105.151 | 107.8621 | continue | 1 | 90 | −314.127 | 495.6517 | continue |
| 2 | 1 | −55.3275 | 58.78291 | continue | 2 | 107 | −196.369 | 407.7699 | continue |
| 3 | 2 | −36.7052 | 41.12448 | continue | 3 | 126 | −116.805 | 367.2043 | continue |
| 4 | 3 | −26.7731 | 32.43642 | continue | 4 | 145 | −63.6092 | 359.5706 | continue |
| 5 | 5 | −20.4124 | 27.67021 | continue | 5 | 171 | −34.4734 | 373.9780 | continue |
| 6 | 5 | −15.8077 | 25.08616 | continue | 6 | 188 | −28.1345 | 398.2559 | continue |
| 7 | 5 | −12.1513 | 23.94599 | continue | 7 | 189 | −34.7014 | 419.2460 | continue |
| 8 | 8 | −9.04072 | 23.89200 | continue | 8 | 190 | −40.7869 | 429.5541 | continue |
| 9 | 9 | −6.28005 | 24.72266 | continue | 9 | 190 | −42.7149 | 432.1846 | continue |
| 10 | 11 | −3.80494 | 26.29212 | continue | 10 | 190 | −42.9682 | 432.4955 | continue |
| 11 | 13 | −1.64563 | 28.46133 | continue | 11 | 192 | −42.9805 | 432.5098 | continue |
| 12 | 15 | 0.107043 | 31.08023 | continue | 12 | 192 | −42.9807 | 432.5099 | continue |
| 13 | 19 | 1.344969 | 33.99174 | continue | 13 | 192 | −42.9807 | 432.5099 | continue |
| 14 | 19 | 1.991195 | 37.04500 | continue | 14 | 192 | −42.9807 | 432.5099 | continue |
| 15 | 22 | 2.038062 | 40.10500 | continue | 15 | 203 | −42.9807 | 432.5099 | continue |
| 16 | 22 | 1.560907 | 43.05311 | continue | 16 | 203 | −42.9807 | 432.5099 | continue |
| 17 | 23 | 0.703089 | 45.78459 | continue | 17 | 204 | −42.9807 | 432.5099 | continue |
| 18 | 24 | −0.36003 | 48.21173 | continue | |||||
| 19 | 24 | −1.46272 | 50.27382 | continue | |||||
| 20 | 24 | −2.4802 | 51.94671 | continue | |||||
| 21 | 26 | −3.34086 | 53.24403 | continue | |||||
| Dataset 1 | Dataset 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| T | N(t) | Acceptance Region | Rejection Region | Result | T | N(t) | Acceptance Region | Rejection Region | Result |
| 1 | 1 | −3.554070 | 6.287044 | continue | 1 | 90 | 11.45807 | 170.0957 | continue |
| 2 | 1 | −0.636960 | 4.216873 | continue | 2 | 107 | 71.55002 | 139.9607 | continue |
| 3 | 2 | 0.776205 | 3.995391 | continue | 3 | 126 | 103.6526 | 146.8394 | continue |
| 4 | 3 | 1.977399 | 4.409981 | continue | 4 | 145 | 129.8891 | 165.5602 | continue |
| 5 | 5 | 3.205886 | 5.201452 | continue | 5 | 171 | 149.0555 | 188.4585 | continue |
| 6 | 5 | 4.434785 | 6.177075 | continue | 6 | 188 | 152.8588 | 214.1708 | continue |
| 7 | 5 | 5.509077 | 7.107788 | accept | 7 | 189 | 120.5342 | 261.5581 | continue |
| 8 | 190 | −56.62470 | 444.3444 | continue | |||||
| 9 | 190 | −1258.160 | 1647.398 | continue | |||||
| 10 | 190 | −14,878.80 | 15,268.35 | continue | |||||
| 11 | 192 | −325,116 | 325,505.2 | continue | |||||
| 12 | 192 | −1.8 × 107 | 18,130,355 | continue | |||||
| 13 | 192 | −3.5 × 109 | 3.47 × 109 | continue | |||||
| 14 | 192 | −3.3 × 1012 | 3.28 × 1012 | continue | |||||
| 15 | 203 | -Inf | Inf | continue | |||||
| 16 | 203 | -Inf | Inf | continue | |||||
| 17 | 204 | -Inf | Inf | continue | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.H.; Chang, I.H.; Pham, H. Software Reliability Model with Dependent Failures and SPRT. Mathematics 2020, 8, 1366. https://doi.org/10.3390/math8081366
Lee DH, Chang IH, Pham H. Software Reliability Model with Dependent Failures and SPRT. Mathematics. 2020; 8(8):1366. https://doi.org/10.3390/math8081366
Chicago/Turabian StyleLee, Da Hye, In Hong Chang, and Hoang Pham. 2020. "Software Reliability Model with Dependent Failures and SPRT" Mathematics 8, no. 8: 1366. https://doi.org/10.3390/math8081366
APA StyleLee, D. H., Chang, I. H., & Pham, H. (2020). Software Reliability Model with Dependent Failures and SPRT. Mathematics, 8(8), 1366. https://doi.org/10.3390/math8081366




