New Stability Criteria for Discrete Linear Systems Based on Orthogonal Polynomials
Abstract
1. Introduction
1.1. Stability of Linear Systems
1.2. Stable Polynomials
- (i)
- has exactly n zeros in ,
- (ii)
- has exactly zeros in ,
- (iii)
- The zeros of and interlace.
- (i)
- and are polynomials of degree n with coefficients of the same sign.
- (ii)
- and have simple and interlaced zeros on the unit circle .
2. Orthogonal Polynomials and the Szegő Transformation
2.1. Orthogonal Polynomials on the Real Line
- If , then
- If , then
2.2. Orthogonal Polynomials on the Unit Circle
- (i)
- Forward recurrence:
- (ii)
- Backward recurrence:where .
2.3. The Szegő Transformation
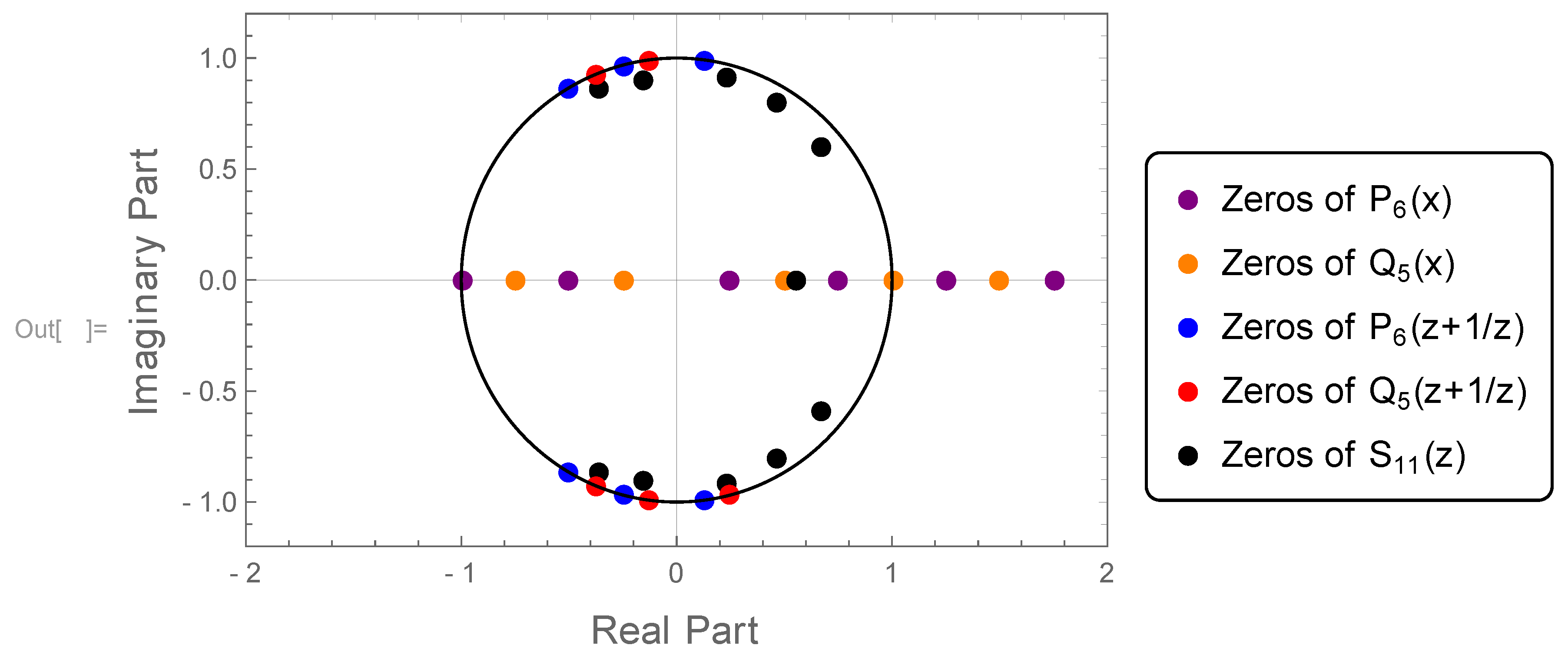
3. Stability Criteria via Orthogonality
| Algorithm 1: Algorithm to determine if a given polynomial is Schur |
 |
4. Conclusions and Further Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Åström, K.J.; Wittenmark, B. Computer-Controlled Systems; Prentice Hall: Upper Saddle River, NJ, USA, 1990. [Google Scholar]
- Kuo, B.C. Digital Control Systems; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Jalili-Kharaajoo, M.; Araabi, B.N. The Schur stability via the Hurwitz stability analysis using a biquadratic transformation. Automatica 2005, 41, 173–176. [Google Scholar] [CrossRef]
- Fleming, R.; Grossman, G.; Lenker, T.; Narayan, S. On Schur D-Stable matrices. Linear Algebra Appl. 1988, 279, 39–50. [Google Scholar] [CrossRef]
- Xu, H.; Datta, A.; Bhattacharyya, S.P. Computation of all stabilizing PID gains for digital control systems. IEEE Trans. Autom. Control 2001, 46, 647–652. [Google Scholar] [CrossRef]
- Jury, E.I.; Blanchard, J. A stability test for linear discrete system in table form. Proc. IRE 1961, 49, 1947–1948. [Google Scholar]
- Jury, E.I.; Blanchard, J. A stability test for linear discrete system using a simple division. Proc. IRE 1961, 49, 1948–1949. [Google Scholar]
- Choo, Y. An elementary proof of the Jury test for real polynomials. Automatica 2011, 47, 249–252. [Google Scholar] [CrossRef]
- Pérez, F.; Abdallah, C.; Docampo, D. Extreme-point stability test for discrete-time polynomials. In Proceedings of the 31st Conference on Decision and Control, Tucson, AZ, USA, 16–18 December 1992; pp. 1552–1553. [Google Scholar]
- Shiomi, K.; Otsuka, N.; Inaba, H.; Ishii, R. The property of bilinear transformation matrix and Schur stability for a linear combination of polynomials. J. Frankl. Inst. 1999, 336, 533–541. [Google Scholar] [CrossRef]
- Ackermann, J.E.; Barmish, B.R. Robust Schur stability of a polytope of polynomials. IEEE Trans. Autom. Control 1988, 33, 984–986. [Google Scholar] [CrossRef]
- Bose, N.K.; Jury, E.I.; Zeheb, E. On robust hurwitz and Schur polynomials. IEEE Trans. Autom. Control 1988, 33, 1166–1168. [Google Scholar] [CrossRef]
- Greiner, R. Necessary conditions for Schur-stability of interval polynomials. IEEE Trans. Autom. Control 2004, 49, 740–744. [Google Scholar] [CrossRef]
- Kraus, F.; Mansour, M.; Jury, E.I. Robust Schur stability of interval polynomials. IEEE Trans. Autom. Control 1992, 37, 141–143. [Google Scholar] [CrossRef]
- Shih, M.H.; Pang, C.T. Simultaneous Schur stability of interval matrices. Automatica 2008, 44, 2621–2627. [Google Scholar] [CrossRef]
- Pastravanu, O.; Matcovschi, M.H. Sufficient conditions for Schur and Hurwitz diagonal stability of complex interval matrices. Linear Algebra Appl. 2015, 467, 149–173. [Google Scholar] [CrossRef]
- Torres-Muñoz, J.A.; Rodríguez-Ángeles, E.; Kharitonov, V.L. On Schur stable multivariate polynomials. IEEE Trans. Circuits Syst. I Regul. Pap. 2006, 53, 1166–1173. [Google Scholar] [CrossRef]
- Dumitrescu, B.; Chang, B.C. Robust Schur stability with polynomial parameters. IEEE Trans. Circuits Syst. II Exp. Briefs 2006, 53, 535–537. [Google Scholar] [CrossRef]
- Dabbene, F.; Henrion, D.; Lagoa, C.M. Simple approximations of semialgebraic sets and their applications to control. Automatica 2017, 78, 110–118. [Google Scholar] [CrossRef]
- Gantmacher, F.R. The Theory of Matrices; Chelsea Publishing Co.: New York, NY, USA, 1959; Volumes 1–2. [Google Scholar]
- Lancaster, P.; Tismenetsky, M. The Theory of Matrices and Applications; Academic Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Bhattacharyya, S.P.; Chapellat, H.; Keel, L.H. Robust Control: The Parametric Approach; Prentice-Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Hermite, C. Sur le nombre des racines dune equation algebrique comprise entre des limites donnes. J. Reine Angew. Math. 1856, 52, 39–51. [Google Scholar]
- Bäckström, T.; Magi, C. Properties of line spectrum pair polynomials—A review. Signal Process. 2006, 86, 3286–3298. [Google Scholar] [CrossRef]
- Szegő, G. Orthogonal Polynomials, 4th ed.; American Mathematical Society Colloquium Publications: Providence, RI, USA, 1975; Volume 23. [Google Scholar]
- Chihara, T.S. An Introduction to Orthogonal Polynomials; Mathematics and Its Applications Series; Gordon and Breach: New York, NY, USA, 1978. [Google Scholar]
- Simon, B. Orthogonal Polynomials on the Unit Circle; American Mathematical Society Colloquium Publications: Providence, RI, USA, 2005; Volume 54. [Google Scholar]
- Ismail, M.E.H. Classical and Quantum Orthogonal Polynomials in One Variable; Encyclopedia of Mathematics and Its Applications; Cambridge University Press: Cambridge, UK, 2005; Volume 98. [Google Scholar]
- Huertas, E.J.; Marcellán, F.; Rafaeli, F.R. Zeros of orthogonal polynomials generated by canonical perturbations of measures. Appl. Math. Comput. 2012, 218, 7109–7127. [Google Scholar] [CrossRef]
- Brezinski, C. Padé-Type Approximation and General Orthogonal Polynomials; International Series of Numerical Mathematics, SO; Birkhäuser Verlag: Basel, Switzerland, 1980. [Google Scholar]
- Genin, I.V. Euclid algorithm, orthogonal polynomials, and generalized routh-hurwitz algorithm. Linear Algebra Appl. 1996, 246, 131–158. [Google Scholar] [CrossRef][Green Version]
- Holtz, O. Hermite-Biehler, Routh–Hurwitz, and total positivity. Linear Algebra Appl. 2003, 372, 105–110. [Google Scholar] [CrossRef][Green Version]
- Lange, L.J. Continued fraction applications to zero location. In Analytic Theory of Continued Fractions II, Lecture Notes in Math., Vol. 1199, Proceedings of a Seminar-Worship, Pitlochry and Aviemore, Scotland, UK, 13–29 June 1985; Thron, W.J., Ed.; Springer: Berlin/Heidelberg, Germany, 1986; pp. 220–262. [Google Scholar]
- Martínez, N.; Garza, L.E.; Aguirre-Hernández, B. On sequences of Hurwitz polynomials related to orthogonal polynomials. Linear Multilinear A 2019, 67, 2191–2208. [Google Scholar] [CrossRef]
- Arceo, A.; Garza, L.E.; Romero, G. Robust stability of hurwitz polynomials associated with modified classical weights. Mathematics 2019, 7, 818. [Google Scholar] [CrossRef]
- Simon, B. Szegő’s Theorem and Its Descendants: Spectral Theory for L2 Perturbations of Orthogonal Polynomials; M. B. Porter Lectures; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garza, L.E.; Martínez, N.; Romero, G. New Stability Criteria for Discrete Linear Systems Based on Orthogonal Polynomials. Mathematics 2020, 8, 1322. https://doi.org/10.3390/math8081322
Garza LE, Martínez N, Romero G. New Stability Criteria for Discrete Linear Systems Based on Orthogonal Polynomials. Mathematics. 2020; 8(8):1322. https://doi.org/10.3390/math8081322
Chicago/Turabian StyleGarza, Luis E., Noé Martínez, and Gerardo Romero. 2020. "New Stability Criteria for Discrete Linear Systems Based on Orthogonal Polynomials" Mathematics 8, no. 8: 1322. https://doi.org/10.3390/math8081322
APA StyleGarza, L. E., Martínez, N., & Romero, G. (2020). New Stability Criteria for Discrete Linear Systems Based on Orthogonal Polynomials. Mathematics, 8(8), 1322. https://doi.org/10.3390/math8081322





