Entrainment of Weakly Coupled Canonical Oscillators with Applications in Gradient Frequency Neural Networks Using Approximating Analytical Methods
Abstract
:1. Introduction
2. Methods
2.1. The Canonical Model of Single Oscillators
2.1.1. Wilson–Cowan Model
2.1.2. The Normal Form
2.1.3. The Normal Form about a Hopf Bifurcation Point: The Canonical Model
2.2. The Canonical Model of Two Coupled Oscillators
2.2.1. The General Normal Form
2.2.2. Hopf Normal Form: The Canonical Model
2.2.3. Radial and Angular Equations
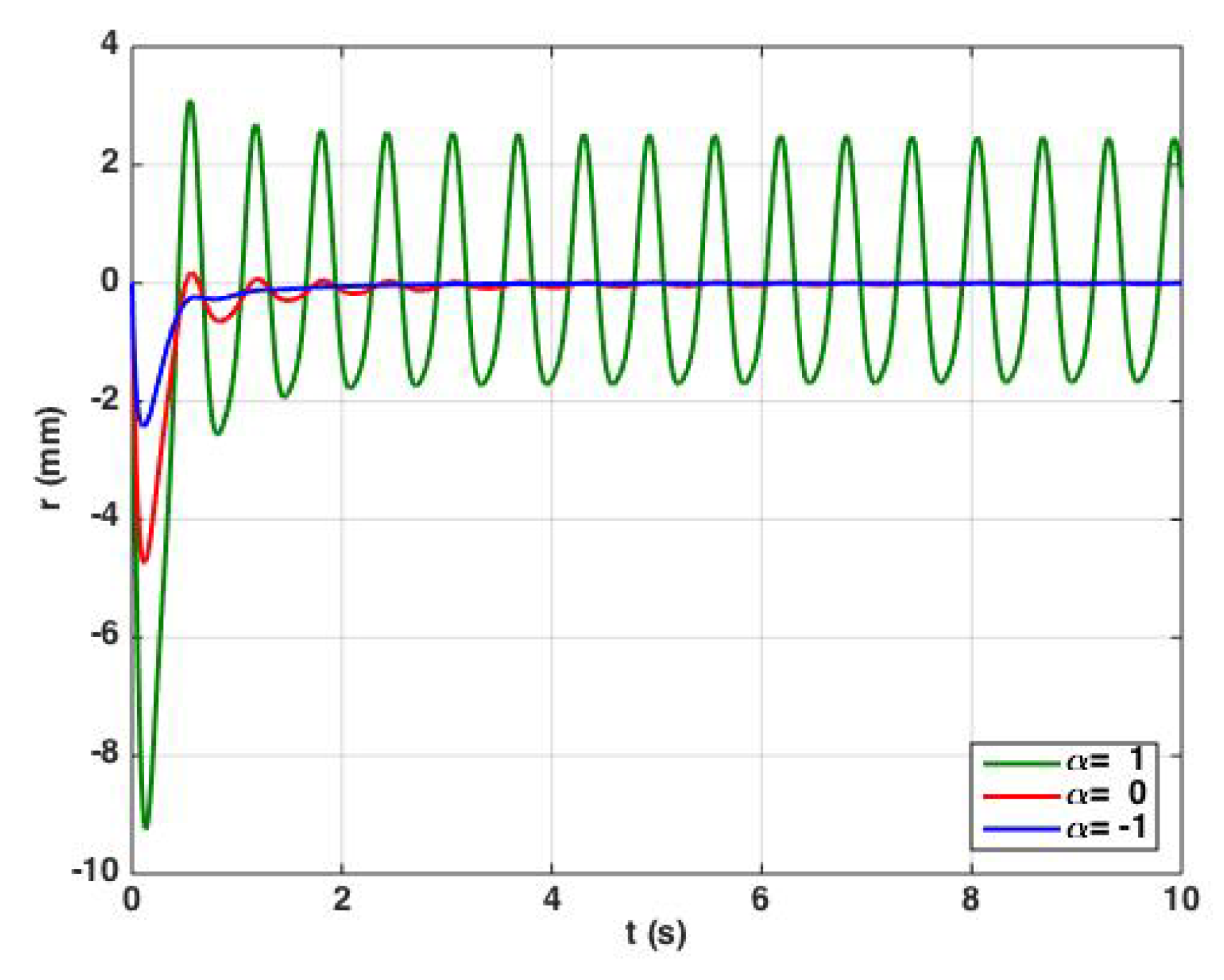
3. Results
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| GFNNs | Gradient Frequency Neural Networks |
| CNF | Conventional Normal Form |
Appendix A
- .
- .
Appendix B
Appendix C
References
- Fuchs, A. Nonlinear Dynamics in Complex Systems: Theory and Applications for the Life-, Neuro- and Natural Sciences; Springer: Berlin, Germany, 2013. [Google Scholar]
- Izhikevich, E.M. Dynamical Systems in Neuroscience; The MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Large, E.W.; Almonte, F.V.; Velasco, M.J. A canonical model for gradient frequency neural networks. Phys. D 2010, 239, 905–911. [Google Scholar] [CrossRef]
- Kim, J.C.; Large, E.W. Signal Processing in Periodically Forced Gradient Frequency Neural Networks. Front. Comput. Neurosci. 2015, 9, 152. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duke, T.; Andor, D.; Julicher, F. Physical Basis of Interference Effects in Hearing. Ann. Henri Poincaré 2003, 4, 667–669. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method for bifurcation of nonlinear problems. Int. J. Nonlinear Sci. Numer. Simul. 2005, 6, 207–208. [Google Scholar] [CrossRef]
- Bayat, M.; Pakar, I.; Emadi, A. Vibration of electrostatically actuated microbeam by means of homotopy perturbation method. Struct. Eng. Mech. 2013, 48, 823–831. [Google Scholar] [CrossRef]
- Bayat, M.; Pakar, I.; Domairry, G. Recent developments of some asymptotic methods and their applications for nonlinear vibration equations in engineering problems: A review. Lat. Am. J. Solids Struct. 2012, 9, 1–93. [Google Scholar] [CrossRef] [Green Version]
- Bogoliubov, N.N.; Mitropolsky, Y.A. Asymptotic Methods in the Theory of Nonlinear Oscillators; Hindustan Publishing Corporation: Delhi, India, 1961. [Google Scholar]
- Wiggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos; Text in Applied Mathematics; Springer: Berlin, Germany, 2003; Volume 2. [Google Scholar]
- Yu, P. Computation of the simplest normal forms with perturbation parameters based on Lie transformation and rescaling. J. Comput. Appl. Math. 2002, 144, 359–373. [Google Scholar] [CrossRef] [Green Version]
- Wilson, H.R.; Cowan, J.D. Excitatory and Inhibitory Interactions in Localized Populations of Modeled Neurons. Biophys. J. 1972, 12, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Hoppensteadt, F.C.; Izhikevich, E.M. Weakly Connected Neural Networks; Appied Mathematical Sciences; Springer: Berlin, Germany, 1997; Volume 126. [Google Scholar]
- Fuchs, A.; Jirsa, V.K.; Haken, H.; Kelso, J.A. Scott Extending the HKB model of coordinated movement to oscillators with different eigenfrequencies. Biol. Cybern. 1996, 74, 21–30. [Google Scholar] [CrossRef]
- Marsden, J.E.; McCracken, M. The Hopf Bifurcation and Its Applications; Applied Mathematical Sciences; Springer: Berlin, Germany, 1976; Volume 19. [Google Scholar]
- Lerud, K.D.; Almonte, F.V.; Kim, J.C.; Large, E.W. Mode-locking neurodynamics predict human auditory brainstem responses to musical intervals. Hear. Res. 2014, 308, 41–49. [Google Scholar] [CrossRef] [PubMed]
- Farokhniaee, A.A. Simulation and Analysis of Gradient Frequency Neural Networks. Ph.D. Thesis, University of Connecticut Graduate School, Mansfield, CT, USA, 2016. [Google Scholar]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farokhniaee, A.; Almonte, F.V.; Yelin, S.; Large, E.W. Entrainment of Weakly Coupled Canonical Oscillators with Applications in Gradient Frequency Neural Networks Using Approximating Analytical Methods. Mathematics 2020, 8, 1312. https://doi.org/10.3390/math8081312
Farokhniaee A, Almonte FV, Yelin S, Large EW. Entrainment of Weakly Coupled Canonical Oscillators with Applications in Gradient Frequency Neural Networks Using Approximating Analytical Methods. Mathematics. 2020; 8(8):1312. https://doi.org/10.3390/math8081312
Chicago/Turabian StyleFarokhniaee, AmirAli, Felix V. Almonte, Susanne Yelin, and Edward W. Large. 2020. "Entrainment of Weakly Coupled Canonical Oscillators with Applications in Gradient Frequency Neural Networks Using Approximating Analytical Methods" Mathematics 8, no. 8: 1312. https://doi.org/10.3390/math8081312




