A New ODE-Based Model for Tumor Cells and Immune System Competition

Abstract

Changes in diet are heavily associated with high mortality rates in several types of cancer. In this paper, a new mathematical model of tumor cells growth is established to dynamically demonstrate the effects of abnormal cell progression on the cells affected by the tumor in terms of the immune system’s functionality and normal cells’ dynamic growth. This model is called the normal-tumor-immune-unhealthy diet model (NTIUNHDM) and governed by a system of ordinary differential equations. In the NTIUNHDM, there are three main populations normal cells, tumor cell and immune cells. The model is discussed analytically and numerically by utilizing a fourth-order Runge–Kutta method. The dynamic behavior of the NTIUNHDM is discussed by analyzing the stability of the system at various equilibrium points and the Mathematica software is used to simulate the model. From analysis and simulation of the NTIUNHDM, it can be deduced that instability of the response stage, due to a weak immune system, is classified as one of the main reasons for the coexistence of abnormal cells and normal cells. Additionally, it is obvious that the NTIUNHDM has only one stable case when abnormal cells begin progressing into early stages of tumor cells such that the immune cells are generated once. Thus, early boosting of the immune system might contribute to reducing the risk of cancer.

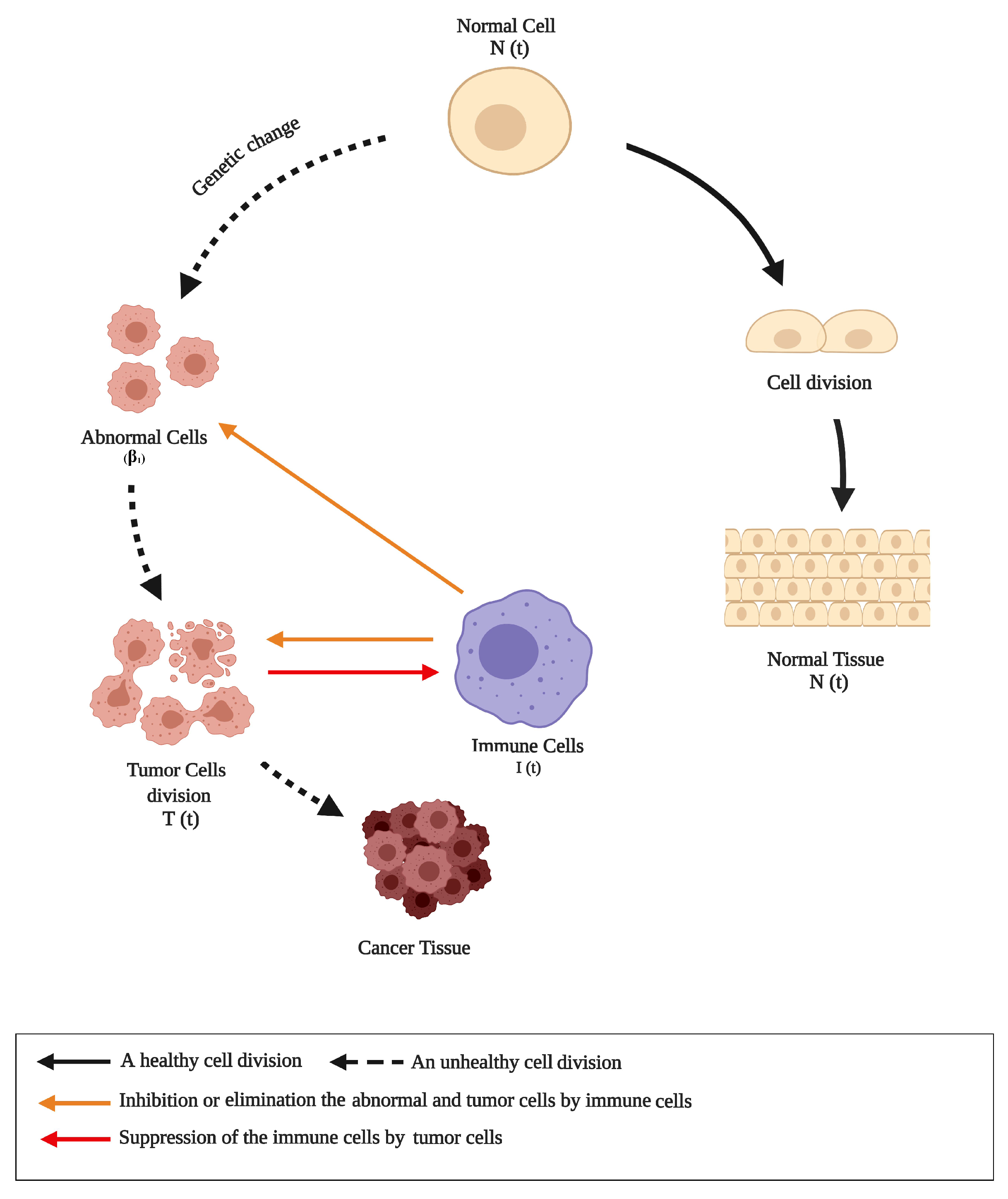
1. Introduction

In 1982, Witten [1] postulated the first mathematical model to illustrate the interactivity between normal and tumor cells. In 1994, researchers began using the functionality of Michaelis–Menten [2,3] for formulating interaction models concerning tumor-immune cells. In 1995, another mathematical model was proposed that entailed the use of two equations for elucidating the engagement between a pathogen-like virus and a human system. It is possible to dynamically explain the process whereby the pathogens engage with the immune system [4]. Based on these models, researchers proposed many models that involve the application of different therapeutic approaches, such as immunotherapy and chemotherapy [5,6,7,8]. Numerical, as well as mathematical, models have been used to examine how a drug’s resistance levels impact tumor cells, which show resistance toward certain medications [9,10,11,12]. In 2003, Kuznetsov–Taylor’s simplified model was put forward by Magda Galach [13], regarding one of the precursors in the emergence of cancer that enables the success of abnormal cells to coexist with normal cells for a prolonged period of time. Agent-based models (ABM) and kinetic theory have helped to explain the dynamics of a complex biological system [14,15] as well as pedestrian dynamics [16,17]. ABM are typically utilized in the cancer micro-environment for modeling tumor growth (drug response) and angiogenesis [18,19]. The thermostatted kinetic theory is suggested for the simulation of complex biological systems [20,21]. In 2016, Bianca and Lemarchand [22] used the principle of thermostatted kinetics to build a simplified model containing three cell types (cancer cell, immune cell, normal cell). The findings indicate that the model can replicate cancer cell’s elimination, equilibrium and how they evade immune system surveillance. Moreover, in the context of thermostatted kinetic theory, the correlations between the immune system and a tumor are defined at cell scales [22]. Ordinary differential equations (ODEs) [23,24,25], partial differential equations (PDEs) [26,27], and delay differential equations (DDEs) [28,29] have been used to suggest cancer models and study the effects of tumor growth on the dynamics of other cells or dynamics of brain diseases [30].

Cancer is a public health disease that causes an increased global mortality level. The majority of cancers develop as a consequence of multiple abnormalities, which accumulate over many years (10–15 years) [31]. One of the main functions of the immune systems is to prevent the body from developing cancer. Previous studies have shown some unhealthy diets, such as a Western-style diet, can damage the capability of the immune system to interact with abnormal cells and result in cancer development [32,33,34]. Alharbi and others deduced dynamically that the immune system has a responsibility to prevent abnormal cells from surviving in tissue [35]. Dynamically, Alharbi and Rambely deduced that it was possible for the immune system to remove abnormal cells, in which case, the functionality goes through the response stage, the interaction stage, and then the recovery stage. These stages are not satisfied when the immune system is weakened as a result of following an unhealthy diet [36]. According to this, the tumor-normal model (TNM) was proposed by considering two main populations of tumor cells and normal cells to dynamically demonstrate the effect of abnormal cells that progress to cells that form tumors in terms of normal cell dynamic growth [37].

In this paper, a new mathematical model was proposed by referring to [1,4,36,37], which is called the normal-tumor-immune-unhealthy diet model (NTIUNHDM). This model was proposed by considering the main population cells, which had a significant effect on the tumor cell appearance in a tissue (normal cells, immune cells, and tumor cells). The dynamics of NTIUNHDM were analyzed and simulated by assuming that the immune system was weak due to a person’s continuous unhealthy diet. The appearance of abnormal cells and their successful growth in tissue are classified as an emergency case of cancer; thus, the NTIUNHDM dynamically demonstrates the effect that the progression of abnormal cells into tumor cells has on the behavior of the immune system and the normal cell cycle. As a consequence, understanding the dynamics of progressive tumor cells contributes to introducing important health advice, reducing the rates of cancer, and increasing the awareness in health care.

The remainder of this paper is arranged as follows. The NTIUNHDM is presented and analyzed in Section 2 and Section 3, respectively. The numerical simulation of the NTIUNHDM is presented in Section 4. This paper is concluded in Section 5.

2. Normal-Tumor-Immune-Unhealthy Diet Model (Ntiunhdm)

Based on the dynamic results of [1,4,36,37], one of the primary reasons for cancer development is the failure of the immune system to accomplish the interaction stage that occurs when a person follows an unhealthy diet as indicated dynamically by the immune-unhealthy diet model (IUNHDM). The continuous division of normal cells leading to cell mutation is classified as one of the precursors in the emergence of cancer cells, as indicated dynamically by the tumor–normal model (TNM). Thus, the normal-tumor-immune-unhealthy diet model (NTIUNHDM) is formulated to suggest a dynamic model that entails the development of various stages of tumor cells (from a state of emergency to stages I and II). Figure 1 is a suggestion of a biological scenario of progressive cancer that is related to the NTIUNHDM. The NTIUNHDM is governed by a system of ordinary differential equations and designed based on the dynamic results of the mathematical models, which are known as IUNHDM [36], and TNM [37].

Our model is hypothesized in the following manner: there is a significant growth in the cell population, which means that it can take a long time for a tissue’s abnormal cells to transition into tumor cells. In accordance with our model, the human tissue cell population is divided in a particular time gap, and the immune system is entrusted with the responsibility of preventing the proliferation of cancerous cells in humans. Hence, The NTIUNHDM is formulated using three main populations: Normal cells, Tumor cells, and Immune cells. The dynamic behaviors of all these cells are demonstrated by the following nonlinear ordinary differential equations:

The independent variable $N\left(t\right)$ was utilized to denote normal cells that can either be destroyed or grown using stable DNA that rules out all activities of the cell. After being targeted by tumors cells, normal cells could not grow. The behavior of normal cells, denoted by N, is elucidated by the following ordinary differential equation:

$$\frac{dN}{dt}=rN(1-{\beta }_{1}N)-\eta NI-\gamma NT.$$

The parameters $r,{\beta }_1,\eta$, and $\gamma$ are real, positive, and defined as follows: r denotes grown-up normal cells while ${\beta }_1$ refers to the division rate of normal cells to their abnormal counterparts. The parameter $\eta$ denotes immune cells that inhibit or eradicate abnormal cells, whereas $\gamma$ denotes the rate at which tumor cells inhibit or attack normal cells. The fact that cancer cells have a continuous cycle is attributed to changes in DNA [38].

The independent variable T signifies how tumors cells emerge—the failure of the immune system to curtail or eradicate abnormal cells. Such types of cells can divide rapidly and attack normal cells that are situated across from the surrounding tissues when there is a weakness in how the immune system responds. This ordinary differential equation shows the abnormal growth of tumors cells:

$$\frac{dT}{dt}={\alpha }_{1}T(1-{\alpha }_{2}T)+{\beta }_{2}NT-{\alpha }_{3}TI.$$

The parameters ${\alpha }_1,{\alpha }_2,{\beta }_2$, and ${\alpha }_3$ are real, positive, and defined as follows; ${\alpha }_1$ denotes the limited growth of tumor cells and the parameter ${\alpha }_2$ means that tumor cells are confronting a decline caused by the body’s ingrown tumor during the process of dietary metabolism. On the other hand, parameter ${\beta }_2$, denotes the pace at which abnormal cells become converted into their tumors counterparts. Although a weak immune system was assumed to be attributed to unhealthy diet in an individual, ${\alpha }_3$ signifies the rate of inhibition or the eradication of tumor cells caused by the immune cells’ response.

One of the most important responsibilities of the immune system is to safeguard the body from cancerous cells. Due to the appearance of abnormal cells, several immune cells can be generated and converted into tumor cells in the tissue. Oftentimes, the activation of these cells mean they are unable to eliminate abnormal and tumor cells or delay their progression. The independent variable $I,$ which denotes the behavior of the immune system, is elucidated by the following ordinary differential equations:

$$\frac{dI}{dt}=\sigma -\delta I+\frac{\rho NI}{m+N}+\frac{{\rho }_{1}TI}{m_1+T}-\mu NI-{\mu }_{1}TI.$$

The first parameter, $\sigma$, denotes a constant source of the immune system response, which is generated in the body on a daily basis. The second parameter, $\delta$, signifies the natural rate at which immune cells die. Depending on the progressive series of cancer, two types of Michaelis–Menten terms are known to exist. The first Michaelis–Menten term is depicted by $\frac{\rho NI}{m+N}$, which eradicates or inhibits abnormal cells in such a manner that the abnormal cell appearance stimulates the immune system to respond. The first parameter $\rho$ denotes this response rate, while the immune system’s threshold rate is given by $m.$ The second Michaelis–Menten term is denoted by $\frac{{\rho }_{1}TI}{m_1+N}$, which inhibits or eradicates tumors cells in such a manner that causes the activity of tumor cells to stimulate the immune system to respond [23]. The parameter $\mu$ signifies reduced immune cells due to the manner in which they interact with abnormal cells. Additionally, the tumor cells’ rapid division and activity can suppress the activity of their immune counterparts. This suppression is denoted by the parameter ${\mu }_1$.

Thus, the following system expresses the normal-tumor-immune-unhealthy diet model (NTIUNHDM).

$$\begin{array}{ccc}\hfill \frac{dN}{dt}& =& rN(1-{\beta }_{1}N)-\eta NI-\gamma NT,\hfill \\ \hfill \frac{dT}{dt}& =& {\alpha }_{1}T(1-{\alpha }_{2}T)+{\beta }_{2}NT-{\alpha }_{3}TI,\hfill \\ \hfill \frac{dI}{dt}& =& \sigma -\delta I+\frac{\rho NI}{m+N}+\frac{{\rho }_{1}TI}{m_1+T}-\mu NI-{\mu }_{1}TI.\hfill \end{array}$$

(1)

3. The Model Analysis

3.1. Conditions and Solution Positivity

The NTIUNHDM (1) showcases the behavior of normal, as well as tumor cells, caused by the weak immune system. Thus, the independent variables $N,T$, and I are positive. In addition, all the parameters are positive, real and their values are between zero and one. Hence, the following set explains the variable regions:

$$\mathrm{\Omega }=\{(N,T,I)\in R_{+}^3\}.$$

The initial values of the NTIUNHDM (1) are assumed to be [36,37]

$$N\left(0\right)=1,T\left(0\right)=1\mathrm{and}I\left(0\right)=1.22.$$

In addition, all solutions with positive conditions are positive for all time t. Thus, we can estimate the following theorem

Theorem 1.

The dynamic system region of the NTIUHDM (1), $\mathrm{\Omega }\subset R_{+}^3,$ is positivity-invariant and a positive solution exists for all time t.

Proof. 

By applying Bernoulli’s method, it is possible to obtain solutions offered by the first and second equations of NTIUNHDM (1) as the following:

From the first population of the NTIUNHDM (1), we have

$$\frac{dN}{dt}\le rN\left(t\right)-r{\beta }_1{N}^2\left(t\right).$$

(2)

By applying Bernoulli’s method, the solution of Equation (1) is given by

$$N\left(t\right)\le \frac{1}{{\beta }_1+c_1{e}^{-rt}}.$$

As $t\to \infty ,$ the solution is given by

$$N\left(t\right)\le \frac{1}{{\beta }_1}.$$

From the second equation of the NTIUNHDM (1), we obtain

$$\frac{dT}{dt}\le {\alpha }_{1}T(1-{\alpha }_{2}T).$$

(3)

By using Bernoulli’s method, the Equation (3) solution will be

$$T\left(t\right)\le \frac{1}{{\alpha }_2+c{e}^{-{\alpha }_{1}t}}.$$

As $t\to \infty ,$ we find

$$T\left(t\right)\le \frac{1}{{\alpha }_2}.$$

The solution of the third equation is computed by using a separable variables method as follows: From the third equations of the NTIUNHDM (1), we have

$$\frac{dI}{dt}\le \sigma -\delta I.$$

(4)

By applying the separable variables method, the solution of Equation (4) is given by

$$I\left(t\right)\le \frac{\sigma }{\delta }+c_2{e}^{-\delta t}.$$

As $t\to \infty ,$ the solution is given by

$$I\left(t\right)\le \frac{\sigma }{\delta }.$$

Then, it can be seen that all the solutions $\left(N\right(t),T(t),I(t\left)\right)$ of NTIUNHDM (1) are positive for all time $t,$

$$\mathrm{\Omega }={\mathrm{\Omega }}_c:=\{(N,T,I)\in R_{+}^3,N=\frac{1}{{\beta }_1},T=\frac{1}{{\alpha }_2}\mathrm{and}I=\frac{\sigma }{\delta }\}.$$

 □

Remark 1.

According to the physiological meaning of cell cycle life, we can deduce that the rate of division normal cell as abnormal cells is very small compared with the rate of the natural divide of cell. Thus, $0<{\beta }_1<<0.1.$

3.2. Equilibrium Points

The steady states occur when the left hand side of the dynamic system of the NTIUNHDM (1) is set to zero as follows:

• $\frac{dN}{dt}=0\iff$

  $$N(r-{\beta }_{1}N-\eta I-\gamma T)=0$$

  (5)
• $\frac{dT}{dt}=0\iff$

  $$T({\alpha }_1(1-{\alpha }_{2}T)+{\beta }_{2}N-{\alpha }_{3}I)=0$$

  (6)
• $\frac{dI}{dt}=0\iff$

  $$\begin{array}{cc}\hfill & \sigma -\delta I+\frac{\rho NI}{m+N}+\frac{{\rho }_{1}TI}{m_1+T}+\mu NI+{\mu }_{1}TI=0\hfill \\ \hfill & (\sigma -\delta I)(m+N)(m_1+T)+\rho (m_1+T)N+\hfill \\ \hfill & {\rho }_1(m+N)TI+\mu (m+N)(m_1+T)NI+\hfill \\ \hfill & {\mu }_1(m+N)(m_1+T)TI=0.\hfill \end{array}$$

  (7)

Thus, by solving the Equations (5)–(7), we can compute and classify the equilibrium points of NTIUNHDM (1) in the following manner:

(1)

The response stage, $p_0$: This response stage indicates that the immune system is capable of responding when abnormal cells start appearing within a tissue. The progression of abnormal cells and their tumors counterparts is governed by the stability case of this particular stage. Thus, the equilibrium point of the response stage is given as follows:

$$p_0=(0,0,\frac{\sigma }{\delta }).$$

(2)

The coexisting stage, $p_1$: The NTIUNHDM is built based on the IUNHDM [36] which is characterised by the loss of the interaction stage. In this case, the immune cells respond to abnormal cells as if they were normal cells, which gives abnormal cells a chance to occur in the tissue as non-active cells for a long time (10–15 years). The equilibrium point of this stage is given as follows:

$$p_1=({\beta }_1^{-1},0,\frac{{\beta }_1(1+m{\beta }_1)\sigma }{(1+m{\beta }_1)({\beta }_1\delta +{\mu }_1)-{\beta }_1\rho }),\mathrm{where}0<{\beta }_1<<0.1.$$

(3)

The resisting stage, $p_2$: This stage is generated when abnormal cells begin to turn into tumor cells. The equilibrium point at this stage is given as follows:

$$p_2=(0,T_1,I_1),$$

where

$$T_1=\frac{1}{6{\alpha }_2}\left[6-\frac{2^{\frac{2}{3}}{\left({\mathrm{\Psi }}_3+\sqrt{{\mathrm{\Psi }}_3^2+4{\mathrm{\Psi }}_4}\right)}^{\frac{1}{3}}+2{\alpha }_1{\alpha }_3{\mathrm{\Psi }}_1}{{\alpha }_1{\alpha }_3\mu }+\frac{2^{\frac{4}{3}}{\alpha }_3(-{\alpha }_1{\mathrm{\Psi }}_1^2+{\mathrm{\Psi }}_2)}{\mu {\left({\mathrm{\Psi }}_3+\sqrt{{\mathrm{\Psi }}_3^2+4{\mathrm{\Psi }}_4}\right)}^{\frac{1}{3}}}\right],$$

$$\begin{array}{ccc}\hfill I_1& =& \frac{1}{6{\alpha }_3^2\mu }\left[2{\alpha }_2{\alpha }_3{\mathrm{\Psi }}_1+\frac{2^{\frac{4}{3}}{\alpha }_1{\alpha }_3^2(-{\alpha }_1{\mathrm{\Psi }}_1^2+{\mathrm{\Psi }}_2)}{{\left({\mathrm{\Psi }}_3+\sqrt{{\mathrm{\Psi }}_3^2+4{\mathrm{\Psi }}_4}\right)}^{\frac{1}{3}}}\right]\hfill \\ \hfill & +& \frac{1}{3\ast 2^{\frac{1}{3}}{\alpha }_3^2\mu }{\left[{\mathrm{\Psi }}_3+\sqrt{{\mathrm{\Psi }}_3^2+4{\mathrm{\Psi }}_4}\right]}^{\frac{1}{3}},\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill {\mathrm{\Psi }}_1& =& 2{\mu }_1+{\alpha }_2(\delta +m_1{\mu }_1-{\rho }_1)\hfill \\ & >& 0,\hfill \\ \hfill {\mathrm{\Psi }}_2& =& 3{\mu }_1({\alpha }_1(1+m_1{\alpha }_2)({\alpha }_2\delta +{\mu }_1)-{\alpha }_1{\alpha }_2{\rho }_1\hfill \\ & +& {\alpha }_2{\alpha }_3\sigma )\hfill \\ & >& 0,\hfill \\ \hfill {\mathrm{\Psi }}_3& =& {\alpha }_1^2{\alpha }_3^3\left({\alpha }_1{\mathrm{\Psi }}_1\right(-\mu ({\mathrm{\Psi }}_1-\mu )\hfill \\ & +& {\alpha }_2^2(2{\delta }_2^2+2{(-m_1{\mu }_1+{\rho }_1)}^2\hfill \\ \hfill & -& \delta (5m_1{\mu }_1+4{\rho }_1)\left)\right))\hfill \\ & +& 9({\mu }_1+{\alpha }_2(\delta +2m_1{\mu }_1+{\rho }_1){\alpha }_1^2{\alpha }_2{\alpha }_3^4{\mu }_1\sigma \hfill \\ & <& 0,\hfill \\ \hfill {\mathrm{\Psi }}_4& =& -{\alpha }_1^3{\alpha }_3^6({\alpha }_1({\mu }_1({\mathrm{\Psi }}_1-{\mu }_1)+{\alpha }_2^2({\delta }^2\hfill \\ & +& {(-m_1{\mu }_1+{\rho }_1)}^2-{\delta }_2(m_1{\mu }_1+2{\rho }_1)\left)\right)\hfill \\ & -& 3{\alpha }_2{\alpha }_3{\mu }_1{\sigma }_2{)}^3\hfill \\ & >& 0.\hfill \end{array}$$

Remark 2.

By applying Theorem 1 and the biological meaning of the equilibrium point $p_2$, we deduced that:

• The tumor cells compete for survival at the resisting stage by rapidly dividing and growing. Therefore,

  $$1\le T_1<\frac{1}{{\alpha }_2}\mathrm{where}0<{\alpha }_2<1.$$
• There is a suppression to the activity of immune cells as a consequence of rapid growth and division of tumors cells [23]. Therefore,

  $$1\le I_1<\frac{\sigma }{\delta }\mathrm{where}0<\frac{\sigma }{\delta }=I\left(0\right)=1.22.$$

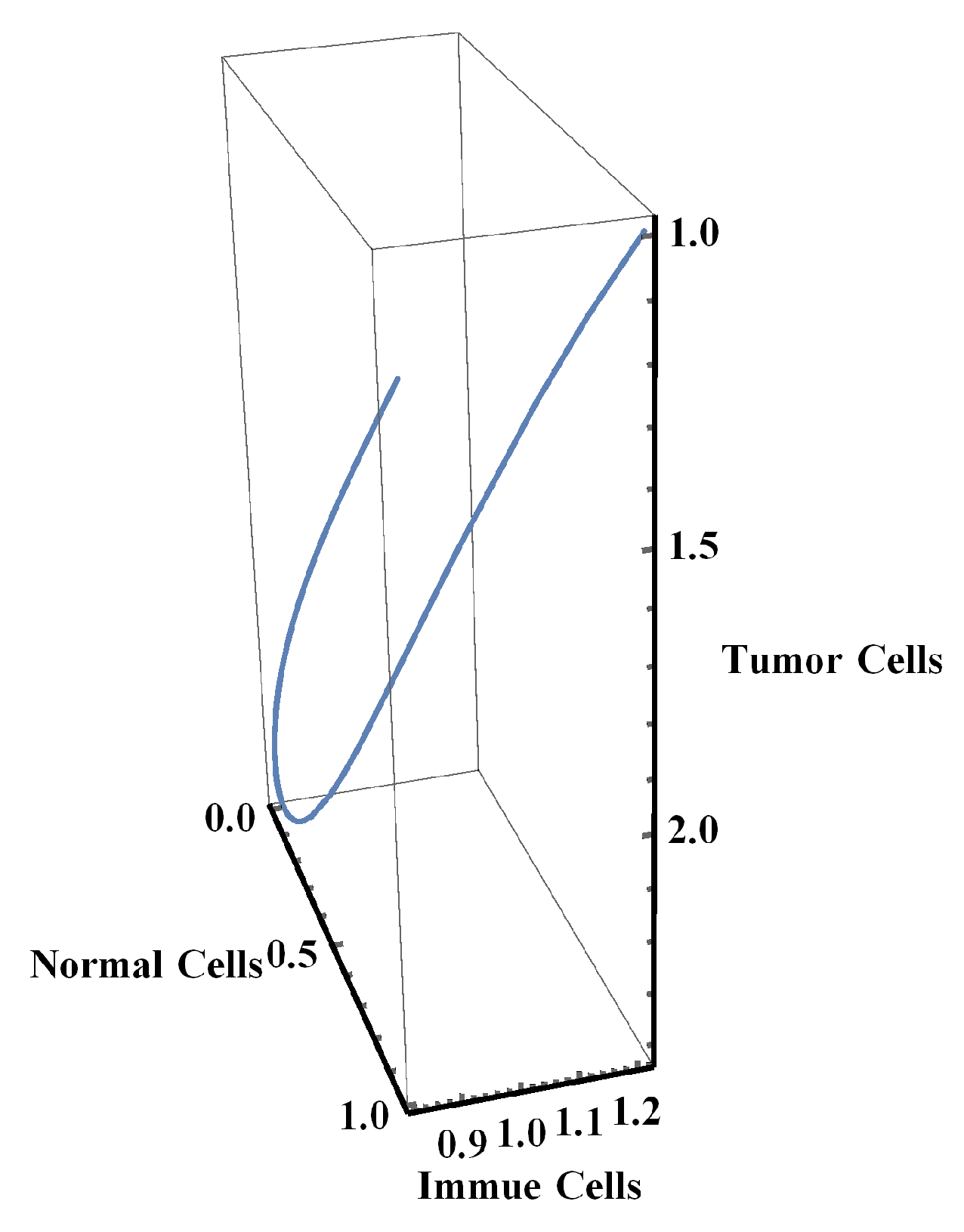
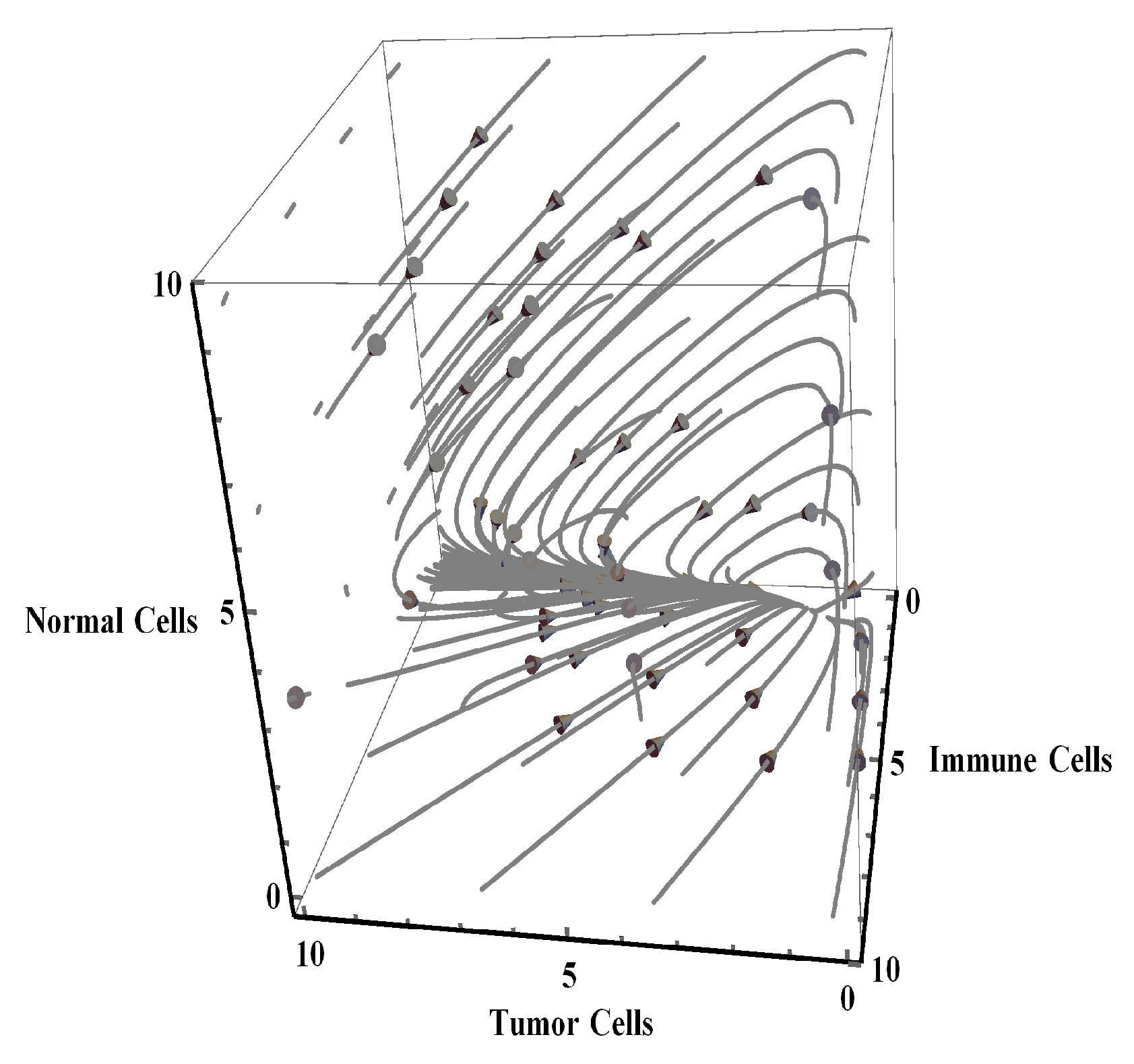
3.3. Stability of Equilibrium Points

The Hartman–Grobman Theorem [39] posits that stability of the equilibrium points are estimated by the following theorems:

Theorem 2.

Assume that the function $f:\mathrm{\Omega }\to R_{+}^3$ where $\mathrm{\Omega }$ is a domain in $R_{+}^3,$ and the equilibrium point $p_0=(0,0,I)\in \mathrm{\Omega }$ is demonstrated in the response stage such that $I\left(0\right)=\frac{\sigma }{\delta }$. Thus, there is at least one of the eigenvalues of the Jacobian matrix at $p_0$ has a positive sign. Hence, the equilibrium point $p_0$ is unstable of f.

Proof. 

The Jacobian matrix of NTIUNHDM (1) at $p_0$ is computed as follows;

$$J{[N,T,I]}_{p_0}=\left[\begin{array}{ccc}r-\frac{\eta \sigma }{\delta }\hfill & 0\hfill & 0\hfill \\ 0\hfill & {\alpha }_1-\frac{{\alpha }_3\sigma }{\delta }\hfill & 0\hfill \\ \frac{(\rho -\mu m)\sigma }{m\delta }\hfill & \frac{({\rho }_1-{\mu }_{1}m)\sigma }{m_1\delta }\hfill & -\delta \hfill \end{array}\right].$$

(8)

Then, the eigenvalues are given as the following:

$$\begin{array}{ccc}\hfill {\lambda }_1& =& -\delta ,\hfill \\ \hfill {\lambda }_2& =& r-\frac{\eta \sigma }{\delta }=r-\eta I\left(0\right),\hfill \\ \hfill {\lambda }_3& =& {\alpha }_1-\frac{{\alpha }_3\sigma }{\delta }={\alpha }_1-{\alpha }_{3}I\left(0\right).\hfill \end{array}$$

It is evident that the stability of the equilibrium point $p_0$ is governed by the immune system’s status. As the immune system is weak, this implies that the response stage is unstable.  □

Physiologically, the instability of the immune system response indicates that the abnormal cells might develop in the tissue. This is considered as an emergency situation, with any progression being able to trigger the formation of tumor cells and the development of cancer [23,36]. The following theorem discusses the dynamic case of coexistence between these cells.

Theorem 3.

Assume that the function $f:\mathrm{\Omega }\to R_{+}^3$ where $\mathrm{\Omega }$ is a domain in $R_{+}^3,$ and the equilibrium point $p_1=(N,0,I)\in \mathrm{\Omega }$ is demonstrated at the coexisting stage such that $0<{\beta }_1<<0.1$. Thus, one of the eigenvalues of the Jacobian matrix at $p_1$ has a positive sign if and only. Hence, the equilibrium point $p_1$ is a semi-stable case of f.

Proof. 

The Jacobian matrix of NTIUNHDM (1) at $p_1,$ is computed as the following:

$$J{[N,T,I]}_{p_1}=\left[\begin{array}{ccc}r-\frac{({\beta }_1(1+m{\beta }_1)\eta \sigma }{(1+m{\beta }_1)(\delta {\beta }_1+\mu )-\rho {\beta }_1}\hfill & \frac{-\gamma }{{\beta }_1}\hfill & \frac{-\eta }{{\beta }_1}\hfill \\ 0\hfill & {\alpha }_1+\frac{{\beta }_2}{{\beta }_1}-\frac{{\alpha }_3{\beta }_1(1+m{\beta }_1)\sigma }{(1+m{\beta }_1)(\delta {\beta }_1+\mu )-\rho {\beta }_1}\hfill & 0\hfill \\ \frac{{\beta }_1(-{(1+m{\beta }_1)}^2{\mu }_1+m_1\rho {\beta }_1^2)\sigma }{(1+m{\beta }_1)((1+m{\beta }_1)(\delta {\beta }_1+\mu )-\rho {\beta }_1)}\hfill & \frac{{\beta }_1(1+m{\beta }_1)({\rho }_1-{\mu }_2{m}_2))\sigma }{m_1((1+m{\beta }_1)(\delta {\beta }_1+\mu )-\rho {\beta }_1)}\hfill & -\delta -\frac{\mu (1+m{\beta }_1)-\rho {\beta }_1}{{\beta }_1(1+m{\beta }_1)}\hfill \end{array}\right].$$

(9)

Since $0<{\beta }_1<<0.1$, the simplified form of the characteristic equation of the matrix (9) can be written as follows

$$(r+\lambda )({\alpha }_1+\frac{{\beta }_2}{{\beta }_1}-\frac{{\alpha }_3{\beta }_1(1+m{\beta }_1)\sigma }{(1+m{\beta }_1)(\delta {\beta }_1+\mu )-{\beta }_1}-\lambda )(\mu +2{\beta }_1(\delta +m\mu -\rho )+{\beta }_1\lambda )=0.$$

(10)

By solving Equation (10), we obtain the following roots:

$$\begin{array}{ccc}\hfill {\lambda }_1& =& -r,\hfill \\ \hfill {\lambda }_2& =& \frac{{\alpha }_1{\beta }_1+{\beta }_2}{{\beta }_1}-\frac{{\alpha }_3(1+m{\beta }_1)\sigma {\beta }_1}{(1+m{\beta }_1)(\mu +\delta {\beta }_1)-\rho {\beta }_1},\hfill \\ \hfill {\lambda }_3& =& -2(\delta -m\mu +2\rho )-\frac{\mu }{{\beta }_1}.\hfill \end{array}$$

By using $0<{\beta }_1<<0.1$, it is possible to deduce that there is one positive eigenvalue ${\lambda }_2$ as well as two negative eigenvalues, ${\lambda }_1\mathrm{and}{\lambda }_3.$ This shows that the coexisting stage, $p_1$ is semi-stable.  □

There is a type of correspondence between the mathematical and physiological meaning, which is indicated as the following: although the abnormal cells are considered as an emergent case of cancer, the success of these cells at coexisting with other cells is shown in [36]. Additionally, if any cell of the abnormal cells begins to be active, this indicates that it has been converted into a tumors cell [31]. Thus, the semi-stability of the coexisting point dynamically indicates that the tumor cells began to appear in the tissue as a consequence of abnormal cell activity.

Theorem 4.

Assume that the function $f:\mathrm{\Omega }\to R_{+}^3$ where $\mathrm{\Omega }$ is a domain in $R_{+}^3,$ and the equilibrium point $p_2=(0,T,I)\in \mathrm{\Omega }$ is demonstrated in the resisting stage. If $\eta +\gamma >r$, then all the eigenvalues of the Jacobian matrix at $p_2$ have a positive sign. Hence, the equilibrium point $p_2$ is stable of f.

Proof. 

The Jacobian matrix of NTIUNHDM (1) at $p_2$, is given as

$$J{[N,T,I]}_{p_2}=\left[\begin{array}{ccc}r-\gamma T_1-\eta I_1\hfill & 0\hfill & 0\hfill \\ {\beta }_2{T}_1\hfill & {\alpha }_1-2{\alpha }_1{\alpha }_2{T}_1-{\alpha }_3{I}_1\hfill & -{\alpha }_3\hfill \\ (-\mu +\frac{\rho }{m})I_1\hfill & (-{\mu }_1+\frac{m_1{\rho }_1}{{(1+m_1)}^2})I_1\hfill & -\delta -{\mu }_1{T}_1+\frac{{\rho }_1{T}_1}{T_1+m_1}\hfill \end{array}\right].$$

(11)

Considering a remark in (2), we rewrite the Jacobian matrix (11) at $p_1$, such that $T_1=1$ and $I_1=1$ as follows:

$$J{[N,T,I]}_{p_2}=\left[\begin{array}{ccc}r-\gamma -\eta \hfill & 0\hfill & 0\hfill \\ {\beta }_2\hfill & {\alpha }_1-2{\alpha }_1{\alpha }_2-{\alpha }_3\hfill & -{\alpha }_3\hfill \\ -\mu +\frac{\rho }{m}\hfill & -{\mu }_1+\frac{m_1{\rho }_1}{{(1+m_1)}^2}\hfill & -\delta -{\mu }_1+\frac{{\rho }_1}{1+m_1}\hfill \end{array}\right].$$

(12)

Then, we can compute the characteristic equation of the matrix (12) as follows:

$$(r-\gamma -\eta -\lambda )({\lambda }^2+B\lambda +C)=0,$$

(13)

where

$$\begin{array}{ccc}\hfill B& =& -{\alpha }_1+2{\alpha }_1{\alpha }_2+{\alpha }_3+\delta +{\mu }_1-\frac{{\rho }_1}{1+m_1}>0,\hfill \\ \hfill C& =& \frac{(1+m_1(2{\alpha }_2-1)((1+m_1)(\delta +{\mu }_1)-{\rho }_1){\alpha }_1}{{(1+m_1)}^2}\hfill \\ & +& \delta {\alpha }_3\hfill \\ & >& 0.\hfill \end{array}$$

All of the eigenvalues have a negative sign when $\eta +\gamma >r.$ This shows that there is indeed a stable case during the resisting immune system.  □

The stability of the resisting point indicates that although the immune system eliminates abnormal cells in the initial stage, the immune system is stimulated again as a consequence of the activity of abnormal cells and their progression to tumor cells. In the case of rapid division and growth of tumor cells and a weak immune system, the generation of new immune cells might convert to immune cell cancer [23].

Remark 3.

From the stability cases of the equilibrium points for the NTIUNHDM (1), we can summarize the following remarks:

• The immune system in the NTIUNHDM failed to eliminate or inhibit the abnormal cells.
• The semi-stable state of the coexisting stage indicated a probability of abnormal cells progressing into their tumors counterparts at any stage.
• The appearance of tumors cells stimulated the immune cells to react, but the growth and division of tumor cells was rapid when compared to the number of immune cells generated to inhibit or remove tumor cells. This generation of cells might convert to immune cell cancer [23].
• The parametric solution of the NTIUNHDM and the behavior solutions around the equilibrium points are shown in Figure 2 and Figure 3. There is one stable equilibrium point called the resisting immune system equilibrium point and it is affected by the dynamic behavior of the tumor and immune cells.

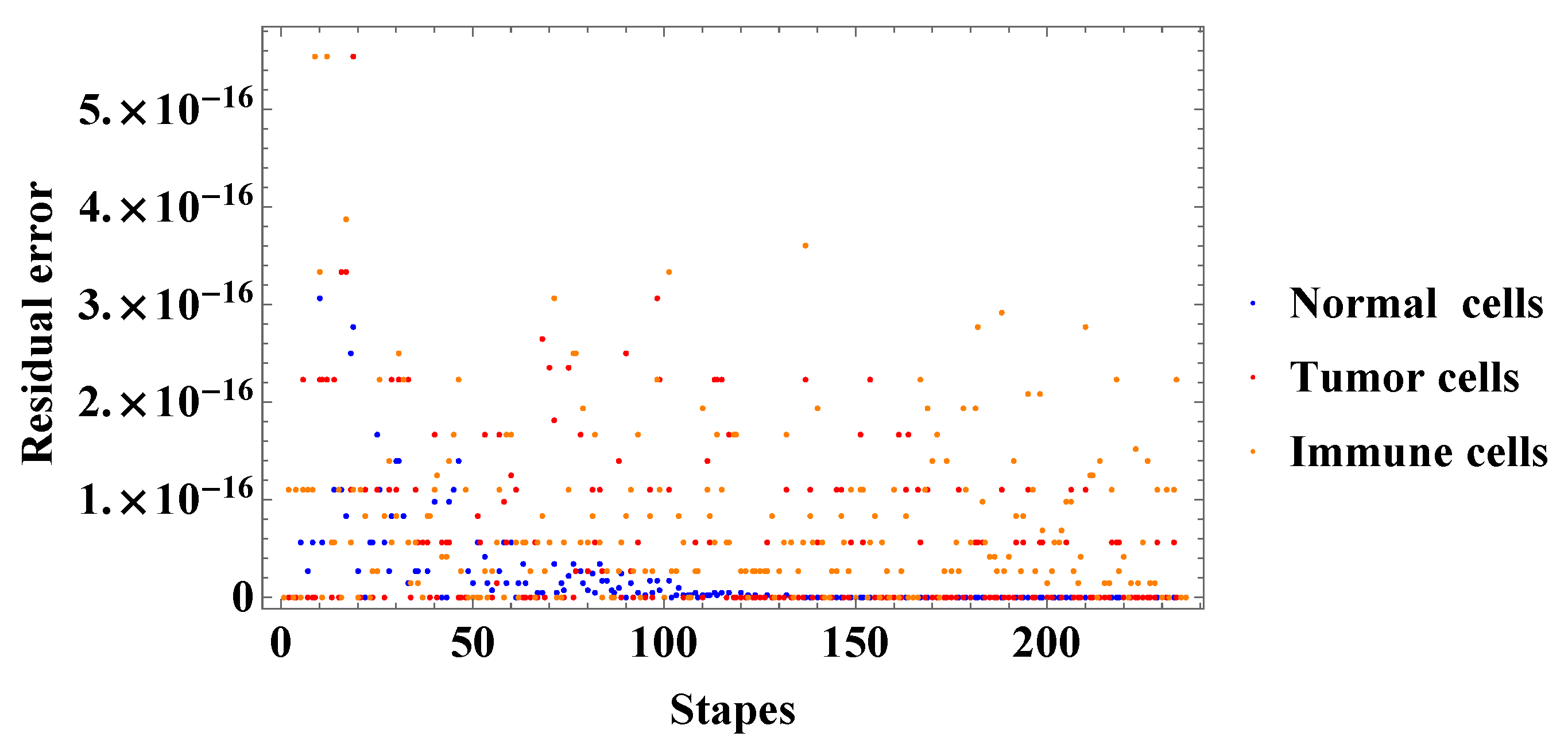
4. Numerical Simulation

The NTIUNHDM was simulated by using Mathematica 11.0 Software and was built by NDSolve commend. A fourth-order Runge–Kutta method was used via NDSolve to obtain a stable and convergent solution for the model simulations. The simulation of NTIUNHDM was carried out by selecting step integration as $0.125$ and thirty days as a time unit. This simulation demonstrated the general dynamic behavior of the immune system when abnormal cells successfully established themselves in the tissue and began to progress as tumor cells. All the parameters in NTIUNHDM were simulated by referring to simulated models in [36,37]. As is illustrated in Figure 4, the residual error values validated the accuracy and reliability of the proposed method. The simulation results of the NTIUNHDM were compared with the numerical simulation of elimination and inhibition of the abnormal cells by the immune system [36] and with the numerical solution of the effect of the estrogen factor on the developing breast cancer cells [23]. Generally, the numerical simulation of the NTIUNHDM showed that the number of tumor cells increased while the number of immune cells and normal cells decreased.

From the simulation of the NTIMUNHDM, it is obvious that when tumor cells began to grow rapidly, the normal cells’ growth retarded. Numerically, the rapid growth of tumor cells is affected by the rate of abnormal cells that progressed into their tumors counterparts, which is indicated by the parameter ${\beta }_2=1.1890,$, while the reduced growth of normal cells is affected by the rate of inhibition or attack from tumor cells, which is indicated by the parameter $\gamma =0.9314.$

Furthermore, there is a suppression of the immune cells as a consequence of the rapid growth of tumor cells at the start. Although the immune system is weak, when thed number of tumor cells reached a peak point, this stimulated the generation of immune cells again. In addition, the behavior of tumor cells is governed by the following condition:

The suppression rate of tumor cells > The suppression rate of immune cells.

If this condition is satisfied, the tumor cells might be delayed by the immune system and other internal factors; otherwise, the tumor cells might have a chance to invade other cells and upgrade progressively.

From the simulation of the NTIMUNHDM, it is obvious that the response of the immune system is affected specifically by the two parameters, ${\rho }_1$ and $m_1$, which are simulated as ${\rho }_1=0.7829$ and $m_1=0.8620.$ However, the behaviors of tumor and immune cells are affected by two parameters, namely the suppression rate of the tumor cells by immune cells, which is denoted by ${\alpha }_3=0.1469$, and the suppression rate of immune cells as a result of being attacked by tumor cells, which is denoted by the parameter ${\mu }_1=0.3634$. The results of the numerical simulation indicated that the weakening of the immune system encourages the abnormal cells to progress into their tumors counterparts and provides the tumor cells a chance to invade other cells and upgrade progressively. The dynamic behavior of the normal cells, tumor cells and immune cells is shown by Figure 5.

5. Conclusions

Mathematical and computer science have worked interactively to understand biological processes better. In this paper, the NTIUNHDM was established to give a dynamical, analytical, and numerical examination of the impact of a weak immune system on developing cancer. There was an evident linkage between the mathematical and biological mechanisms. From the analytical results, we can deduce that the instability of the response to the abnormal cells allowed abnormal cells to develop in the tissue. This triggered cancers since there was a case of semi-stability in the coexistence stage, meaning that it was possible to formulate tumor cells at any time. This indicates that the cells fail to survive together as shown in [31,36].

Additionally, both abnormal and tumor cells were seen to stimulate the immune system in order to generate new cells, but there was a risk of recognising tumor cells as foreign, which explains why they were not attacked directly. The simulation of the NTIMUNHDM indicated that the new immune cell generation delayed the resistance of the immune system when the abnormal cells began manifesting in the tissue. After a matter of days, there was a weak resistance from a slight increase in the immune cells.

To sum up, the NTIUNHDM generally demonstrated a dynamic behavior of the immune system when abnormal cells succeeded in establishing themselves in the tissue and began to progress as tumor cells. It was evident that there is a linkage between the mathematical mechanisms of the NTIUNHDM and the biological mechanisms of the progressive stages of cancer. We recommend conducting more experimental studies to clinically investigate the results of this paper and contribute to the consideration of real cases in order to confirm the results of our mathematical model and to show more precise results. In future studies, we will develop this model by studying the effects of the factors are correlated with an increase in the risk of cancer, such as the effects of diet and the dynamics of other diseases.