The Reduced-Order Extrapolating Method about the Crank-Nicolson Finite Element Solution Coefficient Vectors for Parabolic Type Equation
Abstract
1. Introduction
2. The CNFE Method for the Parabolic Type PDE
3. The ROECNFE Method for the Parabolic Type PDE
3.1. Generation of POD Bases
3.2. Formulation of Matrix-Form ROECNFE Model
3.3. The Stability and Error Estimates to the ROECNFE Solutions
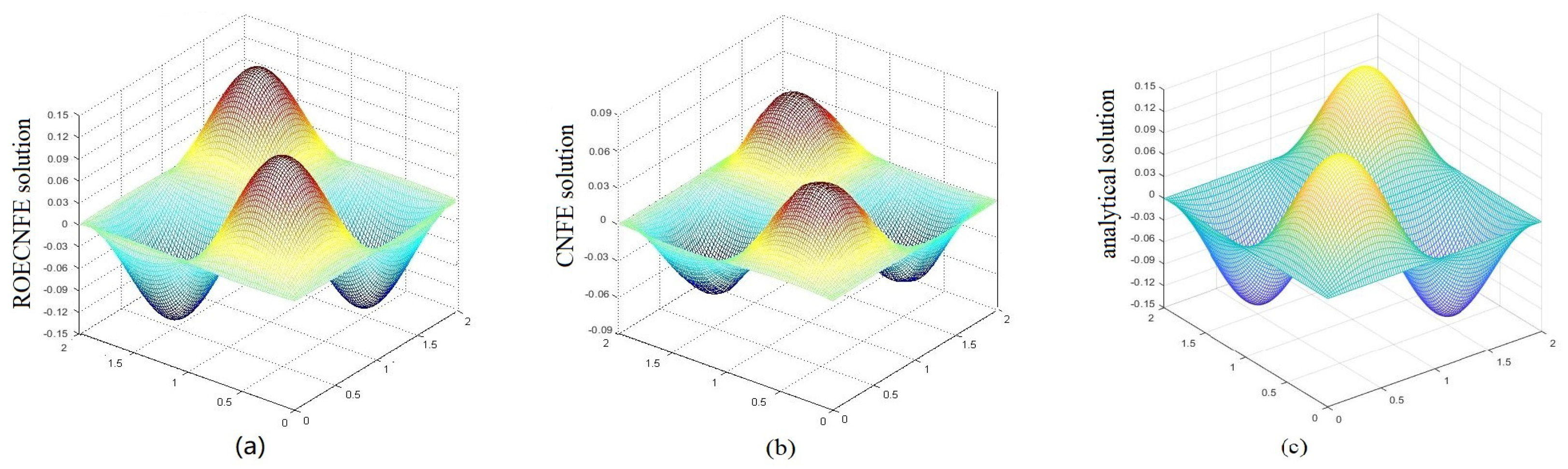
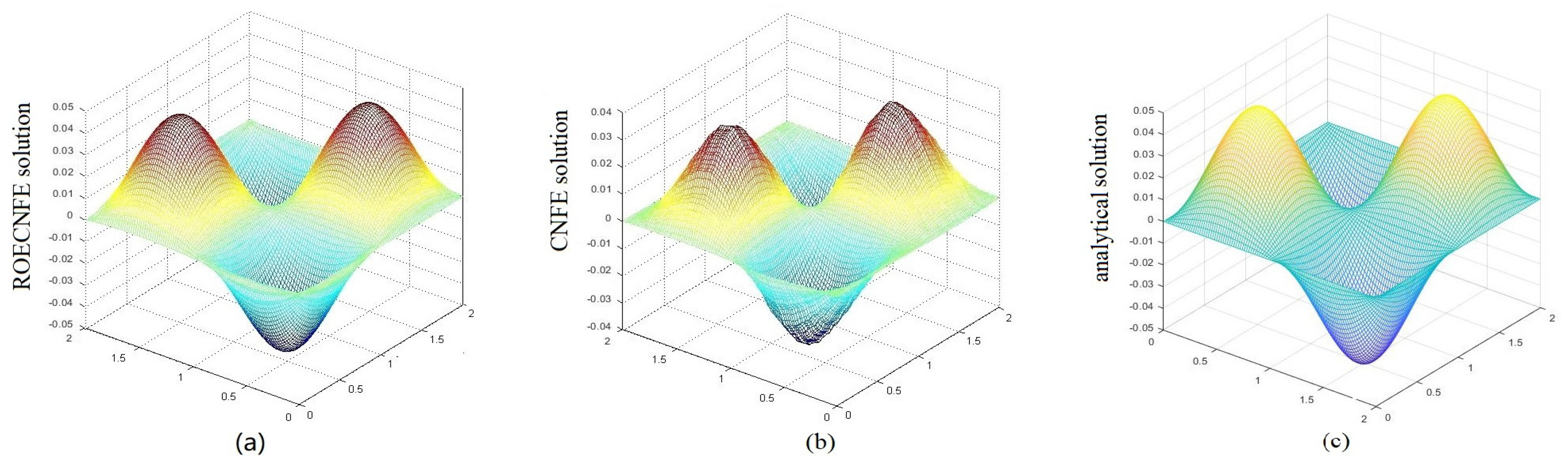
4. Some Numerical Tests
5. Conclusions and Discussions
Funding
Conflicts of Interest
References
- Turner, M.J.; Clough, R.W.; Martin, H.C.; Topp, L.J. Stiffness and deflection analysis of complex structures. J. Aeronaut. Sci. 1956, 23, 805–823. [Google Scholar] [CrossRef]
- Alekseev, A.K.; Bistrian, D.A.; Bondarev, A.E.; Navon, I.M. On linear and nonlinear aspects of dynamic mode decomposition. Int. J. Numer. Meth. Fluids 2016, 82, 348–371. [Google Scholar] [CrossRef]
- Dua, J.; Navon, I.M.; Zhu, J.; Fang, F.; Alekseev, A.K. Reduced order modeling based on POD of a parabolized Navier-Stokes equations model II: Trust region POD 4D VAR data assimilation. Comput. Math. Appl. 2013, 65, 380–394. [Google Scholar] [CrossRef]
- Ghaffari, R.; Ghoreishi, F. Reduced spline method based on a proper orthogonal decomposition technique for fractional sub-diffusion equations. Appl. Numer. Math. 2019, 137, 62–79. [Google Scholar] [CrossRef]
- Hinze, M.; Kunkel, M. Residual based sampling in POD model order reduction of drift-diffusion equations in parametrized electrical networks. J. Appl. Math. Mech. 2012, 92, 91–104. [Google Scholar] [CrossRef]
- Luo, Z.D.; Chen, G. Proper Orthogonal Decomposition Methods for Partial Differential Equations; Academic Press of Elsevier: San Diego, CA, USA, 2018. [Google Scholar]
- Pearson, K. On lines and planes of closest fit to systems of points in space. Philos. Mag. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the dynamics of coherent structures: Part I-III. Quart. Appl. Math. 1987, 45, 561–590. [Google Scholar] [CrossRef]
- Aubry, N.; Holmes, P.; Lumley, J.L.; Stone, E. The dynamics of coherent structures in the wall region of a turbulent boundary layer. J. Fluid Dyn. 1988, 192, 115–173. [Google Scholar] [CrossRef]
- Moin, P.; Moser, R.D. Characteristic-eddy decomposition of turbulence in channel. J. Fluid Mech. 1989, 200, 417–509. [Google Scholar] [CrossRef]
- Kunisch, K.; Volkwein, S. Galerkin proper orthogonal decomposition methods for parabolic problems. Numer. Math. 2001, 90, 117–148. [Google Scholar] [CrossRef]
- Luo, Z.D. An optimized FD extrapolated scheme based on POD for the 2D integro-differential equation of parabolic type. J. Integral Equ. Appl. 2020, 32, 35–50. [Google Scholar] [CrossRef]
- Luo, Z.D.; Ren, H.L. A reduced-order extrapolated finite difference iterative method for the Riemann-Liouville tempered fractional derivative equation. Appl. Numer. Math. 2020, 157, 307–314. [Google Scholar] [CrossRef]
- Luo, Z.D.; Wang, H. A highly efficient reduced-order extrapolated finite difference algorithm for time-space tempered fractional diffusion-wave equation. Appl. Math. Lett. 2020, 102, 106090. [Google Scholar] [CrossRef]
- Luo, Z.D.; Jiang, W.R. A reduced-order extrapolated finite spectral element method for the 2D non-stationary Navier-Stokes equations about vorticity-stream functions. Appl. Numer. Math. 2020, 147, 161–173. [Google Scholar] [CrossRef]
- Teng, F.; Luo, Z.D. A reduced-order extrapolation technique for solution coefficient vectors in the mixed finite element method for the 2D nonlinear Rosenau equation. J. Math. Anal. Appl. 2020, 485, 123761. [Google Scholar] [CrossRef]
- Yang, J.; Luo, Z.D. A reduced-order extrapolating space-time continuous finite element model based on POD for the 2D Sobolev equation. Numer. Methods Partial Differ. Equ. 2020. [Google Scholar] [CrossRef]
- Luo, Z.D.; Teng, F.; Chen, J. A POD-based reduced-order Crank-Nicolson finite volume element extrapolating algorithm for 2D Sobolev equations. Math. Comput. Simul. 2018, 146, 118–133. [Google Scholar] [CrossRef]
- Luo, Z.D.; Xie, Z.H.; Shang, Y.Q.; Chen, J. A reduced finite volume element formulation and numerical simulations based on POD for parabolic problems. J. Comput. Appl. Math. 2011, 235, 2098–2111. [Google Scholar] [CrossRef]
- Jin, S.J.; Luo, Z.D. A reduced-order extrapolating collocation spectral method based on POD for the 2D Sobolev equations. Bound. Value Prob. 2019, 63, 1–19. [Google Scholar] [CrossRef]
- Luo, Z.D.; Jin, S.J. A reduced-order extrapolated Crank-Nicolson collocation spectral method based on POD for the 2D viscoelastic wave equations. Numer. Methods Partial Differ. Equ. 2020, 36, 49–65. [Google Scholar] [CrossRef]
- Teng, F.; Luo, Z.D.; Yang, J. A reduced order extrapolated natural boundary element method based on POD for the 2D hyperbolic equation in unbounded domain. Math. Methods Appl. Sci. 2019, 42, 4273–4291. [Google Scholar] [CrossRef]
- Teng, F.; Luo, Z.D.; Yang, J. A reduced order extrapolated NBE format based on POD for the 2D parabolic equation in unbounded domain. Comput. Appl. Math. 2019, 38, 1–21. [Google Scholar] [CrossRef]
- Benner, P.; Cohen, A.; Ohlberger, M.; Willcox, A.K. Model Rduction and Approximation: Theory and Algorithm; Computational Science & Engineering; SIAM: Philadelphia, PA, USA, 2017. [Google Scholar]
- Quarteroni, A.; Manzoni, A.; Negri, F. Reduced Basis Methods for Partial Differential Equations; Springer International Publishing: Berlin, Germany, 2016. [Google Scholar]
- Kunisch, K.; Volkwein, S. Galerkin proper orthogonal decomposition methods for a general equation in fluid dynamics. SIAM J. Numer. Anal. 2002, 40, 492–515. [Google Scholar] [CrossRef]
- Li, K.; Huang, T.Z.; Li, L.; Lanteri, S. POD-based model order reduction with an adaptive snapshot selection for a discontinuous Galerkin approximation of the time-domain Maxwell’s equations. J. Comput. Phys. 2019, 396, 106–128. [Google Scholar] [CrossRef]
- Thomée, V. Galerkin Finite Element Methods for Parabolic Problems; Springer: Berlin, Germany, 2006. [Google Scholar]
- Luo, Z.D.; Li, H.; Shang, Y.Q.; Fang, Z.C. A reduced-order LSMFE formulation based on POD method and implementation of algorithm for parabolic equations. Finite Elem. Anal. Des. 2012, 60, 1–12. [Google Scholar] [CrossRef]
- Luo, Z.D.; Li, H.; Sun, P. A reduced-order Crank-Nicolson finite volume element formulation based on POD method for parabolic equations. Appl. Math. Comput. 2013, 219, 5887–5900. [Google Scholar] [CrossRef]
- Luo, Z.D.; Li, L.; Sun, P. A reduced-order MFE formulation based on POD method for parabolic equations. Acta Math. Sci. 2013, 33B, 1471–1484. [Google Scholar] [CrossRef]
- Luo, Z.D.; Chen, J.; Sun, P.; Yang, X. Finite element formulation based on proper orthogonal decomposition for parabolic equations. Sci. China Math. 2009, 52, 587–596. [Google Scholar] [CrossRef]
- Luo, Z.D.; Chen, J.; Xie, Z.H.; An, J.; Sun, P. A reduced second-order time accurate finite element formulation based on POD for parabolic equations (in Chinese). Sci. Sin. Math. 2011, 41, 447–460. [Google Scholar]
- Luo, Z.D. The Foundations and Applications of Mixed Finite Element Methods; Chinese Science Press: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Zhang, G.; Lin, Y. Notes on Functional Analysis; Peking University Press: Beijing, China, 1987. (In Chinese) [Google Scholar]
- Luo, Z.D.; Teng, F.; Xia, H. A reduced-order extrapolated Crank-Nicolson finite spectral element method based on POD for the 2D non-stationary Boussinesq equations. J. Math. Anal. Appl. 2019, 71, 564–583. [Google Scholar] [CrossRef]
- Yang, J.; Luo, Z.D. Proper orthogonal decomposition reduced-order extrapolation continuous space-time finite element method for the two-dimensional unsteady Stokes equation. J. Math. Anal. Appl. 2019, 475, 123–138. [Google Scholar] [CrossRef]
- Zhang, W.S. Finite Difference Methods for Partial Differential Equations in Science Computation; Higher Education Press: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Li, H.R.; Song, Z.Y. A reduced-order energy-stability-preserving finite difference iterative scheme based on POD for the Allen-Cahn equation. J. Math. Anal. Appl. 2020, 491, 124245. [Google Scholar] [CrossRef]

| CNFE Model | ROECNFE Matrix-Model | |||||
|---|---|---|---|---|---|---|
| t | n | CPU Run Time | CPU Run Time | |||
| 250 | 1.010356 × | 43.568 s | 4.050523 × | 1.623 s | ||
| 500 | 2.012083 × | 86.865 s | 4.350732 × | 2.265 s | ||
| 750 | 3.125338 × | 129.914 s | 4.671732 × | 2.873 s | ||
| 1000 | 1.015376 × | 172.931 s | 4.952762 × | 3.492 s | ||
| 1250 | 1.414376 × | 215.982 s | 5.251718 × | 4.013 s | ||
| 1500 | 2.534283 × | 259.173 s | 5.552123 × | 4.621 s | ||
| 1750 | 3.241232 × | 302.842 s | 5.856431 × | 5.276 s | ||
| 2000 | 2.562183 × | 345.874 s | 6.172762 × | 5.813 s | ||
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Z. The Reduced-Order Extrapolating Method about the Crank-Nicolson Finite Element Solution Coefficient Vectors for Parabolic Type Equation. Mathematics 2020, 8, 1261. https://doi.org/10.3390/math8081261
Luo Z. The Reduced-Order Extrapolating Method about the Crank-Nicolson Finite Element Solution Coefficient Vectors for Parabolic Type Equation. Mathematics. 2020; 8(8):1261. https://doi.org/10.3390/math8081261
Chicago/Turabian StyleLuo, Zhendong. 2020. "The Reduced-Order Extrapolating Method about the Crank-Nicolson Finite Element Solution Coefficient Vectors for Parabolic Type Equation" Mathematics 8, no. 8: 1261. https://doi.org/10.3390/math8081261
APA StyleLuo, Z. (2020). The Reduced-Order Extrapolating Method about the Crank-Nicolson Finite Element Solution Coefficient Vectors for Parabolic Type Equation. Mathematics, 8(8), 1261. https://doi.org/10.3390/math8081261





