A Partial Allocation Local Search Matheuristic for Solving the School Bus Routing Problem with Bus Stop Selection

Abstract

This paper addresses the school bus routing problem with bus stop selection, which jointly handles the problems of determining the set of bus stops to visit, allocating each student to one of these bus stops and computing the routes that visit the selected bus stops, so that the total routing cost is minimized and the walking distance of the students is limited by a given value. A fast and efficient matheuristic is developed based on an innovative approach that first partially allocates the students to a set of active stops that they can reach, and computes a set of routes that minimizes the routing cost. Then, a refining process is performed to complete the allocation and to adapt the routes until a feasible solution is obtained. The algorithm is tested on a set of benchmark instances. The computational results show the efficiency of the algorithm in terms of the quality of the solutions yielded and the computing time.

1. Introduction

The school bus routing problem (SBRP) basically consists of designing a set of routes for transporting students to schools. Park and Kim [1] provide a review of studies published up until 2009. They emphasize three issues that are relevant to this problem: Are the bus stops fixed a priori or not? Is there a single objective or are there multiple objectives? Which constraints are taken into account? As pointed out by Park and Kim, most studies assume that the bus stop locations as well as the number of students at each stop are given and concentrate on designing the bus routes, aiming to minimize the number of buses used, the total bus travel distance or time, or the total cost. These problems are variants of the well-known Capacitated Vehicle Routing Problem (CVRP). Ellegood et al. [2] update the literature review and show that nowadays this problem still attracts the attention of many researchers. Moreover, these authors identify a shift in the SBRP characteristics being examined towards more real-world problem settings, as well as an increase in the use of metaheuristic solution approaches.

Just to mention a few recent papers on this topic, Bögl et al. [3] deal with the SBRP with transfers, i.e., the possibility that students may change buses. In addition to the bus stop selection and bus routing problems, they consider the bus scheduling problem that concerns the computation of a feasible schedule for the buses and the school start time adjustment problem, which aims to optimize the school start times to allow buses to service multiple schools. These authors propose a heuristic based on a destroy and repair optimization approach. The case of mixed loads, where the buses are allowed to carry students from more than one school at the same time, is dealt with by Ellegood et al. [4], who provide a general analysis to assess the conditions under which mixed loading is likely to be beneficial. Souza Lima et al. [5,6], deal with a multiobjective capacitated rural school bus routing problem with heterogeneous fleet and mixed loads. Miranda et al. [7] expand the concept of mixed-load to multi-load, which means that the students can be picked up and delivered simultaneously. Taking into account that the use of private cars depends on how well public transportation systems operate, Parvasi et al. [8] formulate a bilevel mathematical model, which considers the possibility of estimating the number of students who choose the public transport system. Mokhtari and Ghezavati [9] also consider a mixed load school bus routing problem and propose a hybrid multiobjective ant colony optimization algorithm to solve it, which involves two objectives: minimizing the number of the buses and minimizing the average riding time of the students. Lewis and Smith-Miles [10] propose a heuristic algorithm to find cost-effective solutions to real-world problems, which allow for splitting and merging routes, gauging vehicle dwell times, selecting bus stops, and minimizing walking distances. Caceres et al. [11] propose a greedy heuristic coupled with a column generation approach for solving the problem arising when students with special needs are involved. This problem includes the need to pick up special education students from their home, the need to configure buses appropriately for them, and the need to provide a higher level of service. A variant of the SBRP, arising when students are allowed to choose their preferred stop among the selected ones, has recently been introduced by Calvete et al. [12], who propose a bilevel optimization model and a metaheuristic for the solution of the considered problem. On the other hand, metaheuristic algorithms are widely used in routing problems. Toth and Vigo [13], Elshaer and Awad [14] and Vidal et al. [15] provide recent and complete reviews on the variants of the Vehicle Routing Problems and the use of metaheuristic algorithms for solving them.

This paper addresses the School Bus Routing Problem with bus Stop Selection and a Maximum walking Distance constraint (SBRP-SS-MD) as defined by Schittekat et al. [16] and usually associated with urban areas. This problem deals simultaneously with selecting the bus stops among a set of potential locations, allocating the students to the bus stops and designing the bus routes, while minimizing the total distance traveled by all the buses and taking into account that there is an upper bound on the distance that the students can walk to reach their assigned bus stop. Since the earliest studies on the problem were published, the authors who have studied the SBRP-SS-MD have focused on the three sub-problems involved—location, allocation and routing—and how they are handled to construct a feasible solution. Needless to say, all the three sub-problems are highly interconnected. Taking a solution from one of these sub-problems, even if it is optimal, as the basis from which to build an overall solution of the problem can result in a solution far from the optimal one.

We now review the main papers on the SBRP-SS-MD. A location-allocation-routing approach is taken by Dulac et al. [17] who propose a two-stage approach. In the first stage, the bus stops are selected and the students are assigned to these selected stops. In the second stage, the routes are generated. The constraints are that the bus capacities cannot be exceeded, there are upper bounds on the number of stops and the length of each route, and there is an upper bound on the total distance that a student can walk.

Chapleau et al. [18] change the focus and propose to take advantage of the interaction between the selection of the bus stops and the construction of the routes by determining a minimum number of clusters, each including a number of students close to the route capacity. Then, for each cluster the bus stops are selected and a route is generated. This allocation-routing-location strategy is also followed by Bowerman et al. [19] who consider a multiobjective approach to the problem of providing school bus transportation in urban areas. The optimization criteria are the number of routes, the total bus route length, the load balancing, the length balancing and the student walking distance. The last criterion balances the total distance the students walk from home to and from their bus stops against the route length. They propose a heuristic method for solving the problem in which the students are first partitioned into clusters so that each cluster can be serviced by a single bus route. Then, for each cluster, the bus stops are selected and a bus route that visits the selected stops is generated. The goal of minimizing the number of routes is the dominant objective. The other objectives are combined into a single overall objective using the weighting method.

Riera-Ledesma and Salazar-González [20] propose to combine the bus stop selection and the bus route generation. They focus on a family of school bus routing problems, which look simultaneously for a set of bus stops, for assigning students to them and for designing bus routes visiting such stops. They approach the problem by introducing a generalization of the CVRP called the multiple vehicle traveling purchaser problem. In this problem there is a set of users going to a common destination and a set of potential bus stops, each one reachable by a subset of users. A fleet of homogeneous vehicles is available at a central depot. Each connection between each pair of bus stops has an asymmetric cost. A nonnegative cost is also associated with each potential assignment of a user to a bus stop. This cost is related to the distance walked by a user from his/her home to a bus stop. They also consider a fixed cost for using each vehicle. The aim of the problem is to assign each user to a potential bus stop and to find least cost routes in such a way that each bus stop with assigned users is served by a route. The total number of users assigned to the stops on a route cannot exceed the capacity of the vehicle. The total length of all the routes plus the total assignment cost must be minimized. The authors propose a branch-and-cut approach to solve the problem. Riera-Ledesma and Salazar-González [21] work on the same problem, but including additional ‘resource’ constraints. These ‘resources’ refer to constraints involving the quality of the service: bounds on the length of the bus route from the bus stop at which the first student is collected, bounds on the maximum time a student remains on the bus, and bounds on the number of stops visited by the bus. They propose several formulations of the problem and a branch-and-cut-and-price algorithm.

Schittekat et al. [16] emphasize that, “when a student can be assigned to multiple stops along the same route, the allocation of this student to a particular stop is arbitrary. This is not the case if a student can be assigned to multiple stops in different routes. All students that can be assigned to multiple routes need to be distributed over those routes in such a way that the capacity of the buses is not exceeded. Compared to traditional CVRPs, the possibility to assign students to different stops offers the possibility to incur potential savings; at the same time, it introduces an extra decision level that makes the problem much more difficult to solve”. They propose a location-routing-allocation approach and develop a GRASP+VND matheuristic that integrates the bus stop selection and the bus route construction sub-problems. Once the bus stops have been selected and the routes have been fixed, the problem of allocating students to the bus stops in such a way that the capacity of the buses is not exceeded is solved by an exact method. Kinable et al. [22] propose an exact branch-and-price algorithm for the same problem.

From the previous literature review, we notice that two factors are relevant when studying the SBRP-SS-MD: (i) the settings of the problem and (ii) the approach to deal with the three sub-problems. Regarding the settings of the problem, we conclude that there are two issues that are of interest: the routing cost for the company owning the buses, and the walking distance for the students. This has been studied as a single-objective problem, either by combining the routing cost and the walking distance in the objective function [20,21] or by treating the walking distance as a constraint [16,22] and minimizing only the routing cost. As mentioned above, in this paper we assume the formulation of the SBRP-SS-MD proposed in [16], i.e., a single-objective problem that minimizes the total distance traveled by all the buses, while the distance that students can walk is constrained. Concerning the way of handling the above mentioned three sub-problems, the contribution of this paper is to develop an innovative matheuristic that follows a location-partial-allocation-routing approach. After selecting a subset of bus stops from which we are able to get a feasible solution, in order to compute it the procedure partially allocates the students to the selected bus stops and constructs the routes for serving these students. Then, if possible, the remaining students are allocated to the current routes. Otherwise, the number of students in the initial allocation is increased. This process is done in a smart way, so that the routing cost is kept low and diversified feasible solutions are found. Another important feature of the matheuristic proposed in this paper is the absence of parameters that need to be tuned. As stated in [16] “a good metaheuristic should generate high-quality solutions in little time without the need for excessive parameter tuning”. Finally, it is worth pointing out two main differences between the algorithm discussed in [16] and the matheuristic developed in this paper. First, in the construction phase, we propose to integrate the allocation of the students and the route construction, while in [16] the integrated sub-problems are the bus stop selection and the route generation. Second, our procedure includes the solution of four purpose-built Mixed Integer Linear Programming (MILP) problems for selecting the bus stops, together with a more general random selection, which contributes to diversifying the considered solutions. The performance of the matheuristic is tested on the 112 benchmark instances dealt with in the literature [16,22], obtaining good results in terms of both the quality of the solution provided and the computational time.

The paper is organized as follows. After the Introduction Section, the SBRP-SS-MD and the Integer Linear Programming (ILP) model are described in Section 2. The matheuristic is developed in Section 3. In Section 4 the computational performance of the proposed algorithm is evaluated. Finally, Section 5 concludes the paper with some final remarks.

2. Definition and ILP Model of the SBRP-SS-MD

We assume we have a single school, a set of identical buses located at a depot, each with a fixed capacity Q, a set of available bus stops, and a set of students to be transported to the school. Each bus may operate at most one route, and there are as many buses as needed. Moreover, the students can only be allocated to bus stops within a predetermined walking distance. The SBRP-SS-MD consists of selecting a subset of bus stops to be visited, determining for each student which bus stop he/she should walk to, and designing a set of bus routes through the visited bus stops, so that the total cost of the bus routes is minimized.

Let $G=(V,A)$ be a directed graph, where V is the node set and A is the arc set. The node set is defined as $V=\left\{0\right\}\cup U\cup W$, where node 0 is the depot, U is the set of student locations and W is the set of available bus stops. The set of arcs is defined as $A=A_1\cup A_2$, where $A_1=\{(i,j):i,j\in \left\{0\right\}\cup W,i\ne j\}$ and $A_2=\{(k,i):k\in U,i\in W\}$. Arcs in $A_1$ refer to links which are used to construct the routes. Arcs in $A_2$ are used to allocate students to bus stops. We assume that there are no loop arcs.

Each route starts from node 0, visits a subset of bus stops (nodes of W) and finishes visiting node 0. Bus stops do not need to be visited by a route, but if they are, they can be visited by a single route, i.e., the routes are node-disjoint (except for node 0). Every student is allocated to a visited bus stop which he/she can reach by walking, in such a way that the total number of students allocated to the bus stops visited by a bus route is limited by the capacity of the bus. As mentioned above, this problem is not a classical CVRP since the bus stops that are visited and how many students are allocated to each of them are not known a priori.

We assume that there is a nonnegative routing cost $c_{ij}$ associated with each arc $(i,j)\in A_1$, representing the cost of traveling from node i to node j. The cost $c_{0i}$, $i\in W$, includes the routing cost from the depot to the bus stop i, and the fixed cost of using a bus. The cost $c_{i0}$, $i\in W$, includes the routing cost from the bus stop i to the depot passing by the school. We assume that these costs satisfy the triangle inequality, i.e., $c_{it}+c_{tj}⩾c_{ij}$ for all $i,t,j\in \left\{0\right\}\cup W$. There is also a nonnegative allocation cost $d_{ki}$ associated with each arc $(k,i)\in A_2$, which refers to the distance walked by the student located at node k to reach bus stop i. Let D be the maximum walking distance. Taking into account that each student needs to be allocated to a bus stop he/she can reach, we redefine $A_2=\{(k,i):k\in U,i\in W,d_{ki}⩽D\}$.

In order to formulate the SBRP-SS-MD as an ILP model, we define the binary decision variables:

$$\begin{array}{ccc}\mathrm{For}(i,j)\in A_1,\hfill & x_{ij}\hfill & =\left\{\begin{array}{cc}\hfill 1,& \mathrm{if} \mathrm{arc} (i,j) \mathrm{is} \mathrm{in} \mathrm{a} \mathrm{route}\hfill \\ \hfill 0,& \mathrm{otherwise}\hfill \end{array}\right.\hfill \\ \mathrm{For}(k,i)\in A_2,\hfill & y_{ki}\hfill & =\left\{\begin{array}{cc}\hfill 1,& \mathrm{if} \mathrm{student} k \mathrm{is} \mathrm{allocated} \mathrm{to} \mathrm{bus} \mathrm{stop} i\hfill \\ \hfill 0,& \mathrm{otherwise}\hfill \end{array}\right.\hfill \\ \mathrm{For}i\in W,\hfill & z_i\hfill & =\left\{\begin{array}{cc}\hfill 1,& \mathrm{if} \mathrm{bus} \mathrm{stop} i \mathrm{is} \mathrm{selected} \mathrm{to} \mathrm{be} \mathrm{visited}\hfill \\ \hfill 0,& \mathrm{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

For simplicity, when there is no room for confusion, we denote $\{x_{ij},(i,j)\in A_1;y_{ki},(k,i)\in A_2;z_i,i\in W\}$ by $\{x,y,z\}$. Then, the SBRP-SS-MD can be formulated as follows:

$$\begin{array}{c}\underset{x,y,z}{min}\sum _{(i,j)\in A_1}{c}_{ij}{x}_{ij}\hfill \\ \mathrm{s}.\mathrm{t}.\hfill \end{array}$$

(1)

$$\begin{array}{c}\sum _{i\in W}{x}_{0i}=\sum _{i\in W}{x}_{i0}\hfill \end{array}$$

(2)

$$\begin{array}{c}\sum _{(i,j)\in A_1}{x}_{ij}=z_i,i\in W\hfill \end{array}$$

(3)

$$\begin{array}{c}\sum _{(j,i)\in A_1}{x}_{ji}=z_i,i\in W\hfill \end{array}$$

(4)

$$\begin{array}{c}\sum _{i\in W:(k,i)\in A_2}{y}_{ki}=1,k\in U\hfill \end{array}$$

(5)

$$\begin{array}{c}\sum _{k\in U:(k,i)\in A_2}{y}_{ki}⩽Q{z}_i,i\in W\hfill \end{array}$$

(6)

$$\begin{array}{c}\sum _{k\in U,i\in S:(k,i)\in A_2}{y}_{ki}⩽Q\sum _{i\in S}\sum _{j\in S^{\prime }}{x}_{ij},S\subseteq W,S\ne \varnothing ,S^{\prime }=(\left\{0\right\}\cup W)\setminus S\hfill \end{array}$$

(7)

$$\begin{array}{c}{x}_{ij}\in \{0,1\},(i,j)\in A_1\hfill \end{array}$$

(8)

$$\begin{array}{c}{y}_{ki}\in \{0,1\},(k,i)\in A_2\hfill \end{array}$$

(9)

$$\begin{array}{c}{z}_i\in \{0,1\},i\in W\hfill \end{array}$$

(10)

The objective function (1) minimizes the routing cost. Constraint (2) enforces that as many buses leave the depot (node 0) as enter the depot. Constraints (3) and (4) ensure that exactly one arc enters and leaves a bus stop if and only if the bus stop is selected. Constraints (5) and (6) guarantee that every student is allocated to a single bus stop, which must be selected to be visited. Constraints (7) impose the connectivity of the solution and the bus capacity requirement. Constraints (8)–(10) guarantee that all variables are binary. In this formulation, the constraints have been adapted from the two-index vehicle flow formulation of the CVRP proposed in [13]. Notice that, although constraints (7) would allow the existence of isolated cycles not connected to the depot, these cycles would involve only bus stops with no students allocated. As we are looking for solutions minimizing the global routing cost, these cycles cannot belong to an optimal solution because a smaller routing cost is obtained if they are eliminated.

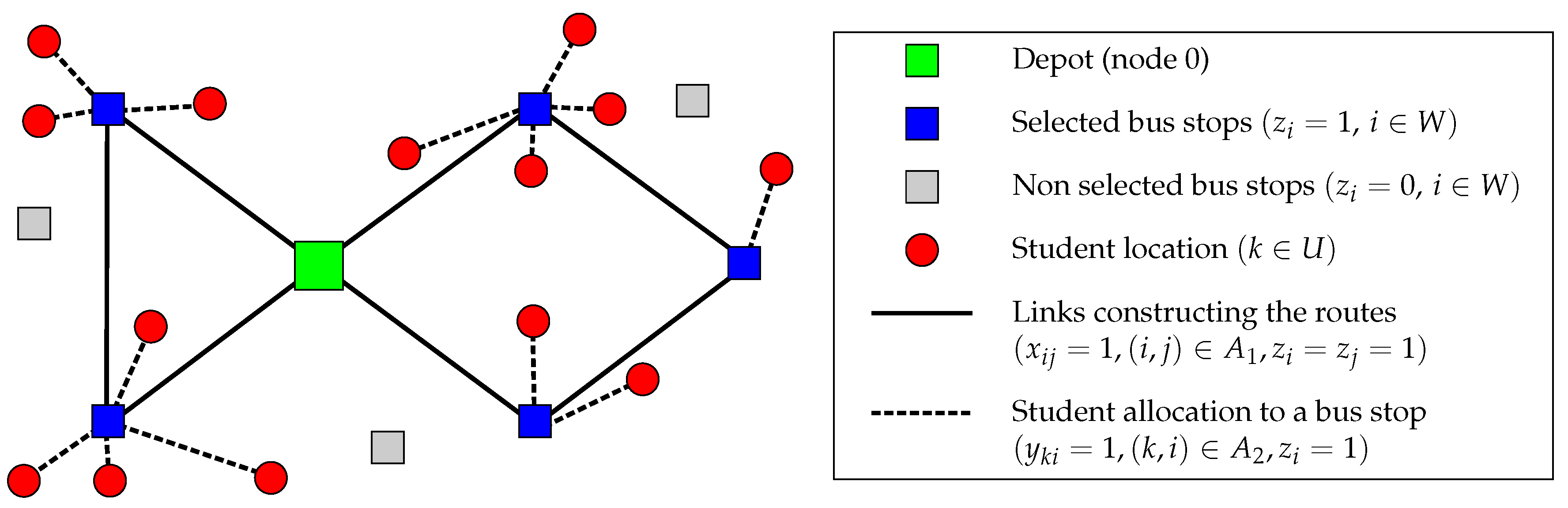
Figure 1 shows a feasible solution of the SBRP-SS-MD. The large green square represents the depot. Small squares represent the bus stops (in blue those which are selected and in grey those which are not selected). Red circles are the student locations. The routes are represented by solid lines. The two routes involve, respectively, two and three bus stops. Three of the five available bus stops are not used. The links allocating students to bus stops are represented by dashed lines. Both routes transport seven students.

3. A Partial Allocation Local Search Algorithm for Solving the SBRP-SS-MD

The matheuristic developed in this paper for solving the SBRP-SS-MD (called PALS hereafter) proceeds by constructing a feasible solution in each iteration while the termination condition is not met. Each iteration consists of three steps:

Step 1: 

The selection of the bus stops that can be visited (active stops) and the computation of a feasible allocation of the students to these active stops.

Step 2: 

The construction of a feasible solution of the SBRP-SS-MD by partially using the allocation determined in Step 1, computing the routes, and finally allocating all the students.

Step 3: 

The application of several local search procedures.

The algorithm also includes an initialization step to obtain some insight into the characteristics of the instance analyzed. We now explain all these steps in detail.

3.1. Initialization Step

First, we determine which bus stops must be always active because they are the only available bus stops for some students due to the maximum walking distance constraint. These are named fixed stops. Every feasible solution of the problem needs to have these bus stops activated. Moreover, those students that can only reach one fixed stop are allocated to it.

Second, we determine a lower bound on the minimum number of routes (MNR) that are needed, $⌈\frac{\left|U\right|}{Q}⌉$, where $\lceil .\rceil$ denotes the ceiling function, i.e., $\lceil a\rceil$ is the least integer greater than or equal to a.

3.2. Step 1: Selection of the Active Stops and Computation of a Feasible Allocation

There are two procedures for selecting the active stops. The first one, which is applied in the first four iterations of algorithm PALS, is based on solving a MILP problem. The purpose is to obtain good feasible solutions of the SBRP-SS-MD. The second procedure selects the active stops randomly, aiming to diversify the feasible solutions constructed by the algorithm.

3.2.1. Solving a MILP Problem for Selecting the Active Stops

This procedure identifies four ad hoc sets of active stops and the corresponding allocations aiming at being able to obtain good feasible solutions of the SBRP-SS-MD. These sets are provided by the optimal solutions of the following MILP problems. In these problems, students are allocated to bus stops, and bus stops to buses, without actually constructing the routes. A similar procedure has been proposed in [12] for the solution of the bilevel version of the SBRP. For the sake of comprehension and because there are some differences with the MILP problems defined in that paper, we briefly explain below the characteristics of the four MILP problems considered.

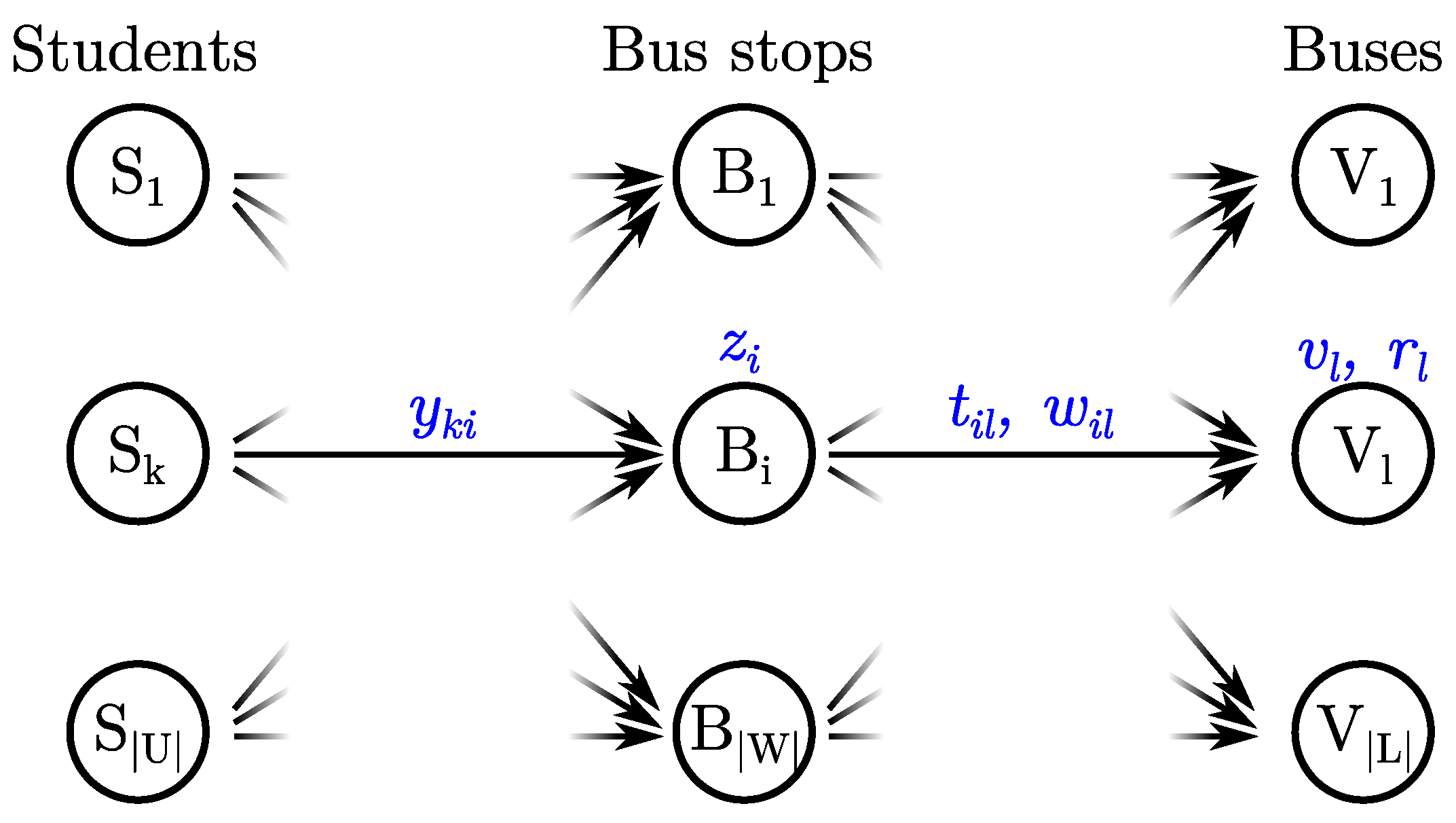
In addition to the variables y and z already introduced, we define the variables:

$$\begin{array}{cc}{v}_l=\hfill & \left\{\begin{array}{cc}1\hfill & \mathrm{if} \mathrm{bus} l \mathrm{is} \mathrm{used}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.l\in L\hfill \\ w_{il}=\hfill & \left\{\begin{array}{cc}1\hfill & \mathrm{if} \mathrm{bus} \mathrm{stop} i \mathrm{is} \mathrm{visited} \mathrm{by} \mathrm{bus} l\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.i\in W,l\in L\hfill \\ t_{il}=\hfill & \multicolumn{3}{c}{\mathrm{number} \mathrm{of} \mathrm{students} \mathrm{allocated} \mathrm{to} \mathrm{bus} \mathrm{stop} i \mathrm{who} \mathrm{are} \mathrm{picked} \mathrm{by} \mathrm{the} \mathrm{bus}}\\ \hfill & l,i\in W,l\in L\hfill \\ r_l=\hfill & \multicolumn{3}{c}{\mathrm{maximum} \mathrm{routing} \mathrm{cost} \mathrm{from} \mathrm{the} \mathrm{bus} \mathrm{stop} \mathrm{visited} \mathrm{by} \mathrm{the} \mathrm{bus} l \mathrm{to} \mathrm{the} \mathrm{depot}}\\ \hfill & \mathrm{and} \mathrm{back},l\in L\hfill \end{array}$$

where L denotes the set of buses. We assume that $\left|L\right|=\left|W\right|$. Figure 2 gives a scheme of the decision variables. The four problems considered are:

• Problem I: Minimize the sum of the maximum routing costs from the bus stops visited by each bus to the depot and back
  Before formulating the problem, we pay attention to the objective function. The idea is to minimize, for each bus, the cost of going from the school to the farthest bus stop in its route and back. This objective function can be written as

  $$\begin{array}{cc}min\hfill & {\displaystyle \sum _{l\in L}}\underset{i\in W}{max}\{(c_{i0}+c_{0i})w_{il}:i\in W\}\hfill \end{array}$$

  (11)
  This is a nonlinear objective function that can be linearized by including in the formulation of the model the variables $r_l$, $l\in L$ as well as the constraints

  $$(c_{i0}+c_{0i})w_{il}⩽r_l,i\in W,l\in L$$
  Then, the objective function is $min{\sum }_{l\in L}{r}_l$. Bearing this in mind, Problem I can be formulated as:

  $$\begin{array}{c}min\sum _{l\in L}{r}_l\hfill \\ \mathrm{s}.\mathrm{t}.\hfill \end{array}$$

  (12)

  $$\begin{array}{c}\sum _{i\in W:(k,i)\in A_2}{y}_{ki}=1,k\in U\hfill \end{array}$$

  (13)

  $$\begin{array}{c}\sum _{l\in L}{w}_{il}=z_i,i\in W\hfill \end{array}$$

  (14)

  $$\begin{array}{c}{z}_i⩽\sum _{k\in U:(k,i)\in A_2}{y}_{ki},i\in W\hfill \end{array}$$

  (15)

  $$\begin{array}{c}{t}_{il}⩽Q{w}_{il},i\in W,l\in L\hfill \end{array}$$

  (16)

  $$\begin{array}{c}\sum _{k\in U:(k,i)\in A_2}{y}_{ki}=\sum _{l\in L}{t}_{il},i\in W\hfill \end{array}$$

  (17)

  $$\begin{array}{c}\sum _{i\in W}{t}_{il}⩽Q{v}_l,l\in L\hfill \end{array}$$

  (18)

  $$\begin{array}{c}{w}_{il}⩽t_{il},i\in W,l\in L\hfill \end{array}$$

  (19)

  $$\begin{array}{c}(c_{i0}+c_{0i})w_{il}⩽r_l,i\in W,l\in L\hfill \end{array}$$

  (20)

  $$\begin{array}{c}{y}_{ki}\in \{0,1\},(k,i)\in A_2\hfill \end{array}$$

  (21)

  $$\begin{array}{c}{w}_{il},z_i,v_l\in \{0,1\},t_{il},r_l⩾0,i\in W,l\in L\hfill \end{array}$$

  (22)
  Constraints (13) ensure that each student is allocated to a single bus stop. Constraints (14) guarantee that each active stop is visited by one bus and no bus visits a bus stop which is non-active. Constraints (15) make sure that those bus stops with no students allocated remain non-active. Constraints (16) ensure that only the bus stops that are visited by a bus can receive students that will be picked up by that bus, and that the bus stops receive at most a number of students equal to the capacity of the bus. Constraints (17) guarantee that the students allocated to a bus stop are picked up by a bus that visits that bus stop. Constraints (18) ensure that only buses that are used can receive students, and that the number of students received by the bus does not exceed the bus capacity. Constraints (19) impose that bus stops which do not receive students for a bus are not visited by that bus. Constraints (20) are included to linearize the objective function (11) as explained above. Finally, constraints (21) and (22) set the characteristics of the variables.
• Problem II: Minimize the total routing cost from the active stops to the depot and back

  $$\begin{array}{cc}min\hfill & {\displaystyle \sum _{i\in W}}(c_{i0}+c_{0i})z_i\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & \left(13\right)–\left(22\right)\hfill \end{array}$$
• Problem III: Lexicographically minimize the sum of the maximum routing costs from the bus stops visited by each bus to the depot and back, and the total routing cost from the active stops to the depot and back

  $$\begin{array}{cc}\mathrm{lex}min\hfill & \left({\displaystyle \sum _{l\in L}}{r}_l,{\displaystyle \sum _{i\in W}}(c_{i0}+c_{0i})z_i\right)\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & \left(13\right)–\left(22\right)\hfill \end{array}$$
• Problem IV: Lexicographically minimize the total routing cost from the active stops to the depot and back, and the sum of the maximum routing costs from the bus stops visited by each bus to the depot and back

  $$\begin{array}{cc}\mathrm{lex}min\hfill & \left({\displaystyle \sum _{i\in W}}(c_{i0}+c_{0i})z_i,{\displaystyle \sum _{l\in L}}{r}_l\right)\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & \left(13\right)–\left(22\right)\hfill \end{array}$$

Lexicographic optimization assumes that the objectives are ranked in order of importance and the objective functions are minimized one at a time in order of priority. Hence, the main criterion is minimized first. Then, the second criterion is minimized subject to achieving the optimum with respect to the first criterion [23].

Thus, in the first iteration, after solving Problem I, algorithm PALS goes to step 2 (described in Section 3.3) with the set of active stops $W_a$ and the feasible allocation FA corresponding to the active stops and the allocation of the students provided by the optimal solution of Problem I. The following three iterations do the same with Problems II to IV.

3.2.2. Selecting the Active Stops Randomly

In this procedure, which is applied from the fifth iteration, in order to select the active stops we look for a covering of the students, i.e., we select the active stops in such a way that each student has at least one bus stop within his/her neighborhood defined by the maximum walking distance D. For this purpose, we activate the fixed stops and randomly select the remaining bus stops which will be activated to have all the students covered. In order to promote the selection of those bus stops that seem to be more promising since they appear frequently in the best solutions, a pool with the best solutions found in the previous iterations is maintained. This pool is initialized in the first iteration with the empty set. Each non-active stop is assigned a weight equal to the number of times that this bus stop appears in the solutions of the pool plus one. Then, a non-active stop is randomly selected, according to probabilities that are proportional to these weights, and activated. Every active stop covers all the students that can reach it. The above process of activating bus stops is repeated until every student is covered by at least one active stop. Figure 3 displays a covering. The radius of each circle is the maximum distance D.

A set of active stops, denoted by $W_a$, is now available and every student can reach at least one active stop. However, since every bus stop can handle at most Q students, which is the capacity of the bus, we need to check if it is possible to allocate every student to an active stop. If this is the case, we have to determine a feasible allocation. Otherwise, it is impossible to construct a feasible solution of the SBRP-SS-MD with the current set of active stops. In this case, we are interested in modifying the current set of active stops to be able to achieve a feasible allocation. For this purpose, for $k\in U$, $i\in W$, we define the binary decision variables

$${\delta }_{ki}=\left\{\begin{array}{cc}\hfill 1,& \mathrm{if} \mathrm{student} k \mathrm{is} \mathrm{allocated} \mathrm{to} \mathrm{bus} \mathrm{stop} i\hfill \\ \hfill 0,& \mathrm{otherwise}\hfill \end{array}\right.$$

and then solve the following ILP problem:

$$\begin{array}{cc}min\hfill & {\displaystyle \sum _{k\in U}}{\displaystyle \sum _{i\in W}}{a}_{ki}{\delta }_{ki}\hfill \\ \mathrm{s}.\mathrm{t}.\hfill \\ \hfill & {\displaystyle \sum _{i\in W}}{\delta }_{ki}=1,\hfill & k\in U\hfill \\ \hfill & {\displaystyle \sum _{k\in U}}{\delta }_{ki}⩽Q,\hfill & i\in W\hfill \\ \hfill & {\delta }_{ki}\in \{0,1\},\hfill & k\in U,i\in W\hfill \end{array}$$

(23)

where the objective function coefficients are defined as:

$$a_{ki}=\left\{\begin{array}{cc}rand(0,1)\hfill & \mathrm{if} i\in W_a \mathrm{and} d_{ki}⩽D\hfill \\ \left|U\right|+rand(0,1)\hfill & \mathrm{if} i\notin W_a \mathrm{and} d_{ki}⩽D\hfill \\ \left|U\right|\times \left|U\right|\hfill & \mathrm{if} d_{ki}>D\hfill \end{array}\right.$$

(24)

and $rand(0,1)$ is a random uniformly distributed number between 0 and 1. Taking into account that the coefficient matrix of problem (23) is unimodular, the integrality constraint on the variables $\delta$ can be relaxed to a nonnegativity constraint, and so problem (23) is a Transportation Problem. Let $Z^{*}$ be the optimal objective function value of problem (23) and let $\{{\delta }_{ki}^{*},k\in U,i\in W\}$ be an optimal solution.

• If $Z^{*}⩽\left|U\right|$, the current set of active stops $W_a$ allows us to allocate every student to an active stop. Let FA be the feasible allocation provided by the optimal solution, i.e., FA = $\{k\in U,i\in W:{\delta }_{ki}^{*}=1\}$. It will be partially used in the following step of the algorithm.
• If $\left|U\right|<Z^{*}<\left|U\right|\times \left|U\right|$ it is not possible to allocate every student to an active stop, but there exists a feasible allocation using non-active stops. Since only active stops can be used, a non-active stop with students allocated is randomly selected and activated, i.e., it is inserted in the set $W_a$. Problem (23) is updated and solved again. This process is repeated until the optimal objective function value of problem (23) is lower than or equal to $\left|U\right|$ and so a feasible allocation is available.
• If $Z^{*}⩾\left|U\right|\times \left|U\right|$, the SBRP-SS-MD is not feasible.

It is worth mentioning that, when the set of active stops $W_a$ provides a feasible allocation FA, in general it is able to provide a lot of feasible allocations. The use of the coefficients (24) allows us to diversify, since different feasible allocations can be obtained for the same set $W_a$ as the algorithm proceeds.

3.3. Step 2: Construction of a Feasible Solution from a Partial Allocation of the Students to the Active Stops

At the beginning of this step the set of active stops $W_a$ is available. These are the only bus stops that will be used in the incumbent solution. The allocation FA, which is also at hand, could be used to solve a CVRP to build the routes. In this case, the algorithm would follow a location-allocation-routing approach. However, we have found that this approach usually leads to solutions that are very costly in terms of the routing cost. Therefore, we propose to use partially the allocation FA, to solve a CVRP for building the routes in accordance with this partial allocation, and then try to allocate all the students using these routes. Since using a very limited partial allocation can result in a non feasible solution, a trade-off is needed between the initial number of students whose allocation is taken from FA and the number of times that we need to repeat this process to construct a feasible solution.

Algorithm 1 provides a pseudocode of the proposed procedure. The main steps are as follows. The students who can only reach one of the active stops are allocated to it. These are the fixed students in the incumbent solution. Let $nMin$ be the number of these students. Let $nMax=\left|U\right|$. Also, let RS be a vector of size $\left|U\right|$ in which the first components are the indices of the fixed students. The remaining components contain the indices of the other students in random order. Then, a partial allocation PFA is obtained by allocating, in accordance with FA, $nAve$ students, with:

$$nAve=⌊{\displaystyle \frac{nMin+nMax}{2}}⌋$$

(25)

where $\lfloor .\rfloor$ denotes the floor function, i.e., $\lfloor a\rfloor$ is the greatest integer less than or equal to a. Apart from the fixed students, the remaining students to complete PFA are selected according to vector RS.

Algorithm 1: Construction of a feasible solution of the SBRP-SS-MD.

Then, a CVRP is solved to obtain the routes, where the demand of each bus stop is the number of its allocated students in accordance with PFA. In order to avoid an active stop not being included in any route if it does not have students allocated in the incumbent PFA, and therefore not taken into account when completing the allocation of the students, these stops are assigned a dummy demand equal to one. Let H be the set of routes obtained.

If $\left|H\right|<\mathrm{MNR}$, it is not possible to allocate all the students to the current routes. Hence, we increase the number of allocated students in the incumbent partial allocation PFA by setting $nMin=nAve$, and updating $nAve$, the partial allocation PFA and the CVRP solution.

If $\left|H\right|$ (with $\left|H\right|⩾\mathrm{MNR}$) routes are available, we compute a feasible assignment of the students to the current set of routes. For this purpose, for $h\in H$, $k\in U$, we define the binary decision variables

$${\theta }_{hk}=\left\{\begin{array}{cc}\hfill 1,& \hfill \mathrm{if} \mathrm{student} k \mathrm{is} \mathrm{assigned} \mathrm{to} \mathrm{route} h\\ \hfill 0,& \mathrm{otherwise}\hfill \end{array}\right.$$

and then solve the following ILP problem:

$$\begin{array}{cc}min\hfill & G={\displaystyle \sum _{h\in H}}{\displaystyle \sum _{k\in U}}{\tilde{a}}_{hk}{\theta }_{hk}\hfill \\ \mathrm{s}.\mathrm{t}.\hfill \\ \hfill & {\displaystyle \sum _{k\in U}}{\theta }_{hk}⩽Q,\hfill & h\in H\hfill \\ \hfill & {\displaystyle \sum _{h\in H}}{\theta }_{hk}=1,\hfill & k\in U\hfill \\ \hfill & {\theta }_{hk}\in \{0,1\},\hfill & h\in H,k\in U\hfill \end{array}$$

(26)

where the objective function coefficients are defined as:

$${\tilde{a}}_{hk}=\left\{\begin{array}{cc}0\hfill & \mathrm{if} (k,i)\in \mathrm{PFA} \mathrm{for} \mathrm{a} \mathrm{bus} \mathrm{stop} i \mathrm{in} \mathrm{the} \mathrm{route}h\hfill \\ rand(0,1)\hfill & \mathrm{if} (k,i)\notin \mathrm{PFA} \mathrm{for} \mathrm{all} \mathrm{the} \mathrm{bus} \mathrm{stop} i \mathrm{in} \mathrm{the} \mathrm{route}, \mathrm{but} d_{ki}⩽D \mathrm{for}\hfill \\ \hfill & \mathrm{a} \mathrm{bus} \mathrm{stop} i \mathrm{in} \mathrm{the} \mathrm{route}h\hfill \\ \left|U\right|\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

Notice that the coefficient matrix of problem (26) is unimodular. Hence, the integrality constraint on the variables can be relaxed to a nonnegativity constraint, and so problem (26) is a Transportation Problem in which the origins are the routes, each with a supply equal to the bus capacity Q, and the destinations are the students, each with demand equal to one.

Let $G^{*}$ be the optimal objective function value of problem (26).

• If $G^{*}<\left|U\right|$, a feasible solution of the SBRP-SS-MD can be obtained. A set $W_a$ of active stops and a set of routes H are available. Moreover, each student has been assigned to a route according to the optimal solution of problem (26). Regarding the specific bus stop to which the student is allocated, he/she could select any achievable bus stop in his/her assigned route. In the algorithm, each student selects his/her nearest bus stop on that route. This solution is saved if it is the best solution obtained up to this time.
  At this time we ask if it is possible to reduce the number of students in the current PFA to try to construct a less costly solution of the corresponding CVRP. For this purpose, we set $nMax=nAve$, and repeat the process of updating $nAve$, the partial allocation PFA and the CVRP solution, and possibly solving again the problem (26).
• If $G^{*}⩾\left|U\right|$, the optimal solution of problem (26) includes students who are allocated to a route for which none of its bus stops is achievable. Hence, it is not possible to get a feasible solution of the SBRP-SS-MD with the current routes. Therefore, we increase the number of students allocated in the current PFA by setting $nMin=nAve$, and repeating the process.

The process of increasing or decreasing the number of students in the partial allocation finishes when $nMax-nMin⩽1$.

3.4. Step 3: Improving Routing Cost Procedures

Three local search procedures (LSP) are applied aiming to improve the objective function value (1).

• LSP 1: Remove active stops and reallocate their students
  Selecting every active non-fixed stop in random order, the stop is removed from the corresponding route, the two adjacent bus stops are linked, and problem (26) is solved in order to get a feasible assignment of the students to the updated routes. If there is a feasible assignment, the bus stop is removed. Taking into account the triangle inequality, this procedure reduces the global routing cost.
• LSP 2: Change active stops for non-active ones
  For every active stop without fixed students in every route, in random order, we look for a non-active stop, which would reduce the routing cost if it replaces the incumbent active stop. If such a bus stop is found, it is located in the route position of the incumbent active stop, and this stop is deactivated. Then, problem (26) is solved. If the optimal solution provides a feasible assignment, the bus stops are interchanged.
  When the active stop considered is a fixed bus stop in the incumbent solution, the search is carried out only among the non-active stops that can be reached by all the students for which that was the only bus stop reachable in the incumbent solution.
• LSP 3: Interchange active stops in different bus routes
  For every pair of active stops belonging to different routes, we check if the routing cost is reduced when exchanging their position in their respective routes. If so, the bus stops are interchanged, and problem (26) is solved. If there is a feasible assignment of students to routes, the bus stops are interchanged.

To finish the process, those bus stops with no students allocated are removed from the routes. Since in the implementation of the algorithm we use a heuristic to solve the CVRP, after applying the three local search procedures we solve again the CVRP with the current allocation of students, providing the current routes as initial routes. If this results in improving the objective function value, the local search procedures are applied once again and the bus stops with no students allocated are removed from the routes.

4. Computational Experiments

This section presents and discusses the computational experiments carried out to analyze the behavior of the proposed matheuristic PALS. These experiments aim to show the performance of PALS in terms of the quality of the solution provided and the CPU time involved. For this purpose, the results obtained by the matheuristic are compared with those provided in the literature [16,22]. The numerical experiments have been performed on a PC Intel Core i7-9700 with 3.0 gigahertz, having 32.0 gigabytes of RAM and Windows 10 64-bit as the Operating System. The code has been written in C++, TDM-GCC 4.9.2. In the computational experiments we have selected the algorithm VRP_RTR developed by C. Goer, which is an implementation of the RTR metaheuristic to generate good solutions to a CVRP instance. This algorithm is available at the VRPH library: https://sites.google.com/site/vrphlibrary/home. Also, for solving the Transportation Problems (23) and (26) we have used the simplex algorithm for Transportation Problems developed by D.T. MacDonald and available at https://github.com/engine99/transport-simplex.

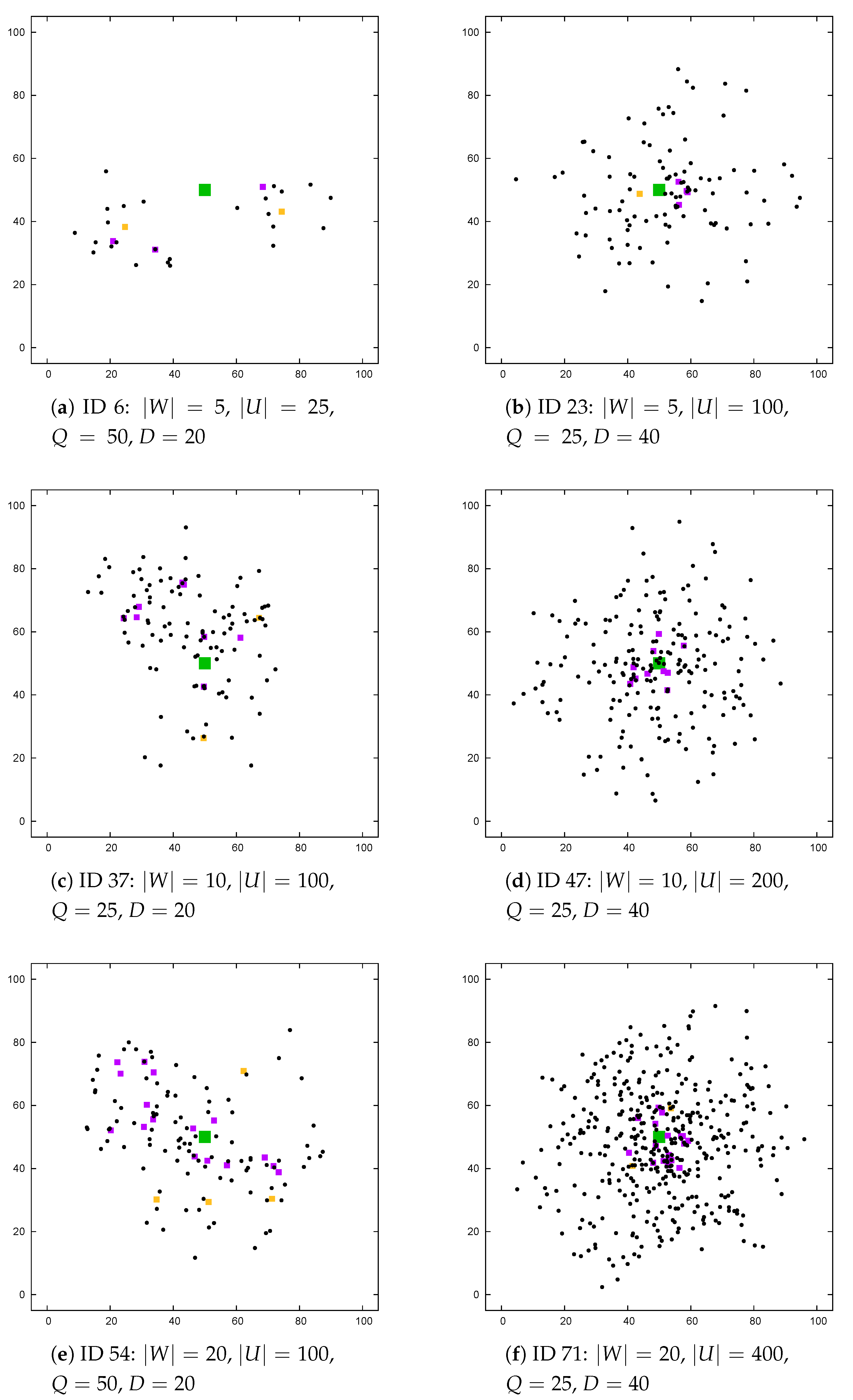
The performance of algorithm PALS has been tested on the set of benchmark instances proposed in [16]. This is a set of 112 instances in which the number of potential bus stops varies from 5 to 80, the number of students ranges between 25 and 800, the bus capacity is 25 or 50, and the maximum walking distance varies from 5 to 40. To improve the presentation of the results, we have classified the instances according to the number of potential bus stops. There are five sets. Set $S_1$ involves the instances with ID from 1 to 24, which have 5 bus stops; set $S_2$ involves the instances with ID from 25 to 48, which have 10 bus stops; set $S_3$ involves the instances with ID from 49 to 72, which have 20 bus stops; set $S_4$ involves the instances with ID from 73 to 96, which have 40 bus stops; and set $S_5$ involves the instances with ID from 97 to 112, which have 80 bus stops. The school and the depot are located at the same place. These instances are very different from each other as regards the geographical distribution of the bus stops and of the students. As an illustration, Figure 4 and Figure 5 show a subset of these instances. Each of the benchmark instances has been solved five times. The size of the pool mentioned in Section 3.2 has been set at 10.

We have solved problems I to IV (defined in Section 3.2.1) using IBM ILOG CPLEX 12.9.0 with the default settings and the stopping criterion set at a time limit of 30 s for each problem. When the CPLEX run is interrupted before providing the optimal solution, the best solution at this time is saved. The termination condition of algorithm PALS has been established in terms of computing time (10 min) or number of iterations without improvement of the objective function (20 iterations), whichever is earlier. This computing time does not include the CPLEX computation time involved in solving Problems I to IV, which is evaluated separately.

We now assess the performance of algorithm PALS by comparing its results with the results presented in the literature. For this purpose, for each benchmark instance we label $f_{min}$, $f_{max}$ and $\overline{f}$, respectively, the best objective function value, the worst objective function value and the average objective function value obtained in the five runs of the experiments. The corresponding values for the CPU times are denoted by $t_{min}$, $t_{max}$ and $\overline{t}$. We denote $t_{cplex}$ the total CPU time required by CPLEX for solving problems I to IV, obtained as the sum of the CPU times required to solve each of the four problems. These values are displayed in

Table 1. Results of the benchmark instances.

Set	Inst	Objective Function Value					CPU Times
		PALS			Literature		PALS				Literature
		${\mathit{f}}_{\mathit{min}}$	${\mathit{f}}_{\mathit{max}}$	$\overline{\mathit{f}}$	${\mathit{f}}_{\mathit{e}}$ [22]	${\mathit{f}}_{\mathit{h}}$ [16]	${\mathit{t}}_{\mathit{min}}$	${\mathit{t}}_{\mathit{max}}$	$\overline{\mathit{t}}$	${\mathit{t}}_{\mathit{cplex}}$	${\mathit{t}}_{\mathit{e}}$ [22]	${\mathit{t}}_{\mathit{h}}$ [16]
$S_1$	1	141.01	=	=	141.01	141.01	0.04	0.04	0.04	0.01	1.78	0.16
	2	161.62	=	=	161.62	161.62	0.04	0.04	0.04	0.01	0.10	0.26
	3	182.14	=	=	182.14	182.14	0.12	0.13	0.12	0.01	0.20	0.39
	4	195.80	=	=	195.80	195.80	0.04	0.04	0.04	0.01	0.09	0.29
	5	111.65	=	=	111.65	111.65	0.47	0.52	0.49	0.01	0.16	0.49
	6	103.18	=	=	103.18	103.18	0.07	0.07	0.07	0.01	0.10	0.52
	7	7.63	=	=	7.63	7.63	0.17	0.33	0.24	0.02	0.04	0.29
	8	25.64	=	=	25.64	25.64	0.75	0.86	0.79	0.03	0.09	0.25
	9	286.68	=	=	286.68	286.68	0.04	0.04	0.04	0.02	0.18	0.39
	10	197.20	=	=	197.20	197.20	0.13	0.13	0.13	0.02	0.10	0.35
	11	193.55	=	=	193.55	193.55	0.32	0.34	0.33	0.04	3.04	0.43
	12	215.86	=	=	215.86	215.86	0.12	0.12	0.12	0.02	0.07	0.74
	13	130.53	=	=	130.53	130.53	1.46	1.67	1.60	0.04	0.25	1.68
	14	96.26	=	=	96.26	96.26	1.90	2.09	1.97	0.03	0.11	1.69
	15	12.89	=	=	12.89	12.89	1.28	1.50	1.38	0.05	0.26	1.38
	16	30.24	=	=	30.24	30.24	0.65	0.81	0.75	0.02	0.15	1.17
	17	360.35	=	=	360.35	360.35	0.03	0.03	0.03	0.03	0.09	1.15
	18	304.23	=	=	304.23	304.23	0.03	0.03	0.03	0.02	0.11	0.90
	19	294.21	=	=	294.21	294.21	1.83	1.97	1.87	0.05	1.87	2.08
	20	229.41	=	=	229.41	229.41	0.04	0.04	0.04	0.02	1.63	1.67
	21	134.95	=	=	134.95	134.95	2.00	2.11	2.04	0.11	0.54	2.89
	22	144.41	=	=	144.41	144.41	0.51	0.52	0.51	0.03	12.97	1.34
	23	58.95	=	=	58.95	58.95	2.00	2.12	2.04	0.16	1.39	4.24
	24	39.44	=	=	39.44	39.44	2.16	2.20	2.19	0.10	0.79	2.89
$S_2$	25	242.85	=	=	242.85	242.85	0.11	0.11	0.11	0.03	0.47	1.55
	26	282.12	=	=	282.12	282.12	0.45	0.45	0.45	0.01	0.32	1.32
	27	244.54	=	=	244.54	244.54	2.10	2.42	2.29	0.03	0.81	2.45
	28	288.33	=	=	288.33	288.33	0.36	0.39	0.37	0.01	0.63	1.60
	29	108.98	=	=	108.98	108.98	2.19	2.42	2.28	0.07	5.68	2.86
	30	157.48	=	=	157.48	157.48	2.94	2.99	2.96	0.02	0.41	2.28
	31	32.25	=	=	32.25	32.25	2.33	2.49	2.39	0.11	0.43	2.84
	32	36.66	=	=	36.66	36.66	1.69	2.07	1.89	0.05	0.26	2.76
	33	403.18	=	=	403.18	403.18	2.71	3.13	3.00	0.12	0.83	0.90
	34	296.53	=	=	296.53	296.53	0.99	1.04	1.02	0.03	5.40	0.54
	35	388.87	=	=	388.87	388.87	0.98	1.06	1.03	0.11	20.58	3.82
	36	294.80	=	=	294.80	294.80	1.80	2.03	1.91	0.04	3.03	4.18
	37	178.28	=	=	178.28	178.28	2.63	2.99	2.83	0.22	29.68	5.58
	38	175.96	=	=	175.96	175.96	3.05	3.26	3.18	0.08	131.05	7.98
	39	57.50	=	=	57.50	57.50	2.39	2.74	2.55	0.66	1.82	7.38
	40	31.89	=	=	31.89	31.89	2.32	2.38	2.35	0.13	1.52	5.90
	41	735.27	=	=	735.27	735.27	0.04	0.04	0.04	0.42	0.02	8.49
	42	506.06	=	=	506.06	512.16	0.06	0.06	0.06	0.11	0.07	4.45
	43	513.00	=	=	513.00	513.00	4.06	4.27	4.15	2.65	124.69	27.17
	44	475.21	=	=	475.21	475.21	2.00	2.10	2.04	0.18	69.69	12.09
	45	347.29	=	=	347.29	347.29	3.52	3.66	3.58	0.86	30.22	25.61
	46	217.46	=	=	217.46	217.46	3.32	4.11	3.71	0.36	3600.00	20.58
	47	102.93	=	=	102.93	102.93	3.45	6.05	4.26	1.64	5.89	33.35
	48	55.05	=	=	55.05	55.05	2.86	3.08	2.94	0.81	8.20	13.05
$S_3$	49	507.81	=	=	507.81	520.24	2.30	2.47	2.37	0.28	6.00	8.85
	50	406.65	=	=	406.65	420.64	4.65	4.90	4.79	0.05	2920.37	3.40
	51	419.17	=	=	419.17	422.21	12.56	20.80	15.52	0.60	708.64	7.84
	52	360.86	=	=	360.86	360.86	9.58	13.74	10.70	0.09	3600.00	3.88
	53	245.17	=	=	245.17	245.17	6.30	7.98	7.09	1.89	71.46	10.32
	54	184.38	=	=	185.06	185.06	5.39	6.26	5.82	0.30	3600.00	5.60
	55	52.52	=	=	52.52	52.52	3.29	4.76	4.15	0.50	16.49	10.40
	56	19.05	=	=	19.05	19.05	3.54	4.62	4.16	0.39	2.67	23.73
	57	875.46	=	=	875.46	903.84	6.76	8.12	7.50	10.48	1564.37	10.60
	58	476.05	=	=	476.05	485.65	6.12	6.80	6.53	0.37	472.16	29.27
	59	615.08	=	=	606.80	616.93	13.08	13.28	13.19	8.71	3600.00	28.85
	60	462.31	=	=	462.31	462.31	13.86	14.39	14.15	0.84	3600.00	18.48
	61	373.21	=	=	373.21	373.21	7.99	11.21	9.31	37.98	3600.00	50.39
	62	252.84	254.30	253.13	250.75	250.75	9.23	14.13	11.69	1.36	3600.00	26.94
	63	93.01	=	=	93.01	93.01	6.61	11.29	8.26	13.49	62.59	67.73
	64	45.40	=	=	45.40	45.40	4.32	6.64	5.09	4.01	28.62	33.50
	65	1323.35	=	=	1323.35	1323.35	9.49	10.16	9.89	60.15	1446.74	234.66
	66	725.75	=	=	720.83	733.54	12.57	12.94	12.78	25.36	1058.96	37.64
	67	975.12	=	=	975.12	975.12	14.21	15.31	14.75	23.64	3600.00	139.12
	68	616.31	=	=	614.67	614.67	16.38	17.10	16.72	90.13	3600.00	73.23
	69	763.76	=	=	763.76	763.76	9.66	10.05	9.90	36.36	3111.86	132.47
	70	298.47	=	=	298.47	298.47	7.84	8.74	8.19	29.63	3600.00	90.54
	71	239.58	=	=	239.58	239.58	8.73	9.10	8.98	37.60	92.36	307.20
	72	84.49	=	=	84.49	84.49	10.74	12.18	11.44	49.02	190.20	127.08
$S_4$	73	808.70	=	=	831.94	831.94	44.39	45.95	45.13	64.40	3600.00	60.10
	74	556.27	556.72	556.36	593.35	593.35	44.24	89.45	56.62	6.96	3600.00	40.00
	75	716.47	725.98	720.55	728.44	728.44	62.62	137.49	95.56	90.44	3600.00	709.28
	76	475.65	475.68	475.67	481.05	481.05	41.39	56.38	44.81	16.11	3600.00	91.71
	77	339.26	342.83	342.12	339.75	339.75	19.77	26.68	23.05	35.65	3600.00	153.04
	78	278.94	=	=	273.88	273.88	13.86	15.73	14.83	24.43	3600.00	53.84
	79	76.77	=	=	76.77	76.77	7.39	11.53	9.15	32.34	137.93	132.52
	80	58.46	61.79	59.13	58.46	58.46	8.40	23.06	13.50	5.98	330.24	77.92
	81	1356.50	1369.35	1366.78	1394.23	1407.05	63.17	84.08	68.62	90.19	3600.00	353.09
	82	834.81	=	=	858.80	858.80	57.87	60.93	59.90	60.15	3600.00	585.98
	83	900.87	912.48	905.87	891.02	891.02	86.15	141.39	108.79	90.26	3600.00	496.35
	84	740.49	748.54	742.95	757.42	757.42	73.53	136.27	110.15	62.79	3600.00	413.29
	85	586.29	589.05	588.50	586.29	586.29	41.59	67.86	52.63	73.28	3600.00	739.56
	86	401.65	=	=	395.95	395.95	30.18	38.14	34.87	62.32	3600.00	242.91
	87	195.33	=	=	195.33	195.33	16.39	21.59	19.13	42.92	333.99	1186.56
	88	70.77	=	=	70.77	70.77	34.58	60.25	43.45	36.66	449.24	549.07
	89	2900.14	=	=	2900.14	2900.14	51.90	61.71	57.83	60.66	3600.00	3529.15
	90	1326.78	=	=	1345.70	1345.70	91.31	94.87	92.56	90.24	3600.00	1257.96
	91	2212.99	=	=	2200.57	2200.57	76.48	85.90	79.22	66.38	3600.00	3495.62
	92	1032.10	1042.78	1037.96	1025.16	1025.16	98.43	143.63	119.07	90.52	3600.00	3600.03
	93	1409.03	=	=	1404.16	1404.16	54.20	85.69	67.51	52.02	542.64	3600.18
	94	624.04	625.64	624.68	616.58	616.58	61.95	112.41	80.44	40.09	3600.00	3600.12
	95	396.92	=	=	396.92	396.92	66.30	71.89	68.02	47.70	790.50	3600.81
	96	200.79	=	=		200.94	37.90	40.29	39.05	62.12		3074.14
$S_5$	97	1455.04	1458.44	1456.68		1546.23	206.90	292.18	235.04	65.82		958.12
	98	993.97	1002.97	999.84		1048.56	160.06	602.74	317.52	90.21		471.89
	99	1220.67	1228.57	1224.39		1216.74	168.09	348.45	240.57	66.21		1833.44
	100	736.81	747.36	740.58		760.61	141.68	340.52	220.63	90.43		576.26
	101	574.01	=	=		565.49	80.00	89.73	84.41	61.93		1224.64
	102	383.94	=	=		372.05	66.60	170.88	129.10	70.56		878.86
	103	131.43	133.60	132.30		131.75	75.81	115.15	94.09	63.67		1116.28
	104	90.27	=	=		95.84	18.30	20.04	19.17	64.54		3600.05
	105	2495.97	2506.21	2502.14		2527.96	422.03	607.06	515.29	67.80		3433.78
	106	1442.57	1446.97	1444.62		1530.58	266.32	464.73	345.72	62.01		3600.03
	107	1807.87	1823.32	1814.62		1809.90	408.76	611.18	528.00	109.66		3600.05
	108	1171.59	1180.77	1174.59		1187.51	363.18	608.33	495.42	66.37		3600.04
	109	1115.51	1128.52	1119.70		1110.44	183.92	435.88	264.85	63.11		3600.10
	110	644.11	662.05	653.86		623.03	187.22	336.36	260.98	62.48		3600.62
	111	311.41	=	=		311.41	150.03	160.47	154.77	72.32		3600.21
	112	126.06	=	=		126.06	60.89	67.05	63.28	67.64		3600.05

for each of the 112 benchmark instances. To facilitate the reading of the table, when either $f_{max}$ or $\overline{f}$ are equal to $f_{min}$, a symbol ‘=’ is written in the corresponding column. The table also shows the values of the objective function and the CPU times provided in the two papers that have dealt with these benchmark instances. The values are denoted by $f_e$ and $t_e$ when referring to the exact method proposed in [22], and by $f_h$ and $t_h$ when referring to the heuristic method proposed in [16]. It is worth pointing out that in [22] the exact algorithm was stopped at 3600 s of computing time with the best solution found at that time. Moreover, in [16] only the results of one run of the heuristic algorithm are presented. None of the two references [16,22] include the characteristics of the computer that was used in the numerical experiments. Finally, we define $f_{best}^{lit}=min\{f_e,f_h\}$, the best objective function value provided in the literature. In Table 1, $f_{min}$, $f_{max}$ or $\overline{f}$ are written in bold if they are less than $f_{best}^{lit}$. Also, they are underlined if they are equal to $f_{best}^{lit}$ (except in the cases in which the symbol ‘=’ is written).

For all the instances in sets $S_1$ and $S_2$, algorithm PALS provides the optimal solution or the best known value of the objective function in all the five runs, i.e., $f_{min}=f_{max}=f_e=f_h$. Notice that the optimal solution is known for all these instances, except instance 46.

Concerning set $S_3$, the optimal solution is known for 15 out of the 24 instances. In all of them, except instance 66, the optimal solution is provided in all the five runs, i.e., $f_{min}=f_{max}=f_e$. It is worth pointing out that $f_e$ is less than $f_h$ in six out of these 15 instances. Although PALS does not provide the optimal solution in instance 66, we can note that $f_e<f_{min}=f_{max}<f_h$. With respect to the nine remaining instances of set $S_3$, in one instance PALS provides the best value, i.e., $f_{min}=f_{max}<f_e=f_h$; in five instances we have $f_{min}=f_{max}=f_e=f_h$; in one instance $f_e<f_{min}=f_{max}<f_h$, and in two instances $f_e=f_h<f_{min}⩽f_{max}$. Summarizing, in 20 out of the 24 instances, PALS provides an objective function value at least as good as the best value provided in the literature and in one instance the value is better. By comparing PALS with the heuristic proposed in [16], we can note that for eight instances $f_{min}$ is less than $f_h$, while for two instances $f_h$ is less than $f_{min}$.

Regarding set $S_4$, only six instances are solved to optimality, and in four of them we have $f_{min}=f_{max}=f_e$. PALS provides a better value of the objective function, i.e., $f_{min}<f_e⩽f_h$ in 10 out of the 24 instances, the same value $f_{min}=f_e=f_h$ in 7 out of the 24 instances, and a worse value $f_e=f_h<f_{min}$ in 7 out of the 24 instances. Notice that the instance 96 has not been solved with the exact method [22]. It is worth pointing out that, when $f_{min}<f_{best}^{lit}$, then the maximum gap $(f_{best}^{lit}-f_{min})/f_{min}$ is less than $0.07$. Conversely, if $f_{best}^{lit}<f_{min}$, then the maximum gap $(f_{min}-f_{best}^{lit})/f_{best}^{lit}$ is less than $0.02$.

Finally, with respect to set $S_5$, only the results of the heuristic algorithm [16] are available. In 9 out of the 16 instances we have $f_{min}<f_h$; in two instances $f_{min}=f_h$ and in the remaining five instances $f_h<f_{min}$. In this set, when $f_{min}<f_{best}^{lit}$, then the maximum gap $(f_{best}^{lit}-f_{min})/f_{min}$ is not greater than $0.06$. In contrast, if $f_{best}^{lit}<f_{min}$, then the maximum gap $(f_{min}-f_{best}^{lit})/f_{best}^{lit}$ is not greater than $0.03$.

Summarizing, in 20 out of the 112 instances algorithm PALS provides an objective function value that is better than the best value in the literature, and in 76 instances provides the same value. It is also noted that for 27 instances $f_{min}$ is less than $f_h$, while for 14 instances $f_h$ is less than $f_{min}$. As a consequence, we can conclude that PALS performs very well in terms of the objective function value.

Regarding the CPU times, the performance of PALS is even better.

Table 2. Average and standard deviation of the CPU times by set.

Set	PALS		Exact [22]		Heuristic [16]
	Average	St. Dev.	Average	St. Dev.	Average	St. Dev.
$S_1$	0.74	0.82	1.09	2.60	1.15	1.02
$S_2$	2.51	1.69	168.40	716.45	8.28	9.02
$S_3$	27.34	25.26	1839.73	1581.98	61.74	75.85
$S_4$	112.85	52.25	2773.24	1395.50	1318.47	1437.62
$S_5$	319.60	161.22			2455.90	1306.91

summarizes, for each set of instances, the average and the standard deviation of the time required by PALS computed as $\overline{t}+t_{cplex}$ in the second and third columns, of the time $t_e$ required by the exact method in the fourth and fifth columns, and of the time $t_h$ required by the heuristic method in the sixth and seventh columns. The increase in the average CPU time is quite evident in all the sets when comparing PALS with the exact method [22], and is marked in sets $S_4$ and $S_5$ when comparing PALS with the heuristic procedure [16] (even when we consider that, for each instance, the value of $\overline{t}$ corresponds to an average of five runs of PALS, while the value of $t_h$ corresponds to a single run). Moreover, it is worth mentioning that the variability of the total time required by PALS is significantly lower than the variability of the computing times required by the exact and the heuristic methods proposed, respectively, in [22] and [16]. Finally, it should be noted that the CPU times required by PALS are small enough to make the application of the algorithm interesting in real situations.

5. Conclusions

A fast and efficient matheuristic for the School Bus Routing problem with bus stop selection and a maximum walking distance constraint (SBRP-SS-MD) has been presented in this paper. It is based on an innovative approach in which, after selecting the bus stops to be visited from the set of available bus stops and computing a feasible allocation of the students to them, only a partial allocation of the students is used to design the initial routes aiming to reduce the routing cost. Then, a process to complete the partial allocation and to redesign the routes is carried out to achieve a feasible solution. The algorithm is very competitive in terms of the closeness of the solution provided to the optimal solution or to the best known solution in the literature. In fact, in 81.25% of the benchmark instances, the best known result in the literature is improved (15.18%) or matched (66.07%) in all the five runs executed for each instance. In 85.72% of the instances, the best known result is improved (17.86%) or matched (67.86%) in at least one run. The computing times can be considered very short (on average, they range from 0.05 and 637.66 s).