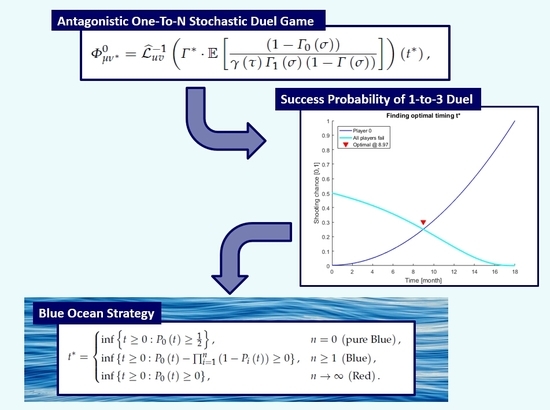
Antagonistic One-To-N Stochastic Duel Game
Abstract
1. Introduction
2. Antagonistic One-To-N Duel Game
Preliminaries
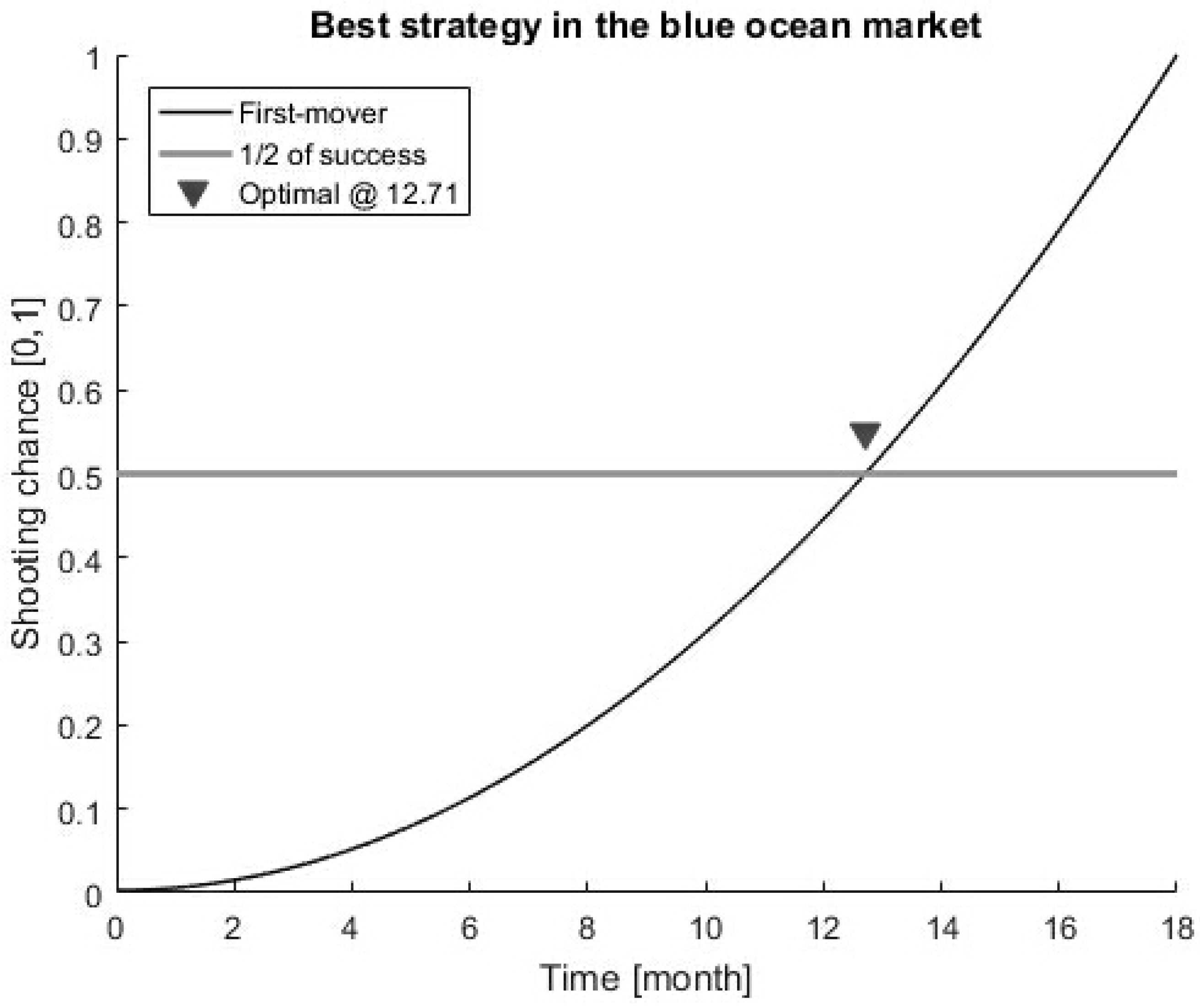
3. Best Strategies in Blue and Red Ocean Markets
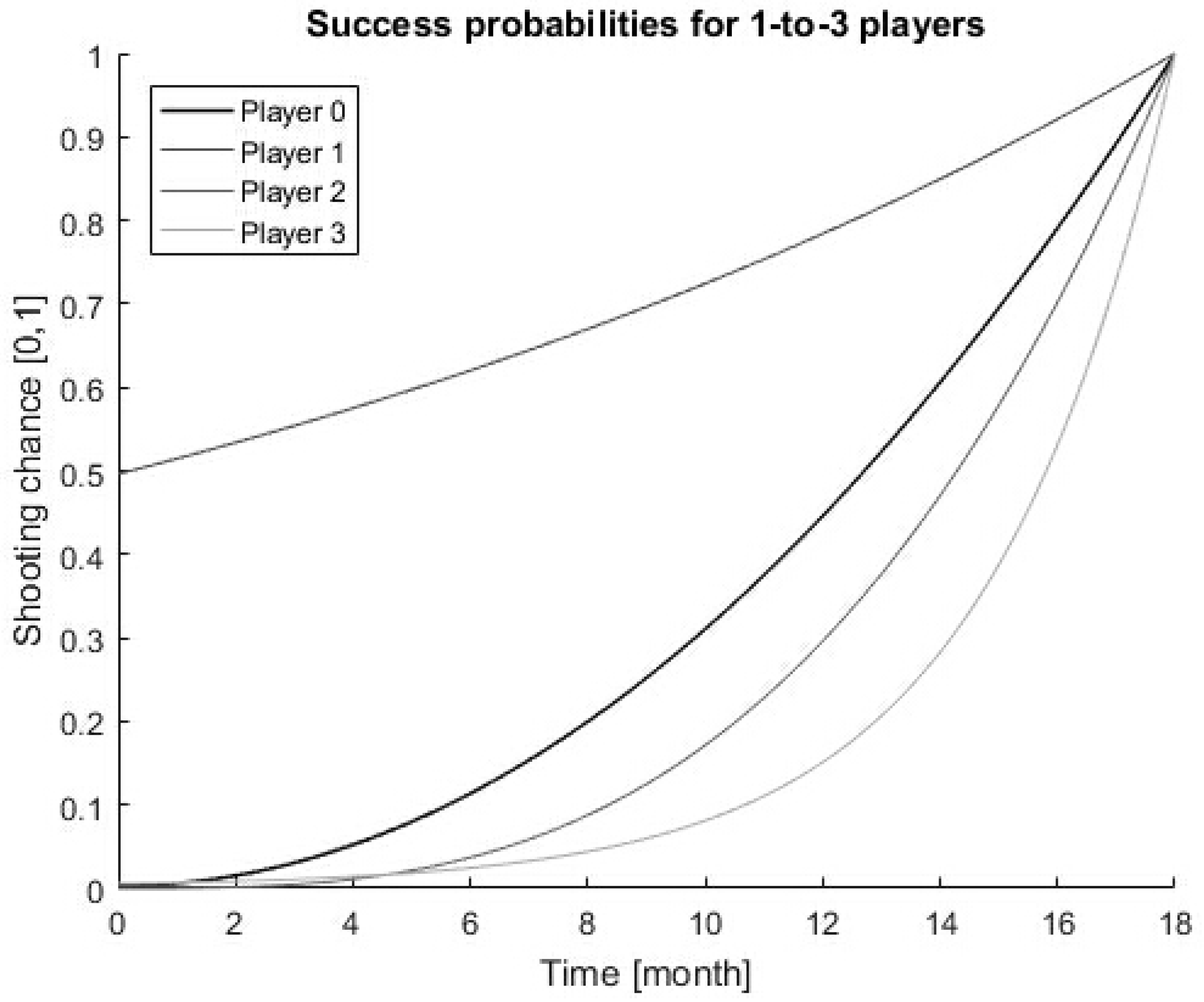
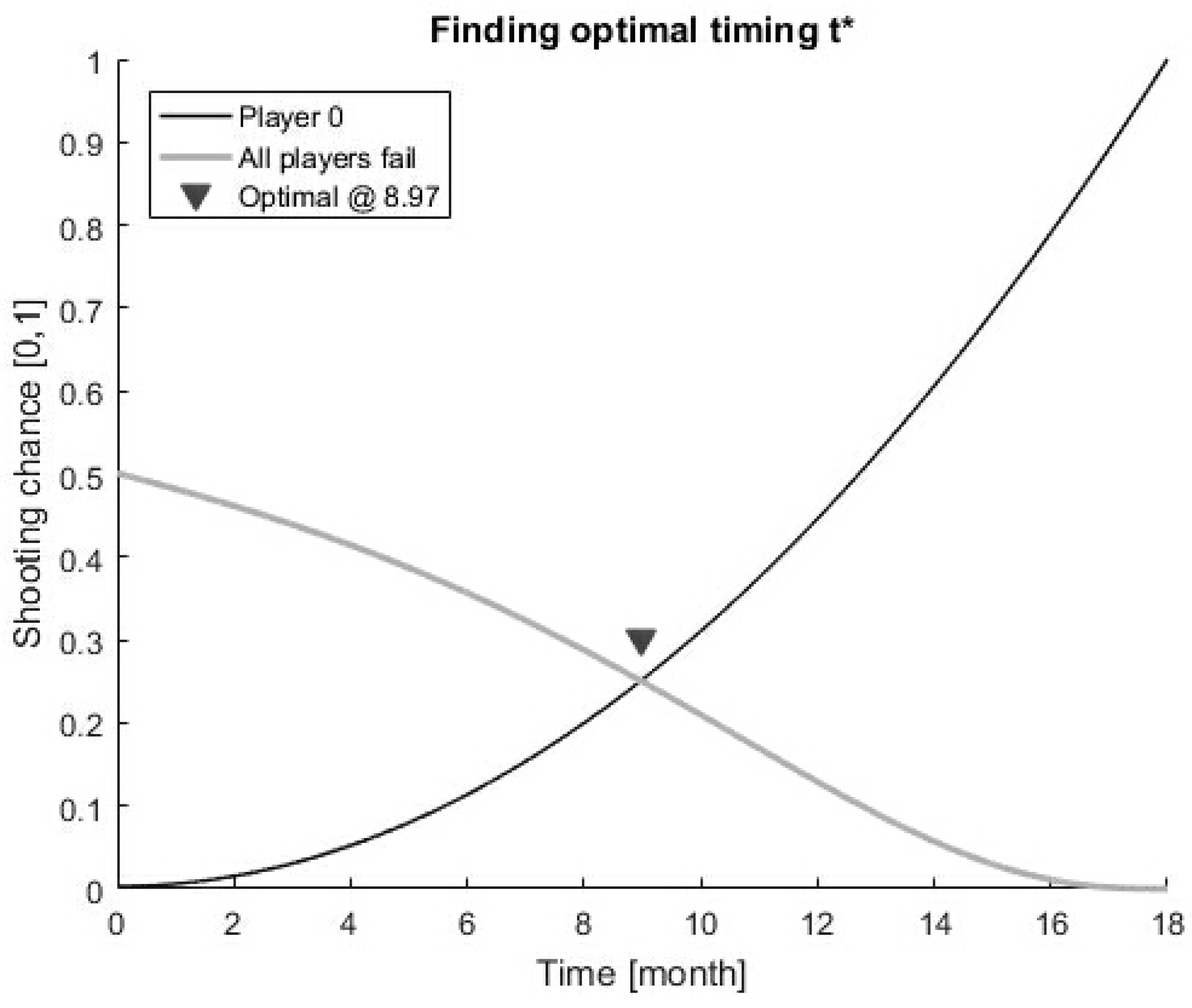
4. Memoryless Case: IT Product Launch Strategy for Multiple Competitors
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Dshalalow, J.H.; White, R. On Reliability of Stochastic Networks. Neural Parallel Sci. Comput. 2013, 21, 141–160. [Google Scholar]
- Dshalalow, J.H.; Iwezulu, K.; White, R.T. Discrete Operational Calculus in Delayed Stochastic Games. Neural Parallel Sci. Comput. 2016, 24, 55–64. [Google Scholar]
- Kim, S.-K. Blockchain Governance Game. Comp. Indust. Eng. 2019, 136, 373–380. [Google Scholar] [CrossRef]
- Kim, S.-K. A Versatile Stochastic Duel Game. Mathematics 2020, 8, 678. [Google Scholar] [CrossRef]
- Thomas, R.J. Timing—The Key to Market Entry. J. Consum. Mark. 1985, 2, 77–87. [Google Scholar] [CrossRef]
- Saylor Academy, Fundamentals of Global Strategy, 2019. Available online: https://saylordotorg.github.io/text/fundamentals-of-global-strategy/index.html (accessed on 1 May 2019).
- GTellis, J.; Golder, P.N.; Christensen, C.M. Will and Vision: How Latecomers Grow to Dominate Markets; McGraw-Hill: Princeton, NJ, USA, 2001. [Google Scholar]
- Eliashberg, J.; Jeuland, A.P. The Impact of Competitive Entry in a Developing Market upon Dynamic Pricing Strategies. Mark. Sci. 1986, 5, 20–36. [Google Scholar] [CrossRef]
- Kalyanaram, G.; Gurumurthy, R. Market Entry Strategies: Pioneers Versus Late Arrivals. Available online: http://www.strategy-business.com/article/18881?gko=c8128 (accessed on 1 May 2019).
- Lilien, G.L.; Yoon, E. The Timing of Competitive Market Entry: An Exploratory Study of New Industrial Products. Manag. Sci. 1990, 36, 519–641. [Google Scholar] [CrossRef]
- Singh, D. First Mover Or Fast Follower—Why It is Okay to be Either in Tech. 2018. Available online: https://blog.alore.io/first-movers-vs-fast-followers/ (accessed on 1 May 2019).
- Birger, J. Second-Mover Advantage. CNN Money. 2006. Available online: https://money.cnn.com/magazines/fortune/fortune_archive/2006/03/20/8371782/ (accessed on 1 May 2019).
- Shevlin, R. The Fast Follower Fallacy. The Financial Brand, 2016. Available online: https://thefinancialbrand.com/59369/fast-follower-fallacy/ (accessed on 1 May 2019).
- Anthony, S.D. First Mover or Fast Follower. Harv. Bus. Rev. 2012. Available online: https://hbr.org/2012/06/first-mover-or-fast-follower (accessed on 1 May 2019).
- Querbes, A.; Frenken, K. Evolving user needs and late-mover advantage. Strateg. Organ. 2017, 15, 67–90. [Google Scholar] [CrossRef] [PubMed]
- Shankar, V.; Carpenter, G.S.; Krishnamurthi, L. Late Mover Advantage: How Innovative Late Entrants Outsell Pioneers. J. Mark. Res. 1998, 35, 54–70. [Google Scholar] [CrossRef]
- Wunker, S. Better growth decisions: Early mover, fast follower or late follower? Strategy Leadersh. 2012, 40, 43–48. [Google Scholar] [CrossRef]
- Kim, W.C.; Mauborgne, R. Blue Ocean Strategy: How to Create Uncontested Market Space and Make the Competition Irrelevant; Harvard Business School Press: Boston, MA, USA, 2004. [Google Scholar]
- Internet Archive, A Conversation with W. Chan Kim and Renee Mauborgne, 2005. Available online: https://web.archive.org/web/20081203070029/http://www.insead.edu/alumni/newsletter/February2005/Interview.pdf (accessed on 1 May 2019).
- Radzik, T. Games of Timing Related to Distribution of Resources. J. Optim. Theory Appl. 1988, 58, 443–471. [Google Scholar] [CrossRef]
- Radzik, T. Silent Mixed Duels. Optimization 1989, 20, 553–556. [Google Scholar] [CrossRef]
- Khalfallah, H.; Rious, V. A game theoretical analysis of the design options of the realtime electricity market. Energy Stud. Rev. 2013, 20, 34–64. [Google Scholar] [CrossRef]
- Kuenle, H.-U. Markov Games under a Geometric Drift Condition; Advances in Dynamic Games; Springer: New York, NY, USA, 2005; pp. 21–38. [Google Scholar]
- Nikoukhah, R.; Delebecque, F. On a stochastic differential game and its relationship with mixed H/H control. In Proceedings of the American Control Conference, Chicago, IL, USA, 24–26 June 1992; IEEE: Piscataway, NJ, USA, 1992; pp. 1380–1384. [Google Scholar]
- Lang, J.P.; Kimeldorf, G. Duels with continuous firing. Manag. Sci. 1975, 22, 470–476. [Google Scholar] [CrossRef]
- Polak, B. Discussion of Duel. Open Yale Courses, 2008. Available online: http://oyc.yale.edu/economics/econ-159/lecture-16 (accessed on 1 May 2019).
- Lang, J.P.; Kimeldorf, G. Silent Duels with Non Discrete Firing. SIAM J. Appl. Math. 1976, 31, 9–110. [Google Scholar] [CrossRef]
- Schwalbe, U.; Walker, P. Zermelo and the Early History of Game Theory. Games Econ. Behav. 2001, 34, 123–137. [Google Scholar] [CrossRef]
- Dshalalow, J.H.; Ke, H.-J. Layers of noncooperative games. Nonlinear Anal. 2009, 71, 283–291. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-K. Antagonistic One-To-N Stochastic Duel Game. Mathematics 2020, 8, 1114. https://doi.org/10.3390/math8071114
Kim S-K. Antagonistic One-To-N Stochastic Duel Game. Mathematics. 2020; 8(7):1114. https://doi.org/10.3390/math8071114
Chicago/Turabian StyleKim, Song-Kyoo (Amang). 2020. "Antagonistic One-To-N Stochastic Duel Game" Mathematics 8, no. 7: 1114. https://doi.org/10.3390/math8071114
APA StyleKim, S.-K. (2020). Antagonistic One-To-N Stochastic Duel Game. Mathematics, 8(7), 1114. https://doi.org/10.3390/math8071114