Projection Methods for Uniformly Convex Expandable Sets
Abstract
1. Introduction
1.1. Background and Goal of the Paper
1.2. Preliminary on Projections and Expansion into Convex Sets
1.3. The Projection Algorithm
1.4. Our Contributions
2. Ottavy’s Framework
2.1. Successive Projection Point-to-Set Mapping
2.2. Ottavy’s Lemma
3. A Strong Convergence Result
- either there exist in and in , such that ,
- or .
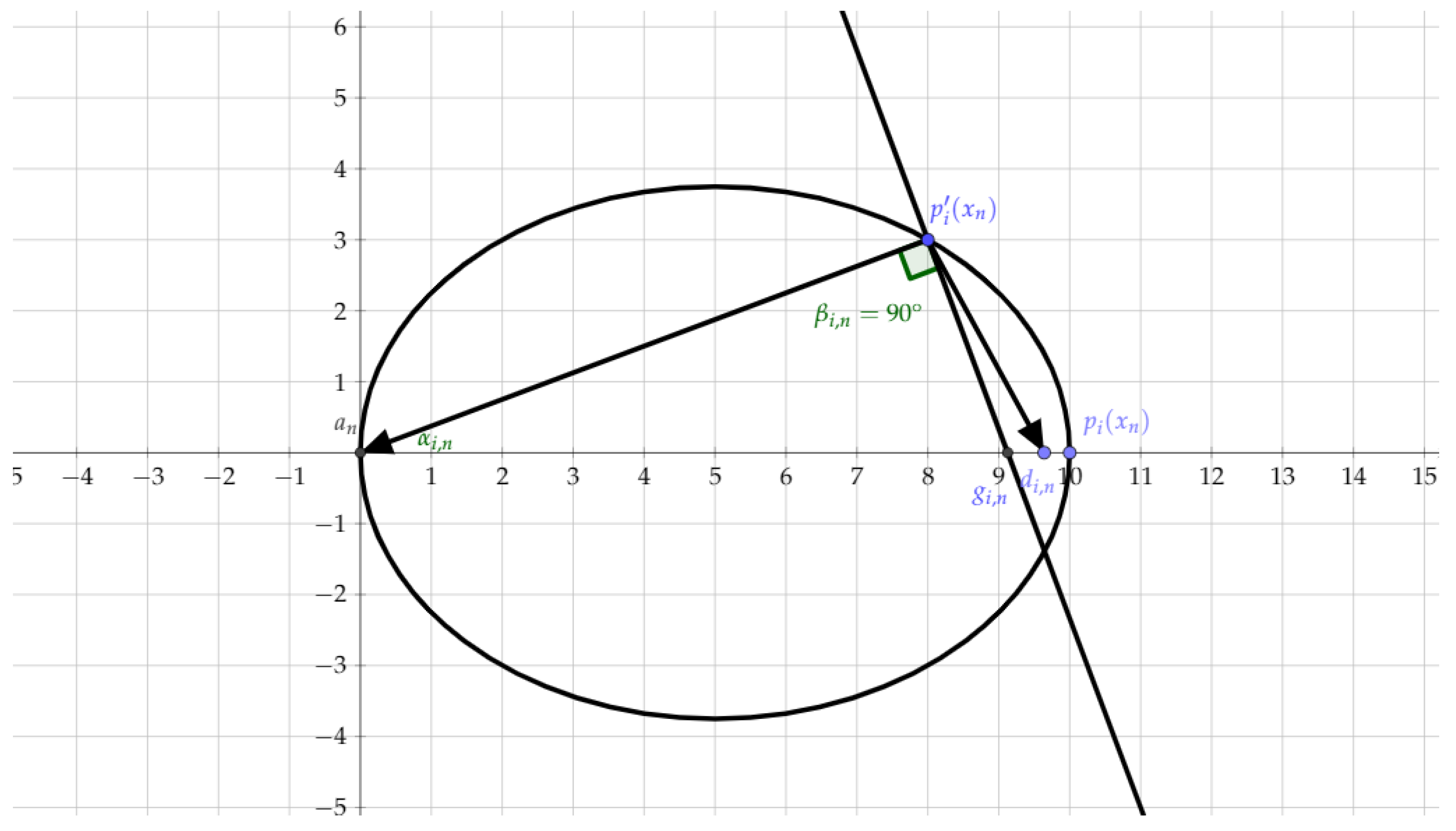
4. Projections onto Stepwise Generated Uniformly Convex Sets
- If the sequence converges to zero, then using Claim 2, also converges to zero. Therefore, is also strongly convergent to for each i in I. Since each set is closed, we again conclude that .
- If the sequence does not converge to zero, and the sequence converges to zero, then we must have for some and some subsequence indexed by an appropriately chosen increasing function . This implies in particular thatAs a result, eitherorNotice further that (16) holds only if converges to zero. Thus, both cases simplify into the conclusion that converges to zero. Therefore is also strongly convergent to for each i in I. Since each set is closed, we again conclude that .
- If both sequences and do not converge to zero, then and for some and for some subsequence indexed by an appropriately chosen increasing function . Since is the length of the main axis of , and, as such, bounds from above the distance between any two points in , we deduce that . Furthermore, since the sequences and are bounded, we deduce thatfor some . Then using the Cauchy-Schwarz inequality in the numerator in (14), we getfor some . Since , we deduce from (11) and (15) that converges to zero. Therefore, is also strongly convergent to for each i in I. Since each set is closed, we again conclude that .
5. Applications
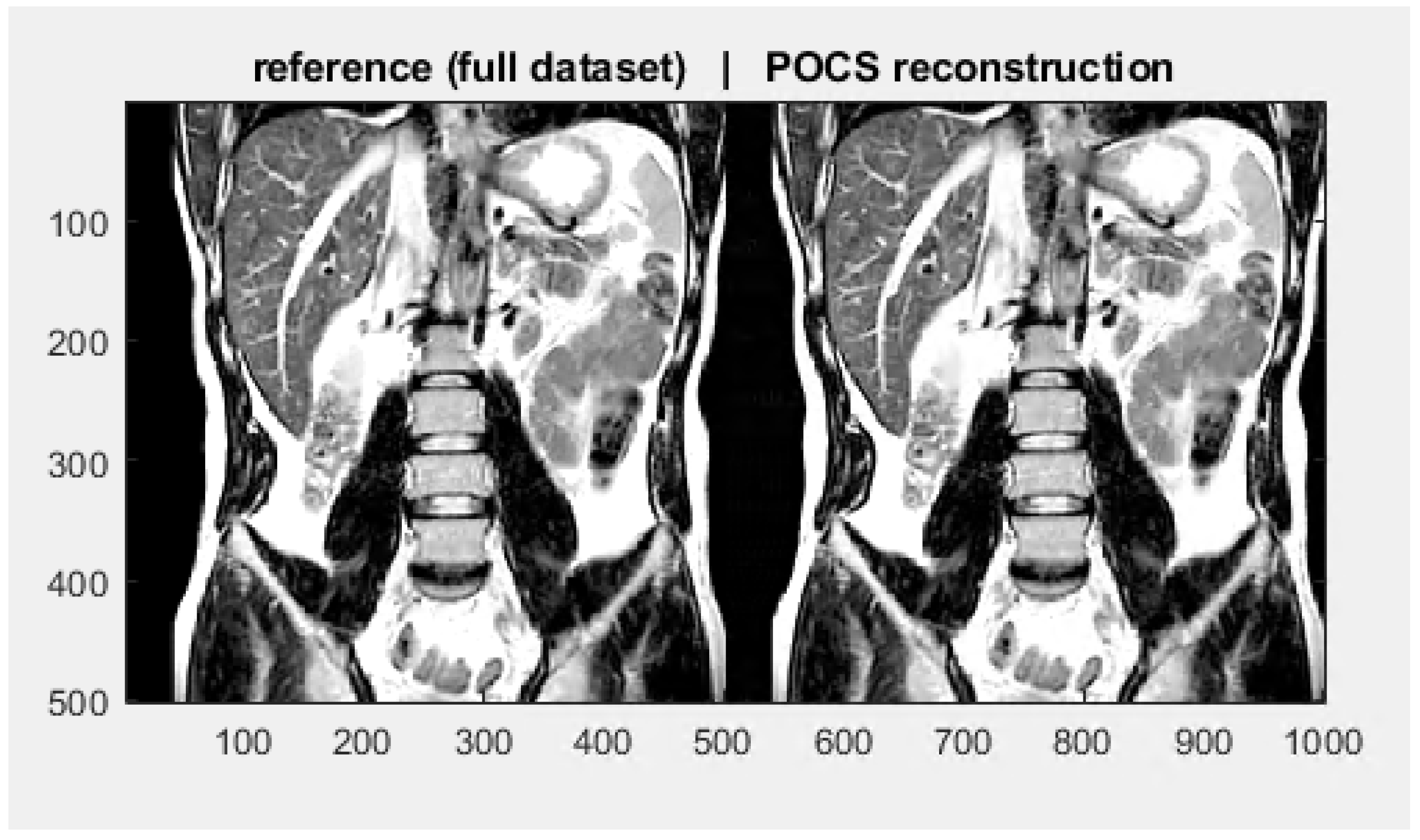
5.1. MRI Image Reconstruction: The Infinite-Dimensional Hilbert Space Setting
| Algorithm 1: Alternating projection method for MRI for . |
 |
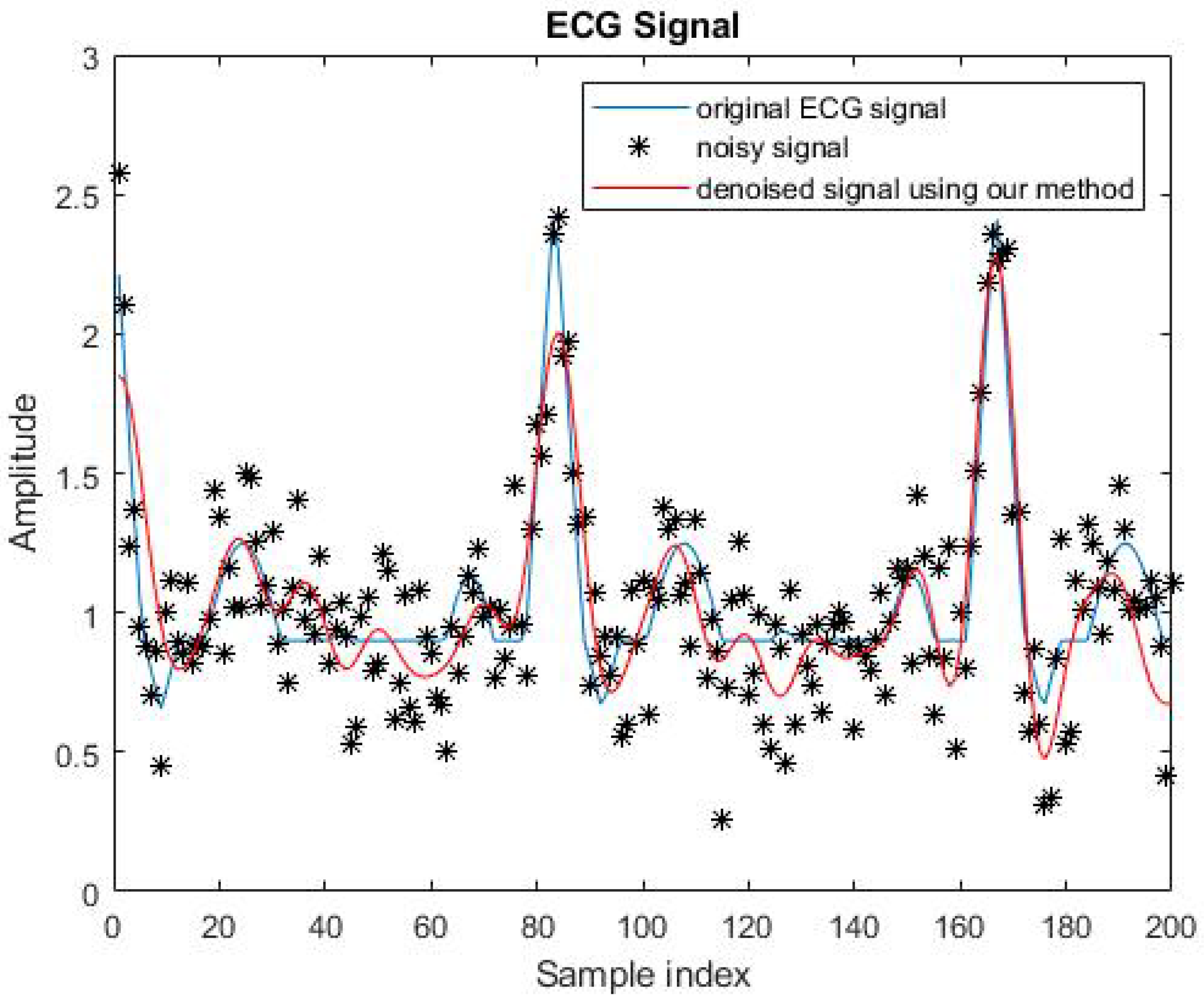
5.2. A Uniformly Convex Version of Cadzow’s Method
- is a sum of damped exponential components, i.e.,with , a real damping factor satisfying , a real number representing a frequency and a complex coefficient,
- is a random noise.
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Definition of the Total Variation (TV) Norm
Appendix B. Niculescu’ Lemma
References
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; Springer: Berlin/Heidelberg, Germany, 2011; Volume 408. [Google Scholar]
- Escalante, R.; Raydan, M. Alternating Projection Methods; SIAM: Philadelphia, PA, USA, 2011. [Google Scholar]
- Gurin, L.; Polyak, B.T.; Raik, È.V. The method of projections for finding the common point of convex sets. Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki 1967, 7, 1211–1228. [Google Scholar]
- Ottavy, N. Strong convergence of projection-like methods in Hilbert spaces. J. Optim. Theory Appl. 1988, 56, 433–461. [Google Scholar] [CrossRef]
- Combettes, P.L.; Puh, H. Iterations of parallel convex projections in Hilbert spaces. Numer. Funct. Anal. Optim. 1994, 15, 225–243. [Google Scholar] [CrossRef]
- Grigoriadis, K.M. Optimal H∞ model reduction via linear matrix inequalities: Continuous-and discrete-time cases. Syst. Control Lett. 1995, 26, 321–333. [Google Scholar] [CrossRef]
- Babazadeh, M.; Nobakhti, A. Direct Synthesis of Fixed-Order H∞ Controllers. IEEE Trans. Autom. Control 2015, 60, 2704–2709. [Google Scholar] [CrossRef]
- Li, Z.; Dai, Y.H.; Gao, H. Alternating projection method for a class of tensor equations. J. Comput. Appl. Math. 2019, 346, 490–504. [Google Scholar] [CrossRef]
- Combettes, P. The convex feasibility problem in image recovery. In Advances in Imaging and Electron Physics; Elsevier: Amsterdam, The Netherlands, 1996; Volume 95, pp. 155–270. [Google Scholar]
- Krol, A.; Li, S.; Shen, L.; Xu, Y. Preconditioned alternating projection algorithms for maximum a posteriori ECT reconstruction. Inverse Probl. 2012, 28, 115005. [Google Scholar] [CrossRef]
- Herman, G.T. Fundamentals of Computerized Tomography: Image Reconstruction From Projections; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- McGibney, G.; Smith, M.; Nichols, S.; Crawley, A. Quantitative evaluation of several partial Fourier reconstruction algorithms used in MRI. Magn. Reson. Med. 1993, 30, 51–59. [Google Scholar] [CrossRef]
- Ticozzi, F.; Zuccato, L.; Johnson, P.D.; Viola, L. Alternating projections methods for discrete-time stabilization of quantum states. IEEE Trans. Autom. Control 2017, 63, 819–826. [Google Scholar] [CrossRef]
- Drusvyatskiy, D.; Li, C.K.; Pelejo, D.C.; Voronin, Y.L.; Wolkowicz, H. Projection methods for quantum channel construction. Quantum Inf. Process. 2015, 14, 3075–3096. [Google Scholar] [CrossRef]
- Grigoriadis, K.M.; Beran, E.B. Alternating projection algorithms for linear matrix inequalities problems with rank constraints. In Advances in Linear Matrix Inequality Methods in Control; SIAM: Philadelphia, PA, USA, 2000; pp. 251–267. [Google Scholar]
- Cadzow, J.A. Signal enhancement-a composite property mapping algorithm. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 49–62. [Google Scholar] [CrossRef]
- Bauschke, H.H.; Combettes, P.L.; Luke, D.R. Phase retrieval, error reduction algorithm, and Fienup variants: A view from convex optimization. J. Opt. Soc. Am. A 2002, 19, 1334–1345. [Google Scholar] [CrossRef] [PubMed]
- Chu, M.T.; Funderlic, R.E.; Plemmons, R.J. Structured low rank approximation. Linear Algebra Its Appl. 2003, 366, 157–172. [Google Scholar] [CrossRef]
- Markovsky, I.; Usevich, K. Structured low-rank approximation with missing data. SIAM J. Matrix Anal. Appl. 2013, 34, 814–830. [Google Scholar] [CrossRef]
- Elser, V. Learning Without Loss. arXiv 2019, arXiv:1911.00493. [Google Scholar]
- Combettes, P.L.; Trussell, H.J. Method of successive projections for finding a common point of sets in metric spaces. J. Optim. Theory Appl. 1990, 67, 487–507. [Google Scholar] [CrossRef]
- Chretien, S.; Bondon, P. Cyclic projection methods on a class of nonconvex sets. Numer. Funct. Anal. Optim. 1996, 17, 37–56. [Google Scholar]
- Chrétien, S. Methodes de projection pour L’optimisation ensembliste non convexe. Ph.D. Thesis, Sciences Po, Paris, France, 1996. [Google Scholar]
- Bauschke, H.H.; Borwein, J.M. On projection algorithms for solving convex feasibility problems. SIAM Rev. 1996, 38, 367–426. [Google Scholar] [CrossRef]
- Censor, Y.; Chen, W.; Combettes, P.L.; Davidi, R.; Herman, G.T. On the effectiveness of projection methods for convex feasibility problems with linear inequality constraints. Comput. Optim. Appl. 2012, 51, 1065–1088. [Google Scholar] [CrossRef]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Michael, V. MRI Partial Fourier Reconstruction with POCS. Available online: https://fr.mathworks.com/matlabcentral/fileexchange/39350-mri-partial-fourier-reconstruction-with-pocs?s_tid=prof_contriblnk (accessed on 13 February 2020).
- Condat, L. Discrete total variation: New definition and minimization. SIAM J. Imaging Sci. 2017, 10, 1258–1290. [Google Scholar] [CrossRef]
- Plonka, G.; Potts, D.; Steidl, G.; Tasche, M. Numerical Fourier Analysis: Theory and Applications; Book Manuscript; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Al Sarray, B.; Chrétien, S.; Clarkson, P.; Cottez, G. Enhancing Prony’s method by nuclear norm penalization and extension to missing data. Signal Image Video Process. 2017, 11, 1089–1096. [Google Scholar] [CrossRef]
- Barton, E.; Al-Sarray, B.; Chrétien, S.; Jagan, K. Decomposition of Dynamical Signals into Jumps, Oscillatory Patterns, and Possible Outliers. Mathematics 2018, 6, 124. [Google Scholar] [CrossRef]
- Moitra, A. Super-resolution, extremal functions and the condition number of Vandermonde matrices. In Proceedings of the Forty-Seventh Annual ACM Symposium on Theory Of Computing, Chicago, IL, USA, 22–26 June 2015; pp. 821–830. [Google Scholar]
- Chrétien, S.; Tyagi, H. Multi-kernel unmixing and super-resolution using the Modified Matrix Pencil method. J. Fourier Anal. Appl. 2020, 26, 18. [Google Scholar] [CrossRef]
- Bach, F. On the Unreasonable Effectiveness of Richardson Extrapolation. Available online: https://francisbach.com/richardson-extrapolation/ (accessed on 13 February 2020).
- Dragomir, S.S. A generalisation of the Cassels and Greub-Reinboldt inequalities in inner product spaces. arXiv 2003, arXiv:math/0306352. [Google Scholar]
- Niculescu, C.P. Converses of the Cauchy-Schwartz Inequality in the C*-Framework. RGMIA Research Report Collection. 2001, Volume 4. Available online: https://rgmia.org/v4n1.php (accessed on 15 February 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chrétien, S.; Bondon, P. Projection Methods for Uniformly Convex Expandable Sets. Mathematics 2020, 8, 1108. https://doi.org/10.3390/math8071108
Chrétien S, Bondon P. Projection Methods for Uniformly Convex Expandable Sets. Mathematics. 2020; 8(7):1108. https://doi.org/10.3390/math8071108
Chicago/Turabian StyleChrétien, Stéphane, and Pascal Bondon. 2020. "Projection Methods for Uniformly Convex Expandable Sets" Mathematics 8, no. 7: 1108. https://doi.org/10.3390/math8071108
APA StyleChrétien, S., & Bondon, P. (2020). Projection Methods for Uniformly Convex Expandable Sets. Mathematics, 8(7), 1108. https://doi.org/10.3390/math8071108




