Simplified Analytical Solution of the Contact Problem on Indentation of a Coated Half-Space by a Conical Punch
Abstract
1. Introduction
- The solution of the problem is constructed in an explicit analytical form;
- The dependence of the only parameter of approximation from the elastic parameters is obtained;
- Numerical calculations become much faster and require much less attention from a specialist.
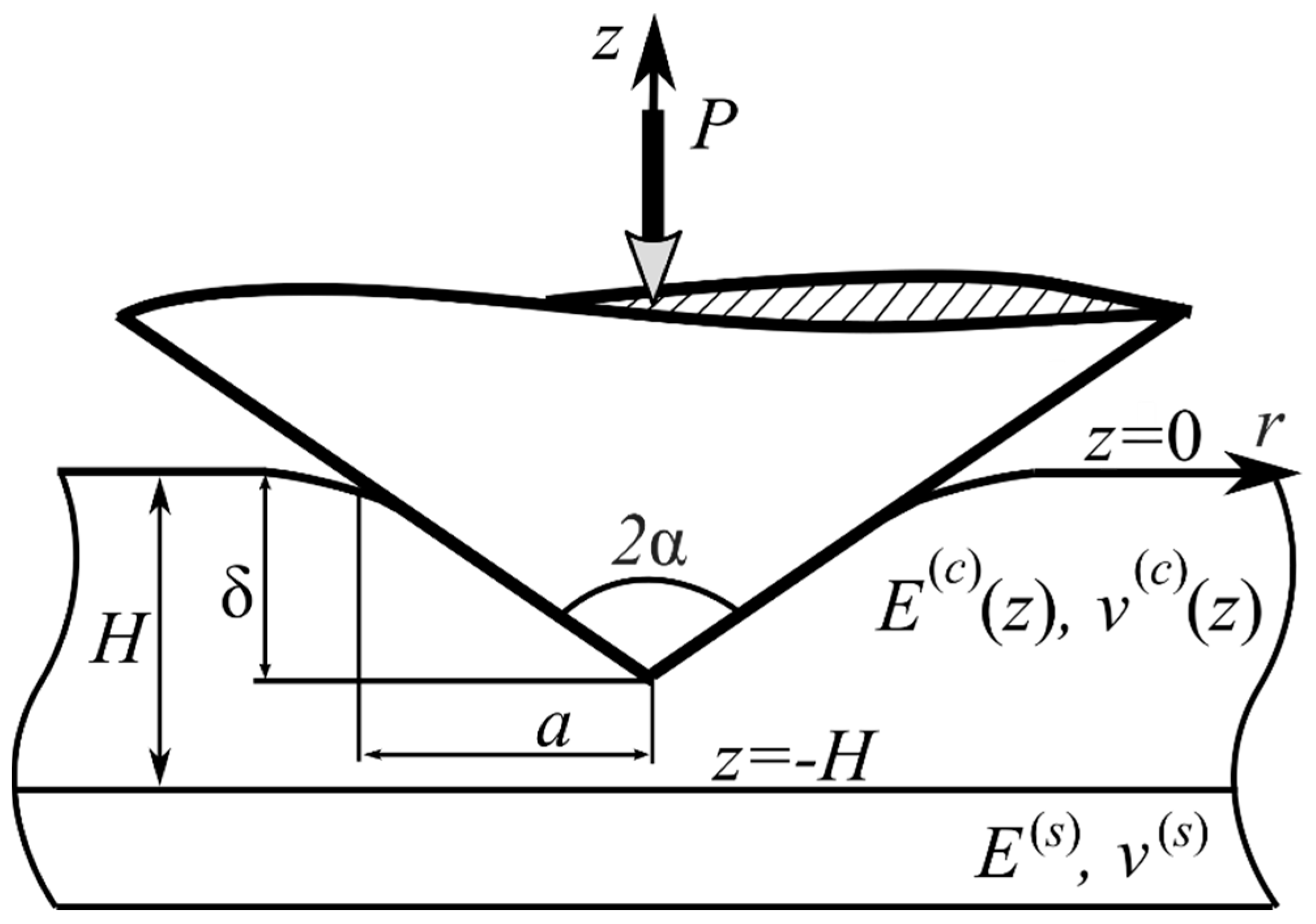
2. Materials and Methods
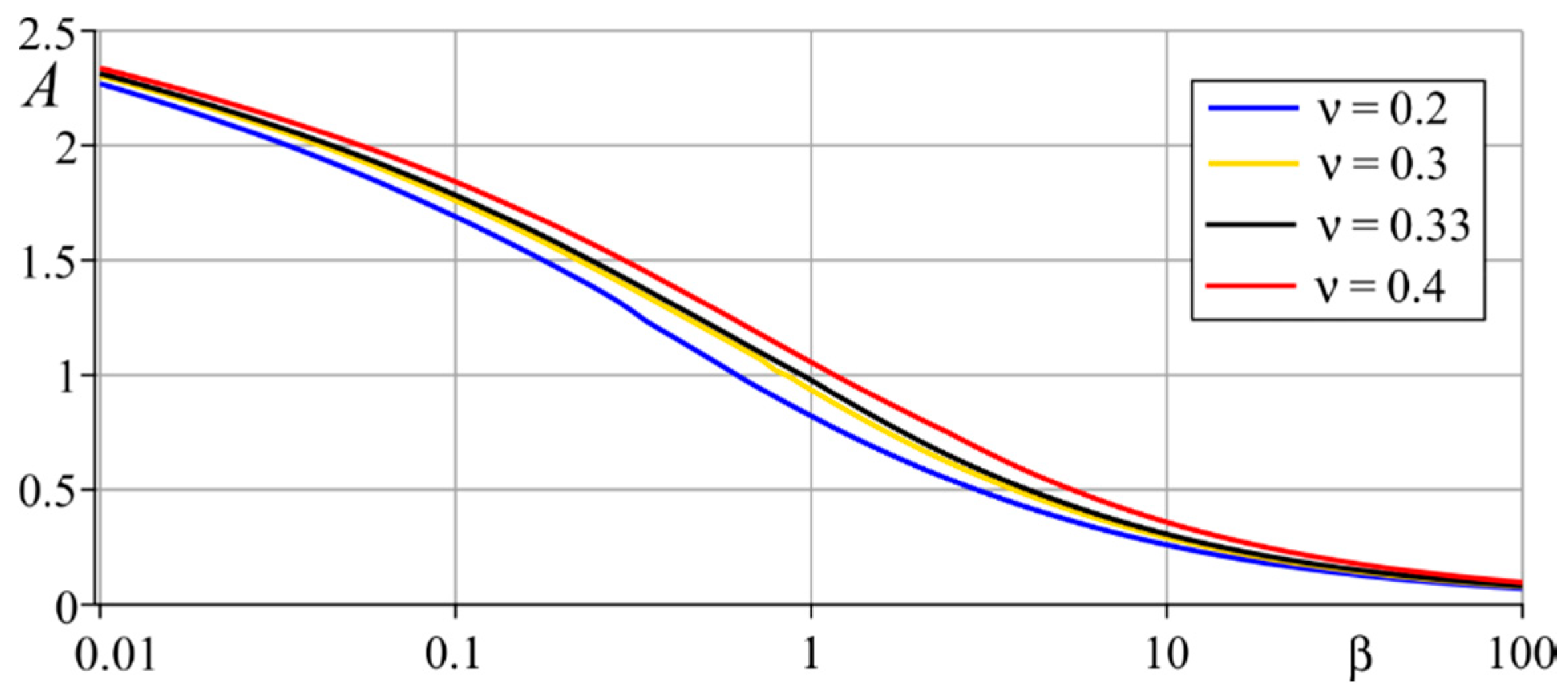
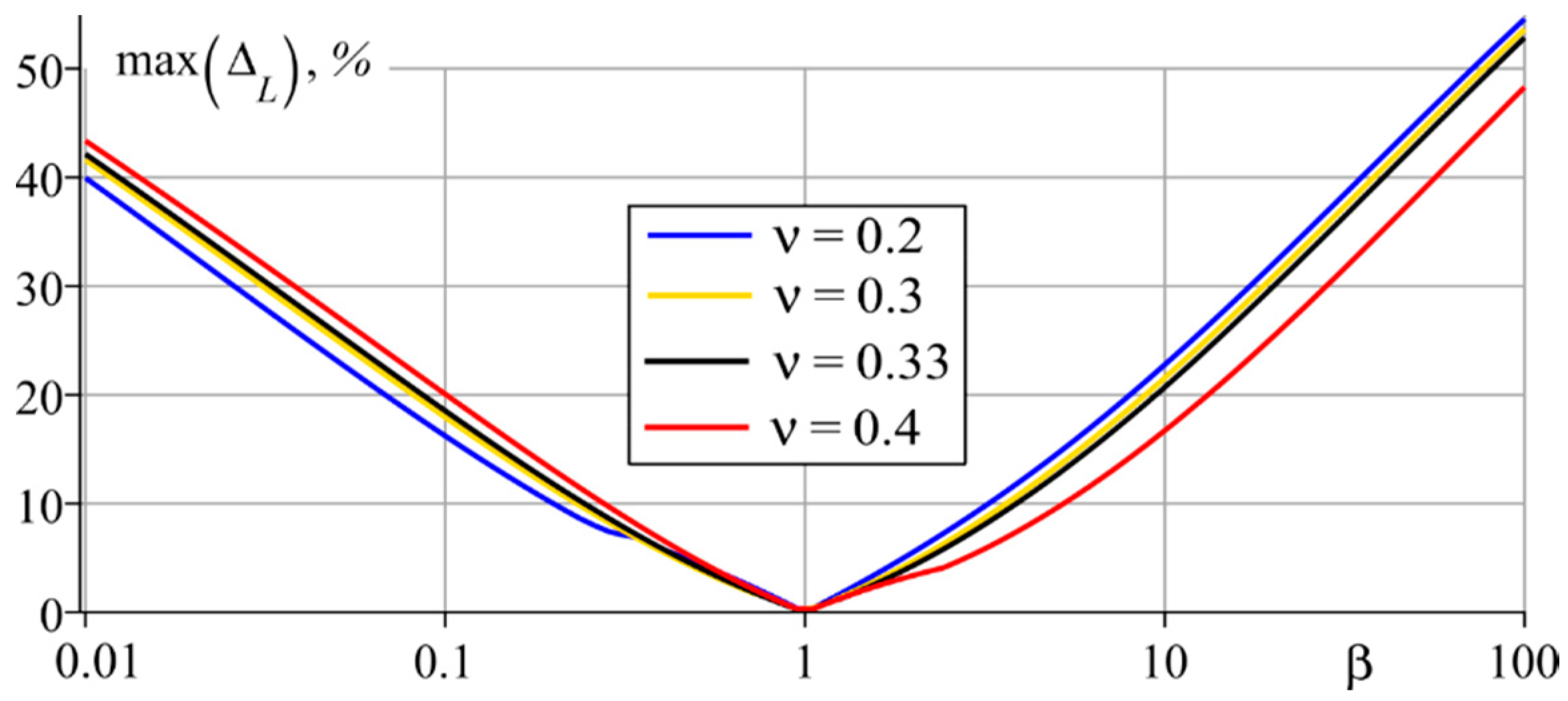
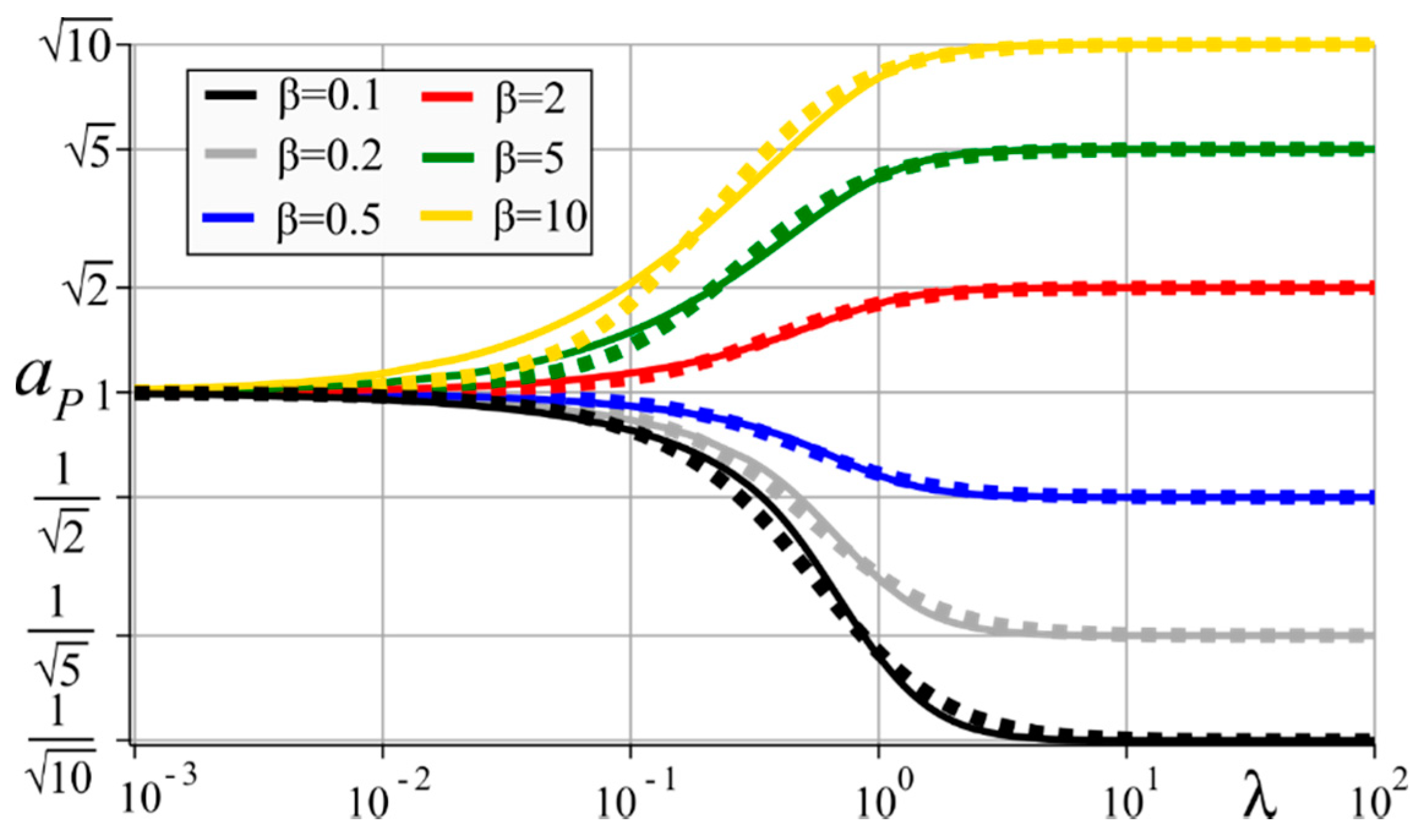
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Asri, R.I.M.; Harun, W.S.W.; Samykano, M.; Lah, N.A.C.; Ghani, S.A.C.; Tarlochan, F.; Raza, M.R. Corrosion and surface modification on biocompatible metals: A review. Mater. Sci. Eng. C 2017, 77, 1261–1274. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Wang, S.; Bi, P.; Zhao, G.; Jin, Y. Super-Hydrophobic Co–Ni Coating with High Abrasion Resistance Prepared by Electrodeposition. Coatings 2019, 9, 232. [Google Scholar] [CrossRef]
- Yang, J.; Odén, M.; Johansson-Jõesaar, M.P.; Esteve, J.; Llanes, L. Mechanical strength of ground WC-Co cemented carbides after coating deposition. Mater. Sci. Eng. A 2017, 689, 72–77. [Google Scholar] [CrossRef]
- Elkhoshkhany, N.; Hafnway, A.; Khaled, A. Electrodeposition and corrosion behavior of nano-structured Ni-WC and Ni-Co-WC composite coating. J. Alloy. Compd. 2017, 695, 1505–1514. [Google Scholar] [CrossRef]
- Zelentsov, V.B.; Mitrin, B.I.; Lubyagin, I.A. Wear resistance of coating materials under the frictional heating conditions. J. Frict. Wear 2017, 38, 265–271. [Google Scholar] [CrossRef]
- Warcholinski, B.; Gilewicz, A.; Kuprin, A.S.; Tolmachova, G.N.; Ovcharenko, V.D.; Kuznetsova, T.A.; Lapitskaya, V.A.; Chizhik, S.A. Comparison of mechanical and tribological properties of nitride and oxynitride coatings based on chrome and zirconium obtained by cathodic arc evaporation. J. Frict. Wear 2019, 40, 163–170. [Google Scholar] [CrossRef]
- Yuan, Z.; Tao, B.; He, Y.; Liu, J.; Lin, C.; Shen, X.; Ding, Y.; Yu, Y.; Mu, C.; Liu, P.; et al. Biocompatible MoS2/PDA-RGD coating on titanium implant with antibacterial property via intrinsic ROS-independent oxidative stress and NIR irradiation. Biomaterials 2019, 217, 119290. [Google Scholar] [CrossRef]
- Mandracci, P.; Mussano, F.; Rivolo, P.; Carossa, S. Surface treatments and functional coatings for biocompatibility improvement and bacterial adhesion reduction in dental implantology. Coatings 2016, 6, 7. [Google Scholar] [CrossRef]
- Golovin, Y.I. Nanoindentation and Its Capabilities; Mashinostroenie: Moscow, Russia, 2009; pp. 8–32. (In Russian) [Google Scholar]
- Ogbonna, N.; Needleman, A. Conical indentation of thick elastic spherical shells. J. Mech. Mater. Struct. 2011, 6, 443–451. [Google Scholar] [CrossRef]
- Taljat, B.; Zacharia, T.; Pharr, G.M. Pile-up behavior of spherical indentations in engineering materials. In Fundamentals of Nanoindentation and Nanotribology; Moody, N.R., Gerberich, W.W., Burnham, N., Baker, S.P., Eds.; Materials Research Society: Warrendale, PA, USA, 1998; Volume 522, p. 33. [Google Scholar]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Sneddon, I.N. The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- ISO 14577-1:2015. Metallic Materials—Instrumented Indentation Test for Hardness and Materials Parameters—Part 1: Test Method. Available online: https://www.iso.org/standard/56626.html (accessed on 13 May 2020).
- Field, J.S.; Swain, M.V. Determining the mechanical properties of small volumes of material from submicrometer spherical indentations. J. Mater. Res. 1995, 10, 101–112. [Google Scholar] [CrossRef]
- Buckle, H. The Science of Hardness Testing and Its Research Applications; American Society for Metals: Cleveland, OH, USA, 1973; pp. 453–491. [Google Scholar]
- Chen, J.; Bull, S.J. On the factors affecting the critical indenter penetration for measurement of coating hardness. Vacuum 2009, 83, 911–920. [Google Scholar] [CrossRef]
- Veprek-Heijman, M.G.; Veprek, S. The deformation of the substrate during indentation into superhard coatings: Bückle’s rule revised. Surf. Coat. Technol. 2015, 284, 206–214. [Google Scholar] [CrossRef]
- Manika, I.; Maniks, J. Effect of substrate hardness and film structure on indentation depth criteria for film hardness testing. J. Phys. D Appl. Phys. 2008, 41, 074010. [Google Scholar] [CrossRef]
- Chen, W.; Xu, K.; Tao, B.; Dai, L.; Yu, Y.; Mu, C.; Shen, X.; Hu, Y.; He, Y.; Cai, K. Multilayered coating of titanium implants promotes coupled osteogenesis and angiogenesis in vitro and in vivo. Acta Biomater. 2018, 74, 489–504. [Google Scholar] [CrossRef]
- Go, A.; Kim, H.T.; Park, Y.J.; Park, S.R.; Lee, M.H. Fabrication of Repeatedly Usable Pt-Electrode Chip Coated With Solidified Glucose Oxidase and Ascorbate Oxidase for the Quantification of Glucose in Urine. IEEE Sens. Lett. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Mohanty, A.; Gangopadhyay, S.; Thakur, A. On applicability of multilayer coated tool in dry machining of aerospace grade stainless steel. Mater. Manuf. Process. 2016, 31, 869–879. [Google Scholar] [CrossRef]
- Nikitin, V.I.; Smyslov, A.M.; Lisyansky, A.S.; Smyslova, M.K.; Simin, O.N.; Shelyapina, N.M. Corrosion resistance of nitride coatings of steam turbine blades. Therm. Power Eng. 2009, 2, 2–6. (In Russian) [Google Scholar]
- Sneddon, I.N. Fourier Transforms; McGraw-Hill: New York, NY, USA, 1951. [Google Scholar]
- Gladwell, G.M.L. Contact Problems in the Classical Theory of Elasticity; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Alexandrov, V.M.; Pozharskii, D.A. Three-Dimensional Contact Problems; Solid Mechanics and Its Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Vorovich, I.I.; Ustinov, I.A. Pressure of a die on an elastic layer of finite thickness. J. Appl. Math. Mech. 1959, 23, 637–650. [Google Scholar] [CrossRef]
- Alexandrov, V.M. Asymptotic solution of the contact problem for a thin elastic layer. J. Appl. Math. Mech. 1969, 33, 49–63. [Google Scholar] [CrossRef]
- Zelentsov, V.B.; Lapina, P.A.; Mitrin, B.I.; Eremeyev, V.A. Characterization of the functionally graded shear modulus of a half-space. Mathematics 2020, 8, 640. [Google Scholar] [CrossRef]
- Zelentsov, V.B.; Sakhabudinov, R.V. Uniform motion of a plane punch on the boundary of an elastic half-plane. Mech. Solids 2014, 49, 208–217. [Google Scholar] [CrossRef]
- Zelentsov, V.B.; Lapina, P.A.; Mitrin, B.I.; Kudish, I.I. An antiplane deformation of a functionally graded half-space. Contin. Mech. Thermodyn. 2019. [Google Scholar] [CrossRef]
- Popov, G.I. On the method of orthogonal polynomials in contact problems of the theory of elasticity. J. Appl. Math. Mech. 1969, 33, 503–517. [Google Scholar] [CrossRef]
- Liu, T.J.; Wang, Y.S.; Xing, Y.M. The axisymmetric partial slip contact problem of a graded coating. Meccanica 2012, 47, 1673–1693. [Google Scholar] [CrossRef]
- Guler, M.A.; Erdogan, F. Contact mechanics of two deformable elastic solids with graded coatings. Mech. Mater. 2006, 38, 633–647. [Google Scholar] [CrossRef]
- Su, J.; Ke, L.L.; Wang, Y.S. Axisymmetric frictionless contact of a functionally graded piezoelectric layered half-space under a conducting punch. Int. J. Solids Struct. 2019, 90, 45–59. [Google Scholar] [CrossRef]
- Ke, L.L.; Yang, J.; Kitipornchai, S.; Wang, Y.S. Electro-mechanical frictionless contact behavior of a functionally graded piezoelectric layered half-plane under a rigid punch. Int. J. Solids Struct. 2008, 45, 3313–3333. [Google Scholar] [CrossRef]
- Su, J.; Ke, L.-L.; Wang, Y.-S.; Xiang, Y. The axisymmetric torsional contact problem of a functionally graded piezoelectric coated half-space. Acta Mech. Sin. 2017, 33, 406–414. [Google Scholar] [CrossRef]
- Vasiliev, A.S.; Volkov, S.S.; Aizikovich, S.M. Approximated Analytical Solution of a Problem on Indentation of an Electro-Elastic Half-Space with Inhomogeneous Coating by a Conductive Punch. Doklady Phys. 2018, 63, 18–22. [Google Scholar] [CrossRef]
- Wang, L.; Rokhlin, S.I. Universal scaling functions for continuous stiffness nanoindentation with sharp indenters. Int. J. Solids Struct. 2005, 42, 3807–3832. [Google Scholar] [CrossRef]
- Ogasawara, N.; Chiba, N.; Chen, X. Representative strain of indentation analysis. J. Mater. Res. 2005, 20, 2225–2234. [Google Scholar] [CrossRef]
- Vasiliev, A.S.; Swain, M.V.; Aizikovich, S.M.; Sadyrin, E.V. Torsion of a circular punch attached to an elastic half-space with a coating with periodically depth-varying elastic properties. Arch. Appl. Mech. 2016, 86, 1247–1254. [Google Scholar] [CrossRef]
- Vasiliev, A.S.; Volkov, S.S.; Belov, A.A.; Litvinchuk, S.Y.; Aizikovich, S.M. Indentation of a hard transversely isotropic functionally graded coating by a conical indenter. Int. J. Eng. Sci. 2017, 112, 63–75. [Google Scholar] [CrossRef]
- Aizikovich, S.M.; Vasil’ev, A.S.; Volkov, S.S. The axisymmetric contact problem of the indentation of a conical punch into a half-space with a coating inhomogeneous in depth. J. Appl. Math. Mech. 2015, 79, 500–505. [Google Scholar] [CrossRef]
- Sadyrin, E.V.; Vasiliev, A.S.; Volkov, S.S.; Mitrin, B.I.; Aizikovich, S.M. Simplified analytical solution of the contact problem on indentation of a coated half-space by a spherical punch. WIT Trans. Eng. Sci. 2019, 122, 209–221. [Google Scholar]
- Vasiliev, A.S.; Sadyrin, E.V.; Volkov, S.S.; Kislyakov, E.A.; Sevostianov, I. Construction of the simplified analytical solution of the flat punch indentation contact problem. AIP Conf. Proc. 2019, 2188, 040017. [Google Scholar]
- Vasiliev, A.S. Compliance functions of electromagnetoelastic piezoelectric and piezomagnetic half-plane and half-space with functionally graded or layered coatings. J. Samara State Tech. Univ. Ser. Phys. Math. Sci. 2019, 23, 475–496. [Google Scholar]
- Volkov, S.S.; Vasiliev, A.S.; Aizikovich, S.M.; Sadyrin, E.V. Compliance functions for a thermoelastic FGM coated half-plane with incomplete adhesion between the coating and substrate. J. Phys. Conf. Ser. 2020, 1474, 012034. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Ronnquist, A.; Navik, P.; Liu, Z. Contact Wire Irregularity Stochastics and Effect on High-speed Railway Pantograph-Catenary Interactions. IEEE Trans. Instrum. Meas. 2020. [Google Scholar] [CrossRef]
- Peng, B.; Iwnicki, S.; Shackleton, P.; Song, Y. General conditions for railway wheel polygonal wear to evolve. Veh. Syst. Dyn. 2019. [Google Scholar] [CrossRef]


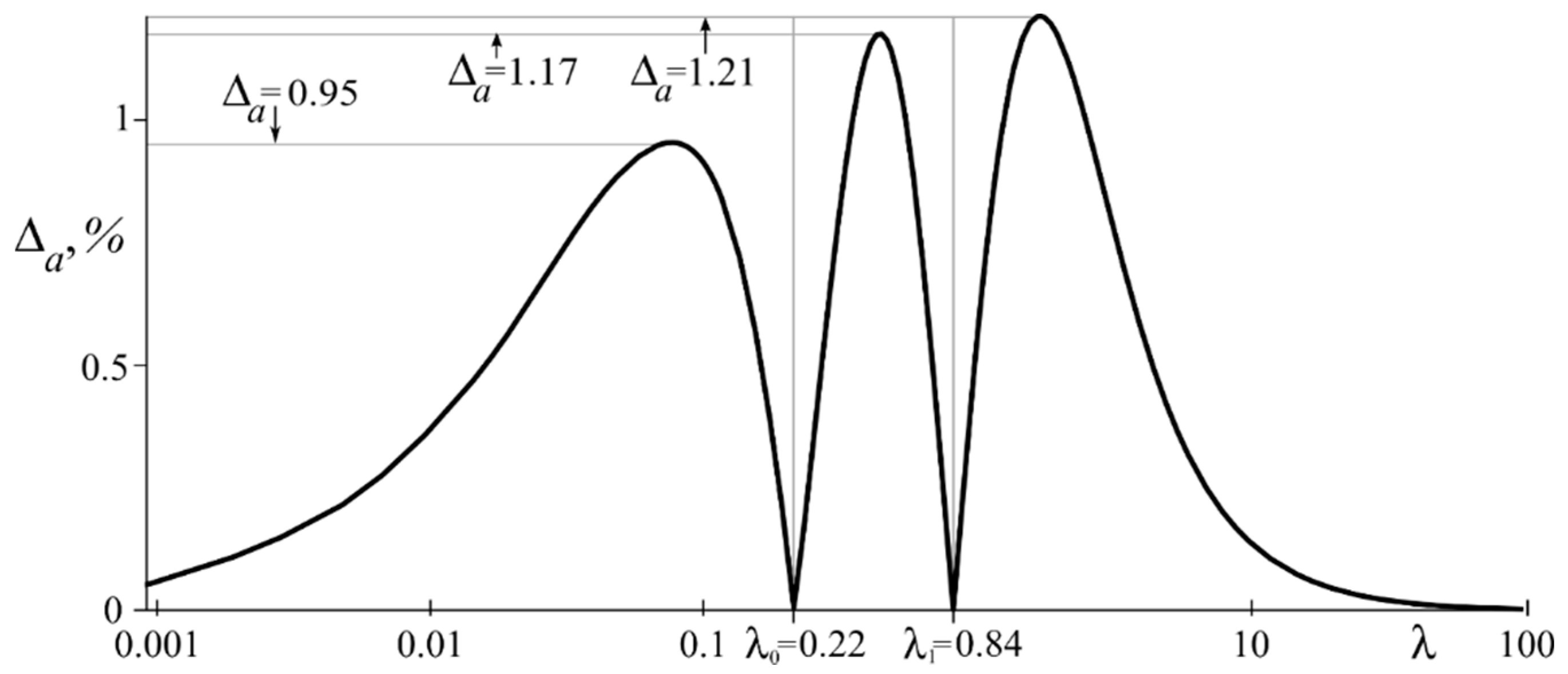
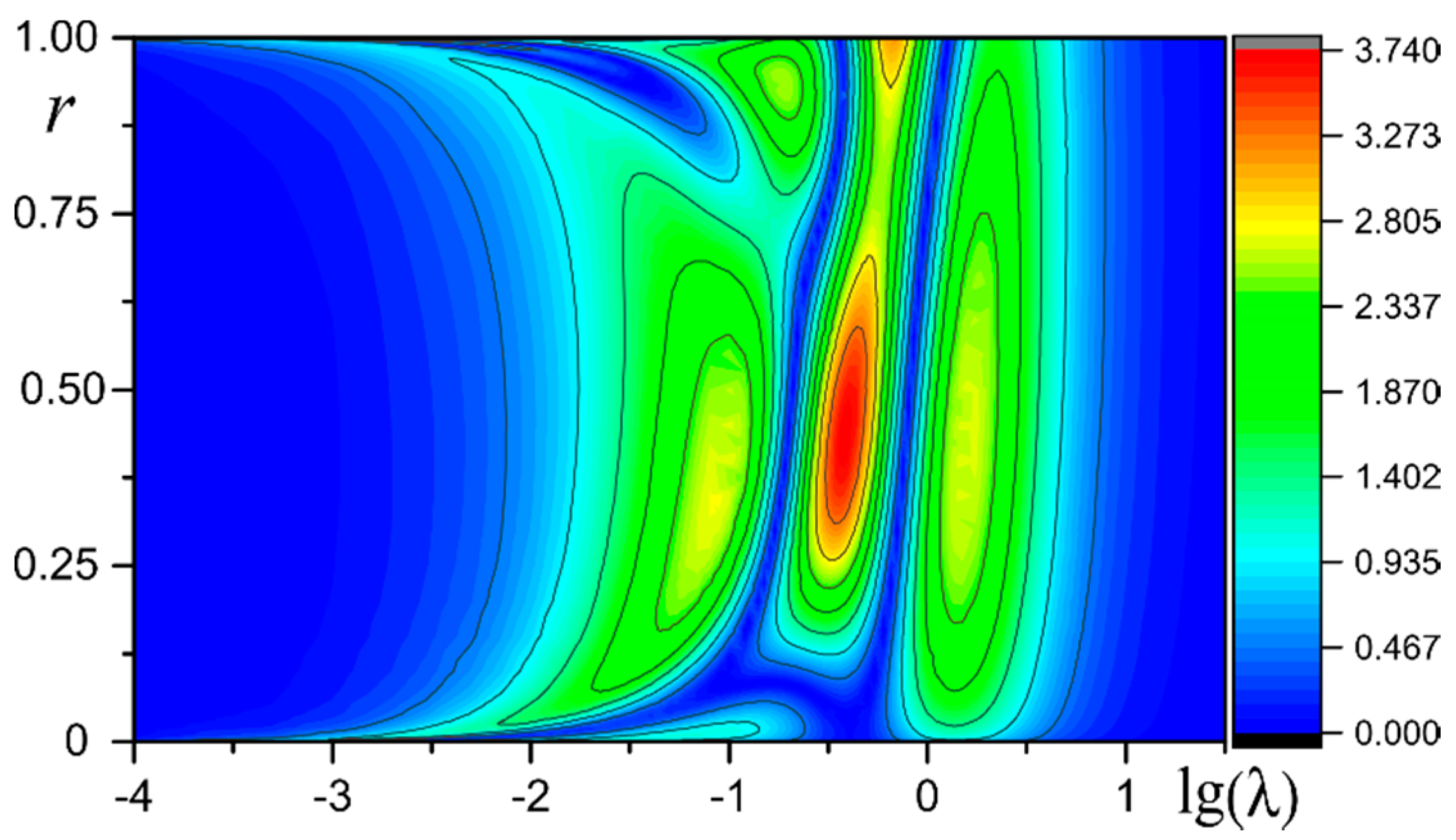
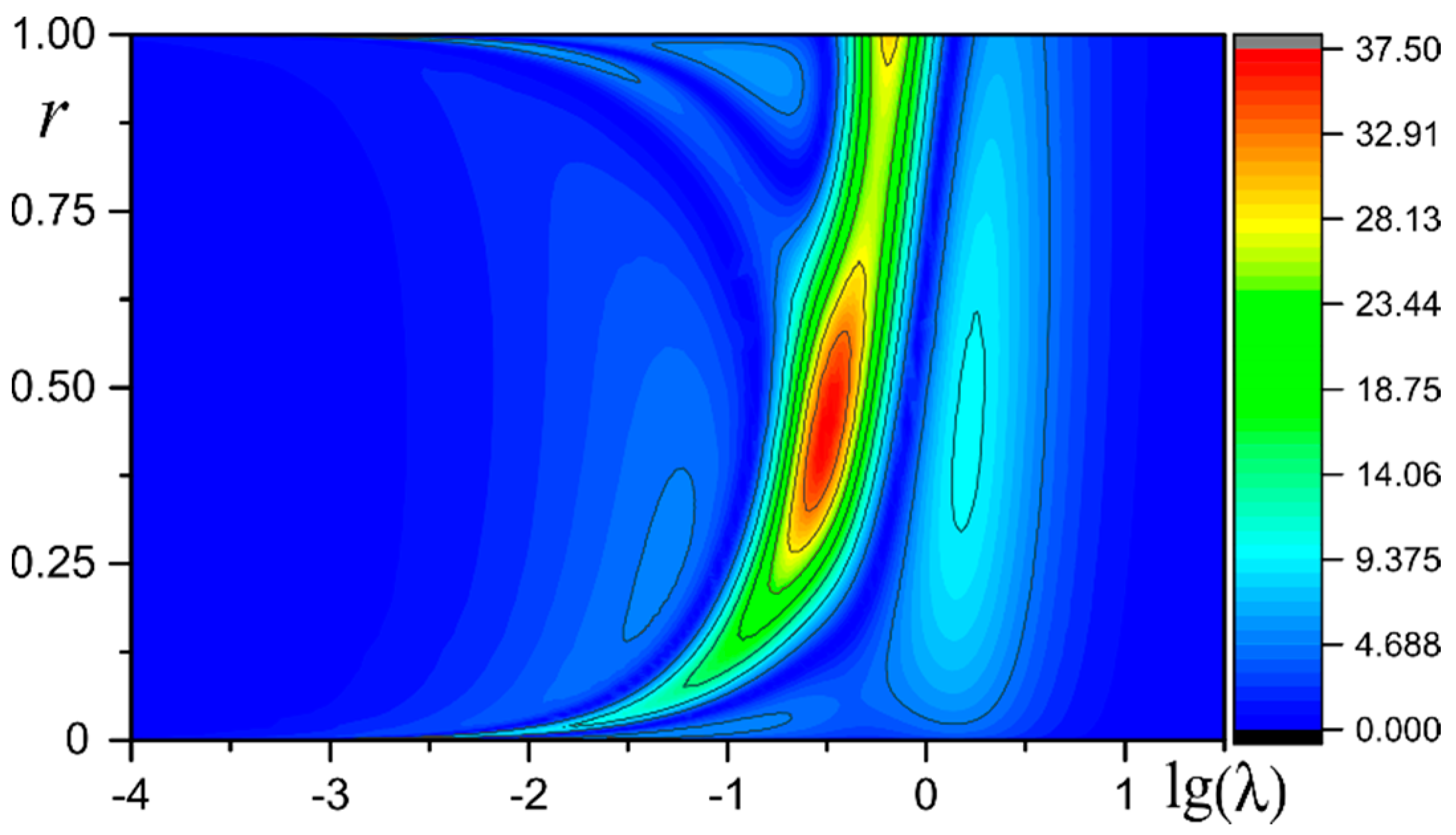
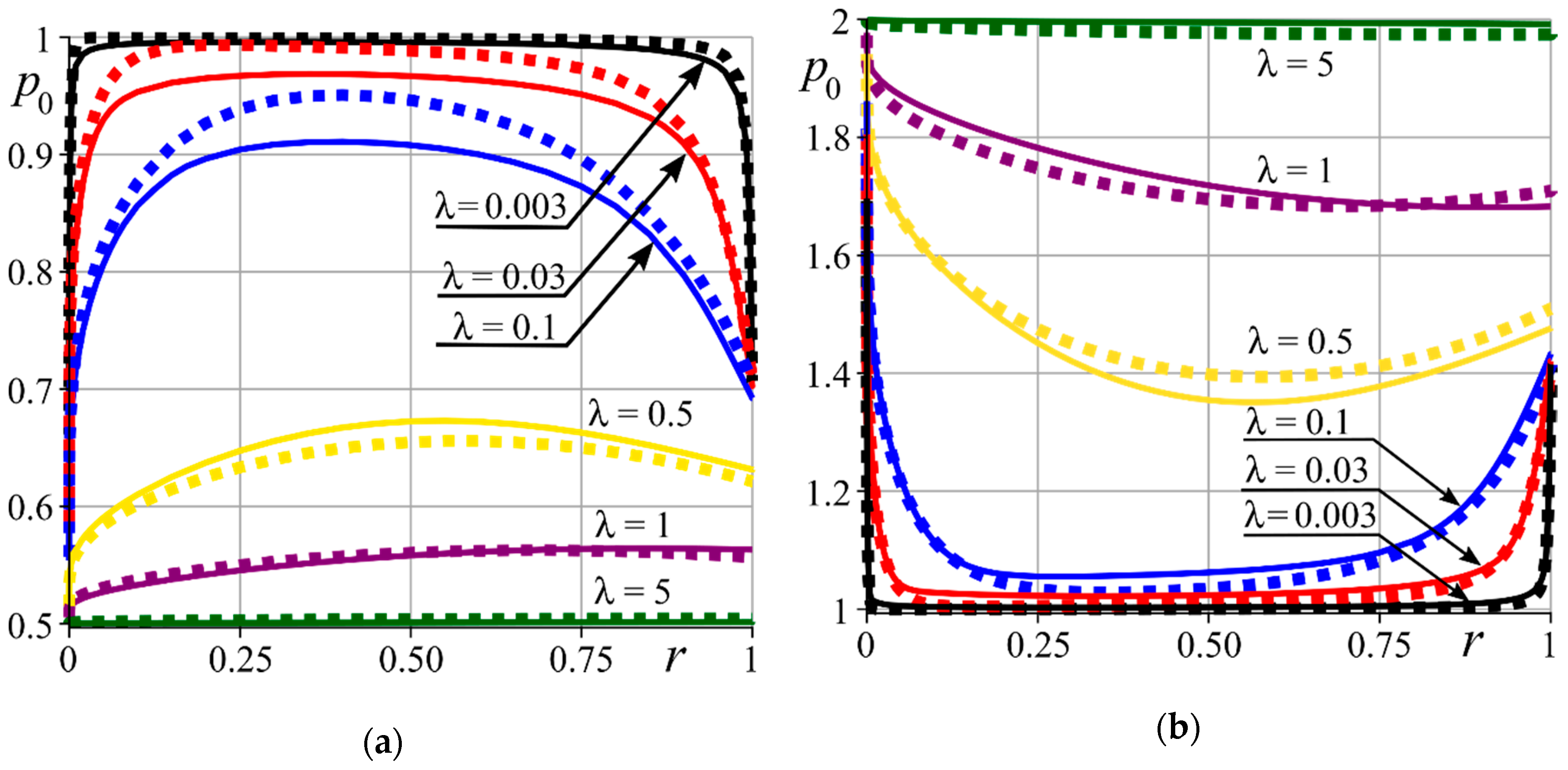
| β = 2 | β = 5 | β = 10 | ||||
|---|---|---|---|---|---|---|
| 0.28 | 0.36 | 0.5 | 0.52 | 0.38 | 0.31 | |
| 6.8 | 3.3 | 1.85 | 1.65 | 2.6 | 4.7 | |
| , % | 1.68 | 1.49 | 0.95 | 1.64 | 5.08 | 8.99 |
| , % | 6.42 | 2.98 | 0.56 | 0.46 | 2.28 | 4.58 |
| , % | 0.49 | 0.88 | 0.62 | 0.43 | 0.38 | 0.18 |
| β = 2 | β = 5 | β = 10 | ||||
|---|---|---|---|---|---|---|
| 0.09 | 0.14 | 0.22 | 0.25 | 0.21 | 0.18 | |
| 0.9 | 0.88 | 0.84 | 0.95 | 1.15 | 1.35 | |
| , % | 1.42 | 1.35 | 0.95 | 1.69 | 5.06 | 8.62 |
| , % | 7.23 | 4.11 | 1.17 | 1.11 | 3.7 | 6.39 |
| , % | 4.56 | 3.11 | 1.21 | 0.72 | 0.94 | 0.82 |
| β = 2 | β = 5 | β = 10 | ||||
|---|---|---|---|---|---|---|
| 0.27 | 0.36 | 0.5 | 0.52 | 0.39 | 0.31 | |
| 6.2 | 3.3 | 1.88 | 1.7 | 2.6 | 4.7 | |
| , % | 1.71 | 1.51 | 0.96 | 1.61 | 4.9 | 8.5 |
| , % | 6.03 | 2.89 | 0.55 | 0.46 | 2.33 | 4.8 |
| , % | 0.49 | 0.89 | 0.62 | 0.43 | 0.38 | 0.18 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasiliev, A.S.; Volkov, S.S.; Sadyrin, E.V.; Aizikovich, S.M. Simplified Analytical Solution of the Contact Problem on Indentation of a Coated Half-Space by a Conical Punch. Mathematics 2020, 8, 983. https://doi.org/10.3390/math8060983
Vasiliev AS, Volkov SS, Sadyrin EV, Aizikovich SM. Simplified Analytical Solution of the Contact Problem on Indentation of a Coated Half-Space by a Conical Punch. Mathematics. 2020; 8(6):983. https://doi.org/10.3390/math8060983
Chicago/Turabian StyleVasiliev, Andrey S., Sergey S. Volkov, Evgeniy V. Sadyrin, and Sergei M. Aizikovich. 2020. "Simplified Analytical Solution of the Contact Problem on Indentation of a Coated Half-Space by a Conical Punch" Mathematics 8, no. 6: 983. https://doi.org/10.3390/math8060983
APA StyleVasiliev, A. S., Volkov, S. S., Sadyrin, E. V., & Aizikovich, S. M. (2020). Simplified Analytical Solution of the Contact Problem on Indentation of a Coated Half-Space by a Conical Punch. Mathematics, 8(6), 983. https://doi.org/10.3390/math8060983




