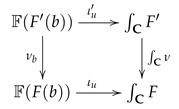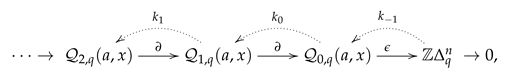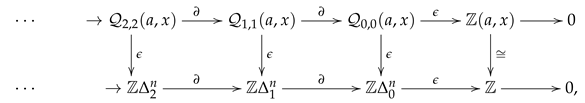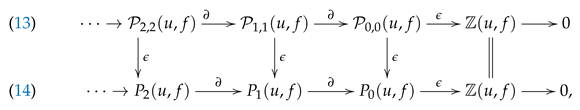Cohomology of Homotopy Colimits of Simplicial Sets and Small Categories

Abstract

This paper deals with well-known weak homotopy equivalences that relate homotopy colimits of small categories and simplicial sets. We show that these weak homotopy equivalences have stronger cohomology-preserving properties than for local coefficients.

1. Introduction

Since the 1980 paper by Thomason [1], we know that the categories $\mathbf{SSet}$, of simplicial sets, and $\mathbf{Cat}$, of small categories, are equivalent from a homotopical point of view. Indeed, there are several basic functorial constructions by which one can pass freely between these categories, preserving all the homotopy invariants of their objects and morphisms. For instance, we have the functor $\mathrm{N}:\mathbf{Cat}\to \mathbf{SSet}$ which assigns to each small category $\mathbf{C}$ its nerve $\mathrm{N}(\mathbf{C})$, and the functor $\mathsf{\Delta }:\mathbf{SSet}\to \mathbf{Cat}$ sending each simplicial set X to its category of simplices $\mathsf{\Delta }(X)$.

Nevertheless, there are interesting algebraic constructions, both on simplicial sets and on small categories, that are not invariants of their homotopy type. This is the case for Gabriel–Zisman cohomology groups $H^n(X,\mathcal{A})$ ([2] Appendix II), of simplicial sets X with arbitrary coefficient systems on them, that is, with coefficients in abelian group valued functors $\mathcal{A}:\mathsf{\Delta }(X)\to \mathbf{Ab}$. Recall from Quillen ([3] II §3, Prop. 4) that a simplicial map $f:Y\to X$ is a weak homotopy equivalence if and only if it induces an equivalence of fundamental groupoids $\mathsf{\Pi }(X)\simeq \mathsf{\Pi }(Y)$, as well isomorphisms $H^n(X,\mathcal{A})\cong H^n(Y,f^{*}A)$, for all $n\ge 0$, whenever $\mathcal{A}$ is a local coefficient system on X, that is, whenever $\mathcal{A}$ is a morphism-inverting functor or, equivalently, if $\mathcal{A}:\mathsf{\Pi }(X)\to \mathbf{Ab}$ is actually an abelian group valued functor on the fundamental groupoid of X. Similarly, Baues–Wirsching cohomology groups$H^n(\mathbf{C},\mathcal{A})$ [4], of a small category $\mathbf{C}$ with coefficients in natural systems$\mathcal{A}$ on it, that is, with coefficients in abelian group valued functors on its category of factorizations $\mathcal{A}:\mathbb{F}(\mathbf{C})\to \mathbf{Ab}$, are homotopy invariants of $\mathbf{C}$ only for local coefficients $\mathcal{A}:\mathsf{\Pi }(\mathbf{C})\to \mathbf{Ab}$.

There are, however, some particular weak homotopy equivalences that have a stronger conservation property of cohomology than for local coefficients. For instance, for any small category $\mathbf{C}$, the morphism between end vertices functor$e:\mathsf{\Delta }\mathrm{N}(\mathbf{C})\to \mathbb{F}(\mathbf{C})$ is a weak homotopy equivalence of categories which induces isomorphisms $H^n(\mathbf{C},\mathcal{A})\cong H^n(\mathrm{N}(\mathbf{C}),e^{*}\mathcal{A})$ for any natural system of coefficients $\mathcal{A}$ on $\mathbf{C}$. The aim of this paper is to prove that two relevant and well-known weak homotopy equivalences have similar strong cohomology-preserving properties. These come respectively associated to diagrams of small categories and simplicial sets. The first of them arises from the seminal Homotopy Colimit Theorem by Thomason ([5] Theorem 1.2). This theorem states that, for any indexing small category $\mathbf{C}$ and any functor $F:{\mathbf{C}}^{op}\to \mathbf{Cat}$, there is a natural weak homotopy equivalence of simplicial sets

$$\eta :{\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F\to \mathrm{N}({\int }_{\mathbf{C}}F)$$

between the homotopy colimit of the $\mathbf{C}$-diagram of simplicial sets $\mathrm{N}F$, obtained by applying the nerve construction $\mathrm{N}(F(c))$ to each category $F(c)$, and the nerve of the category obtained by applying the Grothendieck construction on F, see (9) below for details. Thus, the Grothendieck construction on a diagram of small categories represents its homotopy colimit with respect to the Thomason model structure in $\mathbf{Cat}$ [1]. Since one easily sees that the simplicial map $\eta$ induces an isomorphism between the associated fundamental groupoids $\mathsf{\Pi }({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F)\cong \mathsf{\Pi }(\mathrm{N}{\int }_{\mathbf{C}}F)=\mathsf{\Pi }({\int }_{\mathbf{C}}F)$ (see ([5] p. 95)), Thomason’s theorem is actually equivalent to the fact that $\eta$ induces isomorphisms

$$H^n({\int }_{\mathbf{C}}F,\mathcal{A})\cong H^n({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F,{\eta }^{*}\mathcal{A})(n\ge 0)$$

(1)

for every local coefficient system $\mathcal{A}:\mathsf{\Pi }({\int }_{\mathbf{C}}F)\to \mathbf{Ab}$ on the category ${\int }_{\mathbf{C}}F$. We prove here the following stronger result.

Theorem 1.

For any natural system $\mathcal{A}:\mathbb{F}({\int }_{\mathbf{C}}F)\to \mathbf{Ab}$, the isomorphisms (Equation (1)) hold.

The proof we give of this theorem is independent of that given by Thomason in [5] of his Homotopy Colimit Theorem, so that this latter appears now as a consequence.

Going in the opposite direction, we also consider diagrams of simplicial sets. For any functor $G:{\mathbf{C}}^{op}\to \mathbf{SSet}$, there is a known natural weak homotopy equivalence in $\mathbf{Cat}$

$$\mu :\mathsf{\Delta }({\mathrm{hocolim}}_{\mathbf{C}}G)\to {\int }_{\mathbf{C}}\mathsf{\Delta }G,$$

between the category of simplices of the homotopy colimit of G and the Grothendieck construction on the diagram of small categories $\mathsf{\Delta }G$, obtained by applying the category of simplices construction $\mathsf{\Delta }(G(c))$ to each simplicial set $G(c)$, see Equation (29) below for details. Then, for any local coefficient system $\mathcal{A}:\mathsf{\Pi }({\int }_{\mathbf{C}}\mathsf{\Delta }G)\to \mathbf{Ab}$, the functor $\mu$ induces isomorphisms

$$H^n({\int }_{\mathbf{C}}\mathsf{\Delta }G,\mathcal{A})\cong H^n({\mathrm{hocolim}}_{\mathbf{C}}G,{\mu }^{*}\mathcal{A})(n\ge 0).$$

(2)

Our second main result in the paper is the following.

Theorem 2.

For any coefficient system $\mathcal{A}:{\int }_{\mathbf{C}}\mathsf{\Delta }G\to \mathbf{Ab}$, the isomorphisms (Equation (2)) hold.

We show several consequences of the above theorems. For instance, given a functor $F:{\mathbf{C}}^{op}\to \mathbf{Cat}$ and a natural system $\mathcal{A}$ on ${\int }_{\mathbf{C}}F$, for any morphism $u:c^{\prime }\to c$ in $\mathbf{C}$, there is an induced natural system ${\iota }_u^{*}\mathcal{A}$ on the category $F(c)$. We describe a first quadrant spectral sequence

$$E_2^{p,q}=H^p(\mathbf{C},{\mathcal{H}}^q(F,{\iota }^{*}\mathcal{A}))\Rightarrow H^{p+q}({\int }_{\mathbf{C}}F,\mathcal{A}),$$

where ${\mathcal{H}}^q(F,{\iota }^{*}\mathcal{A})$ is the natural system on $\mathbf{C}$ that assigns to each morphism $u:c^{\prime }\to c$ the cohomology group $H^q(F(c),{\iota }_u^{*}\mathcal{A})$. This spectral sequence reduces to that constructed by Pirashvili–Redondo in ([6] Theorem 5.2) when the natural system of coefficients $\mathcal{A}$ is h-local (see also Gálvez–Neumann–Tonks ([7] Theorem 2.5) and ([8] Theorem 2.16)). In the other direction, given a functor $G:{\mathbf{C}}^{op}\to \mathbf{SSet}$, for a coefficient system $\mathcal{A}$ on ${\int }_{\mathbf{C}}\mathsf{\Delta }G$ and an object c of $\mathbf{C}$, there is an induced coefficient system ${\iota }_c^{*}\mathcal{A}$ on the simplicial set $G(c)$. We describe a Bousfield–Kan type first quadrant spectral sequence (cf. ([9] XII, 4.5, 5.8))

$$E_2^{p,q}=H^p(\mathbf{C},{\mathcal{H}}^q(G,{\iota }^{*}\mathcal{A}))\Rightarrow H^{p+q}({\mathrm{hocolim}}_{\mathbf{C}}G,{\mu }^{*}\mathcal{A}),$$

where ${\mathcal{H}}^q(G,{\iota }^{*}\mathcal{A}):\mathbf{C}\to \mathbf{Ab}$ is the functor that assigns to each object c of $\mathbf{C}$ the cohomology group $H^q(G(c),{\iota }_c^{*}\mathcal{A})$. Various invariance results appears here as corollaries. Some of them are already known, such as the Invariance Theorem by Moerdijk–Svensson ([10] Theorem 2.3), but others are new. For example, if $F,F^{\prime }:{\mathbf{C}}^{op}\to \mathbf{Cat}$ are diagrams of categories and $\nu :F^{\prime }\Rightarrow F$ a natural transformation such that every functor ${\nu }_c:F^{\prime }(c)\to F(c)$, $c\in \mathrm{Ob}\mathbf{C}$, is a weak homotopy equivalence having the Baues–Wirsching cohomology-preserving property, then the induced ${\int }_{\mathbf{C}}\nu :{\int }_{\mathbf{C}}{F}^{\prime }\to {\int }_{\mathbf{C}}F$ is also a weak homotopy equivalence with the same cohomology-preserving property.

The plan of the paper is simple. After this introductory section, the preliminary Section 2 comprises some notations and a brief review of notions and facts concerning cohomology of small categories and simplicial sets, and Section 3 and Section 4 are essentially dedicated to proving Theorems 1 and 2 above, respectively. Although the proofs of both theorems follow a similar strategy, they are independent.

2. Preliminaries

This section aims to make this paper as self-contained as possible; hence, at the same time as fixing notations and terminology, we review some needed constructions and facts concerning cohomology of small categories and simplicial sets.

Throughout the paper, the composition of maps between sets, homomorphisms between abelian groups, and functors between categories, is written by juxtaposition. The composition of arrows in any abstract small category $\mathbf{C}$ is denoted by the symbol ∘.

2.1. Cohomology of Small Categories

If $\mathbf{C}$ is any small category, then the category of $\mathbf{C}$-modules, denoted $\mathbf{C}$-Mod, has as objects the abelian group valued functors $\mathcal{A}:\mathbf{C}\to \mathbf{Ab}$, with morphisms the natural transformations between them. If $\mathcal{A}$ is any $\mathbf{C}$-module and $u:a\to b$ is a morphism in $\mathbf{C}$, then we write the associated homomorphism $\mathcal{A}(u)$ by $u_{*}:\mathcal{A}(a)\to \mathcal{A}(b)$.

The category $\mathbf{C}$-Mod is abelian. We refer to Mac Lane ([11] Chapter IX, §3) for details, but recall that the set of morphisms between two $\mathbf{C}$-modules $\mathcal{A}$ and ${\mathcal{A}}^{\prime }$, denoted by ${\mathrm{Hom}}_{\mathbf{C}}(\mathcal{A},{\mathcal{A}}^{\prime })$, is an abelian group by pointwise addition, that is, if $f,g:\mathcal{A}\to {\mathcal{A}}^{\prime }$ are morphisms, then $f+g:\mathcal{A}\to {\mathcal{A}}^{\prime }$ is defined by setting ${(f+g)}_a=f_a+g_a$, for each object $a\in \mathrm{Ob}\mathbf{C}$. The zero $\mathbf{C}$-module is the constant functor $0:\mathbf{C}\to \mathbf{Ab}$ defined by the trivial abelian group 0, and a sequence of $\mathbf{C}$-modules $\mathcal{A}\to {\mathcal{A}}^{\prime }\to {\mathcal{A}}^{″}$ is exact if and only if all the induced sequences of abelian groups $\mathcal{A}(a)\to {\mathcal{A}}^{\prime }(a)\to {\mathcal{A}}^{″}(a)$ are exact.

Furthermore, the category $\mathbf{C}$-Mod has enough projective objects. A way to see this is by means of free $\mathbf{C}$-modules: There is a forgetful functor $\mathcal{U}:\mathbf{C}-\mathrm{Mod}\to \mathbf{Set}\downarrow {}_{\mathrm{Ob}\mathbf{C}}$, from the category of $\mathbf{C}$-modules to the comma category of sets over the set of objects of $\mathbf{C}$, which carries a $\mathbf{C}$-module $\mathcal{A}$ to the disjoint union set

$$\mathcal{U}\mathcal{A}={\bigcup }_{a\in \mathrm{Ob}\mathbf{C}}\mathcal{A}(a)=\{(a,x)\mid a\in \mathrm{Ob}\mathbf{C},x\in \mathcal{A}(a)\},$$

endowed with the projection map $\pi :\mathcal{U}\mathcal{A}\to \mathrm{Ob}\mathbf{C}$, given by $\pi (a,x)=a$. If $f:\mathcal{A}\to {\mathcal{A}}^{\prime }$ is any morphism of $\mathbf{C}$-modules, then $\mathcal{U}f:\mathcal{U}\mathcal{A}\to \mathcal{U}{\mathcal{A}}^{\prime }$ is defined by $\mathcal{U}f(a,x)=(a,f_a(x))$. This functor $\mathcal{U}$ has a left adjoint, the free $\mathbf{C}$-module functor, $\mathcal{F}:\mathbf{Set}\downarrow {}_{\mathrm{Ob}\mathbf{C}}\to \mathbf{C}-\mathrm{Mod}$, which is defined as follows. If $S=(S,\pi :S\to \mathrm{Ob}\mathbf{C})$ is any set over $\mathrm{Ob}\mathbf{C}$, then

$$\mathcal{F}S=\underset{s\in S}{⨁}\mathbb{Z}{\mathrm{Hom}}_{\mathbf{C}}(\pi s,-)$$

is the $\mathbf{C}$-module that assigns to each $a\in \mathrm{Ob}\mathbf{C}$ the free abelian group $\mathcal{F}S(a)=\mathbb{Z}\{(s,u)\}$ with generators all pairs $(s,u)$ consisting of an element $s\in S$ together with a morphism $u:\pi s\to a$ of $\mathbf{C}$. We usually write $(s,i{d}_{\pi s})$ simply by s, so that each element of $s\in S$ is regarded as an element of $\mathcal{F}S(\pi s)$. For any morphism $v:a\to b$ in $\mathbf{C}$, the homomorphism $v_{*}:\mathcal{F}S(a)\to \mathcal{F}S(b)$ is defined on generators by $v_{*}(s,u)=(s,v\circ u)$. Thus, for any generator $(s,u)$ of $\mathcal{F}S(a)$, we have the equality $u_{*}(s)=(s,u)$, where $u_{*}:\mathcal{F}S(\pi s)\to FS(a)$ is the homomorphism induced by u. If $\lambda :S\to S^{\prime }$ is any map of sets over $\mathrm{Ob}\mathbf{C}$ (so that ${\pi }^{\prime }\lambda =\pi$), the induced $\mathcal{F}\lambda :\mathcal{F}S\to \mathcal{F}{S}^{\prime }$ is the morphism whose component at an object a of $\mathbf{C}$ is the homomorphism ${(\mathcal{F}\lambda )}_a:\mathcal{F}S(a)\to \mathcal{F}{S}^{\prime }(a)$ such that ${(\mathcal{F}\lambda )}_a(s,u)=(\lambda (s),u)$.

Proposition 1.

The functor $\mathcal{F}$ is left adjoint to the functor $\mathcal{U}$. Thus, for $S=(S,\pi )$ any set over $\mathrm{Ob}\mathbf{C}$ and any $\mathbf{C}$-module $\mathcal{A}$, there is a natural isomorphism

$${\mathrm{Hom}}_{\mathbf{C}}(\mathcal{F}S,\mathcal{A})\cong \mathsf{\prod }_{s\in S}\mathcal{A}(\pi s),f\mapsto {\left(f_{\pi s}(s)\right)}_{s\in S}.$$

Proof. 

This follows from the Yoneda Lemma. For any list $\phi \in {\mathsf{\prod }}_{s\in S}\mathcal{A}(\pi s)$, the unique morphism of $\mathbf{C}$-modules $f:\mathcal{F}S\to \mathcal{A}$ such that $f_{\pi s}(s)=\phi (s)$, for all $s\in S$, consists of the homomorphisms $f_a:\mathcal{F}S(a)\to \mathcal{A}(a)$, $a\in \mathrm{Ob}\mathbf{C}$, defined on generators by $f_a(s,u)=u_{*}\phi (s)$. □

From the above proposition, it is plain to see that any free $\mathbf{C}$-module is projective and, moreover, the counit $\mathcal{F}\mathcal{U}\mathcal{A}\to \mathcal{A}$ is a projective presentation of any $\mathbf{C}$-module $\mathcal{A}$.

Let

$$\mathbb{Z}:\mathbf{C}\to \mathbf{Ab}$$

be the $\mathbf{C}$-module that associates to each $a\in \mathrm{Ob}\mathbf{C}$ the free abelian group on the generator a, and to each morphism $u:a\to b$ the isomorphism of abelian groups $u_{*}:\mathbb{Z}(a)\to \mathbb{Z}(b)$ such that $u_{*}a=b$. This is isomorphic to the constant functor on $\mathbf{C}$ defined by the abelian group $\mathbb{Z}$.

The cohomology groups $H^n(\mathbf{C},\mathcal{A})$ of a small category $\mathbf{C}$ with coefficients in a $\mathbf{C}$-module $\mathcal{A}$ (cf., e.g., Gabriel–Zisman [2], Illusie [12], Roos [13], and Watts [14]), are defined as

$$H^n(\mathbf{C},\mathcal{A})={\mathrm{Ext}}_{\mathbf{C}}^n(\mathbb{Z},\mathcal{A})(n\ge 0).$$

(3)

2.2. Baues–Wirsching Cohomology of Small Categories

If $\mathbf{C}$ is any small category, its category of factorizations, $\mathbb{F}(\mathbf{C})$, is the category whose objects are the morphisms $u:a\to b$ in $\mathbf{C}$, and whose morphisms $(v,v^{\prime }):u\to u^{\prime }$ are pairs of morphisms of $\mathbf{C}$ such that $v\circ u\circ v^{\prime }=u^{\prime }$, that is, making commutative the square below.

Composition is given by the formula $(w,w^{\prime })\circ (v,v^{\prime })=(w\circ v,v^{\prime }\circ w^{\prime })$. The identity arrow at any $u:a\to b$ is the pair $(1_a,1_b):u\to u$. In [4], Baues and Wirsching call such $\mathbb{F}(\mathbf{C})$-modules by the name of natural systems on $\mathbf{C}$, and they define the cohomology groups $H^n(\mathbf{C},\mathcal{A})$ of $\mathbf{C}$ with coefficients in a natural system $\mathcal{A}$ to be those of its category of factorizations (see ([4] Theorem (4.4))):

$$H^n(\mathbf{C},\mathcal{A})=H^n(\mathbb{F}(\mathbf{C}),\mathcal{A})(n\ge 0).$$

(4)

Notation: If $\mathcal{A}:\mathbb{F}(\mathbf{C})\to \mathbf{Ab}$ is a natural system, for $a\stackrel{u}{\to }b\stackrel{v}{\to }c$ any two composible arrows in $\mathbf{C}$, we denote the induced homomorphisms ${(v,1_a)}_{*}$ and ${(1_c,u)}_{*}$ briefly by

$$v_{*}:\mathcal{A}(u)\to \mathcal{A}(v\circ u),u^{*}:\mathcal{A}(v)\to \mathcal{A}(v\circ u),$$

respectively. Thus, for any composible arrows $a\stackrel{u}{\to }b\stackrel{v}{\to }c\stackrel{w}{\to }d$, the equalities below hold.

$$\begin{array}{cc}\hfill {(w,u)}_{*}=w_{*}{u}^{*}=u^{*}{w}_{*}:& \mathcal{A}(v)\to \mathcal{A}(w\circ v\circ u),\hfill \\ \hfill {(w\circ v)}_{*}=w_{*}{v}_{*}:& \mathcal{A}(u)\to \mathcal{A}(w\circ v\circ u),\hfill \\ \hfill {(v\circ u)}^{*}=u^{*}{v}^{*}:& \mathcal{A}(w)\to \mathcal{A}(w\circ v\circ u).\hfill \end{array}$$

Baues–Wirsching cohomology recovers the cohomology of a small category $\mathbf{C}$ with coefficients in $\mathbf{C}$-modules, as follows. There is a canonical target functor

$$t:\mathbb{F}(\mathbf{C})\to \mathbf{C}$$

(5)

sending a morphism $(v,v^{\prime }):u\to u^{\prime }$ in $\mathbb{F}(\mathbf{C})$ to $t(v,v^{\prime })=v:b\to b^{\prime }$. By composing with this functor t, every $\mathbf{C}$-module $\mathcal{A}$ gives rise to a natural system on $\mathbf{C}$, which is equally denoted $\mathcal{A}$. This way, every $\mathbf{C}$-module $\mathcal{A}$ is regarded as a natural system on $\mathbf{C}$ and, by ([4] Proposition (8.5)), there are natural isomorphisms ${\mathrm{Ext}}_{\mathbf{C}}^n(\mathbb{Z},\mathcal{A})\cong {\mathrm{Ext}}_{\mathbb{F}(\mathbf{C})}^n(\mathbb{Z},\mathcal{A})$, so that both Equations (3) and (4), for coefficients in $\mathbf{C}$-modules, are the same.

2.3. Cohomology of Simplicial Sets

As usual, let $\mathsf{\Delta }$ denote the simplicial category, whose objects are the finite ordered sets $\mathbf{n}=\{0,1,\dots ,n\}$, and morphisms the weakly order-preserving maps between them. The coface maps are denoted by $d^i:\mathbf{n}-\mathbf{1}\to \mathbf{n}$, $0\le i\le n$. Recall that these are the injections that omit the ith element. We denote by $\mathbf{SSet}$ the category of simplicial sets. If $X:{\mathsf{\Delta }}^{op}\to \mathbf{Set}$ is any simplicial set, for any map $\alpha :\mathbf{m}\to \mathbf{n}$ in $\mathsf{\Delta }$, we write the attached map $X(\alpha ):X(\mathbf{n})\to X(\mathbf{m})$ by ${\alpha }^{*}:X_n\to X_m$. In particular, the face maps ${(d^i)}^{*}$ are denoted by $d_i:X_n\to X_{n-1}$.

The category of simplices of a simplicial set X is denoted by $\mathsf{\Delta }(X)$. This has as objects the pairs $(\mathbf{n},x)$ where $\mathbf{n}\in \mathsf{\Delta }$ and $x\in X_n$, and an arrow $\alpha :(\mathbf{m},x^{\prime })\to (\mathbf{n},x)$ is map $\alpha :\mathbf{m}\to \mathbf{n}$ in $\mathsf{\Delta }$ such that ${\alpha }^{*}x=x^{\prime }$. The assignment $X\mapsto \mathsf{\Delta }(X)$ is the function on objects of a functor $\mathsf{\Delta }:\mathbf{SSet}\to \mathbf{Cat}$, from the category of simplicial sets to the category of small categories, which carries a simplicial map $f:X\to Y$ to the functor $\mathsf{\Delta }(f):\mathsf{\Delta }(X)\to \mathsf{\Delta }(Y)$ sending an arrow $\alpha :(\mathbf{m},x^{\prime })\to (\mathbf{n},x)$ of $\mathsf{\Delta }(X)$ to the arrow $\alpha :(\mathbf{m},f{x}^{\prime })\to (\mathbf{n},fx)$ of $\mathsf{\Delta }(Y)$.

A coefficient system on a simplicial set X is a $\mathsf{\Delta }(X)$-module, that is, a functor $\mathcal{A}:\mathsf{\Delta }(X)\to \mathbf{Ab}$. To shorten notation, for an object $(\mathbf{n},x)$ of $\mathsf{\Delta }(X)$, we usually write $\mathcal{A}(x)$ instead of $\mathcal{A}(\mathbf{n},x)$, leaving understood the dimension n of the simplex x. Thus, if $\alpha :(\mathbf{m},{\alpha }^{*}x)\to (\mathbf{n},x)$ is a morphism in $\mathsf{\Delta }(X)$, the associated homomorphism is written as ${\alpha }_{*}:\mathcal{A}({\alpha }^{*}x)\to \mathcal{A}(x)$. In particular, for any $x\in X_n$, we have the coface homomorphisms

$$\begin{array}{cc}{d}_{*}^i:\mathcal{A}(d_{i}x)\to \mathcal{A}(x),\hfill & 0\le i\le n.\hfill \end{array}$$

The cohomology groups $H^n(X,\mathcal{A})$ of a simplicial set X with coefficients $\mathsf{\Delta }(X)$-module $\mathcal{A}$ are defined to be those of its category of simplices (cf., e.g., Illusie ([12] Chapitre VI §3) and Gabriel–Zisman ([2] Appendix II)), that is,

$$H^n(X,\mathcal{A})=H^n(\mathsf{\Delta }(X),\mathcal{A})(n\ge 0).$$

Remark 1.

A $\mathsf{\Delta }(X)$-module $\mathcal{A}$ is called a local coefficient system on the simplicial set X (see Goerss–Jardine ([15] Chapter III §1) and Gabriel–Zisman ([2] Appendix II, 4.7)) whenever, for any map $\alpha :\mathbf{m}\to \mathbf{n}$ of Δ and any n-simplex x of X, the induced homomorphism ${\alpha }_{*}:\mathcal{A}({\alpha }^{*}x)\cong \mathcal{A}(x)$ is an isomorphism. A weak homotopy equivalence $f:Y\to X$ induces isomorphisms $H^n(X,\mathcal{A})\cong H^n(Y,f^{*}\mathcal{A})$, provided $\mathcal{A}$ is a local coefficient system on X, see Quillen ([3] Chapter II, §3, Prop. 4). However, for arbitrary coefficient systems $\mathcal{A}$ on a simplicial set X, the cohomology groups $H^n(X,\mathcal{A})$ are not invariants of the homotopy type of X.

The standard cochain complex $C(X,\mathcal{A})$, of a simplicial set X with coefficients in a $\mathsf{\Delta }(X)$-module $\mathcal{A}$, consists of the abelian groups

$$C^n(X,\mathcal{A})=\mathsf{\prod }_{x\in X_n}\mathcal{A}(x),$$

with coboundary $\partial :C^{n-1}(X,\mathcal{A})\to C^n(X,\mathcal{A})$ given by $(\partial \phi )(x)={\sum }_{i=0}^n{(-1)}^i{d}_{*}^i\phi (d_{i}x)$. In Section 4 below (see Corollary 8) there is a proof of the following well-known fact (see Illusie ([12] Chapitre VI, (3.4.3))) and Gabriel–Zisman ([2] Appendix II, Prop. 4.2).

Fact 1.

For any coefficient system $\mathcal{A}$ on a simplicial set X, there are natural isomorphisms

$$H^n(X,\mathcal{A})\cong H^{n}C(X,\mathcal{A})(n\ge 0).$$

2.4. The Nerve of a Small Category

We usually regard the ordered sets $\mathbf{n}$ of $\mathsf{\Delta }$ as categories with only one arrow $(i,j):i\to j$ whenever $i\le j$, and the maps $\alpha :\mathbf{m}\to \mathbf{n}$ in $\mathsf{\Delta }$ as functors. The nerve $\mathrm{N}(\mathbf{C})$ of any small category $\mathbf{C}$ is the simplicial set whose n-simplices are the functors $\sigma :\mathbf{n}\to \mathbf{C}$, and the map ${\alpha }^{*}:\mathrm{N}{(\mathbf{C})}_n\to \mathrm{N}{(\mathbf{C})}_m$, induced by a map $\alpha :\mathbf{m}\to \mathbf{n}$, is given by ${\alpha }^{*}\sigma =\sigma \alpha$. The functor nerve $\mathrm{N}:\mathbf{Cat}\to \mathbf{SSet}$ carries a functor $f:\mathbf{C}\to {\mathbf{C}}^{\prime }$ to the simplicial map $\mathrm{N}(f):\mathrm{N}(\mathbf{C})\to \mathrm{N}({\mathbf{C}}^{\prime })$ such that $\mathrm{N}(f)(\sigma )=f\sigma$.

From now on, we will employ several times the following notation: If $\sigma :\mathbf{n}\to \mathbf{C}$ is a functor, then we write ${\sigma }_i:\sigma (i-1)\to \sigma i$ for the morphism $\sigma (i-1,i)$. Thus, for any $i<j$ in $\mathbf{n}$, we have

$$\sigma (i,j)={\sigma }_j\circ \cdots \circ {\sigma }_{i+1}:\sigma i\to \sigma j.$$

(6)

The morphism between end vertices functor is denoted by

$$e:\mathsf{\Delta }\mathrm{N}(\mathbf{C})\to \mathbb{F}(\mathbf{C}).$$

(7)

This carries any object $(\mathbf{n},\sigma )$ of $\mathsf{\Delta }\mathrm{N}(\mathbf{C})$ to the morphism $\sigma (0,n):\sigma 0\to \sigma n$ of $\mathbf{C}$, and carries a morphism $\alpha :(\mathbf{m},\sigma \alpha )\to (\mathbf{n},\sigma )$ of $\mathsf{\Delta }\mathrm{N}(\mathbf{C})$ to the morphism of $\mathbb{F}(\mathbf{C})$

$$\left(\sigma (\alpha m,n),\sigma (0,\alpha 0)\right):\sigma \alpha (0,m)\to \sigma (0,n),$$

depicted as below.

By composing with this functor e, every natural system $\mathcal{A}:\mathbb{F}(\mathbf{C})\to \mathbf{Ab}$ on $\mathbf{C}$ produces a coefficient system on the simplicial set $\mathrm{N}(\mathbf{C})$, which is denoted also by $\mathcal{A}$. In Section 3 below (see Corollary 1) there is a proof of the following well-known fact (cf. Baues–Wirsching ([4] Definition (1.4), Theorem (4.4)), Illusie ([12] Chapitre VI, (3.4.2)), and Gabriel–Zisman ([2] Appendix II, Proposition 3.3)).

Fact 2.

For any natural system $\mathcal{A}$ on a small category $\mathbf{C}$, there are natural isomorphisms

$$H^n(\mathbf{C},\mathcal{A})\cong H^n(\mathrm{N}(\mathbf{C}),\mathcal{A})(n\ge 0).$$

Let us stress that, after Fact 1, it is implicit in the above Fact 2 that, for any natural system $\mathcal{A}$ on $\mathbf{C}$, the cohomology groups $H^n(\mathbf{C},\mathcal{A})$ can be computed by means of the standard cochain complex $C(\mathrm{N}(\mathbf{C}),\mathcal{A})$, which is denoted in [4] by $\mathbb{F}(\mathbf{C},\mathcal{A})$. Thus,

$${\mathbb{F}}^n(\mathbf{C},\mathcal{A})=\mathsf{\prod }_{\sigma :\mathbf{n}\to \mathbf{C}}\mathcal{A}(\sigma (0,n))$$

and the coboundary $\partial :{\mathbb{F}}^{n-1}(\mathbf{C},\mathcal{A})\to {\mathbb{F}}^n(\mathbf{C},\mathcal{A})$ is given by

$$(\partial \phi )(\sigma )={\sigma }_1^{*}\phi (d_0\sigma )+\sum _{i=1}^{n-1}{(-1)}^i\phi (d_i\sigma )+{(-1)}^n{\sigma }_{n*}\phi (d_n\sigma ).$$

Also, let us point out that the composition of the functors in Equations (7) and (5),

$$l=te:\mathsf{\Delta }\mathrm{N}(\mathbf{C})\stackrel{e}{\to }\mathbb{F}(\mathbf{C})\stackrel{t}{\to }\mathbf{C},$$

(8)

is just the last vertex functor, which sends each object $(\mathbf{n},\sigma )$ of $\mathsf{\Delta }\mathrm{N}(\mathbf{C})$ to the object $\sigma n$ of $\mathbf{C}$. By composition with it, any $\mathbf{C}$-module defines a coefficient system on $\mathrm{N}(\mathbf{C})$ and, in this way, Fact 2 applies to the ordinary cohomology groups of $\mathbf{C}$ with coefficients in $\mathbf{C}$-modules.

Remark 2.

For a small category $\mathbf{C}$, arbitrary coefficient systems on $\mathrm{N}(\mathbf{C})$, that is, arbitrary functors $\mathcal{A}:\mathsf{\Delta }\mathrm{N}(\mathbf{C})\to \mathbf{Ab}$, are called Thomason natural systems on $\mathbf{C}$ by Gálvez–Carrillo–Neumann–Tonks in [8], where the cohomology groups $H^n(\mathrm{N}(\mathbf{C}),\mathcal{A})$ are denoted by $H_{Th}^n(\mathbf{C},\mathcal{A})$ and studied under the name of Thomason cohomology groups of the category.

3. On the Weak Equivalence $\mathbf{\eta }:{\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}\mathit{F}\to \mathrm{N}({\int }_{\mathbf{C}}\mathit{F})$

Throughout this section, $F:{\mathbf{C}}^{op}\to \mathbf{Cat}$ denotes a functor, where $\mathbf{C}$ is a small category. For a morphism $u:a\to b$ of $\mathbf{C}$, we write $u^{*}:F(b)\to F(a)$ for the functor $F(u)$. Thus, for any n-simplex $\sigma$ of $\mathrm{N}(\mathbf{C})$, that is, for any functor $\sigma :\mathbf{n}\to \mathbf{C}$, we have functors (see Equation (6) for the notation)

$$\sigma {(i,j)}^{*}={\sigma }_{i+1}^{*}\cdots {\sigma }_j^{*}:F(\sigma j)\to F(\sigma i)(0\le i\le j\le n).$$

3.1. The Involved Constructions

By composing F with the nerve functor, we get a diagram of simplicial sets $\mathrm{N}F:{\mathbf{C}}^{op}\to \mathbf{SSet}$, whose homotopy colimit ([9] Chapter XII, §5) is denoted by ${\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F$. This simplicial set has as n-simplices pairs of functors $(\sigma ,\tau )$, where $\sigma :\mathbf{n}\to \mathbf{C}$ and $\tau :\mathbf{n}\to F(\sigma n)$ and, for any map $\alpha :\mathbf{m}\to \mathbf{n}$ in $\mathsf{\Delta }$, the induced ${\alpha }^{*}:{({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F)}_n\to {({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F)}_m$ acts by

$${\alpha }^{*}(\sigma ,\tau )=(\sigma \alpha ,\sigma {(\alpha m,n)}^{*}\tau \alpha ).$$

In particular, its face operators are given by

$$d_i(\sigma ,\tau )=\left\{\begin{array}{cc}(d_i\sigma ,d_i\tau ),\hfill & 0\le i<n,\hfill \\ (d_n\sigma ,{\sigma }_n^{*}{d}_n\tau ),\hfill & i=n.\hfill \end{array}\right.$$

On the other hand, the Grothendieck construction [5,16,17] on the diagram F yields a small category, denoted by ${\int }_{\mathbf{C}}F$, whose objects are pairs $(a,x)$ where a is an object of $\mathbf{C}$ and x is an object of $F(a)$. A morphism form $(a,x)$ to $(b,y)$ in ${\int }_{\mathbf{C}}F$ is a pair $(u,f)$ with $u:a\to b$ a morphism in $\mathbf{C}$ and $f:x\to u^{*}y$ a morphism in $F(a)$. Arrows in ${\int }_{\mathbf{C}}F$ compose by the formula

$$(v,g)\circ (u,f)=(v\circ u,u^{*}g\circ f).$$

The Thomason weak equivalence ([5] Theorem 1.2) is the simplicial map

$$\eta :{\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F\to \mathrm{N}({\int }_{\mathbf{C}}F),$$

(9)

which carries an n-simplex $(\sigma ,\tau )$ of the homotopy colimit to the n-simplex of the nerve of the Grothendieck construction $\eta (\sigma ,\tau ):\mathbf{n}\to {\int }_{\mathbf{C}}F$ defined by

$$\left\{\begin{array}{c}\eta (\sigma ,\tau )i=(\sigma i,\sigma {(i,n)}^{*}\tau i),\hfill \\ \eta (\sigma ,\tau )(i,j)=((\sigma i,\sigma {(i,n)}^{*}\tau i)\stackrel{\left(\sigma (i,j),\sigma {(i,n)}^{*}\tau (i,j)\right)}{\to }\hfill & (\sigma j,\sigma {(j,n)}^{*}\tau j)).\hfill \end{array}\right.$$

3.2. A Free Resolution of the Natural System $\mathbb{Z}$ over ${\int }_{\mathbf{C}}F$

The following construction is key for our main result in this section.

Let $\mathsf{\Psi }={\mathsf{\Psi }}_{\mathbf{C}}(F)$ be the simplicial replacement construction of Bousfield–Kan ([9] Chapter XII, §5) on $\mathrm{N}F$: that is, the bisimplicial set

$$\mathsf{\Psi }:{\mathsf{\Delta }}^{op}\times {\mathsf{\Delta }}^{op}\to \mathbf{Set},$$

whose $(p,q)$-simplices are pairs of functors $(\sigma ,\tau )$ where $\sigma :\mathbf{p}\to \mathbf{C}$ and $\tau :\mathbf{q}\to F(\sigma p)$. If $\alpha :{\mathbf{p}}^{\prime }\to \mathbf{p}$ and $\beta :{\mathbf{q}}^{\prime }\to \mathbf{q}$ are maps in $\mathsf{\Delta }$, the induced maps

$${\mathsf{\Psi }}_{p^{\prime },q}\stackrel{{\alpha }_h^{*}={(\alpha ,1_{\mathbf{q}})}^{*}}{\leftarrow }{\mathsf{\Psi }}_{p,q}\stackrel{{\beta }_v^{*}={(1_{\mathbf{p}},\beta )}^{*}}{\to }{\mathsf{\Psi }}_{p,q^{\prime }}$$

are defined on a $(p,q)$-simplex $(\sigma ,\tau )$ as above by

$${\alpha }_h^{*}(\sigma ,\tau )=(\sigma \alpha ,\sigma {(\alpha p^{\prime },p)}^{*}\tau ),{\beta }_v^{*}(\sigma ,\tau )=(\sigma ,\tau \beta ).$$

In particular, its face operators ${\mathsf{\Psi }}_{p-1,q}\stackrel{d_i^h}{\leftarrow }{\mathsf{\Psi }}_{p,q}\stackrel{d_j^v}{\to }{\mathsf{\Psi }}_{p,q-1}$ act by

$$d_i^h(\sigma ,\tau )=\left\{\begin{array}{cc}(d_i\sigma ,\tau )\hfill & 0\le i<p,\\ (d_p\sigma ,{\sigma }_p^{*}\tau )\hfill & i=p,\end{array}\right.d_j^v(\sigma ,\tau )=(\sigma ,d_j\tau ),0\le j\le q.$$

Now, for each integers $p,q\ge 0$, let the set ${\mathsf{\Psi }}_{p,q}$ be endowed with the morphism between end vertices map $\pi :{\mathsf{\Psi }}_{p,q}\to \mathrm{Ob}\mathbb{F}({\int }_{\mathbf{C}}F)$, defined by

$$\pi (\sigma ,\tau )=\left((\sigma 0,\sigma {(0,p)}^{*}\tau 0)\stackrel{\left(\sigma (0,p),\sigma {(0,p)}^{*}\tau (0,q)\right)}{\to }\left(\sigma p,\tau q\right)\right)$$

and let ${\mathcal{P}}_{p,q}=\mathcal{F}{\mathsf{\Psi }}_{p,q}$ be the corresponding free $\mathbb{F}({\int }_{\mathbf{C}}F)$-module (i.e., free natural system on ${\int }_{\mathbf{C}}F$). Thus, for each morphism $(u,f):(a,x)\to (b,y)$ in ${\int }_{\mathbf{C}}F$,

$${\mathcal{P}}_{p,q}(u,f)=\mathbb{Z}\left\{(\sigma ,\tau ,v,g,v^{\prime },g^{\prime })\right\}$$

(10)

is the free abelian group with generators the sextuples $(\sigma ,\tau ,v,g,v^{\prime },g^{\prime })$, where

$$\left\{\begin{array}{c}\sigma :\mathbf{p}\to \mathbf{C}\mathrm{is}\mathrm{a}\mathrm{functor},\hfill \\ \tau :\mathbf{q}\to F(\sigma p)\mathrm{is}\mathrm{a}\mathrm{functor},\hfill \\ v:\sigma p\to b\mathrm{is}\mathrm{a}\mathrm{morphism}\mathrm{in}\mathbf{C},\hfill \\ g:\tau q\to v^{*}y\mathrm{is}\mathrm{a}\mathrm{morphism}\mathrm{in}F(\sigma p),\hfill \\ v^{\prime }:a\to \sigma 0\mathrm{is}\mathrm{a}\mathrm{morphism}\mathrm{in}\mathbf{C},\hfill \\ g^{\prime }:x\to v^{\prime *}\sigma {(0,p)}^{*}\tau 0\mathrm{is}\mathrm{a}\mathrm{morphism}\mathrm{in}F(a),\hfill \end{array}\right.$$

such that

$$\left\{\begin{array}{c}u=v\circ \sigma (0,p)\circ v^{\prime },\hfill \\ f=v^{\prime *}\sigma {(0,p)}^{*}(g\circ \tau (0,q))\circ g^{\prime }.\hfill \end{array}\right.$$

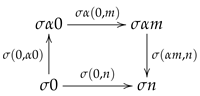
Note that the latter equations mean that the square in the category ${\int }_{\mathbf{C}}F$ below commutes.

For any three composible morphisms in ${\int }_{\mathbf{C}}F$,

$$(a^{\prime },x^{\prime })\stackrel{(u^{\prime },f^{\prime })}{\to }(a,x)\stackrel{(u,f)}{\to }(b,y)\stackrel{(u^{″},f^{″})}{\to }(b^{\prime },y^{\prime }),$$

the induced homomorphisms

$$\begin{array}{c}{(u^{\prime },f^{\prime })}^{*}:{\mathcal{P}}_{p,q}(u,f)⟶{\mathcal{P}}_{p,q}(u\circ u^{\prime },u^{\prime *}f\circ f^{\prime }),\hfill \\ {(u^{″},f^{″})}_{*}:{\mathcal{P}}_{p,q}(u,f)⟶{\mathcal{P}}_{p,q}(u^{″}\circ u,u^{*}{f}^{″}\circ f),\hfill \end{array}$$

are, respectively, given on generators by

$$\begin{array}{c}{(u^{\prime },f^{\prime })}^{*}(\sigma ,\tau ,v,g,v^{\prime },g^{\prime })=(\sigma ,\tau ,v,g,v^{\prime }\circ u^{\prime },{u^{\prime }}^{*}{g}^{\prime }\circ f^{\prime }),\hfill \\ {(u^{″},f^{″})}_{*}(\sigma ,\tau ,v,g,v^{\prime },g^{\prime })=(\sigma ,\tau ,u^{″}\circ v,v^{*}{f}^{″}\circ g,v^{\prime },g^{\prime }).\hfill \end{array}$$

These ${\mathcal{P}}_{p,q}$ provide a bisimplicial natural system on ${\int }_{\mathbf{C}}F$

$$\mathcal{P}={\mathcal{P}}_{\mathbf{C}}(F):{\mathsf{\Delta }}^{op}\times {\mathsf{\Delta }}^{op}⟶\mathbb{F}({\int }_{\mathbf{C}}F)-\mathrm{Mod},$$

(11)

where, for any maps in the simplicial category, $\alpha :{\mathbf{p}}^{\prime }\to \mathbf{p}$ and $\beta :{\mathbf{q}}^{\prime }\to \mathbf{q}$, the induced ${\alpha }_h^{*}:{\mathcal{P}}_{p,q}\to {\mathcal{P}}_{p^{\prime },q}$ and ${\beta }_v^{*}:{\mathcal{P}}_{p,q}\to {\mathcal{P}}_{p,q^{\prime }}$ are the morphisms whose respective components at a morphism $(u,f):(a,x)\to (b,y)$ of ${\int }_{\mathbf{C}}F$ are the homomorphisms ${\alpha }_h^{*}:{\mathcal{P}}_{p,q}(u,f)\to {\mathcal{P}}_{p^{\prime },q}(u,f)$ and ${\beta }_v^{*}:{\mathcal{P}}_{p,q}(u,f)\to {\mathcal{P}}_{p,q^{\prime }}(u,f)$ respectively defined on generators by

$$\begin{array}{c}{\alpha }_h^{*}(\sigma ,\tau ,v,g,v^{\prime },g^{\prime })=\left(\sigma \alpha ,\sigma {(\alpha p^{\prime },p)}^{*}\tau ,v\circ \sigma (\alpha p^{\prime },p),\sigma {(\alpha p^{\prime },p)}^{*}g,\sigma (0,\alpha 0)\circ v^{\prime },g^{\prime }\right),\hfill \\ {\beta }_v^{*}(\sigma ,\tau ,v,g,v^{\prime },g^{\prime })=\left(\sigma ,\tau \beta ,v,g\circ \tau (\beta q^{\prime },q),v^{\prime },(v^{\prime *}\sigma {(0,p)}^{*}\tau (0,\beta 0))\circ g^{\prime }\right).\hfill \end{array}$$

In particular, the horizontal and vertical face homomorphisms

$${\mathcal{P}}_{p-1,q}(u,f)\stackrel{d_i^h}{\leftarrow }{\mathcal{P}}_{p,q}(u,f)\stackrel{d_j^v}{\to }{\mathcal{P}}_{p,q-1}(u,f)$$

act on generators by

$$\begin{array}{cc}\hfill d_i^h(\sigma ,\tau ,v,g,v^{\prime },g^{\prime })& =\left\{\begin{array}{cc}(d_0\sigma ,\tau ,v,g,{\sigma }_1\circ v^{\prime },g^{\prime })\hfill & i=0,\hfill \\ (d_i\sigma ,\tau ,v,g,v^{\prime },g^{\prime })\hfill & 0<i<p,\hfill \\ (d_p\sigma ,{\sigma }_p^{*}\tau ,v\circ {\sigma }_p,{\sigma }_p^{*}g,v^{\prime },g^{\prime })\hfill & i=p,\hfill \end{array}\right.\hfill \\ \hfill d_j^v(\sigma ,\tau ,v,g,v^{\prime },g^{\prime })& =\left\{\begin{array}{cc}(\sigma ,d_0\tau ,v,g,v^{\prime },(v^{\prime *}\sigma {(0,p)}^{*}{\tau }_1)\circ g^{\prime })\hfill & j=0,\hfill \\ (\sigma ,d_j\tau ,v,g,v^{\prime },g^{\prime })\hfill & 0<j<q,\hfill \\ \left(\sigma ,d_q\tau ,v,g\circ {\tau }_q,v^{\prime },g^{\prime }\right)\hfill & j=q,\hfill \end{array}\right.\hfill \end{array}$$

Let $\mathrm{diag}\mathcal{P}$ be the complex associated to the simplicial natural system diagonal of $\mathcal{P}$: that is, the cochain complex of natural systems on ${\int }_{\mathbf{C}}F$ with ${(\mathrm{diag}\mathcal{P})}_n={\mathcal{P}}_{n,n}$, and whose differential $\partial :{\mathcal{P}}_{n,n}(u,f)\to {\mathcal{P}}_{n-1,n-1}(u,f)$, at a morphism $(u,f):(a,x)\to (b,y)$ of ${\int }_{\mathbf{C}}F$, is given on generators by

$$\begin{array}{cc}\hfill \partial (\sigma ,\tau ,v,g,v^{\prime },g^{\prime })=& \left(d_0\sigma ,d_0\tau ,v,g,{\sigma }_1\circ v^{\prime },(v^{\prime *}\sigma {(0,n)}^{*}{\tau }_1)\circ g^{\prime }\right)+\sum _{i=1}^{n-1}{(-1)}^i(d_i\sigma ,d_i\tau ,v,g,v^{\prime },g^{\prime })\hfill \\ \hfill & +{(-1)}^n\left(d_n\sigma ,{\sigma }_n^{*}{d}_n\tau ,v\circ {\sigma }_n,{\sigma }_n^{*}(g\circ {\tau }_n),v^{\prime },g^{\prime }\right).\hfill \end{array}$$

(12)

Lemma 1.

$\mathrm{diag}{\mathcal{P}}_{\mathbf{C}}(F)$ is a projective resolution of the natural system $\mathbb{Z}$ on ${\int }_{\mathbf{C}}F$. Therefore, for any natural system $\mathcal{A}$ on ${\int }_{\mathbf{C}}F$,

$$H^n\left({\int }_{\mathbf{C}}F,\mathcal{A}\right)=H^n\left({\mathrm{Hom}}_{\mathbb{F}({\int }_{\mathbf{C}}F)}(\mathrm{diag}{\mathcal{P}}_{\mathbf{C}}F,\mathcal{A})\right)(n\ge 0).$$

Proof. 

Let us write $\mathcal{P}={\mathcal{P}}_{\mathbf{C}}(F)$ as in Equation (11). Let $ϵ:{\mathcal{P}}_{0,0}\to \mathbb{Z}$ be the morphism of natural systems whose component $ϵ:{\mathcal{P}}_{0,0}(u,f)\to \mathbb{Z}(u,f)$, at a morphism $(u,f):(a,x)\to (b,y)$ of ${\int }_{\mathbf{C}}F$, is the homomorphism defined on generators by

$$ϵ(a_0,x_0,a_0\stackrel{v}{\to }b,x_0\stackrel{g}{\to }{v}^{*}y,a\stackrel{v^{\prime }}{\to }{a}_0,x\stackrel{g^{\prime }}{\to }{v}_{*}^{\prime }{x}_0)=(u,f),$$

where we have identified any object $a_0$ of $\mathbf{C}$ with the functor $\sigma :\mathbf{0}\to \mathbf{C}$ such that $\sigma 0=a_0$ and, similarly, an object $x_0$ of $F(a_0)$ with the functor $\tau :\mathbf{0}\to F(a_0)$ with $\tau 0=x_0$. It is easily seen that this morphism $ϵ:{\mathcal{P}}_{0,0}\to \mathbb{Z}$ determines an augmentation $ϵ:\mathrm{diag}\mathcal{P}\twoheadrightarrow \mathbb{Z}$.

Since every natural system ${\mathcal{P}}_{n,n}$ is free, whence projective, it suffices to prove that, for any morphism $(u,f):(a,x)\to (b,y)$ of ${\int }_{\mathbf{C}}F$, the augmented chain complex of abelian groups

$$\cdots \to {\mathcal{P}}_{2,2}(u,f)\stackrel{\partial }{⟶}{\mathcal{P}}_{1,1}(u,f)\stackrel{\partial }{⟶}{\mathcal{P}}_{0,0}(u,f)\stackrel{ϵ}{⟶}\mathbb{Z}(u,f)\to 0$$

(13)

is exact. To do this, let us fix such a morphism $(u,f)$ and proceed as follows.

For each $q\ge 0$, let $P_q(u,f)=\mathbb{Z}\left\{(\tau ,w,w^{\prime })\right\}$ be the free abelian group on the set of triples $(\tau ,w,w^{\prime })$ consisting of a functor $\tau :\mathbf{q}\to F(b)$ and morphisms $w:\tau q\to u^{*}y$ and $w^{\prime }:x\to \tau 0$ of $F(a)$ with $f=w\circ \tau (0,q)\circ w^{\prime }$, that is, making commutative the square

These $P_q(u,f)$ define a simplicial abelian group $P(u,f)$, where each map $\beta :{\mathbf{q}}^{\prime }\to \mathbf{q}$ of $\mathsf{\Delta }$ induces the homomorphism ${\beta }^{*}:P_q(u,f)\to P_{q^{\prime }}(u,f)$ defined on generators by

$${\beta }^{*}(\tau ,w,w^{\prime })=\left(\tau \beta ,w\circ \tau (\beta q^{\prime },q),\tau (0,\beta 0)\circ w^{\prime }\right).$$

In particular, its face homomorphisms $d_i:P_q(u,f)\to P_{q-1}(u,f)$ are defined by

$$d_j(\tau ,w,w^{\prime })=\left\{\begin{array}{cc}(d_0\tau ,w,{\tau }_1\circ w^{\prime }),\hfill & j=0,\hfill \\ (d_j\tau ,w,w^{\prime }),\hfill & 0<j<q,\hfill \\ (d_q\tau ,w\circ {\tau }_q,w^{\prime }),\hfill & j=q.\hfill \end{array}\right.$$

This simplicial abelian group $P(u,f)$ can be endowed with an augmentation over $\mathbb{Z}(u,f)$ by the homomorphism $ϵ:P_0(u,f)\twoheadrightarrow \mathbb{Z}(u,f)$ which acts on generators by $ϵ(x_0,x_0\stackrel{w}{\to }{u}^{*}y,x\stackrel{w^{\prime }}{\to }{x}_0)=(u,f)$. Let us also denote by $P(u,f)$ the associated chain complex, in which the differentials $\partial =\sum {(-1)}^i{d}_i$ are obtained by taking alternating sums. The resulting augmented chain complex of abelian groups admits a contracting homotopy k

(14)

whence it is exact. Such a contraction k is given by the homomorphisms $k_{-1}:\mathbb{Z}(u,f)\to P_0(u,f)$ and $k_q:P_q(u,f)\to P_{q+1}(u,f)$, $q\ge 0$ which act on generators by

$$k_{-1}(u,f)=(u^{*}y,1_{u^{*}y},f),k_q(\tau ,w,w^{\prime })={(-1)}^{q+1}(w⭑\tau ,1_{u^{*}y},w^{\prime }).$$

In the above formula, for any functor $\tau :\mathbf{q}\to F(a)$ and any morphism $w:\tau q\to u^{*}y$, the functor $w⭑\tau :\mathbf{q}+\mathbf{1}\to F(a)$ is defined by

$$\begin{array}{c}(w⭑\tau )i=\left\{\begin{array}{cc}\tau i\hfill & i\le q,\hfill \\ u^{*}y\hfill & i=q+1,\hfill \end{array}\right.\hfill \\ (w⭑\tau )(i,j)=\left\{\begin{array}{cc}\tau (i,j):\tau i\to \tau j,\hfill & j\le q,\hfill \\ w\circ \tau (i,q):\tau i\to u^{*}y,\hfill & j=q+1.\hfill \end{array}\right.\hfill \end{array}$$

(15)

To check that $k:i{d}_{P(u,f)}\Rightarrow 0$ is actually a chain homotopy, we first observe the equalities

$$d_j(w⭑\tau )=\left\{\begin{array}{cc}w⭑d_j\tau ,\hfill & 0\le j<q,\hfill \\ (w\circ {\tau }_q)⭑d_q\tau ,\hfill & j=q,\hfill \\ \tau \hfill & j=q+1.\hfill \end{array}\right.$$

From these, it is not hard to see that the operators $k_q$ satisfy the equations

$$d_j{k}_q=\left\{\begin{array}{cc}-k_{q-1}{d}_j\hfill & 0\le j\le q,\hfill \\ i{d}_{P_q(u,f)}\hfill & j=q+1,\hfill \end{array}\right.$$

whence the equality $\partial k_q+k_{q-1}\partial =i{d}_{P_q(u,f)}$ follows for all $q\ge 0$.

Consider now the simplicial abelian group $P(u,f)$ as a bisimplicial abelian group which is constant in the horizontal direction. Then, the homomorphisms $ϵ:{\mathcal{P}}_{0,q}(u,f)\twoheadrightarrow P_q(u,f)$ defined on generators by

$$ϵ\left(a_0,\mathbf{q}\stackrel{\tau }{\to }F(a_0),a_0\stackrel{v}{\to }b,v_{*}\tau q\stackrel{g}{\to }y,a\stackrel{v^{\prime }}{\to }{a}_0,v_{*}^{\prime }x\stackrel{g^{\prime }}{\to }\tau 0\right)=(v_{*}^{\prime }\tau ,v^{\prime *}g,g^{\prime }),$$

determine a bisimplicial homomorphism $ϵ:\mathcal{P}(u,f)\to P(u,f)$. For every $q\ge 0$, the associated augmented chain complex of abelian groups

is exact, because of it admits a contracting homotopy h given by the homomorphisms $h_{-1}:P_q(u,f)\to {\mathcal{P}}_{0,q}(u,f)$ and $h_p:{\mathcal{P}}_{p,q}(u,f)\to {\mathcal{P}}_{p+1,q}(u,f)$ which act on generators by

$$\left\{\begin{array}{c}{h}_{-1}(\tau ,w,w^{\prime })=(a,\tau ,u,w,1_a,w^{\prime }),\hfill \\ h_p(\sigma ,\tau ,v,g,v^{\prime },g^{\prime })=(\sigma ⭑v^{\prime },\tau ,v,g,1_a,g^{\prime }),\hfill \end{array}\right.$$

where, for any functor $\sigma :\mathbf{p}\to \mathbf{C}$ and any morphism $v^{\prime }:a\to \sigma 0$, the functor $\sigma ⭑v^{\prime }:\mathbf{p}+\mathbf{1}\to \mathbf{C}$ is defined by the formulas

$$\begin{array}{c}(\sigma ⭑v^{\prime })i=\left\{\begin{array}{cc}a& i=0,\hfill \\ \sigma (i-1)& i>0,\hfill \end{array}\right.\hfill \\ (\sigma ⭑v^{\prime })(i,j)=\left\{\begin{array}{cc}\sigma (0,j-1)\circ v^{\prime }:a\to \sigma (j-1),\hfill & i=0,\hfill \\ \sigma (i-1,j-1):\sigma (i-1)\to \sigma (j-1),\hfill & i>0.\hfill \end{array}\right.\hfill \end{array}$$

As above, to check that h is actually a contracting chain homotopy, we first observe the equalities

$$d_i(\sigma ⭑v^{\prime })=\left\{\begin{array}{cc}\sigma & i=0,\hfill \\ d_0\sigma ⭑({\sigma }_1\circ v^{\prime })& i=1,\hfill \\ d_{i-1}\sigma ⭑v^{\prime }& 1<i\le p+1.\hfill \end{array}\right.$$

From these, we see that the operators $h_p$ satisfy the equations

$$d_i^h{h}_p=\left\{\begin{array}{cc}i{d}_{{\mathcal{P}}_{p,q}(u,f)}\hfill & i=0,\hfill \\ h_{p-1}{d}_{i-1}^h\hfill & 0<i\le p+1,\hfill \end{array}\right.$$

whence the equality $\partial h_p+h_{p-1}\partial =i{d}_{{\mathcal{P}}_{p,q}(u,f)}$ follows.

Finally, the Dold–Puppe theorem implies that the induced map on the associated augmented diagonal complexes $ϵ:\mathrm{diag}\mathcal{P}(u,f)\to P(u,f)$,

is a homology isomorphism. Therefore, the chain complex Equation (13) is exact, since the chain complex Equation (14) is such. □

Let us now consider the category of simplices $\mathsf{\Delta }({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F)$, whose objects are triples $(\mathbf{n},\sigma ,\tau )$, where $\sigma :\mathbf{n}\to \mathbf{C}$ and $\tau :\mathbf{n}\to F(\sigma 0)$ are functors, and whose morphisms $\alpha :(\mathbf{m},\gamma ,\delta )\to (\mathbf{n},\sigma ,\tau )$ are those maps $\alpha :\mathbf{m}\to \mathbf{n}$ in $\mathsf{\Delta }$ such that $\sigma \alpha =\gamma$ and $\sigma {(\alpha m,n)}^{*}\tau \alpha =\delta$. We have the composite functor $e\mathsf{\Delta }(\eta )$,

$$\mathsf{\Delta }({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F)\stackrel{\mathsf{\Delta }(\eta )}{\to }\mathsf{\Delta }(\mathrm{N}{\int }_{\mathbf{C}}F)\stackrel{e}{\to }\mathbb{F}({\int }_{\mathbf{C}}F),$$

(16)

of the functor $\mathsf{\Delta }(\eta )$ induced by Thomason simplicial map Equation (9) with the morphism between end vertices functor e Equation (7). This functor $e\mathsf{\Delta }(\eta )$ carries each object $(\mathbf{n},\sigma ,\tau )$ to the morphism of ${\int }_{\mathbf{C}}F$

$$(\sigma 0,\sigma {(0,n)}^{*}\tau 0)\stackrel{(\sigma (0,n),\sigma {(0,n)}^{*}\tau (0,n))}{\to }(\sigma n,\tau n),$$

and a morphism $\alpha :(\mathbf{m},\gamma ,\delta )\to (\mathbf{n},\sigma ,\tau )$, as above, to the morphism of the category of factorizations $\mathbb{F}({\int }_{\mathbf{C}}F)$ given by the broken arrows below.

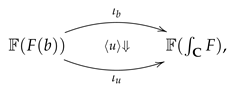
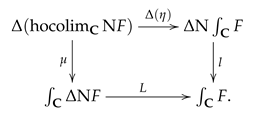
Then, by composition with $e\mathsf{\Delta }(\eta )$, any natural system $\mathcal{A}$ on ${\int }_{\mathbf{C}}F$ gives rise to a coefficient system, denoted by ${\eta }^{*}\mathcal{A}$, on the simplicial set ${\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F$. As a main result in this paper, we have

Theorem 3.

For any natural system $\mathcal{A}$ on ${\int }_{\mathbf{C}}F$, the Thomason map η in Equation (9) induces isomorphisms

$$H^n({\int }_{\mathbf{C}}F,\mathcal{A})\cong H^n({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F,{\eta }^{*}\mathcal{A}).$$

Proof. 

For any given natural system $\mathcal{A}$ on ${\int }_{\mathbf{C}}F$, the coefficient system ${\eta }^{*}\mathcal{A}$ on the homotopy colimit ${\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F$ carries an n-simplex $(\sigma ,\tau )$ to the abelian group

$${\eta }^{*}\mathcal{A}(\sigma ,\tau )=\mathcal{A}(\sigma (0,n),\sigma {(0,n)}^{*}\tau (0,n))$$

and, for any map $\alpha :\mathbf{m}\to \mathbf{n}$ in the simplicial category, the induced homomorphism ${\alpha }_{*}:{\eta }^{*}\mathcal{A}({\alpha }^{*}(\sigma ,\tau ))\to {\eta }^{*}\mathcal{A}(\sigma ,\tau )$ is the homomorphism

$$\begin{array}{cc}\hfill {\alpha }_{*}& ={\left(\sigma (\alpha m,n),\sigma {(\alpha m,n)}^{*}\tau (\alpha m,n)\right)}_{*}{\left(\sigma (0,\alpha 0),\sigma {(0,n)}^{*}\tau (0,\alpha 0)\right)}^{*}\hfill \\ \hfill & :\mathcal{A}(\sigma (\alpha 0,\alpha m),\sigma {(\alpha 0,n)}^{*}\tau (\alpha 0,\alpha m))⟶\mathcal{A}(\sigma (0,n),\sigma {(0,n)}^{*}\tau (0,n)).\hfill \end{array}$$

In particular, for any n-simplex $(\sigma ,\tau )$ of ${\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F$, the coface homomorphisms

$$d_{*}^i:{\eta }^{*}\mathcal{A}(d_i(\sigma ,\tau ))\to {\eta }^{*}\mathcal{A}(\sigma ,\tau )$$

are

$$\begin{array}{cc}\hfill d_{*}^0=& {({\sigma }_1,\sigma {(0,n)}^{*}{\tau }_1)}^{*}:\mathcal{A}(\sigma (1,n),\sigma {(1,n)}^{*}\tau (1,n))⟶\mathcal{A}(\sigma (0,n),\sigma {(0,n)}^{*}\tau (0,n)),\hfill \\ \hfill d_{*}^i=& id:\mathcal{A}(\sigma (0,n),\sigma {(0,n)}^{*}\tau (0,n))⟶\mathcal{A}(\sigma (0,n),\sigma {(0,n)}^{*}\tau (0,n))0<i<n,\hfill \\ \hfill d_{*}^n=& {({\sigma }_n,{\sigma }_n^{*}{\tau }_n)}_{*}:\mathcal{A}(\sigma (0,n-1),\sigma {(0,n)}^{*}\tau (0,n-1))⟶\mathcal{A}(\sigma (0,n),\sigma {(0,n)}^{*}\tau (0,n)).\hfill \end{array}$$

Then, the standard cochain complex $C({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F,{\eta }^{*}\mathcal{A})$ consists of the abelian groups

$$C^n({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F,{\eta }^{*}\mathcal{A})=\mathsf{\prod }_{\begin{array}{c}\sigma :\mathbf{n}\to \mathbf{C}\\ \tau :\mathbf{n}\to F(\sigma n)\end{array}}\mathcal{A}(\sigma (0,n),\sigma {(0,n)}^{*}\tau (0,n)),$$

(17)

with coboundary $\partial :C^{n-1}({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F,{\eta }^{*}\mathcal{A})\to C^n({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F,{\eta }^{*}\mathcal{A})$ given by

$$\begin{array}{cc}\hfill (\partial \phi )(\sigma ,\tau )=& {({\sigma }_1,\sigma {(0,n)}^{*}{\tau }_1)}^{*}\phi (d_0\sigma ,d_0\tau )+\sum _{i=1}^{n-1}{(-1)}^i\phi (d_i\sigma ,d_i\tau )\hfill \\ \hfill & +{(-1)}^n{\left({\sigma }_n,{\sigma }_n^{*}{\tau }_n\right)}_{*}\phi (d_n\sigma ,{\sigma }_n^{*}{d}_n\tau ).\hfill \end{array}$$

(18)

Now, let $\mathcal{P}={\mathcal{P}}_{\mathbf{C}}(F)$ be the bisimplicial natural system in Equation (11). By Proposition 1, for every $n\ge 0$, there is an isomorphism of abelian groups

$$\mathsf{\Gamma }:C^n({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F,{\eta }^{*}\mathcal{A})\cong {\mathrm{Hom}}_{\mathbb{F}({\int }_{\mathbf{C}}F)}({\mathcal{P}}_{n,n},\mathcal{A}),$$

which carries any n-cochain $\phi \in C^n({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F,\mathcal{A})$ to the morphism of natural systems $\mathsf{\Gamma }\phi :{\mathcal{P}}_{n,n}\to \mathcal{A}$ whose component at every morphism $(u,f):(a,x)\to (b,y)$ of ${\int }_{\mathbf{C}}F$ is the homomorphism of abelian groups

$$\mathsf{\Gamma }\phi :{\mathcal{P}}_{n,n}(u,f)\to \mathcal{A}(u,f)\mid (\sigma ,\tau ,v,g,v^{\prime },g^{\prime })\mapsto {(v,g)}_{*}{(v^{\prime },g^{\prime })}^{*}\phi (\sigma ,\tau ).$$

These morphisms $\mathsf{\Gamma }$ fit together to define an isomorphism of cochain complexes

$$\mathsf{\Gamma }:C({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F,{\eta }^{*}\mathcal{A})\cong {\mathrm{Hom}}_{\mathbb{F}({\int }_{\mathbf{C}}F)}(\mathrm{diag}\mathcal{P},\mathcal{A}).$$

In effect, for any $\phi \in C^{n-1}({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F,{\eta }^{*}\mathcal{A})$, any morphism $(u,f):(a,x)\to (b,y)$ of ${\int }_{\mathbf{C}}F$, and any generator $(\sigma ,\tau ,v,g,v^{\prime },g^{\prime })$ of ${\mathcal{P}}_{n,n}(u,f)$, we have

$$\begin{array}{cc}\hfill (\mathsf{\Gamma }& (\partial \phi ))(\sigma ,\tau ,v,g,v^{\prime },g^{\prime })={(v,g)}_{*}{(v^{\prime },g^{\prime })}^{*}\left((\partial \phi )(\sigma ,\tau )\right)\hfill \\ \hfill & \stackrel{(18)}{=}{(v,g)}_{*}{(v^{\prime },g^{\prime })}^{*}{({\sigma }_1,\sigma {(0,n)}^{*}{\tau }_1)}^{*}\phi (d_0\sigma ,d_0\tau )+\sum _{i=1}^{n-1}{(-1)}^i{(v,g)}_{*}{(v^{\prime },g^{\prime })}^{*}\phi (d_i\sigma ,d_i\tau )\hfill \\ \hfill & +{(-1)}^n{(v,g)}_{*}{(v^{\prime },g^{\prime })}^{*}{({\sigma }_n,{\sigma }_n^{*}{\tau }_n)}_{*}\phi (d_n\sigma ,{\sigma }_n^{*}{d}_n\tau )\hfill \\ \hfill & ={(v,g)}_{*}{({\sigma }_1\circ v^{\prime },(v^{\prime *}\sigma {(0,n)}^{*}{\tau }_1)\circ g^{\prime })}^{*}\phi (d_0\sigma ,d_0\tau )+\sum _{i=1}^{n-1}{(-1)}^i{(v,g)}_{*}{(v^{\prime },g^{\prime })}^{*}\phi (d_i\sigma ,d_i\tau )\hfill \\ \hfill & +{(-1)}^n{(v\circ {\sigma }_n,{\sigma }_n^{*}g\circ {\sigma }_n^{*}{\tau }_n)}_{*}{(v^{\prime },g^{\prime })}^{*}\phi (d_n\sigma ,{\sigma }_n^{*}{d}_n\tau )\hfill \\ \hfill & =(\mathsf{\Gamma }\phi )((d_0\sigma ,d_0\tau ,v,g,{\sigma }_1\circ v^{\prime },(v^{\prime *}\sigma {(0,n)}^{*}{\tau }_1)\circ g^{\prime })+\sum _{i=1}^{n-1}{(-1)}^i(d_i\sigma ,d_i\tau ,v,g,v^{\prime },g^{\prime })\hfill \\ \hfill & +{(-1)}^n(d_n\sigma ,{\sigma }_n^{*}{d}_n\tau ,v\circ {\sigma }_n,{\sigma }_n^{*}(g\circ {\tau }_n),v^{\prime },g^{\prime }))\hfill \\ \hfill & \stackrel{(12)}{=}\left((\mathsf{\Gamma }\phi )\partial \right)(\sigma ,\tau ,v,g,v^{\prime },g^{\prime }).\hfill \end{array}$$

Hence, the result follows from Lemma 1 and Fact 1 (=Corollary 8 below). □

Theorem 3 above is actually a natural generalization of the useful and well-known result below, already presented as Fact 2 in the preliminary Section 2.

Corollary 1.

Let $\mathbf{C}$ be a small category. For any natural system $\mathcal{A}$ on $\mathbf{C}$, there are natural isomorphisms

$$H^n(\mathbf{C},\mathcal{A})\cong H^n(\mathrm{N}(\mathbf{C}),\mathcal{A})(n\ge 0).$$

Proof. 

Let us specialize Theorem 3 to the case when $F=\mathbf{0}:{\mathbf{C}}^{op}\to \mathbf{Cat}$ is the constant functor defined by the only-one-arrow category $\mathbf{0}$. In this case, ${\int }_{\mathbf{C}}\mathbf{0}=\mathbf{C}$, ${\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}\mathbf{0}=\mathrm{N}(\mathbf{C})$, and the Thomason simplicial map Equation (9), $\eta :{\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}\mathbf{0}\to \mathrm{N}({\int }_{\mathbf{C}}\mathbf{0})$, is the identity map on $\mathrm{N}\mathbf{C}$. Therefore, Theorem 3 just says that, for any natural system $\mathcal{A}$ on $\mathbf{C}$, there are isomorphisms $H^n(\mathbf{C},\mathcal{A})\cong H^n(\mathrm{N}(\mathbf{C}),\mathcal{A})$. □

Particular cases of the following corollary have been used several times in homological algebra to compute cohomology of semidirect products of groups or monoids, diagrams of groups, etc. (see, e.g., Cegarra [18,19]), by means of certain chain complexes more manageable than the standard ones.

Let $\mathcal{P}={\mathcal{P}}_{\mathbf{C}}(F)$ be the bisimplicial natural system on ${\int }_{\mathbf{C}}F$ in Equation (11), and let $\mathcal{A}$ be any given natural system on ${\int }_{\mathbf{C}}F$. By Proposition 1, there is a natural isomorphism of bicosimplicial abelian groups

$${\mathrm{Hom}}_{\mathbb{F}({\int }_{\mathbf{C}}F)}(\mathcal{P},\mathcal{A})\cong \tilde{C}({\int }_{\mathbf{C}}F,\mathcal{A}),$$

where $\tilde{C}({\int }_{\mathbf{C}}F,\mathcal{A})$ is the bicosimplicial abelian group described as follows: for every integers $p,q\ge 0$,

$${\tilde{C}}^{p,q}({\int }_{\mathbf{C}}F,\mathcal{A})=\mathsf{\prod }_{\begin{array}{c}\sigma :\mathbf{p}\to \mathbf{C}\\ \tau :\mathbf{q}\to F(\sigma p)\end{array}}\mathcal{A}(\sigma (0,p),\sigma {(0,p)}^{*}\tau (0,q)),$$

(19)

and, for any maps $\alpha :{\mathbf{p}}^{\prime }\to \mathbf{p}$ and $\beta :{\mathbf{q}}^{\prime }\to \mathbf{q}$ in the simplicial category, the induced homomorphisms

$${\tilde{C}}^{p^{\prime },q}({\int }_{\mathbf{C}}F,\mathcal{A})\stackrel{{\alpha }_{*}^h}{\to }{\tilde{C}}^{p,q}({\int }_{\mathbf{C}}F,\mathcal{A})\stackrel{{\beta }_{*}^v}{\leftarrow }{\tilde{C}}^{p,q}({\int }_{\mathbf{C}}F,\mathcal{A})$$

are defined by

$$\begin{array}{cc}\hfill ({\alpha }_h^{*}\phi )(\sigma ,\tau )=& {(\sigma (\alpha p^{\prime },p),1_{\sigma {(\alpha p^{\prime },p)}^{*}\tau q})}_{*}{(\sigma (0,\alpha 0),1_{\sigma {(0,p)}^{*}\tau 0})}^{*}(\sigma \alpha ,\sigma {(\alpha p^{\prime },p)}^{*}\tau ),\hfill \\ \hfill ({\beta }_{*}^v\phi )(\sigma ,\tau )=& {(1_{\sigma p},\tau (\beta q^{\prime },q))}_{*}{(1_{\sigma 0},\sigma {(0,p)}^{*}\tau (0,\beta 0))}^{*}(\sigma ,\tau \beta ).\hfill \end{array}$$

In particular, its horizontal and vertical coface homomorphisms

$${\tilde{C}}^{p-1,q}({\int }_{\mathbf{C}}F,\mathcal{A})\stackrel{d_h^i}{\to }{\tilde{C}}^{p,q}({\int }_{\mathbf{C}}F,\mathcal{A})\stackrel{d_v^j}{\leftarrow }{\tilde{C}}^{p,q-1}({\int }_{\mathbf{C}}F,\mathcal{A})$$

are given by the formulas

$$\begin{array}{cc}\hfill d_h^i\phi (\sigma ,\tau )& =\left\{\begin{array}{ccc}{({\sigma }_1,1_{\sigma {(0,p)}^{*}\tau 0})}^{*}\phi (d_0\sigma ,\tau )\hfill & \hfill & i=0,\hfill \\ \phi (d_i\sigma ,\tau )\hfill & \hfill & 0<i<p,\hfill \\ {({\sigma }_p,1_{{\sigma }_p^{*}\tau q})}_{*}\phi (d_p\sigma ,\tau )\hfill & \hfill & i=p,\hfill \end{array}\right.\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill d_v^j\phi (\sigma ,\tau )& =\left\{\begin{array}{ccc}{(1_{\sigma 0},\sigma {(0,p)}^{*}{\tau }_1)}^{*}\phi (\sigma ,d_0\tau )\hfill & \hfill & j=0,\hfill \\ \phi (\sigma ,d_j\tau )\hfill & \hfill & 0<j<q,\hfill \\ {(1_{\sigma p},{\tau }_q)}_{*}\phi (\sigma ,d_q\tau )\hfill & \hfill & j=q,\hfill \end{array}\right.\hfill \end{array}$$

(21)

Define the non-standard cochain complex of ${\int }_{\mathbf{C}}F$ with coefficients in a natural system $\mathcal{A}$ to be $\mathrm{Tot}\tilde{C}({\int }_{\mathbf{C}}F,\mathcal{A})$, the total cochain complex of the associated double cochain complex to $\tilde{C}({\int }_{\mathbf{C}}F,\mathcal{A})$. Thus, it consists of the abelian groups

$${\mathrm{Tot}}^n\tilde{C}({\int }_{\mathbf{C}}F,\mathcal{A})=\mathsf{\prod }_{\begin{array}{c}\sigma :\mathbf{p}\to \mathbf{C}\\ \tau :\mathbf{q}\to F(\sigma p)\\ p+q=n\end{array}}\mathcal{A}(\sigma (0,p),\sigma {(0,p)}^{*}\tau (0,q)),$$

with coboundary $\partial :{\mathrm{Tot}}^{n-1}\tilde{C}({\int }_{\mathbf{C}}F,\mathcal{A})\to {\mathrm{Tot}}^n\tilde{C}({\int }_{\mathbf{C}}F,\mathcal{A})$ given by

$$\begin{array}{cc}\hfill (\partial \phi )(\sigma ,\tau )=& {({\sigma }_1,1_{\sigma {(0,p)}^{*}\tau 0})}_{*}\phi (d_0\sigma ,\tau )+\sum _{i=1}^{p-1}{(-1)}^i\phi (d_i\sigma ,\tau )+{(-1)}^p{\left({\sigma }_p,1_{{\sigma }_p^{*}\tau q}\right)}_{*}\phi (d_p\sigma ,{\sigma }_p^{*}\tau )\hfill \\ \hfill & +{(-1)}^p\left[{(1_{\sigma 0},\sigma {(0,p)}^{*}{\tau }_1)}^{*}\phi (\sigma ,d_0\tau )+\sum _{j=1}^{q-1}{(-1)}^j\phi (\sigma ,d_j\tau )+{(-1)}^q{\left(1_{\sigma p},{\tau }_q\right)}_{*}\phi (\sigma ,d_q\tau )\right].\hfill \end{array}$$

Corollary 2.

For any natural system $\mathcal{A}$ on ${\int }_{\mathbf{C}}F$, there are natural isomorphisms

$$H^n({\int }_{\mathbf{C}}F,\mathcal{A})\cong H^n\mathrm{Tot}\tilde{C}({\int }_{\mathbf{C}}F,\mathcal{A})(n\ge 0).$$

Proof. 

From the descriptions of the bicomplex $\tilde{C}({\int }_{\mathbf{C}}F,\mathcal{A})$ in Equations (18) and (17) and the complex $C({\mathrm{hocolim}}_{\mathbf{C}}NF,{\eta }^{*}\mathcal{A})$ in Equations (19)–(21), a straightforward comparison shows that $\mathrm{diag}\tilde{C}({\int }_{\mathbf{C}}F,\mathcal{A})=C({\mathrm{hocolim}}_{\mathbf{C}}NF,{\eta }^{*}\mathcal{A})$. Then the result follows from Theorem 3, since both cochain complexes $\mathrm{diag}\tilde{C}({\int }_{\mathbf{C}}F,\mathcal{A})$ and $\mathrm{Tot}\tilde{C}({\int }_{\mathbf{C}}F,\mathcal{A})$ are cohomology equivalent by the generalized Eilenberg–Zilber theorem of Dold and Puppe (see, e.g., Goerss–Jardine ([15] Chapter IV, Theorem 2.4)). □

Spectral sequences for the cohomology of the Grotendieck construction are implicit in the above corollary. Let $\mathcal{A}$ be a natural system on ${\int }_{\mathbf{C}}F$. Every arrow $u:a\to b$ in $\mathbf{C}$ determines a functor between the categories of factorizations

$${\iota }_u:\mathbb{F}(F(b))\to \mathbb{F}({\int }_{\mathbf{C}}F),$$

(22)

which acts on objects by

$${\iota }_u(x\stackrel{f}{\to }y)=\left((a,u^{*}x)\stackrel{(u,u^{*}f)}{\to }(b,y)\right)$$

and on morphisms by

Then, by composition with ${\iota }_u$, the natural system $\mathcal{A}$ on the Grothendieck construction gives rise to a natural system on the category $F(b)$, denoted by ${\iota }_u^{*}\mathcal{A}$, so that the cohomology groups

$$H^q(F(b),{\iota }_u^{*}\mathcal{A})$$

(23)

are defined. For any integer $q\ge 0$, there is a natural system on $\mathbf{C}$,

$${\mathcal{H}}^q(F,{\iota }^{*}\mathcal{A}):\mathbb{F}(\mathbf{C})\to \mathbf{Ab},\mid (a\stackrel{u}{\to }b)\mapsto H^q(F(b),{\iota }_u^{*}\mathcal{A}),$$

(24)

which acts on morphisms as follows: For any morphism $(v,v^{\prime }):u\to u^{\prime }$ in $\mathbb{F}(\mathbf{C})$,

one has the natural transformation $⟨v,v^{\prime }⟩:{\iota }_u{v}^{*}\Rightarrow {\iota }_{u^{\prime }}$

whose component at a morphism $f:x\to y$ of $F(b^{\prime })$ is the morphism of $\mathbb{F}({\int }_{\mathbf{C}}F)$

$$⟨v,v^{\prime }⟩(f)=\left((v,1_{v^{*}y}),(v^{\prime },1_{u^{\prime *}x})\right):(u,u^{*}{v}^{*}f)\to (u^{\prime },u^{\prime *}f)$$

depicted as

Then, the induced homomorphism

$$v_{*}{v}^{\prime *}:H^q(F(b),{\iota }_u^{*}\mathcal{A})\to H^q(F(b^{\prime }),{\iota }_{u^{\prime }}^{*}\mathcal{A})$$

is the composite of the homomorphisms

$$H^q(F(b),{\iota }_u^{*}\mathcal{A})\stackrel{{(v^{*})}^{*}}{\to }{H}^q(F(b^{\prime }),v^{*}{\iota }_u^{*}\mathcal{A})\stackrel{{⟨v,v^{\prime }⟩}_{*}}{\to }{H}^q(F(b^{\prime }),{\iota }_{u^{\prime }}^{*}\mathcal{A}).$$

Corollary 3.

For any natural system $\mathcal{A}$ on ${\int }_{\mathbf{C}}F$ there is a natural first quadrant spectral sequence

$$E_2^{p,q}=H^p(\mathbf{C},{\mathcal{H}}^q(F,{\iota }^{*}\mathcal{A}))\Rightarrow H^{p+q}({\int }_{\mathbf{C}}F,\mathcal{A})$$

where ${\mathcal{H}}^q(F,{\iota }^{*}\mathcal{A})$ is the natural system on $\mathbf{C}$ defined in Equation (24).

Proof. 

Let $\tilde{C}({\int }_{\mathbf{C}}F,\mathcal{A})$ be the double cochain complex associated to the bicosimplicial abelian group in Equation (19). Fixing any $p\ge 0$, and taking homology in the vertical complex ${\tilde{C}}^{p,•}({\int }_{\mathbf{C}}F,\mathcal{A})$, we have

$$\begin{array}{cc}\hfill H_v^q{\tilde{C}}^{p,•}({\int }_{\mathbf{C}}F,\mathcal{A})=& H^q\left(\mathsf{\prod }_{\sigma :\mathbf{p}\to \mathbf{C}}\mathbb{F}(F(\sigma p),{\iota }_{\sigma (0,p)}^{*}\mathcal{A})\right)=\mathsf{\prod }_{\sigma :\mathbf{p}\to \mathbf{C}}{H}^q(F(\sigma p),{\iota }_{\sigma (0,p)}^{*}\mathcal{A})\hfill \\ \hfill =& \mathsf{\prod }_{\sigma :\mathbf{p}\to \mathbf{C}}{\mathcal{H}}^q(F,\mathcal{A})(\sigma (0,p)).\hfill \end{array}$$

Taking now the cohomology again, we have $H_h^p{H}_v^q\tilde{C}({\int }_{\mathbf{C}}F,\mathcal{A})=H^p(\mathbf{C},{\mathcal{H}}^q(F,{\iota }^{*}A))$, whence the result follows from Corollary 2. □

Note that, when $u=1_b$ is the identity arrow of any object b of $\mathbf{C}$, then functor ${\iota }_{1_b}:\mathbb{F}(F(b))\to \mathbb{F}({\int }_{\mathbf{C}}F)$ in (22) is the induced one on the category of factorizations by the canonical inclusion functor

$${\iota }_b:F(b)\hookrightarrow {\int }_{\mathbf{C}}F\mid (x\stackrel{f}{\to }y)\to \left((b,x)\stackrel{(1_b,f)}{\to }(b,y)\right).$$

(25)

So, in this case, we can write the corresponding cohomology group Equation (23) simply as $H^q(F(b),{\iota }_b^{*}\mathcal{A})$. For any $q\ge 0$, we have the $\mathbf{C}$-module

$$H^q(F,{\iota }^{*}\mathcal{A}):\mathbf{C}\to \mathbf{Ab}\mid b\mapsto H^q(F(b),{\iota }_b^{*}\mathcal{A}),$$

(26)

which carries every morphism $v:b\to b^{\prime }$ to the composite homomorphism

$$H^q(F(b),{\iota }_b^{*}\mathcal{A})\stackrel{{(v^{*})}^{*}}{\to }{H}^q(F(b^{\prime }),v^{*}{\iota }_b^{*}\mathcal{A})\stackrel{{⟨v⟩}_{*}}{\to }{H}^q(F(b^{\prime }),{\iota }_{b^{\prime }}^{*}\mathcal{A}),$$

where $⟨v⟩:{\iota }_b{v}^{*}\Rightarrow {\iota }_{b^{\prime }}$

is the natural transformation defined, at any object x of $F(b^{\prime })$, by

$$⟨v⟩(x)=(v,1_{v^{*}x}):(b,v^{*}x)\to (b^{\prime },x).$$

There is, for any integer $q\ge 0$, a morphism of natural systems on $\mathbf{C}$

$${⟨⟩}_{*}:H^q(F,{\iota }^{*}\mathcal{A})\to {\mathcal{H}}^q(F,{\iota }^{*}\mathcal{A}),$$

(27)

where, recall, the $\mathbf{C}$-module $H^q(F,{\iota }^{*}\mathcal{A})$ is regarded as a natural system by composition with the target functor $t:\mathbb{F}(\mathbf{C})\to \mathbf{C}$ in Equation (5). Its component at any morphism $u:a\to b$ in $\mathbf{C}$ is the homomorphism

$${⟨u⟩}_{*}:H^q(F(b),{\iota }_b^{*}\mathcal{A})\to {\mathcal{H}}^q(F(b),{\iota }_u^{*}\mathcal{A})$$

induced by the natural transformation $⟨u⟩:{\iota }_b\Rightarrow {\iota }_u$,

which is defined on any morphism $f:x\to y$ of $F(b)$ by

$$⟨u⟩(f)=\left(1_{(b,y)},(u,1_{u^{*}x})\right):(1_b,f)\to (u,u^{*}f)$$

Following to Pirsahvili–Redondo [6], we say that the natural system $\mathcal{A}$ is h-local provided the morphism ${⟨⟩}_{*}:H^q(F,{\iota }^{*}\mathcal{A})\cong {\mathcal{H}}^q(F,{\iota }^{*}\mathcal{A})$ in Equation (27) is an isomorphism, for all $q\ge 0$. This means that, for any arrow $u:a\to b$ in $\mathbf{C}$, the cochain map ${⟨u⟩}_{*}:\mathbb{F}(F(b),{\iota }_b^{*}\mathcal{A})\to \mathbb{F}(F(b),{\iota }_u^{*}\mathcal{A})$

is a homology isomorphism. We call the natural system $\mathcal{A}$local whenever the natural transformations $⟨u⟩:{\iota }_b\Rightarrow {\iota }_u$ induces an isomorphism ${\iota }_b^{*}\mathcal{A}\cong {\iota }_u^{*}\mathcal{A}$ of natural systems on $F(b)$, that is, if for any $f:x\to y$ in $F(b)$,

$${(u,1_{u^{*}x})}^{*}:\mathcal{A}(1_b,f)\cong \mathcal{A}(u,u^{*}f)$$

is an isomorphism (note that this condition is a bit weaker than the corresponding one stated in [6]). Clearly every local natural system on ${\int }_{\mathbf{C}}F$ is h-local, as well as every ${\int }_{\mathbf{C}}F$-module is a local natural system. The spectral sequence by Pirsahvili–Redondo in ([6] Theorem 5.2) (cf. also Gálvez–Neumann–Tonks ([7] Theorem 2.5)) and ([8] Theorem 2.16)) appears now as a particular case of the spectral sequence in the above Corollary 3.

Corollary 4.

For any h-local natural system $\mathcal{A}$ on ${\int }_{\mathbf{C}}F$ there is a natural spectral sequence

$$E_2^{p,q}=H^p(\mathbf{C},H^q(F,{\iota }^{*}\mathcal{A}))\Rightarrow H^{p+q}({\int }_{\mathbf{C}}F,\mathcal{A})$$

where $H^q(F,{\iota }^{*}\mathcal{A})$ is the natural system on $\mathbf{C}$ defined in Equation (26).

The spectral sequence in Corollary 3 involves some invariance results, as we show below.

Corollary 5.

Let $F,F^{\prime }:{\mathbf{C}}^{op}\to \mathbf{Cat}$ be functors, let $\nu :F^{\prime }\Rightarrow F$ be a natural transformation, and let $\mathcal{A}$ be a natural system on ${\int }_{\mathbf{C}}F$. If, for any arrow $u:a\to b$ in $\mathbf{C}$, the functor ${\nu }_b:F^{\prime }(b)\to F(b)$ induces isomorphisms

$$H^n(F(b),{\iota }_u^{*}\mathcal{A})\cong H^n(F^{\prime }(b),{\nu }_b^{*}{\iota }_u^{*}\mathcal{A}),n\ge 0,$$

then the functor ${\int }_{\mathbf{C}}\nu :{\int }_{\mathbf{C}}{F}^{\prime }\to {\int }_{\mathbf{C}}F$ also induces isomorphisms

$$H^n({\int }_{\mathbf{C}}F,\mathcal{A})\cong H^n({\int }_{\mathbf{C}}{F}^{\prime },{({\int }_{\mathbf{C}}\nu )}^{*}\mathcal{A}),n\ge 0.$$

Proof. 

For any arrow $u:a\to b$ of $\mathbf{C}$, the square

commutes. Therefore ${\nu }_b$ induces isomorphisms

$$H^n(F(b),{\iota }_u^{*}\mathcal{A})\cong H^n(F^{\prime }(b),{\iota }_u^{\prime *}{({\int }_{\mathbf{C}}\nu )}^{*}\mathcal{A}).$$

Since these are natural in u, it follows that $\nu$ induces an isomorphism of natural systems on $\mathbf{C}$ between ${\mathcal{H}}^n(F,{\iota }^{*}\mathcal{A})$ and ${\mathcal{H}}^n(F^{\prime },{\iota }^{\prime *}{({\int }_{\mathbf{C}}\nu )}^{*}\mathcal{A})$. Then, for any integers $p,q\ge 0$, there are natural isomorphisms

$$H^p(\mathbf{C},{\mathcal{H}}^q(F,{\iota }^{*}\mathcal{A}))\cong H^p(\mathbf{C},{\mathcal{H}}^q(F^{\prime },{\iota }^{\prime *}{({\int }_{\mathbf{C}}\nu )}^{*}\mathcal{A}))$$

and the result follows from the spectral sequences in Corollary 3 for F and $\mathcal{A}$ and $F^{\prime }$ and ${({\int }_{\mathbf{C}}\nu )}^{*}\mathcal{A}$, respectively. □

Recall now that a functor $\mathcal{A}:{\int }_{\mathbf{C}}F\to \mathbf{Ab}$ is called a twisted system of coefficients on the diagram of categories $F:{\mathbf{C}}^{op}\to \mathbf{Cat}$ whenever, for any object b of $\mathbf{C}$, $i_b^{*}\mathcal{A}$ is a local system of coefficients on the category $F(b)$; that is, provided that, for any arrow $f:x\to y$ in $F(b)$, the induced ${(1_b,f)}_{*}:\mathcal{A}(b,x)\cong \mathcal{A}(b,y)$ is an isomorphism, see ([10] Definition 2.1). The following invariance result was proved by Moerdijk–Svensson in ([10] Theorem 2.3).

Corollary 6.

Let $F,F^{\prime }:{\mathbf{C}}^{op}\to \mathbf{Cat}$ be functors. Suppose $\nu :F^{\prime }\Rightarrow F$ is a natural transformation such that all the functors ${\nu }_b:F^{\prime }(b)\to F(b)$, $b\in \mathrm{Ob}\mathbf{C}$, are weak homotopy equivalences of categories. Then, for any twisted system of coefficients $\mathcal{A}$ on F, ν induces natural isomorphisms

$$H^n({\int }_{\mathbf{C}}F,\mathcal{A})\cong H^n({\int }_{\mathbf{C}}{F}^{\prime },{({\int }_{\mathbf{C}}\nu )}^{*}\mathcal{A}),n\ge 0.$$

Proof. 

For any twisted system of coefficients $\mathcal{A}$ on F, the induced homomorphisms ${\nu }_b^{*}:H^n(F(b),{\iota }_b^{*}\mathcal{A})\cong H^n(F^{\prime }(b),{\nu }_b^{*}{\iota }_b^{*}\mathcal{A})$ are isomorphisms. Since, for any $u:a\to b$ in $\mathbf{C}$, we have $i_b^{*}\mathcal{A}={\iota }_u^{*}\mathcal{A}$, the hypothesis of Corollary 5 above hold, whence the result follows. □

The following terminology is suggested by T. Pirashvili.

Definition 1.

A weak homotopy equivalence of categories $f:{\mathbf{C}}^{\prime }\to \mathbf{C}$ is a Baues–Wirsching weak homotopy equivalence (resp. a Roos–Watts weak homotopy equivalence) provided that, for any natural system $\mathcal{A}$ on $\mathbf{C}$ (resp. $\mathbf{C}$-module), the induced homomorphisms $H^n(\mathbf{C},\mathcal{A})\cong H^n({\mathbf{C}}^{\prime },f^{*}\mathcal{A})$, $n\ge 0$, are all isomorphisms.

For instance, if $f:{\mathbf{C}}^{\prime }\to \mathbf{C}$ is any functor with a left or right adjoint, then it is a Baues–Wirsching weak homotopy equivalence. This fact follows from ([20] Lemma 1.5, p. 10). See also ([6] Lemma 2.2), ([8] Corollary 2.3), and ([21] Corollary 4.3).

Corollary 7.

Let $F,F^{\prime }:{\mathbf{C}}^{op}\to \mathbf{Cat}$ be functors. Suppose $\nu :F^{\prime }\Rightarrow F$ is a natural transformation such that all the functors ${\nu }_b:F^{\prime }(b)\to F(b)$, $b\in \mathrm{Ob}\mathbf{C}$, are Baues–Wirsching (resp. Roos–Watts) weak homotopy equivalences, then ${\int }_{\mathbf{C}}\nu :{\int }_{\mathbf{C}}{F}^{\prime }\to {\int }_{\mathbf{C}}F$ also is.

Proof. 

This follows from Corollary 5. □

4. On the Weak Equivalence $\mathbf{\mu }:\mathsf{\Delta }({\mathrm{hocolim}}_{\mathbf{C}}\mathbf{G})\to {\int }_{\mathbf{C}}\mathsf{\Delta }\mathbf{G}$

Throughout this section, $\mathbf{C}$ is a small category and $G:{\mathbf{C}}^{op}\to \mathbf{SSet}$ is a functor. For any morphism $u:a\to b$ of $\mathbf{C}$, we write $u^{*}:G(b)\to G(a)$ for the simplicial map $G(u)$. Since $u^{*}$ is simplicial, for any map $\alpha :\mathbf{m}\to \mathbf{n}$ in $\mathsf{\Delta }$, we have ${\alpha }^{*}{u}^{*}=u^{*}{\alpha }^{*}$, that is, the square below commutes.

In particular, every functor $\sigma :\mathbf{n}\to \mathbf{C}$ gives rise to the simplicial maps, see Equation (6),

$$\sigma {(i,j)}^{*}={\sigma }_{i+1}^{*}\cdots {\sigma }_j^{*}:G(\sigma j)\to G(\sigma i)(0\le i\le j\le n).$$

4.1. The Involved Constructions

The simplicial replacement of G of Bousfield–Kan ([9] Chapter XII, §5) produces the bisimplicial set

$$\mathsf{\Psi }={\mathsf{\Psi }}_{\mathbf{C}}(G):{\mathsf{\Delta }}^{op}\times {\mathsf{\Delta }}^{op}\to \mathbf{Set},$$

(28)

whose $(p,q)$-simplices are pairs $(\sigma ,x)$ where $\sigma :\mathbf{p}\to \mathbf{C}$ is a functor and $x\in G{(\sigma p)}_q$ is a q-simplex of $G(\sigma p)$. If $\alpha :{\mathbf{p}}^{\prime }\to \mathbf{p}$ and $\beta :{\mathbf{q}}^{\prime }\to \mathbf{q}$ are maps in $\mathsf{\Delta }$, the induced maps

$${\mathsf{\Psi }}_{p^{\prime },q}\stackrel{{\alpha }_h^{*}={(\alpha ,1_{\mathbf{q}})}^{*}}{\leftarrow }{\mathsf{\Psi }}_{p,q}\stackrel{{\beta }_v^{*}={(1_{\mathbf{p}},\beta )}^{*}}{\to }{\mathsf{\Psi }}_{p,q^{\prime }}$$

are respectively defined on any $(p,q)$-simplex $(\sigma ,x)$ as above by

$${\alpha }_h^{*}(\sigma ,x)=(\sigma \alpha ,\sigma {(\alpha p^{\prime },p)}^{*}x),{\beta }_v^{*}(\sigma ,x)=(\sigma ,{\beta }^{*}x).$$

In particular, its horizontal and vertical face maps ${\mathsf{\Psi }}_{p-1,q}\stackrel{d_i^h}{\leftarrow }{\mathsf{\Psi }}_{p,q}\stackrel{d_j^v}{\to }{\mathsf{\Psi }}_{p,q-1}$ act by

$$\begin{array}{cc}\hfill d_i^h(\sigma ,x)& =\left\{\begin{array}{cc}(d_i\sigma ,x)\hfill & 0\le i<p,\hfill \\ (d_p\sigma ,{\sigma }_p^{*}x)\hfill & i=p,\hfill \end{array}\right.\hfill \\ \hfill d_j^v(\sigma ,x)& =(\sigma ,d_{j}x),0\le j\le q.\hfill \end{array}$$

The homotopy colimit construction on G is the simplicial set

$${\mathrm{hocolim}}_{\mathbf{C}}G=\mathrm{diag}{\mathsf{\Psi }}_{\mathbf{C}}(G).$$

Its n-simplices are then pairs $(\sigma ,x)$ where $\sigma :\mathbf{n}\to \mathbf{C}$ is a functor and $x\in G{(\sigma p)}_n$. If $\alpha :\mathbf{m}\to \mathbf{n}$ is any map in $\mathsf{\Delta }$, then the induced map ${\alpha }^{*}:{({\mathrm{hocolim}}_{\mathbf{C}}G)}_n\to {({\mathrm{hocolim}}_{\mathbf{C}}G)}_m$ acts by

$${\alpha }^{*}(\sigma ,x)=(\sigma \alpha ,\sigma {(\alpha m,n)}^{*}{\alpha }^{*}x).$$

In particular, its face maps are given by

$$d_i(\sigma ,x)=\left\{\begin{array}{cc}(d_i\sigma ,d_{i}x)\hfill & 0\le i<n,\hfill \\ (d_n\sigma ,{\sigma }_n^{*}{d}_{n}x)\hfill & i=n.\hfill \end{array}\right.$$

On the other hand, by composing G with the category of simplices functor $\mathsf{\Delta }:\mathbf{SSet}\to \mathbf{Cat}$, we get a diagram of categories $\mathsf{\Delta }G:{\mathbf{C}}^{op}\to \mathbf{Cat}$ on which we can apply the Grothendieck construction. This yields the small category

$${\int }_{\mathbf{C}}\mathsf{\Delta }G,$$

whose objects are triples $(\mathbf{n},a,x)$, where $\mathbf{n}\in \mathrm{Ob}\mathsf{\Delta }$, $a\in \mathrm{Ob}\mathbf{C}$, and $x\in G{(a)}_n$ is a n-simplex of $G(a)$. A morphism $(\alpha ,u):(\mathbf{m},b,y)\to (\mathbf{n},a,x)$ consists of morphisms $\alpha :\mathbf{m}\to \mathbf{n}$, of $\mathsf{\Delta }$, and $u:b\to a$, of $\mathbf{C}$, such that $y=u^{*}{\alpha }^{*}x$. Composition in ${\int }_{\mathbf{C}}\mathsf{\Delta }G$ is given by $(\beta ,v)\circ (\alpha ,u)=(\beta \alpha ,v\circ u)$.

Let $\mathsf{\Delta }({\mathrm{hocolim}}_{\mathbf{C}}G)$ be the category of simplices of the homotopy colimit of G. Its objects are triples $(\mathbf{n},\sigma ,x)$, where $\sigma :\mathbf{n}\to \mathbf{C}$ is a functor and $x\in G{(\sigma n)}_n$. Its morphisms $\alpha :(\mathbf{m},\tau ,y)\to (\mathbf{n},\sigma ,x)$ are those maps $\alpha :\mathbf{m}\to \mathbf{n}$ in $\mathsf{\Delta }$ such that $\tau =\sigma \alpha$ and $y=\sigma {(\alpha m,n)}^{*}{\alpha }^{*}x$. We have the functor

$$\mu :\mathsf{\Delta }({\mathrm{hocolim}}_{\mathbf{C}}G)\to {\int }_{\mathbf{C}}\mathsf{\Delta }G,$$

(29)

which is defined on objects by $\mu (\mathbf{n},\sigma ,x)=(\mathbf{n},\sigma n,x)$, and on morphisms $\alpha :(\mathbf{m},\tau ,y)\to (\mathbf{n},\sigma ,x)$ by

$$\mu (\alpha )=(\alpha ,\sigma (\alpha m,n)):(\mathbf{m},\tau m,y)⟶(\mathbf{n},\sigma n,x).$$

4.2. A Projective Resolution of the ${\int }_{\mathbf{C}}\mathsf{\Delta }G$-module $\mathbb{Z}$

To shorten some expressions, if $\mathcal{A}$ is any ${\int }_{\mathbf{C}}\mathsf{\Delta }G$-module and $(\mathbf{n},a,x)$ is an object of ${\int }_{\mathbf{C}}\mathsf{\Delta }G$, then we write $\mathcal{A}(a,x)$ for $\mathcal{A}(\mathbf{n},a,x)$, leaving understood the dimension n of the simplex x of $G(a)$.

Let $\mathsf{\Psi }={\mathsf{\Psi }}_{\mathbf{C}}(G)$ be as in Equation (28). For any integers $p,q\ge 0$, let the set ${\mathsf{\Psi }}_{p,q}$ be equipped with the map

$$\pi :{\mathsf{\Psi }}_{p,q}\to \mathrm{Ob}{\int }_{\mathbf{C}}\mathsf{\Delta }G,(\sigma ,x)\mapsto \left(\mathbf{q},\sigma p,x\right),$$

and let ${\mathcal{Q}}_{p,q}=\mathcal{F}{\mathsf{\Psi }}_{p,q}$ be the associated free ${\int }_{\mathbf{C}}\mathsf{\Delta }G$-module. Thus, for each object $(\mathbf{n},a,x)$ of ${\int }_{\mathbf{C}}\mathsf{\Delta }G$, ${\mathcal{Q}}_{p,q}(a,x)=\mathbb{Z}\left\{(\sigma ,z,\alpha ,u)\right\}$ is the free abelian group on the set of lists $(\sigma ,z,\alpha ,u)$ consisting of a functor $\sigma :\mathbf{p}\to \mathbf{C}$, a simplex $z\in G{(\sigma p)}_q$, a map $\alpha :\mathbf{q}\to \mathbf{n}$ in $\mathsf{\Delta }$, and a morphism $u:\sigma p\to a$ in $\mathbf{C}$, such that $z=u^{*}{\alpha }^{*}x$. Equivalently, we can take

$${\mathcal{Q}}_{p,q}(a,x)=\mathbb{Z}\left\{(\sigma ,u,\alpha )\right\}$$

(30)

the free abelian group on the set of triples $(\sigma ,u,\alpha )$ consisting of a functor $\sigma :\mathbf{p}\to \mathbf{C}$, a morphism $u:\sigma p\to a$ in $\mathbf{C}$, and a map $\alpha :\mathbf{q}\to \mathbf{m}$ in $\mathsf{\Delta }$. If $(\beta ,v):(\mathbf{m},b,y)\to (\mathbf{n},a,x)$ is any morphism of the category ${\int }_{\mathbf{C}}\mathsf{\Delta }G$, then the induced homomorphism ${(\beta ,v)}_{*}:{\mathcal{Q}}_{p,q}(b,y)\to {\mathcal{Q}}_{p,q}(a,x)$ is given on generators by ${(\beta ,v)}_{*}(\sigma ,\alpha ,u)=(\sigma ,\beta \alpha ,v\circ u)$.

These ${\mathcal{Q}}_{p,q}$ provide us of a bisimplicial ${\int }_{\mathbf{C}}\mathsf{\Delta }G$-module

$$\mathcal{Q}={\mathcal{Q}}_{\mathbf{C}}(G):{\mathsf{\Delta }}^{op}\times {\mathsf{\Delta }}^{op}⟶{\int }_{\mathbf{C}}\mathsf{\Delta }G-\mathrm{Mod},$$

(31)

in which, for any maps $\beta :{\mathbf{p}}^{\prime }\to \mathbf{p}$ and $\gamma :{\mathbf{q}}^{\prime }\to \mathbf{q}$ in the simplicial category, the induced morphisms at any object $(\mathbf{n},a,x)$ of ${\int }_{\mathbf{C}}\mathsf{\Delta }G$,

$${\mathcal{Q}}_{p^{\prime },q}(a,x)\stackrel{{\beta }_h^{*}}{\leftarrow }{\mathcal{Q}}_{p,q}(a,x)\stackrel{{\gamma }_v^{*}}{\to }{\mathcal{Q}}_{p,q^{\prime }}(a,x)$$

are the homomorphisms acting on generators by

$$\left\{\begin{array}{c}{\beta }_h^{*}(\sigma ,\alpha ,u)=\left(\sigma \beta ,\alpha ,u\circ \sigma (\beta p^{\prime },p)\right),\hfill \\ {\gamma }_v^{*}(\sigma ,\alpha ,u)=\left(\sigma ,\alpha \gamma ,u\right).\hfill \end{array}\right.$$

In particular, the horizontal and vertical face homomorphisms

$${\mathcal{Q}}_{p-1,q}(a,x)\stackrel{d_i^h}{\leftarrow }{\mathcal{Q}}_{p,q}(a,x)\stackrel{d_j^v}{\to }{\mathcal{Q}}_{p,q-1}(a,x)$$

are defined on generators by

$$\begin{array}{cc}\hfill d_i^h(\sigma ,\alpha ,u)& =\left\{\begin{array}{ccc}(d_i\sigma ,\alpha ,u),\hfill & \hfill & 0\le i<p,\hfill \\ (d_p\sigma ,\alpha ,u\circ {\sigma }_p)\hfill & \hfill & i=p,\hfill \end{array}\right.\hfill \\ \hfill d_j^v(\sigma ,\alpha ,u)& =(\sigma ,\alpha d^j,u),0\le j\le q.\hfill \end{array}$$

Let $\mathrm{diag}\mathcal{Q}$ be the complex associated to the simplicial ${\int }_{\mathbf{C}}\mathsf{\Delta }G$-module diagonal of $\mathcal{Q}$. Thus, ${(\mathrm{diag}\mathcal{Q})}_m={\mathcal{Q}}_{m,m}$ and, at any object $(\mathbf{n},a,x)$ of ${\int }_{\mathbf{C}}\mathsf{\Delta }G$, the differential $\partial :{\mathcal{Q}}_{m,m}(a,x)\to {\mathcal{Q}}_{m-1,m-1}(a,x)$ is given on generators by

$$\begin{array}{c}\hfill \partial (\sigma ,\alpha ,u)=\sum _{i=0}^{m-1}{(-1)}^i(d_i\sigma ,\alpha d^i,u)+{(-1)}^m\left(d_m\sigma ,\alpha d^m,u\circ {\sigma }_m\right).\end{array}$$

(32)

Lemma 2.

$\mathrm{diag}{\mathcal{Q}}_{\mathbf{C}}(F)$ is a projective resolution of the ${\int }_{\mathbf{C}}\mathsf{\Delta }G$-module $\mathbb{Z}$. Hence, for any ${\int }_{\mathbf{C}}\mathsf{\Delta }G$-module $\mathcal{A}$,

$$H^n\left({\int }_{\mathbf{C}}\mathsf{\Delta }G,\mathcal{A}\right)=H^n\left({\mathrm{Hom}}_{{\int }_{\mathbf{C}}\mathsf{\Delta }G}(\mathrm{diag}{\mathcal{Q}}_{\mathbf{C}}(F),\mathcal{A})\right).$$

Proof. 

Let us write $\mathcal{Q}={\mathcal{Q}}_{\mathbf{C}}(F)$ as in Equation (31). There is an augmentation $ϵ:\mathrm{diag}\mathcal{Q}\twoheadrightarrow \mathbb{Z}$ which, at any object $(\mathbf{n},a,x)$ of ${\int }_{\mathbf{C}}\mathsf{\Delta }G$, is given by the homomorphism

$$ϵ:{\mathcal{Q}}_{0,0}(a,x)\to \mathbb{Z}(a,x)$$

that carries all generators $(\sigma ,\alpha ,u)$ of ${\mathcal{Q}}_{0,0}(a,x)$ to the generator $(\mathbf{n},a,x)$ of $\mathbb{Z}(a,x)$. Since every ${\int }_{\mathbf{C}}\mathsf{\Delta }F$-module ${\mathcal{Q}}_{n,n}$ is free, whence projective, it suffices to prove that, for any object $(\mathbf{n},a,x)$ of ${\int }_{\mathbf{C}}\mathsf{\Delta }F$, the augmented chain complex of abelian groups

$$\cdots \to {\mathcal{Q}}_{2,2}(a,x)\stackrel{\partial }{⟶}{\mathcal{Q}}_{1,1}(a,x)\stackrel{\partial }{⟶}{\mathcal{Q}}_{0,0}(a,x)\stackrel{ϵ}{⟶}\mathbb{Z}(a,x)\to 0$$

(33)

is exact. To do this, let us fix any such $(\mathbf{n},a,x)$ and proceed as follows.

Let ${\mathsf{\Delta }}^n={\mathrm{Hom}}_{\mathsf{\Delta }}(-,\mathbf{n})$ be the standard simplicial n-simplex, and let us consider the simplicial abelian group $\mathbb{Z}{\mathsf{\Delta }}^n$, $\mathbf{q}\mapsto \mathbb{Z}{\mathrm{Hom}}_{\mathsf{\Delta }}(\mathbf{q},\mathbf{n})$, as a bisimplicial abelian group which is constant in the horizontal direction. Then, a bisimplicial homomorphism $ϵ:\mathcal{Q}(a,x)\to \mathbb{Z}{\mathsf{\Delta }}^n$ is given by the homomorphisms $ϵ:{\mathcal{Q}}_{0,q}(a,x)\to \mathbb{Z}{\mathsf{\Delta }}_q^{\mathbf{n}}$ defined on generators by

$$ϵ(a_0,\mathbf{q}\stackrel{\alpha }{\to }\mathbf{n},a_0\stackrel{u}{\to }a)=\alpha ,$$

where we have identified any object $a_0$ of $\mathbf{C}$ with the functor $\sigma :\mathbf{0}\to \mathbf{C}$ such that $\sigma 0=a_0$. For any $q\ge 0$, the associated augmented chain complex of abelian groups admits a contracting homotopy k

whence it is exact. Such a homotopy k is given by the homomorphisms

$$k_{-1}:\mathbb{Z}{\mathsf{\Delta }}_q^n\to {\mathcal{Q}}_{0,q}(a,x),k_p:{\mathcal{Q}}_{p,q}(a,x)\to {\mathcal{Q}}_{p+1,q}(a,x),$$

which act on generators by

$$k_{-1}(\alpha )=(a,\alpha ,1_a),k_p(\sigma ,\alpha ,u)={(-1)}^{p+1}(u⭑\sigma ,\alpha ,1_a),$$

where, for any $\sigma :\mathbf{p}\to \mathbf{C}$ and $u:\sigma p\to a$, $u⭑\sigma :\mathbf{p}+\mathbf{1}\to \mathbf{C}$ is defined as in Equation (15). It follows from Dold–Puppe Theorem that the induced map on the associated augmented diagonal complexes $ϵ:\mathrm{diag}\mathcal{Q}(a,x)\to \mathrm{diag}\mathbb{Z}{\mathsf{\Delta }}^n=\mathbb{Z}{\mathsf{\Delta }}^n$,

is a homology isomorphism. Then, the exactness of Equation (33) follows from the exactness of the augmented chain complex at the bottom in the above diagram, as it has a contracting homotopy given by the homomorphisms

$$h_{-1}:\mathbb{Z}\to \mathbb{Z}{\mathsf{\Delta }}_0^n,h_q:\mathbb{Z}{\mathsf{\Delta }}_q^n\to \mathbb{Z}{\mathsf{\Delta }}_{q+1}^n,$$

(34)

which are defined on generators as follows: $h_{-1}(1):\mathbf{0}\to \mathbf{n}$ is the map $0\mapsto 0$, and, for any $\alpha :\mathbf{q}\to \mathbf{n}$, $h_q(\alpha ):\mathbf{q}+\mathbf{1}\to \mathbf{n}$ is the map $0\mapsto 0$ and $i+1\mapsto \alpha (i)$. □

By composing with the functor $\mu :\mathsf{\Delta }({\mathrm{hocolim}}_{\mathbf{C}}G)\to {\int }_{\mathbf{C}}\mathsf{\Delta }G$ in Equation (29), every ${\int }_{\mathbf{C}}\mathsf{\Delta }G$-module $\mathcal{A}$ gives rise to a coefficient system ${\mu }^{*}\mathcal{A}$ on ${\mathrm{hocolim}}_{\mathbf{C}}G$, and we have

Theorem 4.

For any ${\int }_{\mathbf{C}}\mathsf{\Delta }G$-module $\mathcal{A}$, there are natural isomorphisms

$$H^n({\int }_{\mathbf{C}}\mathsf{\Delta }G,\mathcal{A})\cong H^{n}C({\mathrm{hocolim}}_{\mathbf{C}}G,{\mu }^{*}\mathcal{A}).$$

Proof. 

Let $\mathcal{A}$ be any given ${\int }_{\mathbf{C}}\mathsf{\Delta }G$-module. As we did before, for any object $(\mathbf{n},a,x)$ of ${\int }_{\mathbf{C}}\mathsf{\Delta }G$ we write $\mathcal{A}(a,x)$ instead of $\mathcal{A}(\mathbf{n},a,x)$, and also, for any morphism $u:b\to a$ of $\mathbf{C}$ we write

$$u_{*}:\mathcal{A}(b,u^{*}x)\to \mathcal{A}(a,x)$$

for the induced homomorphism ${(i{d}_{\mathbf{n}},u)}_{*}:\mathcal{A}(\mathbf{n},b,u^{*}x)\to \mathcal{A}(\mathbf{n},a,x)$. Similarly, for $\alpha :\mathbf{m}\to \mathbf{n}$ any map in $\mathsf{\Delta }$, we write

$${\alpha }_{*}:\mathcal{A}(a,{\alpha }^{*}x)\to \mathcal{A}(a,x)$$

by the homomorphism ${(\alpha ,1_a)}_{*}:\mathcal{A}(\mathbf{m},a,{\alpha }^{*}x)\to \mathcal{A}(\mathbf{n},a,x)$. Thus, we have the equalities

$${\alpha }_{*}{u}_{*}={(\alpha ,u)}_{*}=u_{*}{\alpha }_{*}:\mathcal{A}(b,u^{*}{\alpha }^{*}x)\to \mathcal{A}(a,x),$$

(35)

that is, both inner triangles in the diagram below commutes.

The induced coefficient system ${\mu }^{*}\mathcal{A}$ on ${\mathrm{hocolim}}_{\mathbf{C}}G$ carries an n-simplex $(\sigma ,x)$ to the abelian group ${\mu }^{*}\mathcal{A}(\sigma ,x)=\mathcal{A}(\sigma n,x)$ and, for any map $\alpha :\mathbf{m}\to \mathbf{n}$ in $\mathsf{\Delta }$, the attached ${\mu }^{*}\mathcal{A}(\alpha ):{\mu }^{*}\mathcal{A}({\alpha }^{*}(\sigma ,x))\to {\mu }^{*}\mathcal{A}(\sigma ,x)$ is the homomorphism

$${\alpha }_{*}\sigma {(\alpha m,n)}_{*}:\mathcal{A}(\sigma \alpha m,\sigma {(\alpha m,n)}^{*}{\alpha }^{*}x)\to \mathcal{A}(\sigma n,x).$$

In particular, the cofaces ${\mu }^{*}\mathcal{A}(d^i):{\mu }^{*}\mathcal{A}(d_i(\sigma ,x))\to {\mu }^{*}\mathcal{A}(\sigma ,x)$ are the homomorphisms

$$\left\{\begin{array}{cc}{d}_{*}^i:\mathcal{A}(\sigma n,d_{i}x)\to \mathcal{A}(\sigma n,x),\hfill & 0\le i<n,\hfill \\ d_{*}^n{\sigma }_{n*}:\mathcal{A}(\sigma (n-1),{\sigma }_n^{*}{d}_{n}x)\to \mathcal{A}(\sigma n,x),\hfill & i=n.\hfill \end{array}\right.$$

Then, the standard cochain complex $C({\mathrm{hocolim}}_{\mathbf{C}}G,{\mu }^{*}\mathcal{A})$ consists of the abelian groups

$$C^m({\mathrm{hocolim}}_{\mathbf{C}}G,{\mu }^{*}\mathcal{A})=\mathsf{\prod }_{\begin{array}{c}\sigma :\mathbf{m}\to \mathbf{C}\\ x\in F{(\sigma m)}_m\end{array}}\mathcal{A}(\sigma m,x),$$

with coboundary $\partial :C^{m-1}({\mathrm{hocolim}}_{\mathbf{C}}G,{\mu }^{*}\mathcal{A})\to C^m({\mathrm{hocolim}}_{\mathbf{C}}G,{\mu }^{*}\mathcal{A})$ given by

$$(\partial \phi )(\sigma ,x)=\sum _{i=0}^{m-1}{(-1)}^i{d}_{*}^i\phi (d_i\sigma ,d_{i}x)+{(-1)}^m{d}_{*}^m{\sigma }_{m*}\phi (d_m\sigma ,{\sigma }_m^{*}{d}_{m}x).$$

(36)

Now, let $\mathcal{Q}={\mathcal{Q}}_{\mathbf{C}}(G)$ be the bisimplicial ${\int }_{\mathbf{C}}\mathsf{\Delta }G$-module in Equation (31). By Proposition 1, there are isomorphisms of abelian groups

$${\mathsf{\Gamma }}^{\prime }:C^m({\mathrm{hocolim}}_{\mathbf{C}}G,{\mu }^{*}\mathcal{A})\cong {\mathrm{Hom}}_{{\int }_{\mathbf{C}}\mathsf{\Delta }G}({\mathcal{Q}}_{m,m},\mathcal{A})(m\ge 0)$$

which carry an m-cochain $\phi \in C^m({\mathrm{hocolim}}_{\mathbf{C}}G,\mathcal{A})$ to the morphism of ${\int }_{\mathbf{C}}\mathsf{\Delta }G$-modules ${\mathsf{\Gamma }}^{\prime }\phi$ given, at any object $(\mathbf{n},a,x)$ of ${\int }_{\mathbf{C}}\mathsf{\Delta }F$, by the homomorphism of abelian groups

$${\mathsf{\Gamma }}^{\prime }\phi :{\mathcal{Q}}_{m,m}(a,x)\to \mathcal{A}(a,x)\mid (\sigma ,\alpha ,u)\mapsto {\alpha }_{*}{u}_{*}\phi (\sigma ,{\alpha }^{*}{u}^{*}x).$$

These ${\mathsf{\Gamma }}^{\prime }$ fit together to define an isomorphism of cochain complexes

$${\mathsf{\Gamma }}^{\prime }:C({\mathrm{hocolim}}_{\mathbf{C}}G,{\mu }^{*}\mathcal{A})\cong {\mathrm{Hom}}_{{\int }_{\mathbf{C}}\mathsf{\Delta }G}(\mathrm{diag}\mathcal{Q},\mathcal{A}).$$

In effect, for any $\phi \in C^{m-1}({\mathrm{hocolim}}_{\mathbf{C}}G,{\mu }^{*}\mathcal{A})$, any object $(\mathbf{n},a,x)$ of ${\int }_{\mathbf{C}}\mathsf{\Delta }F$, and any generator $(\sigma ,\alpha ,u)$ of ${\mathcal{Q}}_{m,m}(a,x)$, we have

$$\begin{array}{cc}\hfill \left({\mathsf{\Gamma }}^{\prime }(\partial \phi )\right)& (\sigma ,\alpha ,u)={\alpha }_{*}{u}_{*}(\partial \phi )(\sigma ,u^{*}{\alpha }^{*}x)\hfill \\ \hfill & \stackrel{(36)}{=}\sum _{i=0}^{m-1}{(-1)}^i{\alpha }_{*}{u}_{*}{d}_{*}^i\phi (d_i\sigma ,d_i{u}^{*}{\alpha }^{*}x)+{(-1)}^m{\alpha }_{*}{u}_{*}{d}_{*}^m{\sigma }_{m*}\phi (d_m\sigma ,{\sigma }_m^{*}{d}_m{u}^{*}{\alpha }^{*}x)\hfill \\ \hfill & \stackrel{(35)}{=}\sum _{i=0}^{m-1}{(-1)}^i{\alpha }_{*}{d}_{*}^i{u}_{*}\phi (d_i\sigma ,d_i{\alpha }^{*}{u}^{*}x)+{(-1)}^m{\alpha }_{*}{d}_{*}^m{u}_{*}{\sigma }_{m*}\phi (d_m\sigma ,d_m{\alpha }^{*}{\sigma }_m^{*}{u}^{*}x)\hfill \\ \hfill & =\sum _{i=0}^{m-1}{(-1)}^i{(\alpha d^i)}_{*}{u}_{*}\phi (d_i\sigma ,{(\alpha d^i)}^{*}{u}^{*}x)\hfill \\ \hfill & +{(-1)}^m{(\alpha d^m)}_{*}{(u\circ {\sigma }_m)}_{*}\phi (d_m\sigma ,{(\alpha d^m)}^{*}{(u\circ {\sigma }_m)}^{*}x)\hfill \\ \hfill & \stackrel{(32)}{=}({\mathsf{\Gamma }}^{\prime }\phi )(\partial (\sigma ,\alpha ,u))=\left(({\mathsf{\Gamma }}^{\prime }\phi )\partial \right)(\sigma ,\alpha ,u).\hfill \end{array}$$

Hence, the result follows from Lemma 2. □

Let X be a simplicial set. When we specialize Theorem 4 above to the case when $\mathbf{C}=\mathbf{0}$ is the only-one-arrow category and $G:\mathbf{0}\to \mathbf{SSet}$ the functor with $G(0)=X$, then ${\mathrm{hocolim}}_{\mathbf{C}}G=X$, the simplicial set X, ${\int }_{\mathbf{C}}\mathsf{\Delta }G=\mathsf{\Delta }(X)$, the category of simplices of X, and the comparison functor (Equation (29)), $\mu :\mathsf{\Delta }({\mathrm{hocolim}}_{\mathbf{C}}G)\to {\int }_{\mathbf{C}}\mathsf{\Delta }G$, is the identity on $\mathsf{\Delta }(X)$. Therefore, we obtain the following well-known result, already mentioned in Section 2 as Fact 1.

Corollary 8.

For any simplicial set X and any $\mathsf{\Delta }(X)$-module $\mathcal{A}$, there are natural isomorphisms

$$H^n(X,\mathcal{A})\cong H^{n}C(X,\mathcal{A})(n\ge 0).$$

Returning to the general case, if $\mathcal{A}$ is any ${\int }_{\mathbf{C}}\mathsf{\Delta }G$-module, we have are natural isomorphisms

$$\begin{array}{cc}\hfill H^n({\int }_{\mathbf{C}}\mathsf{\Delta }G,\mathcal{A})& \stackrel{4}{\cong }{H}^{n}C({\mathrm{hocolim}}_{\mathbf{C}}G,{\mu }^{*}\mathcal{A})\stackrel{8}{\cong }{H}^n({\mathrm{hocolim}}_{\mathbf{C}}G,{\mu }^{*}\mathcal{A}),\hfill \end{array}$$

whence our second main result in the paper follows

Corollary 9.

The functor μ in Equation (29) is a Roos–Watts weak homotopy equivalence; that is, for any ${\int }_{\mathbf{C}}\mathsf{\Delta }G$-module $\mathcal{A}$, μ induces isomorphisms

$$H^n({\int }_{\mathbf{C}}\mathsf{\Delta }G,\mathcal{A})\cong H^n({\mathrm{hocolim}}_{\mathbf{C}}G,{\mu }^{*}\mathcal{A}).$$

Remark 3.

For any ${\int }_{\mathbf{C}}\mathsf{\Delta }G$-module $\mathcal{A}$, the spectral sequence in Corollary 4 can be written as

$$E_2^{p,q}=H^p(\mathbf{C},H^q(G,{\iota }^{*}\mathcal{A}))\Rightarrow H^{p+q}({\mathrm{hocolim}}_{\mathbf{C}}G,{\mu }^{*}\mathcal{A}),$$

where $H^q(G,{\iota }^{*}\mathcal{A}):\mathbf{C}\to \mathbf{Ab}$ is the $\mathbf{C}$-module assigning to each object b of $\mathbf{C}$ the q-th cohomology group of the simplicial set $G(b)$ with coefficients in the $\mathsf{\Delta }G(b)$-module obtained by restriction of $\mathcal{A}$ via the inclusion functor $i_b:\mathsf{\Delta }G(b)\hookrightarrow {\int }_{\mathbf{C}}\mathsf{\Delta }G$ (25).

Remark 4.

Let us say that a weak homotopy equivalence of simplicial sets $f:Y\to X$ is Gabriel–Zisman weak homotopy equivalence provided that, for any coefficient system $\mathcal{A}$ on Y, the induced $f^{*}:H^n(X,\mathcal{A})\cong H^n(Y,f^{*}A)$ are isomorphisms for all $n\ge 0$. That is, whenever $\mathsf{\Delta }(f):\mathsf{\Delta }(X)\to \mathsf{\Delta }(Y)$ is a Roos–Watts weak homotopy equivalence. The invariance result in Corollary 7, tell us that if $\nu :G^{\prime }\Rightarrow G$ is a natural transformation between diagrams of simplicial sets $G^{\prime },G:{\mathbf{C}}^{op}\to \mathbf{SSet}$, such that every ${\nu }_a:G^{\prime }(a)\to G(a)$, $a\in \mathrm{Ob}\mathbf{C}$, is a Gabriel–Zisman weak homotopy equivalence, then the induced functor ${\int }_{\mathbf{C}}\nu :{\int }_{\mathbf{C}}{G}^{\prime }\to {\int }_{\mathbf{C}}G$ is a Roos–Watts weak homotopy equivalence (cf. Moerdijk–Svensson ([10] Corollary 2.5)).

Finally, it is worth noting that both Theorem 3 and Corollary 9 can be useful in combination. For example, for any diagram of categories $F:{\mathbf{C}}^{op}\to \mathbf{Cat}$, there is a canonical functor

$$L={\int }_{\mathbf{C}}lF:{\int }_{\mathbf{C}}\mathsf{\Delta }\mathrm{N}F\to {\int }_{\mathbf{C}}F,$$

induced by the natural transformation $lF:\mathsf{\Delta }\mathrm{N}F\to F$, whose component at any object $a\in \mathrm{Ob}\mathbf{C}$, is the last vertex functor $l_{F(a)}:\mathsf{\Delta }\mathrm{N}(F(a))\to F(a)$, see Equation (8). We now can prove

Corollary 10.

For any functor $F:{\mathbf{C}}^{op}\to \mathbf{Cat}$, the functor L above is a Roos–Watts weak homotopy equivalence.

Proof. 

We know that every last vertex functor $l_{F(a)}:\mathsf{\Delta }\mathrm{N}(F(a))\to F(a)$ is a weak homotopy equivalence (see, e.g., Illusie ([12] Chapitre VI, Thèormé 3.3)). Then, the functor L is also a weak homotopy equivalence by Thomason ([5] Corollary 3.3.1). Furthermore, since the square of functors

commutes, for any ${\int }_{\mathbf{C}}F$-module $\mathcal{A}$, the induced homomorphisms $H^n({\int }_{\mathbf{C}}F,\mathcal{A})\to H^n({\int }_{\mathbf{C}}\mathsf{\Delta }\mathrm{N}F,L^{*}\mathcal{A})$ are the composite of the isomorphisms

$$\begin{array}{c}\hfill H^n({\int }_{\mathbf{C}}F,\mathcal{A})\stackrel{3}{\cong }{H}^n({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F,{\eta }^{*}{l}^{*}\mathcal{A})=H^n({\mathrm{hocolim}}_{\mathbf{C}}\mathrm{N}F,{\mu }^{*}{L}^{*}\mathcal{A})\stackrel{9}{\cong }{H}^n({\int }_{\mathbf{C}}\mathsf{\Delta }\mathrm{N}F,L^{*}\mathcal{A}).\end{array}$$

□