Mathematical Model for Production Plan Optimization—A Case Study of Discrete Event Systems ^†

Abstract

This paper proposes an optimal scheduling model under production and maintenance constraints for a real case of a discrete event system. The intent was to use the rich mathematical theory and algorithms of optimization in the study of this important class of systems. The current study detailed firstly a new approach for mapping a simulation event relationship graph into a mixed-integer program, with a flexible workshop real case. Several other potential applications of the mathematical model are examined, thanks to the model constraints flexibility characteristics, including a general case of a manufacturing system for optimal resource scheduling, an application on the case of hospital beds’ management. The model extension could be also interesting for other applications like museum systems or the case of big data in complex and social networks.

1. Introduction

For most companies, maintenance represents a very significant function within the overall production environment. The developments in automation, and the resulting complexity of the systems involved, have made the reliability of the machines even more important. This is especially true in the process industry, characterized by expensive, specialized equipment and stringent environmental considerations. Nowadays, with profit margins decreasing, there is need for a good maintenance planning and control, especially for discrete event systems (DES). The evolution of DES is defined by the instantaneous occurrence of events at possibly unknown and/or irregular time intervals (e.g., communication and transport systems, computer systems, and manufacturing systems). Today, these systems are so complex that intuitive methods are no longer enough to ensure efficient and operational supervision and scheduling. The theory of supervision of DES was developed by Wonham and Ramadge [1,2]. Thanks to formal languages and automata, these authors have introduced concepts like those used in the theory of automatic control of continuous systems. Thus, the synthesized supervisor ensures the desired legal behavior. Indeed, Petri nets (PNs) are shown to be more powerful than automata for modeling DES with synchronization and parallelism. In addition, the PNs are more advantageous for dealing with the control problems defined by specifications on the states of the system [3,4]. They represent a very suitable tool for studying manufacturing systems thanks to their modeling power and mathematical properties. In our previous work [5,6,7] we focused on the development of methods of control and production optimization of the computation time to calculate controllers that satisfy control specifications and constraints related to manufacturing systems.

The production and maintenance management using new strategies differs greatly from management policies in traditional manufacturing. These strategies are more deterministic and more flexible since they could consider different parameters impacting production and control activities’ performances. Production scheduling is considered as a determinant functionality in the production management. Since production activities depend on several parameters, production scheduling may need to consider the manufacturing system status and operational conditions in the production layer.

In a more general context, decision support systems continue to be very popular in industrial engineering thanks to their ability to help decision makers managing their resources in function of several manufacturing constraints. However, manufacturing systems are complex since they are connecting many technical and human resources. These systems are often looking for more efficiency and, so, new strategies are developed, especially in production planning.

The importance of considering production management components linked to manufacturing execution systems (MES) has hugely increased during the last years. The Figure 1 [8] illustrates the MES growth between 2006 and 2016. In literature, many proposals deal with manufacturing system allocation and production planning.

Several research works [9,10,11] focused on mathematical modeling to express the production scheduling problem in terms of variables and constraints. In [9], a set of algorithms to minimize the length of production planning was proposed. The proposed algorithms are used to generate all possible optimal schedules grouped into subsets. The authors propose computational algorithms in order to evaluate these performances and select the best ones in function of given performances’ parameters. In [10], a hybrid policy to deal with the optimal production scheduling complexity due to various kinds of uncertain factors, such as breakdowns, maintenance actions, and production parameters, was developed. The authors used the genetic algorithm as a resolution tool to minimize the total completion time. In [11], the production planning computation complexity for various types of cost functions, maintenance costs, and production capacity limits was summarized. Many research works deal with several industrial constraints such as subcontracting, warranty, and quality in manufacturing and logistic fields [12].

For more details about determination of production and maintenance control policies under different types of constraints, the reader may refer to the work of Rezg et al. [13].

An application example of our methodology such as hospital beds’ management is presented in this paper to show the effectiveness of our mathematical model. Then, two illustrative examples are given to highlight, firstly, the importance of the model in a real production issue for a discrete event system and, secondly, to demonstrate the mathematical model efficiency for a typical case of an industrial production unit. The main goal was to find a schedule that satisfies all resource constraints while minimizing the total cost. Other proposals integrate different parameters as subject of optimization conducive to get the best decisions from which we cite tasks’ selection and sizing, assignment of tasks to manufacturing systems, and jobs’ sequencing.

In other proposals [14], simulation and meta-heuristics tools are used to highlight operating issues and evaluate different decisions of resources’ management. In [15], the authors proposed an algorithm dealing with beds’ management issues in hospital centers. Maintenance strategies currently used by decision makers are generally classified into two main classes: The corrective maintenance and the preventive one. Corrective maintenance actions are realized when a machine breaks down. The main task of such maintenance activities is to restore the machine to a desired condition. Preventive actions are performed regularly to increase the machine availability and to avoid, as possible, its breaking down. In this paper, we studied preventive maintenance actions that are already planned in the initial production planning.

The junction of maintenance and production scheduling [16] was the subject of many proposals in the literature. In particular, [17] discusses the optimal joint production and maintenance plan in the case of a system consisting of several identical machines. In [18], a new approach for joint production and maintenance scheduling in the case of multiple machines was developed. Machines are subject to failures and an age-dependent preventive maintenance policy was used. The main improvement of this work was to implement a PN supervisor on a flexible manufacturing system (FMS) under production and control constraints using a developed JAVA application. Therefore, we considered merging an efficient mathematical model in order to provide an optimal production planning. This paper is organized thusly: Section 2 presents briefly the Petri nets and the theory of regions concepts and describes the FMS in our laboratory. Then, Section 3 develops the production planning mathematical model. Next, Section 4 provides a numerical example on a real experimental environment. Finally, the Section 5 shows the mathematical model efficiency on a given industrial production unit.

2. Mathematical Model Description

In this part, a planning for manufacturing systems production is presented. Our proposition was to develop a production plan under production constraints. The mathematical model was based on [15]’s proposal.

The proposed model was based on the following assumptions:

• The production duration was considered as known in advance.
• Batches could not be operated on more than one manufacturing system.
• Each batch was associated to two dates: Earliest manufacturing date and latest manufacturing date. Real manufacturing date must be included between these two dates.
• Two type of workshops: Workshops with two manufacturing systems and ones with only one manufacturing system.
• Manufacturing of different types of batches in the same workshop at the same time was forbidden.

Hence, the essential objective consisted of assigning the maximum number of batches. Assignment must have respected constraints and did not disturb current planning. Availability (empty and occupied manufacturing systems) was determined and updated after each assignment.

Algorithm for Production Scheduling

The objective function is expressed as following:

$${\displaystyle {\sum }_{i=1}^{NP}}\left(F_i·M{D}_i\right).$$

(1)

It aims to minimize the non-operated (rejected) batches.

The model constraints are given as following:

$${{\displaystyle \sum }}_{l=1}^{NMS}{X}_{l,t,i}\le 1.$$

(2)

Equation (2), a batch cannot be operated by more than one manufacturing system in a time unit t.

$${\displaystyle \sum }_{l=1}^{NP}{X}_{l,t,i}\le 1$$

(3)

Equation (3), a manufacturing system operates at most one batch in a time unit t.

$${\displaystyle \sum }_{l=1}^{NMS}{\displaystyle \sum }_{t=E{M}_i}^H{F}_i·M{D}_i+X_{i,l,t}=M{D}_i$$

(4)

Equation (4), non-interrupted manufacturing. The model assumes that manufacturing operation is continuous. The length of stay of the batch in the workshop is strictly equal to its manufacturing duration.

$${\displaystyle \sum }_{l=1}^{NMS}{A}_{i,l}\le 1$$

(5)

$$M{D}_i·A_{i,l}={\displaystyle \sum }_{t=E{M}_i}^H{X}_{t,l,i}$$

(6)

Equations (5) and (6), a batch can occupy at most one manufacturing system.

$$J_i\ge E{M}_i$$

(7)

$$J_i\le L{M}_i$$

(8)

Equations (7) and (8), upper and lower bounds for manufacturing date.

$${\displaystyle \sum }_{t=E{M}_i}^H{X}_{t,\mathrm{l},i}·B_{l,t}=A_{i,l}·M{D}_i$$

(9)

Equation (9), availability of the manufacturing system to operate the batch i.

$$Wor{k}_i·M_{j,k,l}·\left({\displaystyle \sum }_{i=1}^{NP}{T}_i·\left(X_{i,j,t}-X_{i,k,t}\right)\right)\le 1$$

(10)

$$Wor{k}_i·M_{j,k,l}·\left({\displaystyle \sum }_{i=1}^{NP}{T}_i·\left(X_{i,j,t}-X_{i,k,t}\right)\right)\ge -1$$

(11)

$$Wor{k}_i·M_{j,k,l}·\left(S{P}_{j,t}-{\displaystyle \sum }_{i=1}^{NP}\left(X_{i,j,t}·T_i\right)\right)\ge -1$$

(12)

Equations (10)–(12), batches of different types cannot be operated in the same workshop at a given unit of time.

$${\displaystyle \sum }_{t=E{M}_i}^H{X}_{t,l,i}·B_{l,t}·(1-Mai{n}_{l,t})=A_{i,l}·M{D}_i$$

(13)

Equation (13) expresses the preventive maintenance constraints. Constraint (18) expresses the preventive maintenance constraints. Related to the maintenance planning, we considered the fact that manufacturing systems must be maintained after a given number of operated products. Preventive maintenance is not linked to duration but to a given quantity produced, after which the system must be inspected and maintained. This quantity is mostly fixed based on system characteristics such as the equipment life duration, its mechanic characteristics, and the environmental and operational conditions in which the system operates. It is interpreted to mean that a maintenance action can not interrupt the manufacturing operation, which has to be continuous. This constraint is an extension for the constraint (9) for system availability.

i ≤ NP, l ≤ L, t ≤ T

(14)

Equation (14) expresses the integration constraints.

3. Algorithm Application for a Real Case: Petri Net Modeling

3.1. Petri Net and Theory of Regions’ Concepts

A Petri net (PN) is a graphical modeling and mathematical tool for divers’ systems, especially for discrete event systems. From an informal standpoint, a PN is a directed graph with two types of nodes (transitions and places) and has a dynamic behavior. The transitions and places are connected by oriented arcs. An arc links either a transition to a place/a place to a transition but never links a place to a place/a transition to a transition.

Regularly, a PN is a bipartite graph: $PN=\langle P, T, Pre, Post\rangle$ where: [19]

• $P$ is a set of places.
• $T$ is a set of controllable and uncontrollable transitions: $T=T_c{{\displaystyle \cup }}^{ }{T}_u.$
• $Pre:P\times T$ in N represent a pre-incidence function that specifies weighted arcs from $P$ to $T$. N is a set of non-negative integers.
• $Post:P\times T$ in N is the post-incidence function that specifies weighted arcs from $T$ to $P$.

Let the set $p^{\left(t\right)}$ (respectively, ${}_{}{}^{\left(t\right)}p$) be the output transitions (respectively, input transitions) of a place $p$. Naturally, a PN can be formalized by an indexed matrix C as: $C\left(p_i, t_j\right)=w\left(t_j,p_i\right)$ if $t_j\in {}_{}{}^{\left(t\right)}p{}_i$, $C\left(p_i,t_j\right)=-w\left(t_j,p_i\right)$ if $t_j\in p_i^{\left(t\right)}$, and 0 elsewhere. The $w:F\to N$ is a valuation function of arcs (the finite set of arcs $F\subseteq \left(P*T\right){{\displaystyle \cup }}^{ }\left(T*P\right)$. Moreover, let $t^{\left(p\right)}$ (respectively, ${}_{}{}^{\left(p\right)}t$) be the set of output places (respectively, input places) of a transition $t$. The reachability graph constructed from the initial marking $M_0$ is denoted by $G\left(N, M_0\right)$. The set of generated markings in $G\left(N, M_0\right)$ is denoted by M. A transition enabled from a marking $M\in Ϻ$ (denoted by $M[t>$) if and only if $M\ge Pre\left(·,t\right)$. An enabled transition may fire yield a new marking $M^{\prime }$ such that $M_0=M+C\left(·,t\right)$. This expression can be defined by $M[t>M_0$. A new marking $M_0$ is reachable from a marking $M$ if a firing sequence $\sigma =t_1, t_2\dots t_n$ exists by firing $\sigma$. Any marking $M_0$ reachable from the initial marking $M_0$ satisfies the following PN state equation: $M_0=M_0+C*\overrightarrow{\sigma }$, where $\overrightarrow{\sigma }:T\to N$ is a vector of non-negative integers called the occurrence of $t_i$ in $\sigma$. A Petri net is said to be k-bounded if the number of tokens in each place $p_i\in P$ does not exceed k. A PN is said live if every transition is live. A Petri net is reversible, if from any reachable state, $M$, an enabled sequence exists, transforming $M$ into $M_0$.

The theory of regions in control synthesis was proposed by [19,20,21,22] using the properties of PN tools for adding a PN controller Pc to the initial Petri net model with initial marking $M_0\left(P_c\right)$ and its incidence vectors $C\left(P_c,·\right)$. This theory is represented by a linear system composed of three types of equations: The reachability equations, the marking/transition separation instance (MTSI) equations, and the cycle equations. Its resolution leads to the design of PN supervisor. This control place $P_c$ has to fulfill the reachability conditions, i.e.,

$$M_0\left(P_c\right)+C\left(P_c,·\right)\overrightarrow{{\Gamma }_M}\ge 0$$

(15)

where $\overrightarrow{{\Gamma }_M}$ is the path between $M_0$ and $M$. In addition, each PN controller to add has to solve at least one prohibited event $\left(M,t\right)$ in the set $\mathsf{\Omega }$ of prohibited state transitions. The MTSI condition relative to the couple $\left(M^{*},t\right)$ is:

$$M_0\left(P_c\right)+C\left(P_c,·\right)\overrightarrow{{\Gamma }_{M^{*}}}<0$$

(16)

where $M^{*}$ is a forbidden state.

Finally, $P_c$ must satisfy cycle equations:

$${\displaystyle \sum }_{t\in T}C\left(P_c,t\right)·\overrightarrow{\sigma \left[t\right]}=0$$

(17)

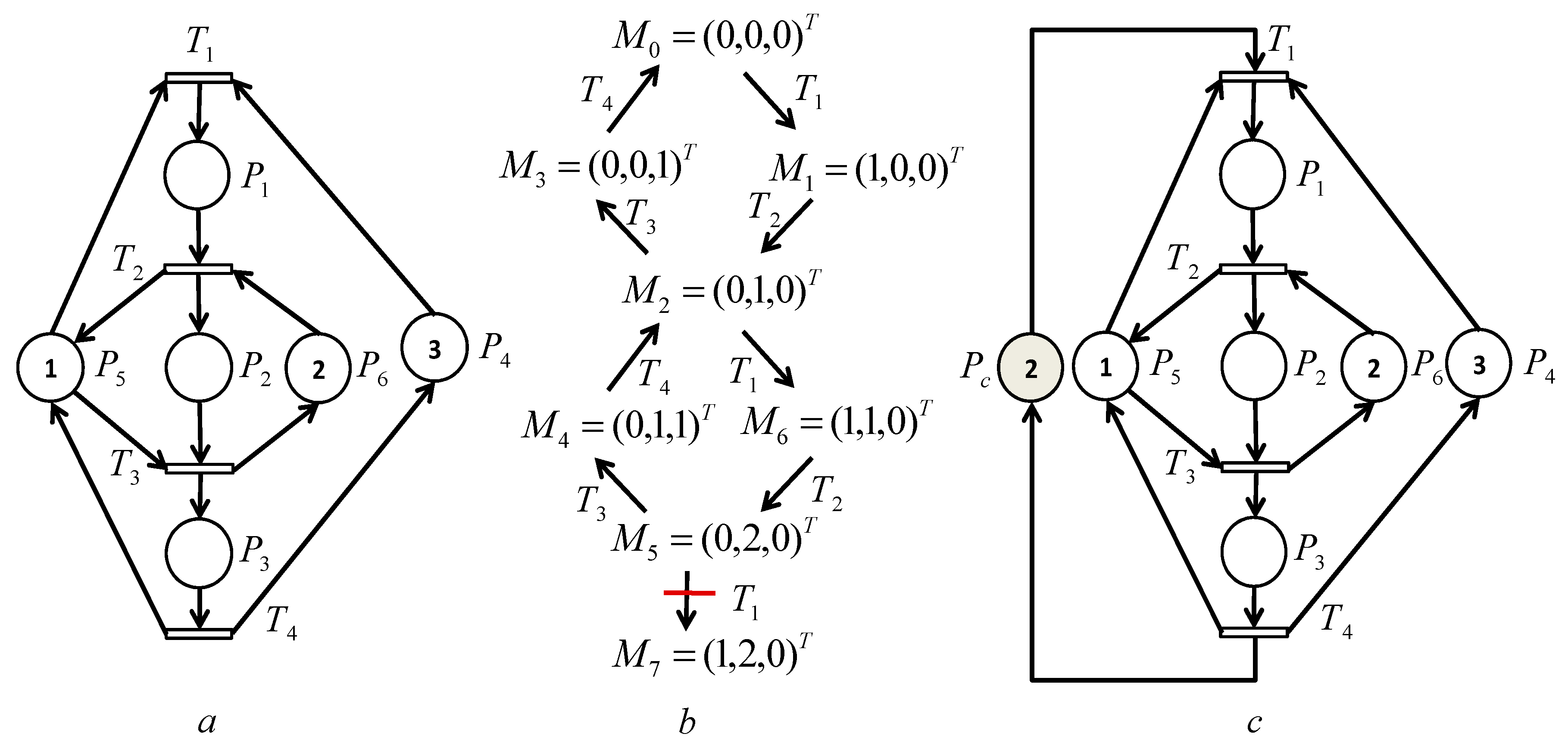
where $\overrightarrow{\sigma \left[t\right]}$ is the algebraic sum of occurrences of $t$ in $\sigma$. Considerably, many MTSI conditions may obtain the same solutions by resolving the linear system composed of Equations (15)–(17). Afterwards, the number of Petri net controllers will be much smaller than the set of MTSI conditions. The following example of Figure 2 is an application of the theory of regions for control synthesis.

For this prohibited state problem, we want to forbid the following event separation instance ($M_5\to M_7$) (i.e., see Figure 2b). Based on the theory of regions, there are seven reachability equations:

• $M_0\left(P_c\right)\ge 0$;
• $M_1\left(P_c\right)=M_0\left(P_c\right)+C\left(P_c,t_1\right)\ge 0$;
• $M_2\left(P_c\right)=M_0\left(P_c\right)+C\left(P_c,t_1\right)+C\left(P_c,t_2\right)\ge 0$;
• $M_3\left(P_c\right)=M_0\left(P_c\right)+C\left(P_c,t_1\right)+C\left(P_c,t_2\right)+C\left(P_c,t_3\right)\ge 0$;
• $M_4\left(P_c\right)=M_0\left(P_c\right)+2C\left(P_c,t_1\right)+2C\left(P_c,t_2\right)+C\left(P_c,t_3\right)\ge 0$;
• $M_5\left(P_c\right)=M_0\left(P_c\right)+2C\left(P_c,t_1\right)+2C\left(P_c,t_2\right)\ge 0$; and
• $M_6\left(P_c\right)=M_0\left(P_c\right)+2C\left(P_c,t_1\right)+C\left(P_c,t_2\right)\ge 0$;

one cycle equation:

$$C\left(P_c,t_1\right)+C\left(P_c,t_2\right)+C\left(P_c,t_3\right)+C\left(P_c,t_4\right)=0;$$

and one MTSI equation:

$$M_7\left(P_c\right)=M_0\left(P_c\right)+2C\left(P_c,t_1\right)+2C\left(P_c,t_2\right)+C\left(P_c,t_1\right)<0·$$

The (LS) linear system of the theory of regions contains nine equations. Its resolution succeeds to the controlled Petri net (i.e., see Figure 2c):

$$\mathrm{PN}\mathrm{Controller}:M_0\left(P_c\right)=2;C\left(P_c,·\right)=\left(-1,0,0,1\right).$$

(18)

3.2. Real Case Presentation

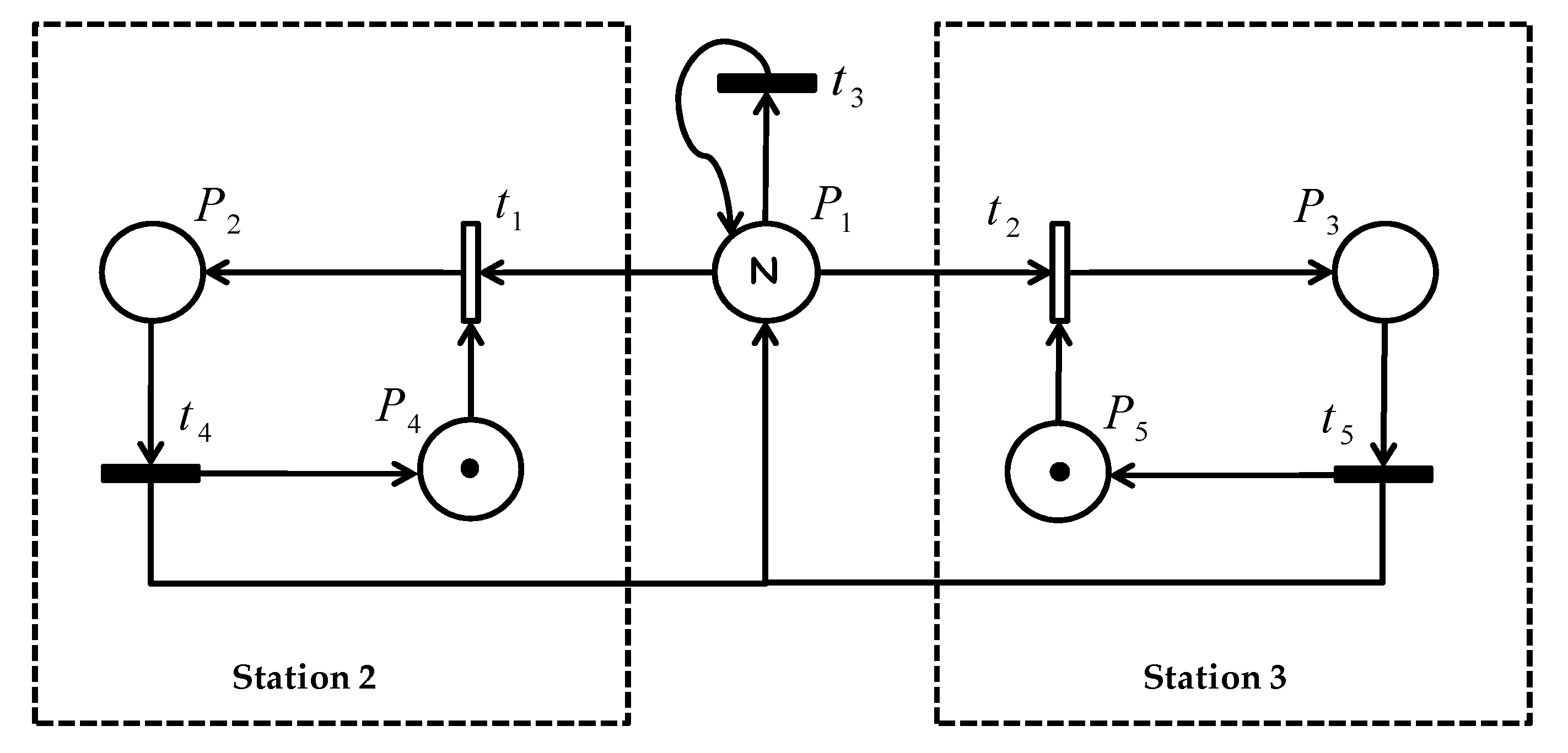
A flexible manufacturing system (FMS), composed of two production stations installed in the university UFR_MIM in Metz-FRANCE and its Petri net model, are presented in Figure 3 and Figure 4. These stations, modeled by the places P2 and P3, pack engraved blue and red pieces in black boxes. The capacity of each station is modeled by P4 and P5. The transitions (t₁, t₂) and (t₄, t₅) represent, respectively, the events of entry and exit of the pallets through their annex’s conveyors. Otherwise, the pallets can continue their way to the main conveyor by crossing t₃. Note that only the transitions t₁ and t₂ are controllable.

The control part of the system makes it imperative not to pack two pieces of different colors for the same unit of time. Our objective in this example was to sort a number N of blue and red engraved pieces in order to package them in black boxes and ship them to customers. In fact, in our previous works, the control constraint was feasible on a number N of pieces in order to dispatch the engraved parts, but the sorting according to the color of the piece remains an insoluble problem in our field. The application of the theory of regions to design the controller was not suitable until now for colored Petri nets. In addition, this work shed new light on the integration of the scheduling in our previous work. In the next section, we develop a mathematical model that will be used to define the optimal production and maintenance planning for the described FMS.

In this section, the algorithm was simulated to highlight its importance in some modeling complex cases. Related to the maintenance planning, we considered the fact that the system must be maintained after a given number of operated batches. Preventive maintenance is not linked to duration but to a given quantity produced, after which the system must be inspected and maintained. This quantity is mostly fixed based on system characteristics such as the equipment life duration, its mechanic characteristics, and the environmental and operational conditions in which the system operates.

The data that will be used in the numerical example are expressed as following:

• The number of machines is two, as mentioned in the previous subsection.
• The two machines are installed in the same workshop.
• Two types of batches are considered: Blue and red.
• The number of production batches is 8 (N=8).
• The time horizon is expressed in hours and is equal to seven.
• Production time of a simple piece is 10 min (1/6 h).
• Each production batch has an execution time proportional to its size, which must be a multiple of 6. For example, a batch having 12 pieces, takes 12*10min= 2 h of production.
• The batches’ characteristics (type, earliest and latest manufacturing dates) are given in the

  Table 1. Data for operated batches.

  Batch i	EM (i)	LM (i)	T (i)	Batch Size (i)	Production Time
  1	6	8	R	12	2
  2	3	4	B	12	2
  3	2	3	B	12	2
  4	5	5	R	24	4
  5	1	2	B	6	1
  6	5	7	B	18	3
  7	2	2	B	6	1

  .

Based on this data, the production program given by the mathematical model application is illustrated as following: The simulation results show a deterministic optimal solution for production and maintenance scheduling. Machines’ unavailability is expressed by three letters: B (respectively, R) for pre-programmed production for a blue batch (respectively, red batch) and M for preventive maintenance.

The results shown in the

Table 2. Production planning for the flexible manufacturing system.

System		Planning Horizon
		1	2	3	4	5	6	7	8
1	S2	B	7	2	2	4	4	4	4
	S3	5	B	3	3	M	R	1	1

led us to conclude that the model constraints were respected (machines’ unavailability and non-mixed batches in each time unit. For example, batch 2 was operated in the station 2, during the third and fourth time units. From a total of 11 batches, one batch was not scheduled for operation. The batch number 6 was rejected. This rejection was due to the production constraints (batch size, earliest and latest manufacturing dates, etc.).

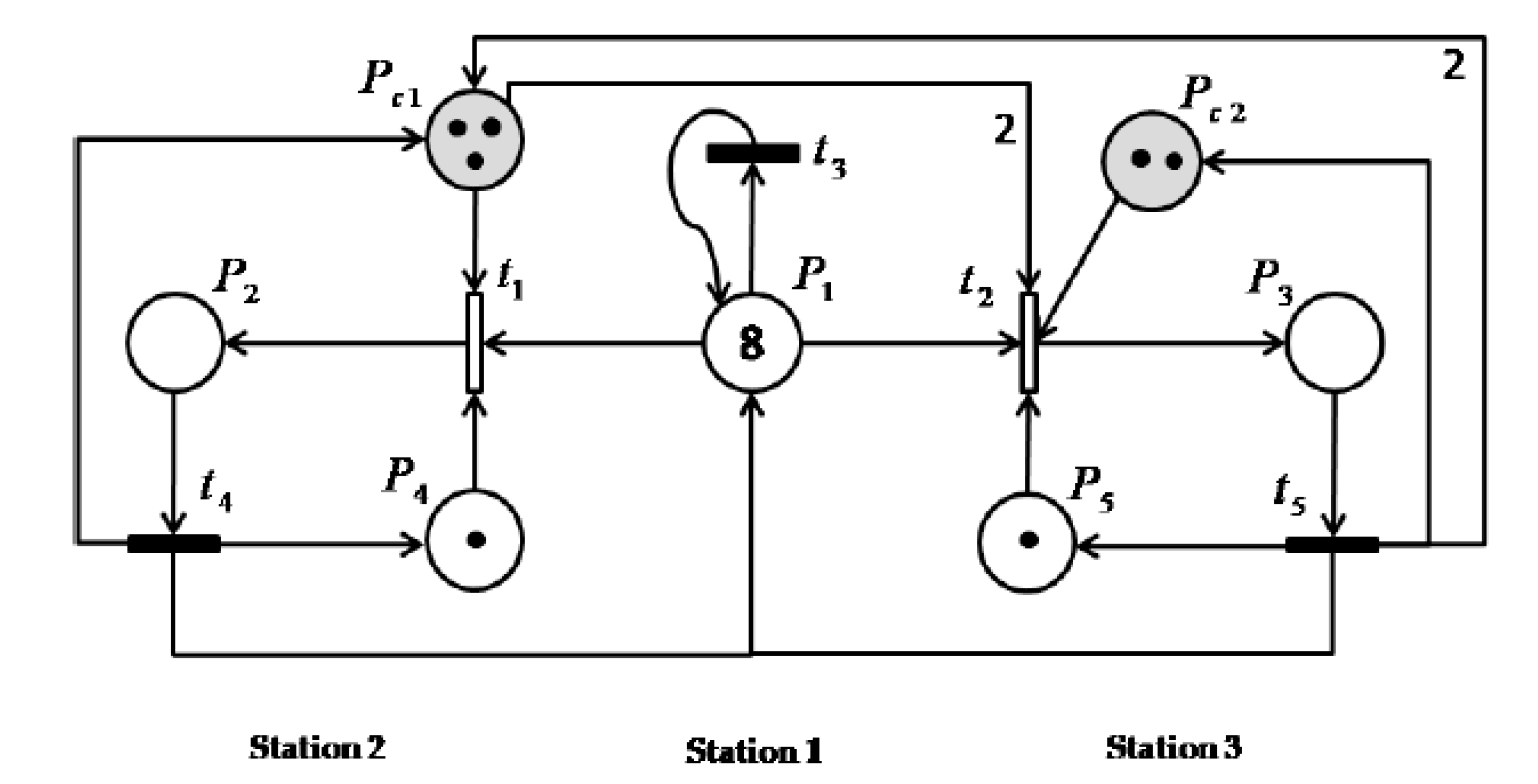
Conforming to our new control methodology, 2 PN monitors, Pc1 and Pc2, can then be located by eliminating redundant PN monitors when the linear system composed of reachability MTSI conditions and cycle equations is solved. The controlled system net is obtained by applying the theory of regions presented in the previous section and shown in the

Table 3. The controlled Petri net model of FMS.

PN Controllers	The Initial Marking	The Incidence Vector
$P_{c1}$	3	(−1, −2, 0, 1, 2)
$P_{c2}$	2	(0, −1, 0, 0, 1)

and the Figure 5.

The proposed policy was implemented in the flexible manufacturing system installed in our laboratory in France and the computation of PN controllers was done by using CPLEX software. The results analysis showed that our control approach using PN was more effective than previous methodologies based on the theory of regions. Indeed, for the same number of controllers, one can supervise the system under less computational burden. Our proposed control approach was merged with mathematical modeling tools to face one of the real constraints in the industrial world.

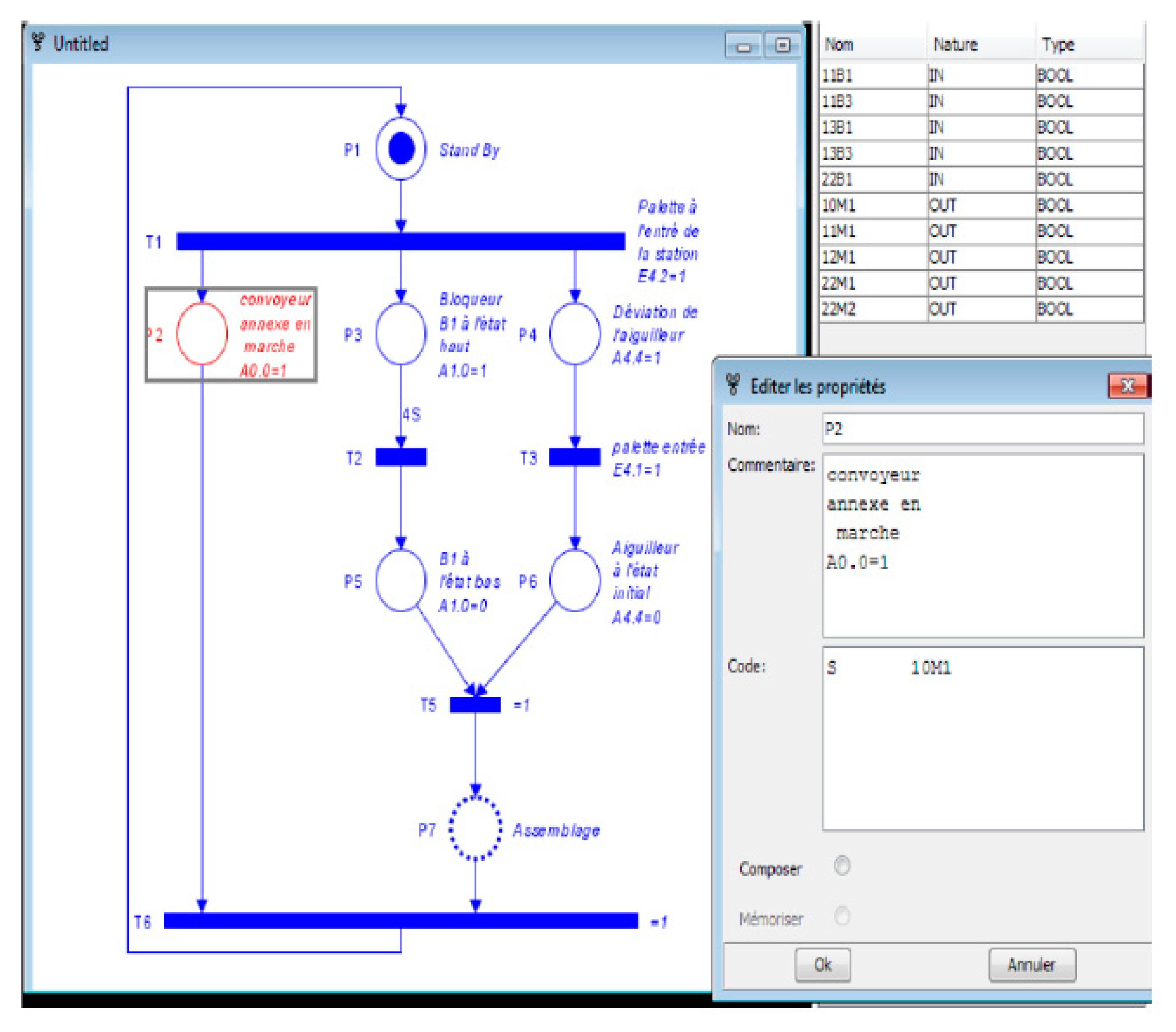
The proposed control policy was implemented in the FMS through a JAVA application (Figure 6), (Rezig et al. 2018) [23], wherein the controlled PN model was edited and then transformed into a comprehensible code supported by the Programmable Logic Controller (PLC). Once the internal input/output signals of the PLC are detected, one can transform the PN model into a language supported by the PLC. The LIST language of IEC norm 61131-3 was chosen.

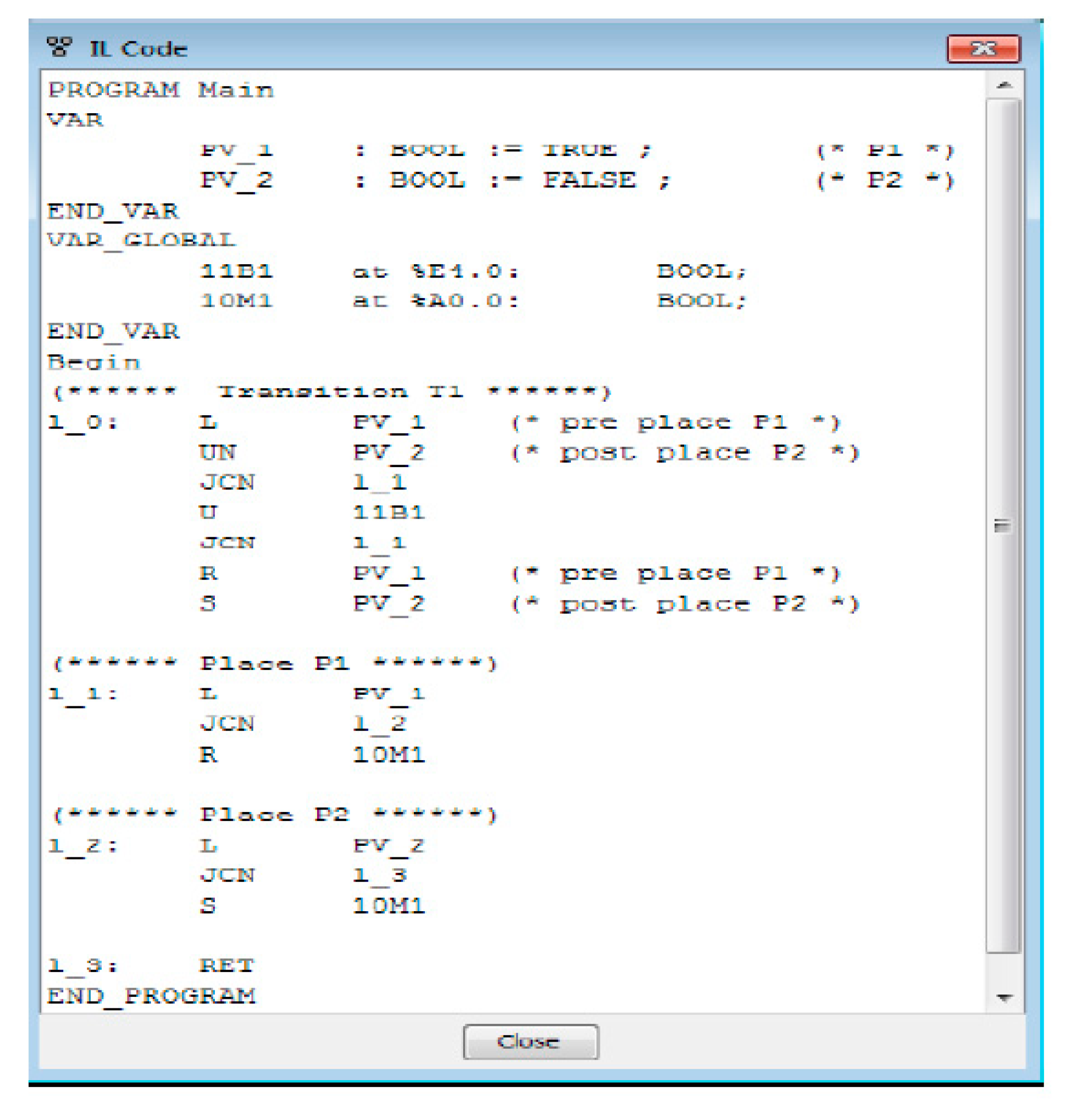
In fact, the JAVA application was developed to model any PN controller and then generate the corresponding LIST code that will be sent to the target in a second time. The interface is functional from the creation of the project until the code generation. It is possible to save a project, to model the controlled PN as in any editor, and to associate the inputs to their addresses in the PLC. 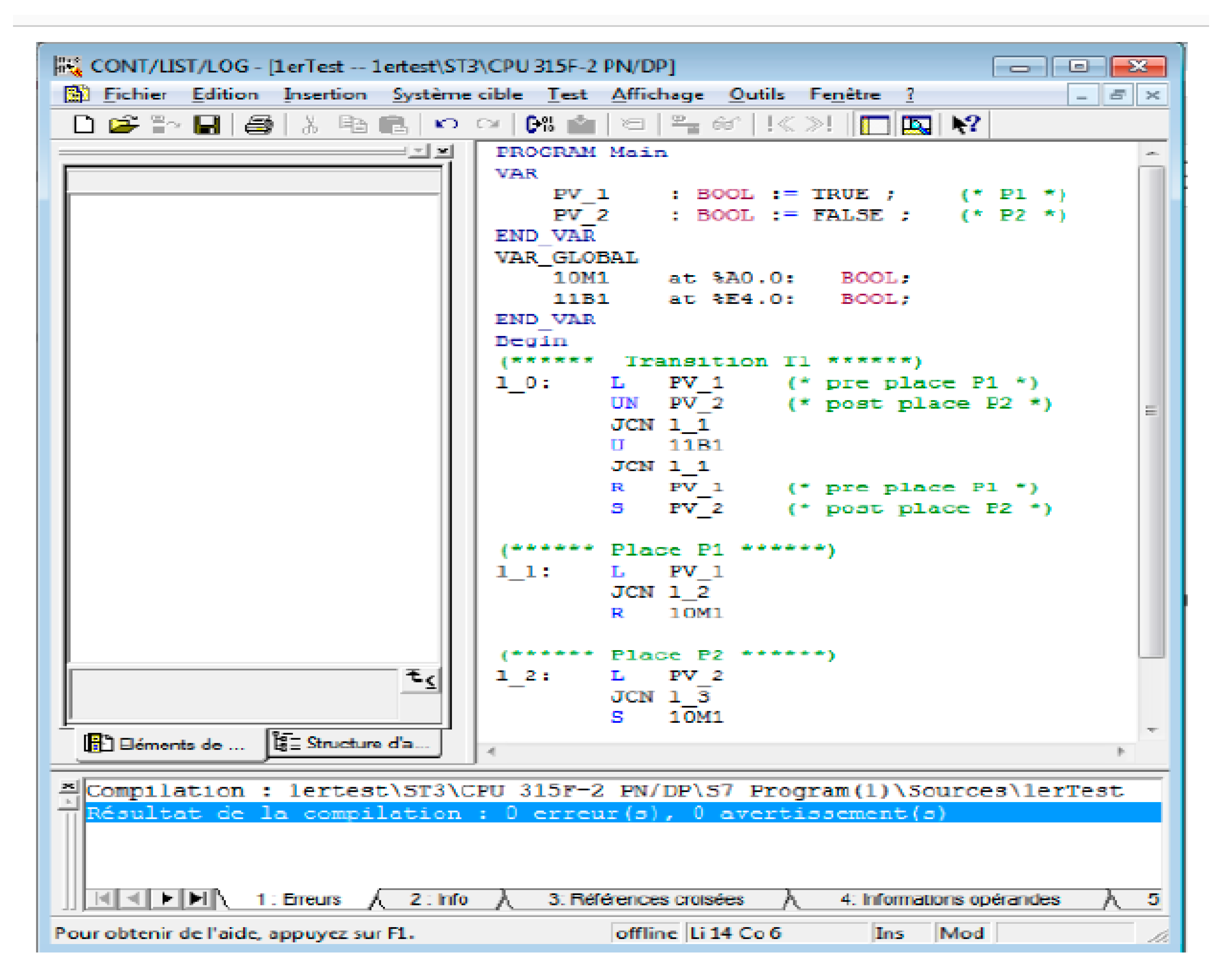Then, the generated code (Figure 7) will be tested using the SIEMENS STEP7 compiler (Figure 8).

4. Mathematical Model Extensions

The main advantage of the current proposed model is its mathematical flexibility that permits adapting it to many production applications by modifying the model constraints.

In this section, we present some different applications where the model has shown its efficiency to validate the flexibility characteristic.

4.1. Case of Manufacturing System

This application was discussed in an existing work in the literature [24] with an algorithm for manufacturing planning under unavailability constraints. In this section, we extended the database used for the numerical example to show the model efficiency dealing with a bigger size problem.

Table 4. Manufacturing systems’ initial unavailability.

Manufacturing Systems		Planning Horizon
		1	2	3	4	5	6	7	8	9	10	11	12	13	14
Workshop 1	1					B	B	A	A
Workshop 2	2					M	M
Workshop 3	3							A	B	B				A	A
	4											B
Workshop 4	5	A	A												B
	6	A	A		B	B	B	B
Workshop 5	7	A	A	A	A	B	B	B					B		A
	8	A	A	A	A	B	B	B	A	A	A				A

* The colored cell means the availability dates of the manufacturing system.

gives the initial unavailability dates of a manufacturing system in the time horizon that will be the subject of scheduling. As mentioned before, the unavailability, in this paper, corresponds to preprogrammed production activities: Based on Table 4, as an example, preprogrammed production actions in the studied time horizon for the system 1 are the manufacturing of batch type B for fifth and sixth time units.

For the numerical example, we considered five workshops having eight manufacturing systems (three double workshops and two single). The following database was considered (

Table 5. Data for operated batches.

Product (i)	EM (i)	LM (i)	T (i)
1	1	2	B
2	2	3	A
3	3	4	A
4	3	6	B
5	9	10	A
6	8	12	A
7	12	12	A
8	9	9	B
9	12	13	A
10	13	13	B
11	13	13	A
12	8	11	A
13	3	9	B
14	8	11	A
15	10	10	A

):

• The horizon time was fixed at 14 units of time.
• The manufacturing duration (MD) was fixed at three units of time for batch type A and two units of time for batch type B.
• Initial unavailability was expressed by the preventive maintenance action plan by the letter M in the Table 4 and

  Table 6. Optimal manufacturing planning.

  Manufacturing Systems		Planning Horizon
  		1	2	3	4	5	6	7	8	9	10	11	12	13	14
  Workshop 1	1		2	2	2	B	B	A	A				7	7	7
  Workshop 2	2			4	4	M	M			8	8			10	10
  Workshop 3	3	1	1					A	B	B	5	5	5	A	A
  	4			3	3	3			6	6	6	B	9	9	9
  Workshop 4	5	A	A	13	13	13		14	14						B
  	6	A	A		B	B	B	B			10	10
  Workshop 5	7	A	A	A	A	B	B	B	12	12			B		A
  	8	A	A	A	A	B	B	B	A	A	A				A

  and preprogrammed production actions expressed by Letter B for batch type B and Letter A for batch type A.

Table 6 illustrates the obtained results. The simulation results highlight the optimal production scheduling in the given time horizon and in function of model constraints. Results led us to conclude that production constraints, that two batches of different types could not be in the same workshop at a given time t, were respected. For instance, batch 2 was operated in the first workshop, on the first machine during the second, third, and the fourth time units. Batch 5 was operated on the third machine of the Workshop 3 on the 10th, the 11th, and 12th time units.

The optimal solution was obtained with the solver CPLEX, after 2 min and 50 s of calculation, which corresponds to 190,134 iterations. From a total of 11 batches, one batch was not scheduled for operation. The batch was rejected due to the earliest and latest manufacturing dates’ constraint.

We proposed a performance comparison between the solvers used, which were, in this case, CPLEX and Xpress. We considered five experiments to schedule 15, 20, 25, 30, and 50 products. The results obtained are illustrated in

Table 7. Results of resolution.

Products Number	Computation Time in s (CPLEX)	Computation Time in s (Xpress)
15	170	190
20	2800	1800
25	2700	1800
30	3600	3800
50	46	3800

.

We note that the results obtained with CPLEX and Xpress were nearly the same for the case of 15 products. For the case of 20 and 25 products, we note that CPLEX was faster with the same given optimal solution. Moreover, in the case of 50 products, CPLEX reached the optimal solution within a few seconds, whereas Xpress spent much more time before getting a solution, which was not the optimal one. We can conclude then that, in the case of this algorithm resolution, it would be better to use the CPLEX solver.

4.2. Case of Hospital Beds’ Management

The proposed mathematical model was also used for beds’ management planning and management in healthcare establishments [15].

Beds’ management is a complex problem that lots of hospital centers decide to integrate, to well manage the financial impact on the budget and to maximize the acceptance rate of patients.

Many proposed models are based on reducing hospitalization cost and optimizing the use of resources. In our proposal [15], the model considered the capacity of beds for two types of patients: Scheduled and non-scheduled patients. Otherwise, the model managed also preventive maintenance actions during the planning horizon.

The idea of our work was to apply the proposed mathematical algorithm with some modifications to be in good agreement with real specific constraints of this application from which we can cite:

• The need of considering some cases where some patients need to be isolated, so assigned to a room with a single bed.
• The need of replanning the refused patients given from the first planning proposal, by modifying, if possible, the earliest and latest acceptance dates.

The model was used in an analogical way with the example presented for manufacturing system. The workshops designed the rooms, the manufacturing systems designed the beds, and the products were assimilated to patients. For more details and numerical illustrations, the reader may refer to our previous work [15].

The actual proposed mathematical model could also be extended to several other applications with adaptations on constraints, objective function, and parameters characteristics such as museum system or the study of big data in complex and social networks [25,26,27,28].

For instance, the problem of visitors’ museum touring could be addressed, while considering physical parameters, as well as visitors’ interests and social interactions, towards maximizing their perceived quality of experience (QoE). In this case, it would be interesting to develop this proposal by establishing an analogy between hospital environment (hospital, patients, beds, and characteristics) and museum case (museum, visitors, resources, and exhibits’ characteristics).

5. Conclusions

This work aimed to propose a new approach in mathematical modeling optimization. The contribution of this paper was, firstly, to propose a linear optimization model for a joint production and maintenance planning and, secondly, to show the importance of such models in different industrial issues and particularly in the case of flexible manufacturing system where the Petri net modeling is more commonly used. Furthermore, an application example of our methodology, such as hospital beds management, was presented in this paper to show the effectiveness of our mathematical model. Thus, we backed up our proposals by another illustrative example and a real case of study. Therefore, the algorithm for solving an optimal production planning under production and unavailability constraints was discussed.

Thanks to the modeling tools, decision makers could optimize the production planning which depends on several constraints. The mathematical model was then applied on a discrete event system installed in our laboratory (University of Lorraine, Metz, France). Even though the main used tool for the flexible manufacturing system was the PN modeling, we showed in this article that it could be controlled with mathematical modeling, in the case of complex production issues and, so, there is no need for more complex tools in PN, such as colored PN tool. Therefore, thanks to the mathematical model solution output, the PN supervisor was implemented via STEP7 software.

Future works aim to integrate other production constraints in the manufacturing planning algorithm to more generalize the model usefulness for other industrial applications.