Effect of a Boundary Layer on Cavity Flow
Abstract
1. Introduction
2. General Approach for Flows with Vorticity
3. Complex Potentials of Flows
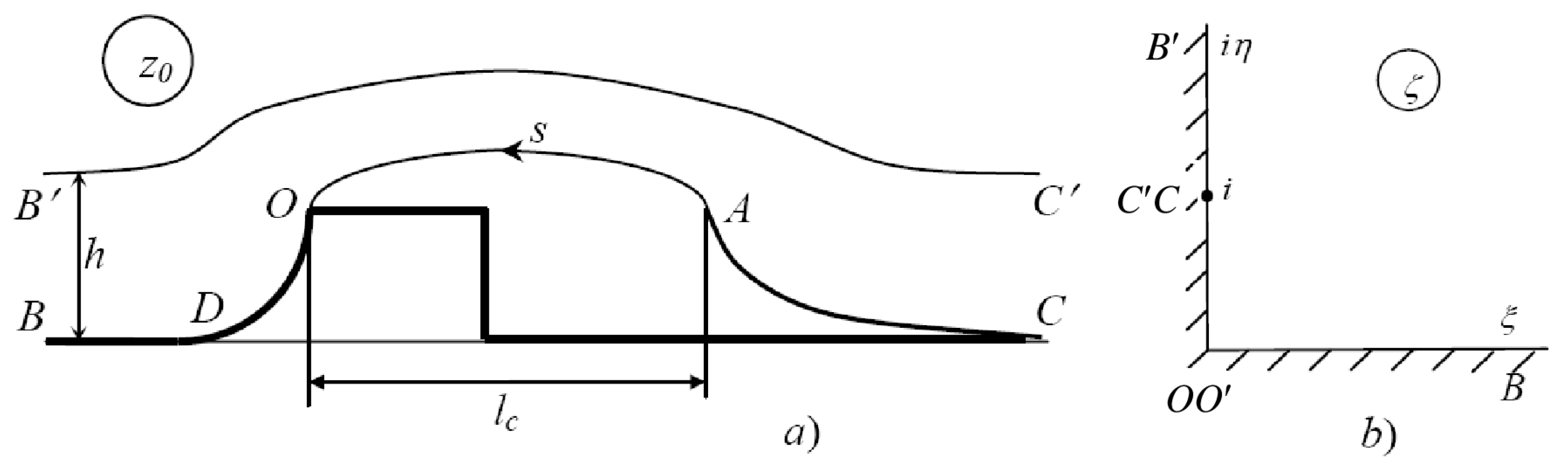
3.1. Cavity Flow in Channels with Curved Walls
3.1.1. Cavity Closure Model
3.1.2. Integro-Differential Equations in the Functions and
3.2. Jet Flow Along a Curved Wall
3.3. Semi-Infinite Flow Passing over a Solid Curved Surface
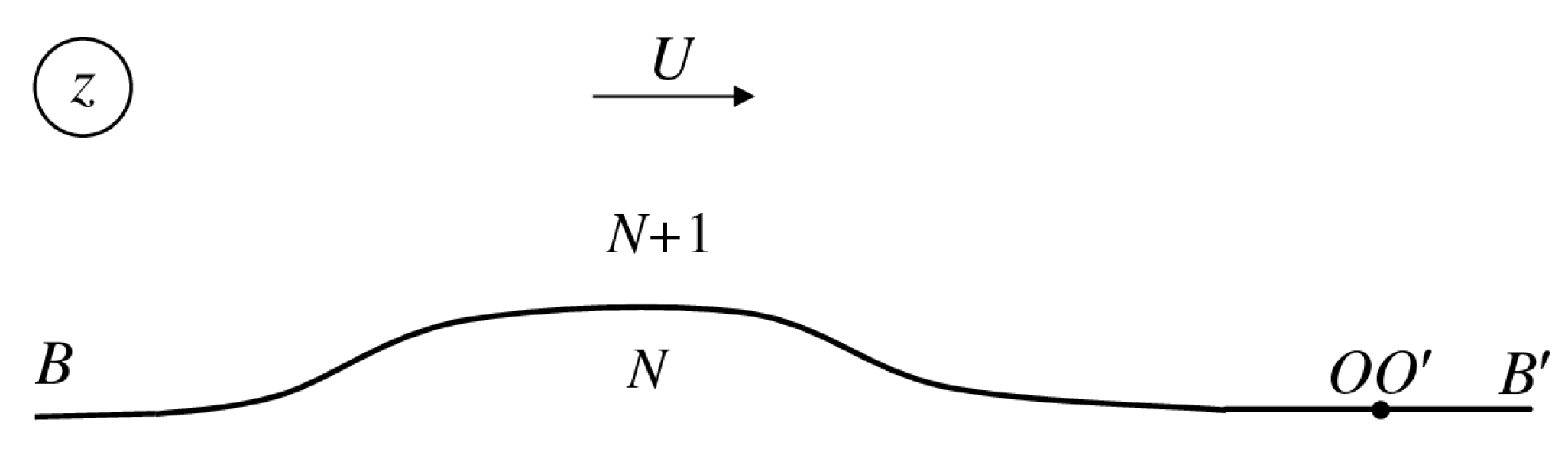
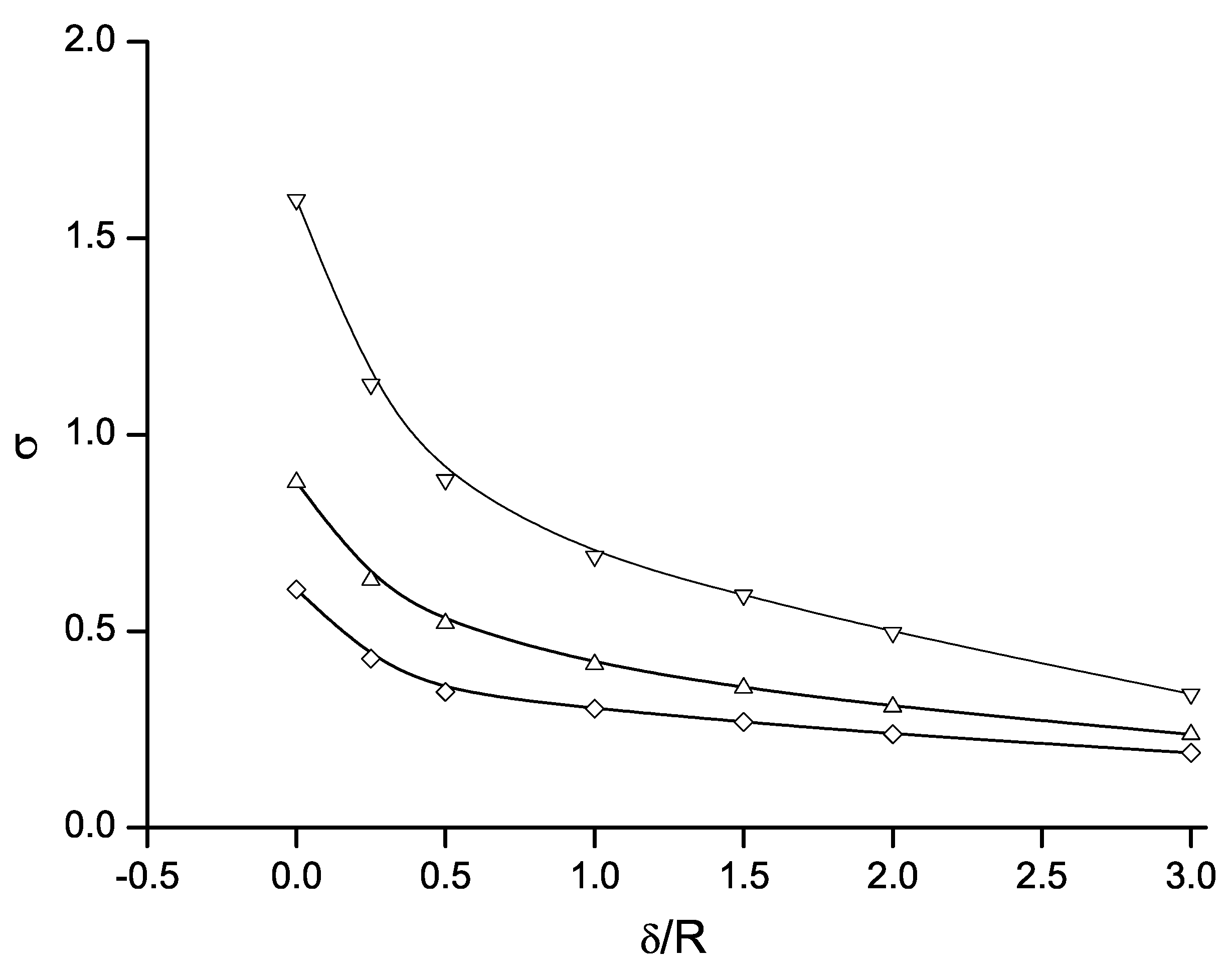
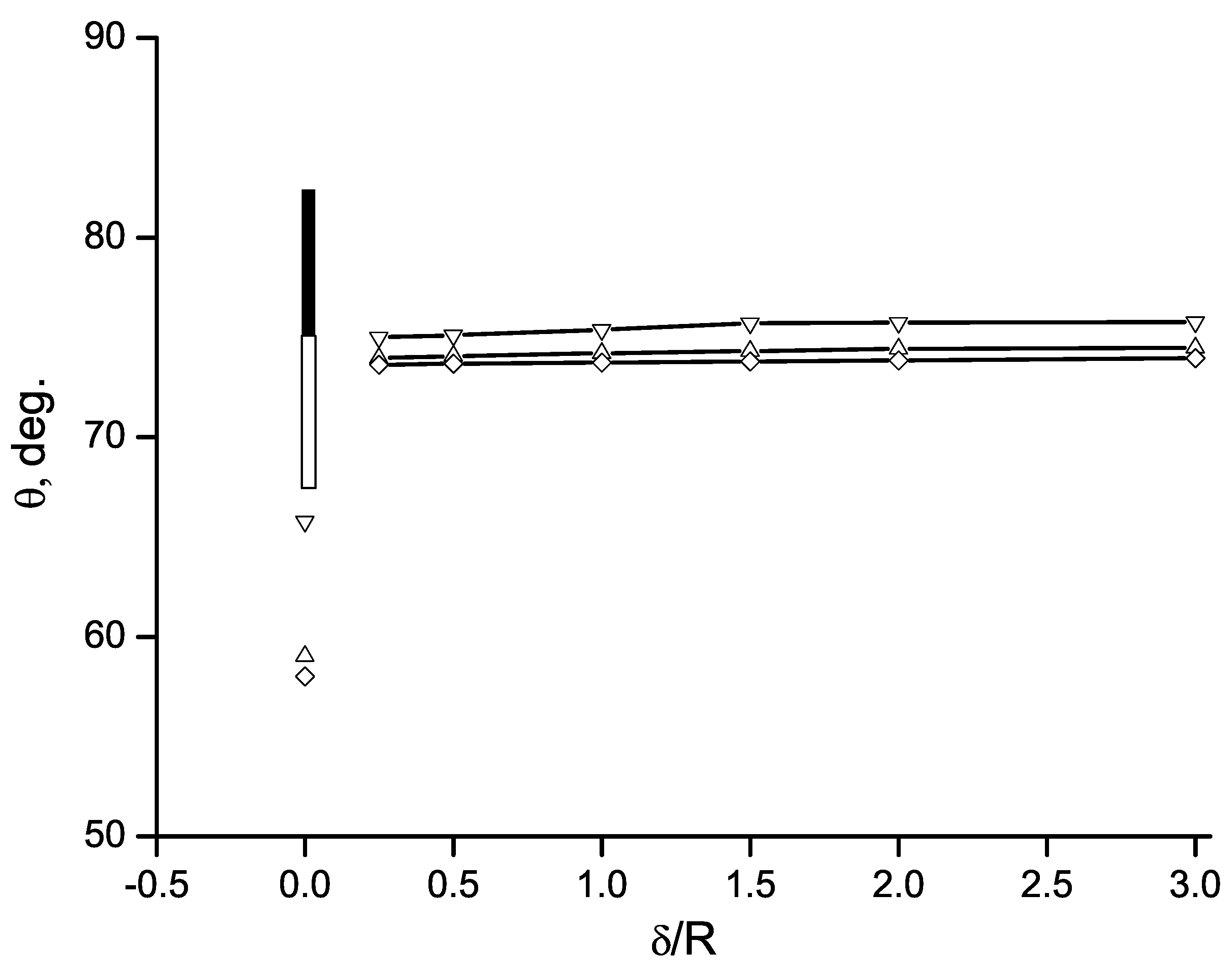
4. Results and Discussion
4.1. Cavity Flow with a Fixed Point of Cavity Detachment
4.2. Cavity Flow Past a Circular Cylinder
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Cartesian coordinates | |
| Complex coordinate/physical plane | |
| parametric variable/parameteric plane | |
| s | arclength coordinate |
| flow potential | |
| stream function | |
| w | complex potential |
| complex velocity | |
| derivative of the complex potential | |
| complex potential | |
| width of the channel i | |
| L | characteristics length |
| R | radius of the cylinder |
| pressure at infinity | |
| pressure in the cavity | |
| U | velocity on the outer boundary |
| V | average velocity across the channels |
| cavitation number based on U | |
| cavitation number based on V | |
| v | velocity magnitude |
| slope of the side of the channel | |
| thickness of the boundary layer |
References
- Street, R.L. A linearized Theory for Rotational Super-Cavitating Flow. J. Fluid Mech. 1963, 17, 513–545. [Google Scholar] [CrossRef][Green Version]
- Vasiliev, V.N. Cavity vortex flow past a curved arc. In Unsteady Motion of Bodies in Liquid; University of Chuvashia: Cheboksary, Russia, 1979; pp. 3–15. [Google Scholar]
- Kotlyar, L.M.; Lazarev, V.A. Cavity vortex flow past a wedge. In Proceedings of the Boundary-Value Problem Workshop; Kazan’ State University: Kazan, Russia, 1971; pp. 15–25. [Google Scholar]
- Sedov, L.I. Plane Problems in Hydrodynamics and Aerodynamics; Nauka: Moscow, Russia, 1980; p. 448. [Google Scholar]
- Muskhelishvili, N.I. Singular Integral Equations: Boundary Problems of Function Theory and Their Applications to Mathematical Physics; Dover Publ.: New York, NY, USA, 1992. [Google Scholar]
- Burov, A.V. Uniformly Whirling Jet Flow Past a Wedge. In High-Speed Hydrodynamics; University of Chuvashia: Cheboksary, Russia, 1985; pp. 22–24. [Google Scholar]
- Yoon, B.S.; Semenov, Y.A. Cavity flow in a boundary layer. In Proceedings of the 26th International Conference on Offshore Mechanics and Arctic Engineering (OMAE), Shanghai, China, 6–11 June 2010. [Google Scholar]
- Brillouin, M. Les surfaces de glissement de Helmholtz et la resistance des fluids. Ann. Chim. Phys. 1911, 23, 145–230. [Google Scholar]
- Villat, H. Sur la validite des solutions de certains problemes d’hydrodynamique. J. Math. Pure Appl. 1914, 20, 231–290. [Google Scholar]
- Arakeri, V.H.; Acosta, A.J. Viscous effects in the inception of cavitation on axisymmetric bodies. Trans. ASME J. Fluids Engng. 1973, 95, 519–527. [Google Scholar] [CrossRef]
- Arakeri, V.H. Viscous effects on the position of cavitation separation from smooth bodies. J. Fluid Mech. 1975, 68, 779–799. [Google Scholar] [CrossRef]
- Tassin Leger, A.; Ceccio, S.L. Examination of the flow near the leading edge of attached cavitation. Part 1. Detachment of two-dimensional and axisymmetric cavities. J. Fluid Mech. 1998, 376, 61–90. [Google Scholar] [CrossRef]
- Yoon, B.S.; Semenov, Y.A. Cavity detachment on a hydrofoil with the inclusion of surface tension effects. Eur. J. Mech. B/Fluids 2011, 30, 17–25. [Google Scholar] [CrossRef]
- Michell, J.H. On the theory of free stream lines. Philos. Trans. R. Soc. Lond. A 1890, 181, 389–431. [Google Scholar] [CrossRef]
- Joukovskii, N.E. Modification of Kirchhof’s method for determination of a fluid motion in two directions at a fixed velocity given on the unknown streamline. Math. Sbornik. 1890, 15, 121–278. [Google Scholar]
- Gurevich, M.I. Theory Jets Ideal Fluids; Academic Press: New York, NY, USA, 1965. [Google Scholar]
- Semenov, Y.A.; Iafrati, A. On the nonlinear water entry problem of asymmetric wedges. J. Fluid Mech. 2006, 547, 231–256. [Google Scholar] [CrossRef]
- Semenov, Y.A.; Yoon, B.S. Onset of flow separation at oblique water impact of a wedge. Phys. Fluids 2009, 21, 112103-1. [Google Scholar] [CrossRef]
- Birkhoff, G.; Zarantonello, E.H. Jets, Wakes and Cavities; Academic Press: New York, NY, USA, 1957. [Google Scholar]
- Crocco, L.; Lees, L. A mixing theory for the interaction between dissipative flows and nearly isentropic streams. J. Aeronaut. Sci. 1952, 19, 649–676. [Google Scholar] [CrossRef]
- Semenov, Y.A.; Tsujimoto, Y. A cavity wake model based on the viscous/inviscid interaction approach and its application to non-symmetric cavity flows in inducers. Trans. ASME J. Fluids Eng. 2003, 125, 758–766. [Google Scholar] [CrossRef]
- Tulin, M.P. Supercavitating flows-small perturbation theory. J. Ship Res. 1964, 7, 16–37. [Google Scholar]
- Farhat, M.; Avellan, F. On the detachment of a leading edge cavitation. In Proceedings of the Fourth International Symposium on Cavitation, Pasadena, CA, USA, 20–23 June 2001. [Google Scholar]


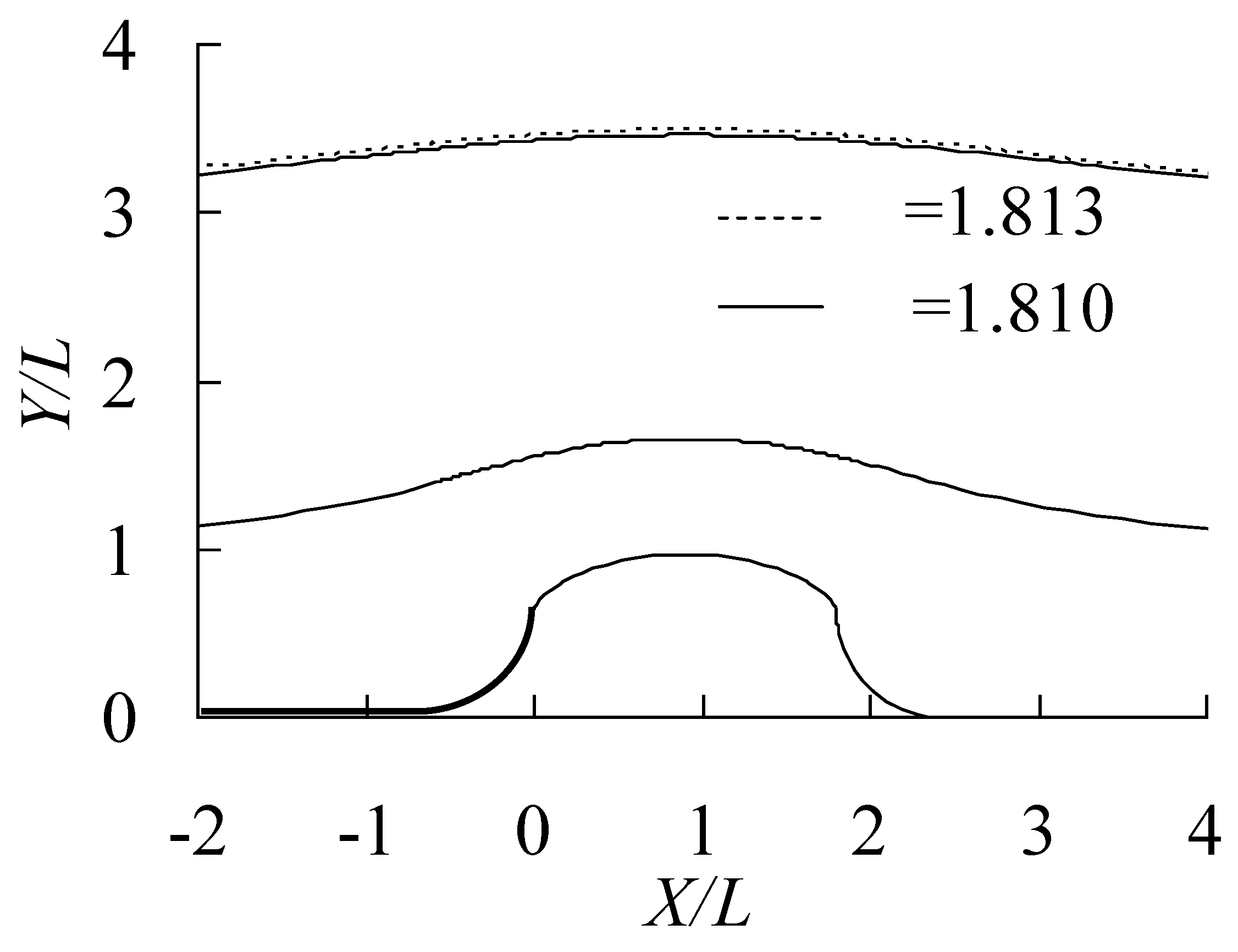
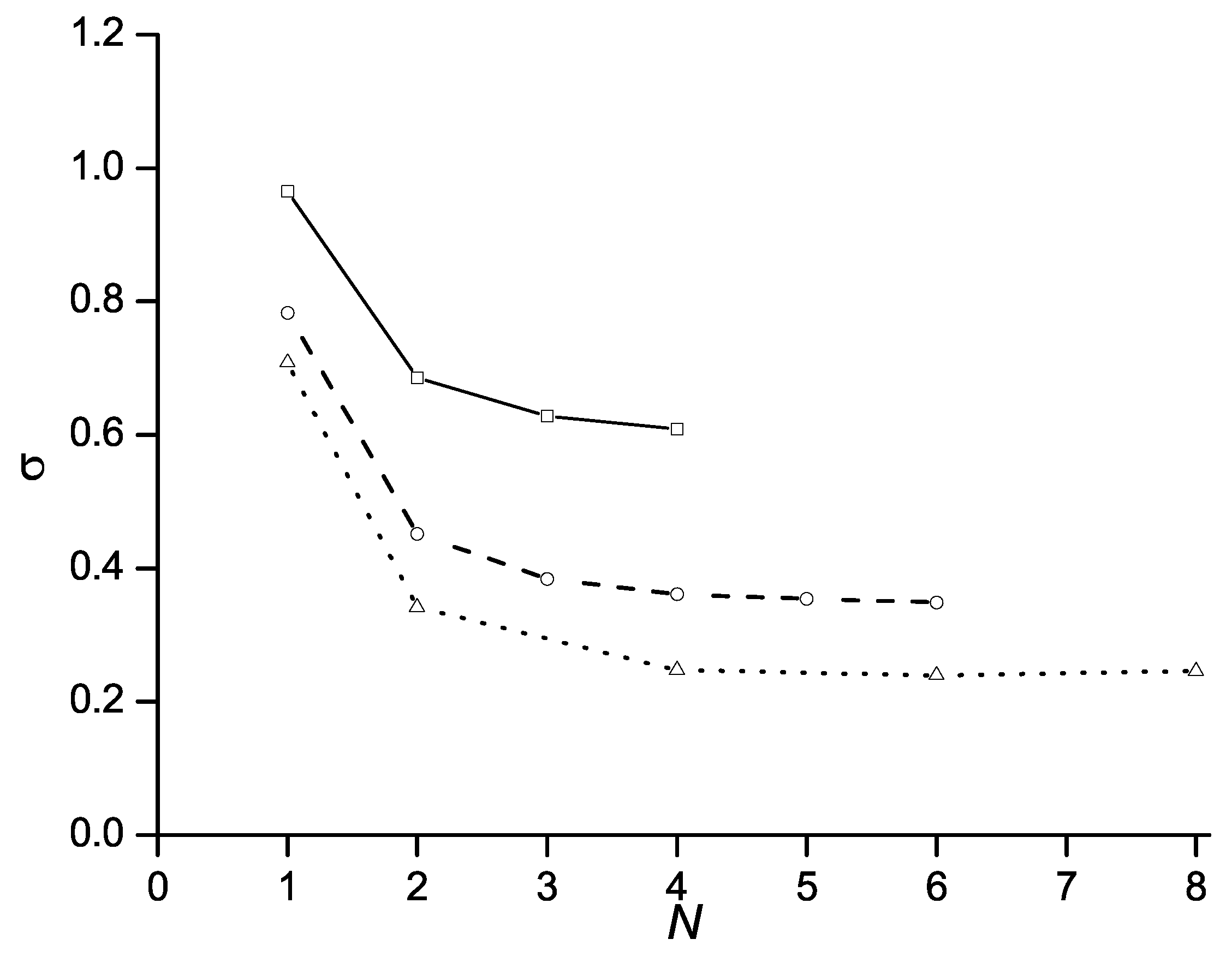



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savchenko, Y.N.; Savchenko, G.Y.; Semenov, Y.A. Effect of a Boundary Layer on Cavity Flow. Mathematics 2020, 8, 909. https://doi.org/10.3390/math8060909
Savchenko YN, Savchenko GY, Semenov YA. Effect of a Boundary Layer on Cavity Flow. Mathematics. 2020; 8(6):909. https://doi.org/10.3390/math8060909
Chicago/Turabian StyleSavchenko, Yuriy N., Georgiy Y. Savchenko, and Yuriy A. Semenov. 2020. "Effect of a Boundary Layer on Cavity Flow" Mathematics 8, no. 6: 909. https://doi.org/10.3390/math8060909
APA StyleSavchenko, Y. N., Savchenko, G. Y., & Semenov, Y. A. (2020). Effect of a Boundary Layer on Cavity Flow. Mathematics, 8(6), 909. https://doi.org/10.3390/math8060909





