The Wright Functions of the Second Kind in Mathematical Physics
Abstract
1. Introduction
2. The Wright Functions of the Second Kind and the Mainardi Auxiliary Functions
- for the first kind, when
- for the second kind, when and putting for convenience so
3. The Wright Functions of the Second Kind and the Time-Fractional Diffusion Wave Equation
- (a)
- Cauchy problem
- (b)
- Signalling problem
3.1. Complements to the Time-Fractional Diffusion-Wave Equations
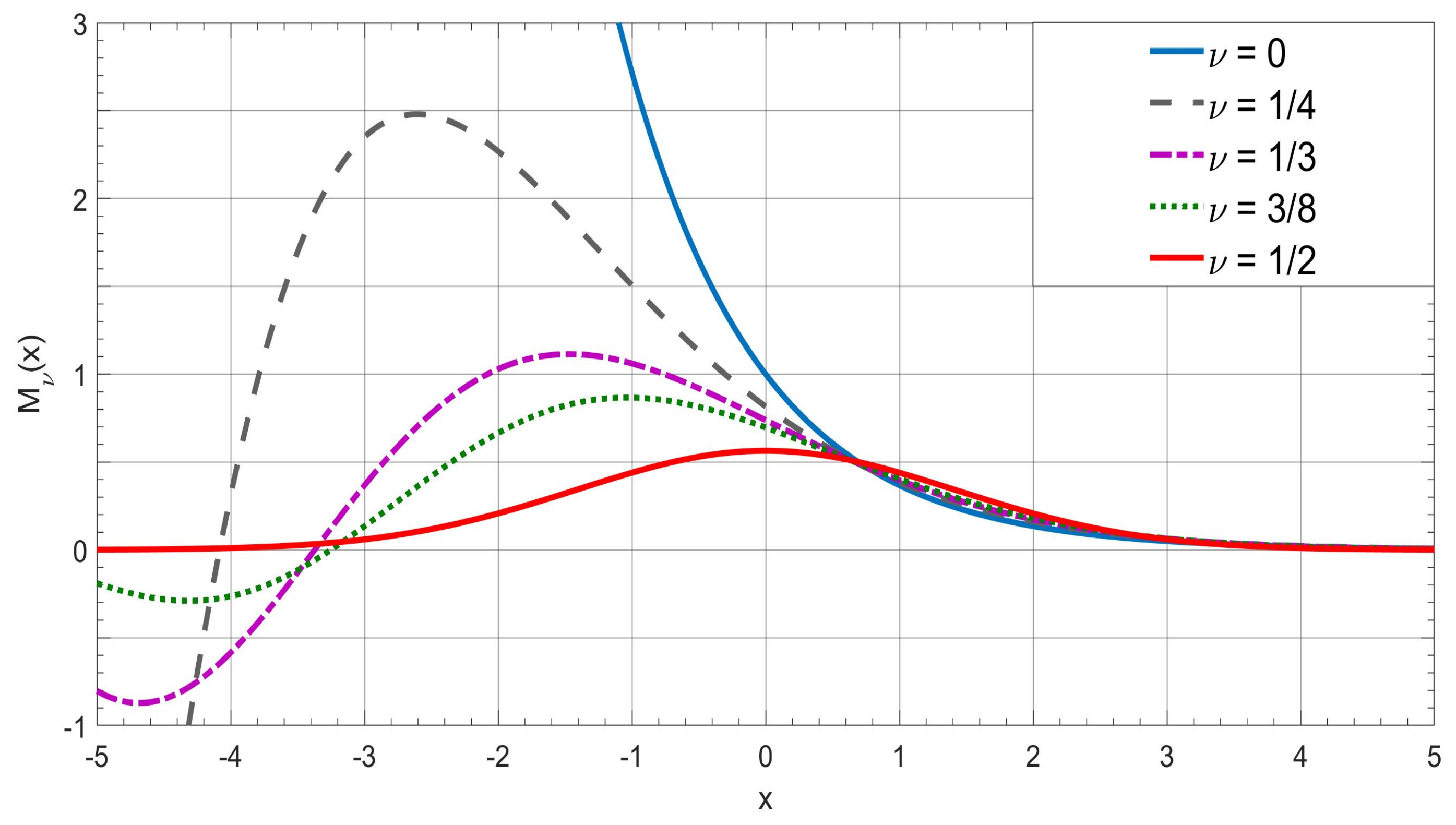
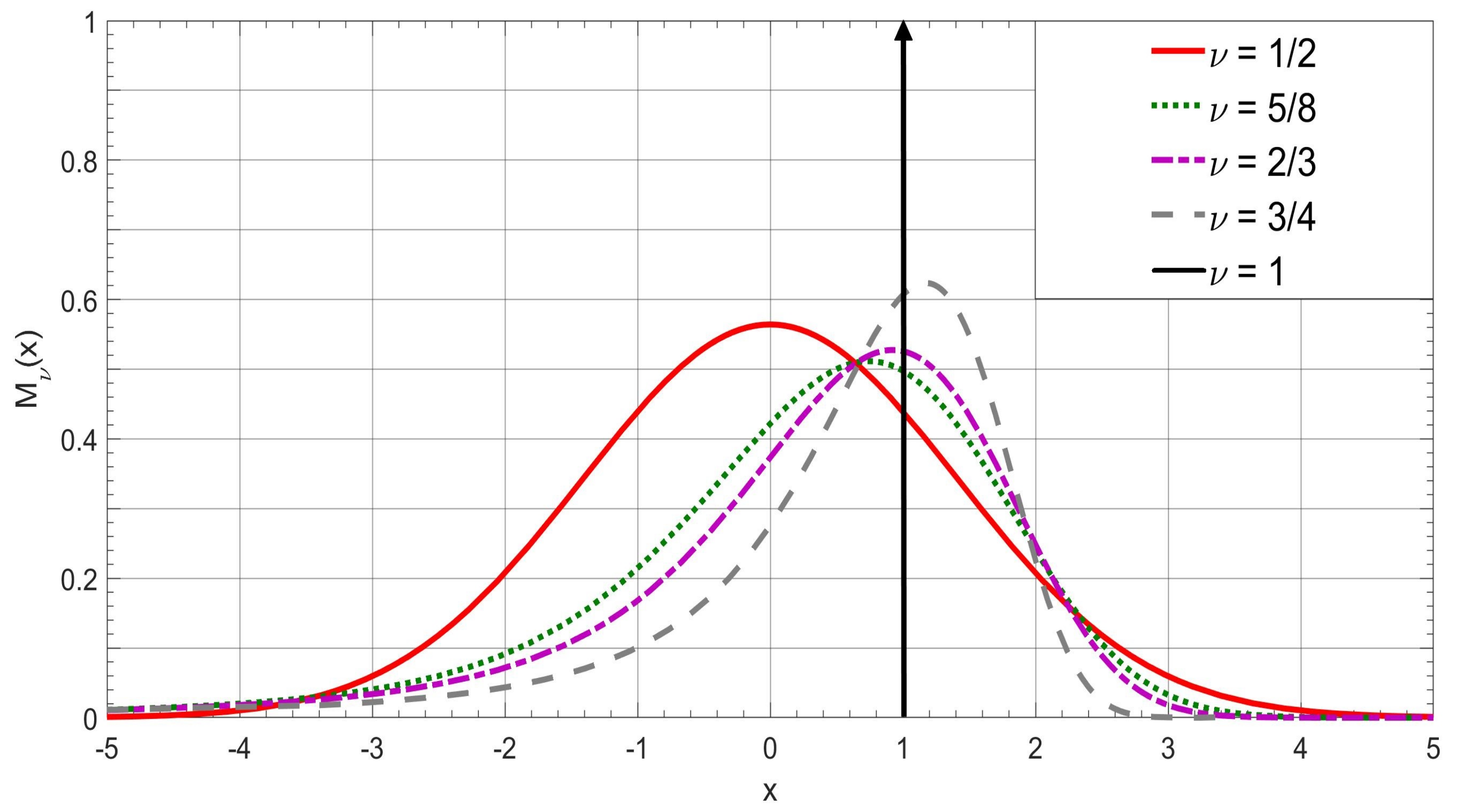
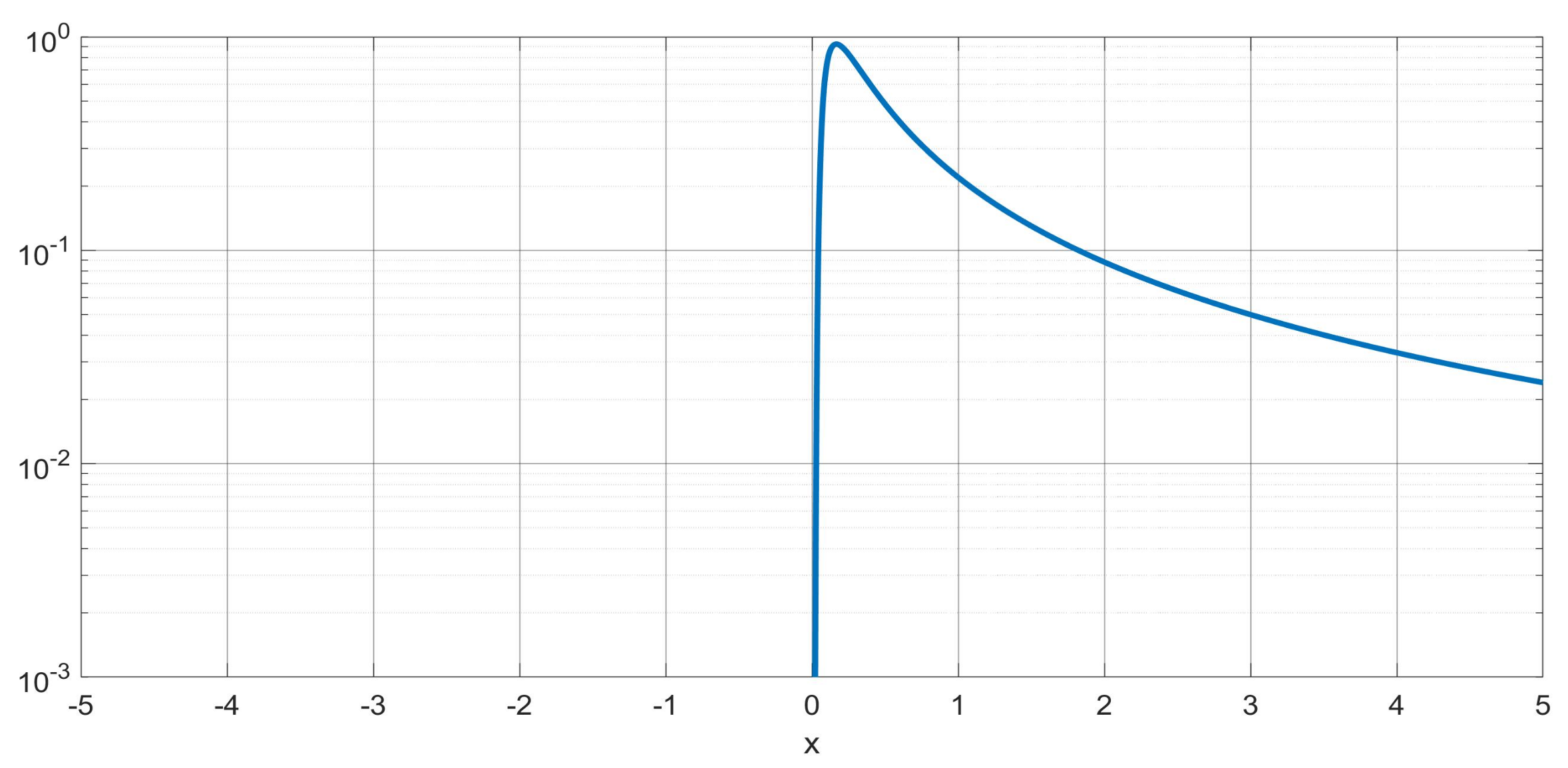
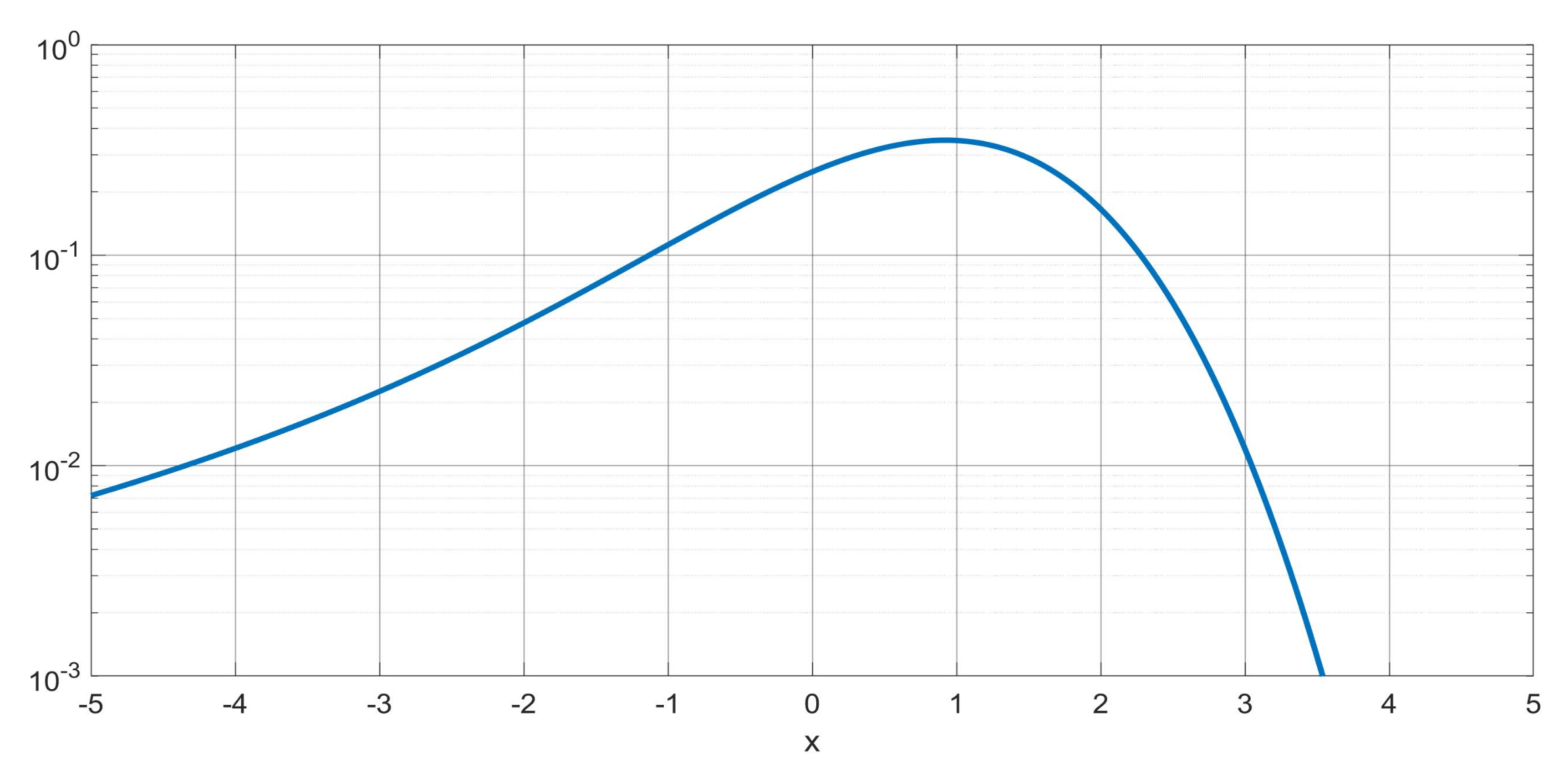
4. The -Wright Functions in Probability Theory and the Stable Distributions
4.1. The Auxiliary Functions versus Extremal Stable Densities
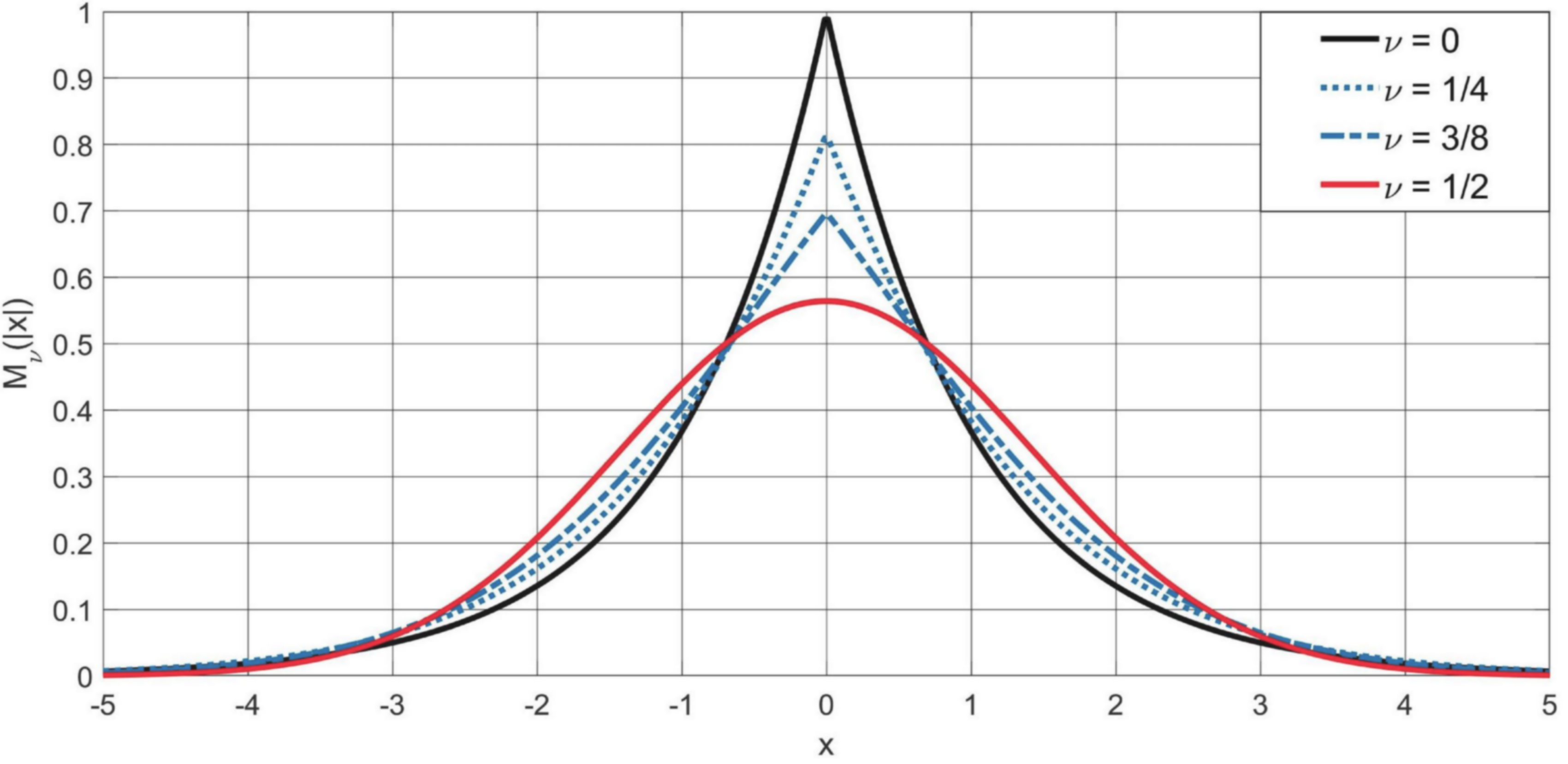
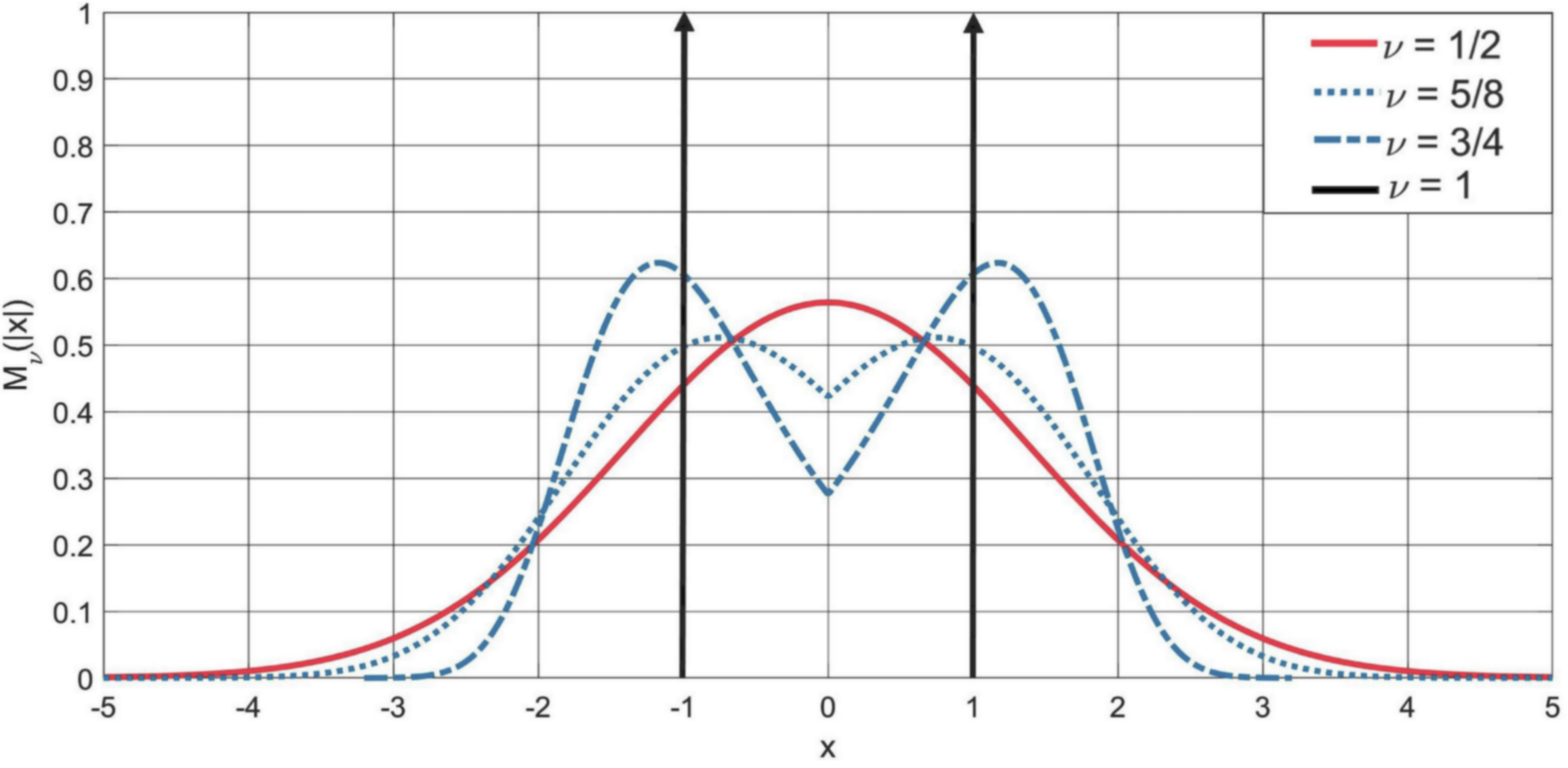
4.2. The Symmetric M-Wright Function
4.3. The Wright -Function in Two Variables
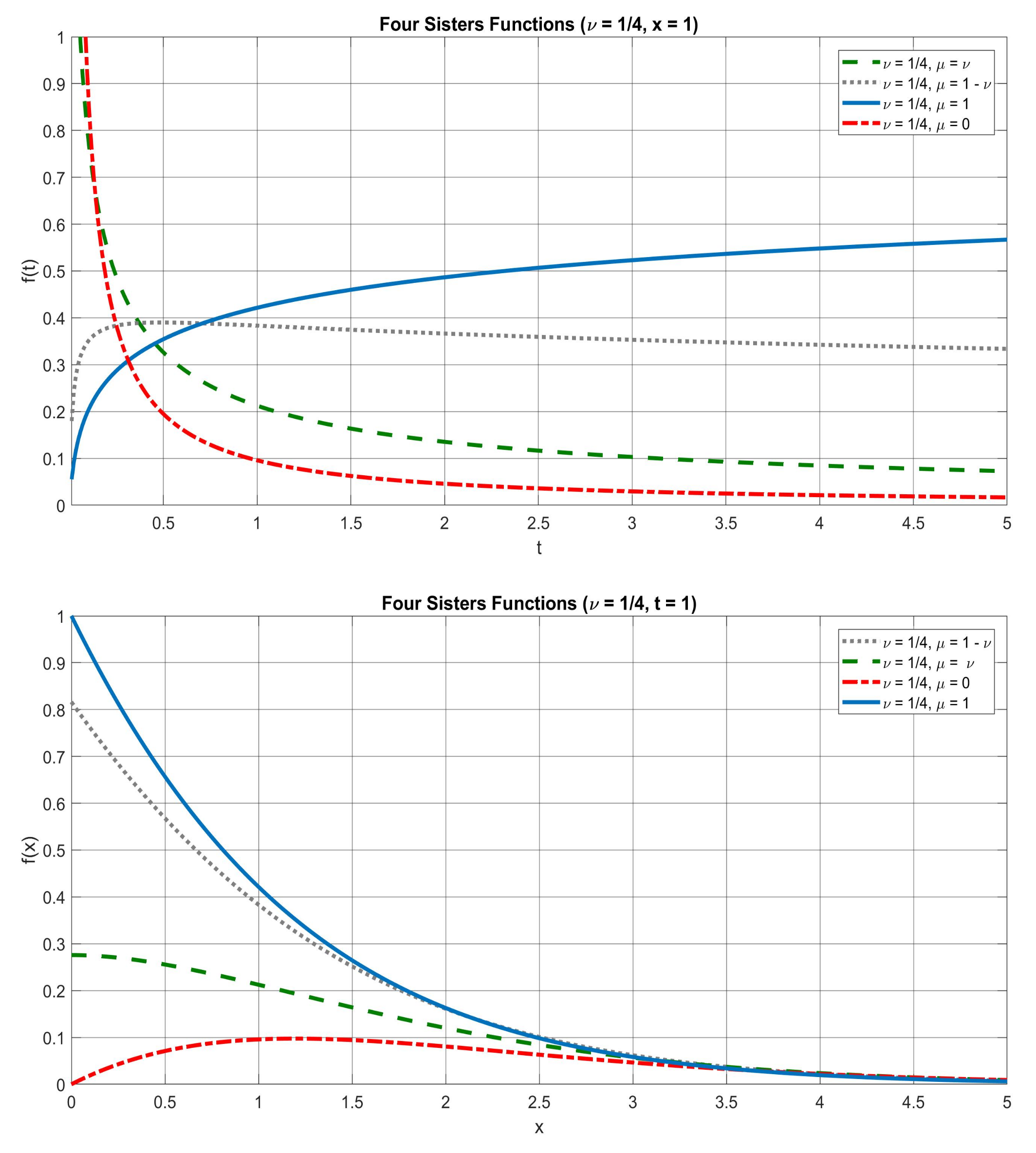
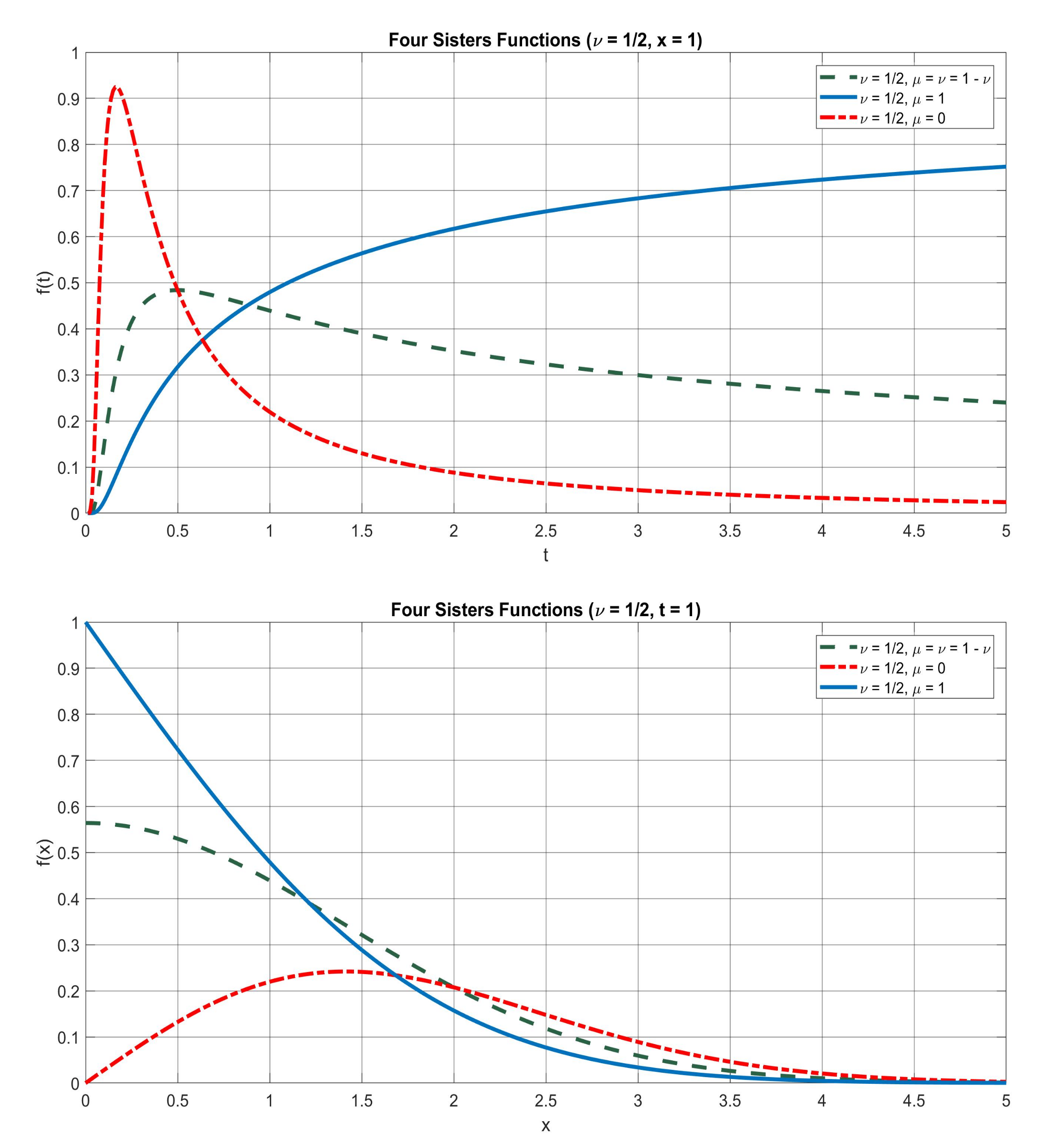
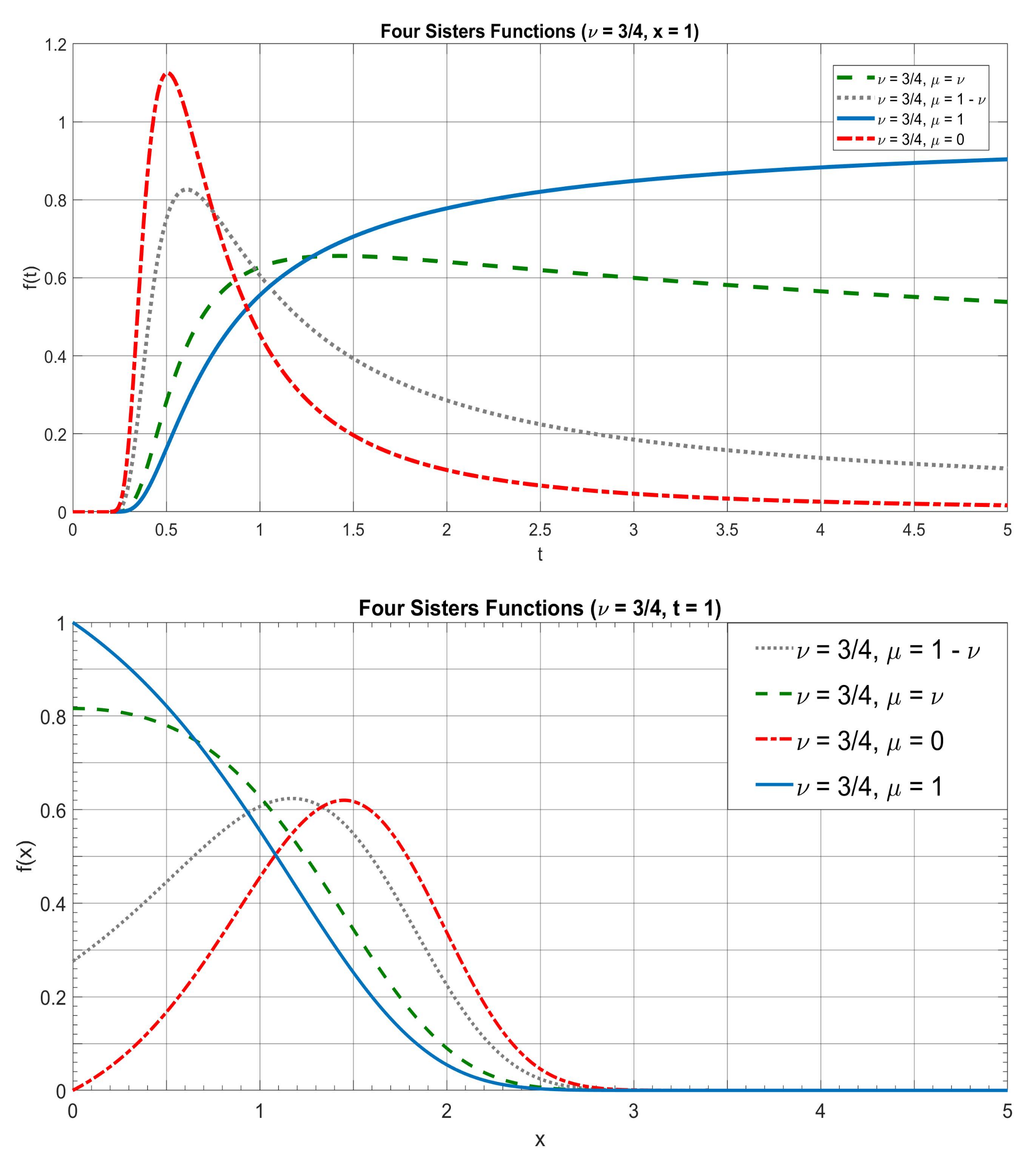
5. The Four Sisters
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Standard Diffusion Equation and the Three Sisters
- -
- from . Indeed, notingsince we can obtain (A12), namely
- -
Appendix B. Essentials of Fractional Calculus
Appendix C. The Lévy Stable Distributions
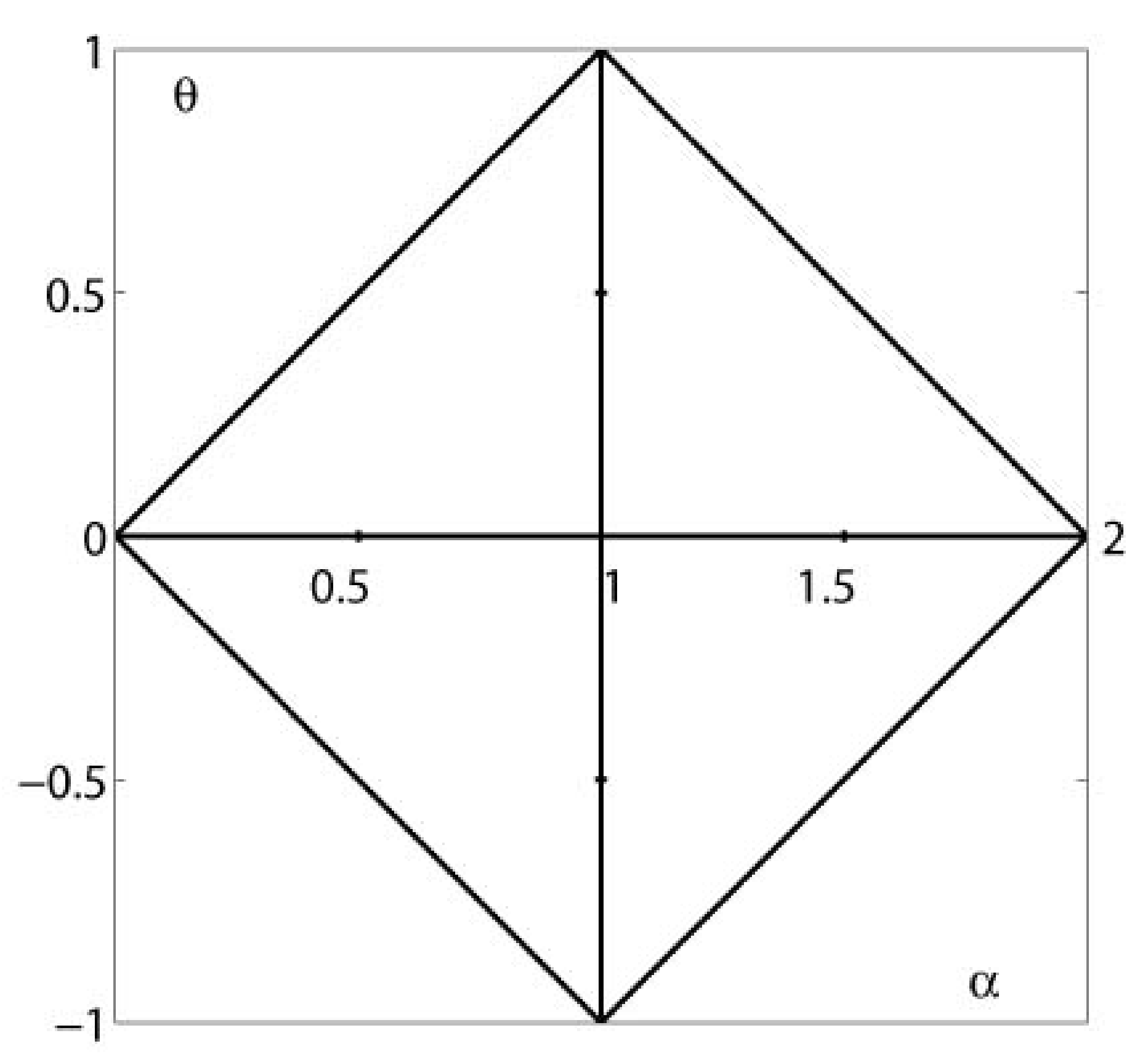
- -
- The class of stable distributions possesses its own domain of attraction, see, e.g., [73].
- -
- -
- The stable distributions are self-similar and infinitely divisible.
References
- Ragab, F.M. The inverse Laplace transform of an exponential function. Comm. Pure Appl. Math. 1958, 11, 115–127. [Google Scholar] [CrossRef]
- Stefański, T.P.; Gulgowski, J. Signal propagation in electromagnetic media described by fractional-order models. Comm. Nonlinear Sci. Numer. Simul. 2020, 82, 105020. [Google Scholar] [CrossRef]
- Garra, R.; Giraldi, F.; Mainardi, F. Wright type generalized coherent states. WSEAS Trans. Math. 2019, 18, 428–431. [Google Scholar]
- Wright, E.M. On the coefficients of power series having exponential singularities. J. Lond. Math. Soc. 1933, 8, 71–79. [Google Scholar] [CrossRef]
- Wright, E.M. The asymptotic expansion of the generalized Bessel function. Proc. Lond. Math. Soc. (Ser. II) 1935, 38, 257–270. [Google Scholar] [CrossRef]
- Wright, E.M. The generalized Bessel function of order greater than one. Quart. J. Math. Oxf. Ser. 1940, 11, 36–48. [Google Scholar] [CrossRef]
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F. Higher Transcendental Functions, 3rd ed.; McGraw-Hill: New York, NY, USA, 1955. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity, 2nd ed.; Imperial College Press: London, UK, 2010. [Google Scholar]
- Wong, R.; Zhao, Y.-Q. Smoothing of Stokes’ discontinuity for the generalized Bessel function. Proc. R. Soc. Lond. 1999, 455, 1381–1400. [Google Scholar] [CrossRef]
- Wong, R.; Zhao, Y.-Q. Smoothing of Stokes’ discontinuity for the generalized Bessel function II. Proc. R. Soc. Lond. A 1999, 455, 3065–3084. [Google Scholar] [CrossRef]
- Luchko, Y. The Wright function and its applications. In Handbook of Fractional Calculus with Applications; Machado, J.A.T., Ed.; De Gruyter GmbH: Berlin, Germany; Boston, MA, USA, 2019; Volume 1: Basic, Theory, pp. 241–268. [Google Scholar]
- Paris, R.B. Asymptotics of the special functions of fractional calculus. In Handbook of Fractional Calculus with Applications; Machado, J.A.T., Ed.; De Gruyter GmbH: Berlin, Germany; Boston, MA, USA, 2019; Volume 1: Basic, Theory, pp. 297–325. [Google Scholar]
- Gorenflo, R.; Luchko, Y.u.; Mainardi, F. Analytical properties and applications of the Wright function. Fract. Calc. Appl. Anal. 1999, 2, 383–414. [Google Scholar]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S. Mittag–Leffler Functions. Related Topics and Applications; Springer: Berlin, Germany, 2014; 2nd Edition to appear. [Google Scholar]
- Mainardi, F. On the initial value problem for the fractional diffusion-wave equation. In Waves and Stability in Continuous Media; Rionero, S., Ruggeri, T., Eds.; World Scientific: Singapore, 1994; pp. 246–251, In Proceedings of the VII-th WASCOM, International Conference “Waves and Stability in Continuous Media”, Bologna, Italy, 4–7 October 1993. [Google Scholar]
- Mainardi, F. The time fractional diffusion-wave-equation. Radiophys. Quantum Electron. 1995, 20–36, (English translation from the Russian of Radiofisika). [Google Scholar] [CrossRef]
- Mainardi, F. The fundamental solutions for the fractional diffusion-wave equation. Appl. Math. Lett. 1996, 9, 23–28. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional relaxation-oscillation and fractional diffusion-wave phenomena. Chaos Solitons Fractals 1996, 7, 1461–1477. [Google Scholar] [CrossRef]
- Liemert, A.; Klenie, A. Fundamental solution of the tempered fractional diffusion equation. J. Math. Phys. 2015, 56, 113504. [Google Scholar] [CrossRef]
- Saa, A.; Venegeroles, R. Alternative numerical computation of one-sided Lévy and Mittag–Leffler distributions. Phys. Rev. 2011, 84, 026702. [Google Scholar]
- Kiryakova, V. The multi-index Mittag–Leffler functions as an important class of special functions of fractional calculus. Comp. Math. Appl. 2010, 59, 1885–1895. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Koroleva, A.A.; Rogosin, S.V. Multi-parametric Mittag–Leffler functions and their extension. Fract. Calc. Appl. Anal. 2013, 16, 378–404. [Google Scholar] [CrossRef]
- Ansari, A.; Refahi Sheikhani, A. New identities for the Wright and the Mittag–Leffler functions using the Laplace transform. Asian-European J. Math. 2014, 7, 1450038. [Google Scholar] [CrossRef]
- Mainardi, F. A tutorial survey on the basic special functions of fractional calculus. WSEAS Trans. Math. 2020, 19, 74–98. [Google Scholar] [CrossRef]
- Luchko, Y. On the asymptotics of zeros of the Wright function. Z. für Analysis und ihre Anwendungen (ZAMP) 2000, 19, 597–622. [Google Scholar] [CrossRef]
- Luchko, Y.; Kiryakova, V. The Mellin integral transform in fractional calculus. Fract. Calc. Appl. Anal. 2013, 16, 405–430. [Google Scholar] [CrossRef]
- Bazhlekova, E. Subordination in a class of generalized time-fractional diffusion-wave equations. Fract. Calc. Appl. Anal. 2018, 21, 869–900. [Google Scholar] [CrossRef]
- D’Ovidio, M. Wright functions governed by fractional directional derivatives and fractional advection diffusion equations. Methods Appl. Anal. 2015, 22, 1–36. [Google Scholar] [CrossRef]
- Gorenflo, R.; Luchko, Y.u.; Mainardi, F. Wright functions as scale-invariant solution of the diffusion-wave equation. J. Comp. Appl. Math. 2000, 118, 175–191. [Google Scholar] [CrossRef]
- Mentrelli, A.; Pagnini, G. Front propagation in anomalous diffusive media governed by time-fractional diffusion. J. Comput. Phys. 2015, 293, 427–441. [Google Scholar] [CrossRef]
- Moslehi, A.; Ansari, A. On M-Wright transforms and time-fractional diffusion equations. Integral Transform. Spec. Funct. 2017, 28, 113–120. [Google Scholar] [CrossRef]
- Pagnini, G. Erdélyi-Kober fractional diffusion. Fract. Calc. Appl. Anal. 2012, 15, 117–127. [Google Scholar] [CrossRef]
- Povstenko, Y. Linear Partial Differential Equations for Engineers; Springer: Heidelberg, Germany, 2015. [Google Scholar]
- Consiglio, A.; Mainardi, F. On the Evolution of Fractional Diffusive Waves. Ric. Mat. 2019. [Google Scholar] [CrossRef]
- Kochubei, A.N. Distributed order calculus and equations of ultraslow diffusion. J. Math. Anal. Appl. 2008, 340, 252–281. [Google Scholar] [CrossRef]
- Li, Z.; Luchko, Y.; Yamamoto, M. Asymptotic estimates of solutions to initial-boundary-value problems for distributed order time-fractional diffusion equations. Fract. Calc. Appl. Anal. 2014, 17, 1114–1136. [Google Scholar] [CrossRef]
- Mainardi, F.; Pagnini, G.; Gorenflo, R. Some aspects of fractional diffusion equations of single and distributed order. Comput. Appl. Math. 2007, 187, 295–305. [Google Scholar] [CrossRef]
- Mainardi, F.; Mura, A.; Pagnini, G.; Gorenflo, R. Time-fractional diffusion of distributed order. Vib. Control. 2008, 14, 1267–1290. [Google Scholar] [CrossRef]
- Luchko, Y. Multi-dimensional fractional wave equation and some properties of its fundamental solution. Commun. Appl. Ind. Math. 2014, 6, 1–21. [Google Scholar] [CrossRef]
- Luchko, Y. On some new properties of the fundamental solution to the multi-dimensional space- and time-fractional diffusion-wave equation. Mathematics 2017, 5, 76. [Google Scholar] [CrossRef]
- Luchko, Y.; Mainardi, F. Cauchy and signaling problems for the time-fractional diffusion-wave equation. ASME J. Vib. Acoust. 2014, 136, 050904/1-7. [Google Scholar] [CrossRef]
- Luchko, Y.; Mainardi, F. Fractional diffusion-wave phenomena. In Handbook of Fractional Calculus with Applications; Tarasov, V., Machado, J.A.T., Eds.; De Gruyter GmbH: Berlin, Germany; Boston, MA, USA, 2019; Volume 5: Applications in physics, Part B, pp. 71–98. [Google Scholar]
- Boyadjiev, L.; Luchko, Y. Mellin integral transform approach to analyze the multidimensional diffusion-wave equations. Chaos, Solitons Fractals 2017, 102, 127–134. [Google Scholar] [CrossRef]
- Hanyga, A. Multidimensional solutions of time-fractional diffusion-wave equations. Soc. Lond Proc. Ser. Math. Phys. Eng. Sci. 2002, 458, 933–957. [Google Scholar] [CrossRef]
- Kemppainen, J. Positivity of the fundamental solution for fractional diffusion and wave wave equations. Math. Meth. Appl. Sci. 2019, 1–19. [Google Scholar] [CrossRef]
- Schneider, W.R.; Wyss, W. Fractional diffusion and wave equations. Math. Phys. 1989, 30, 134–144. [Google Scholar] [CrossRef]
- Mainardi, F.; Luchko, Y.; Pagnini, G. The fundamental solution of the space-time fractional diffusion equation. Fract. Calc. Appl. Anal. 2001, 4, 153–192. [Google Scholar]
- Mainardi, F.; Tomirotti, M. Seismic pulse propagation with constant Q and stable probability distributions. Ann. Geofis. 1997, 40, 1311–1328. [Google Scholar]
- Mainardi, F.; Pagnini, G.; Gorenflo, R. Mellin transform and subordination laws in fractional diffusion processes. Fract. Calc. Appl. Anal. 2003, 6, 441–459. [Google Scholar]
- Beghin, L.; Orsingher, E. Poisson-type processes governed by fractional and higher-order recursive differential equations. Electron. J. Probab. 2010, 15, 684–709. [Google Scholar] [CrossRef]
- Cahoy, D.O. On the parametrization the M-Wright Function. Far East J. Theor. Stat. 2011, 34, 155–164. [Google Scholar]
- Cahoy, D.O. Estimation and Simulation for the M-Wright Function. Commun. Stat. Methods 2012, 41, 1466–1477. [Google Scholar]
- Garra, R.; Orsingher, E.; Polito, F. Fractional diffusions with time-varying coefficients. J. Math. Phys. 2015, 56, 093301. [Google Scholar] [CrossRef]
- Chen, L. Nonlinear stochastic time-fractional diffusion equation on R: Moments, Holder regularity and Intermittency. Trans. Am. Math. Soc. 2017, 369, 8497–8535. [Google Scholar] [CrossRef]
- Consiglio, A.; Luchko, Y.; Mainardi, F. Some notes on the Wright functions in probability theory. WSEAS Trans, Math. 2019, 18, 389–393. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Parametric subordination in fractional diffusion processes. In Fractional Dynamics. Recent Advances; Klafter, J., Lim, S.C., Metzler, R., Eds.; World Scientific: Singapore, 2012; Chapter 10; pp. 227–261. [Google Scholar]
- Mainardi, F.; Mura, A.; Pagnini, G. The M Wright function in time-fractional diffusion processes: A tutorial survey. Int. J. Diff. Eqs. 2010, 104505. [Google Scholar] [CrossRef]
- Pagnini, G. The M-Wright function as a generalization of the Gaussian density for fractional diffusion processes. Fract. Calc. Appl. Anal. 2013, 16, 436–453. [Google Scholar] [CrossRef]
- Scalas, E.; Viles, N. On the convergence of quadratic variation for compound fractional Poisson processes. Fract. Calc. Appl. Anal. 2012, 15, 31–331. [Google Scholar] [CrossRef]
- Koren, T.; Lomholt, M.A.; Chechkin, A.V.; Klafter, J.; Metzler, R. Leapover lengths and first passage time statistics for Lévy flights. Phys. Rev. Lett. 2007, 99, 160602. [Google Scholar] [CrossRef] [PubMed]
- Padash, A.; Chechkin, A.V.; Dybiec, B.; Pavlyukevich, I.; Shokri, B.; Metzler, R. First-passage properties of asymmetric Lé vy flights. J. Phys. Math. Theor. 2019, 52, 454004. [Google Scholar] [CrossRef]
- Stankovič, B. On the function of E.M. Wright. Publ. de l’Institut Mathématique, Beograd, Nouvelle Sér. 1970, 10, 113–124. [Google Scholar]
- Mainardi, F. The Linear Diffusion Equation; Lecture Notes in Mathematical Physics; University of Bologna, Department of Physics: Bologna, Italy, 1996–2006; p. 19, [Available since 2019 at Brown University]; Available online: www.dam.brown.edu/fractional_calculus/documents/THELINEARDIFFUSIONEQUATION.pdf (accessed on 1 June 2020).
- Gorenflo, R.; Mainardi, F. Fractional Calculus: Integral and Differential Equations of Fractional Order. In Fractals and Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer: Wien, Österreich, 1997; pp. 223–276, [E-print arXiv:0805.3823]. [Google Scholar]
- Mainardi, F. Fractional Calculus: Some Basic Problems in Continuum and Statistical Mechanics. In Fractals and Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer Verlag: Wien, Österreich, 1997; pp. 291–348, [E-print arXiv:1201.0863]. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations; An Application-Oriented Exposition Using Differential Operators of Caputo Type, Lecture Notes in Mathematics No 2004; Springer: Berlin, Germany, 2010. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent, Part II. Geophys. J. R. Astr. Soc. 1967, 13, 529–539, [Reprinted in Fract. Calc. Appl. Anal. 2008, 11, 4–14]. [Google Scholar] [CrossRef]
- Caputo, M. Elasticità e Dissipazione; Zanichelli: Bologna, 1969. (In Italian) [Google Scholar]
- Caputo, M.; Mainardi, F. A new dissipation model based on memory mechanism. Pure Appl. Geophys. (PAGEOPH) 1971, 91, 134–147, [Reprinted in Fract. Calc. Appl. Anal. 2007, 10, 309–324]. [Google Scholar] [CrossRef]
- Caputo, M.; Mainardi, F. Linear Models of Dissipation in Anelastic Solids. Riv. Nuovo C. 1971, 1, 161–198. [Google Scholar] [CrossRef]
- Butzer, P.L.; Westphal, U. Introduction to Fractional Calculus. In Fractional Calculus, Applications in Physics; Hilfer, H., Ed.; World Scientific: Singapore, 2000; pp. 1–85. [Google Scholar]
- Feller, W. On a Generalization of Marcel Riesz’ Potentials and the Semi-Groups generated by Them. Meddelanden Lunds Universitets Matematiska Seminarium; Comm. Sém. Mathém. Université de Lund, Tome suppl. dédié à M: Riesz, Lund, 1952; pp. 73–81. [Google Scholar]
- Feller, W. An Introduction to Probability Theory and its Applications; Wiley: New York, NY, USA, 1971; Volume II. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Random walk models for space-fractional diffusion processes. Fract. Calc. Appl. Anal. 1998, 1, 167–191. [Google Scholar]
- Gawronski, W. On the bell-shape of stable distributions. Ann. Probab. 1984, 12, 230–242. [Google Scholar] [CrossRef]
- Simon, T. Positive Stable Densities and the Bell-Shape. Proc. Am. Math. Soc. 2015, 143, 885–895. [Google Scholar] [CrossRef][Green Version]
- Kwaśnicki, M. A new class of bell-shaped functions. Trans. Am. Math. Soc. 2020, 373, 2255–2280. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mainardi, F.; Consiglio, A. The Wright Functions of the Second Kind in Mathematical Physics. Mathematics 2020, 8, 884. https://doi.org/10.3390/math8060884
Mainardi F, Consiglio A. The Wright Functions of the Second Kind in Mathematical Physics. Mathematics. 2020; 8(6):884. https://doi.org/10.3390/math8060884
Chicago/Turabian StyleMainardi, Francesco, and Armando Consiglio. 2020. "The Wright Functions of the Second Kind in Mathematical Physics" Mathematics 8, no. 6: 884. https://doi.org/10.3390/math8060884
APA StyleMainardi, F., & Consiglio, A. (2020). The Wright Functions of the Second Kind in Mathematical Physics. Mathematics, 8(6), 884. https://doi.org/10.3390/math8060884





