1. Introduction
Retaining walls are structures widely used in engineering for supporting soil laterally. The design of these walls is a problem of interaction between the soil and the structure to retain a material safely and economically. When the height of a cantilever wall becomes important, the volume of concrete required begins to be considerable. From a height of 8–10 m, buttressed walls economize its design. The design of these structures is mainly carried out following rules very much linked to the experience of structural engineers [
1]. If the initial design dimensions or material qualities are inadequate, the structure is redefined. With this procedure of trial and error, the different designs obtained do not go beyond a few tests. This process leads to a safe, but not necessarily economic, design [
2]. Structural optimization methods have clear advantages over experience-based design.
Presently, the optimum design of reinforced concrete (RC) structures constitutes a relevant line of research. In practical structural optimization problems, the variables used must be discrete, so they are combinatorial optimization problems. However, combinatorial problems are found in a large number of real problems such as allocation resources [
3,
4], logistics [
5], transport [
6], routing problems [
7,
8], scheduling problems [
6,
9], and engineering design projects [
10,
11], among others. These problems present a space of solutions that grows exponentially with the variables used, so the metaheuristics, which were inspired by natural phenomena for continuous spaces, are a good approach to obtain optimum solutions to engineering problems. However, two important characteristics of metaheuristics, intensification and diversification, must be preserved to design discrete versions of these algorithms.
While structural optimization began by minimizing the weight or cost of structures [
12,
13], other objective functions related to the social, Reference [
14] and environmental sustainability of structures [
15] throughout their entire life cycle have subsequently been incorporated. Reducing the carbon footprint of RC structures is currently investigated as an optimization target. In particular, a hybrid multistart optimization strategic method based on a variable neighborhood search threshold acceptance strategy [
16] was used to reduce the cost and carbon-emissions in cantilever retaining walls. A hybrid harmony search together with a threshold acceptance strategy [
17,
18], the black hole algorithm [
17] and a hybrid k-means cuckoo search algorithms [
10] were applied to minimize both the economic cost and the CO
emissions in counterfort retaining walls. A CO
and cost analysis in precast–prestressed concrete road bridges was developed in [
15]. In [
14], the importance of the criteria that define social sustainability was analyzed. These criteria considered the complete life of infrastructure. The social sustainability of infrastructure projects was tackled in [
14] using Bayesian methods. In recent works [
19,
20], different meta-heuristics algorithms were used for optimal design of RC retaining walls. The life cycle assessment of earth-retaining walls was analyzed in [
21,
22].
A strategy that reinforces the results obtained by the metaheuristics has been the hybridization with techniques that deeply modify their way of working. Hybridization is carried out in different ways, the most important of which are: (i) mathematics, integrating mathematical programming and metaheuristics [
23], (ii) hybrid heuristics, combining different metaheuristics [
24], (iii) symmetrical heuristics, where simulation and metaheuristics are combined [
25], and (iv) hybridization between metaheuristics and machine learning.
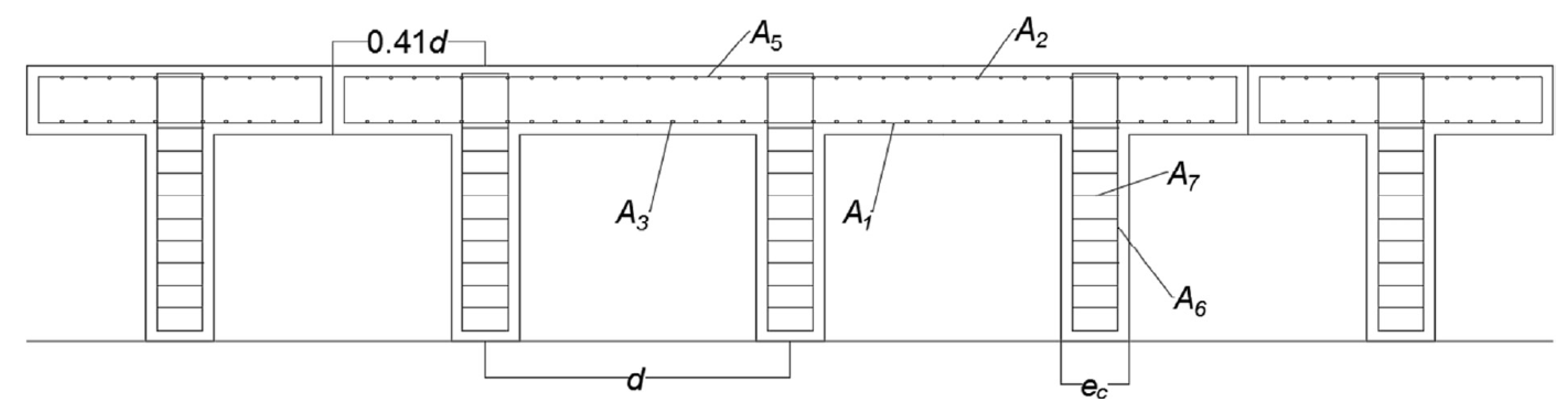
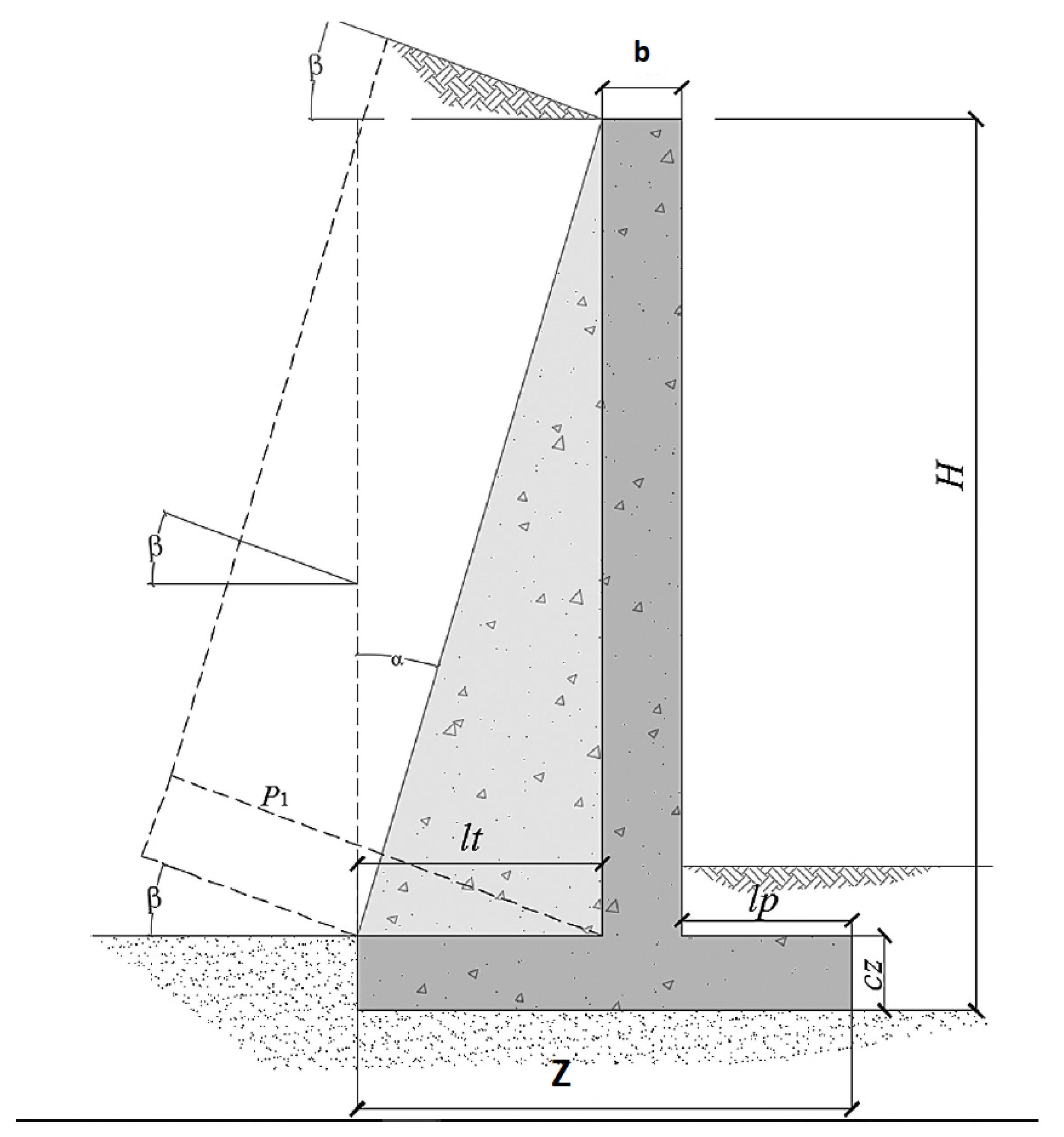
In this article, we used an emerging line of research that integrates the areas of machine learning and metaheuristic algorithms with the goal of tackle the design of reinforced earth retaining walls problem. This problem presents important challenges in computational complexity since it involves 32 design variables, therefore we have on the order of possible combinations. Therefore, it is interesting to understand how these types of hybrid techniques perform in this problem, in addition to comparing these ones with the state-of-the-art solutions that addressed the design of this type of walls.
The proposed hybrid algorithm uses a machine learning algorithm in a discrete operator that allows continuous metaheuristics to tackle combinatorial optimization problems. In this way, a combinatorial optimization problem, such as the buttressed wall design, can be addressed. The contributions of this work are as follows:
A hybrid Particle Swarm Optimization (PSO) based on a db-scan clustering technique is proposed. The db-scan is very effective in binary combinatorial problems [
6,
10]. PSO is often used to solve continuous optimization problems and its tuning is very simple.
The contribution of the db-scan in the discretization process was studied through a random operator. In addition, the discretization performed by db-scan was compared with methods using k-means [
5,
26].
The proposed algorithm is applied to obtain low-carbon, low-cost counterfort wall designs. This hybrid algorithm is compared with an efficient algorithm adapted from the harmony search (HS) proposed in [
18].
The rest of this paper is structured as follows: in
Section 2 we develop a state-of-the-art of hybridizing metaheuristics with machine learning; in
Section 3 we define the optimization problem, the variables involved, and the restrictions; then in
Section 4 we detail the discrete db-scan algorithm; we move on with the experiments and results obtained in
Section 5; and conclude with
Section 6 in which we summarize the conclusions and new lines of research.
2. Hybridizing Metaheuristics with Machine Learning
Metaheuristics is a broad collection of incomplete optimization techniques inspired by some real-world phenomenon in nature or in the behavior of living beings [
27,
28]. The objective is to solve problems of high computational complexity in a reasonable execution time so that its optimization mechanism is not significantly affected when the problem to be solved is altered. Then again, the set of techniques capable of learning from a database are the so-called machine learning algorithms [
29]. Depending on the learning mode, these techniques are divided into learning by reinforcement, supervised learning, and unsupervised learning. It is common for these algorithms to be used in a wide range of problems such as regression, dimensionality reduction, transformation, classification, time series or anomaly detection and computer vision problems.
The integration of the machine learning techniques with the metaheuristic algorithms can be done basically with two approaches [
30]. Either machine learning techniques are used to increase the quality of the solutions and the convergence rates obtained by metaheuristics, or metaheuristic are used to enhance the performance of machine learning techniques [
30]. However, metaheuristics often improves the efficiency of an optimization problem concerning machine learning. Based on the work of [
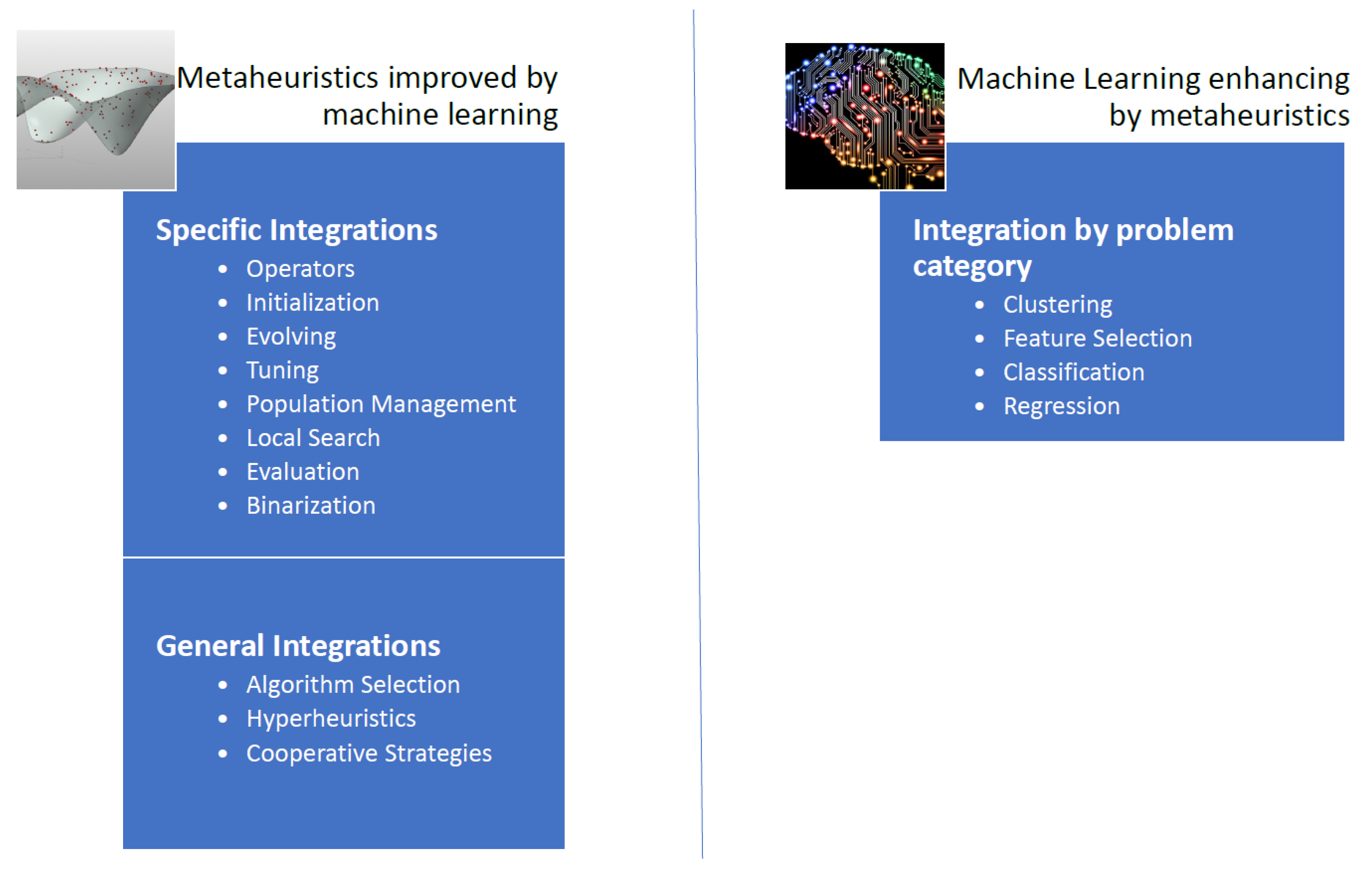
30], we propose an extension of the scheme of techniques in which metaheuristics and machine learning are combined (
Figure 1).
Machine learning can be used as a metamodel to determine from a set of metaheuristics the best one for each instance. In addition, specific machine learning operators can also be embedded into a metaheuristic, resulting in three different groups of techniques: hyper-heuristics, algorithm selection, and cooperative strategies [
30].
If we automate the design and tuning of metaheuristics to solve a large number of problems, we obtain the so-called hyper-heuristics. The aim of the cooperation strategies is to obtain methods that are more robust by combining the algorithms in a parallel or sequential way. The cooperation mechanism can share the whole solution, or only a part of it. In [
31], a multi-objective optimization of an aerogel glazing system through a surrogate model driven by the cross-entropy function was developed with the implementation of the supervised machine-learning method. In [
32] the multilevel thresholding image segmentation-based hyperheuristic method was addressed. Finally, in [
33] an agent-based distributed framework was proposed to solve the problem of permutation flow stores, and in which each agent is implementing a different metaheuristic.
On the other hand, there are operators that allow enhancing the performance of a metaheuristic integrating machine learning operators. Initialization, population management, solution disruption, binaryization, local search operators and parameter setting and are examples of such operators [
30]. Binary operators using unsupervised learning techniques can be integrated into metaheuristics that operate in continuous spaces to perform the binarization process [
6]. In [
34], a percentile transition-ranking algorithm was proposed as a mechanism to binarize continuous metaheuristics. In [
9], the application of Big Data techniques was applied to improve a cuckoo search binary algorithm. The tuning of the parameters of metaheuristics is another line of research of interest. In [
35], a tuning method was applied on different sized problem sets for the real-world integration and test order problem. In [
36] a semi-automatic approach designs the fuzzy logic rule base to obtain instance-specific parameter values using decision trees. The use of machine learning techniques improves the initiation of solutions, without the need to start it randomly. A cluster-based population initialization framework was proposed in [
37] and applied to differential evolution algorithms. In [
38] a case-based reasoning technique was applied to initiate a genetic algorithm in a weighted circle design problem. To solve an economic dispatch problem, Hopfield neural networks were used to start solutions of a genetic algorithm [
39].
Metaheuristics improve the machine learning algorithms in problems such as feature selection, grouping, classification, feature extraction, among others. Image analysis to identify breast cancer can be enhanced by a genetic algorithm [
40] that improves the performance of the Support Vector Machine (SVM). The medical diagnoses and prognoses were tackled in [
41] combining swarm intelligence metaheuristics with the probabilistic search models of estimation of distribution algorithms. In [
42], the authors used swarm intelligence metaheuristics for the convolution neural network hyper-parameters tuning. In [
32], a multiverse optimizer algorithm was used for text documents clustering. An improved normalized mutual information variable selection algorithm for soft sensors in [
43] was used to perform the variable selection and validate error information of artificial neural networks. A dropout regularization method for convolutional neural networks was tackled in [
44] through the use of metaheuristic algorithms. In [
45], a firefly algorithm was combined with the least-squares support vector machine technique to address geotechnical engineering problems. Metaheuristics contributed to the problems of regression, as is the case with the prediction of the strength of high strength concretes in [
46]. Another example is the integration of artificial neural networks and metaheuristics for improved stock price prediction [
47]. In [
48], proposes a sliding-window metaheuristic optimization for predicting the share price of construction companies in Taiwan. In [
49], the least squares support vector machine hybridizing a fruit fly algorithms is applied to simulate the nonlinear system of a MEL time series. Metaheuristics also apply to unsupervised learning techniques, such as clustering techniques. For example, in [
50] a metaheuristic optimization was used for a clustering system for dynamic data streams. Metaheuristics have also been integrated into clustering techniques in the search for the centroids that best group the data under a certain metric. A bee colony metaheuristic was used for energy efficient clustering in wireless sensor networks [
51]. In [
52], a clustering search metaheuristic was applied for the capacitated helicopter routing problem. In [
53], a hybrid-encoding scheme was used to find the optimal number of hidden neurons and connection weights in neutral networks. Four metaheuristic-driven techniques were used in [
44] to determine the dropout probability in convolutional neural networks. In [
54] the bat algorithm and cuckoo search were used to adjust the weights of neural networks. An algorithm was proposed using simulated annealing, differential evolution, and harmony search to optimize convolutional neural networks was proposed in [
55]. In [
56] long-term short memory trained with metaheuristics were applied in healthcare analysis.
In this paper, the study proposes a hybrid algorithm in which the unsupervised db-scan learning technique to obtain binary versions of the PSO optimization algorithm. This hybrid algorithm was used to obtain a sustainable design buttressed walls. Recently, the db-scan binarization algorithm obtained versions of continuous metaheuristics that have been used to solve the set covering problem [
6] and the multidimensional knapsack problem [
10] which are NP-hard problems.
4. The db-Scan Discrete Algorithm
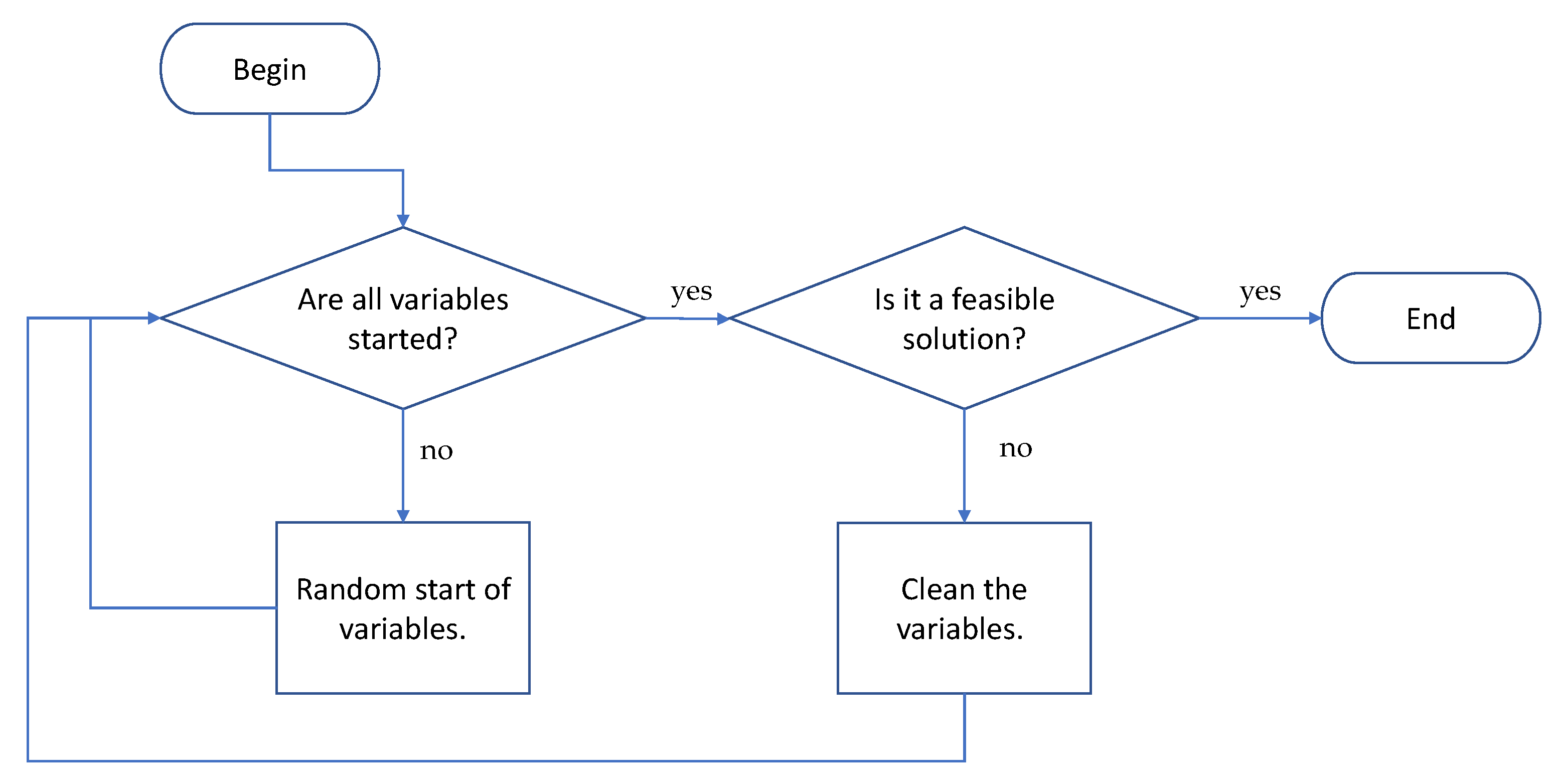
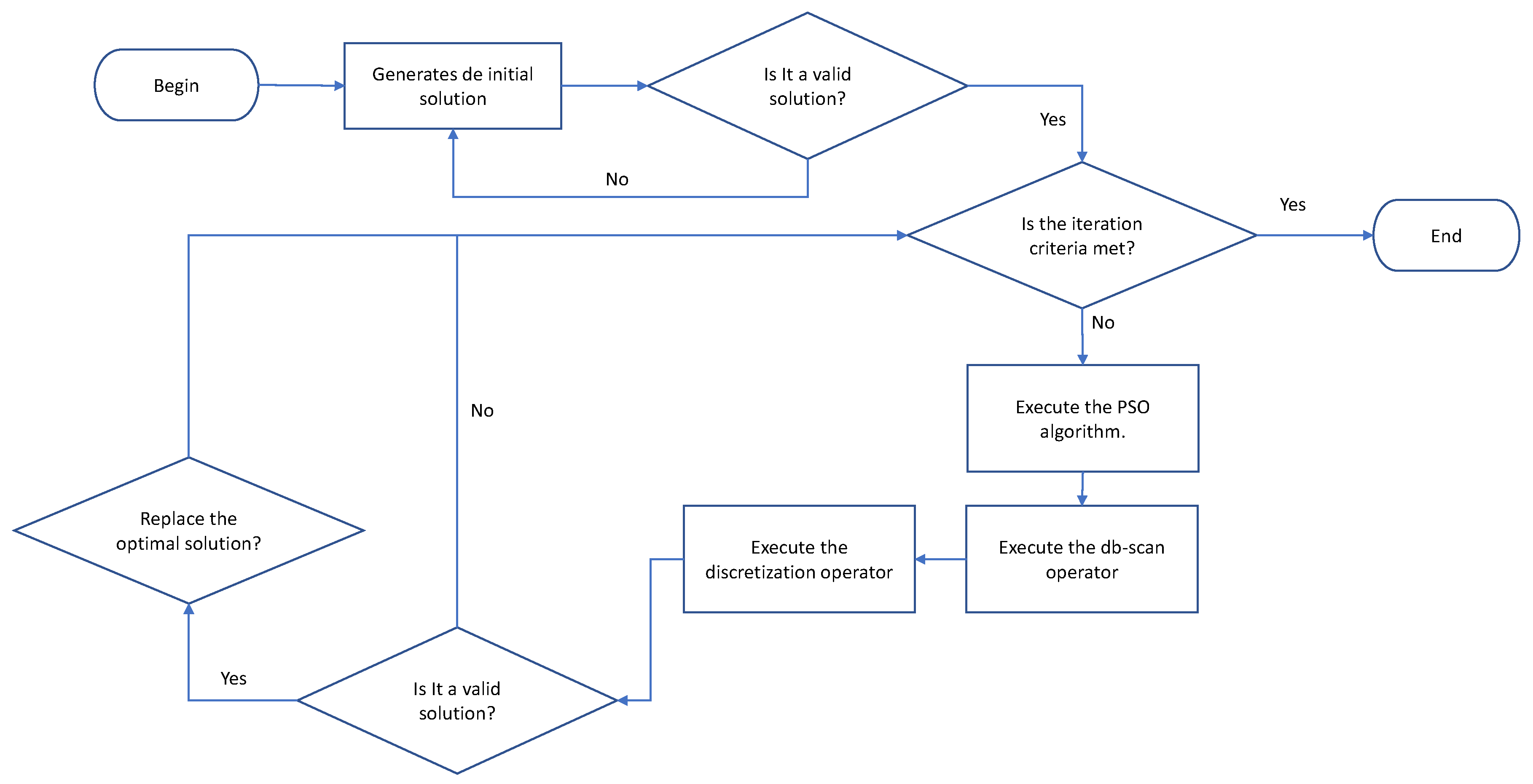
As a first step, the algorithm generates a set of valid solutions. These solutions are randomly generated. In this procedure, first, it is validated if the solution variables are started. In the case that they are not all started, the variables are started randomly. Once all the variables are generated, the next step is to verify if the solution obtained is valid. In the event that it is not valid, all variables are removed and regenerated. The detail of the initiation procedure is shown in
Figure 5. Subsequently, PSO is used to produce a new solution in the continuous space. The PSO algorithm will be described in
Section 4.1. Subsequently, the db-scan operator is applied to the continuous solution in order to transform continuous movements into groups associates to transition probabilities. The db-scan operator will be detailed in
Section 4.2. After the db-scan operator generates the groups, the discretization operator applies the corresponding transition probability to each group, generating a new discrete solution. The discretization operator is detailed in
Section 4.3. Finally, the new solution is validated and, in case it meets the restrictions, it is compared with the best solution obtained. If the new value is higher, it replaces the current one. The detailed flow chart of the hybrid algorithm is shown in
Figure 6.
4.1. Particle Swarm Optimization
For the proper functioning of the PSO algorithm, the concepts of population that are usually called a swarm, and each of these solutions is called a particle. The essence of the algorithm is that each particle is guided by a combination of the best value particle obtained so far in the search space (maximum global) together with the best result obtained by the particle (local maximum). The optimization process is iterative until some termination condition is met.
Formally let
corresponds to the fitness function to be optimized. This function considers a candidate solution that is represented by a vector in
and generates a real value as output. This obtained value, represents the value of the objective function for the given candidate solution. The goal is to find a solution for which
for all b in the search space, which would mean that a is the global minimum. The algorithm pseudo-code is shown in Procedure 1.
| Algorithm 1 Particle swarm optimization algorithm |
- 1:
Objective function f(s) - 2:
Generate initial solutions of n particles. - 3:
Get the particle’s best known position to its initial position: . - 4:
ifthen - 5:
Update the swarm’s best known position: - 6:
end if - 7:
Initialize the particle’s velocity: - 8:
while stop criterion are meet do - 9:
for each particle and dimension do - 10:
Pick random numbers: - 11:
Update the particle’s velocity: - 12:
Update the particle’s position: - 13:
end for - 14:
if < then - 15:
Update the particle’s best known position: . - 16:
if < then - 17:
Update the swarm’s best known position: . - 18:
end if - 19:
end if - 20:
end while
|
4.2. db-Scan Operator
The solutions resulting from the execution of the PSO algorithm are grouped by the db-scan operator. We should note that the db-scan operator can be applied to any swarm intelligence continuous metaheuristics. The spatial clustering technique based on noise density of applications (db-scan), requires for the clustering, a set of points S within a vector space, and a metric, usually, the metric is the Euclidean. Db-scan groups the points of S that meet a minimum density criterion. The rest of the points are considered outliers. As input parameters db-scan requires a radius and the minimum number of neighbors . The main steps of the algorithm are shown below:
Find the points in the neighborhood of every point and identify the core points with more than neighbors.
Find the connected components of core points on the neighbor graph, ignoring all non-core points.
Assign each non-core point to a nearby cluster if the cluster is an neighbor; otherwise, assign it to noise.
In the db-scan (dbscanOp) operator, the db-scan grouping technique is used to make groups of points to which we will assign a probability of transition. This probability of transition will subsequently allow the discretization operator to discretize continuous solutions. The grouping proposal uses the movements obtained by PSO in each dimension for all the particles. Suppose
is a solution in iteration t, then
represents the magnitude of the offset
in the i-th position, considering the iterations
t and
. After all the displacements were obtained, the grouping is carried out. To obtain the groups, the displacement module will be used, which is denoted by
. This grouping is done using the db-scan technique. Finally, a generic function
is used, which is shown in Equation (
2) with the objective of assigning a probability of transition to each group and therefore to each displacement.
Then using the function
, a probability is assigned to each group obtained from the clustering process. In this article, we use the linear function given in Equation (
2), where Clust (
) indicates the location of the group to which
belongs. The coefficient
represents the initial transition coefficient and
models the transition separation for the different groups. Both parameters must be estimated. The pseudo-code of the discretization procedure is shown in Algorithm 2.
where
x represents the value of
. Also, because
, each element of
, is assigned the same value
. That is,
. On the other hand,
are constants that will be determined in the tuning of parameters, where
corresponds to the initial transition coefficient and
represents the transition probability coefficient.
| Algorithm 2 db-scan operator |
- 1:
Function dbscanOp(,) - 2:
Input, - 3:
Output lTransitionProbability - 4:
getDelta(, ) - 5:
getClusters() - 6:
lTransitionProbability ← getTranProb( , )–Equation ( 2) - 7:
return (lTransitionProbability)
|
4.3. Discretization Operator
The discretization operator receives the list lTransitionProbability
. This list contains the values of the transition probabilities which were the result delivered by the db-scan operator. Then given a solution
, we select each of its components
and we proceed to determine through the transition probability if this component should be modified. In the case of large transition probabilities, there is a greater possibility of modification. Then a random number is obtained at [0, 1] and this number is compared with the value of the transition probability assigned to the component. In cases where the modification condition is satisfied, it can increase the value by 1 or decrease it by 1. Finally, the selected value is compared with the best value obtained by the algorithm and remains with the minimum of both. The pseudocode of the discrete procedure is shown in Algorithm 3.
| Algorithm 3 Discretization operator. |
- 1:
Function DiscOperator(lTransitionProbability, ) - 2:
Input lTransitionProbability - 3:
Output–where is discrete. - 4:
movement = 0 - 5:
fordo - 6:
if then - 7:
movement = 1 - 8:
else - 9:
movement = −1 - 10:
end if - 11:
= max(1,min(,+movement)) - 12:
end for
|
6. Conclusions
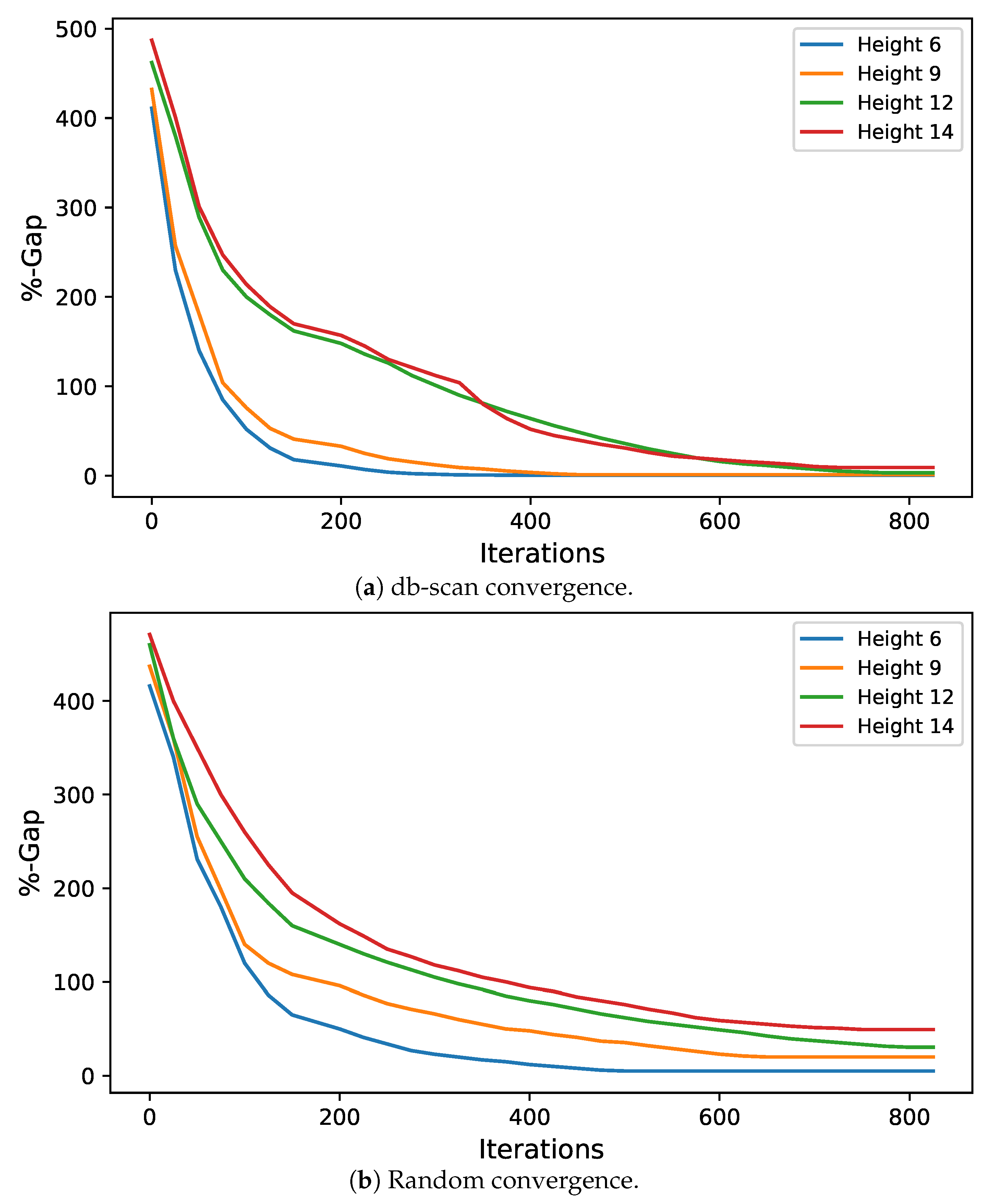
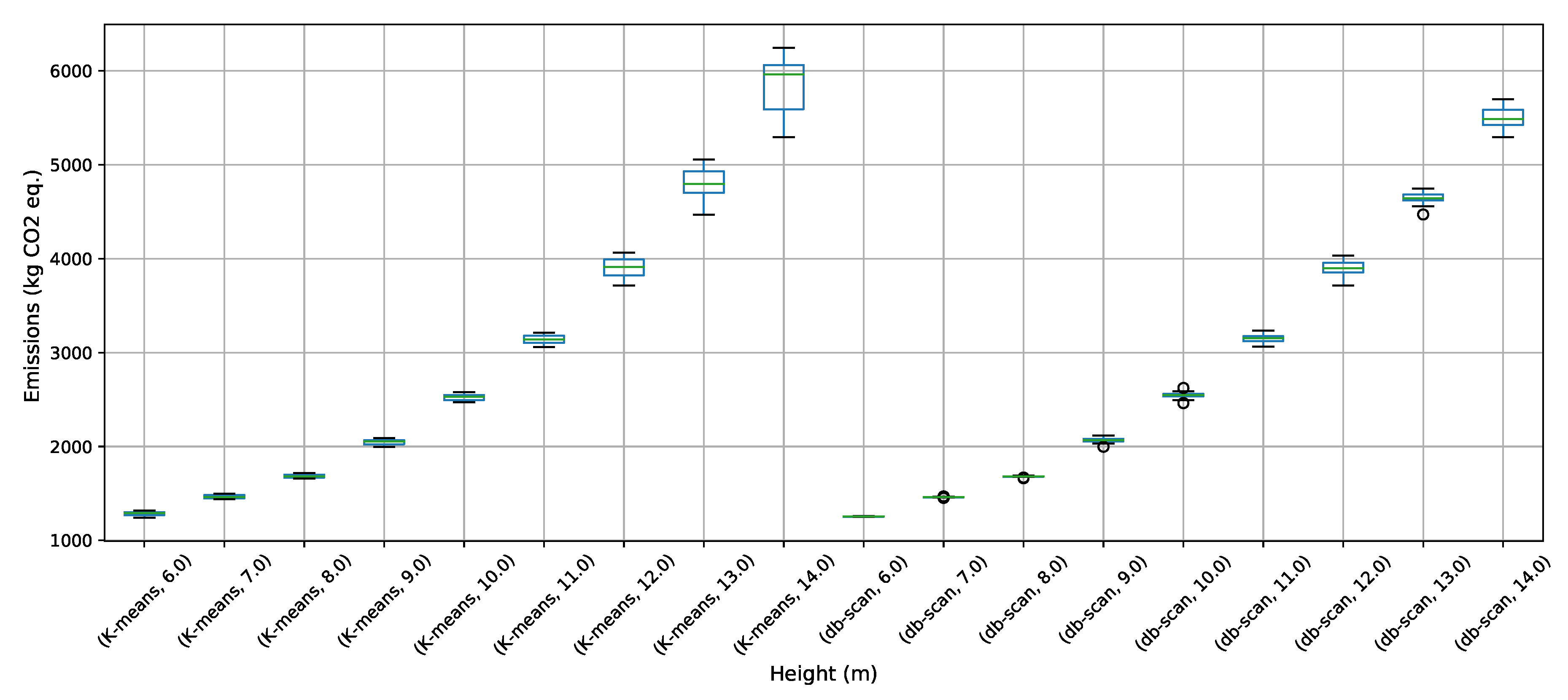
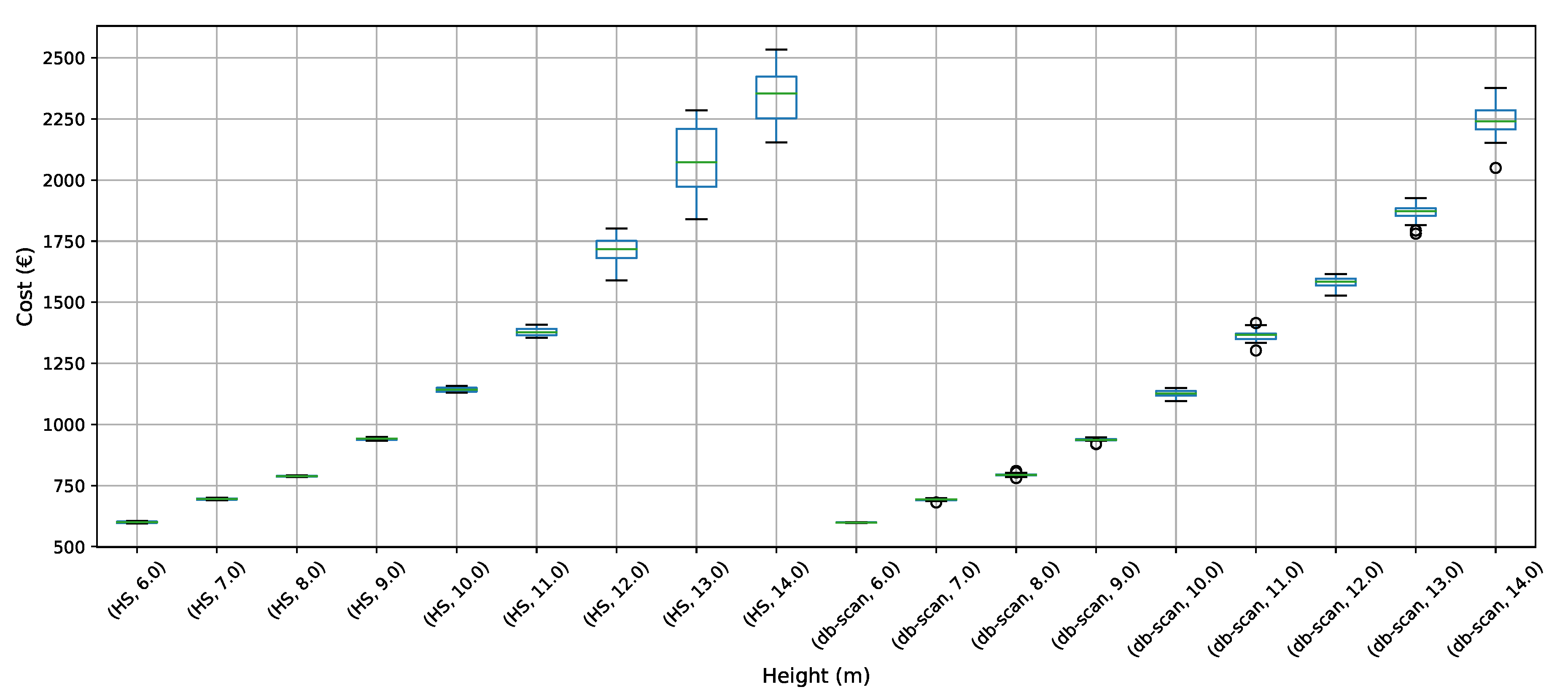
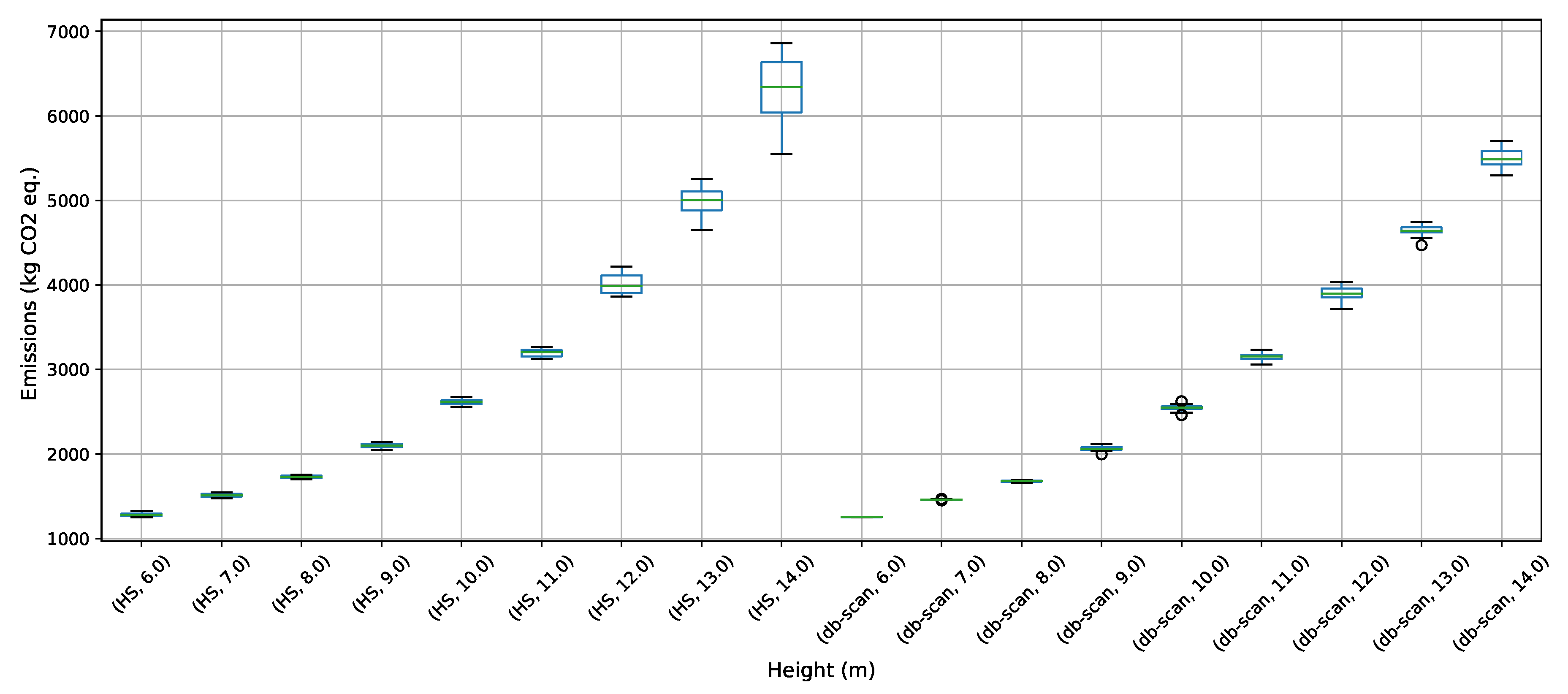
To address the buttressed walls problem, a hybrid algorithm based on the db-scan clustering technique and the PSO optimization algorithm was proposed in this article. This hybridization was necessary because PSO works naturally in continuous spaces and the problem studied is combinatorial. A Db-scan was used as a discretization mechanism. The optimization functions considered were cost and emission of CO. To measure the robustness of our proposal, three experiments were designed. The first evaluates the performance of the hybrid algorithm with respect to a random operator. Later in the second experiment, the performance was compared with respect to the k-means clustering technique. Finally, in the last experiment, we studied the performance of the hybrid algorithm when compared to an HS adaptation described in the literature. The first experiment concludes that the db-scan operator contributes to the quality of the solutions, obtaining better values than the random operator, in addition to reducing the dispersion of these. In comparison with k-means mixed results are obtained, in some cases, k-means is superior to db-scan and in other db-scan improves the solutions obtained by k-means. Regarding the dispersion in the different instances, we observed that from height 12 onwards db-scan obtained much smaller dispersions than k-means. Lastly, in comparison with HS, in general, db-scan surpass HS obtaining better results, especially in the instances where the height was over 12 m.
From the results obtained in this study, several lines of research emerge. The first line is related to population management. In the present work, the population was a static parameter. By analyzing the results generated by the algorithm as it iterates, it is possible to identify regions where search needs to be intensified or regions where further exploration is needed. This would allow for dynamic population management. Another interesting research line is related to the parameters used by the algorithm. According to what is detailed in
Section 5.1, a robust method was used to get the most suitable configuration. However, this configuration is a static one and is not necessarily the best configuration throughout all execution. Proposing a framework that allows adapting the parameters based on the results obtained by the algorithm as it is executed, would allow generating even more robust methods than the current one.