Orbit Growth of Periodic-Finite-Type Shifts via Artin–Mazur Zeta Function
Abstract
1. Introduction
- (i)
- prime orbit counting function
- (ii)
- Mertens’ orbit counting functionsandwhere is the closed orbit, h is the topological entropy of the system and . The functions are well-defined if the number of closed orbits for each period is finite.
2. Orbit Growth via Zeta Function
- (a)
- (Prime Orbit Theorem)
- (b)
- (Mertens’ Orbit Theorem)where γ is Euler–Mascheroni constant, andwhere C is a positive constant that can be specified as
- (a)
- Since is analytic and non-zero for , (3) implies that is also analytic and non-zero for . From (1) and (3), for ,whereEquivalently, for ,Observe that is analytic for and has a power series representation for . Recall that any analytic function has a unique power series representation (see [17,18]). Therefore, the series is also its power series representation for . Overall, (6) is also valid for .For any , the series converges for . Therefore, the terms in the series are bounded, i.e., there exists a real such thatNow, definefor . Please note thatNow, we need to relate both and . First, observe that can be expressed in terms of closed orbits asIndeed, this is true by defining and checking thatFor a closed orbit , the number of times for it to appear in the sum is . So,Define the extension of over asfor . For any real , set such that . So,Now, we need to show that as (and equivalently, ). First, we will prove that is bounded for any real . Indeed, since is analytic for , this implies that converges. From (2),Furthermore, from (9), it is easy to see that is also bounded.Now, choose . Observe thatSince and are bounded, andit is obtained thatPlease note that can be chosen arbitrarily close to 1, so it can be deduced further thatHence,or equivalently,
- (b)
- We begin with proving the result for . From (1) and (3), it can be shown that for ,where is given in (5). Recall that if a power series converges in an open disc, then it is analytic in the same disc (see [17,18]). Please note that the series in (6) is analytic for , and so is the series by comparison.Since , for any ,Recall that for harmonic sum,where is the Euler–Mascheroni constant (see [19]). Therefore, (14) can be written asNow, definefor . Observe that can be expressed in terms of closed orbits asIndeed, this is true by defining and checking thatFurthermore, for a closed orbit , it contributes to the sum for . So,Consider the sumSince , it can be written asWe will prove that the sum in the last line in (19) converges as by using Riemann–Stieltjes integral with respect to (see [20]). We will also use the fact thatfor some positive constants A and B. This is derived from result in part (a). Now,The expression in the last line in (21) converges as , and so is the sum. By using (18), (19) and (21), it is obtained thatThe desired result for is obtained by applying exponent and arranging terms in (23).Now, we will prove the result for . Using (17) and similar calculation as above, it is obtained thatandThe sum in the last line in (25) converges as by using Riemann–Stieltjes integral with respect to . Indeed, it can be checked thatwhere A and B are constants in (20), and the integral converges as by integral test. The calculation is very similar to the previous one, so it is omitted here.Overall, from (24) and (25), the sumconverges to a positive constant C. By using (23), it is obtained thatThe desired result for is obtained by arranging terms in (26). □
- (i)
- the radius of convergence forabout the origin is, and
- (ii)
- there is a pole of order m at, whereis the pth root of unity and.
3. Periodic-Finite-Type Shifts
3.1. Construction
- (i)
- For the sake of simplicity, the restricted mapwill be denoted simply as σ from now on.
- (ii)
- For the sake of this paper, we call the integer r in the above definition as the shifting value of. Please note that r is not necessarily unique for each.
- (i)
- all words in have the same length ℓ, and
- (ii)
- .
3.2. Graph Representation
- (i)
- and , and
- (ii)
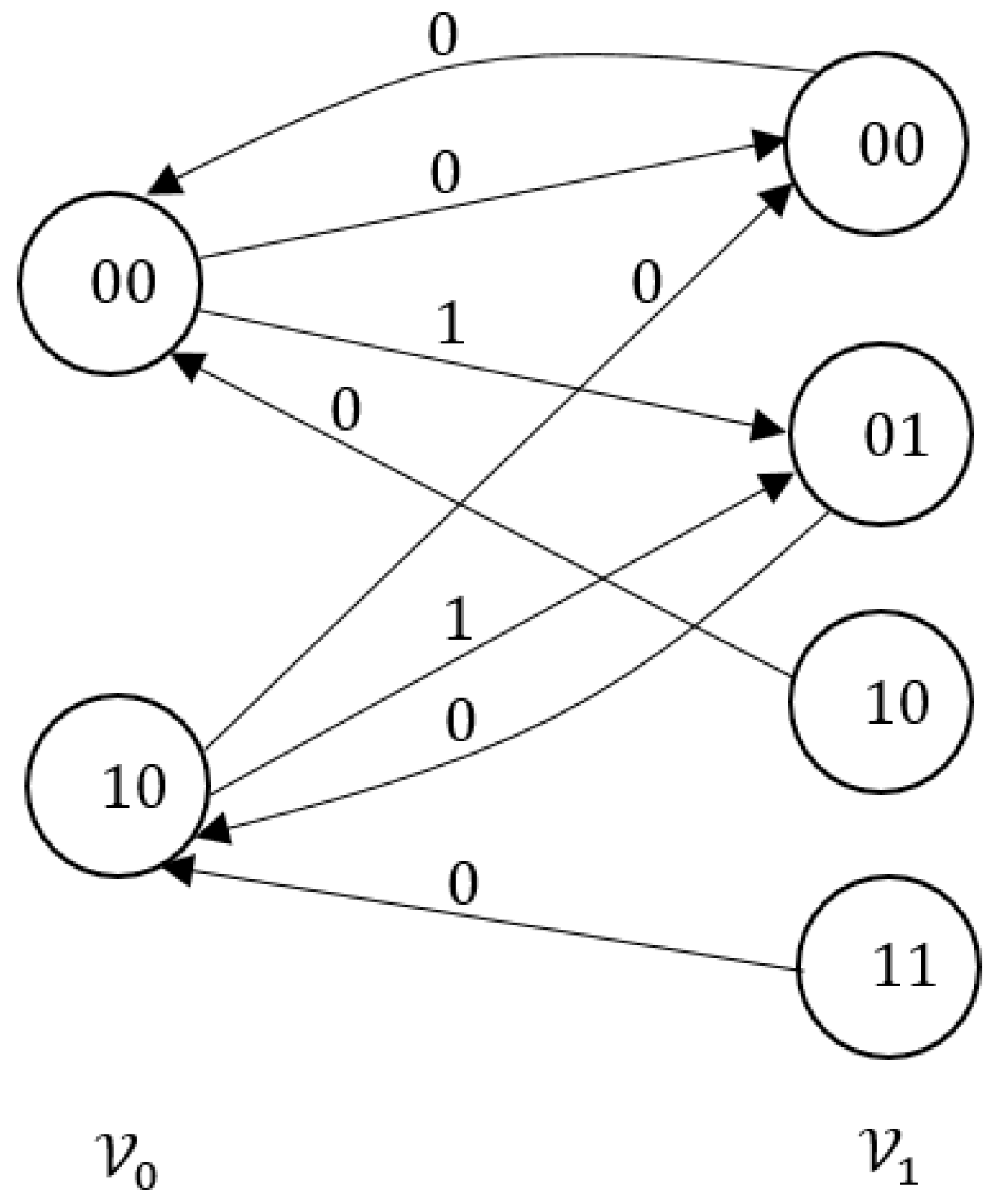
- for and where , there exists an edge from u to v with label if and only if . In this case, u and v are said to overlap progressively.
- (i)
- ifand, then the wordoccurs in the point;
- (ii)
- ifand, then the wordoccurs in the point;
- (iii)
- ifand, then the wordoccurs in the point;
- (iv)
- ifand, then the wordoccurs in the point.
3.3. Zeta Function
- (i)
- the sets of vertices are defined asfor all ;
- (ii)
- for and where , there exists an edge from u to v if and only if u and v overlap progressively.
- (i)
- the set of vertices is ;
- (ii)
- for , there exists an edge from u to v if and only if there is a path of length from u to v in .
4. Orbit Growth of a Periodic-Finite-Type Shift
- (i)
- the only eigenvalues of modulus are of the form where is th root of unity for all . The eigenvalues are simple;
- (ii)
- if a non-negative matrix satisfies , i.e., for every pair of indices i and j, then for any eigenvalue of . The equality holds if and only if .
- (i)
- the sets of vertices are defined asfor all ;
- (ii)
- for and where , there exists an edge from u to v if and only if u and v overlap progressively.
- (i)
- for , the expression gives rise to some simple poles at radius , and also other poles at for other non-zero eigenvalues of . Since by definition of Perron eigenvalue, the other poles are located beyond the radius ;
- (ii)
- for , the expression gives rise to zeros or poles at for every non-zero eigenvalue of . However, Lemma 1 implies that these are located beyond the radius ;
- (iii)
- for , observe thatwhere runs through the eigenvalues of . This gives rise to zeros at radius for every eigenvalue of . However, Lemma 2 implies that these zeros are located beyond the radius .
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hardy, G.H.; Wright, E.M. The series of primes (3). In An Introduction to Theory of Numbers, 6th ed.; Heath-Brown, D.R., Silverman, J.H., Eds.; Oxford University Press: Oxford, UK, 2008; pp. 451–500. [Google Scholar]
- Parry, W. An analogue of the prime number theorem for closed orbits of shifts of finite type and their suspensions. Isr. J. Math. 1983, 45, 41–52. [Google Scholar] [CrossRef]
- Parry, W.; Pollicott, M. Zeta functions and the periodic orbit structure of hyperbolic dynamics. Asterisque 1990, 187–188, 1–255. [Google Scholar]
- Sharp, R. An analogue of Mertens’ theorem for closed orbits of Axiom A flows. Bol. da Soc. Bras. Matemática 1991, 21, 205–229. [Google Scholar] [CrossRef]
- Waddington, S. The prime orbit theorem for quasihyperbolic toral automorphisms. Monatshefte für Math. 1991, 112, 235–248. [Google Scholar] [CrossRef]
- Noorani, M.S.M. Mertens theorem and closed orbits of ergodic toral automorphisms. Bull. Malays. Math. Sci. Soc. 1999, 22, 127–133. [Google Scholar]
- Artin, M.; Mazur, B. On periodic points. Ann. Math. 1965, 81, 82–99. [Google Scholar] [CrossRef]
- Alsharari, F.; Noorani, M.S.M.; Akhadkulov, H. Analogues of the prime number theorem and Mertens’ theorem for closed orbits of the Motzkin shift. Bull. Malays. Math. Sci. Soc. 2017, 40, 307–319. [Google Scholar] [CrossRef]
- Alsharari, F.; Noorani, M.S.M.; Akhadkulov, H. Estimates on the number of orbits of the Dyck shift. J. Inequal. Appl. 2015, 2015, 1–12. [Google Scholar] [CrossRef]
- Akhatkulov, S.; Noorani, M.S.M.; Akhadkulov, H. An analogue of the prime number, Mertens’ and Meissel’s theorems for closed orbits of the Dyck shift. AIP Conf. Proc. 2017, 1830, 1–9. [Google Scholar]
- Pakapongpun, A.; Ward, T. Functorial orbit counting. J. Integer Seq. 2009, 12, 1–20. [Google Scholar]
- Everest, G.; Miles, R.; Stevens, S.; Ward, T. Orbit-counting in non-hyperbolic dynamical systems. J. für die Reine und Angewandte Mathematik 2007, 608, 155–182. [Google Scholar] [CrossRef][Green Version]
- Everest, G.; Miles, R.; Stevens, S.; Ward, T. Dirichlet series for finite combinatorial rank dynamics. Trans. Am. Math. Soc. 2009, 362, 199–227. [Google Scholar] [CrossRef]
- Nordin, A.; Noorani, M.S.M.; Dzul-Kifli, S.C. Counting closed orbits in discrete dynamical systems. In Dynamical Systems, Bifurcation Analysis and Applications; Springer: Singapore, 2019; pp. 147–171. [Google Scholar]
- Béal, M.P.; Crochemore, M.; Moision, B.E.; Siegel, P.H. Periodic-finite-type shift spaces. IEEE Trans. Inf. Theory 2011, 57, 3677–3691. [Google Scholar] [CrossRef]
- Manada, A.; Kashyap, N. On the zeta function of a periodic-finite-type shift. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2013, E96.A, 1024–1031. [Google Scholar] [CrossRef]
- Conway, J.B. Elementary properties and examples of analytic functions. In Functions of One Complex Variable; Springer: New York, NY, USA, 1973; pp. 30–57. [Google Scholar]
- Sinha, R. Holomorphic and harmonic functions. In Real and Complex Analysis; Springer: Singapore, 2018; Volume 2, pp. 1–188. [Google Scholar]
- Alabdulmohsin, I.M. The sum of the approximation errors of harmonic numbers. In Summability Calculus; Springer: Cham, Switzerland, 2018; pp. 151–153. [Google Scholar]
- Lang, S. Riemann-Stieltjes integral and measure. In Real and Functional Analysis; Springer: New York, NY, USA, 1993; pp. 278–294. [Google Scholar]
- Lind, D.; Marcus, B. An Introduction to Symbolic Dynamics and Coding; Cambridge University Press: Cambridge, UK, 1995; pp. 1–135. [Google Scholar]
- Kitchens, B. Background and basics. In Symbolic Dynamics: One-Sided, Two-Sided and Countable State Markov Shifts; Springer: Berlin, Germany, 1998; pp. 1–32. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nordin, A.; Md Noorani, M.S. Orbit Growth of Periodic-Finite-Type Shifts via Artin–Mazur Zeta Function. Mathematics 2020, 8, 685. https://doi.org/10.3390/math8050685
Nordin A, Md Noorani MS. Orbit Growth of Periodic-Finite-Type Shifts via Artin–Mazur Zeta Function. Mathematics. 2020; 8(5):685. https://doi.org/10.3390/math8050685
Chicago/Turabian StyleNordin, Azmeer, and Mohd Salmi Md Noorani. 2020. "Orbit Growth of Periodic-Finite-Type Shifts via Artin–Mazur Zeta Function" Mathematics 8, no. 5: 685. https://doi.org/10.3390/math8050685
APA StyleNordin, A., & Md Noorani, M. S. (2020). Orbit Growth of Periodic-Finite-Type Shifts via Artin–Mazur Zeta Function. Mathematics, 8(5), 685. https://doi.org/10.3390/math8050685




