A Decentralized Framework for Parameter and State Estimation of Infiltration Processes
Abstract
1. Introduction
2. System Description and Problem Formulation
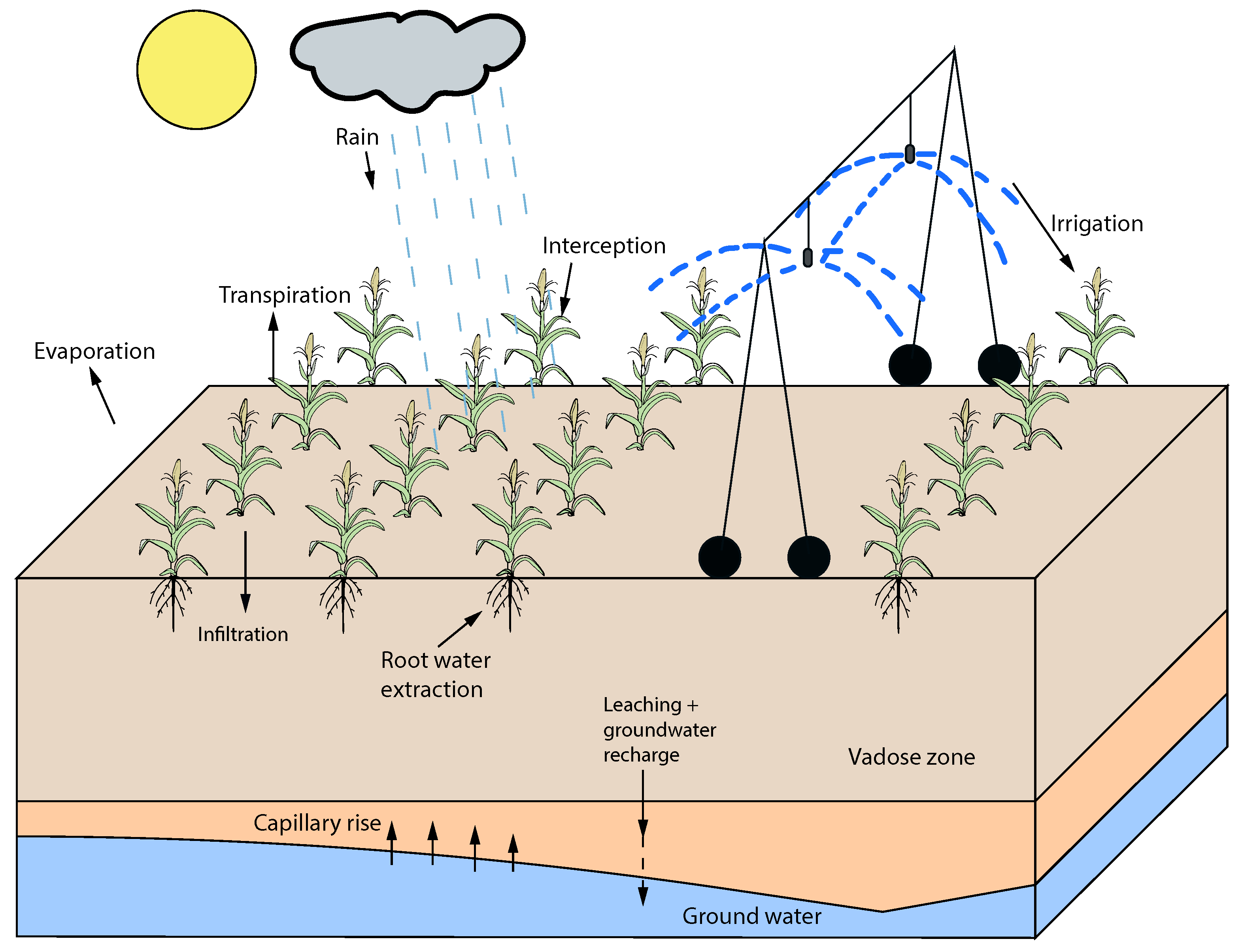
2.1. System Description and Modeling
2.2. Model Discretization
2.3. Augmented Model
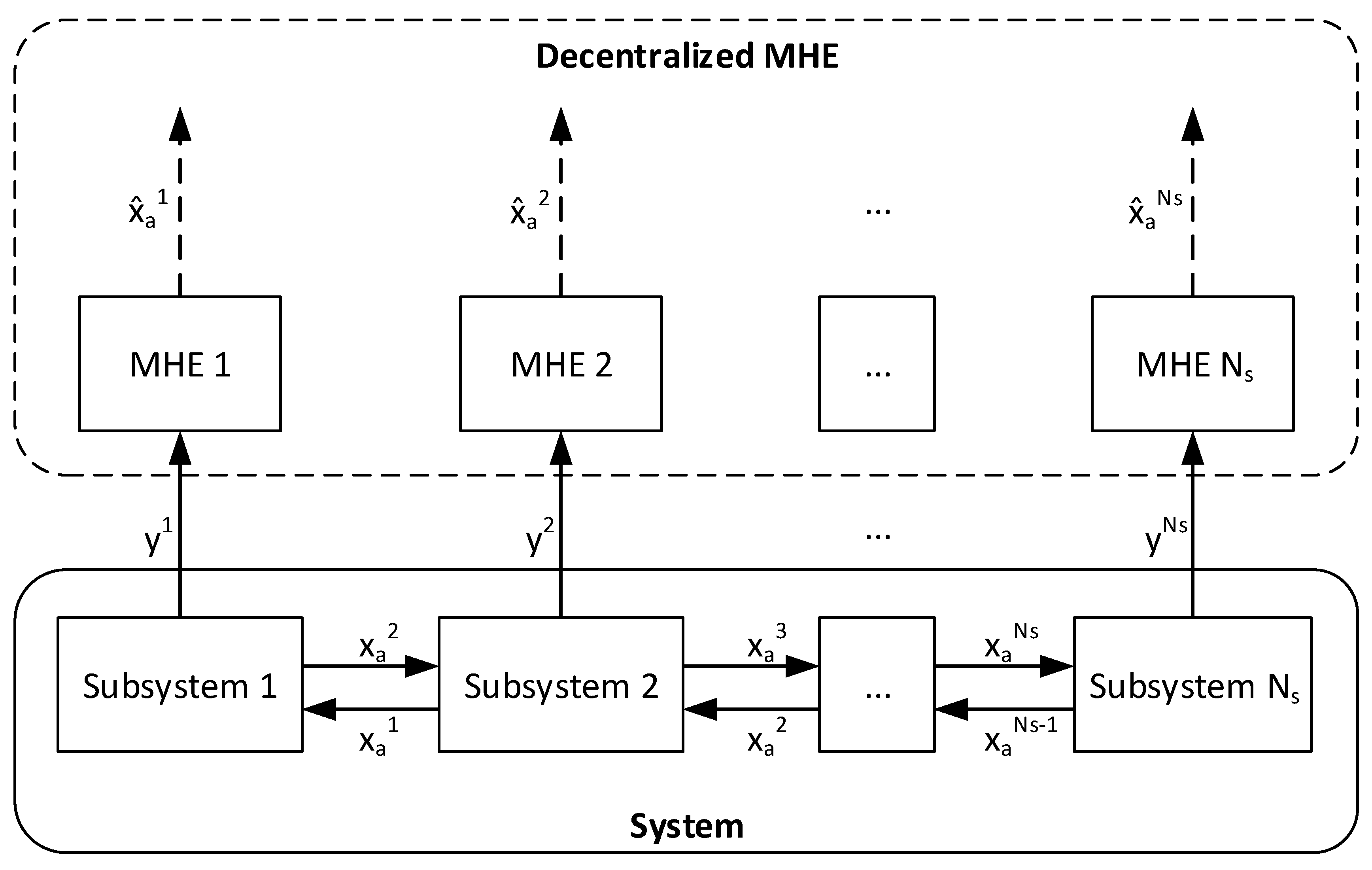
3. Proposed Estimation Method
3.1. Guidelines for Subsystem Decomposition
- it is expected that the numbers of the states in the configured subsystems can be made similar, such that the computational and organizational complexity of the local estimators are not significantly different;
- it is desirable if each subsystem only accounts for one soil type;
- it is expected that the initial values of the states involved in each subsystem are relatively similar;
- it is expected that the areas that are subject to different irrigation schedules are assigned to different subsystems;
- it is expected that each configured subsystem is assigned sufficient sensors such that the subsystem is observable;
- it is important that the dynamical interaction between each two subsystems is made minimal.
3.2. Significant Parameter Selection and Minimal Number of Sensors
3.3. Subsystem Approximation and Motivation of Decentralized Estimation
3.4. Decentralized Moving Horizon Estimation Design
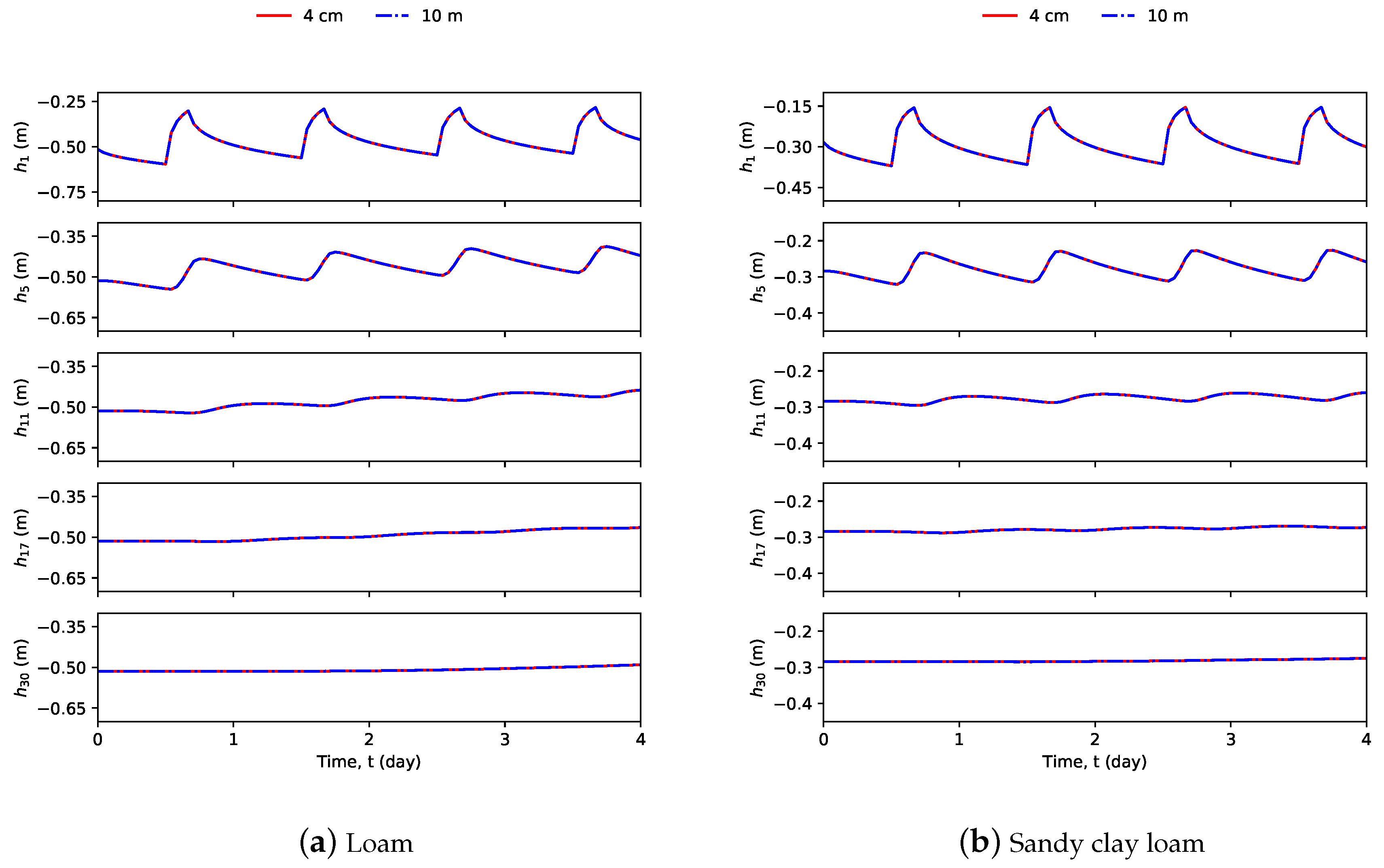
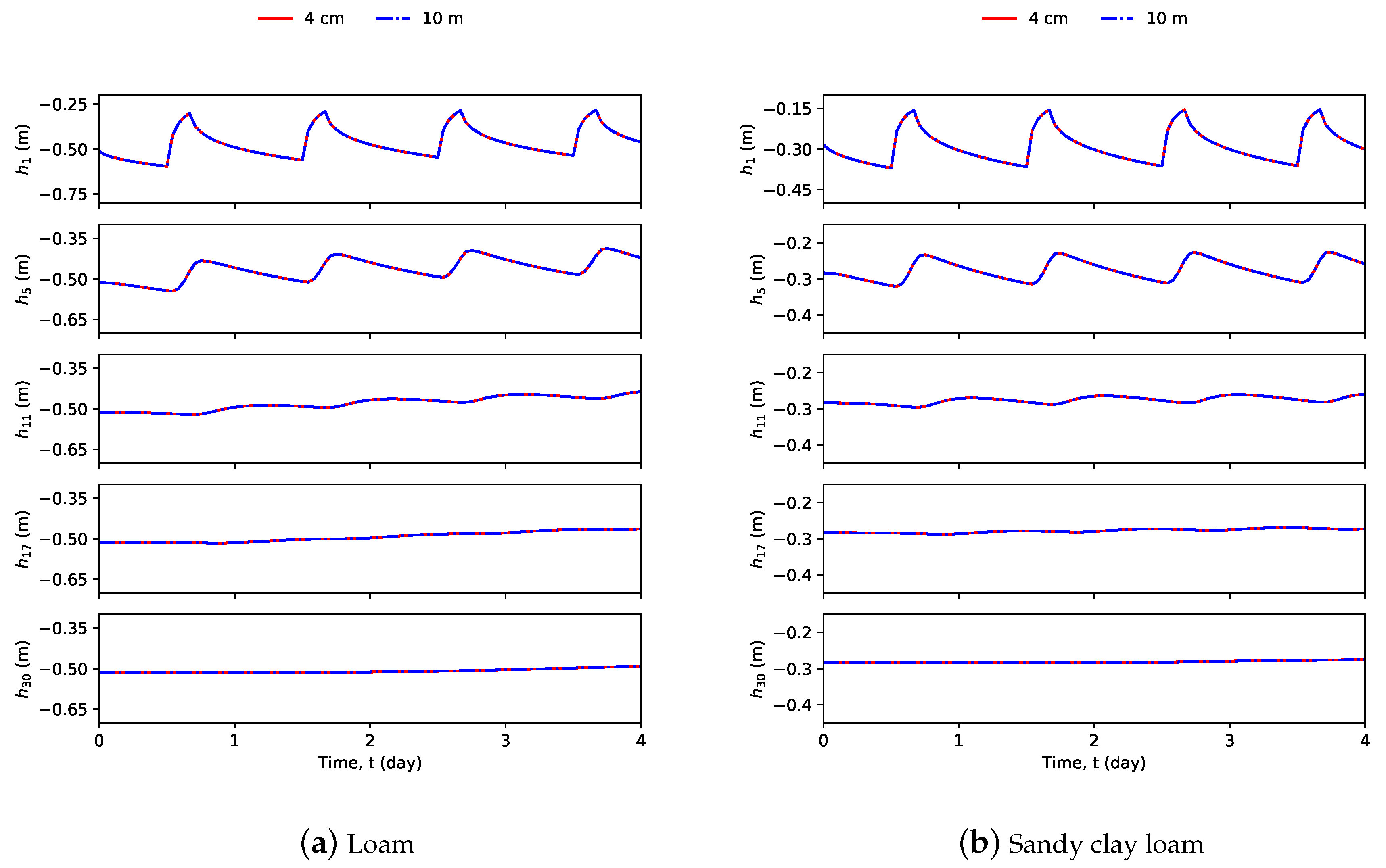
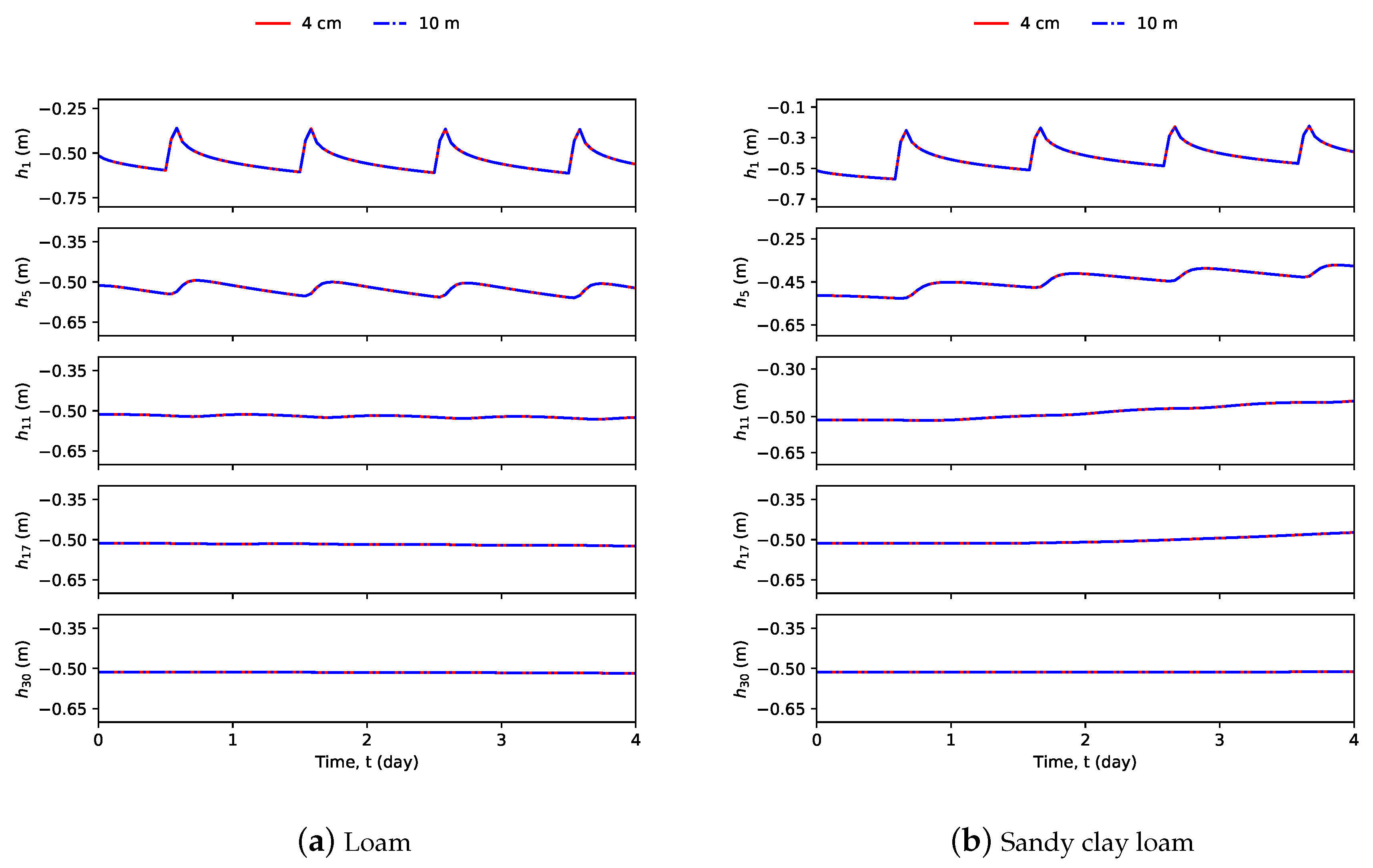
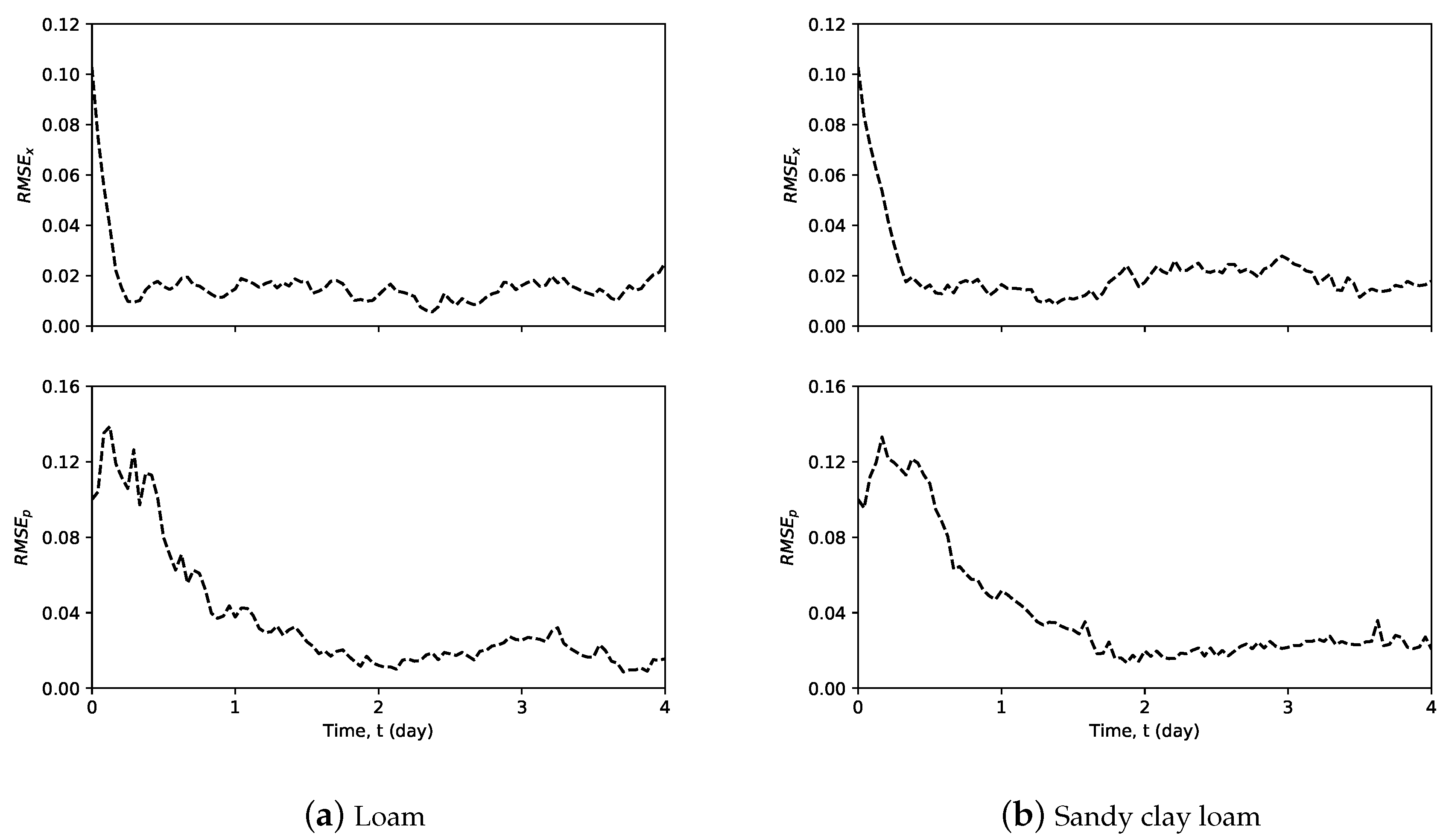
4. Simulation Results and Discussion
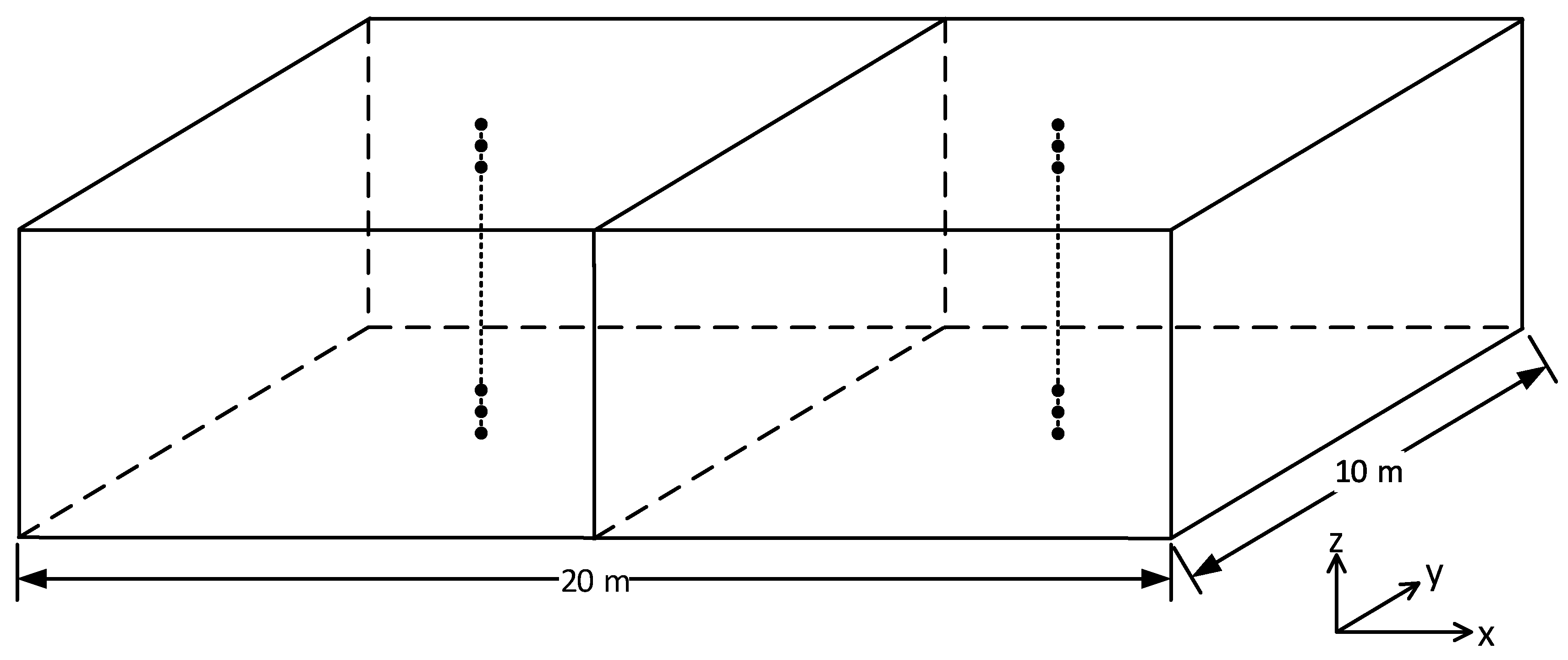
4.1. System Description
4.2. Observability Test on Original System
4.3. Subsystem Decomposition
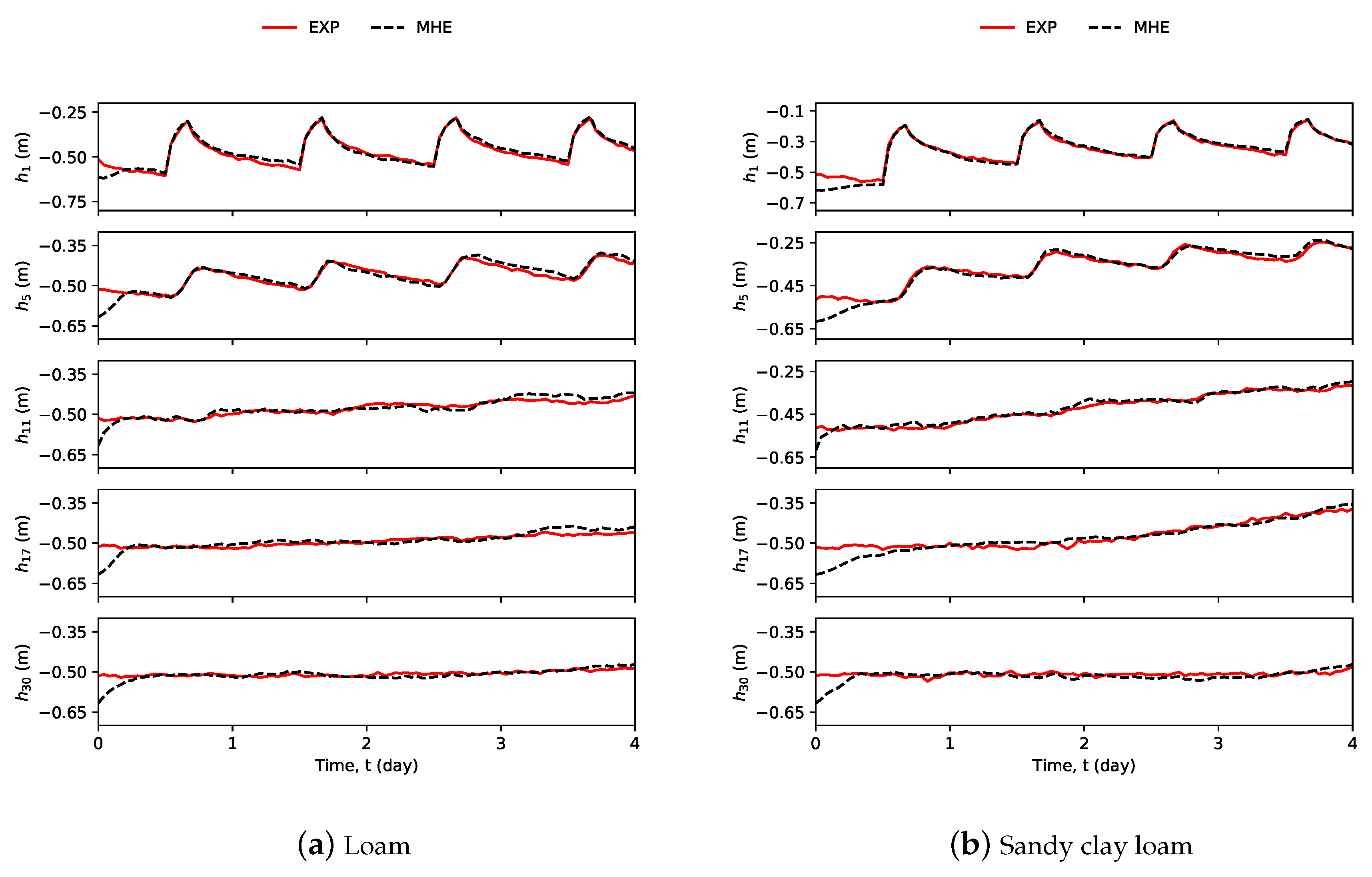
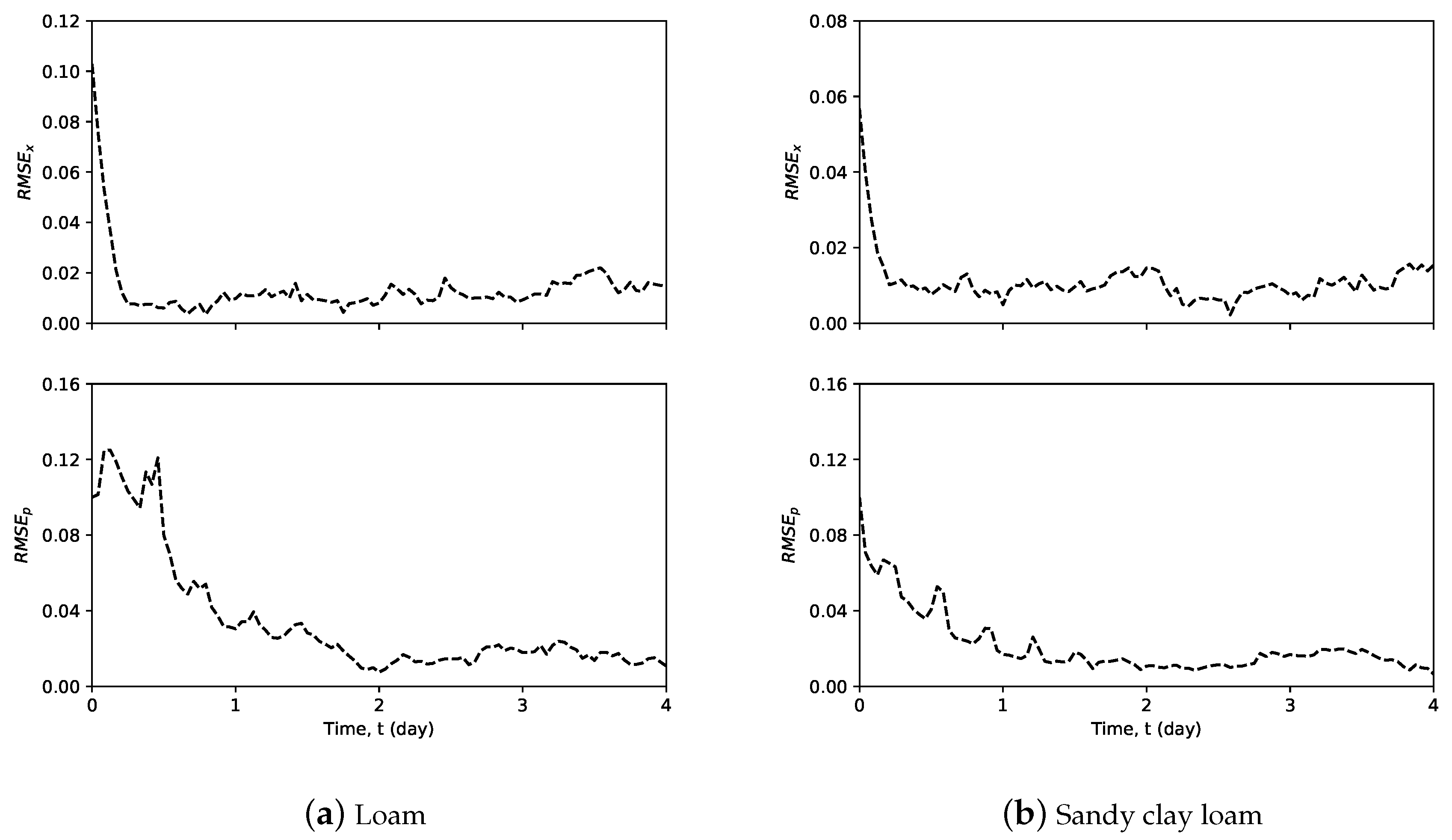
4.4. Simultaneous Parameter and State Estimation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- Food and Agriculture Organization of The United Nations (FAO). AQUASTAT Main Database. Available online: http://www.fao.org/nr/water/aquastat/data/query/index.html?lang=en (accessed on 31 October 2019).
- Fischer, G.; Tubiello, F.N.; van Velthuizen, H.; Wiberg, D.A. Climate change impacts on irrigation water requirements: Effects of mitigation, 1990–2080. Technol. Forecast. Soc. Chang. 2007, 74, 1083–1107. [Google Scholar] [CrossRef]
- Montzka, C.; Moradkhani, H.; Weihermüller, L.; Franssen, H.J.H.; Canty, M.; Vereecken, H. Hydraulic parameter estimation by remotely-sensed top soil moisture observations with the particle filter. J. Hydrol. 2011, 399, 410–421. [Google Scholar] [CrossRef]
- Lü, H.; Yu, Z.; Zhu, Y.; Drake, S.; Hao, Z.; Sudicky, E.A. Dual state-parameter estimation of root zone soil moisture by optimal parameter estimation and extended Kalman filter data assimilation. Adv. Water Resour. 2011, 34, 395–406. [Google Scholar] [CrossRef]
- Medina, H.; Romano, N.; Chirico, G.B. Kalman filters for assimilating near-surface observations into the Richards equation–Part 2: A dual filter approach for simultaneous retrieval of states and parameters. Hydrol. Earth Syst. Sci. 2014, 18, 2521–2541. [Google Scholar] [CrossRef]
- Moradkhani, H.; Sorooshian, S.; Gupta, H.V.; Houser, P.R. Dual state–parameter estimation of hydrological models using ensemble Kalman filter. Adv. Water Resour. 2005, 28, 135–147. [Google Scholar] [CrossRef]
- Chen, W.; Huang, C.; Shen, H.; Li, X. Comparison of ensemble-based state and parameter estimation methods for soil moisture data assimilation. Adv. Water Resour. 2015, 86, 425–438. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Franssen, H.J.H.; Sekhar, M. Iterative filter based estimation of fully 3D heterogeneous fields of permeability and Mualem-van Genuchten parameters. Adv. Water Resour. 2018, 122, 340–354. [Google Scholar] [CrossRef]
- Li, C.; Ren, L. Estimation of unsaturated soil hydraulic parameters using the ensemble Kalman filter. Vadose Zone J. 2011, 10, 1205–1227. [Google Scholar] [CrossRef]
- Bo, S.; Sahoo, S.R.; Yin, X.; Liu, J.; Shah, S.L. Parameter and State Estimation of One-Dimensional Infiltration Processes: A Simultaneous Approach. Mathematics 2020, 8, 134. [Google Scholar] [CrossRef]
- Rao, C.V.; Rawlings, J.B.; Mayne, D.Q. Constrained state estimation for nonlinear discrete-time systems: Stability and moving horizon approximations. IEEE Trans. Autom. Control 2003, 48, 246–258. [Google Scholar] [CrossRef]
- Yin, X.; Liu, J. Distributed moving horizon state estimation of two-time-scale nonlinear systems. Automatica 2017, 79, 152–161. [Google Scholar] [CrossRef]
- Christofides, P.D.; Scattolini, R.; de la Pena, D.M.; Liu, J. Distributed model predictive control: A tutorial review and future research directions. Comput. Chem. Eng. 2013, 51, 21–41. [Google Scholar] [CrossRef]
- Scattolini, R. Architectures for distributed and hierarchical model predictive control—A review. J. Process. Control 2009, 19, 723–731. [Google Scholar] [CrossRef]
- Daoutidis, P.; Zachar, M.; Jogwar, S.S. Sustainability and process control: A survey and perspective. J. Process. Control 2016, 44, 184–206. [Google Scholar] [CrossRef]
- Yin, X.; Liu, J. Subsystem decomposition of process networks for simultaneous distributed state estimation and control. AIChE J. 2019, 65, 904–914. [Google Scholar] [CrossRef]
- Stewart, B.T.; Venkat, A.N.; Rawlings, J.B.; Wright, S.J.; Pannocchia, G. Cooperative distributed model predictive control. Syst. Control Lett. 2010, 59, 460–469. [Google Scholar] [CrossRef]
- Venkat, A.N.; Rawlings, J.B.; Wright, S.J. Stability and optimality of distributed model predictive control. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 12–15 December 2005; pp. 6680–6685. [Google Scholar]
- Heidarinejad, M.; Liu, J.; de la Peña, D.M.; Davis, J.F.; Christofides, P.D. Multirate Lyapunov-based distributed model predictive control of nonlinear uncertain systems. J. Process. Control 2011, 21, 1231–1242. [Google Scholar] [CrossRef]
- Dunbar, W.B. Distributed receding horizon control of dynamically coupled nonlinear systems. IEEE Trans. Autom. Control 2007, 52, 1249–1263. [Google Scholar] [CrossRef]
- Halvgaard, R.; Vandenberghe, L.; Poulsen, N.K.; Madsen, H.; Jørgensen, J.B. Distributed model predictive control for smart energy systems. IEEE Trans. Smart Grid 2016, 7, 1675–1682. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, J. Distributed moving horizon state estimation for nonlinear systems with bounded uncertainties. J. Process. Control 2013, 23, 1281–1295. [Google Scholar] [CrossRef]
- Vadigepalli, R.; Doyle, F.J. A distributed state estimation and control algorithm for plantwide processes. IEEE Trans. Control Syst. Technol. 2003, 11, 119–127. [Google Scholar] [CrossRef]
- Yin, X.; Zeng, J.; Liu, J. Forming Distributed State Estimation Network From Decentralized Estimators. IEEE Trans. Control Syst. Technol. 2019, 27, 2430–2443. [Google Scholar] [CrossRef]
- Xie, L.; Choi, D.H.; Kar, S.; Poor, H.V. Fully distributed state estimation for wide-area monitoring systems. IEEE Trans. Smart Grid 2012, 3, 1154–1169. [Google Scholar] [CrossRef]
- Farina, M.; Ferrari-Trecate, G.; Scattolini, R. Distributed moving horizon estimation for nonlinear constrained systems. Int. J. Robust Nonlinear Control 2012, 22, 123–143. [Google Scholar] [CrossRef]
- Haber, A.; Verhaegen, M. Moving Horizon Estimation for Large-Scale Interconnected Systems. IEEE Trans. Autom. Control 2013, 58, 2834–2847. [Google Scholar] [CrossRef]
- Yin, X.; Decardi-Nelson, B.; Liu, J. Subsystem decomposition and distributed moving horizon estimation of wastewater treatment plants. Chem. Eng. Res. Des. 2018, 134, 405–419. [Google Scholar] [CrossRef]
- Schneider, R.; Marquardt, W. Convergence and Stability of a Constrained Partition-Based Moving Horizon Estimator. IEEE Trans. Autom. Control 2016, 61, 1316–1321. [Google Scholar] [CrossRef]
- Farina, M.; Ferrari-Trecate, G.; Scattolini, R. Distributed moving horizon estimation for sensor networks. IFAC Proc. Vol. 2009, 42, 126–131. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhao, C.; Di, Z.; Wang, W.X.; Lai, Y.C. Exact controllability of complex networks. Nat. Commun. 2013, 4, 1–9. [Google Scholar] [CrossRef]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]



| (m/s) | n | ||||
|---|---|---|---|---|---|
| Loam | 0.430 | 0.0780 | 3.60 | 1.56 | |
| Sandy clay loam | 0.390 | 0.100 | 5.90 | 1.48 |
| Candidate # | Parameters Removed |
|---|---|
| 1 | of loam and of SCL |
| 2 | of loam and of SCL |
| 3 | of loam and of SCL |
| 4 | of loam and of SCL |
| u | Irrigation Schedule | |||||
|---|---|---|---|---|---|---|
| Soil type | Loam | SCL | Loam | SCL | Loam | SCL |
| Scenario 1 | −0.514 | −0.514 | 2.5 | 2.5 | 12PM to 4PM | 12PM to 4PM |
| Scenario 2 | −0.514 | −0.284 | 2.5 | 2.5 | 12PM to 4PM | 12PM to 4PM |
| Scenario 3 | −0.514 | −0.514 | 2.5 | 2.5 | 12PM to 2PM | 2PM to 4PM |
| Variables | True Value | Initial Guess | |
|---|---|---|---|
| MHE 1 | (m/s) | ||
| (m/m) | 0.430 | 0.387 | |
| (1/m) | 3.60 | 3.24 | |
| n | 1.56 | 1.72 | |
| (m/m) | 0.0780 | 0.0780 | |
| MHE 2 | (m/s) | ||
| (m/m) | 0.390 | 0.351 | |
| (1/m) | 5.90 | 5.31 | |
| n | 1.48 | 1.62 | |
| (m/m) | 0.100 | 0.100 | |
| MHE 1 & 2 | (m) | −0.514 | −0.617 |
| Variables | Lower Bounds | Upper Bounds | |
|---|---|---|---|
| MHE 1 | |||
| 0.344 | 0.516 | ||
| 2.88 | 4.32 | ||
| 1.25 | 1.87 | ||
| MHE 2 | |||
| 0.312 | 0.468 | ||
| 4.72 | 7.08 | ||
| 1.18 | 1.78 | ||
| MHE 1 & 2 | −1.00 | ||
| −∞ | ∞ | ||
| 0.00 | 0.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bo, S.; Liu, J. A Decentralized Framework for Parameter and State Estimation of Infiltration Processes. Mathematics 2020, 8, 681. https://doi.org/10.3390/math8050681
Bo S, Liu J. A Decentralized Framework for Parameter and State Estimation of Infiltration Processes. Mathematics. 2020; 8(5):681. https://doi.org/10.3390/math8050681
Chicago/Turabian StyleBo, Song, and Jinfeng Liu. 2020. "A Decentralized Framework for Parameter and State Estimation of Infiltration Processes" Mathematics 8, no. 5: 681. https://doi.org/10.3390/math8050681
APA StyleBo, S., & Liu, J. (2020). A Decentralized Framework for Parameter and State Estimation of Infiltration Processes. Mathematics, 8(5), 681. https://doi.org/10.3390/math8050681






