Modified Inertial-Type Multi-Choice CQ-Algorithm for Countable Weakly Relatively Non-Expansive Mappings in a Banach Space, Applications and Numerical Experiments
Abstract
1. Introduction and Preliminaries
- (1)
- If then p is called a fixed point of The set of fixed points of T is denoted by ;
- (2)
- if there exists a sequence with such that as then p is called an asymptotic fixed point of [4]. The set of asymptotic fixed points of T is denoted by ;
- (3)
- if there exists a sequence with such that as then p is called a strong asymptotic fixed point of [4]. The set of strong asymptotic fixed points of T is denoted by ;
- (4)
- (5)
- (1)
- is closed and convex in E;
- (2)
- if and with or and with then and
2. Improvement and New Proof Techniques for Chidume’s Results
3. Inertial-Type Iterative Algorithms with New Set
- and satisfy
- is a real number sequence in with as
- and are two real number sequences in with and ;
- is a real number sequence in with as ,
4. Applications
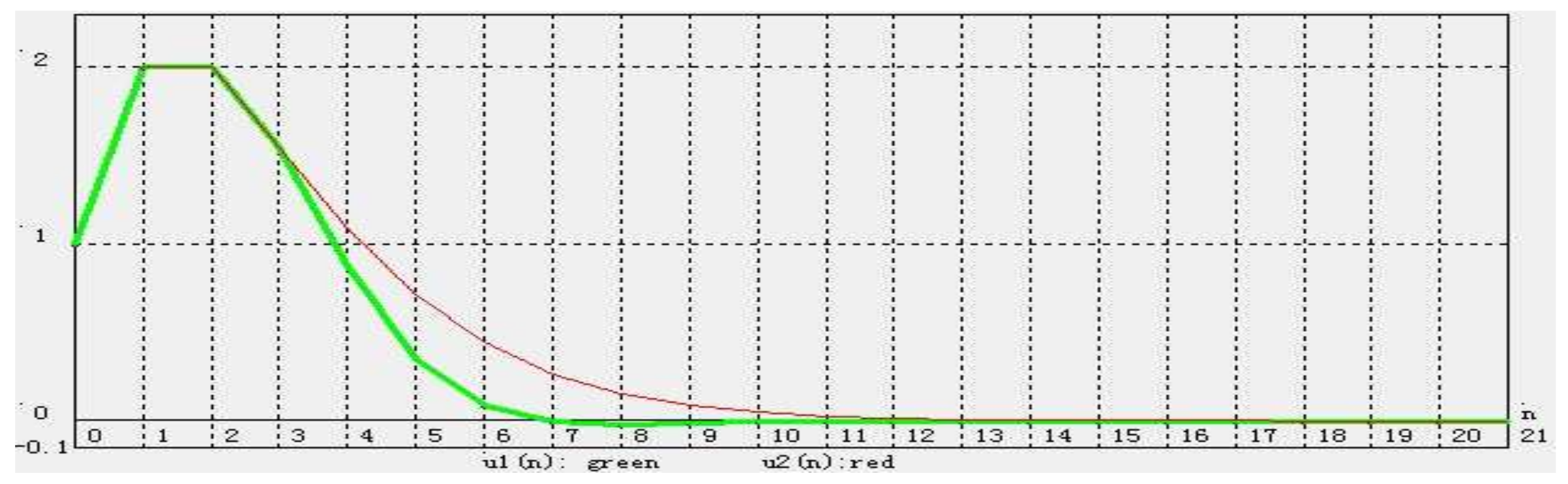
5. Numerical Experiments
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Agarwal, R.P.; O’Regan, D.; Sahu, D.R. Fixed Point Theory for Lipschitz-Type Mappings with Applications; Springer: Berlin, Germany, 2008. [Google Scholar]
- Barbu, V. Nonlinear Semigroups and Differential Equations in Banach Space; Noordhoff: Leiden, The Netherlands, 1976; pp. 10–15. [Google Scholar]
- Alber, Y.I. Metric and generalized projection operators in Banach spaces: Properties and Applications. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type; Dekker: New York, NY, USA, 1996. [Google Scholar]
- Zhang, J.L.; Su, Y.F.; Cheng, Q.Q. Simple projection algorithm for a countable family of weak relatively nonexpansive mappings and applications. Fixed Point Theory Appl. 2012, 2012, 205. [Google Scholar] [CrossRef][Green Version]
- Matsushita, S.Y.; Takahashi, W. An Iterative Algorithm for Relatively Nonexpansive Mappings by a Hybrid Method and Applications in Nonlinear Analysis and Convex Analysis; Yokohama Publishers: Yokohama, Japan, 2004. [Google Scholar]
- Matsushita, S.Y.; Takahashi, W. Weak and strong convergence theorems for relatively nonexpansive mappings in Banach spaces. Fixed Point Theory Appl. 2004, 1, 37–47. [Google Scholar] [CrossRef]
- Matsushita, S.Y.; Takahashi, W. A strong convergence theorem for relatively nonexpansive mappings in a Banach space. J. Approx. Theory. 2005, 134, 257–266. [Google Scholar] [CrossRef]
- Su, Y.F.; Xu, H.K.; Zhang, X. Strong convergence theorems for two countable families of weak relatively nonexpansive mappings and applications. Nonlinear Appl. 2010, 73, 3890–3906. [Google Scholar] [CrossRef]
- Takahashi, W. Nonlinear Functional Analysis; Yokohama Publishers: Yokohama, Japan, 2000. [Google Scholar]
- Pascali, D.; Sburlan, S. Nonlinear Mappings of Monotone Type; Sijthoff and Noordhoff International Publishers: Alphen aan den Rijn, The Netherlands, 1978. [Google Scholar]
- Duan, L.L.; Shi, A.F.; Wei, L.; Agarwal, R.P. Construction techniques of projection sets in hybrid methods for infinite weakly relatively nonexpansive mappings with applications. J. Nonlinear Funct. Anal. 2019, 2019, 14. [Google Scholar]
- Kohsaka, F.; Takahashi, W. The Set of Common Fixed Points of an Infinite Family of Relatively Nonexpansive Mappings in Banach and Function Spaces II; Yokohama Publishers: Yokohama, Japan, 2008. [Google Scholar]
- Nilsrakoo, W.; Saejung, S. On the fixed-point set of a family of relatively nonexpansive and generalized nonexpansive mappings. Fixed Point Theory Appl. 2010, 2010, 414232. [Google Scholar] [CrossRef][Green Version]
- Wei, L.; Cho, Y.J.; Zhou, H.Y. A strong convergence theorem for common fixed points of two relatively nonexpansive mappings and its applications. J. Appl. Math. Comput. 2009, 29, 95–103. [Google Scholar] [CrossRef]
- Zhang, J.; Su, Y.; Cheng, Q. Hybrid algorithm of fixed point for weak relatively nonexpansive multivalued mappings and applications. Abstr. Appl. Anal. 2012, 2012, 479438. [Google Scholar] [CrossRef]
- Chidume, C.E.; Ikechukwu, S.I.; Adamu, A. Inertial algorithm for approximating a common fixed point for a countable family of relatively nonexpansive maps. Fixed Point Theory Appl. 2018, 2018, 9. [Google Scholar] [CrossRef][Green Version]
- Gala, S.; Ragusa, M.A. Logarithmically improved regularity criterion for the Boussinesq equations in Besov spaces with negative indices. Appl. Anal. 2016, 95, 1271–1279. [Google Scholar] [CrossRef]
- Wei, L.; Agarwal, R.P. Simple form of a projection set in hybrid iterative schemes for non-linear mappings, application of inequalities and computational experiments. J. Inequal. Appl. 2018, 2018, 179. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Agarwal, R.P. New construction and proof techniques of projection algorithms for countable maximal monotone mappings and weakly relatively non-expansive mappings in a Banach space. J. Inequal. Appl. 2018, 2018, 64. [Google Scholar] [CrossRef] [PubMed]
- Saleem, N.; Vujakovic, J.; Baloch, W.U.; Radenovic, S. Coincidence point results for multivalued Suzuki type mappings using contraction in b-metric spaces. Mathematics 2019, 7, 1017. [Google Scholar] [CrossRef]
- Nakajo, K.; Takahashi, W. Strong convergence theorems for nonexpansive mappings and nonexpansive semigroups. J. Math. Anal. 2003, 279, 372–379. [Google Scholar] [CrossRef]
- Polyak, B.T. Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Tian, M.; Jiang, B.N. Inertial hybrid algorithm for variational inequality problems in Hilbert spaces. J. Inequal. Appl. 2020, 2020, 12. [Google Scholar] [CrossRef]
- Bot, R.I.; Csetnek, E.R.; Hendrich, C. Inertial Douglas-Rachford splitting for monotone inclusion problems. Appl. Math. Comput. 2015, 256, 472–487. [Google Scholar]
- Lorena, D.A.; Pock, T. An inertial forward-backward algorithm for monotone inclusions. J. Math. Imaging Vis. 2015, 51, 311–325. [Google Scholar] [CrossRef]
- Dong, Q.L.; Yuan, H.B.; Cho, Y.J.; Rassias, T.M. Modified inertial Mann algorithm and inertial CQ-algorithm for nonexpansive mappings. Optim. Lett. 2018, 12, 87–102. [Google Scholar] [CrossRef]
- Mosco, U. Convergence of convex sets and of solutions of variational inequalities. Adv. Math. 1969, 3, 510–585. [Google Scholar] [CrossRef]
- Tsukada, M. Convergence of best approximations in a smooth Banach space. J. Approx. Theory. 1984, 40, 301–309. [Google Scholar] [CrossRef]
- Zhang, J.L.; Su, Y.F.; Xu, H.K.; Cheng, Q.Q. Strong convergence theorems for a common fixed point of two countable families of relatively quasi nonexpansive mappings and applications. Abstr. Appl. Anal. 2012, 2012, 956950. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, L.; Xin, Y.; Zhang, R.; Agarwal, R.P. Modified Inertial-Type Multi-Choice CQ-Algorithm for Countable Weakly Relatively Non-Expansive Mappings in a Banach Space, Applications and Numerical Experiments. Mathematics 2020, 8, 613. https://doi.org/10.3390/math8040613
Wei L, Xin Y, Zhang R, Agarwal RP. Modified Inertial-Type Multi-Choice CQ-Algorithm for Countable Weakly Relatively Non-Expansive Mappings in a Banach Space, Applications and Numerical Experiments. Mathematics. 2020; 8(4):613. https://doi.org/10.3390/math8040613
Chicago/Turabian StyleWei, Li, Yibin Xin, Ruilan Zhang, and Ravi P. Agarwal. 2020. "Modified Inertial-Type Multi-Choice CQ-Algorithm for Countable Weakly Relatively Non-Expansive Mappings in a Banach Space, Applications and Numerical Experiments" Mathematics 8, no. 4: 613. https://doi.org/10.3390/math8040613
APA StyleWei, L., Xin, Y., Zhang, R., & Agarwal, R. P. (2020). Modified Inertial-Type Multi-Choice CQ-Algorithm for Countable Weakly Relatively Non-Expansive Mappings in a Banach Space, Applications and Numerical Experiments. Mathematics, 8(4), 613. https://doi.org/10.3390/math8040613





